Action potentials in basal and oblique dendrites of rat neocortical pyramidal neurons

Abstract

Basal and oblique dendrites comprise ∼2/3 of the total excitable membrane in the mammalian cerebral cortex, yet they have never been probed with glass electrodes, and therefore their electrical properties and overall impact on synaptic processing are unknown. In the present study, fast multi-site voltage-sensitive dye imaging combined with somatic recording was used to provide a detailed description of the membrane potential transients in basal and oblique dendrites of pyramidal neurons during single and trains of action potentials (APs). The optical method allowed simultaneous measurements from several dendrites in the visual field up to 200 μm from the soma, thus providing a unique report on how an AP invades the entire dendritic tree. In contrast to apical dendrites, basal and oblique branches: (1) impose very little amplitude and time course modulation on backpropagating APs; (2) are strongly invaded by the somatic spike even when somatic firing rates reach 40 Hz (activity-independent backpropagation); and (3) do not exhibit signs of a ‘calcium shoulder’ on the falling phase of the AP. A compartmental model incorporating AP peak latencies and half-widths obtained from the apical, oblique and basal dendrites indicates that the specific intracellular resistance (R_i) is less than 100 Ω cm. The combined experimental and modelling results also provide evidence that all synaptic locations along basal and oblique dendrites, situated within 200 μm from the soma, experience strong and near-simultaneous (latency < 1 ms) voltage transients during somatic firing. The cell body, axon hillock and basal dendritic compartments achieve unique synchronization during each AP. Therefore, with respect to a retrograde signal (AP), basal and proximal oblique dendrites should be considered as an integral part of the axo-somatic compartment.

The electrical signal is the primary physical substrate of rapid information processing in the brain (Koch, 1999). Our knowledge about the processing of electrical signals in the dendritic tree of pyramidal neocortical neurons is almost entirely based on physiological measurements performed on the apical trunk (Stuart & Sakmann, 1994; Larkum et al. 2001). However, the apical dendrite receives only a small fraction of the total synaptic drive. A larger fraction of afferent inputs, approximately 2/3 of nerve terminals innervating a layer V pyramidal neuron, terminate on the basal and oblique dendrites (Larkman, 1991). Because the small diameters of basal and oblique dendrites prevent direct electrical recordings, the electrical properties of these neuronal compartments are unknown, and therefore the impact of 2/3 of the total synaptic drive in pyramidal cells of the mammalian cerebral cortex is uncertain. The electrical signals are not only the primary substrate of neuron-to-neuron communication but are also thought to be the primary communication tool between the cell body and distal dendritic regions (Magee & Johnston, 1997; Markram et al. 1997). Very little is known about how well the action potential (AP) propagates from the soma to the distal tip of a basal or oblique dendrite. Microfluorometric measurements of calcium concentration changes in basal dendrites have provided some useful insights (Yuste et al. 1994; Schiller et al. 1995), but the temporal pattern of fast membrane potential transients in distal dendritic tips cannot be extracted from the change in intracellular calcium. The electrical properties of basal and oblique dendrites have also been addressed in multi-compartmental models of individual neocortical neurons (Mainen et al. 1995; Archie & Mel, 2000; Rhodes & Llinas, 2001; Vetter et al. 2001). Computer simulations have proven to be particularly useful in portions of the dendritic tree such as the apical trunk, in which the densities of different membrane conductances have been mapped with patch electrodes (Stuart & Sakmann, 1994; Bekkers, 2000). Although promising, biophysical models of dendritic function incorporating basal and oblique dendrites will remain somewhat speculative in the absence of direct experimental measurements.

In order to understand how fine neocortical dendrites process electrical signals, it is necessary to experimentally characterize the actual membrane potential transients in basal and oblique dendrites just as they were characterized in the apical dendrite (Stuart & Sakmann, 1994; Larkum et al. 2001). The objective of this study was to implement a new technique for optical imaging of membrane potential transients in distal segments of basal and oblique dendrites, and estimate dendritic electrical properties by comparing the actual experimental measurements with traces generated in computer simulations.

METHODS

Intracellular application of the dyes

Sprague-Dawley rats (postnatal day (P)21–35) were deeply anaesthetized with halothane and decapitated according to an animal protocol approved by the Yale University Animal Care and Use Committee. Coronal brain slices (300 μm thick) were harvested from the somatosensory area in gassed (95 % O₂ and 5 % CO₂), ice-cold artificial cerebrospinal fluid (ACSF, mM): 125 NaCl, 26 NaHCO₃, 10 glucose, 2.3 KCl, 1.26 KH₂ PO₄, 2 CaCl₂ and 1 MgSO₄ (pH 7.4, osmolarity 300–310 mosmol l⁻¹). The slices were incubated for 30 min at 35 °C and then kept at room temperature before being transferred to the recording chamber. Somatic whole-cell recordings were made with 7 MΩ patch pipettes and an Axopatch 200B amplifier, under infrared video microscopy. The pipette solution contained (mM): 135 potassium gluconate, 2 MgCl₂, 3 Mg-ATP, 10 phosphocreatine, 0.3 GTP and 10 Hepes (pH 7.3, adjusted with KOH), and 3 mg ml⁻¹ of the voltage-sensitive styryl dye JPW3028 (di-methyl analogue of JPW1114, synthesized by J. P. Wuskell and L. M. Loew, University of Connecticut, Farmington, CT, USA), 150 μM bis-fura or 200–300 μM Calcium Green-1. The osmolarity of the pipette solution was adjusted with distilled water to 275 mosmol l⁻¹. To avoid extracellular deposition of the dye, glass pipettes were filled from the tip with dye-free solution by applying negative pressure for 3 min, and were back-filled with dye solution. Borosilicate electrode glass (o.d. = 1.5, i.d. = 0.86 mm) was pre-washed in boiling ethanol alcohol, rinsed in acetone and dried. Both dye-free and dye-rich solutions were filtered through nylon syringe filters, pore size 0.2 μm (Nalgene 4-mm). Intracellular staining was achieved by free diffusion of the dye from the pipette into the cell body. After 40–60 min of staining an outside-out patch was formed and the patch electrode removed. Stained neurons were incubated for 2–3 h at room temperature and repatched with a dye-free pipette. APs were initiated by somatic current injections (I = 0.2 nA, duration = 50 ms). In some experiments glutamate iontophoresis (duration = 20 ms) was used to induce somatic bursts (40 Hz). For this purpose sharp (60 MΩ) glass pipettes were filled with 200 mM sodium glutamate (pH 9) and positioned in the vicinity of basal or oblique dendrites. All experiments were performed at 23 °C except those shown in Fig. 7 and Fig. 9 (29- 34 °C).

Figure 7. AP-associated calcium transients in distal tips of basal dendrites.

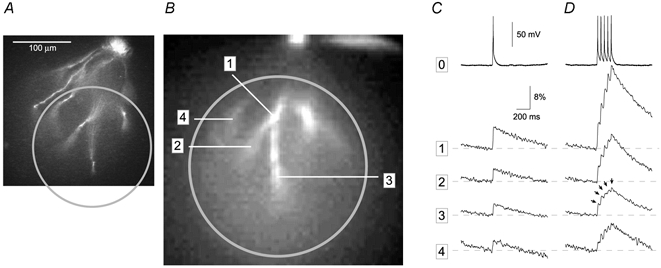
A, microphotograph of a layer V pyramidal neuron filled with Calcium Green-1. B, low spatial resolution fluorescence image (80 pixels × 80 pixels) of the area marked by a circle in A, captured with the data acquisition camera (NeuroCCD). The field diaphragm in the excitation path is partially closed to reduce the exposure of the cell body to strong illumination light. C, a single AP was evoked by direct current injection and simultaneous whole-cell and multi-site optical measurements were performed at 200 Hz frame rate. The whole-cell record (trace 0) is aligned with calcium signals from second- and third-order basal dendrites (1–4). D, the cell body was injected with depolarizing current to produce a train of 5 APs. Each AP in the train is accompanied by a calcium transient at every recording site in the basal dendritic tree, including the most distal recording site ‘3’, located 220 μm from the soma (arrows). The distances between the soma and recording sites 1, 2 and 4 are 165, 205 and 170 μm, respectively. Calcium traces displayed in C and D are products of temporal (4 sweeps) and spatial averaging (9 pixels). This experiment was performed at 34 °C.

Figure 9. Frequency-independent AP backpropagation in basal dendrites – two examples.

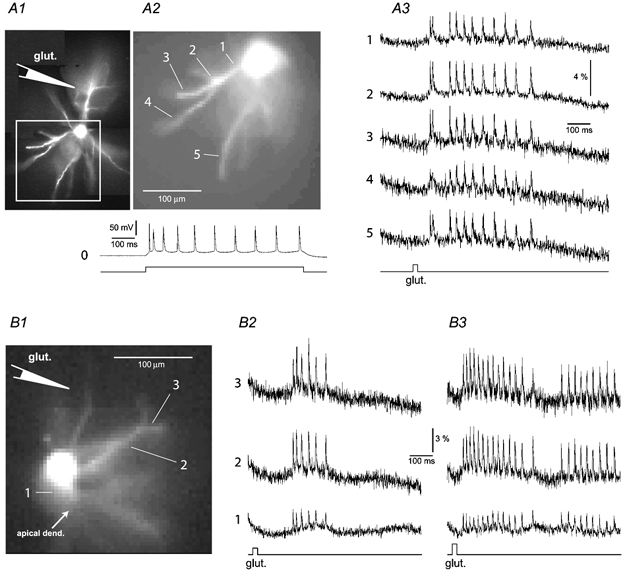
A1, composite high spatial resolution fluorescence image (520 nm) of a pyramidal neuron filled with the voltage-sensitive dye. During the filling procedure a depolarizing current pulse (duration = 700 ms) was injected to produce a burst of APs (trace 0). The loading pipette was then pulled out (outside-out patch) and a glutamate-filled sharp pipette was placed in the position indicated by the schematic drawing. A2, low spatial resolution fluorescence image (80 pixels × 80 pixels) of the area marked by a rectangle in A1, taken with the NeuroCCD camera. A3, glutamate-evoked APs recorded optically from 5 ROI located on the soma-dendrite junction (1), and along primary (2) and secondary (3–5) basal branches. Note that ROI ‘4’ is ∼80 μm beyond the branch point. The timing and duration (20 ms) of the glutamate pulse are indicated below. The experiment was performed at 29 °C bath temperature. B1, frame selected from the sequence of frames captured by the data acquisition camera during the voltage-sensitive dye imaging of glutamate-evoked APs. The apical dendrite is out of focus and oriented down and right. Schematic drawing indicates the relative position of the glutamate-filled stimulation electrode. B2, optical signals from the cell body, and 2 ROI along the basal dendrite (as indicated in B1), 85 and 130 μm from the centre of the soma. B3, same as in B2, except the intensity of the iontophoretic current was adjusted to evoke a 40 Hz somatic firing rate. Note that the amplitude of the optically recorded AP signal is relatively stable throughout the burst. The experiment was performed at 33 °C. Each optical trace in this figure is an averaged output of 16 neighbouring pixels (4 pixels × 4 pixels). There was no temporal averaging.

Optical recordings

Voltage-sensitive and calcium-sensitive imaging were performed using a 250 W xenon arc lamp (Opti-Quip, Highland Mills, NY, USA) mounted on an upright Nikon Eclipse microscope equipped with a × 40, 0.9 NA water-immersion objective, and a nano-k ‘biscuit’ bench-top vibration isolation platform. Frames containing 80 pixels × 80 pixels were captured with a back-illuminated cooled NeuroCCD camera (RedShirtImaging, Fairfield, CT, USA) operated under NeuroPlex software (written in IDL, Research Systems Inc., Boulder, CO, USA), which was also used to drive the mechanically isolated uncased shutter (35 mm Uniblitz) and the programmable pulse-generator (Master-8, A.M.P.I.). JPW3028 signals (excitation 520 ± 45 nm, dichroic 570 nm and emission > 610 nm) were sampled at 2.7 kHz, while bis-fura fluorescence changes (excitation 380 nm, dichroic 400 nm and emission 450 nm) and Calcium Green-1 (excitation 500 nm, dichroic 525 nm and emission 545 nm) were recorded at 200 Hz frame rate. On-line signal averaging was carried out using the spike-triggered mode, but all sweeps were saved and inspected for consistency. Off-line data analysis (spatial averaging and digital filtering) was performed using NeuroPlex (RedShirtImaging). For spatial averaging, 6–16 neighbouring pixels were selected from each region of interest (ROI), and ΔF/F was calculated as average light intensity change/average resting light intensity. Due to signal saturation in the centre of the soma, for somatic ROI, pixels were selected from the periphery of the soma. After averaging, data were temporally filtered with a 0.5 kHz low-pass (low-sharpness) Gaussian filter. Interpolation of data points to create a pseudo-continuous function (oversampling from 2.7 to 27 kHz) was done using a sinc function (sinc (x) = sin (πx)/πx; McClellan et al. 1998), with custom-made software in LabVIEW (National Instruments), kindly provided by Matt Wachowiak. In order to reduce the photodynamic damage of the voltage-sensitive dye (Antic et al. 1999), the following steps were taken to minimize light exposure: (1) during the dye injection and incubation period the microscope and overhead lights were extinguished; (2) focusing of the stained neurons was done with 2–5 % neutral density optical filters inserted into the excitation illumination path; and (3) the duration of the optical recording sweeps was limited to 90 ms, and intersweep intervals were kept above 90 s in the experiments shown in Figs 2, 3, 4 and 8, in which temporal averaging was required to improve the signal-to-noise ratio. The experiments shown in Fig. 9 were performed in 1 s long sweeps, and neurons could not tolerate more than five to six illumination epochs of this duration.

Figure 2. Voltage imaging of AP backpropagation.

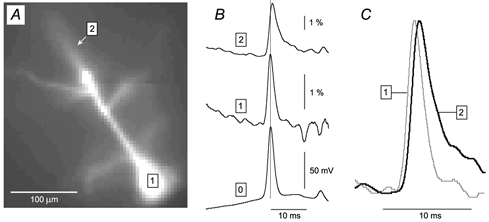
A, microphotograph of a neocortical pyramidal layer V neuron loaded with the fluorescent voltage-sensitive dye JPW3028. The neuron was stimulated by direct current injection to produce a single AP, and subjected to simultaneous whole-cell and multi-site optical measurements (temporal average of 4 trials). B, whole-cell record (trace 0) is aligned with optical signals from the soma (trace 1) and apical dendrite (trace 2 – arrow in A). The thin vertical line marks the peak of the somatic spike. C, optical traces from the soma (grey) and apical dendrite 240 μm from the soma (black) are scaled and superimposed for direct comparison of the timing and shape of the signals. In this and the following figures the upward deflection (positive signal) represents an increase in the fluorescence intensity, and the amplitude is expressed as ΔF/F.

Figure 3. Simultaneous multi-site optical imaging of membrane potential transients from basal, oblique and apical dendrites.

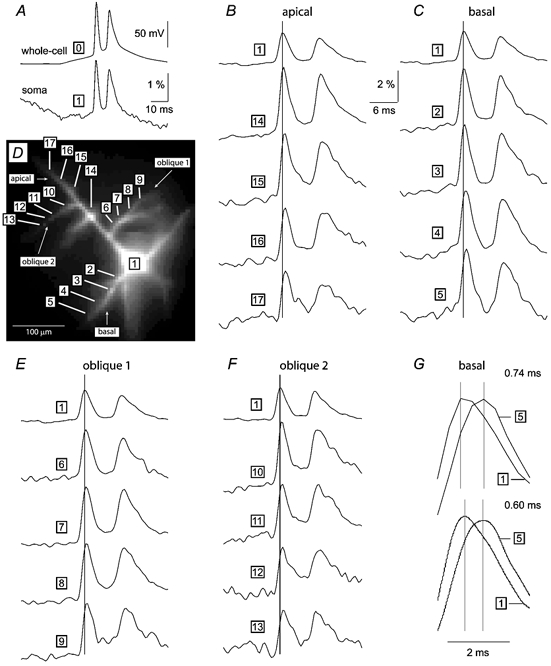
A layer V pyramidal neuron (D) was loaded with fluorescent voltage-sensitive dye, and injected with a current pulse to produce 2 APs. A, the somatic whole-cell record (trace 0) is aligned with the somatic optical signal (trace 1) to show the agreement in respect to timing, time course and relative amplitude of 2 spikes. B, C, E and F each consist of the somatic optical signal (trace 1) aligned with 4 optical signals recorded along apical (A), basal (C) and 2 oblique dendrites (E and F), as indicated by numbers on the microphotograph shown in D. Optical signals are products of: (1) spike-triggered temporal averaging (4 trials); (2) spatial averaging (n = 6–9 neighbouring pixels); and (3) digital filtering (Gaussian low-pass 0.5 kHz). The vertical line marks the peak of the first somatic spike. G, upper, AP-associated optical signal in the basal dendrite 145 μm from the soma (trace 5) is scaled and superimposed on the somatic optical signal (trace 1), to show the propagation latency on a faster time scale. Lower, same two traces as above, but interpolated with sinc function. The corresponding interspike interval, measured as the time difference between two samples of maximum amplitude (marked by vertical lines), is displayed above each trace pair. For multiple-frame and movie presentation of these experimental data see ‘Supplementary material’.

Figure 4. AP peak latencies in apical, oblique and basal dendrites: experimental measurements and computer simulations.

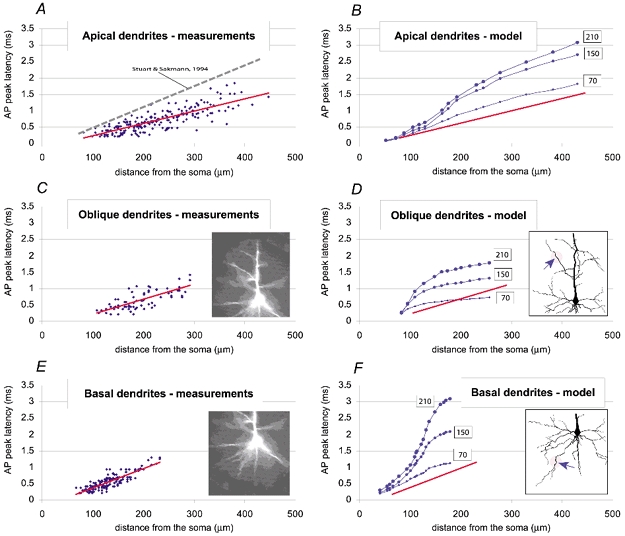
AP peak latencies along apical (A), oblique (C) and basal (E) dendrites are plotted versus the distance from the centre of the soma. Red lines represent the least squares fit of data points. The dashed line in A is a linear regression fit of peak latencies obtained with dual patch electrode measurements (Stuart & Sakmann, 1994). Insets in C and E are microphotographs of a representative neuron filled with JPW3028, taken immediately after the optical imaging. AP peak latencies obtained in computer simulations of apical (B), oblique (D) and basal (F) dendrites are plotted versus the distance from the centre of the soma. Each simulation was carried out using 3 characteristic values of R_i (70, 150 and 210 Ω cm). Red lines are copied from corresponding panels on the left. Insets in D and F depict the morphology of the proximal dendritic tree of the model neuron (Stuart & Spruston, 1998). Arrows mark particular dendritic segments for which plots were made.

Figure 8. The shape of APs in distal segments of basal dendrites: voltage imaging.

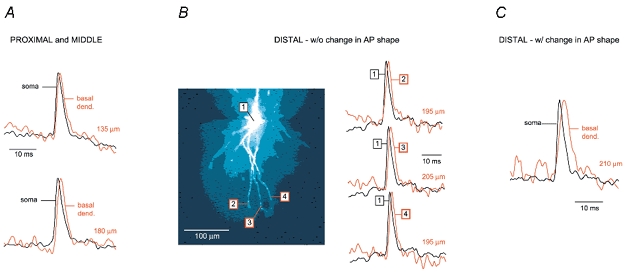
A, 2 examples of voltage imaging performed at proximal and middle recording sites on basal dendrites (less than 180 μm from the cell body). Upper, AP-associated optical signal from basal dendrite (red, 135 μm from the soma) superimposed on the somatic optical record (black). Lower, same as above but different cell and different recording distance from the centre of the soma (180 μm). B, left, composite microphotograph of a layer V pyramidal neuron filled with JPW3028. Right, 3 examples of optical signals sampled from distal dendritic segments at distances larger than 180 μm, as indicated in the left panel. There is no apparent broadening of the backpropagating AP. Note that ROI ‘3’ is ∼150 μm beyond the branch point. C, example of an experiment in which the half-width of the AP increases in distal dendritic segments. Each trace in Fig. 8 is the product of temporal (4 sweeps) and spatial averaging (6–9 pixels). All somatic signals are coloured black and dendritic recordings are coloured red. The distance from the centre of the soma is indicated above each dendritic recording.

Neuronal modelling

Simulations were performed using NEURON 5.1 (available from http://www.neuron.yale.edu) with a backward Euler integration method and a time step of 25 μs. The morphology of the neocortical layer V pyramidal neuron model in Fig. 1 and Fig. 4 was the same as described previously (Stuart & Spruston, 1998). The model neuron in Fig. 5 and Fig. 6 was based on the neurolucida reconstruction of a biocytine-filled layer V pyramidal cell (Sprague-Dawley rat, age P27). To minimize shrinkage, slices were not dehydrated or resliced. They were mounted in water-soluble medium (Aqua-PolyMount, Polysciences Inc., Warrington, PA, USA). Neurolucida data were converted to NEURON format using Robert Cannon's Neuron Morphology and Conversion Tool (CVAPP, available from http://www.compneuro.org). In the standard conditions, R_i, R_m (specific membrane resistance) and C_m (specific membrane capacitance) were uniform and set to 70 Ω cm, 25 kΩ cm² and 1 μF cm⁻², respectively. The effects of spines on membrane area were modelled by decreasing R_m, and increasing C_m by a factor of 2 (‘spine factor’) in all dendritic compartments beyond 30–50 μm from the soma. Hodgkin-Huxley sodium and potassium channels were modelled as described previously (Mainen & Sejnowski, 1996), with densities set to 35 and 30 pS μm⁻² in the soma and dendrites, and 30 000 and 2000 pS μm⁻² in the axon hillock and axon, respectively. High voltage-activated calcium conductance (g_Ca) was modelled as described previously (Mainen & Sejnowski, 1996), with uniform density set to 0.3 pS μm⁻². The effective somatic input resistance of the model neurons (R_i set to 70 Ω cm) measured with long hyperpolarizing pulses (−0.2 nA) was 81 and 55 MΩ. APs were initiated by somatic current injections (I = 0.2–0.4 nA, duration = 25 ms). Simulations were done at a nominal temperature of 23 °C, with all conductance kinetics scaled by a Q₁₀ of 2.3.

Figure 1. Effect of R_i on AP peak latency in basal dendrites: computer simulations.

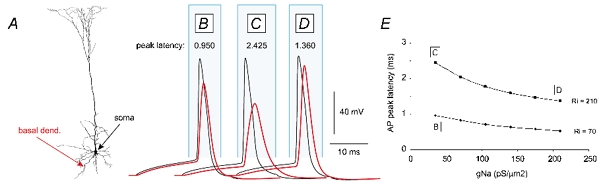
A, reconstructed layer V pyramidal neuron used for the model (provided by N. Spruston). B, AP waveforms in the soma (black trace) and distal basal compartment 150 μm from the soma (red trace), as indicated with arrows in A. The AP peak latency (in ms) is shown above the trace. Global R_i= 70 Ω cm, dendritic g_Na= 35 pS μm⁻², g_K= 30 pS μm⁻², g_Ca= 0.3 pS μm⁻². C, same as in B, except R_i= 210 Ω cm. D, same as in B, except R_i= 210 Ω cm and dendritic g_Na= 210 pS μm⁻². E, plot of AP peak latency in a distal basal dendrite 150 μm from the soma versus dendritic g_Na. Peak latencies were plotted for two R_i values (70 and 210 Ω cm). Points on the graph marked as B, C and D correspond to model parameters used in simulation trials displayed in B, C and D, respectively. An additional set of simulations was carried out to test how different values of specific membrane resistance (R_m), when applied uniformly, affect AP propagation. The results suggest that varying R_m in the range 10–50 kΩ cm² has minimal effects (approximately ±0.1 ms) on AP peak latency in basal dendrites (data not shown).

Figure 5. Effects of dendritic sodium channel density (g_Na) on the AP peak latency: computer simulation.

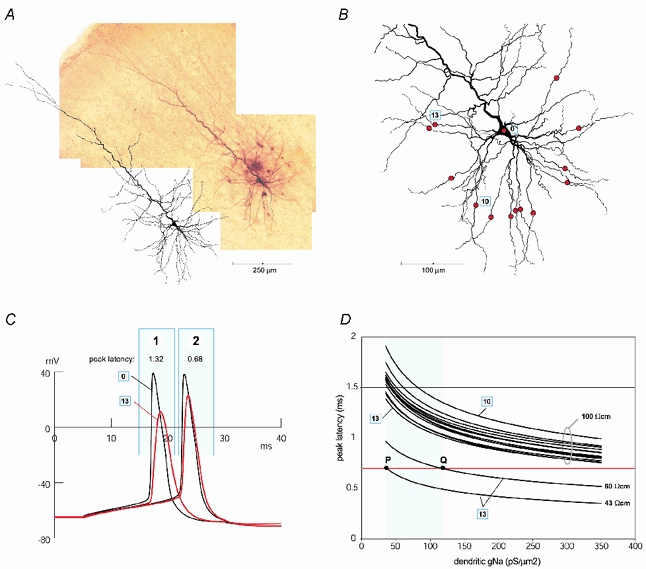
A, composite microphotograph of a biocytin-labelled layer V pyramidal cell in a 300 μm thick slice harvested from the rat somatosensory cortex (P27) aligned with a Neurolucida reconstruction of the same neuron. B, morphology of the pyramidal neuron after incorporation into NEURON (only basolateral dendritic arbor is shown). Red circles indicate recording sites on 13 basal dendrites. Each recording site is 150 μm from the centre of the soma. The somatic recording site is marked ‘0’. The dendrite with the slowest AP propagation velocity (largest peak latency) is marked ‘10’. The dendrite with the fastest AP propagation velocity is marked ‘13’. C, the model output in response to a square current pulse injection into the cell body. If R_i was set to 100 Ω cm the AP would propagate from the recording site ‘0’ to the recording site ‘13’ with 1.32 ms peak latency (sweep 1). If R_i was set to 43 Ω cm, the peak latency would match the experimental value of 0.68 ms (sweep 2). D, AP peak latencies at 13 recording sites marked by red circles in B are plotted versus dendritic g_Na. The g_K/g_Na ratio was kept at 30/35 (Mainen & Sejnowski, 1996). All 13 curves in the upper part of the graph were generated in the model where R_i was set to 100 Ω cm. The curves generated by the slowest and fastest dendrite are marked ‘10’ and ‘13’, respectively. The horizontal red line marks 0.68 ms, the experimentally measured mean value of AP peak latency in basal dendrites 150 μm from the soma. Note that none of the 13 curves in the upper part of the graph cross the red line, thus models with unusually high densities of dendritic sodium channels (350 pS μm⁻²) cannot match experimental data if R_i was set to 100 Ω cm. In the lower part of the graph AP peak latencies obtained from the recording site ‘13’ are plotted versus dendritic g_Na. In these two simulations R_i was set to 43 and 60 Ω cm in order to match the experimental data. The turquoise area represents the region of popular dendritic g_Na values used by computational neuroscientists. The turquoise parameter range begins at 35 pS μm⁻² (Mainen & Sejnowski, 1996) and ends at 120 pS μm⁻² (Rhodes & Llinas, 2001). P and Q mark the interception of the model output (curves 43 and 60 Ω cm) and experimentally obtained peak latency (red horizontal line), inside the plausible range for dendritic g_Na (turquoise area). Note that any model output curve between 43 and 60 Ω cm would intercept the red line inside the turquoise area (between P and Q).

Figure 6. Exploration of the parameter space.

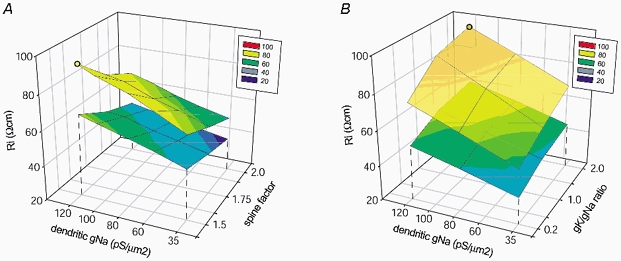
A, a multi-compartmental model (Fig. 5B) was used to determine which R_i values are required to match experimentally measured AP peak latency (0.68 ms) 150 μm from the cell body, when dendritic g_Na and spine factor were varied. Dendritic g_Na was varied within the Mainen-Rhodes range (35–120 pS μm⁻²). Spine factor was varied between 1.5 and 2. The lower mesh plot was obtained from the slowest dendrite (Fig. 5B, ‘10’). The upper mesh plot was obtained from the fastest dendrite (‘13’). The R_i values required to match experimental data in other basal dendrites (‘1–12’) shown in Fig. 5B, are confined to the space between the two mesh plots. The yellow circle is the maximal R_i value (87 Ω cm), which was obtained when high dendritic g_Na (120 pS μm⁻²) was combined with small spine factor (1.5). B, in order to determine what effects different ratios of dendritic g_K and g_Na have on the results shown in A, an additional set of simulations was performed using the same model. This panel depicts the 3-D plot of R_i values (that fulfil the experimental constraint) under different combinations of dendritic g_Na and g_K/g_Na ratios. The spine factor was fixed to 1.5. Dendritic g_Na was varied within the Mainen-Rhodes range (35–120 pS μm⁻²), and g_K/g_Na ratio was varied in the range 0.2–2.0. The lower mesh plot was obtained from the slowest dendrite (Fig. 5B, ‘10’). The upper mesh plot was obtained from the fastest dendrite (‘13’). The R_i values required to match the experimental data in other basal dendrites shown in Fig. 5B are confined to the space between the two mesh plots. The orange circle is the maximal R_i value (95 Ω cm), which was obtained when high dendritic g_Na (120 pS μm⁻²) was combined with high dendritic g_K (240 pS μm⁻²; g_K/g_Na= 2).

RESULTS

The shape of the dendritic AP provides a rough estimate of dendritic electrical properties

It has become possible (at least in theory) for every scientist to begin an experimental project with a simulation of the experiment (Wilson, 2000). Here, a multi-compartmental model (Fig. 1A) was used to test whether the peak latency and the time course of the backpropagating AP in basal dendrites may contain important biophysical clues about the regional electrical properties of these dendrites. Somatic APs were evoked by direct current injections (Fig. 1B-D), and membrane potential waveforms were analysed at two sites: the soma (black trace), and the distal region of a basal dendrite 150 μm from the soma (red trace). Under standard conditions (R_i= 70 Ω cm; Stuart & Spruston, 1998), the AP backpropagates from the soma to a distal segment of the basal dendrite with a peak latency of 0.95 ms (Fig. 1B). A 3-fold increase in R_i (from 70 to 210 Ω cm) caused a dramatic increase in the AP peak latency (Fig. 1C), which could not be totally counterbalanced by a uniform 6-fold increase (from 35 to 210 pS μm⁻²) in the dendritic Hodgkin-Huxley sodium conductance g_Na (Fig. 1D). It can be inferred from computer simulations that the peak latency of a backpropagating AP in basal dendrites is much more sensitive to the specific intracellular resistance than to the density of voltage-gated sodium channels (Fig. 1E), and that a significant increase in the half-width of the backpropagating AP (Fig. 1C) in relatively short basal dendrites is an indication of weak electrical coupling (high specific axial resistance). This modelling study, together with classic work (Goldstein & Rall, 1974), suggests that the AP could be used as an exploration probe. For example, by sending an AP along the basal dendrite and measuring its peak latency and time course en route to and at the distal dendritic segment, we may be able to produce a rough estimate of the dendritic electrical properties.

Voltage imaging of AP backpropagation in apical dendrites

The recently developed voltage-sensitive dye technique was used to monitor the dendritic membrane potential in real cells. Simultaneous optical and electrical measurements were performed on individual neurons in acute brain slices cut from the rat somatosensory area. In our initial effort (Antic et al. 1999), we provided the basic methodology for intracellular dye application and optical recordings from dendrites of individual neurons in brain slices. In the present study, a newly developed fast CCD camera (80 pixels × 80 pixels) replaced the silicon diode array (24 pixels × 24 pixels), which brought substantial improvements in the spatial and temporal resolution (from 600 to 370 μs per whole frame) and, equally importantly, in the sensitivity of the measurements (signal-to-noise ratio). With better signals, experiments were designed to provide a detailed description of AP half-widths and peak latencies along individual dendrites. In a typical experiment, the pyramidal neurons (n = 17) were loaded with the voltage-sensitive dye JPW3028 (Fig. 2A), depolarized to generate a somatic AP, and fluorescent light was measured along the apical dendrite. The optical signal from the soma (Fig. 2B, trace 1) was in good agreement with the whole-cell recording (trace 0), but not with the optical signal from the apical dendrite (trace 2). At a distance of 240 μm from the soma (trace 2), the AP peak latency was 0.56 ms, and the half-width of the backpropagating AP was 135 % of its somatic value (Fig. 1C). These experiments demonstrate that fast voltage-sensitive dye imaging can detect both the peak latency and the broadening of the backpropagating AP in apical dendrites, as previously described (Stuart & Sakmann, 1994).

APs in basal and oblique dendrites

The next set of experiments was carried out with the objective to record membrane potential transients from oblique and basal dendrites of layer V pyramidal cells. The neuron displayed in Fig. 3D was loaded with voltage-sensitive dye and stimulated by somatic current injection to produce a burst of two APs. The optical signal from the somatic region (Fig. 3A, trace 1) captured not only the exact time course of the two APs but also their relative amplitudes. Panels B, C, E and F each consist of the somatic optical signal (trace 1) and four dendritic recordings aligned on a faster time scale. In all neurons examined (n = 25) there was an increase in the peak latency along each dendrite, indicating the direction of propagation from the soma to the periphery. The mean propagation velocity was 0.335, 0.300 and 0.215 m s⁻¹ in apical, oblique and basal dendrites, respectively. Under the present experimental conditions (somatic current injection, in vitro, at room temperature), a failure of the AP to invade a set of dendrites or a particular dendritic region was never observed. In all cases the somatically induced AP invaded every basal and oblique dendrite including second-order branches (general backpropagation). The shapes of the dendritic signals did not show the signs of passive filtering that would have been expected if basal and oblique dendrites were passive and electrotonically distant from the soma (Rall, 1959). In order to improve the accuracy of the measurements, optical signals (Fig. 3G, upper) were subjected to a ‘discrete-to-continuous conversion’ (McClellan et al. 1998), i.e. a smooth continuous-time function was interpolated throughout the sampled points (Fig. 3G, lower).

Using the interpolated data, the peak latencies were measured along dendritic branches of 25 neurons (apical N = 17, oblique N = 12 and basal dendrites N = 31; N = number of dendrites) and plotted versus distance from the soma (Fig. 4). In apical dendrites (Fig. 4A) the backpropagation velocity was larger than that measured with dual patch-electrode recordings (Stuart & Sakmann, 1994). The animals used in the present study (3–5 weeks old) were older than those used by Stuart & Sakmann (1994), and this could explain the observed difference on account of the morphological and physiological maturation of pyramidal neurons (Zhu, 2000). Experimental measurements of AP peak latencies in apical (Fig. 4A), oblique (Fig. 4C) and basal (Fig. 4E) dendrites were compared with results from the computer simulation in Fig. 4B, D and F. The model was the same as that used in Fig. 1A. The simulations were carried out using three characteristic values for R_i (70, 150 and 210 Ω cm), while keeping all other parameters fixed. The peak latencies obtained in the model where global R_i was set to 70 Ω cm were closest to the values obtained in the experimental measurements (red lines, Fig. 4B, D and F).

At this point it is necessary to reflect on two problems that could compromise the conclusions of the modelling study. First, the morphology of the model neuron used in Fig. 4B, D and F was borrowed from a 3-week-old Wistar rat (Stuart & Spruston, 1998), while the experimental data shown in Fig. 4A, C and E were collected from 3- to 5-week-old Sprague-Dawley rats. Second, the density of the dendritic sodium conductance (35 pS μm⁻²) used in the model neuron (Fig. 4) was based on patch electrode measurements along the apical trunk by Stuart & Sakmann (1994). What if the density of voltage-gated sodium channels in basal dendrites was actually higher than that found in the apical trunk? Or, what if the previously reported value was an underestimate of dendritic g_Na (for discussion see Rhodes & Llinas, 2001). Both questions were addressed in the new model depicted in Fig. 5.

To eliminate the discrepancy in animal strain and animal age, a layer V pyramidal cell from one of the animals used in our laboratory (Sprague-Dawley, P27) was reconstructed (Fig. 5A and B). The old model (Fig. 4) was then inserted into a new morphology. With identical channel types and densities, the new morphology produced a nearly identical pattern of backpropagation. As previously described, when R_i was set to 70 Ω cm, the AP peak latencies along basal dendrites were closest to experimentally obtained values (not shown).

Next, while preserving the ratio g_Na/g_K (35/30), higher and higher densities of Hodgkin-Huxley conductances were inserted in the entire dendritic arbor uniformly, and the peak latency was analysed in 13 basal dendrites, 150 μm from the soma (red circles, Fig. 5B). The experimentally measured mean peak latency in basal dendrites at 150 μm from the soma (0.68 ± 0.16 ms; Fig. 5D, horizontal red line) could not have been achieved in neuron models with R_i= 100 Ω cm, even if g_Na was set to 350 pS μm⁻² (Fig. 5D). This sodium channel density is 10 times higher than that used in recent studies (Mainen & Sejnowski, 1996; Vetter et al. 2001), and it is unlikely that basal dendrites of pyramidal neocortical neurons possess such a large number of sodium channels (Rhodes & Llinas, 2001). Within the plausible range for dendritic g_Na (Fig. 5D, turquoise area, 35–120 pS μm⁻²; Mainen & Sejnowski, 1996; Rhodes & Llinas, 2001), the R_i values that fit experimental measurements of AP peak latency in basal dendrite ‘13’ range between 43 and 60 Ω cm. Basal dendrite ‘13’ has the most favourable geometry (larger diameter and fewer branch points than other basal dendrites) for fast AP propagation, and hence would require the largest R_i to match experimental AP peak latency. All other basal branches (‘1–12’; Fig. 5B) have slower conduction velocities, and require R_i lower than 60 Ω cm to match experimental results within the plausible range for the dendritic g_Na (turquoise area).

The result shown in Fig. 5D is based on two assumptions: (1) the specific membrane capacitance (C_m) in neocortical pyramidal neurons is 1 μF cm⁻²; (2) the density of spines, the membrane potential in spine heads and the spine stem currents are distributed variables with continuous rather than discrete spatial arguments (Baer & Rinzel, 1991), and the effect of dendritic spines on membrane area can be simulated by decreasing R_m and increasing C_m by a factor of 2 (Stuart & Spruston, 1998). What if the ‘spine factor’ of 2 is an overestimate of the effective contribution of spine heads to the dendritic capacitance? That is, high-resistance spine necks may prevent the full charging of spine heads during fast membrane potential transients. In order to address this possibility, the spine factor was varied between 1.5, 1.75 and 2. Each spine factor was explored within the plausible range for the dendritic g_Na (35–120 pS μm⁻²). The analysis was done for the fastest (‘13’) and slowest dendrite (‘10’, Fig. 5B). The results in Fig. 6A show that under any possible combination of three parameters (dendritic geometry, dendritic g_Na and spine factor) the experimental data could not be matched in the model with R_i values above 87 Ω cm (yellow circle, Fig. 6A).

In the above modelling, the increase in the dendritic g_Na was accompanied by a proportional increase in dendritic g_K; i.e. the g_K/g_Na ratio of 30/35, established originally by Mainen & Sejnowski (1996), was preserved in every simulation. In the next set of simulations different g_K/g_Na ratios were tested. The spine factor was set to 1.5 to allow for higher R_i estimates, and the g_K/g_Na ratio was varied between 0.2, 1.0 and 2.0 (Fig. 6B). The results show that under any possible combination of three parameters (dendritic geometry, dendritic g_Na and g_K/g_Na ratio) the experimental data could not be matched in the model with R_i values above 95 Ω cm (orange circle, Fig. 6B). Thus even after a radical cut in dendritic membrane capacitance from 2 to 1.5 μF cm⁻², combined with an increase in the dendritic R_m from 12 500 to 16 666 Ω cm², and a radical increase in g_K/g_Na ratio up to 2.0 (Fig. 6B), R_i values required to match the experimental data were lower than the popular neurocomputational range of 150–250 Ω cm (Anderson et al. 1999; Destexhe & Pare, 1999; Archie & Mel, 2000; Durstewitz et al. 2000; Rhodes & Llinas, 2001; Vetter et al. 2001).

Calcium electrogenesis in basal dendrites

The experimental measurements of the AP peak latency and half-width, together with the computer simulation, suggest that distal basal segments experience a substantial depolarization during the somatic spike (Fig. 5C). Is this depolarization large enough to open high voltage-activated calcium channels? Using intracellularly applied calcium-sensitive dye fura-2, Schiller et al. (1995) addressed this question in the most proximal parts of the basal dendrites, less than 80 μm from the cell body. Basal dendrites, however, typically extend up to 250 μm in pyramidal layer V neurons (see Fig. 5). In addition, it is still unknown whether a single AP reliably invades the entire basal bush or fails at particular branch points, so that some distal dendritic segments experience less depolarization than others, and hence less (or zero) calcium influx. The next set of experiments was designed to determine whether a single AP could trigger calcium influx at distal dendritic regions, at distances larger than 150 μm from the soma. In single sweeps calcium signals were sampled simultaneously from all basal dendrites in the visual field; typically three to four basal branches. Particular attention was paid to dendritic segments beyond the branch point (see also ‘Supplementary material’). In the representative example shown in Fig. 7, the pyramidal cell was loaded with the calcium-sensitive dye Calcium Green-1 and a single AP (Fig. 7C, trace 0) was evoked by brief somatic current injection. Optical recordings of intracellular free calcium concentration were performed simultaneously along four basal branches. Four ROI were selected from two basal dendrites for display (traces 1–4). In repeated trials, single APs regularly evoked calcium transients in every basal branch examined. The same result was obtained from 20 basal dendrites in eight neurons (5 neurons at 23 °C, 3 neurons at 32–34 °C). These data indicate that backpropagating APs depolarize the distal tips of basal dendrites (up to 200 μm from the centre of the soma) sufficiently to open voltage-gated calcium channels and trigger the surge of calcium ions into the dendritic cytosol. AP propagation failures were never observed in these experiments. On the contrary, the amplitudes of calcium signals were very similar between different basal dendrites in the visual field (Fig. 7C), thus rejecting the hypothesis that some dendritic segments experience significantly larger voltage transients than others. Moreover, each somatic AP in a 20 Hz train (n = 3) was associated with a distinguishable calcium transient in distal dendrites (Fig. 7D), further supporting the hypothesis that the dendritic membrane potential swing, caused by the backpropagating spike, is both strong and swift.

Recently, patch electrode measurements from apical dendrites have shown that the activation of the voltage-gated calcium channels by backpropagating APs causes a substantial broadening of the dendritic spike, sometimes manifested with a characteristic calcium shoulder on the falling phase of the electrical signal (Stuart et al. 1997; Larkum et al. 2001). Thus one might expect a calcium-dependent plateau in the distal tips of basal dendrites, because these branches experience a 6-fold higher calcium transient than the distal regions of the apical trunk or soma during an AP (Schiller et al. 1995). However, AP-associated voltage-sensitive dye signals from basal dendrites were very similar in shape to somatic optical signals. In the present study, the great majority of optical measurements were performed at distances less than 180 μm from the cell body (79 basal dendrites in 24 pyramidal neurons). In this group of experiments (Fig. 8A) AP half-width in the dendritic segment never exceeded 125 % of the somatic half-width. A considerably smaller number of recordings (7 dendrites in 5 neurons) were done at distances larger than 180 μm. Among these, two different dendritic responses were observed. In the first group (5 dendrites in 3 neurons) there was no significant change in the shape of the AP (Fig. 8B). In the second group (2 dendrites in 2 neurons) an obvious broadening of the AP (half-width increase larger than 25 %) was detected ∼200 μm from the soma (Fig. 8C). However, none of the AP-associated dendritic signals in the present study, regardless of the distance from the cell body, showed any signs of a calcium shoulder.

Activity-independent backpropagation

In order to investigate whether basal and oblique dendrites exhibit activity-dependent backpropagation as observed in the apical trunks of hippocampal (Spruston et al. 1995) and neocortical pyramidal neurons (Stuart et al. 1997), glutamate iontophoresis was used to evoke somatic bursts of APs. The results from two representative cells are displayed in Fig. 9A and B. As part of a standard experimental routine, and for the purpose of electrophysiological identification, a burst of APs was evoked by direct current injection during the dye-loading protocol (Fig. 9A1 bottom, trace 0). The patch electrode was then carefully pulled out and the neuron was left at room temperature for 3 h. Following the incubation period the bath temperature was increased to 29 °C and a glutamate-filled sharp glass electrode was advanced into the brain slice and positioned in the vicinity of the oblique dendrite as indicated by the schematic drawing. A brief glutamate pulse (20 ms) produced a burst, which lasted 480 ms and consisted of 11 APs (Fig. 9A3). Optical signals (traces 1–5) obtained from three different basal branches (as indicated in Fig. 9A2) appeared to have constant amplitudes throughout the bursting episode. In the second example (Fig. 9B1), the basal dendrite of interest was positioned near the centre of the recorded area. Following a 2 h incubation period the bath temperature was increased to 33 °C. The first glutamate pulse delivered in the basal area triggered a 200 ms long burst of APs (Fig. 9B2). A stronger iontophoretic pulse (Fig. 9B3) evoked a long-lasting burst, which consisted of more than 20 APs firing at approximately 40 Hz. Voltage imaging failed to detect frequency-dependent amplitude modulation in basal dendrites (up to 180 μm, n = 7 neurons, 18 basal dendrites) and oblique dendritic regions (up to 220 μm from the soma, n = 2 neurons, 3 oblique dendrites). In basal dendritic segments 150 μm from the cell body, the mean and standard deviation of the ratio of the amplitude of the fifth spike to the first spike in a train (30–40 Hz) was 92.5 ± 11.3 %. The experimental data suggest that the backpropagation of APs in basal and proximal-oblique dendrites of pyramidal layer V neurons is not dynamically regulated at firing rates of up to 40 Hz.

DISCUSSION

Simultaneous whole-cell and multi-site voltage-sensitive dye recordings were used to obtain a detailed description of AP propagation in the basal and oblique dendrites of layer V pyramidal neurons. When neurons were driven to fire bursts of APs at 40 Hz, distal regions of basal and oblique dendrites faithfully followed this firing frequency, in one-to-one fashion. The failure of an AP to invade a distal basal or oblique dendritic segment was never observed. Although the sensitivity of the voltage-sensitive dye recording is very low (for 100 mV voltage change the amplitude of the optical signal ΔF/F is approximately 3 %), AP-associated optical signals were regularly recorded from the distal tips of basal and oblique dendrites. The absolute amplitude of the dendritic transient, however, cannot be determined because the sensitivity of optical measurements, expressed as ΔF/F (light intensity change/ resting light intensity) can vary along the dendrite. This is the consequence of the internal application of the voltage-sensitive dye. The lipophilic fluorescent dye JPW3028 is bound to both the plasmalemma and intracellular membranes, and both populations of dye molecules contribute to the resting fluorescence level F. The distribution of intracellular machinery in the soma and across the dendritic tree is unknown, so dividing the optical signal ΔF by F does not eliminate this uncertainty in the results. However, the conclusions of the present study do not depend on the absolute calibration of optical signals in terms of the amplitude of the voltage signal. They depend on the timing of the peak and the shape of the AP, which are directly available from voltage-sensitive dye recordings (Ross et al. 1977).

In the present study, the AP peak latency and the shape of the electrical signal in the distal segments of individual dendrites were measured with the voltage-sensitive dye method at room temperature. Ideally, one would like to record AP waveforms in basal dendrites at physiological temperatures and apply these data to the model. However, the half-width of APs at 37 °C is 2–3 times smaller than that at 23 °C. With the present sampling interval (0.37 ms), the details of the AP rising and falling phase would be largely lost due to the undersampling of the fast signal, and it would be very difficult to determine the peak latency and the shape of the dendritic AP with the level of confidence present in optical recordings at room temperature (Figs 2, 3 and 8). The complete description of APs in basal dendrites at physiological temperatures will have to await improvements in dendritic patch electrode recordings (Stuart & Sakmann, 1994) or in the sensitivity of the voltage-sensitive dyes (Loew et al. 1992) and optical acquisition apparatus (Bullen & Saggau, 1999). The data displayed in Figs 3, 4 and 8 should not be taken as a result that describes AP propagation in neocortical pyramidal cells of a living brain. Rather, they are an example of the assay designed to estimate the passive parameter (R_i), by comparing the signals obtained from real neurons at room temperature with those generated in the computer simulation. The data described in Fig. 9, however, were acquired at physiological temperature, and provide a more relevant insight into the relative amplitudes of dendritic voltage fluctuations during the train of somatic APs.

Analysis of optical signals obtained in the basal and oblique dendrites at room temperature showed that the peak latency increased with distance from the soma, but the shape of the AP was not noticeably changed up to 200 μm from the cell body. The relatively small average peak latency of less than 1 ms measured in the distal tips of basal and oblique dendrites (Fig. 4), and the lack of a significant change in the shape of the spike (Fig. 3 and Fig. 8) indicate that, at room temperature, basal and oblique dendrites: (1) impose relatively small passive filtering on the backpropagating APs and (2) do not exhibit a prominent calcium shoulder previously seen in distal apical dendrites (Larkum et al. 2001). It is important to limit the conclusions about basal dendrites to the segments measured (200 μm from the soma) because basal dendrites from 3- to 5-week-old animals extend at least 250 μm, and hence the terminal portions of these branches were not investigated. This is especially important as unique non-linear behaviours were limited to the very distal portions of the apical dendrites of the same neuron type, and were not observed in the main apical trunk hundreds of micrometres from the soma (Stuart et al. 1997; Larkum et al. 2001).

Specific intracellular resistance

The impact of R_i on the model output was recognized very early on, in the pioneering works of Wilfrid Rall, and a thorough search for the exact value has a long history (Rall et al. 1992). The strategy of combining experimental measurements with a biophysical model of the cell to determine its passive membrane properties has been described in detail by a number of researchers (Major et al. 1994; Thurbon et al. 1998). Perhaps the most reliable estimate of passive electrical properties of mammalian pyramidal neurons has been achieved by modelling the experimental data obtained from simultaneous somatic and dendritic patch-pipette recordings (Stuart & Spruston, 1998). This remarkable study has suggested R_i values ranging from 70 to 100 Ω cm. Nevertheless, in spite of this strong experimental evidence that R_i is in the range 70–100 Ω cm, a number of important modelling studies of neocortical pyramidal neurons published after the report from Stuart & Spruston (1998) continued to use R_i values of 150 Ω cm (Anderson et al. 1999; Durstewitz et al. 2000; Vetter et al. 2001) or even 200 Ω cm and higher (Destexhe & Pare, 1999; Archie & Mel, 2000; Rhodes & Llinas, 2001). The numerical examples presented in Fig. 1 and Fig. 4 show that different R_i values (70, 150 and 210 Ω cm) have dramatically different effects on the electrical response of the remote dendritic compartment, and hence on the integration of the information in individual neurons (Mel, 1999; Koch & Segev, 2000).

Traditionally, passive cable models were based on somatic voltage transients in response to subthreshold current pulses (Barrett & Crill, 1974; Clements & Redman, 1989; Spruston & Johnston, 1992; Major et al. 1994; Thurbon et al. 1998; Trevelyan & Jack, 2002). In the present study, paradoxically, passive cable properties were addressed by analysing the details of AP propagation along the dendrites of pyramidal neurons (see also Meyer et al. 1997). With the advent of multi-site recordings of voltage transients from an individual neuron, the constraints on the model grew considerably (Stuart & Spruston, 1998). It has recently been shown that different neuron models, which produce identical responses to a somatic current injection, can easily be distinguished by recording from more than one place on the dendritic tree (Trevelyan & Jack, 2002). With optical multi-site data, it is now possible to estimate the specific intracellular resistance (R_i) of relatively short basal dendrites. The reasoning is based on the following arguments.

1. The AP propagation velocity in relatively short basal dendrites is much less sensitive to dendritic g_Na (and g_K) than to the R_i (Fig. 1).

2. The adequate range for apical dendrite g_Na has been established both experimentally (∼40 pS μm⁻²; Stuart & Sakmann, 1994) and in the modelling studies that successfully mimicked the dendritic patch-electrode recordings of backpropagating APs (Mainen et al. 1995; Vetter et al. 2001). We would probably find the right value for g_Na between 35 and 120 pS μm⁻² in non-apical branches, i.e. basal and oblique dendrites (Rhodes & Llinas, 2001). Even with the dendritic g_Na set to 120 pS μm⁻², the experimental measurements of the AP peak latencies in basal dendrites could not have been matched in the model, unless R_i was smaller than 100 Ω cm (Fig. 5 and Fig. 6).

3. Varying the specific membrane resistance (R_m) in the model (Fig. 1), from 10 to 50 kΩ cm², had a very small (approximately ±0.1 ms) effect on the AP peak latency in basal dendrites (not shown). This is in accord with the results of Trevelyan & Jack (2002) who found that for rapid transients, the dendritic transfer function is set mainly by C_m and R_i, so concerns about the wide range of R_m and whether or not it varies along the dendrite are only relevant to synaptic potential decays.

4. The dendritic diameter has a large influence on the AP velocity in basal dendrites. However, this parameter is satisfactorily constrained in morphologically reconstructed neurons. Size variations among different basal dendrites within the same neuron, and between different neurons of the same type, were of the order of ±0.209 μm in the proximal region (measured 50 μm from the soma), and ±0.146 μm in the distal part of the basal dendrite (measured 150 μm from the cell body). This result is based on 91 measurements in three reconstructed pyramidal cells (animal ages P22, P27 and P33). Major (2001) has pointed out that a 0.2 μm error in a 0.6 μm diameter dendrite can lead to the axial resistance being out by a factor of between 0.5 and 2 (axial resistance is proportional to 1/diameter²). Most of our experiments, and modelling were done in the first 150 μm of the basal dendrite, where the dendritic diameter was always greater than 0.75 μm (mean dendritic diameter 150 μm from the cell body = 0.794 ± 0.146 μm, n = 3 neurons, N = 27 dendrites).

5. The specific membrane capacitance (C_m) strongly influences the speed with which electrical signals propagate along dendrites and unmyelinated axons. The generally accepted C_m value for biological membranes is 1 ± 0.1 μF cm⁻² (Hodgkin & Rushton, 1946; Hodgkin et al. 1952). This was recently confirmed in nucleated patches pulled from cortical and hippocampal neurons (Gentet et al. 2000).

With the exception of R_i, the membrane parameters that largely determine the AP propagation velocity in dendrites are either restricted to a very narrow acceptable range (C_m, diameter), or have a small influence in a relatively wide acceptable range (g_Na, R_m). R_i is the only model parameter that both has a great influence on the propagation velocity and, at the same time, is the subject of a long-lasting controversy (Rall et al. 1992). In other words, the R_i acceptable range has been poorly defined by previous research. It has to be noted here that, in part, the responsibility for the great uncertainty about cytoplasmic resistivity lies with the single-electrode technique. The estimate for R_i is most sensitive to the initial part of the voltage decay (Thurbon et al. 1998), and it is this region of the response that is most affected by capacitative artefact, which is notoriously hard to control. Single-electrode studies have yielded R_i values in the range 170–340 Ω cm (Shelton, 1985; Major et al. 1994; Ulrich et al. 1994). Interestingly, multi-electrode, or multi-site experimental measurements (Stuart & Spruston, 1998; Thurbon et al. 1998; Inoue et al. 2001) have arrived at considerably lower R_i values (∼70 Ω cm).

This was also the case in the present study. The neuron models with R_i values of 100 Ω cm and higher could not mimic the experimental measurements of AP peak latencies along basal and oblique dendrites (Fig. 5 and Fig. 6), unless the dendritic membrane was assigned both a low effective membrane capacitance (spine factor < 1.5) and an extraordinarily high density of voltage-gated sodium channels (g_Na > 120 pS μm⁻²). After adopting C_m= 1 μF cm⁻² and spine factor = 1.75, the conclusion of the combined experimental and modelling approach used here is that the specific axial resistance of neocortical pyramidal neurons at room temperature is in the range 50–70 Ω cm (Fig. 6). One important concern is that the lower R_i values were influenced by the long recording times during temporal averaging of AP-associated optical signals; namely, a hypertonicity of the intracellular solution may result in dendrite swelling (Stuart & Spruston, 1998). In the present study the osmolarity of the intracellular solution was typically 25 mosmol l⁻¹ lower than the osmolarity of the ACSF (see Methods). This allowed long-term recordings (∼30 min) without an apparent increase in the diameter of the cell body (hyperosmolarity of the internal solution) or increase in the series resistance (hyposmolarity of the internal solution).

Recent experiment-modelling studies performed on neocortical pyramidal neurons (Stuart & Spruston, 1998), hippocampal pyramidal neurons (Inoue et al. 2001) and motoneurons (Barrett & Crill, 1974; Thurbon et al. 1998), are in accord with our finding that the specific axial resistance of mammalian CNS neurons is likely to be less than 100 Ω cm.

Role of APs in basal dendrites

The AP serves as an important retrograde signal for the induction of synaptic plasticity (Magee & Johnston, 1997; Markram et al. 1997). In apical dendrites of pyramidal neurons the backpropagating APs have been shown to attenuate in amplitude as a function of distance and frequency of firing (Spruston et al. 1995; Stuart et al. 1997). In contrast to apical dendrites, APs in basal and oblique branches appear to have substantial amplitudes and swift time courses (Figs 3, 5C and 8), and do not show signs of frequency-dependent amplitude modulation (Fig. 9). The peak latency of the retrograde signal at the tips of basal branches (Fig. 4) is approximately three times shorter than in the apical tuft (Larkum et al. 2001). Synaptic inputs arriving on basal dendrites are therefore better suited to participate in coincidence detection than their apical tuft counterparts.

Besides the important role that backpropagating APs may play in triggering the synaptic plasticity in distal dendritic segments of neocortical neurons, it is necessary to examine their possible role in the dendritic release of neurotransmitters, which is known to occur in at least three other mammalian neuron types: dopaminergic neurons of the substantia nigra, mitral and periglomerular cells of the olfactory bulb. In fact, the mammalian CNS is rich with examples of dendro-dendritic chemical transmission. So far, electron microscopy of Golgi-impregnated brain sections has revealed dendro-dendritic synapses in the thalamic ventrobasal nucleus, lateral geniculate nucleus, ventromedial tegmentum and locus coeruleus (for references see Peters et al. 1991). But most importantly, dendro-dendritic synapses have been recorded in layer V of the primate motor cortex (Sloper, 1971). This report was based on the ultrastructural analysis of brains harvested from five Rhesus monkeys. Thus, the anatomical data suggest that the cerebral cortex, much like the olfactory bulb, subcortical and brain stem masses, utilizes dendro-dendritic chemical transmission.

Recent cell biological and electrophysiological studies have shown that pyramid-to-pyramid communication through gap junction channels is one of the prominent features of the developing cerebral cortex (Peinado et al. 1993). Occasional dendritic gap junctions have been sighted with electron microscopy in a variety of mammalian CNS neurons, including the cortex of adult rat and humans (Peters et al. 1991). Unlike chemical synaptic communication, the type of gap junctional communication so far seen in the cortex is mediated mostly by dendrites rather than axons. This form of electrical communication necessarily operates between neurons situated within dendritic range of each other. Morphological and anatomical characteristics of basal dendrites, together with the physiological data described here, suggest that basal branches are uniquely suitable for axon-independent communication between pyramidal cells in the same lamina, and may be involved in columnar organization of the mammalian neocortex.

Difference between apical and basal dendrites

Apical tuft and basolateral pyramidal branches receive anatomically (Zeki & Shipp, 1988) and probably functionally (Poirazi & Mel, 2001) segregated synaptic inputs (clustering of synaptic inputs that carry similar or paired information). At moderate firing rates (20–40 Hz), a backpropagating AP interacts with apical tuft and basal populations of synaptic afferents in quantitatively different ways. Due to severe frequency-dependent amplitude attenuation, dendritic spikes in tuft dendrites are drastically reduced in size and delayed in time (Spruston et al. 1995; Stuart et al. 1997; Larkum et al. 2001). In contrast to apical tuft dendrites, basal branches experience frequency-insensitive voltage swings (Fig. 9), characterized by very little shape distortion (Fig. 3 and Fig. 8), and peak latencies of less than 1 ms (Fig. 4). Within 200 μm from the soma, all synaptic contacts along basal and oblique dendrites experience strong and near-simultaneous (latency < 1 ms) voltage transients during somatic firing. During an AP burst, the entire basolateral dendritic bush pulsates in sync with the cell body (Fig. 9). Therefore, with respect to a retrograde signal (AP), basal and oblique dendrites should be considered as an integral part of the axo-somatic compartment. This is not to say that axon, soma and basal dendrites operate as a single compartment during the integration of synaptic inputs. Multi-site optical measurements presented here only reveal that during a somatic AP these three compartments come into a unique synchrony.

Besides the obvious difference in transmission of the retrograde signal, basal and apical dendrites also impose a different degree of attenuation on forward signals (excitatory postsynaptic potentials), and seem to have different amplification mechanisms involved in local synaptic integration. For example, with respect to a synchronous activation of neighbouring synaptic inputs, basal dendrites respond with spatially restricted NMDA-dependent plateau potentials (Schiller et al. 2000), while the apical dendrite generates calcium spikes that propagate for several hundred micrometres into the dendritic tree (Yuste et al. 1994; Schiller et al. 1997).

The above-mentioned physiological differences between basal and apical dendrites add to the list of evidence in support of the view (Larkum et al. 2001) that the distribution of synaptic afferents on different classes of pyramidal dendrites (basal, oblique and apical tuft) plays a crucial role in information processing, and together with local dendritic integration capabilities (Mel, 1999; Koch & Segev, 2000) holds clues about the computational task of an individual pyramidal cell.

Supplementary material

The online version of this paper can be found at:

http://www.jphysiol.org/cgi/content/full/550/1/35 DOI: 10.1113/jphysiol.2003.033746

and contains material entitled: