Sarcoplasmic reticulum calcium release compared in slow-twitch and fast-twitch fibres of mouse muscle

Abstract

Experiments were carried out to compare the amplitude and time course of Ca²⁺ release from the sarcoplasmic reticulum (SR) in intact slow-twitch and fast-twitch mouse fibres. Individual fibres within small bundles were injected with furaptra, a low-affinity, rapidly responding Ca²⁺ indicator. In response to a single action potential at 16 °C, the peak amplitude and half-duration of the change in myoplasmic free [Ca²⁺] (Δ[Ca²⁺]) differed significantly between fibre types (slow-twitch: peak amplitude, 9.4 ± 1.0 μM (mean ± S.E.M.); half-duration, 7.7 ± 0.6 ms; fast-twitch: peak amplitude 18.5 ± 0.5 μM; half-duration, 4.9 ± 0.3 ms). SR Ca²⁺ release was estimated from Δ[Ca²⁺] with a computational model that calculated Ca²⁺ binding to the major myoplasmic Ca²⁺ buffers (troponin, ATP and parvalbumin); buffer concentrations and reaction rate constants were adjusted to reflect fibre-type differences. In response to an action potential, the total concentration of released Ca²⁺ (Δ[Ca_T]) and the peak rate of Ca²⁺ release ((d/dt)Δ[Ca_T]) differed about 3-fold between the fibre types (slow-twitch: Δ[Ca_T], 127 ± 7 μM; (d/dt)Δ[Ca_T], 70 ± 6 μM ms⁻¹; fast-twitch: Δ[Ca_T], 346 ± 6 μM; (d/dt)Δ[Ca_T], 212 ± 4 μM ms⁻¹). In contrast, the half-duration of (d/dt)Δ[Ca_T] was very similar in the two fibre types (slow-twitch, 1.8 ± 0.1 ms; fast-twitch, 1.6 ± 0.0 ms). When fibres were stimulated with a 5-shock train at 67 Hz, the peaks of (d/dt)Δ[Ca_T] in response to the second and subsequent shocks were much smaller than that due to the first shock; the later peaks, expressed as a fraction of the amplitude of the first peak, were similar in the two fibre types (slow-twitch, 0.2–0.3; fast-twitch, 0.1–0.3). The results support the conclusion that individual SR Ca²⁺ release units function similarly in slow-twitch and fast-twitch mammalian fibres.

In mammalian skeletal muscle, contractile properties differ according to fibre type; for example, the duration of the twitch in slow-twitch fibres is about 4 times larger than that in fast-twitch fibres (rat muscle; Close, 1967). A major factor contributing to the differences in contractile properties is thought to be the difference in myosin isoforms in the different fibre types (e.g. Pette & Staron, 1990). There are also quantitative differences between the fibre types in many of the elements that control the myoplasmic Ca²⁺ transient and activation of the contractile filaments. Relative to fast-twitch fibres, slow-twitch fibres have: (i) about 0.25 times the amount of muscle charge movement (rat fibres; Hollingworth & Marshall, 1981), which presumably is due to a smaller density of dihydropyridine receptors (DHPRs) in the membranes of the transverse tubular system; (ii) about 0.4 times the myoplasmic concentration of ryanodine receptors (RYRs), the Ca²⁺ release channels of the sarcoplasmic reticulum (SR) (guinea-pig fibres; Franzini-Armstrong et al. 1988); (iii) 0.3-0.5 times the concentration of SR Ca²⁺ pump molecules (mouse and guinea-pig fibres; Leberer et al. 1988; Ferguson & Franzini-Armstrong, 1988); (iv) a virtual absence of parvalbumin, a soluble Ca²⁺- and Mg²⁺-binding protein found at near millimolar concentrations in the myoplasm of some fast-twitch fibres of some species (e.g. mouse and rat; Heizmann et al. 1982; Ecob-Prince & Leberer, 1989); (v) a troponin isoform with one rather than two Ca²⁺-regulatory sites per molecule (van Eerd & Takahashi, 1976; Potter et al. 1977); and (vi) a more sensitive tension-pCa curve (rat fibres; Kerrick et al. 1976; Stephenson & Williams, 1981), which presumably reflects a troponin isoform with a higher affinity for Ca²⁺ binding than that found in fast-twitch fibres.

To explore how these differences affect Ca²⁺ signalling during excitation-contraction coupling, we have measured the amplitude and time course of the myoplasmic free [Ca²⁺] transient (Δ[Ca²⁺]) in slow-twitch mouse fibres and compared the results with similar measurements in fast-twitch fibres (Hollingworth et al. 1996). In addition, we have used a computational model to calculate the binding of Ca²⁺ to the quantitatively important myoplasmic Ca²⁺ buffers (troponin, ATP and parvalbumin) and to estimate the amplitude and time course of SR Ca²⁺ release in the two fibre types. Dissected bundles of intact fibres (rather than enzyme-dissociated or cut fibres) were used so that the physiological state of the fibres would be as close to normal as possible for fibres outside the whole animal. The reliability of the measurements of Δ[Ca²⁺] was maximized by (i) use of furaptra, a low-affinity, rapidly responding Ca²⁺ indicator (Konishi et al. 1991) that is well suited for monitoring the unusually large and brief Ca²⁺ transients that occur in skeletal muscle (Hirota et al. 1989; Konishi & Baylor, 1991; Delbono & Stefani, 1993; Hollingworth et al. 1996; Delbono & Meissner, 1996), and (ii) microinjection of the membrane-impermeant form of the Ca²⁺ indicator rather than introduction of the membrane-permeant form with ‘AM loading’ (see Zhao et al. 1997).

The results support several novel conclusions. (i) The amplitude of Δ[Ca²⁺] in slow-twitch fibres stimulated by action potentials is about an order of magnitude larger than that found previously (Carroll et al. 1997; Liu et al. 1997). (ii) The peak rate of SR Ca²⁺ release in slow-twitch fibres is also about an order of magnitude larger than previously reported in cut fibres depolarized by voltage clamp (Delbono & Meissner, 1996). (iii) The time course of SR Ca²⁺ release is similar in slow-twitch and fast-twitch fibres, although the peak rate of SR Ca²⁺ release in slow-twitch fibres is only about one-third of that in fast-twitch fibres. (iv) With a high frequency train of action potentials, inactivation of SR Ca²⁺ release occurs with subsequent action potentials in the train and the extent of inactivation is similar in slow-twitch and fast-twitch fibres. (v) The latter two findings, in combination with three other reported findings, namely (a) a 2.4-fold larger concentration of RYRs in fast-twitch fibres compared with slow-twitch fibres (Franzini-Armstrong et al. 1988); (b) a structural similarity between the triadic junctions in the two fibre types (Cullen et al. 1984); and (c) the presence of a common RYR isoform in the two fibre types (RYR1; Otsu et al. 1993; Damiani & Margreth, 1994; Murayama & Ogawa, 1997), support the conclusion that individual SR Ca²⁺ release units function similarly in the two fibre types.

Some of the results have been reported in abstract form (Hollingworth & Baylor, 1998).

METHODS

Slow-twitch fibres from mouse soleus muscle were studied with methods used previously in this laboratory to study fast-twitch fibres from extensor digitorum longus muscle (EDL; Hollingworth et al. 1996). Briefly, Balb-C mice, 8-10 weeks of age, were killed by rapid cervical disarticulation according to protocols approved by the Institutional Animal Care and Use Committee. Muscles were extracted and pared by gross dissection to small bundles that contained 10-15 % of the original mass. The bundles were mounted in a temperature-controlled chamber on an optical bench apparatus and bathed in mammalian Ringer solution, usually at 16 °C. The Ringer solution was bubbled with oxygen and contained (mM): NaCl 150, KCl 2, CaCl₂ 2, MgCl₂ 1, Hepes 5; pH was adjusted to 7.4 at 20 °C.

To reduce movement artifacts in the fluorescence records, the fibre bundles were stretched to long sarcomere lengths (range, 3.3-4.1 μm). Although it is possible that stretch alters the properties of Δ[Ca²⁺], the alterations are not expected to be large. This follows from the work of Konishi et al. (1991) on frog twitch fibres, where the properties of Δ[Ca²⁺] differed in only minor ways between sarcomere lengths of 2.5 and 4.0 μm.

The isometric twitch tension was monitored with a tension transducer (SensoNor, Horten, Norway) attached to the tendon at one end of the fibre bundle. The strength of the external stimulus was adjusted to be just supra-threshold for the detection of an all-or-none Ca²⁺ signal from the indicator-injected fibre (see below). The use of a just supra-threshold stimulus minimized the twitch amplitude from the bundle and thus also reduced movement-related artifacts in the fluorescence records. The recorded twitch tension arose from the injected fibre and an unknown (but small) number of other fibres. Because the cross-sectional area of the fibres that contributed to the tension response was not determined, the amplitudes of the tension records have been left uncalibrated.

Five soleus fibres, each from a different bundle, were successfully studied. Results from these experiments were compared with results from eleven experiments using EDL (three from this study and eight from the study of Hollingworth et al. 1996). No significant differences were found between the EDL fibres of this and the previous study. All soleus and EDL fibres studied appeared to be of the slow-twitch and fast-twitch types, respectively, as both the myoplasmic Ca²⁺ transients and the twitch tension responses measured from these fibres differed in highly consistent ways (see Results). However, it is possible that with more experiments using soleus muscle, some overlap in the properties of Δ[Ca²⁺] and tension might be observed in comparison with the results from EDL, as the fibre-type composition of mouse soleus muscle is reported to be about 60 % slow-twitch and 40 % fast-twitch, whereas the composition of mouse EDL muscle is close to 100 % fast-twitch (Ecob-Prince & Leberer, 1989). Alternatively, the soleus fibres at the surface of the muscle, which was the location that was used in our experiments, might consist predominantly of slow-twitch fibres.

Measurement of Δ[Ca²⁺]

The tetra-potassium salt of furaptra (Raju et al. 1989), which is also known as mag-fura-2, was purchased from Molecular Probes Inc. (Eugene, OR, USA) and pressure-injected into one fibre within a bundle. Short-wavelength light from a tungsten-halogen source was selected by a wide-band interference filter (410 ± 20 nm; Chroma Technology Co., Brattleboro, VT, USA) and used to excite indicator fluorescence from a 0.3 mm length of fibre; the longer wavelength fluorescent light was selected by a second wide-band filter (530 ± 60 nm) and its intensity was measured with a silicon photodiode. The indicator-related resting fluorescence intensity (F) was calculated as the measured resting light intensity minus the non-indicator-related component, which was estimated from a comparable length of the bundle not containing furaptra. The value of F and the measured diameter of the injected fibre were used to estimate the myoplasmic furaptra concentration (Konishi et al. 1991). This concentration was < 0.3 mM in all fibres; thus, any perturbation of Δ[Ca²⁺] due to Ca²⁺ buffering by furaptra is expected to be negligible (Konishi et al. 1991).

Changes in fluorescence (ΔF) were measured in response to action potentials initiated by brief (< 1 ms) external shocks from a point stimulus positioned just above the bundle near the site of indicator injection. An experiment was accepted for study only if its Ca²⁺-related ΔF signal was all-or-none (see discussion of Fig. 1 in Results). Conversion of the F and ΔF signals to Δ[Ca²⁺] was carried out as described previously (Hollingworth et al. 1996):

(1)

(2)

where Δf_CaD denotes the change in the fraction of the indicator in the Ca²⁺-bound form, and K_D is the apparent dissociation constant of furaptra for Ca²⁺ in the myoplasm (estimated value, 96 μM at 16 °C and free [Mg²⁺] of 1 mM). The use of eqns (1) and (2) to estimate Δ[Ca²⁺] is appropriate because (i) the kinetic delay between Δ[Ca²⁺] and Δf_CaD is expected to be negligible (< 1 ms at time of peak Δ[Ca²⁺] in a frog twitch fibre; Konishi et al. 1991), and (ii) the value of f_CaD in a resting fibre should be essentially zero. The zero value is expected because the myoplasmic K_D of furaptra is ≈1000-fold larger than resting myoplasmic [Ca²⁺] ([Ca²⁺]_R, ≈0.1 μM). The scaling factor in eqn (1) of -1.07 (i.e. 1/(0.068 - 1.0)), is based on the expectation that, with 410 ± 20 nm excitation, the relative fluorescence intensities of furaptra in the Ca²⁺-free and Ca²⁺-bound forms are 1.0 and 0.068, respectively (Konishi et al. 1991; Zhao et al. 1996). The value assumed for K_D at 28 °C (108 μM) was calculated from that at 16 °C with a temperature coefficient (Q₁₀) of 1.1.

Figure 1. Ca²⁺ and tension responses from a bundle of soleus fibres that contained one fibre injected with furaptra.

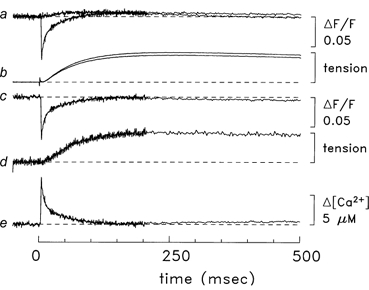
Zero time marks the moment that the bundle was stimulated by a single shock. The top trace in a is the average of four ΔF/F responses that were just sub-threshold for detection of a Ca²⁺ transient by furaptra. The other trace in this pair is the average of four supra-threshold responses; the average amplitude of the supra-threshold stimulus was 2 % larger than that of the sub-threshold stimulus. After 206 ms, the data collection protocol used 4-point averaging, which reduced the noise on the traces. The next pair of traces (b) shows the tension responses associated with the supra- and sub-threshold stimuli; a stimulus artifact is apparent at time zero. Trace c is the supra-threshold ΔF/F response minus the sub-threshold ΔF/F response; prior to the subtraction, a 5-point smoothing algorithm was applied to the sub-threshold response to reduce the influence of high-frequency noise. Trace d is the difference tension record (supra-threshold response minus sub-threshold response), which is displayed at higher vertical gain. (In this and subsequent figures, the amplitude of the tension calibration bar corresponds to the maximum evoked tension response.) Trace e is Δ[Ca²⁺] calculated from the trace c using eqns (1) and (2). Fibre, 062597.1; diameter, 30 μm; sarcomere length, 3.8 μm; estimated furaptra concentration, 200 μM; temperature, 16 °C.

Reliability of the calibration of Δ[Ca²⁺]

The general reliability of these procedures for measuring and calibrating Δ[Ca²⁺] in skeletal muscle with furaptra is supported by the work of Konishi & Baylor (1991) and Konishi et al. (1991) on frog twitch fibres, comparing Δ[Ca²⁺] using furaptra with that measured with PDAA (purpurate-3, 3′-diacetic acid). The PDAA Ca²⁺ signal is considered by us to be the best available calibration standard for Δ[Ca²⁺] in skeletal muscle because (i) the dissociation constant of PDAA for Ca²⁺ is large (K_D, 0.95 mM; Hirota et al. 1989) and (ii) the degree of binding of PDAA to myoplasmic constituents is the smallest of any indicator studied to date in skeletal muscle fibres (Hirota et al. 1989; Zhao et al. 1996). Because of the first property, the response of PDAA to Δ[Ca²⁺] is expected to be linear and without kinetic delay. Because of the second property, the K_D of PDAA in myoplasm is expected to be close to that measured in a simple salt solution (0.95 mM).

The importance of these properties for the calibration of Δ[Ca²⁺] is illustrated by a comparison of results using PDAA and furaptra with those using the high-affinity indicators fura-2 and indo-1. Both in frog twitch fibres and in mammalian fast-twitch fibres stimulated by action potentials, most measurements of Δ[Ca²⁺] with these two types of indicators differ by about an order of magnitude: with PDAA and furaptra, peak Δ[Ca²⁺] is typically 5-20 μM (Hirota et al. 1989; Konishi & Baylor, 1991; Konishi et al. 1991; Hollingworth et al. 1996) whereas, with fura-2 and indo-1, peak Δ[Ca²⁺] is typically 0.5-2 μM (e.g. Suda & Kurihara, 1991; Westerblad & Allen, 1993; Carroll et al. 1995; Abate et al. 2002). The time course of Δ[Ca²⁺] measured with PDAA or furaptra is also significantly briefer than that measured with fura-2 or indo-1. These differences are thought to result from both kinetic and steady-state errors that apply particularly strongly to Δ[Ca²⁺] measurements with fura-2 and indo-1. For example, fura-2 and indo1-1 bind more heavily to myoplasmic constituents than do PDAA or furaptra; in intact frog fibres, the estimated bound fractions are 0.81 for indo-1, 0.76 for fura-2, 0.58 for furaptra, and 0.40 for PDAA (Zhao et al. 1996). When compared with indicator molecules in a simple salt solution, bound indicator molecules undergo an alteration of their on- and off-rate constants for Ca²⁺, an alteration of their effective K_D for Ca²⁺, and an alteration of the optical properties of the indicator that are required for the calibration of [Ca²⁺] (see e.g. Konishi et al. 1988; Harkins et al. 1993; Baker et al. 1994; Baylor & Hollingworth, 1998, 2000). As noted by Hirota et al. (1989), the calibration of Δ[Ca²⁺] in skeletal muscle with the high-affinity indicators thus becomes susceptible to a potentially large underestimation of Δ[Ca²⁺]. Further, because large sarcomeric gradients in Δ[Ca²⁺] occur in twitch fibres stimulated by action potentials (Cannell & Allen, 1984; Baylor & Hollingworth, 1998), high-affinity indicators become heavily saturated with Ca²⁺ in some regions of the sarcomere but not others; this variable saturation makes it difficult to kinetically correct the spatially averaged Δ[Ca²⁺] measurement to yield a reliable time course for Δ[Ca²⁺] (Baylor & Hollingworth, 1998, 2000). Based on these results, we believe that calibrations of Δ[Ca²⁺] in skeletal muscle with PDAA or furaptra are strongly preferable to those with fura-2 or indo-1.

Estimation of Ca²⁺ binding to myoplasmic Ca²⁺ buffers and of SR Ca²⁺ release

The single-compartment kinetic model of Baylor et al. (1983), updated as described by Baylor & Hollingworth (1998), was used to estimate the total concentration of Ca²⁺ released from the SR (Δ[Ca_T]; concentration units are relative to the myoplasmic water volume) and the rate of SR Ca²⁺ release ((d/dt)Δ[Ca_T]). Δ[Ca_T] was calculated as the sum of Δ[Ca²⁺] and the estimated changes in the concentration of Ca²⁺ bound to furaptra (Δ[CaD]) and to the principal myoplasmic Ca²⁺ buffers (troponin, ATP and parvalbumin; denoted Δ[CaTrop], Δ[CaATP] and Δ[CaParv], respectively). Possible contributions to Δ[Ca_T] due to Ca²⁺ binding and transport by the SR Ca²⁺ pump were not included as previous calculations for frog twitch fibres (Pape et al. 1990) indicated that inclusion of a binding and transport scheme for the pump (Fernandez-Belda et al. 1984) resulted in only a minor (≈10 %) increase in Δ[Ca_T]. This error is small in comparison with the approximately 3-fold difference estimated in Results for Δ[Ca_T] and (d/dt)Δ[Ca_T] in slow-twitch vs. fast-twitch mouse fibres.

Table 2 (described in Results) gives the parameter values for the concentrations and rate constants used in the model. Values for fast-twitch fibres at 16 °C are identical to those used previously for frog twitch fibres at the same temperature (Baylor & Hollingworth, 1998). Values for slow-twitch fibres were modified from the fast-twitch values based on the fibre-type differences described in the Introduction. Overall, some uncertainty exists regarding the values listed in Table 2. The single most important uncertainty is probably the value assumed for the association rate constant between Ca²⁺ and troponin, as troponin constitutes the quantitatively most important myoplasmic Ca²⁺ buffer on a rapid time scale. The value of this constant in Table 2 (0.885 × 10⁸ M⁻¹ s⁻¹ at 16 °C) is consistent with biochemical measurements on troponin in fast-twitch mammalian fibres (Johnson et al. 1981; Rosenfeld & Taylor, 1985; see Discussion in Maylie et al. 1987). As far as we know, similar biochemical measurements are not available for troponin in slow-twitch fibres and we have therefore assumed that this rate constant is identical in the two fibre types. If the value of this rate constant in the model is increased or decreased 2-fold, the value estimated for the peak of (d/dt)Δ[Ca_T] is changed by approximately +20 % and -23 %, respectively, for slow-twitch fibres and +13 % and -19 %, respectively, for fast-twitch fibres. Again, these changes are small with respect to the large fibre-type differences in (d/dt)Δ[Ca_T] described in Results. Because the free [Ca²⁺] required for half-activation of tension in slow-twitch fibres is about half that in fast-twitch fibres (≈0.6 and 1.2 μM, respectively; skinned rat fibres at 22-25 °C; Stephenson & Williams, 1981), the Ca²⁺-troponin dissociation rate constant for slow-twitch fibres was selected to be half that for fast-twitch fibres.

Table 2.

Parameter values used in the modelling of SR Ca²⁺ release (16°C)

1	2	3
	Slow-twitch	Fast-twitch
A. Resting concentrations (free)
[Ca2+]R (μM)	0.1	0.1
[Mg2+]R (μM)	1000	1000
B. Site concentrations (total)
Troponin Ca2+ sites (μM)	120	240
ATP Ca2+ sites (μM)	8000	8000
Parvalbumin Ca2+ and Mg2+ sites (μM)	0	1500
C. Reaction rate constants
Ca2+−troponin reaction
On-rate (108M−1 s−1)	0.885	0.885
Off-rate (s−1)	57.5	115
Dissociation constant (μM)	0.65	1.3
Ca2+−parvalbumin reaction
On-rate (108M−1 s−1)	—	0.417
Off-rate (s−1)	—	0.5
Dissociation constant (μM)	—	0.012
Mg2+−parvalbumin reaction
On-rate (108M−1 s−1)	—	0.00033
Off-rate (s−1)	—	3
Dissociation constant (μM)	—	90.9

Concentrations units are relative to the myoplasmic water volume, as with Δ [Ca²⁺]. Free [Mg²⁺] is assumed to be constant at 1mM. The reaction of Ca²⁺ with ATP (not shown) is assumed to be instantaneous, with Δ[CaATP] = 3.6 ×Δ[Ca²⁺]; this assumes that [ATP] = 8 mM and that the effective dissociation constant of ATP for Ca²⁺ is 2.2 mM (Baylor & Holling worth, 1998). Rate constants for the parvalbumin reaction are not listed for slow-twitch fibres because it has been reported taht the parvalbumin concentration in slow-twitch fibres is zero. For model calculations at 28°C, the reaction rate constants were twice those shown here. See Methods for justification of parameter values at 16°C.

The effects of changes in several other parameter values in Table 2 were also explored computationally and these were also found to produce relatively minor changes in the estimates of (d/dt)Δ[Ca_T]: (i) -15 % for slow-twitch and -10 % for fast-twitch fibres for a 2-fold reduction in the ATP concentration; (ii) +8 % for slow-twitch fibres and +6 % for fast-twitch fibres for a 3-fold reduction in [Ca²⁺]_R; (iii) +1 % for fast-twitch fibres for a 3-fold increase in the Ca²⁺-parvalbumin association rate constant; and (iv) -6 % for fast-twitch fibres if the reaction between Ca²⁺ and troponin is changed from the standard one for fast-twitch fibres (in which it is assumed that the two regulatory sites bind Ca²⁺ identically and independently) to a sequential reaction with positive cooperativity (Baylor et al. 2002).

Statistics

Population measurements are reported as mean ± S.E.M. The statistical significance of a difference between means was evaluated with Student's two-tailed t test at P < 0.05.

RESULTS

Δ[Ca²⁺] and tension elicited by a single action potential at 16 °C

Figure 1 shows results from an experiment on a bundle of soleus fibres stimulated by a single external shock; zero time marks the moment of the stimulus. The superimposed pair of traces at the top show the normalized fluorescence changes (ΔF/F) that resulted from stimuli that were either just sub-threshold (top trace) or just supra-threshold for an all-or-none Ca²⁺ signal from the one fibre in the bundle that had been injected with furaptra. The response to the sub-threshold stimulus reveals a small increase in fluorescence that begins 20-30 ms after stimulation. This increase is thought to be due to a movement artifact caused by fibres other than the one injected with furaptra. In contrast, the response to the supra-threshold stimulation reveals an abrupt early downward deflection due to Δ[Ca²⁺] (peak amplitude, -0.069 ΔF/F; time to peak, 4.5 ms). At later times, this trace overshoots the baseline, presumably also due to a movement artifact.

The second pair of superimposed traces in Fig. 1 show the corresponding tension responses. The amplitude of the supra-threshold tension response is about 10 % larger than that of the sub-threshold response. This extra tension from the supra-threshold stimulus, which probably came from the injected fibre only, suggests that about 10 fibres contributed to the sub-threshold tension response.

The ΔF/F and tension traces in the middle of Fig. 1 show the ‘difference’ records for fluorescence and tension, obtained by subtraction of the sub-threshold responses from the corresponding supra-threshold responses. The movement artifact in the corrected ΔF/F record appears to have been reduced by the subtraction procedure. Nevertheless, a small artifact probably remains, as this trace still bows upwards slightly during the period 100-250 ms after stimulation. The difference record for tension and the two original tension records all have very similar time courses.

The bottom trace (trace e) in Fig. 1 shows Δ[Ca²⁺], which was calculated from the corrected ΔF/F record with eqns (1) and (2). Δ[Ca²⁺] has a peak value of 7.6 μM, a time to half-rise of 3.7 ms after stimulation, a time to peak of 4.5 ms and a half-duration (time between half-rise and half-decay) of 8.2 ms. These properties of Δ[Ca²⁺] are expected to be minimally influenced by the residual movement artifact in the corrected ΔF/F trace. In contrast, the amplitude of Δ[Ca²⁺] 100-500 ms after stimulation, when the tension transient is large, is not known. During this period, Δ[Ca²⁺] is small and cannot be reliably distinguished from the movement artifact. In addition, a small contribution to the ΔF/F signal from furaptra may occur at this time due to a change in myoplasmic free [Mg²⁺] (Konishi et al. 1991).

Similar measurements of Δ[Ca²⁺] and tension were recorded in five experiments with soleus muscle. Column 2 of Table 1 gives the mean ± S.E.M. values of several parameters measured in these experiments. For comparison, column 3 gives the values measured from 11 experiments with EDL at the same temperature. With both soleus and EDL muscles, the values in columns 2 and 3 of Table 1 reveal a tight distribution about their means. Significant differences between fibre types were detected in the values of peak amplitude and half-duration of Δ[Ca²⁺] (see asterisks in column 3). The peak amplitude in soleus fibres is about 0.5 times that in EDL fibres (9.4 and 18.5 μM, respectively) whereas the half-duration in slow-twitch fibres is about 1.6 times that in fast-twitch fibres (7.7 and 4.9 ms, respectively). In contrast, the times to half-rise and to peak of Δ[Ca²⁺] are virtually identical in the two fibre types. As expected, the parameters that describe the time course of the tension responses are all significantly larger in the soleus (slow-twitch) fibres than in the EDL (fast-twitch) fibres (see asterisks in Table 1).

Table 1.

Properties of Δ[Ca²⁺] and tension in response to a single action potential

1	2	3	4	5
	16°C		28°C
	Slow-twitch	Fast-twitch	Slow-twitch	Fast-twitch
	(n = 5)	(n = 11)	(n = 1)	(n = 4)
Δ[Ca2+]
Peak amplitude (μM)	6.4 ± 1.0	18.5 ± 0.5*	8.6	21.7 ± 1.8
Time to half-rise (ms)	3.4 ± 0.2	3.2 ± 0.1	2.1	1.4 ± 0.1
Time to peak (ms)	4.8 ± 0.1	4.4 ± 0.2	2.5	2.0 ± 0.1
Half-duration (ms)	7.7 ± 0.6	4.9 ± 0.3*	4.4	2.0 ± 0.1
Twitch tension
Time to half-rise (ms)	38 ± 3	17 ± 0*	22	8 ± 1
Time to peak (ms)	160 ± 5	50 ± 1*	97	23 ± 1
Half-duration (ms)	725 ± 130	199 ± 11*	408	97 ± 8

Measurements for slow-twitch and fast-twitch fibres are from soleus and EDL muscles, respectively. Data are mean ±s.e.m. for the number of experiments (n) indicated at the top of the columns. Values of time to half-rise and time to peak are relative to the time of the external shock. Asterisks in column 3 denote significant differences (P < 0.05) with respect to the corresponding mean in column 2. The mean ±s.e.m. values of indicator concentration, fibre diameter and sarcomere length were: 120 ± 25 μM, 39 ± 4 μM and 3.6 ± 0.1 μM (soleus) and 81 ± 12 μM, 44 ± 2 μM and 3.9 ± 0.1 mm (EDL), respectively.

These differences between slow-twitch and fast-twitch fibres are further illustrated in Fig. 2, which shows Δ[Ca²⁺] and tension responses averaged from four soleus experiments (dotted traces, with identifying arrows) and seven EDL experiments (continuous traces). As expected, the parameter values that describe these average measurements (see legend) are similar to the mean values given in column 2 of Table 1. In Fig. 2B, the records are displayed on a faster time scale than those in Fig. 2A, and the slow-twitch Δ[Ca²⁺] signal has been scaled to have the same displayed amplitude as the fast-twitch signal. A striking feature revealed in Fig. 2B is that the temporal waveforms of the two Δ[Ca²⁺] signals are very similar through time to peak and slightly into the falling phase; thereafter, the slow-twitch Δ[Ca²⁺] decays more slowly. The close similarity of the Δ[Ca²⁺] time courses through time to peak suggests that the time course of SR Ca²⁺ release is likely to be very similar in the two fibre types (see last two sections of Results).

Figure 2. Comparison of Ca²⁺ and tension responses in slow-twitch and fast-twitch fibres.

A, Δ[Ca²⁺] and twitch tension averaged from four experiments with soleus muscle (dotted lines, identified by arrows) and seven experiments with EDL muscle (continuous lines) of the type illustrated in Fig. 1. The selected experiments had minimal contamination of the Δ[Ca²⁺] signal by movements artifacts. The mean diameter of the fibres was 37 ± 6 μm for soleus and 41 ± 2 μm for EDL muscle. Where necessary, records were temporally shifted (average shift, 1 data point = 0.5 ms) to align the rising phases of the Δ[Ca²⁺] signals. The total number of Δ[Ca²⁺] responses averaged was 31 for soleus and 13 for EDL. The slow-twitch Δ[Ca²⁺] record has a peak amplitude of 8.0 μM, a time to half-rise of 3.4 ms, a time to peak of 4.5 ms and a half-duration of 7.6 ms; the corresponding values for the fast-twitch record are 18.2 μM, 3.5 ms, 4.5 ms and 4.8 ms, respectively. The tension response from each experiment was scaled to unity amplitude prior to averaging. The slow-twitch tension record has a time to half-rise of 38 ms, a time to peak of 184 ms and a half-duration of 767 ms; the corresponding values for the fast-twitch record are 17 ms, 54 ms and 215 ms, respectively. B, same traces as in A displayed on a faster time base and with the slow-twitch Δ[Ca²⁺] scaled to have the same peak amplitude as that of the fast-twitch Δ[Ca²⁺]. Temperature, 16 °C.

Characterization of the decay of Δ[Ca²⁺] in response to a single action potential

Figure 2 shows that the time for Δ[Ca²⁺] to return close to baseline is slower in the slow-twitch fibres than in the fast-twitch fibres. The slower return in the slow-twitch fibres indicates that the Ca²⁺ removal systems are less active in slow-twitch than fast-twitch fibres.

To characterize the relative activity of the Ca²⁺ removal systems and to make comparisons with previous characterizations of the decay phase of Δ[Ca²⁺] in the two fibre types (see Discussion), the signals in Fig. 2 were fitted with a decaying single exponential function:

(3)

The fits were carried out for various time intervals after the time to peak, and the method of least squares was used to adjust amplitude A and the time constant τ. To characterize the initial rate of decay of Δ[Ca²⁺] from peak, eqn (3) was fitted from the time of the first data point after the time to peak until the time for Δ[Ca²⁺] to return half-way to baseline. The best-fitted value of τ was 9.4 ms for the slow-twitch signal (rate constant, 106 s⁻¹; 5.0 ≤ t ≤ 11.0 ms) and 4.7 ms for the fast-twitch signal (rate constant, 213 s⁻¹; 5.0 ≤ t ≤ 8.5 ms). To characterize the decay of Δ[Ca²⁺] during the final half of the signals, eqn (3) was fitted for 11.0 ≤ t ≤ 150 ms (slow-twitch) and for 8.5 ≤ t ≤ 150 ms (fast-twitch). The best-fitted values for τ were 39 ms (slow-twitch) and 12 ms (fast-twitch) (rate constants, 26 and 83 s⁻¹, respectively). Thus, the rate constant of the final decay was about 3-fold larger in the fast-twitch fibres than in the slow-twitch fibres, and, in both fibre types, the rate constant of the initial decay was several times larger than that of the final decay.

Δ[Ca²⁺] and tension in response to repetitive stimulation

Figure 3A and B shows superimposed Δ[Ca²⁺] and tension responses from slow-twitch and fast-twitch fibres, respectively, stimulated by a single shock and a 5-shock train at 67 Hz. In both fibre types, the peak Δ[Ca²⁺] due to the second shock in the train was slightly smaller than that due to the first; subsequently, the peak amplitudes either grew slightly larger with increasing shock number (slow-twitch) or were very similar to that triggered by the first shock (fast-twitch). The progressive rise in the amplitude of the later peaks of Δ[Ca²⁺] in the slow-twitch fibre is probably related to the finding that Δ[Ca²⁺] decays more slowly from peak levels in slow-twitch fibres (see above); thus, when a subsequent increment in Δ[Ca²⁺] occurs, it commences from a relatively higher starting level.

Figure 3. Δ[Ca²⁺] and tension responses from fibres stimulated by a single shock and five shocks at 67 Hz.

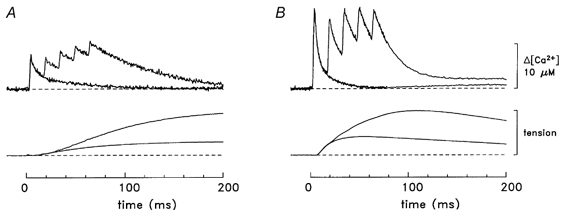
A, slow-twitch responses (fibre, 062597.1). B, fast-twitch responses (averaged results from fibres 032596.2, 040596.1, 040896.1 and 040996.3). In A, the Δ[Ca²⁺] record following a single-shock has a peak amplitude of 7.6 μM, a time to half-rise of 3.7 ms, a time to peak of 4.5 ms and a half-duration of 8.2 ms; the corresponding values in B are 17.5 μM, 3.0 ms, 4.0 ms and 4.5 ms, respectively. For the tension responses in A, the values of time to half-rise, time to peak and half-duration are 55, 307 and 1360 ms, respectively (single shock) and 82, 342 and 1320 ms, respectively (multiple-shock); in B, the values are 16, 55 and 215 ms, respectively (single shock) and 34, 107 and 236 ms, respectively (multiple-shock). Temperature, 16 °C.

In contrast to the single-shock response, the full time course of the decay of Δ[Ca²⁺] from its peak at the end of the 5-shock train was well described in both fibre types by a decaying exponential function to a baseline offset, A₀:

(4)

Least-squares fits were carried out for the time period 65 ≤ t ≤ 500 ms. The best-fitted values of A₀ and τ were -0.4 μM and 68 ms (slow-twitch) and 1.8 μM and 21 ms (fast-twitch), respectively. The corresponding rate constants are 15 and 48 s⁻¹, respectively, which is a 3-fold difference. In both fibre types, the rate constant of the decay of Δ[Ca²⁺] after the 5-shock train is slightly more than half that observed for the final half of the decay of Δ[Ca²⁺] after a single shock (26 and 83 s⁻¹; see above). Thus, the fractional reduction in the (final) decay rate constant with maintained stimulation is similar in the two fibre types.

Figure 3 also shows that, with a 67 Hz train of stimuli, the initial rate at which Δ[Ca²⁺] decays from its individual peaks declines during the train. To characterize this effect, the rate constant of the initial decay of Δ[Ca²⁺] from peak levels was estimated with eqn (3) during each 6 ms period beginning immediately after the corresponding time of peak. Figure 4 shows the results plotted as a function of stimulus time during the train (□, slow-twitch; ○, fast-twitch). In both fibre types, the decay rate constant associated with the first shock (0 ms on the abscissa in Fig. 4) is about 2.5-fold larger than that associated with the second shock (t = 15 ms) and about 5-fold larger than the ‘steady-state’ rate constant observed after 3-8 shocks (t ≥ 30 ms). Qualitatively similar results were reported previously for Δ[Ca²⁺] in fast-twitch fibres at three temperatures (16, 28 and 35 °C; Hollingworth et al. 1996). The explanation suggested for the steep decline in the fast-twitch rate constant with subsequent shocks in the train was that one or more of the myoplasmic Ca²⁺ buffers (troponin, parvalbumin or the SR Ca²⁺ pump) rapidly binds Ca²⁺ to a near-maximal level early in the train and thereafter is unavailable to bind Ca²⁺ and contribute to the rapid lowering of Δ[Ca²⁺] (Hollingworth et al. 1996). Because mouse slow-twitch fibres have little or no parvalbumin (soleus muscle; Heizmann et al. 1982; Ecob-Prince & Leberer, 1989), saturation of Ca²⁺ binding sites on parvalbumin cannot contribute significantly to the decline in the decay rate constant in the slow-twitch fibres. The larger absolute values of the decay rate constants in fast-twitch compared with slow-twitch fibres (Fig. 4) are consistent with the 2-fold greater concentration of Ca²⁺ binding sites on troponin in fast-twitch fibres (van Eerd & Takahashi, 1976; Potter et al. 1977), the 3-fold greater concentration of SR Ca²⁺ pump sites (Leberer et al. 1988) and the presence of parvalbumin.

Figure 4. Initial decay rate constants of Δ[Ca²⁺] at different times during a 67 Hz train of stimuli.

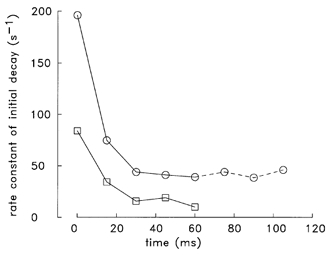
Decay rate constants (1/τ) were estimated for the initial decline of Δ[Ca²⁺] from individual peaks of the type illustrated in Fig. 3: □, slow-twitch fibres; ○, fast-twitch fibres. For each estimate, eqn (3) was fitted to the Δ[Ca²⁺] data during the 6 ms period beginning immediately after peak; similar relative rates (not shown) were obtained from straight line fits to the same data sets. The abscissa shows the time during the train beginning at the time of the first shock. The fibres that contributed to the plot are those of Fig. 3 plus one additional fast-twitch fibre (040996.1, which was stimulated by an 8-shock train; the data for the three extra shocks for this fibre are connected by dashed lines). At t ≤ 60 ms, the fast-twitch data are the average values from five individual experiments; values of S.E.M. for these data are not shown, as, in all cases, they were less than the symbol size.

Estimation of SR Ca²⁺ release

The measurements of Δ[Ca²⁺] were used as input to the computational model described in the Methods to estimate the total concentration of Ca²⁺ released from the SR into the myoplasm (Δ[Ca_T]) and the rate of SR Ca²⁺ release ((d/dt)Δ[Ca_T]). For these calculations, the concentrations and reaction rate constants in the model were selected to match the biochemical characteristics of the fibre types (parts B and C of Table 2). The resting occupancies of the troponin, ATP and parvalbumin sites were calculated from the values of [Ca²⁺]_R and [Mg²⁺]_R, and the site dissociation constants (parts A and C of Table 2). The changes during activity were calculated from [Ca²⁺] (i.e. Δ[Ca²⁺] + [Ca²⁺]_R) and the appropriate rate equations for mass-action binding of Ca²⁺ and (in the case of parvalbumin) Mg²⁺ (Robertson et al. 1981; Baylor et al. 1983; Baylor & Hollingworth, 1998).

Figure 5A shows results of the modelling procedure applied to a slow-twitch fibre stimulated by a single shock. The two traces at the bottom show Δ[Ca²⁺] and Δ[CaD], which were calculated directly from the fluorescence measurements and the estimated total concentration of indicator (see Methods). The middle three traces show the changes in site occupancies (Δ[CaATP], Δ[CaTrop], Δ[CaParv]). The second trace shows Δ[Ca_T], calculated as the sum of the five lower traces. The top trace (labelled Release) shows (d/dt)Δ[Ca_T]. Figure 5B shows corresponding results for a fast-twitch fibre.

Figure 5. Myoplasmic Ca²⁺ binding and SR Ca²⁺ release in response to a single shock.

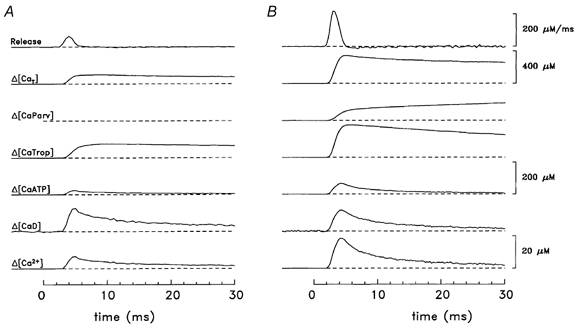
A, slow-twitch (fibre, 062597.1; sarcomere length, 3.8 μm; furaptra concentration, 200 μM). B, fast-twitch (fibre, 040896.1; sarcomere length, 3.8 μm; furaptra concentration, 74 μM). All units of concentration are moles of Ca²⁺ per litre of myoplasmic water. The 20 μM calibration bar applies to Δ[Ca²⁺] and Δ[CaD]; the 200 μM calibration bar applies to Δ[CaATP], Δ[CaTrop], and Δ[CaParv]. The top trace (labelled Release) is (d/dt)Δ[Ca_T]. To reduce noise on the modelled traces during the baseline period, the fluctuations on the Δ[Ca²⁺] traces were set to zero prior to the onset of Δ[Ca²⁺]. The peak occupancies of the troponin sites with Ca²⁺ ([CaTrop]_R + Δ[CaTrop]) are 103 μM (A) and 219 μM (B), corresponding to fractional occupancies of 0.858 and 0.912, respectively. Temperature, 16 °C.

In Fig. 5, the peak value of Δ[Ca_T] in the slow-twitch fibre is only one-third of that in the fast-twitch fibre (115 and 345 μM, respectively), and a similar difference is also found for the peaks of (d/dt)Δ[Ca_T] (65 and 214 μM ms⁻¹, respectively). In contrast, the values of time to half-rise, time to peak and half-duration of (d/dt)Δ[Ca_T] are very similar (slow-twitch, 3.2, 4.0 and 1.8 ms, respectively; fast-twitch, 2.5, 3.0 and 1.6 ms, respectively). Similar features were observed for the mean values from all experiments (columns 2 and 3 of Table 3). Significant differences were found for the peak of Δ[Ca_T], the peak of (d/dt)Δ[Ca_T] and one of the temporal parameters (half-duration of (d/dt)Δ[Ca_T]). In the case of the half-duration of (d/dt)Δ[Ca_T], the value for slow-twitch fibres differed only slightly (< 15 %) from that for fast-twitch fibres.

Table 3.

Properties of SR Ca²⁺ release in response to a single action potential

1	2	3	4	5
	16°C		28°C
	Slow-twitch	Fast-twitch	Slow-twitch	Fast-twitch
	(n = 5)	(n = 11)	(n = 1)	(n = 4)
Δ[Ca2+]
Peak amplitude (μM)	127 ± 7	346 ± 6*	120	358 ± 9
(d/dt)Δ[CaT]
Peak amplitude (μM ms−1)	70 ± 6	212 ± 4*	105	473 ± 28
Time to half-rise (ms)	2.8 ± 0.2	2.6 ± 0.1	1.8	1.2 ± 0.1
Time to peak (ms)	3.5 ± 0.2	3.3 ± 0.1	2.3	1.6 ± 0.1
Half-duration (ms)	1.8 ± 0.1	1.6 ± 0.0*	1.2	0.8 ± 0.0

Release parameters were estimated from the single-compartment model, as described in the text. Values of time to half-rise and time to peak are relative to the time of the external shock. Asterisks in column 3 denote significant differences between the means in columns 2 and 3 (P < 0.05).

Figure 6 shows similar results for Δ[Ca²⁺] measured in response to a 5-shock train at 67 Hz for slow-twitch (Fig. 6A) and fast-twitch (Fig. 6B) fibres. In both fibre types, the peaks of (d/dt)Δ[Ca_T] in response to shocks 2-5 are much smaller than that due to the first shock. The amplitude of the subsequent peaks, if expressed as a fraction of that of the first peak, are: 0.33, 0.28, 0.18 and 0.23 (slow-twitch) and 0.29, 0.17, 0.13 and 0.09 (fast-twitch). For the four fast-twitch fibres stimulated as in Fig. 6, the mean values for shocks 2-5 were: 0.32 ± 0.02, 0.21 ± 0.02, 0.15 ± 0.01 and 0.12 ± 0.01. These reductions are probably due to the process of Ca²⁺-dependent inactivation of Ca²⁺ release, in which the rise in [Ca²⁺] in response to prior shocks acts to inhibit SR Ca²⁺ release in subsequent shocks (see also Discussion). The slightly larger fractional reductions calculated for the fast-twitch fibres are consistent with the larger amplitude Δ[Ca²⁺] in the fast-twitch fibres.

Figure 6. Myoplasmic Ca²⁺ binding and SR Ca²⁺ release in response to a 5-shock train at 67 Hz.

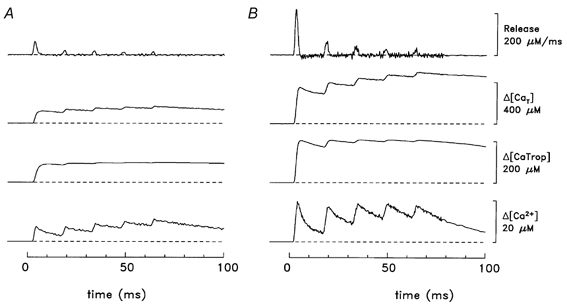
A, slow-twitch; B, fast-twitch (same fibres as in Fig. 5.) For simplicity, the traces for Δ[CaD], Δ[CaATP] and Δ[CaParv] are not shown. In response to the first shock, the peaks of release were 64 and 215 μM ms⁻¹ (A and B, respectively). During the period 10-70 ms, the average occupancies of the troponin sites with Ca²⁺ ([CaTrop]_R + Δ[CaTrop]) are 109 μM (A) and 216 μM (B), corresponding to fractional occupancies of 0.908 and 0.900, respectively. Temperature, 16 °C.

Regarding the Δ[CaTrop] waveforms in Fig. 5 and Fig. 6, it is of interest that, with both the slow-twitch and fast-twitch fibres, the fractional occupancy of the troponin regulatory sites with Ca²⁺ is large (close to 0.9; see legends to Fig. 5 and Fig. 6). Thus, in both fibre types, the amount of Ca²⁺ release calculated from the model appears to be well suited to nearly saturate the troponin sites with Ca²⁺, both in response to a single action potential and to a high-frequency train of action potentials.

Measurements at 28 °C

In our previous study of fast-twitch fibres (Hollingworth et al. 1996), Δ[Ca²⁺] was measured at 16 and 28 °C in four experiments. In the present study, a successful experiment of this type was completed on one slow-twitch bundle (single-shock stimulation; data not shown). Columns 4 and 5 of Table 1 give the measured parameter values for Δ[Ca²⁺] and tension in the five experiments at 28 °C. Differences between the fibre types are apparent that are qualitatively similar to those described above at 16 °C (columns 2 and 3 of Table 1). As expected, all temporal parameters at 28 °C are substantially smaller than the corresponding values at 16 °C.

Equation (3) was used to characterize the decay phase of the Δ[Ca²⁺] signals at 28 °C with the same procedures used at 16 °C. The values of the initial rate constant of decay were 147 s⁻¹ for slow-twitch (3.0 ≤ t ≤ 7.0 ms; n = 1) and 577 ± 68 s⁻¹ for fast-twitch (2.2 ± 0.1 ≤ t ≤ 3.4 ± 0.2 ms; n = 4). In contrast, the values of the rate constant for the final half of the decay were 59 s⁻¹ for slow-twitch and 270 ± 45 s⁻¹ for fast-twitch fibres. Thus, as at 16 °C, in both fibre types the initial decay of Δ[Ca²⁺] was several times faster than the final decay, and the final decay of Δ[Ca²⁺] in the fast-twitch fibres was several times faster than that of Δ[Ca²⁺] in the the slow-twitch fibres.

To estimate the properties of SR Ca²⁺ release at 28 °C, calculations like those described in the preceding section were carried out; the values of the kinetic parameters in the model were adjusted to the higher temperature as described in the legend of Table 2. Columns 4 and 5 of Table 3 show the results. As at 16 °C, the peak amplitudes of Δ[Ca_T] and (d/dt)Δ[Ca_T] reveal large differences between the fibre types (120 μM and 105 μM ms⁻¹, respectively, in slow-twitch vs. 358 ± 9 μM and 473 ± 28 μM ms⁻¹ in fast-twitch), whereas the parameters that describe the time course of (d/dt)Δ[Ca_T] (time to half-rise, time to peak and half-duration) are similar in the two fibre types. As expected, all temporal parameters are smaller at 28 °C than at 16 °C.

DISCUSSION

Δ[Ca²⁺] in slow-twitch fibres stimulated by action potentials

In this article we describe what we believe are the most accurate measurements to date of the amplitude and time course of spatially averaged Δ[Ca²⁺] in mammalian slow-twitch fibres stimulated by action potentials. The measurements rely on the injection of furaptra, a low-affinity, rapidly responding fluorescent Ca²⁺ indicator, into a single intact muscle cell within a fibre bundle. Accurate measurements of Δ[Ca²⁺] in twitch muscle fibres stimulated by action potentials are greatly facilitated by the use of low-affinity, rapidly responding indicators that do not bind strongly to myoplasmic constituents (Hirota et al. 1989; see Methods). Further, the amplitude of Δ[Ca²⁺] is more accurately measured if the indicator is microinjected rather than introduced by AM loading (Zhao et al. 1997). The importance of this methodological approach has been demonstrated previously in mammalian fast-twitch fibres, where the amplitude of Δ[Ca²⁺] measured with furaptra (Delbono & Stefani, 1993; Hollingworth et al. 1996; Delbono & Meissner, 1996) is about an order of magnitude larger than that measured with the metallochromic indicator antipyrylazo III (Garcia & Schneider, 1993) or with the high-affinity fluorescent indicators fura-2 (Carroll et al. 1995) and indo-1 (e.g. Westerblad & Allen, 1993; Abate et al. 2002). The new measurements of Δ[Ca²⁺] in mouse slow-twitch fibres reported here complement our previous measurements in fast-twitch fibres (Hollingworth et al. 1996) and thus facilitate a meaningful comparison of Ca²⁺ signalling events in the two mammalian fibre types.

Differences between Δ[Ca²⁺] in slow-twitch and fast-twitch fibres

In response to an action potential, Δ[Ca²⁺] in mouse slow-twitch (soleus) fibres differs in two highly reproducible ways when compared with Δ[Ca²⁺] in fast-twitch (EDL) fibres. First, the peak of Δ[Ca²⁺] in slow-twitch fibres is about half that in fast-twitch fibres (≈9 μM and ≈19 μM, respectively; Table 1 and Fig. 2 and Fig. 3). This difference correlates with a difference in the steady-state tension vs. pCa relation measured in skinned rat fibres, in which the free [Ca²⁺] required for half-activation of tension (Ca₅₀) in slow-twitch fibres is about half that in fast-twitch fibres (0.6 and 1.2 μM, respectively, at 22-25 °C; Stephenson & Williams, 1981). Similar correlations with fibre-type and contractile speed have been observed in three twitch fibres from toadfish muscle: slow-twitch and fast-twitch fibres from the trunk musculature, and super-fast fibres from swimbladder muscle. In these fibres, the mean peak amplitudes of Δ[Ca²⁺] in response to an action potential (also measured with furaptra) were 7, 11 and 50 μM, respectively, and the corresponding values of Ca₅₀ were 0.5, 2 and 6 μM, respectively (16 °C; Rome et al. 1996). Second, the half-duration of Δ[Ca²⁺] in slow-twitch fibres is about 1.6 times that in fast-twitch fibres (7.7 and 4.9 ms, respectively, at 16 °C; Table 1) and the rate constant for the final decay of Δ[Ca²⁺] to baseline is about one-third that in fast-twitch fibres (26 and 83 s⁻¹, respectively, at 16 °C; see Results). These differences are consistent with other findings that indicate that the Ca²⁺ removal systems in slow-twitch fibres are less well developed than those in fast-twitch fibres. For example, mouse slow-twitch fibres have little or no parvalbumin (Heizmann et al. 1982; Ecob-Prince & Leberer, 1989) and only about one-third the myoplasmic concentration of SR Ca²⁺ pump molecules as fast-twitch fibres (Leberer et al. 1988).

Comparisons with other reports of Δ[Ca²⁺] in slow-twitch and fast-twitch mammalian fibres

Others have also found that Δ[Ca²⁺] decays more slowly in slow-twitch than fast-twitch fibres; in some studies, a smaller peak amplitude of Δ[Ca²⁺] has also been detected in slow-twitch fibres. Eusebi et al. (1980, 1985) microinjected individual intact fibres of rat muscle with the Ca²⁺ indicator aequorin and activated the fibres with 20-25 ms depolarizations with a two-microelectrode voltage clamp. The mean rate constant for the decay of the aequorin signal, which responds to [Ca²⁺] with a substantial kinetic delay (Blinks et al. 1978), was 24 s⁻¹ in slow-twitch (soleus) fibres and 63 s⁻¹ in fast-twitch (EDL) fibres (25 °C). The amplitude of the Ca²⁺ transient was judged to be smaller in slow-twitch fibres, although it was difficult to make an accurate comparison because of the difficulty in estimating the aequorin concentration in the experiments.

Carroll et al. (1997) also found that Δ[Ca²⁺] decayed more slowly in rat slow-twitch (soleus) fibres than in fast-twitch (flexor digitorum brevis) fibres. The experiments were carried out on enzyme-dissociated single fibres suspended in an agarose gel (sarcomere length, 1.8-2.4 μm) and relied on fura-2 introduced by AM loading. Fibres were activated by action potentials initiated by external shocks, and the fura-2 signal was corrected for a kinetic delay in the reaction between Ca²⁺ and fura-2. In response to a single action potential, the mean rate constant for the final decay of Δ[Ca²⁺] to baseline was ≈23 s⁻¹ for slow-twitch fibres and ≈40 s⁻¹ for fast-twitch fibres (26-28 °C). The estimated peak amplitudes of Δ[Ca²⁺] did not differ significantly (≈0.8 μM in slow-twitch fibres and ≈0.9 μM in fast-twitch fibres). In a related study on mouse fibres using similar techniques, Liu et al. (1997) found that Δ[Ca²⁺] was larger and had faster final decay rate constants than Δ[Ca²⁺] in rat fibres (slow-twitch mouse fibres, 1.3 μM and 45 s⁻¹, respectively; fast-twitch mouse fibres, 2.4 μM and 92 s⁻¹, respectively; 28 °C). These peaks of Δ[Ca²⁺] in rat and mouse fibres are much smaller than the values reported here (Table 1), and the decay rate constants are somewhat smaller. As mentioned in the Methods and the first section of the Discussion, these differences are probably caused by inaccuracies in the estimation of Δ[Ca²⁺] when fura-2 is used as the indicator.

Delbono & Meissner (1996) also measured Δ[Ca²⁺] in slow-twitch (soleus) and fast-twitch (EDL) rat fibres. Cut fibre segments were mounted in a Vaseline-gap voltage-clamp apparatus and furaptra was introduced by diffusion from the cut ends (20-22 °C). Fibres were activated by depolarizations from -90 to +10 mV for variable durations (12.5-200 ms). In response to depolarization for a duration of 12.5 ms, the peak amplitude of Δ[Ca²⁺] was 5-6 μM in both fibre types. These values are smaller than those reported here with furaptra for intact mouse fibres stimulated by an action potential (slow twitch fibres, ≈9 μM; fast-twitch fibres, 19-22 μM; columns 2-5 of Table 1).

Estimation of SR Ca²⁺ release in slow-twitch and fast-twitch fibres

In response to an action potential, the time course of (d/dt)Δ[Ca_T] is very similar in mouse slow-twitch and fast-twitch fibres; in contrast, the peak amplitudes of (d/dt)Δ[Ca_T] and Δ[Ca_T] in slow-twitch fibres are only about one-third of those in fast-twitch fibres (columns 2 and 3 of Table 3; see also columns 4 and 5). Although these conclusions depend on model estimates of myoplasmic Ca²⁺ buffering, which involves some uncertainty, the greatly reduced values of the release parameters in slow-twitch fibres are largely attributable to known differences: (i) the 2-fold smaller concentration of Ca²⁺ regulatory sites in this fibre type; (ii) the absence of parvalbumin; and (iii) from the present study, the 2-fold smaller amplitude of the myoplasmic Ca²⁺ transient. Some residual uncertainty in the conclusions remains due to the assumption in the model that the Ca²⁺-troponin association rate constant is similar in the two fibre types (see Methods). The 3-fold larger Ca²⁺ release rate in fast-twitch fibres is consistent with the higher concentration of RYRs in fast-twitch fibres (2.4-fold larger in guinea-pig muscle; Franzini-Armstrong et al. 1988) and the greater amount of muscle charge movement in fast-twitch fibres (4-fold larger in rat muscle; Hollingworth & Marshall, 1981).

In response to a high-frequency train of action potentials, the peak values of (d/dt)Δ[Ca_T] triggered by action potentials subsequent to the first are markedly smaller than that triggered by the first action potential, and the fractional reductions in release rate are similar in the two fibre types (see Fig. 6 and associated text). Similar reductions in the peak values of (d/dt)Δ[Ca_T] during a train also occur in frog twitch fibres (Maylie et al. 1987; Baylor & Hollingworth, 1988). The similar magnitude of the reductions in all three fibre types is consistent with the idea that a common mechanism is responsible. The likely explanation, first proposed for frog fibres, is that the rise in myoplasmic free [Ca²⁺] that occurs initially in response to membrane depolarization has a strong negative-feedback effect on continued SR Ca²⁺ release (‘Ca²⁺-inactivation of Ca²⁺ release’) (Baylor et al. 1983; Schneider & Simon, 1988; Baylor & Hollingworth, 1988; Simon et al. 1991; Jong et al. 1995). This inhibition, which presumably evolved to prevent [Ca²⁺] from exceeding the concentration required to saturate the Ca²⁺ regulatory sites on troponin, avoids unnecessary delays in fibre relaxation, unnecessary expenditure of energy for the re-sequestration of Ca²⁺ and possible toxic effects that could result from unusually high levels of [Ca²⁺].

A reasonable working hypothesis suggested by these findings is that, within any given SR Ca²⁺ release unit, the release mechanism functions similarly in slow-twitch and fast-twitch mammalian fibres. The idea of an essential similarity in the Ca²⁺ release mechanism in these fibre types is consistent with the structural similarity of the triadic junctions in slow-twitch and fast-twitch fibres (Cullen et al. 1984) and the presence of a common RYR isoform, RYR1 (Otsu et al. 1993; Damiani & Margreth, 1994; Murayama & Ogawa, 1997). Because, in both fibre types, the release of Ca²⁺ from the SR during stimulation by an action potential appears to lead rapidly to a large fractional occupancy of the troponin regulatory sites with Ca²⁺ (described in connection with Fig. 5 and Fig. 6), the differences in the contractile speed of the two fibre types appear to be related to differences in fibre properties and events subsequent to SR Ca²⁺ release and the association of Ca²⁺ with troponin.

Comparisons with other estimates of SR Ca²⁺ release in slow-twitch and fast-twitch fibres

Our conclusions about the peak rates of SR Ca²⁺ release in mammalian fibres and about the essential similarity of the SR Ca²⁺ release mechanism in slow-twitch and fast-twitch fibres differ from those of Delbono & Meissner (1996). These authors estimated SR Ca²⁺ release in rat fibres stimulated by voltage-clamp depolarizations from -90 to +10 mV for 200 ms; the peak release rates (slow-twitch, 10.4 ± 1.6 μM ms⁻¹; fast-twitch, 15.6 ± 1.3 μM ms⁻¹; 20-22 °C) are about an order of magnitude smaller than the values shown in Table 3 with stimulation via an action potential. Delbono & Meissner also reported that the extent of inactivation of SR Ca²⁺ release during sustained depolarization was substantially greater in slow-twitch fibres than fast-twitch fibres. Based on this finding and the detection of a smaller ratio of DHPRs to RYRs in slow twitch than fast-twitch fibres (0.34 ± 0.05 and 0.92 ± 0.11, respectively; estimated from high-affinity radioligand binding assays), these workers proposed that the SR Ca²⁺ release mechanism in slow-twitch fibres depends more heavily on Ca²⁺-induced Ca²⁺ release than in fast-twitch fibres.

Although it is possible that a significant fibre-type difference in the mechanism controlling SR Ca²⁺ release exists in rat muscle but not in mouse muscle, it is also possible that the different conclusions of Delbono & Meissner compared with our own arise because of methodological differences. With regard to the estimation of SR Ca²⁺ release, these differences include the methods of fibre preparation (cut fibres vs. intact fibres), fibre activation (voltage-clamp depolarization vs. action-potential stimulation) and of modelling SR Ca²⁺ release using the measurement of Δ[Ca²⁺] with furaptra (model of Melzer et al. 1987vs. the model described in connection with Table 2). Of these differences, our use of action potential rather than voltage-clamp stimulation may result in a less reliable estimate of the extent of inactivation of SR Ca²⁺ release during maintained stimulation. For example, with a 67 Hz stimulus, reductions in action potential size might occur that are not the same in the two fibre types. However it should be noted that any reduction in the action potential during a 67 Hz stimulus is likely to be less marked in fast-twitch fibres than in slow-twitch fibres, yet the extent of inactivation of SR Ca²⁺ release during the train was, if anything, less marked in slow-twitch fibres than in fast-twitch fibres.

Regarding the use of intact vs. cut fibres, experiments on frog fibres indicate that this difference in fibre preparation may be quite important. For example, in experiments in which a large myoplasmic fura-2 concentration (1-3 mM) was used to perturb SR Ca²⁺ release, results from one set of experiments on frog cut fibres were consistent with an important underlying contribution from Ca²⁺-induced Ca²⁺ release (Jacquemond et al. 1991) whereas results on frog intact fibres (Baylor & Hollingworth, 1988; Hollingworth et al. 1992) and from another set of experiments on frog cut fibres (Jong et al. 1993) were not. Moreover, the properties of Ca²⁺ sparks in frog cut fibres (Tsugorka et al. 1995; Klein et al. 1996) appear to vary with the laboratory in which the measurements are made and to differ substantially from spark properties in intact fibres (Table VII of Hollingworth et al. 2001). A possible explanation for the difference between Ca²⁺ sparks in cut and intact fibres is that Ca²⁺-induced Ca²⁺ release may make a stronger contribution to RYR activation in cut fibres than in intact fibres (Hollingworth et al. 2001; Chandler et al. 2003). Based on these results from amphibian muscle, the conclusion that the SR Ca²⁺ release mechanism in slow-twitch mammalian fibres depends more heavily on Ca²⁺-induced Ca²⁺ release than in fast-twitch fibres may be a peculiarity of the cut fibre preparation. Because the condition of intact fibres is close to that of fibres in the native environment, the results from this preparation are more likely to reflect the true physiological properties of the underlying mechanisms.