Abstract
We present here a new technique with which to visualize nuclei in living muscle fibres in the intact animal, involving injection of labelled DNA into single cells. This approach allowed us to determine the position of all of nuclei within a sarcolemma without labelling satellite cells. In contrast to what has been reported in tissue culture, we found that the nuclei were immobile, even when observed over several days. Nucleic density was uniform along the fibre except for the endplate and some myotendinous junctions, where the density was higher. The perijunctional region had the same number of nuclei as the rest of the fibre. In the extensor digitorum longus (EDL) muscle, the extrajunctional nuclei were elongated and precisely aligned to the long axis of the fibre. In the soleus, the nuclei were rounder and not well aligned. When comparing small and large fibres in the soleus, the number of nuclei varied approximately in proportion to cytoplasmic volume, while in the EDL the number was proportional to surface area. Statistical analysis revealed that the nuclei were not randomly distributed in either the EDL or the soleus. For each fibre, actual distributions were compared with computer simulations in which nuclei were assumed to repel each other, which optimizes the distribution of nuclei with respect to minimizing transport distances. The simulated patterns were regular, with clear row-like structures when the density of nuclei was low. The non-random and often row-like distribution of nuclei observed in muscle fibres may thus reflect regulatory mechanisms whereby nuclei repel each other in order to minimize transport distances.
The largest cells in the vertebrate body are the muscle fibres. In mouse limb muscle fibres, in vivo injection of cytosolic dye has revealed a typical cellular volume of 5 nl (Utvik et al. 1999). In larger animals, volumes can be much greater. Thus a cylinder with a diameter of 50 μm and a length of 0.5 m, dimensions not unrealistic in larger mammals, has a volume of about 1 μl. Most other mammalian cells are more spherical in shape, with diameters in the range 5–20 μm and volumes thus ranging from 10−5 to 10−3 nl. Thus, even in small animals like mice, the muscle fibres have a volume that is almost five orders of magnitude larger than that of small uninucleated cells. Muscle cells, however, possess multiple nuclei and constitute one of the few syncytia in the mammalian body, other examples being osteoclasts and some large macrophages. There is an old concept that states that a certain volume of cytoplasm is required to serve a certain volume of karyoplasm (e.g. Strassburger, 1893). Although modern biologists rather envisage the nucleus as supporting the cytoplasm, the ‘karyoplasmic-ratio hypothesis’ is still relevant, and it is argued that the link between DNA content and cell volume is a fundamental principle in biology (Gregory, 2001). The mechanistic background for such correlations remains obscure. It is possible that each nucleus has only a limited synthetic capacity, or that there are some other rate-limiting steps (e.g. the number of nuclear pores could be limiting the passage of RNA from the nucleus to the cytoplasm; Cavalier-Smith, 1978, 1980).
As a mechanistic substrate for the karyoplasmic ratio hypothesis in muscle, it is believed that each nucleus serves a certain domain. Some proteins are localized to the site of expression (Hall & Ralston, 1989; Ralston & Hall, 1992), most notably, but not exclusively, at the synapse (Merlie & Sanes, 1985; Sanes et al. 1991; Gundersen et al. 1993). Thus, mRNA does not diffuse far from its nucleus of origin. In addition to having a voluminous cytoplasm, muscle cells span vast geometrical distances. The only other cells reaching further are some types of neuron. In axons, however, there are specialized mechanisms for axonal transport. Similar systems have not been described in muscle, and proteins might rely mainly on diffusion to get from where they are synthesized to where they are needed. Consequently, not only the number, but also the spatial distribution of nuclei might be crucial in order to minimize the transport problem. To our knowledge, the distribution of nuclei in muscle fibres has not previously been addressed quantitatively.
Here we describe a new technique in which nuclei are labelled in intact mice by intercellular injection of labelled DNA. This offers three important advantages compared to previous studies: (1) living cells are studied directly in vivo, (2) single cells can be followed over time, and (3) all of the nuclei within a cell are visualized but, importantly, the nuclei in satellite cells are not labelled. We report that in vivo muscle nuclei are stationary and seem to be spatially distributed as if to minimize transport distances. The number of nuclei increases with fibre calibre, but in distinctly different ways in the EDL and soleus muscles.
METHODS
Animal operation procedures
Female NMRI mice, 7–15 weeks old, were anaesthetized with an intraperitoneal injection of 5 μl (g body weight)−1 of Equithesin (Ullevål Sykehus, Norway; 42.5 mg of chloral hydrate and 9.7 mg pentobarbitone per ml). The mice were placed on a heated plate that was designed to keep the body temperature stable throughout the experiment. The leg was pinned out and the EDL or soleus muscle was exposed by pulling the overlaying muscles to one side. The exposed muscle was covered with Ringer-lactate and held in place with a coverslip mounted 2 mm above the muscle. In some muscles, the neuromuscular junction was visualized by applying rhodamine-conjugated α-bungarotoxin (1 μg ml−1; Molecular Probes, Eugene, OR, USA) to the surface of the muscle for 2–3 min. This allows good visualization, but is not sufficient to block neuromuscular transmission (Balice-Gordon & Lichtman, 1990).
Some mice were re-sutured and allowed to recover for 1–4 days, and then re-anaesthetized to allow a second observation of the same fibres. After the experiments, the mice were killed by neck dislocation while still under deep anaesthesia.
These animal experiments were approved by the Norwegian Animal Research Authority and were conducted in accordance with the Norwegian Animal Welfare Act of 20 December 1974 (no. 73, chapter VI, sections 20–22), and the Regulation on Animal Experimentation of 15 January 1996.
In vivo imaging
The heated animal platform was placed on the specimen stage of an upright, fixed-stage fluorescence microscope (Olympus BX50WI, Norwood, MA, USA) and the muscle surface was viewed by in vivo imaging techniques similar to those pioneered by Lichtman and collaborators (Lichtman et al. 1987; Balice-Gordon & Lichtman, 1990). During and after injections, muscles were viewed through water-immersion objectives with long working distances. An adjustable 12 V, 100 W halogen lamp was used for epi-illumination, and precautions were taken to minimize the time and intensity of light exposure (the lamp was operated at 3–5 V) in order to avoid phototoxicity. The muscle was viewed with a SIT camera (Hamamatsu C2400-08) coupled to an image processor (Hamamatsu ARGUS-20) and a Macintosh computer running Adobe Photoshop and NIH Image software. All of the pictures shown are from living muscles in vivo.
Intracellular injections
The labelled DNA injections were performed essentially as described previously (Utvik et al. 1999). Borosilicate 1.0/1.5 mm glass micropipettes with a filament (World Precision Instruments, Sarasota, FL, USA) were pulled on a laser-heated puller (P2000, Sutter Instruments, Novato, CA, USA) and bevelled on an audiocassette tape moving at playing speed, to a resistance of about 100 MΩ. The pipette was filled by capillary forces by dipping its base into a solution containing phosphorothioated 5′-Oregon Green-labelled oligonucleotides (5.0 × 10−4 M; Biognostik, Göttingen, Germany) mixed with 2 g l−1 of Cascade Blue dextran (Molecular Probes). The DNA was dissolved in a buffer containing 10 mm NaCl, 10 mm Tris (pH 7.5), 0.1 mm EDTA and 100 mm potassium gluconate. The filled pipettes were placed in a micromanipulator (Sutter Instruments) and used to penetrate the cells. To verify the penetration, the membrane potential was recorded on a Duo 773 electrometer (World Precision Instruments). The solution was ejected by pulses of pressurized nitrogen (100–150 hPa) lasting 20 ms and delivered at 500 ms intervals by a PV820 pneumatic pico-pump (World Precision Instruments). A constant holding pressure of about 1 hPa was also applied to prevent the solution from moving back into the pipette between pulses.
The injected oligonucleotides were rapidly taken up by the myonuclei, probably by active transport (Hartig et al. 1998). The labelled DNA was never seen to leak out of the fibres or to label more than one fibre, thus only the nuclei confined within one plasma membrane were labelled. Importantly, injected DNA did not label nuclei in satellite cells. Thus, both ultrastructural (Schmalbruch, 1978) and electrophysiological evidence (Bader et al. 1988) indicates that there are no gap junctions between the satellite cells and their muscle fibres.
Fibre typing
After the in vivo analysis, the muscles were frozen and sectioned for immunohistochemistry. The injected fibres were identified by the injected fluorescent dyes, and the fibre type was determined with the following monoclonal antibodies: type 2a, SC-71; type 1, BS-D5; and type 2b, BF-F3 (gift from Stefano Schiaffino; Schiaffino et al. 1989). In the EDL the surface fibres are generally type 2b, and all of the injected fibres were identified as type 2b fibres. In the soleus, nine fibres were identified as type 2a, while for five fibres the fluorescent dye was not detectable. All of the injected fibres in this muscle were located on the dorsolateral surface of the muscle, and in this region the majority of the fibres are type 2a and the rest are type 1.
Reconstruction of fibre segments
Most of the data were derived after allowing the labelled oligonucleotides to diffuse over a 400–600 μm stretch of each fibre. A diffusion time of 2 h was typically required, during which the animal was kept anaesthetized.
Some fibres were studied after longer time periods in order to reconstruct longer stretches (Fig. 1) or to study single cells over time (Fig. 3). In the latter case, some fibres were re-injected to ensure that the original injection would also label new nuclei. No new nuclei were ever revealed after re-injection (data not shown).
Figure 1. Density of nuclei along the length of the fibre, from the endplate (0 μm) to the distal tendon.
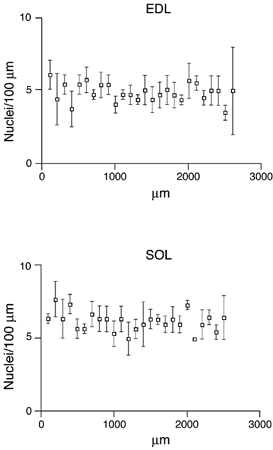
Each point represents the mean ± s.e.m. of three fibres taken from the EDL and soleus (SOL).
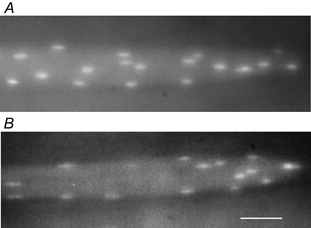
Figure 3. The position of nuclei observed with an interval of 24 h to 4 days.
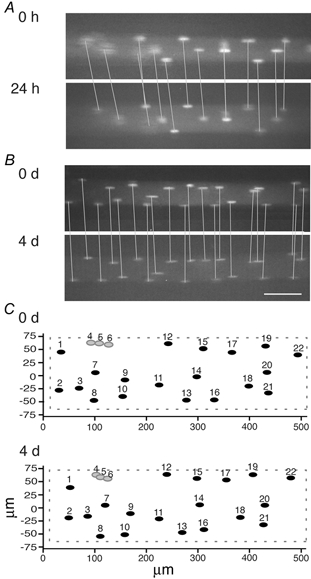
A and B are micrographs of two different fibres observed with an interval of 24 h and 4 days (4 d), respectively. Corresponding nuclei are connected by lines. Scale bar = 50 μm. C, surface foldout of a third fibre; corresponding nuclei are given the same number designation. Note the constancy of nuclear positions. Grey symbols indicate synaptic nuclei.
After diffusion of the oligonucleotides, pictures of fibre segments were taken at focal planes spaced 5 μm apart. The pictures were exported to the program NIH Image in which the x and y coordinates were determined. The plane in which a given nucleus was in focus determined the z coordinate for that nucleus.
Once the coordinates for each nucleus were obtained, the numbers were exported to the program MacSpin (Abacus Concepts, Berkeley, CA, USA). This program depicts data in a three-dimensional coordinate system and allows them to be viewed from different angles. MacSpin was used to proofread the data and to check whether the nuclear positions were reasonably well confined to a tubular surface. After they had been proof read, the coordinates were transposed to a new coordinate system. This transposition was done in such a way that the fibre was virtually aligned with two of the axes. This simplified the further geometrical and statistical analysis.
Statistical and geometrical analysis
Since nuclei are usually distributed close to the surface of the fibre, the statistical evaluation of the distribution was based on a projection of the nuclei onto an idealized surface. When selecting an idealized form, flexibility has to be weighted against robustness and the danger of over-fitting. We selected a form that in a cross-sectional view is elliptical. Along the fibre, the axes of the ellipse may vary linearly and proportionally. Although fibres may have more irregular forms, with the exception of a few, the distribution of nuclei around this form appeared as random variations rather than systematic deviations. The optimal fit was defined as that with the smallest squared distance from the nuclei to the idealized surface measured along radians from the fibre centre. The ideal surface was subsequently found in the following way: if the centre and the tilting of the fibre are known, non-linear regression may be used to find the parameters defining the ellipse and its cross-sectional variation. We thus searched over a grid of possible centres and different degrees of tilting, carried out the regression for each centring/tilting-combination, and used the overall result corresponding to the smallest squared distance from the nucleus to the surface.
To reveal whether or not the actual distributions of nuclei were consistent with random distributions, we used Monte Carlo tests. As a test statistic, we used the average of the distance from each nucleus to its nearest neighbour, measured either along the surface or directly (see Results). The test then compared the average of the nearest neighbour distances for the fibre under consideration with the average obtained for a large number of similarly sized artificial fibres in which the same number of nuclei was distributed randomly. If the actual positioning of the nuclei is more regular than random, nearest neighbour distances will be longer; if nuclei are clustered, the distances will be shorter than in the random case. Thus, the test will detect and identify both kinds of deviation from random positioning.
In general, it is difficult to determine the optimal positioning of nuclei to minimize transport distances. In a certain mathematical sense, positioning nuclei at the corners of equilateral triangles (so that a nucleus and its six neighbours form a hexagon) is optimal. In tubes, the optimal positioning will depend upon the number of nuclei per area (or volume) unit. With low densities, positioning the nuclei at equal distances along the fibre, with neighbours shifted 180 deg around the fibre will be optimal (still in a certain mathematical sense). On a foldout of the fibre, this will appear as two rows of nuclei. With high densities of nuclei, distributions approximating the above-mentioned hexagons will be optimal, while at intermediate densities the optimal distributions may be complex. If one considers direct distances (through the cytoplasm) rather than surface distances, the optimal positioning will be more difficult to determine since the solutions will depend on the cross-sectional form
To study near-optimal distributions for the idealized fibres that were fitted to our real fibres, we used a stochastic relaxation type of optimization procedure, where nuclei were assumed to repel each other (Geman & Geman, 1984). When optimizing with respect to direct distances, we assumed a cylindrical form for the fibre.
To describe the eccentricity of the ellipsoid nuclei, an index e was calculated, which satisfied the equation: b2 = a2 (1 –e2), where a and b are the semi-major and semi-minor axes. For a circle, e = 0 and for an ellipsis, 0 < e < 1.
Non-linear least-squares regression was used when modelling the relationship between nucleic density and cross-sectional area.
RESULTS
Reconstruction of nuclear distributions in single fibres
We investigated muscle fibres from 33 different animals. Data are derived from 47 fibres from the EDL and 17 fibres from the soleus. In three fibres from each of the two muscles, the position of all of the nuclei in the fibre all the way from the endplate to the tendon was photographed and then determined by three-dimensional reconstruction. In these fibres, there was no systematic variability along the length of the fibre (Fig. 1) except for at the specialized neuromuscular and myotendinous junctions described below. Similar findings have been obtained with different methods by previous investigators (Merlie & Sanes, 1985; Tseng et al. 1994). The rest of our data are derived from 34 segments on the lateral muscle surface either distal (EDL) or proximal (soleus) to the endplate. These choices were dictated by anatomical accessibility. In the EDL the fibres had a nuclear density of 30–57 nuclei mm−1, while in the soleus fibres nuclear density ranged from 35 to 77 nuclei mm−1. Given a fibre length of 4–6 mm, this gives a total of one- to a few hundred nuclei per cell.
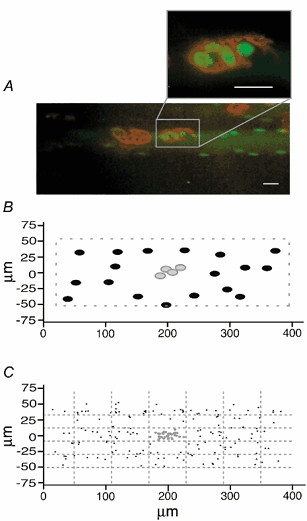
In order to simplify the visualization of nuclear positions, we have taken advantage of the fact that the nuclei of normal muscle fibres are confined to a folded two-dimensional plane, the surface. First, three-dimensional coordinates for each nuclei were determined from photomicrographs taken at different focal planes (Fig. 2A and B). Second, an elliptical tube was fitted to the spatial three-dimensional coordinates of each nucleus in each fibre segment (Fig. 2B). Third, each nucleus was assigned a two-dimensional coordinate for the closest point on the surface. Fourth, the surface was ‘cut open’ so as to yield a two-dimensional foldout representation of the nuclear distribution (Fig. 2C).
Figure 2. Three- and two-dimensional reconstruction of nucleic positions in a fibre segment.
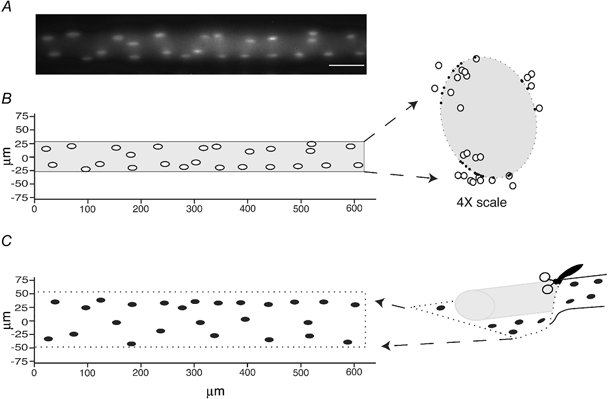
A, averaged micrograph of 17 focal planes of the segment. Scale bar = 50 μm. B, reconstruction seen from the same angle as in A, and from the end (× 4 higher magnification). An oval cylindrical surface (dotted) was fitted to the data and the positions of the nuclei were projected onto this virtual surface. C, for further analysis, the surface was ‘cut open’ and folded out so as to give the positions of the nuclei in the two-dimensional cell. The borders of the foldout, roughly corresponding to the sarcolemma, are indicated by the dotted line.
The number and position of nuclei are constant over time
Previous data from tissue culture have suggested that nuclei in myotubes are quite mobile (Englander & Rubin, 1987). We investigated positional stability in muscle fibres by observing the same fibre at intervals of 1–4 days. In eight EDL fibres from eight different animals we saw no significant change in nuclear position (Fig. 3). Some fibres had rotated slightly between observations, but surface foldouts revealed that the relative positions of the nuclei were the same (Fig. 3C). While the visual inspections suggested that the nuclei maintained roughly their relative positions, relative distances were also measured numerically in three fibres with a 4 day interval. On average, there was a 5.9 μm difference between corresponding internuclear distances measured at the two time points. Only six distances out of 43 were altered by more than 10 μm, which roughly corresponds to the diameter of a nucleus. All types of imperfections in the positioning connected to data acquisition and, perhaps more importantly, to differences in stretch or other mechanical distortion of the fibre would contribute to differences when the same fibre is measured on different days. In our opinion, these uncertainties might have led to similar deviations without any nuclear movement. However, although the data suggest that nuclei are fixed at their exact positions, we cannot exclude the possibility that a certain wobbling takes place within a confined territory for each nucleus.
One of the eight fibres studied over time displayed one extra nucleus at the second examination, but apart from this, the number of nuclei was the same for the first and second observation in all the fibres. The near absence of new nuclei is consistent with the view of muscle as a permanent tissue with a turnover of less than 1–2 % per week (Schmalbruch & Lewis, 2000).
The shape and orientation of nuclei varies between fibre types
Figure 4A shows micrographs of 30 randomly selected nuclei from EDL and soleus fibres that could be photographed en face. The EDL nuclei had a long axis of 18 ± 2 μm and a short axis of 5 ± 1 μm (mean ± S.D.). The corresponding numbers for soleus fibres were 14 ± 2 μm and 8 ± 1 μm, respectively. Thus, EDL nuclei were rather elongated, with their eccentricity index (see Methods) averaging 0.96 (Fig. 4B). The EDL nuclei were also strictly aligned parallel to the long axis of the fibre, with an average deviation of only 4 deg between the long axis of the nuclei and that of the fibre (Fig. 4C). In contrast, soleus nuclei varied more in shape, and in general were less oval, with an eccentricity index of 0.83 (Fig. 4B). They were also less well aligned, with some nuclei even deviating more than 45 deg from the long axis of the fibre (Fig. 4C).
Figure 4. The shape and orientation of single nuclei in soleus and EDL.
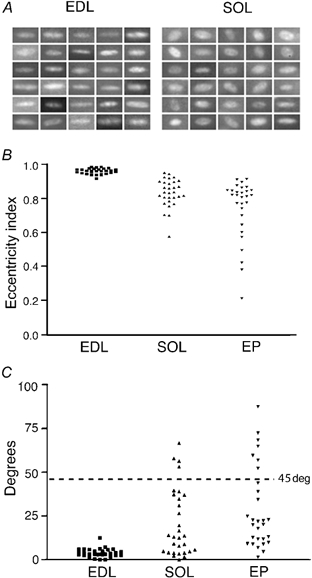
A, micrographs of 30 nuclei from both the EDL and soleus (each square is 20 μm wide). B, eccentricity indices (see Methods) of the same nuclei as depicted in A, and of synaptic (end plate, EP) nuclei in the EDL. C, orientation of the long axis of the non-synaptic nuclei relative to the long axis of the fibre for the EDL and soleus, and for EP nuclei from an EDL fibre.
The endplate and the myotendinous junction are specialized regions
As observed already by Ranvier, there is a cluster of nuclei with different morphology at the endplate. We confirmed these observations with our techniques in vivo (Fig. 5A and B). Thus, in 19 EDL fibres investigated there were on average four nuclei that were in close proximity to α-bungarotoxin staining. The centre-to-centre distance between neighbouring synaptic nuclei was 11–14 μm, while for extrasynaptic nuclei the distance was 30–32 μm (95 % confidence intervals). Thus, synaptic nuclei are strongly clustered compared to extrasynaptic nuclei. In the EDL, the synaptic nuclei were also more rounded than the extrasynaptic nuclei, and had an average eccentricity index of 0.74 (Fig. 4B). In the soleus the extrasynaptic nuclei were as round as the synaptic nuclei, although synaptic nuclei were quite varied in orientation (Fig. 4C); 75 % had an angle of less than 45 deg relative to the fibre axis, so there was a tendency towards alignment with the long axis of the fibre, even for endplate nuclei.
Figure 5. Endplate nuclei and nuclei in the perisynaptic region.
Micrograph (A, scale bar 20 μm) and foldout (B) of a fibre segment in the endplate region. In A, acetylcholine receptors labelled with α-bungarotoxin (red) and nuclei labelled with fluorescein-conjugated DNA (green) is shown. C, the nuclear position relative to the endplate on foldouts from nine fibres superimposed. No perisynaptic specialization was apparent.
The perijunctional membrane is considered to be specialized, and we speculated that it might have fewer nuclei since the synaptic nuclei are supposed to be ‘clustered’ from the region adjacent to that of nerve contact. Positions on the membrane foldout are shown in Fig. 5B for the same fibre as shown in Fig. 5A. Although it looked like there might be fewer nuclei around the endplate in some fibres, this was not supported by statistical evidence. Surface foldouts for nine fibres were aligned according to endplate position (200, 0), and then the position of all the nuclei from the foldouts were plotted (Fig. 5C). If anything, there were more nuclei in areas close to the endplate, but the differences were not statistically significant.
Another specialized part of the muscle fibre is the myotendinous region. Eleven out of 19 myotendinous junctions investigated in the EDL showed no significant specialization with regard to nuclear distribution or density. The five remaining fibres, one of which is shown in Fig. 6B, showed an increase in nuclear density of 80–100 %. This would be consistent with some fibres undergoing in repair or growth. The myotendinous junction is particularly vulnerable to damage during stretch or eccentric work (Tidball, 1991; Frenette & Cote, 2000).
Figure 6. Nuclei at the myotendinous region.
Micrographs of examples of fibre segments at the distal end of the fibre, showing the myotendinous junction without specialization (A) and with an increased density of nuclei (B) as observed in five out of 19 fibres. Scale bar = 50 μm.
How does nuclear number vary with fibre size?
The notion that large cells have multiple nuclei because there is a limit to how much cytoplasm each nucleus can serve has led to the concept of nuclear domains, most often given as the total cytoplasmic volume divided by the number of nuclei. If spherical mononucleated cells have diameters in the range 5–25 μm, their corresponding nuclear domains vary by a factor of 125. This is illustrated with crosses and a connecting line in Fig. 7A, where volume is plotted as a function of cell cross-sectional area. When nuclear domain data from EDL fibres (open circles) were plotted the same way, it became apparent that the greater number of nuclei that comes with larger fibres contributed only slightly to reducing nuclear domain volumes in these multinucleated cells. In contrast, soleus fibres had a rather constant nuclear domain volume (filled circles), suggesting that the number of nuclei is proportional to fibre volume.
Figure 7. Cell size and nuclear domains.
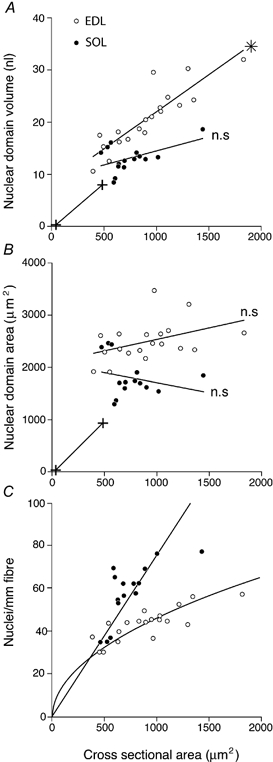
A, average nuclear cytoplasmic domain volumes; B, average cell surface domain areas; and C, nuclear density of EDL and soleus fibres with different cross-sectional areas. In C, the theoretical nuclear density with a constant nuclear cytoplasmic domain volume is denoted by a straight line and that with a constant nuclear sarcolemmal domain area by a curved line. The curves were constructed by least-squares linear and non-linear regression, assuming an unchanged form of the fibre. The linear regression coefficients were statistically different (*) or not different (n.s.) from 0.
It is a peculiarity that muscle nuclei are located at the surface, and it is possible that each nucleus is ‘serving’ a cell surface area rather than a volume. Figure 7B shows how nuclear surface domain varies with fibre size. Domain sizes for EDL fibres were reasonably constant (open circles), indicating that in this muscle the number of nuclei could be proportional to surface area.
The straight line through the origin in Fig. 7C represents a model where the number of nuclei keeps the nuclear domain constant with respect to cytoplasmic volume. The observations for the soleus fibres (filled circles) fitted this model reasonably well. If we fit a linear model to the EDL data, the intercept deviates significantly from zero; thus, the cytoplasmic nuclear domain would decrease with increasing fibre size. If, however, we use a model where the number of nuclei per millimetre of fibre length was required to keep the nuclear domain constant with respect to surface area (Fig. 7C, curved line through the origin), the observations for the EDL fit well. Thus, we suggest that in the soleus, the number of nuclei could be regulated so as to keep a close-to-constant nuclear cytoplasmic volume, while in the EDL it could be regulated to keep the surface area per nucleus constant.
Nuclei are distributed in an orderly manner
The distribution of nuclei is probably important to minimize the transport problem in these large cells, and we hypothesized that mechanisms might operate to optimize nuclear placement within the fibre. From the point of view of minimizing transport distances from nuclei to various locations in the cell, paradoxically, the ‘best’ distribution is the one with the greatest average distance between nuclei. The ‘worst’ would be to cluster all of the nuclei in one position, leading to very short distances between the nuclei, but with vast transport distances to reach the other end of the cell.
If nuclear distribution was not somehow regulated, the distribution should be random. We found that in all EDL fibres and in 12 out of 14 soleus fibres investigated, the positions of nuclei were significantly different from those that would be expected if they were positioned randomly on the surface (P < 0.05). In all of the fibres, the average distance between the nuclei and their nearest neighbour was longer than obtained by a random distribution, indicating that the nuclei are more evenly distributed than random (Table 1). An example fibre is shown in Fig. 8. The fibre depicted in Fig. 8A is shown as a surface foldout in Fig. 8B and can be compared to a computer simulation where the same number of nuclei was positioned randomly on the same surface (Fig. 8C). Figure 8D shows a computer simulation where the nuclei were assumed to repel each other (see Methods), resulting in a regular pattern that should be near optimal in avoiding long transport distances. We proceeded with a third simulation, where nuclei were distributed on the surface, but the optimization was performed with respect to transport distances directly through the cytosol (Fig. 8E). Such simulations generally led to a less ordered impression when viewed on two-dimensional foldouts; moreover, nuclei often appeared to be organized in apparent rows. A final simulation is shown in Fig. 8F, where normally distributed noise has been added to the pattern shown in Fig. 8E. Note that the row-like structure is still visible. The non-random and often row-like structure of nuclei in real muscle fibres may be the result if mechanisms operate as if to repel nuclei from each other, such as in our simulations.
Table 1.
Distances to the nearest neighbouring nuclei as observed and with simulated random or optimal positioning
| Direct | Along surface | |
|---|---|---|
| EDL | ||
| Observed (μm) | 31.0 ± 2.5 | 35 ± 2.6 |
| Random (μm) | 23.6 ± 1.8 | 25.5 ± 2.7 |
| Optimal (μm) | 41.0 ± 0.9 | 50.0 ± 1.0 |
| Improvement random → optimal (%) | 43 ± 7 | 43 ± 12 |
| Soleus | ||
| Observed (μm) | 25.1 ± 3.3 | 27.8 ± 5.2 |
| Random (μm) | 20.0 ± 2.8 | 22.2 ± 2.5 |
| Optimal (μm) | 34.4 ± 0.8 | 41.2 ± 1.3 |
| Improvement random → optimal (%) | 35 ± 18 | 31 ± 24 |
The average distance to the nearest neighbouring nuclei was calculated based on observed and simulated posistioning of nuclei. The data are given as mean (± s.e.m.) nearest for 15–17 fibres. The improvement factor was calculated such that if nuclei had an average distance equal to that obtained by random simulation this would yield 0% ‘improvement’ for the fibre, while 100% would be the distance obtained by the simulation of optimal distribution. The observed distances were statistically different (P < 0.05) from the distances obtained by positioning the nuclei randomly.
Figure 8. Distribution patterns of nuclei in one fibre segment as observed and as obtained by positioning the same nuclei by computer simulations.
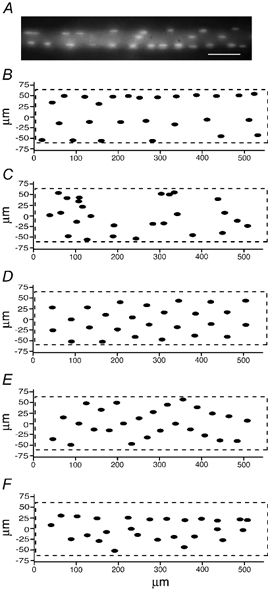
A, averaged micrograph of 17 focal planes of the segment. Scale bar = 50 μm. B, observed nuclear positions on the surface foldout. C, a computer simulation where the same number of nuclei were positioned randomly on the same surface. D, a computer simulation where the nuclei were assumed to repel each other in order to form patterns that should be near optimal in avoiding long transport distances along the surface of the fibre. E, a computer simulation where nuclei were assumed to repel each other and distances were measured directly through the cytosol. F, same fibre as in E but with added normally distributed noise (s.d. equal to one-third of the average distances in E).
Considering all of the fibre segments we reconstructed, the observed distance from each nucleus to its nearest neighbour was 3–10 μm longer than obtained by random distribution (Table 1). In fact, the whole distribution of distances was shifted towards the theoretical optimal longest distance obtained by the simulations (Fig. 9). We calculated an ‘improvement’ factor, where an average nearest neighbour distance equal to that obtained by the random simulation would yield a 0 % improvement for the fibre, while a distance equal to that obtained by the simulation of optimal distribution would yield 100 % improvement. Measured this way, EDL fibres exhibited a 43 % improvement with respect to both direct and along the surface distances. The factors of 31 and 35 % found for the soleus were lower, and the analysis therefore confirmed the impression that the nuclei of EDL fibres have a more even, and thus ‘better’ distribution than in the soleus. Interestingly, in the soleus, the observed improvement was better with respect to optimal direct distances than with respect to optimizing along the surface distances for 11 of the 14 fibres investigated (P = 0.05, Wilcoxon signed-rank test). This could hint that whatever mechanism is operating, it is optimizing direct distances rather than along the surface distances in this muscle.
Figure 9. Distribution of nearest neighbour distances for nuclei as observed or by random positioning.
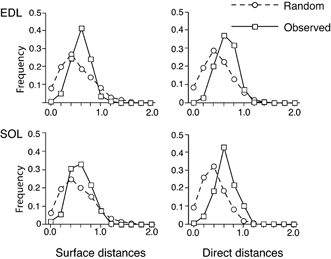
Data are the mean of 19 EDL fibres and 14 soleus fibres. The distances are given relative to the optimal distance given by the computer simulations (direct and along the surface) calculated for each fibre. The optimal (maximal) distance was set to 1.
We also investigated row formation in a similar way to that used to investigate spatial distribution, but this time analysing the distribution of all of the nuclei in the fibre around the circumference (Fig. 10). As can be seen from the examples in Fig. 2B and Fig. 10, nuclei often seemed to be clustered in selected sectors of the ‘tube’ when observed from the end of the fibre segment. Out of 30 fibres, all but three cases had an average distance to the nearest neighbour shorter than that obtained by simulated random positioning. In 12 cases, the deviation was significant (P < 0.05), indicating a clustering in certain sectors. Observed from the side of the fibre, these clusters would represent rows.
Figure 10. Nuclear row formation.
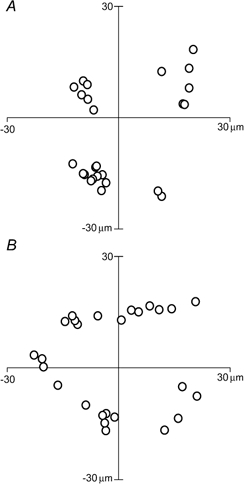
The distribution of the nuclei in two fibre segments seen from the end. A, the best example of nuclear preference for selected sectors of the circumference (P = 0.0006, Monte Carlo simulation). B, in this fibre the nuclei had a more random distribution around the circumference (not significant, Monte Carlo simulation).
DISCUSSION
Our data indicate that the number and position of nuclei are constant over time. This is different from previous observations of fibres in culture, where 85 % of the nuclei in myotubes were shown to move at a rate greater than 3–4 μm h−1. We show that the spatial distribution of the fixed nuclei is not random, but appears to be with respect to minimizing transport distances. The number of nuclei seems to vary in relation to fibre size, but is distinctly differently in the soleus and the EDL.
Most studies hitherto have been performed on sections of fixed or frozen material. Differences in freezing and stretching procedures can introduce a variability in cell volume assessments of more than 50 %, and deviations vary according to fibre position and type within the same specimen (Roy et al. 1996). Moreover, without resorting to electron microscopy it has been difficult to distinguish between myonuclei and satellite cells. In normal adult rodents, the nuclei of satellite cells can comprise up to 10 % of the nuclei within the fibre basal membrane (Schmalbruch & Hellhammer, 1977; Snow, 1977). During growth, and under normal, experimental and pathological conditions where the muscle is undergoing changes the numbers can be considerably higher, and the number varies between muscles and between different parts of the fibre (for review see Hawke & Garry, 2001). Such problems were circumvented in this study because we observed living fibres in a normal stretched position using a staining procedure to label the nuclei confined by one sarcolemma.
Nuclear patterning
Landing et al. (1974) speculated that the nuclei fitted in a hexagonal pattern projected on the membrane, but to our knowledge the positional distribution of nuclei within the muscle fibre syncytium has not been analysed quantitatively before. We show that the distribution is not random, but is rather approximated by patterns that optimize cytosolic transport distances. In order to simulate such distributions, we used an algorithm where nuclei repel each other. While the actual mechanism might be more complex, relevant ‘repellent’ phenomena have been described. Thus, in microfabricated chambers under chemical conditions favourable for microtubule formation, microtubule asters will position a microtubule-organizing centre (MTOC) in the centre of the chamber. Two MTOCs will position themselves apart from each other and the walls (Holy et al. 1997). This happens in the absence of molecular motors, just by the growing microtubules pushing against the walls. In muscle cells, nuclei seem to be surrounded by a network of microtubules (Ralston et al. 1999, 2001). Some of the mechanisms underlying nuclear positioning in fungi are relatively well understood, but much less is known about animals (Morris, 2003). In both animals and fungi, however, nuclear movement and positioning seem be related to dynein and other proteins on the plus end of microtubules interacting with the cytoskeleton at the cell cortex to generate force on nuclear MTOCs and the nuclear envelope (Holy et al. 1997).
Interestingly, in muscle the only nuclei that are clustered together, the synaptic nuclei, have high concentrations of syne-1 located to their nuclear envelopes. Syne-1 levels are much lower in extrasynaptic nuclei, but it is expressed at high levels in myotubes in culture and in central nuclei during regeneration (Apel et al. 2000). Syne-1 is related to klarsict, which is a protein thought to have a direct mechanical role in nucleic migration in the Drosophila eye (Mosley-Bishop et al. 1999).
The ordered pattern is a distinct feature of healthy muscle fibres, although more so in the EDL than in the soleus. Distinct differences in the organization of microtubules between the EDL and soleus have been observed (Ralston et al. 2001). Denervation alters microtubular organization (Ralston et al. 1999), and after denervation nuclei tend to cluster, eventually leaving significant territories of cytoplasm devoid of nuclei (Viguie et al. 1997; Ralston et al. 1999).
Interestingly, pericentrin, which corresponds to microtubule nucleation sites, is located at the pointed end of the nuclei in the EDL, but not in the soleus (Ralston et al. 2001). This could be related to our finding that nuclei in the EDL are more precisely aligned to the long axis of the fibre than in the soleus.
The observation that nuclei appear in rows seems to be an emergent property of the simulations with nuclei repelling each other, particularly in fibres with low nuclear density. ‘Rows’ have often been assumed to be the result of myoblast fusion during muscle growth. Our data suggest that if forces are operating so as to cause nuclei to repel each other, rows are likely to form as a consequence, irrespective of muscle development.
Nuclear number and domains
The nuclear domain concept has been addressed in numerous muscle fibre studies spanning more than a century. Qualitatively, most of the modern literature concludes that when fibres get larger as a result of growth or hypertrophy, the number of nuclei increases (Enesco & Puddy, 1964; Moss, 1968; Cheek et al. 1971; Seiden, 1976; Cabric & James, 1983; Cabric et al. 1987; Giddings & Gonyea, 1992; Winchester & Gonyea, 1992; Allen et al. 1995; McCall et al. 1998; Kadi et al. 1999; Roy et al. 1999). Conversely, during atrophy the number decreases (Darr & Schultz, 1989; Giddings & Gonyea, 1992; Allen et al. 1995, 1996, 1997; Hikida et al. 1997; Viguie et al. 1997; Ohira et al. 1999). It is thought that when fibre size increases, nuclei from satellite cells are inserted, while during atrophy nuclei are removed by apoptosis (Allen et al. 1999). The mechanisms linking cell size and nuclear number remain unknown.
While there is reasonable agreement at the qualitative level, reports of the quantitative link between fibre size and nucleus number are more variable. Most studies on atrophy suggest that fibre volume is reduced more than the number of nuclei (Darr & Schultz, 1989; Giddings & Gonyea, 1992; Allen et al. 1995, 1996, 1997; Hikida et al. 1997; Viguie et al. 1997; Ohira et al. 1999). Similarly, during hypertrophy, some studies suggest that the increase in the number of nuclei is less than sufficient to keep constant volume domains (Cheek et al. 1971; Giddings & Gonyea, 1992; Winchester & Gonyea, 1992; Kadi et al. 1999), while others suggest that the number of nuclei increases in proportion to volume (Enesco & Puddy, 1964; Moss, 1968; Seiden, 1976; McCall et al. 1998; Roy et al. 1999). Only a few studies suggest that the number of nuclei increases more than the volume (Cabric & James, 1983; Cabric et al. 1987; Allen et al. 1995).
Some of the controversy regarding the relationship between fibre size and nucleus number could be related to methodological imperfections, but also to the fact that most of the studies focus on muscle undergoing changes. During the dynamic phase of adaptation, loss or gain in cytoplasm might be disproportionate to the rate of loss or gain of nuclei. In the present study we have focused on the correlation between size and nucleus number under stable conditions. We find that for the normal size distribution in freely moving mice, oxidative soleus fibres display nucleus numbers that seem to vary in proportion to volume. In glycolytic EDL fibres this seems not to be the case, and the number of nuclei is more closely related to surface area. In support of these conclusions, it has been reported that in fibres from oxidative muscles the number of nuclei is more dependent on fibre size than in fibres from fast muscles (Tseng et al. 1994; Dupont-Versteegden et al. 2000). This might be related to the fact that the EDL is a much more stable structure than the soleus, with an average protein half-life of more than 14 days, about twice that of the soleus (Goldberg, 1967; Kelly et al. 1984). We speculate that in at least some muscles the interior is rather stable, containing proteins with long half-lives, and that the surface membrane and cytoskeleton might be the most dynamic part. This might also explain one of the more enigmatic properties of muscle, namely the finding that all nuclei are located at the surface, a rather suboptimal positioning with respect to minimizing transport distances to the interior. Central nuclei are found only during growth or related to pathology and repair where the fibre is remodelled.
In conclusion, we suggest that both the spatial distribution and density of nucleic are regulated in muscle. The number of nuclei seems to be approximately proportional either to cytoplasmic volume or to the cell surface area. It seems unlikely that the latter is a mere imperfect or insufficient adaptation to volume, since few fibres had nucleic densities corresponding to values between those predicted by each model.
REFERENCES
- Allen DL, Linderman JK, Roy RR, Bigbee AJ, Grindeland RE, Mukku V, Edgerton VR. Apoptosis: a mechanism contributing to remodeling of skeletal muscle in response to hindlimb unweighting. Am J Physiol. 1997;273:C579–587. doi: 10.1152/ajpcell.1997.273.2.C579. [DOI] [PubMed] [Google Scholar]
- Allen DL, Monke SR, Talmadge RJ, Roy RR, Edgerton VR. Plasticity of myonuclear number in hypertrophied and atrophied mammalian skeletal muscle fibers. J Appl Physiol. 1995;78:1969–1976. doi: 10.1152/jappl.1995.78.5.1969. [DOI] [PubMed] [Google Scholar]
- Allen DL, Roy RR, Edgerton VR. Myonuclear domains in muscle adaptation and disease. Muscle Nerve. 1999;22:1350–1360. doi: 10.1002/(sici)1097-4598(199910)22:10<1350::aid-mus3>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Allen DL, Yasui W, Tanaka T, Ohira Y, Nagaoka S, Sekiguchi C, Hinds WE, Roy RR, Edgerton VR. Myonuclear number and myosin heavy chain expression in rat soleus single muscle fibers after spaceflight. J Appl Physiol. 1996;81:145–151. doi: 10.1152/jappl.1996.81.1.145. [DOI] [PubMed] [Google Scholar]
- Apel ED, Lewis RM, Grady RM, Sanes JR. Syne-1, a dystrophin- and klarsicht-related protein associated with synaptic nuclei at the neuromuscular junction. J Biol Chem. 2000;275:31986–31995. doi: 10.1074/jbc.M004775200. [DOI] [PubMed] [Google Scholar]
- Bader CR, Bertrand D, Cooper E, Mauro A. Membrane currents of rat satellite cells attached to intact skeletal muscle fibers. Neuron. 1988;1:237–240. doi: 10.1016/0896-6273(88)90144-4. [DOI] [PubMed] [Google Scholar]
- Balice-Gordon RJ, Lichtman JW. In vivo visualization of the growth of pre- and postsynaptic elements of neuromuscular junctions in the mouse. J Neurosci. 1990;10:894–908. doi: 10.1523/JNEUROSCI.10-03-00894.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabric M, Appell HJ, Resic A. Effects of electrical stimulation of different frequencies on the myonuclei and fiber size in human muscle. Int J Sports Med. 1987;8:323–326. doi: 10.1055/s-2008-1025677. [DOI] [PubMed] [Google Scholar]
- Cabric M, James NT. Morphometric analyses on the muscles of exercise trained and untrained dogs. Am J Anat. 1983;166:359–368. doi: 10.1002/aja.1001660309. [DOI] [PubMed] [Google Scholar]
- Cavalier-Smith T. Nuclear volume control by nucleoskeletal DNA, selection for cell volume and cell growth rate, and the solution of the DNA C-value paradox. J Cell Sci. 1978;34:247–278. doi: 10.1242/jcs.34.1.247. [DOI] [PubMed] [Google Scholar]
- Cavalier-Smith T. How selfish is DNA. Nature. 1980;285:617–618. doi: 10.1038/285617a0. [DOI] [PubMed] [Google Scholar]
- Cheek DB, Holt AB, Hill DE, Talbert JL. Skeletal muscle cell mass and growth: the concept of the deoxyribonucleic acid unit. Pediatr Res. 1971;5:312–328. [Google Scholar]
- Darr KC, Schultz E. Hindlimb suspension suppresses muscle growth and satellite cell proliferation. J Appl Physiol. 1989;67:1827–1834. doi: 10.1152/jappl.1989.67.5.1827. [DOI] [PubMed] [Google Scholar]
- Dupont-Versteegden EE, Murphy RJ, Houle JD, Gurley CM, Peterson CA. Mechanisms leading to restoration of muscle size with exercise and transplantation after spinal cord injury. Am J Physiol. 2000;279:C1677–1684. doi: 10.1152/ajpcell.2000.279.6.C1677. [DOI] [PubMed] [Google Scholar]
- Enesco M, Puddy D. Increase in the number of nuclei and weight in skeletal muscle of rats of various ages. Am J Anat. 1964;114:235–244. doi: 10.1002/aja.1001140204. [DOI] [PubMed] [Google Scholar]
- Englander LL, Rubin LL. Acetylcholine receptor clustering and nuclear movement in muscle fibers in culture. J Cell Biol. 1987;104:87–95. doi: 10.1083/jcb.104.1.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frenette J, Cote CH. Modulation of structural protein content of the myotendinous junction following eccentric contractions. Int J Sports Med. 2000;21:313–320. doi: 10.1055/s-2000-3774. [DOI] [PubMed] [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distribution and the restoration of images. IEEE Trans PAMI. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Giddings CJ, Gonyea WJ. Morphological observations supporting muscle fiber hyperplasia following weight-lifting exercise in cats. Anat Rec. 1992;233:178–195. doi: 10.1002/ar.1092330203. [DOI] [PubMed] [Google Scholar]
- Goldberg AL. Protein synthesis in tonic and phasic skeletal muscles. Nature. 1967;216:1219–1220. doi: 10.1038/2161219a0. [DOI] [PubMed] [Google Scholar]
- Gregory TR. Coincidence, coevolution, or causation? DNA content, cell size, and the C-value enigma. Biol Rev Camb Philos Soc. 2001;76:65–101. doi: 10.1017/s1464793100005595. [DOI] [PubMed] [Google Scholar]
- Gundersen K, Sanes JR, Merlie JP. Neural regulation of muscle acetylcholine receptor ɛ- and α-subunit gene promoters in transgenic mice. J Cell Biol. 1993;123:1535–1544. doi: 10.1083/jcb.123.6.1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall ZW, Ralston E. Nuclear domains in muscle cells. Cell. 1989;59:771–772. doi: 10.1016/0092-8674(89)90597-7. [DOI] [PubMed] [Google Scholar]
- Hartig R, Shoeman RL, Janetzko A, Grub S, Traub P. Active nuclear import of single-stranded oligonucleotides and their complexes with non-karyophilic macromolecules. Biol Cell. 1998;90:407–426. [PubMed] [Google Scholar]
- Hawke TJ, Garry DJ. Myogenic satellite cells: physiology to molecular biology. J Appl Physiol. 2001;91:534–551. doi: 10.1152/jappl.2001.91.2.534. [DOI] [PubMed] [Google Scholar]
- Hikida RS, Van Nostran S, Murray JD, Staron RS, Gordon SE, Kraemer WJ. Myonuclear loss in atrophied soleus muscle fibers. Anat Rec. 1997;247:350–354. doi: 10.1002/(SICI)1097-0185(199703)247:3<350::AID-AR6>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Holy TE, Dogterom M, Yurke B, Leibler S. Assembly and positioning of microtubule asters in microfabricated chambers. Proc Natl Acad Sci U S A. 1997;94:6228–6231. doi: 10.1073/pnas.94.12.6228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadi F, Eriksson A, Holmner S, Butler-Browne GS, Thornell LE. Cellular adaptation of the trapezius muscle in strength-trained athletes. Histochem Cell Biol. 1999;111:189–195. doi: 10.1007/s004180050348. [DOI] [PubMed] [Google Scholar]
- Kelly FJ, Lewis SE, Anderson P, Goldspink DF. Pre- and postnatal growth and protein turnover in four muscles of the rat. Muscle Nerve. 1984;7:235–242. doi: 10.1002/mus.880070309. [DOI] [PubMed] [Google Scholar]
- Landing BH, Dixon LG, Wells T. Studies on isolated human skeletal muscle fibers. Hum Pathol. 1974;5:441–461. doi: 10.1016/s0046-8177(74)80023-7. [DOI] [PubMed] [Google Scholar]
- Lichtman JW, Magarassi L, Purves D. Visualization of neuromuscular junctions over periods of several months in living mice. J Neurosci. 1987;7:1215–1222. doi: 10.1523/JNEUROSCI.07-04-01215.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCall GE, Allen DL, Linderman JK, Grindeland RE, Roy RR, Mukku VR, Edgerton VR. Maintenance of myonuclear domain size in rat soleus after overload and growth hormone/ IGF-I treatment. J Appl Physiol. 1998;84:1407–1412. doi: 10.1152/jappl.1998.84.4.1407. [DOI] [PubMed] [Google Scholar]
- Merlie JP, Sanes JR. Concentration of acetylcholine receptor mRNA in synaptic regions of adult muscle fibers. Nature. 1985;317:66–68. doi: 10.1038/317066a0. [DOI] [PubMed] [Google Scholar]
- Morris NR. Nuclear positioning: the means is at the ends. Curr Opin Cell Biol. 2003;15:54–59. doi: 10.1016/s0955-0674(02)00004-2. [DOI] [PubMed] [Google Scholar]
- Mosley-Bishop KL, Li Q, Patterson L, Fischer JA. Molecular analysis of the klarsicht gene and its role in nuclear migration within differentiating cells of the Drosophila eye. Curr Biol. 1999;9:1211–1220. doi: 10.1016/s0960-9822(99)80501-6. [DOI] [PubMed] [Google Scholar]
- Moss FP. The relationship between the dimensions of the fibers and the number of nuclei during normal growth of skeletal muscle in the domestic fowl. Am J Anat. 1968;122:555–564. doi: 10.1002/aja.1001220308. [DOI] [PubMed] [Google Scholar]
- Ohira Y, Yoshinaga T, Ohara M, Nonaka I, Yoshioka T, Yamashita-Goto K, Shenkman BS, Kozlovskaya IB, Roy RR, Edgerton VR. Myonuclear domain and myosin phenotype in human soleus after bed rest with or without loading. J App Pysiol. 1999;87:1776–1785. doi: 10.1152/jappl.1999.87.5.1776. [DOI] [PubMed] [Google Scholar]
- Ralston E, Hall ZW. Restricted distribution of mRNA produced from a single nucleus in hybrid myotubes. J Cell Biol. 1992;119:1063–1068. doi: 10.1083/jcb.119.5.1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ralston E, Lu Z, Ploug T. The organization of the Golgi complex and microtubules in skeletal muscle is fiber type-dependent. J Neurosci. 1999;19:10694–10705. doi: 10.1523/JNEUROSCI.19-24-10694.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ralston E, Ploug T, Kalhovde J, Lomo T. Golgi complex, endoplasmic reticulum exit sites, and microtubules in skeletal muscle fibers are organized by patterned activity. J Neurosci. 2001;21:875–883. doi: 10.1523/JNEUROSCI.21-03-00875.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy RR, Monke SR, Allen DL, Edgerton VR. Modulation of myonuclear number in functionally overloaded and exercised rat plantaris fibers. J Appl Physiol. 1999;87:634–642. doi: 10.1152/jappl.1999.87.2.634. [DOI] [PubMed] [Google Scholar]
- Roy RR, Pierotti DJ, Edgerton VR. Skeletal muscle fiber cross-sectional area: effects of freezing procedures. Acta Anat (Basel) 1996;155:131–135. doi: 10.1159/000147798. [DOI] [PubMed] [Google Scholar]
- Sanes JR, Johnson YR, Kotzbauer PT, Mudd J, Hanley T, Martinou JC, Merlie JP. Selective expression of an acetylcholine receptor-lacZ transgene in synaptic nuclei of adult muscle fibres. Development. 1991;113:1181–1191. doi: 10.1242/dev.113.4.1181. [DOI] [PubMed] [Google Scholar]
- Schiaffino S, Gorza L, Sartore S, Saggin L, Ausoni S, Vianello M, Gundersen K, Lømo T. Three myosin heavy chain isoforms in type 2 skeletal muscle fibres. J Muscle Res Cell Motil. 1989;10:197–205. doi: 10.1007/BF01739810. [DOI] [PubMed] [Google Scholar]
- Schmalbruch H. Satellite cells of rat muscles as studied by freeze-fracturing. Anat Rec. 1978;191:371–376. doi: 10.1002/ar.1091910309. [DOI] [PubMed] [Google Scholar]
- Schmalbruch H, Hellhammer U. The number of nuclei in adult rat muscles with special reference to satellite cells. Anat Rec. 1977;189:169–176. doi: 10.1002/ar.1091890204. [DOI] [PubMed] [Google Scholar]
- Schmalbruch H, Lewis DM. Dynamics of nuclei of muscle fibers and connective tissue cells in normal and denervated rat muscles. Muscle Nerve. 2000;23:617–626. doi: 10.1002/(sici)1097-4598(200004)23:4<617::aid-mus22>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- Seiden D. Quantitative analysis of muscle cell changes in compensatory hypertrophy and work-induced hypertrophy. Am J Anat. 1976;145:459–465. doi: 10.1002/aja.1001450405. [DOI] [PubMed] [Google Scholar]
- Snow MH. The effects of ageing on satellite cells in skeletal muscles of mice and rats. Cell Tissue Res. 1977;185:399–408. doi: 10.1007/BF00220299. [DOI] [PubMed] [Google Scholar]
- Strassburger E. Über die Wirkungssphäre der kerne und die zellgrösse. Histol Beitr. 1893;5:97–124. [Google Scholar]
- Tidball JG. Myotendinous junction injury in relation to junction structure and molecular composition. Exerc Sport Sci Rev. 1991;19:419–445. [PubMed] [Google Scholar]
- Tseng BS, Kasper CE, Edgerton VR. Cytoplasm-to-myonucleus ratios and succinate dehydrogenase activities in adult rat slow and fast muscle fibers. Cell Tissue Res. 1994;275:39–49. doi: 10.1007/BF00305374. [DOI] [PubMed] [Google Scholar]
- Utvik JK, Njå A, Gundersen K. DNA injection into single cells of intact mice. Hum Gene Ther. 1999;10:291–300. doi: 10.1089/10430349950019075. [DOI] [PubMed] [Google Scholar]
- Viguie CA, Lu DX, Huang SK, Rengen H, Carlson BM. Quantitative study of the effects of long-term denervation on the extensor digitorum longus muscle of the rat. Anat Rec. 1997;248:346–354. doi: 10.1002/(SICI)1097-0185(199707)248:3<346::AID-AR7>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- Winchester PK, Gonyea WJ. A quantitative study of satellite cells and myonuclei in stretched avian slow tonic muscle. Anat Rec. 1992;232:369–377. doi: 10.1002/ar.1092320306. [DOI] [PubMed] [Google Scholar]


