Proteins unfold in steps

Abstract

I present results from an experiment on the dynamics of folding of a globular protein (bovine serum albumin). Employing a micro-mechanical technique, I perform the measurements on very few molecules (1–100). I observed a sequence of steps in time for both unfolding and refolding. The overall characteristic time of the process is thus built up of waiting times between successive steps. The pattern of steps is reproducible, demonstrating the existence of deterministic pathways for folding and unfolding. Certain symmetries in the patterns of steps may reflect the architecture of the protein’s structure.

How do proteins fold, or, more generally, how do they change conformation? This is a question about dynamics, and it represents the logical next step after the elucidation of the structure of the native state. Work on protein folding can be catalogued into studies of equilibrium conformations and studies of dynamics. I now briefly consider both.

One important question about equilibrium states is how many different ones there are—i.e., how complex is the phase diagram of a protein. There is probably no single answer valid for all proteins. For small, single domain proteins (e.g., ribonuclease) the claim is that there are only two states, native and unfolded (1–4). However, for several proteins—e.g., α-lactalbumins (5–7) and cytochrome c (8)—it has been shown that there exists at least a third phase, called “molten globule.” For large, multidomain proteins the phase diagram could be more complex.

Studies of the dynamics of folding and unfolding generally find at least one characteristic time scale (an exponential relaxation) (4, 9–11) and sometimes two (12–15). These time scales vary over orders of magnitude (from milliseconds to minutes) depending on the particular protein and the conditions, but they are extremely large compared with the typical time scales of molecular processes, which are measured in picoseconds. As in the static case, all experiments are performed on bulk samples of protein in solution, so one measures the dynamics averaged over the whole population of molecules. The dynamics of a single molecule can only be inferred.

Probes of conformation used in the experiments include (16) measurements of the hydrodynamic size (by viscosity, dynamic light scattering, electrophoresis, etc.), of the radius of gyration (scattering experiments), optical rotation (which measures the amount of secondary structure), fluorescence (monitors the environment of tryptophane residues), NMR (probes the chemical environment of certain H atoms), and fluorescence energy transfer, which measures the distance between two specific sites on the polypeptide chain (17–19). This latter technique is closest to the one used in the present study, in that we also measure an “end-to-end” distance.

To study dynamics, ideally one would like to look at a single molecule. This is because in a bulk sample, since it is not possible to synchronize the molecules, one measures what is effectively a time average, and the details are lost. The present experiment is performed on a sample consisting of very few molecules (1–100), and there is a mechanism for synchronization. As a result, I unveil a stepwise process in time for unfolding and refolding. The overall characteristic time of the process is seen to break up into a succession of shorter waiting times separating discrete steps in the protein’s conformation. The pattern of steps is reproducible. I thus provide part of the answer to the question posed in the beginning.

EXPERIMENTAL METHOD

A description of the technique has been given elsewhere (20). It is a micro-mechanical measurement of size. The molecules to be studied are sandwiched in a monolayer between a glass plate and a micrometer size sphere. If, responding to changes in the ambient solution, the molecules swell, they push the sphere away from the plate; if they contract, they pull the sphere toward the plate. These movements of the sphere are detected with a resolution of a fraction of a nanometer, using a near-field optical technique. Namely, the sphere is illuminated by the evanescent light created by the total internal reflection of a laser beam at the glass–water interface that is the bottom of the cell. Light scattered by the sphere is collected through a microscope objective and the intensity measured with a photodiode. Because of the rapid decay of the electromagnetic fields away from the surface of the plate, this intensity is a sensitive measure of the separation between the sphere and the plate (21, 22): I(z) = I(0) e^−z/δ, where I(z) is the scattered intensity if the sphere is at height z above the plate and 2 δ is the decay length of the fields. For example, with our light source (He–Ne laser, λ = 633 nm) and geometry, the decay length for the intensity is of order δ ≈ 100 nm; this means that a 1-nm movement of the sphere results in approximately a 1% change in intensity of the scattered light, which is easily detectable. Under the conditions of the present experiment the noise level of the measurement was 2–3 Å in a frequency band from 0 (!) to 20 Hz, dominated by the Brownian motion of the sphere. Because in my setup the sphere is not held by a macroscopic arm, but rather by the molecules themselves, I circumvent the problems of stability that affect other mechanical devices—e.g., the atomic force microscope. The interaction between the sphere and the plate, which is the sum of an attractive (Van der Waals) term and a repulsive (electrostatic) term (see, for example, ref. 23): F = AR/6D² − CR e^−D/Δ (A = the Hamaker constant, R = the radius of the sphere, D = the separation between the sphere and the plate, Δ = the Debye screening length, and C = a constant that depends on ionic strength, surface charge, and temperature), results in the surfaces exerting a force on the molecules. At a separation of ≈8 nm, and in my conditions (A = 10⁻²⁰ J; R = 5 μm; Δ = 1 nm; C = 10⁻¹ N/m), the two terms roughly balance, each being of order ≈100 pN. However, due to the roughness of the surfaces, the actual average distance between the sphere and the plate is more likely to be on the order of ≈20 nm or more, as discussed below. The net force is then attractive and small (F ≤ 20 pN). For comparison, in an experiment in which the interaction between biotin–avidin pairs is measured with the atomic force microscope (24), forces as large as 160 pN apparently do not disrupt the folded albumin molecule to which the biotin is attached. In summary, the technique allows detection of changes in the “mechanical size” (thus operationally defined) of macromolecules; the quantity being measured is similar to the end to end distances obtained by the method of fluorescence energy transfer.

The results reported here were obtained with bovine serum albumin (BSA), a globular protein of 585 amino acids. The three-dimensional structure of human albumin is known (25–27); it is dominated by α-helices, and the dimensions are approximately 80 × 80 × 40 Å. To fix the protein to the surfaces I used the following procedure: a suspension of the spheres was incubated (10 μm diameter polystyrene spheres from Polysciences) with an excess of 10 mg/ml BSA (from Sigma; catalogue no. B4287) in 0.1 M NaCl for 6 hr at room temperature; BSA adsorbs on the spheres. After washing the spheres (to eliminate BSA in solution) a dilute suspension is introduced in the cell (made from a microscope slide, Chase Scientific catalogue no. 600, and a cover glass supported on 75-μm spacers); the spheres settle at the bottom and BSA molecules on the surface of the spheres readily adsorb onto the glass slide, thus “gluing” the spheres to the plate. Spheres that are not thus attached are washed off when the cell is flushed. A single sphere is brought in the field of view of the microscope and the light intensity is recorded in the course of time as unfolding is enduced by exposing the molecules to an acid solution. The motion of the sphere is calculated from the change in light intensity using the formula for I(z) given above. Because the relative changes in intensity are small, a linearization can be used (Δz = −δΔI/I).

RESULTS

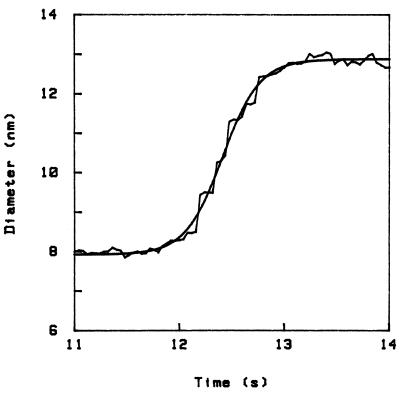
In Fig. 1 I present a curve of the unfolding in the course of time obtained with the above technique. The ordinate is the height of the sphere above the plate (which represents the diameter of the molecules); I measure only height differences, but I have set the initial height at 8 nm, which corresponds to the diameter of the albumin molecule in the native state. The rugged curve is the experiment, and the smooth curve is a fit through the data. At time t ≈ 12 s I replace the initial 0.1 M NaCl in water solution with a 4% trichloroacetic acid (TCA) solution, this exchange taking place in a time which is short compared with the time scales discussed here. The effect is that the molecules unfold and push the sphere up (20) by about 4 nm, in a process that overall takes about 1 s. [The correction to the light intensity due to the change in index of refraction, coming mainly from the change in penetration depth δ, is small (corresponding to an apparent movement < 0.5 nm).] This swelling of the molecules is comparable to figures quoted in ref. 28 for the acid unfolding of albumin (60% increase in linear dimension). Because the swelling of the molecule is not isotropic, in this case the actual movement of the sphere will also depend on the orientation of the molecules relative to the surfaces.

Figure 1.

Unfolding curve in time for BSA in 4% TCA, showing a stepwise increase in size (diameter of the molecule). The system was quenched at t ≈ 12 s (the origin of time is arbitrary). The initial diameter is set to be 8 nm (corresponding to the folded dimensions). The smooth curve is a fit using the form D = D₀ + A tanh[(t − t₀)/τ], where D = diameter and t = time, which gives τ = 0.35 s in this case.

The main observation contained in this report is that this process occurs in steps. There is a step, then a waiting time, then a step, and so on. In the figure we can clearly identify five steps, and there may be two smaller ones at the beginning and end. Step heights are, in this case, on the order of 1 nm, and waiting times on the order of 0.1 s.

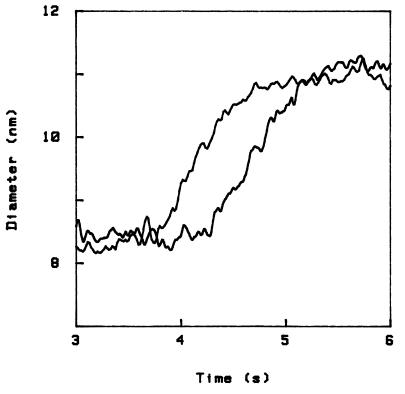
The unfolding is reversible—i.e., when we restore the initial NaCl solution the sphere jumps back to the original position. Therefore the experiment can be performed several times on the same sample (the same sphere), and we then find that the pattern of steps is reproducible. This is shown in Fig. 2, where I have plotted side-by-side, for ease of comparison, the curves from two independent runs. In fact, by comparing several such curves, even quite small steps can be clearly distinguished from the random Brownian fluctuations of the sphere. For example, for the sample corresponding to Fig. 2 we obtain a list of the steps that reads as follows: 3.5 - 3 - 4.5 - 1.5 - 4.5 - 4 - 1 - 1 - 1 - 2.5, where the step height is in angstroms, and I feel shy to quote a resolution of better than 0.5 Å.

Figure 2.

Comparison of two independent unfolding curves obtained with the same sample.

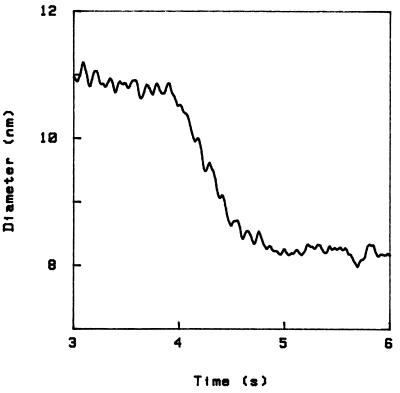
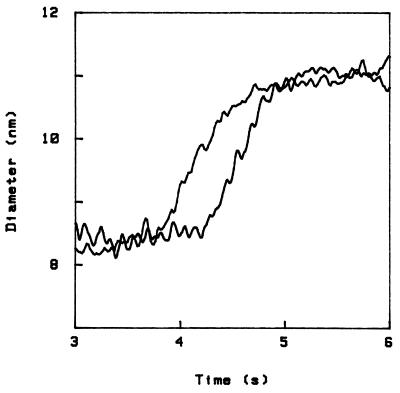
The process of refolding occurs on a similar time scale, and also in steps. This is shown in Fig. 3, where we start from the final state of Fig. 2 (4% TCA) and restore the initial NaCl solution (the sample is the same as for Fig. 2). The pattern of steps is related to the steps upon unfolding through a simple transformation, namely reversal of the diameter axis. This is shown in Fig. 4, where I have again plotted the first curve in Fig. 2 and the curve in Fig. 3, the latter with ordinate reversed. Note, however, that (i) this symmetry is at best an approximate one; for example, in Fig. 4 a small (1.5 Å) step occurs in two different positions in the two curves, and three small (1.1 Å) steps toward the end of unfolding appear merged into one bigger step in the curve to the right; and (ii) another symmetry operation that also allows to approximately superpose folding and unfolding patterns is reversal of the time axis; although the previous transformation generally leads to a better superposition, with the present data it is not easy to decide this question. The difficulty is that, in addition, all curves possess an approximate symmetry under simultaneous reversal of both axis. In fact, the overall shape of any curve can be fitted by a hyperbolic tangent, as shown in Fig. 1.

Figure 3.

Refolding in 0.1 M NaCl.

Figure 4.

Comparison of unfolding and refolding curves, the latter after reversal of the diameter axis.

DISCUSSION

Let us first consider an alternative interpretation of the data. Namely, the steps could correspond to the molecules that hold the sphere unfolding one after the other, each individual molecule unfolding in a “one step” process. I believe this explanation is not correct for the following reasons. Let us suppose that the sphere is held by six molecules (because I observed roughly six main steps). First, if one molecule unfolds but the others do not, it is hard to see how the sphere would lift at all. Second, quenching time (i.e., the time it takes for the TCA concentration to rise from 0 to its final value in the gap between the sphere and the plate, when solution is changed) is estimated to be ≈50 ms, and moreover, within an even shorter time all molecules involved see identical conditions, because the diffusion time for both H₃O⁺ and trichloroacetate ions over the distances that separate the molecules involved (<100 nm) is in the microsecond range. Therefore, with respect to the time scales characteristic of the steps, the quenching is instantaneous, and there is no reason for different molecules to unfold at different times, except as a manifestation of a stochastic process. However, in this case the number of “events” (unfolding of a single molecule) should be distributed exponentially in time, whereas we observe a linear distribution (single events separated by roughly constant waiting times). Third, in this scenario the steps could not occur in a reproducible pattern.

Another possibility is that the sphere is supported by an aggregate of molecules, and the steps are a manifestation of the sequential unfolding of the molecules within the aggregate. This, however is unlikely: it is known that albumin adsorbs on surfaces in a monolayer, not a multilayer (29)—i.e., it does not show any tendency to aggregate. This is confirmed, in the present case, by the following two observations. It is possible to cause the sphere to collapse on the plate, using a different denaturant (urea). The collapse is then of order the size of one molecule (20). Alternatively, a partial collapse of the sphere on the plate can be obtained by digesting with trypsin; in this case also the sphere moves by an amount smaller than the diameter of one molecule. This observation will be reported in more detail elsewhere. If we can exclude a multilayered structure, any state along the transition curve (Fig. 1), which is intermediate between the initial and final states, must correspond to a partial expansion of all the molecules supporting the sphere, rather than a complete expansion of only some of the molecules.

Assuming then that what we observe corresponds to steps in the dynamics of unfolding of a single molecule, note that because of the geometry (sphere against a plate), the number of “active” molecules (i.e., molecules that make contact on one side with the sphere and on the other with the plate) is at most (that is, if the molecules were densely packed on the surface of the sphere) ≈100. The actual number is probably much smaller. Walz and Suresh (30) estimate (from transmission electron micrographs and other observations) that the surface of latex spheres of the kind used in this experiment presents asperities that we can roughly think of as hemispheres with an ≈20 nm radius, with a surface coverage sufficient to support the sphere (≈1%). The sphere is then most likely resting on few (≈3) such (albumin covered) hills; with the relevant radius of curvature being now ≈20 nm, the number of albumin molecules making contact is correspondingly small (on the order of 1 per asperity). With very few molecules, the mechanism for synchronization is the perturbation (force exerted by the sphere) on the other molecules when one makes a step.

This experiment is performed on a protein bound to a surface. Although this situation is interesting in its own right, as proteins in the cell often function in interaction with surfaces (membranes, ribosomes, etc.), the question arises whether the dynamics is different for the protein in solution. While a definitive answer will have to wait for a corresponding experiment on single molecules in solution, which may be feasible, I note that many enzymes can be attached to surfaces while retaining their enzymatic activity, which indicates that the structure of the active site, and therefore probably the overall structure of the molecule, remains substantially unaltered. In such a case one would not expect drastic differences in the dynamics.

If we forget about the details of the steps and just look at the overall shape of the unfolding and refolding curves, a time scale τ can be extracted by fitting with a function which depends on a single characteristic time, as done in Fig. 1. This is the time scale measured in all experiments on bulk samples; as already noted, it can be extremely large. For example, for the present experiment τ ≈ 0.4 s, which is huge compared with the time scales of molecular motion. Indeed, it is very surprising that there should be such a characteristic time scale at all. However, a staircase-like curve accounts for it, simply by introducing waiting times. Namely, if we write the unfolding process as a “reaction” with one or more intermediate states: F → I₁ → I₂ … → U (where F = folded form, U = unfolded form, and I = intermediates) and consider a quantity Q (such as the size of the molecule) which takes different values q₀, q₁, … , q_n for the different states (say q₀ < q₁ < … < q_n for the sake of the argument), then a bulk experiment measures, to a first approximation, an average 〈Q〉 ∝ q₀ [F] + q₁ [I₁] + … q_n [U], where [F] means the concentration of the form F. It is easy to see that the resulting dynamics for 〈Q(t)〉 is a sum of exponentials, but if the rate constants are all nearly equal, it will be difficult to distinguish this from a single exponential dynamics. If one of the rate constants is sensibly different from the others, one will see double exponential dynamics, and so on.

We can think of the waiting times as energy barriers in an appropriate conformation space, or we can simply think in terms of breaking bonds (hydrogen bonds, effective bonds due to hydrophobicity, etc.). Because for the same sample we observe always the same sequence of steps, this must have a structural basis. Note that we see roughly six main steps, and the protein consists of six domains (27). In fact, it has been suggested that the acid unfolding of albumin consists essentially in the different domains coming apart from each other (31), and what we observe in this experiment may correspond, at least in part, to this process.

For refolding, we observe again the same sequence of steps, occurring in the same order (assuming that the correct transformation for superposing folding and unfolding curves is reversal of the diameter axis). This means that in conformation space folding and unfolding take different paths. However, these paths are related in the following way. Let us suppose that, during unfolding, first the big structures break apart, then smaller structures within the big ones break apart, and so on. Then we would find that in refolding first the big structures are assembled, and only then the smaller ones within these. In fact, the reproducibility of the pattern of steps is a demonstration of the existence of deterministic folding pathways both for folding and unfolding. The existence of such pathways has been recognized before in the formation of covalent bonds (disulfide bridges) during refolding (32, 33), and they are thought to occur more generally (see the discussion of “adhesion steps” in ref. 34); indeed, a deterministic folding route could already be surmised from the fact that under appropriate conditions folding and unfolding times can be comparable. In my case, ascribing certain symmetries to the pattern of steps is an attempt to extract some general features of these pathways.

Individual waiting times vary from run to run (as expected for a stochastic process like the overcoming of barriers), but they are of order 1/10 s (a simple estimate shows that this corresponds to barrier heights of order 20 kT; for comparison, the binding energy of one hydrogen bond is ≈7 kT). However, we would not be able to see steps occurring much faster due to the time resolution of the experiment in its present form. In fact, it is necessary to “tune” the acid concentration of the quenching to see the steps clearly, for the following reason. If we compare, for the same sample, unfolding in 4% and 6% TCA, we see in the second case the same steps as before plus probably some more (although the additional steps are not very clear), so that the total expansion of the molecule is larger. In addition, all waiting times are reduced, so that the overall characteristic time of the process is shortened, by a factor ≈0.7 in this case. Already under these conditions, two or sometimes three successive steps may appear as one bigger step. At a concentration of 10%, we do not see any clear steps; presumably they are too fast to be resolved. Finally, were we to perform the experiment with a better resolution in time and space, it is possible that we would find steps within steps.

In conclusion, by performing an experiment on very few molecules I have shown that albumin folds and unfolds in steps. These steps are not seen in other experiments because in a bulk sample they average out. They provide an explanation for the very long time scales observed in protein folding. The reproducibility of the pattern of steps demonstrates that folding and unfolding follows deterministic pathways.

Of the results reported here, what we expect to be general is the occurrence of deterministic steps. The particular sequence of steps, the waiting times, etc. must be system-dependent: a different protein (or even different orientations of the same molecule) will show a different pattern. This experiment was performed on a large, multidomain protein. One would like to know whether the observed dynamics is characteristic of this class of proteins only, or extends to smaller, single domain proteins. Whether certain approximate symmetries that I have pointed out in this work are general or not is another interesting open question.

ABBREVIATIONS

BSA

bovine serum albumin

TCA

trichloroacetic acid