Abstract
This study investigates the effect of class imbalance in training data when developing neural network classifiers for computer aided medical diagnosis. The investigation is performed in the presence of other characteristics that are typical among medical data, namely small training sample size, large number of features, and correlations between features. Two methods of neural network training are explored: classical backpropagation (BP) and particle swarm optimization (PSO) with clinically relevant training criteria. An experimental study is performed using simulated data and the conclusions are further validated on real clinical data for breast cancer diagnosis. The results show that classifier performance deteriorates with even modest class imbalance in the training data. Further, it is shown that BP is generally preferable over PSO for imbalanced training data especially with small data sample and large number of features. Finally, it is shown that there is no clear preference between oversampling and no compensation approach and some guidance is provided regarding a proper selection.
1. Introduction
In computer aided decision (CAD) systems, computer algorithms are used to help a physician in diagnosing a patient. One of the most common tasks performed by a CAD system is the classification task where a label is assigned to a query case (i.e., a patient) based on a certain number of features (i.e., clinical findings). The label determines the query’s membership in one of predefined classes representing possible diagnoses. CAD systems have been investigated and applied for the diagnosis of various diseases, especially for cancer. Some comprehensive reviews on the topic can be found in (Kawamoto et al., 2005; Sampat et al., 2005; Lisboa and Taktak, 2006). CAD systems rely on a wide range of classifiers, such as traditional statistical and Bayesian classifiers (Duda et al., 2000), case-base reasoning classifiers (Aha et al., 1991), decision trees (Mitchell, 1997), and neural networks (Zhang, 2000). In particular, neural network classifiers are a very popular choice for medical decision making and they have shown to be very effective in the clinical domain (Lisboa, 2002; Lisboa and Taktak, 2006).
To construct a classifier, a set of examples representing previous experience is essential. In general, the larger and more representative the set of available examples is, better classification of future query cases can be obtained (Raudys and Jain, 1991). In the medical domain, however, there are several challenges and practical limitations associated with data collection. First, collecting data from patients is time-consuming. Second, acquiring large volumes of patients representing certain diseases is often challenging due to the low prevalence of the disease. This is the case, for example, with CAD systems developed to support cancer screening. Cancer prevalence is particularly low among screening populations which results in class imbalance in the collected set of examples; a phenomenon where one of the disease states is underrepresented. In addition, the clinical presentation of patients with the same disease varies dramatically. Due to this inherent variability, CAD systems are often asked to handle large numbers of features, many of which are correlated and/or of no significant diagnostic value. The issues described above (i.e., finite sample size, imbalanced datasets, and large numbers of potentially correlated features) can have a detrimental effect on the development and performance evaluation of typical CAD classifiers.
Several investigators have addressed classification in the presence of these issues from both general machine learning and CAD perspectives. Most attention has been given to the effects of finite sample size (Fukunaga and Hayes, 1989; Raudys and Jain, 1991; Raudys, 1997; Wagner et al., 1997; Sahiner et al., 2000; Beiden et al., 2003; Chan et al., 2004). The problem of large data dimensionality (i.e., large number of features) has been addressed in (Hamamoto et al., 1996) for neural networks and in (Raudys and Jain, 1991) and (Raudys, 1997) for other types of classifiers. In addition, researchers have examined the effect of finite sample selection (Jain and Zongker, 1997; Sahiner et al., 2000). Finally, the implications of data handling and CAD evaluation with limited datasets have been discussed in detail in several recent publications (Gur et al., 2004; Li and Doi, 2006; Li and Doi, 2007).
In contrast, the problem of classification using imbalanced data has attracted less attention. It has been mainly addressed in the literature on machine learning (Barnard and Botha, 1993; Japkowicz, 2000; Weiss and Provost, 2001; Japkowicz and Stephen, 2002; Chawla et al., 2002; Maloof, 2003; Zhou and Liu, 2006; Elazmeh et al., 2006). These studies were mostly performed using real life problems, where the effects of particular properties of the training data cannot be easily determined (Weiss and Provost, 2001; Chawla et al., 2002; Maloof, 2003). A study oriented on isolating the effect of some data properties was presented in (Japkowicz, 2000) and (Japkowicz and Stephen, 2002). However, the investigators did not include the impact of the number of features in the dataset, correlation among features, and the effect of random sampling from the population. In another study (Weiss and Provost, 2001), the authors evaluated the effect of the extent of data imbalance on classifier performance. However, their study was restricted to the classical C4.5 classifier. Moreover, in general machine learning applications, classification performance is often measured using the average classification error as the figure of merit (FOM). Unfortunately, classification error is not a suitable FOM for medical decision support systems where diagnostic sensitivity and specificity are more clinically relevant and better accepted by the physicians.
Although some CAD researchers have dealt with class imbalance within their own application domain (Boroczky et al., 2006), to the best of our knowledge, no systematic evaluation its effect has been reported from this perspective. The purpose of this investigation is to extend the previously reported studies by providing a more comprehensive evaluation of the effect of class imbalance in the training dataset for the performance of neural network classifiers in medical diagnosis. This effect is studied in the presence of the following other, commonly occurring limitations in clinical data:
limited training sample size,
large number of features, and
correlation among extracted features.
In this study, we also compare two common class imbalance compensation methods (i) over-sampling and (ii) undersampling. Since the study targets specifically CAD applications, two distinct neural network training methods are also investigated. The first method is the traditional backpropagation (BP) and the second one is particle swarm optimization (PSO) with clinically relevant performance criteria. This additional factor will allows us to assess whether the neural network training algorithm has any impact on the conclusions.
The article is organized as follows. Section 2 provides a brief description of clinically relevant FOMs for assessing the performance of classifiers for binary classification problems. Section 3 describes the training algorithms employed in this study. Section 4 provides description of the study design and data. Results and discussion follow in Section 5 and Section 6, respectively.
2. A clinically relevant FOM: Receiver Operator Characteristic (ROC) Curve
Traditionally, the average classification error has been used to evaluate classifier performance. It is defined as the total number of misclassified example divided by the total number of available examples for a given operating point of a classifier. For instance, in a 2-class classification problem with two predefined classes (e.g., positive diagnosis, negative diagnosis) the classified test cases are divided into four categories:
true positives (TP) - correctly classified positive cases,
true negatives (TN) - correctly classified negative cases,
false positives (FP) - incorrectly classified negative cases, and
false negatives (FN) - incorrectly classified positive cases
Therefore, the misclassification error is
| (1) |
This evaluation criterion is of a limited use in clinical applications for many reasons. First, misclassification error varies dramatically depending on class prevalence and it can be very misleading in clinical applications where the most important class is typically underepresented. For example, if the presence of cancer is 5% in the test dataset (a typical clinical scenario), a classifier that detects 100% of cancer-free cases and 0% of cancer cases achieves a seemingly low 5% misclassification error. From a clinical perspective, however, this is an unacceptable performance since all cancer patients are misdiagnosed and thus left untreated. Second, in medical decision making, different types of misclassifications have different cost. For example, in breast cancer diagnosis, a false positive classification translates into an unnecessary breast biopsy, associated with both emotional and financial cost. False negative, however, means a missed cancer which in turn can be deadly. Such differences are not taken into account by the average classification error. Finally, the average classification error depends on the classifier’s operating threshold. Since many classification systems (such as neural networks) provide a decision variable of multiple possible values, choosing the optimal decision threshold can be challenging. It also makes impossible direct comparisons among CAD systems that are designed to operate with different decision thresholds.
To account for these issues, Receiver Operator Characteristic (ROC) analysis is commonly used in the clinical CAD community (Obuchowski, 2003). ROC curve describes the relation between two indices: true positive fraction (TPF) and (ii) false positive fraction (FPF), defined as follows:
| (2) |
| (3) |
A conventional ROC curve plots TPF (or sensitivity) vs. FPF (or [1 – specificity]) for every possible decision threshold imposed on the decision variable. By providing such a complete picture, ROC curves are often used to select the optimal decision threshold by maximizing any pre-selected measure of clinical efficacy (e.g., accuracy, average benefit, etc.).
In CAD studies, the most commonly used FOM is the area under the ROC curve (AUC). The AUC index for useful classifiers is constrained between 0.5 (representing chance behavior) and 1.0 (representing perfect classification performance). CAD classifiers are typically designed to maximize the ROC area index. However, in cancer screening applications, it is often critical to achieve sufficiently high sensitivity (also known as detection rate). In such applications, it is expected that the CAD classifier will need to achieve at least 90% sensitivity. Accordingly, researchers have proposed the partial AUC index (pAUC, where p indicates the lowest acceptable sensitivity level) as a more meaningful FOM (Jiang et al., 1996). Detailed description of ROC analysis and its utilization for CAD evaluation can be found in (Jiang et al., 1996; Bradley, 1997; Metz et al., 1998).
3. Training algorithms for neural networks
Training feedforward neural networks is an optimization problem of finding the set of network parameters (weights) that provide the best classification performance. Traditionally, the backpropagation method (Rumelhart et al., 1986) is used to train neural network classifiers. This method is a variation of the gradient descent method to find a minimum of an error function in the weight space. The error measure is typically the mean squared error (MSE). Although there is a correlation between MSE and the classification performance of the classifier, there is no simple relation between them. In fact, it is possible that an MSE decrease may cause a decline in classification performance. Moreover, the MSE is very sensitive to class imbalances in the data. For example, if positive training examples are severely underrepresented in the training dataset, an MSE-trained classifier will tend to assign objects to the negative class. As described before, such classification is of no use in the clinical domain.
To overcome this limitation, a particle swarm optimization (PSO) algorithm with clinically relevant objectives is also implemented for training neural network classifiers (Habas et al., 2007). The study compares the results of training classifiers using BP method with MSE as an objective with those using the PSO algorithm.
Particle swarm optimization (Kennedy and Eberhart, 1995) is an iterative optimization algorithm inspired by the observation of collective behavior in animals (eg. bird flocking and fish schools). In PSO each candidate solution to the optimization problem of a D-variable function is represented in one particle. Each particle i is described by its position xi (a D-dimensional vector representing a potential solution to the problem) and its velocity υi. The algorithm typically starts with a random initialization of the particles. Then, in each iteration, the particles change their position according to their velocity. In each iteration the velocity is updated. Given that pi is the best position (i.e. one that correspond to the best value of the objective function) found by an individual i in all the preceding iterations and pg is the best position found so far by the entire population, the velocity of a particle changes according to the following formula (Clerc and Kennedy, 2002; van den Bergh and Engelbrecht, 2004)
| (4) |
where υid(t) is the d-th component of the velocity vector of a particle i in iteration t (analogous notation is used for xi, pi, and pg), φ1(t) and φ2(t) are random numbers between 0 and c1 and 0 and c2, respectively, and ω is an inertia coefficient. c1, c2 and ω are parameters of the algorithm deciding on significance of particular factors while adjusting the velocity. Position of the particle i is simply adjusted as
| (5) |
The output of the algorithm is the best global position found during all iterations. Even though PSO convergence to a global optimum has not been proven for the general case (some results on the convergence can be found in (Clerc and Kennedy, 2002)), the algorithm has been shown efficient for many optimization problems including training neural networks (Kennedy and Eberhart, 1995).
From the clinical perspective, the most attractive aspect of PSO-based training is that it can be conducted using clinically relevant evaluation criteria. This means that the objective function for the PSO algorithm can be chosen to be AUC, pAUC or other clinically relevant criteria (e.g., specific combinations of desired sensitivity and specificity). In this study, the PSO-based neural network training consists of finding the set of weights that provides the best classification performance in terms of AUC or 0:9AUC.
Applying ROC-based evaluation during the classifier training could provide multiple benefits. First, since the final evaluation criterion fits the training criterion, the overall performance of the classifier can be potentially improved. Second, since AUC is basically independent of class prevalence, dataset imbalance is of lower concern when training the neural network with clinically relevant objectives. PSO has been successfully applied in CAD for training classifiers with ROC-based objectives (Habas et al., 2007), but its effectiveness with imbalanced datasets has not been yet evaluated.
4. Study design
The study is designed to assess systematically the impact of imbalanced training data on classifier performance while taking into account other factors such as the size of the training dataset, the number of features available, and presence of correlation among features. The study was conducted with simulated data and the conclusions were further validated using a clinical dataset for breast cancer diagnosis.
The neural networks used in the study were feed forward networks with a single output neuron and one hidden layer consisting of three neurons. A network with three hidden neurons was chosen to keep the network complexity low and prevent overtraining. Sigmoidal activation functions were used for all neurons. The neural networks were trained using (i) BP with MSE, (ii) PSO with AUC and (iii) PSO with 0:9AUC as the objective functions. When applying the BP method, all the networks were trained for 1000 iterations with a learning rate of 0.1. For the PSO training, the following standard algorithm parameters were used: c1 = 2, c2 = 2, ω = 0:9. The number of particles was set to the number of parameters of each neural network (varying based on the number of features) multiplied by 10. The number of iterations was set to 100. The parameters for this study were chosen empirically to provide good performance while at the same time keeping the time complexity feasible.
To prevent overtraining, the examples available for the development of the network were divided into two sets: a training set and a validation set. The training and validation sets were characterized by the same size and positive class prevalence and both were used to construct a classifier. Although choosing equal-size training and validation sets is unusual (usually a validation set is substantially smaller), it was necessary due to the class imbalance factor. For instance, given a training set with 100 examples and 1% prevalence of positive examples, choosing a validation set smaller than the training would result in no positive validation examples. The training set was used to calculate the MSE and the gradient for BP and to calculate AUC or 0:9AUC for the PSO-based training. During the training process, classifier performance on the validation set was repeatedly evaluated. The network that provided the best performance on the validation set during training was selected at the end of the training process. Such practice was applied to prevent possible overfitting of the network to the training examples.
To obtain an accurate estimation of the network performance, a hold-out technique was applied in which a separate test set was used to evaluate the network after the training process. For the BP method, one network was trained and finally tested using both FOMs (AUC and 0:9AUC). For the PSO training method, a separate classifier was trained for each FOM separately and each trained network was tested on the final test set according to its corresponding FOM.
To account for the class imbalance, two standard ways of compensation were evaluated, namely oversampling and undersampling. In oversampling, examples from the underrepresented class are copied several times to produce a balanced dataset. This means that the size of the training dataset increases up to two times. Note that in the case of batch BP training, this method is equivalent to the commonly used approach where the changes of weights induced by a particular example are adjusted according to the prevalance of its class in the training set (lower prevalence, higher weight). Also, note that oversampling has no effect on the PSO training as class prevalence does not affect the ROC-based assessment. In undersampling, examples from the overrepresented class are randomly removed, resulting in a smaller dataset. Although the computational complexity of the training process for this method decreases, the main drawback is that potentially useful examples are discarded from training. In both scenarios, the resulting datasets are characterized by equal class prevalence.
4.1. Experiment 1: simulated data
In the first experiment, simulated data were generated to evaluate the combined effect of all examined factors on classifier performance. Such an evaluation would not be possible with data coming from a real clinical problem since the proposed experiments require a very large number of examples. Furthermore, in simulated data, important parameters can be strictly controlled which allows for assessing their separate as well as combined impact on classifier performance. In this experiment we followed the experimental design similar to one presented in (Sahiner et al., 2000).
The simulated datasets were generated using multivariate normal distributions separately for each class:
| (6) |
where p(x) is a probability density function, x is a d-dimensional vector of features, µ is a vector of means and ∑ is a covariance matrix. Furthermore, it was assumed that the covariance matrices for both classes are equal (∑ = ∑1 = ∑2). Based on the above assumptions, the best achievable AUC performance is given by the following equation (Sahiner et al., 2000):
| (7) |
where Δ(∞) is the Mahalanobis distance between the two classes:
| (8) |
To evaluate how different levels of imbalances in training dataset affect performance in the presence or absence of feature correlation and for different number of features, two general cases were considered: (i) uncorrelated features and (ii) correlated features. For each of these cases three data distributions were created with 5, 10 and 20 features. For each of the resulting combinations, it was assumed that the two classes have multivariate Gaussian distributions with unequal means and equal covariance matrices.
4.1‥1 Distributions for uncorrelated data
For this scenario, it was assumed that the covariance matrices were the indentity matrices (∑1 = ∑2 = I) and the difference of means between the classes for feature i was
| (9) |
where M is the number of features and α is a constant. A similar distribution of Δµ(i) was observed in the clinical data used in this study. The parameter α was selected separately for each number of features to provide Δ(∞) = 3:28 which corresponds to the ideal observer performance Az = 0:9.
4.1‥2 Distributions for correlated data
In this scenario, it was also assumed that the covariance matrices for the two classes are equal (∑ = ∑1 = ∑2) but they are not identity matrices. For each of the number of features M, a 5 × 5 matrix AM was constructed. Then the covariance matrix was generated as a block-diagonal matrix based on AM, i.e., a matrix that has AM on its diagonal and matrices containing zeros outside the diagonal. For example, the matrix for 10 features was
| (10) |
And the corresponding covariance matrix was ∑ was
| (11) |
Note that for 5 features ∑ = A5. The values on the diagonal of AM were always ones. The values outside the diagonal were selected such that for each number of features the classwise correlations averaged in 0.08 with standard deviation of 0.2. The correlations in general varied between −0.3 and 0.8. These values were selected to reflect the correlation structure observed in the clinical data used in this study.
Mean differences between the two classes were selected using equation (9). The parameter α was selected to provide ideal observer performance Az = 0:9 for each number of features.
4.1‥3 Other data parameters
The positive class prevalence index c was defined as
| (12) |
where Npos is the number of positive examples and Ntot is the total number of examples in the training dataset. Six levels of c were used: 0.01, 0.02, 0.05, 0.1, 0.2 and 0.5 where the last one corresponds to the equal prevalence of both classes. Positive class prevalence described the extent of imbalance in the training dataset. Additionally, two sizes of the training dataset were investigated (1000 and 100 examples).
4.1‥4 Neural networks training and testing
Neural networks were trained for all possible combinations of the described factors. For each combination, 50 training and validation datasets were independently drawn from a given distribution and a separate set of neural networks was trained to account for data variability and random factors inherent in neural network training. For each pair of training and validation datasets, the BP training was conducted three times: (i) with original data, (ii) with oversampled data, and (iii) with undersampled data. The PSO-based training was conducted six times for each one of the following combinations: 3 compensation schemes (oversampling + undersampling + no compensation) × 2 neural networks (one trained using AUC + one trained using 0:9AUC as the training objective).
For the final evaluation, a separate dataset of 10,000 test examples was created. This set was drawn from the same distribution as the training and validation sets (once for each pair of distributions). Such large testing sample size was used to minimize the uncertainty of the classifier’s performance estimation. The testing sets were characterized by equal class prevalence (5000 positive and 5000 negative examples). To compare the results for different scenarios a t-test with no assumption about equal variances was applied.
4.2. Experiment 2: breast cancer diagnosis data
For further validation, the real life problem of breast cancer diagnosis was also studied. Specifically, the problem was to assess the malignancy status of a breast mass. The diagnosis is made based on clinical and image findings (i.e., features extracted by physicians from mammograms and sonograms and clinical features from the patient’s history). The original data used in this experiment consisted of 1005 biopsy-proven masses (370 malignant and 645 benign). Each mass was described by a total number of 45 features. The data used in this experiment is an extended version of the data described in detail in (Jesneck et al., 2007). It was collected at Duke University Medical Center according to an IRB-approved protocol.
The original set of 1,005 masses was resampled to obtain training sets that reflected the class imbalance simulated in Experiment 1. Due to limited sample size, only one size of the training dataset was investigated. The training and validation sets consisted of 200 examples each throughout the entire experiment. This number was selected to ensure that a sufficient number of cases are excluded for final testing to reduce the estimation variance in testing performance. Actually, 415 examples were excluded for testing. The test set was fairly balanced with 41% cancer prevalence (170 malignant and 245 benign masses). The number of test examples was kept constant so that the variability of the classifier performance will be similar across all studied combinations of parameters. Furthermore, with these examples excluded, there were still enough left to obtain 200 training and 200 validation examples for all class imbalance scenarios considered in this analysis. As in Experiment 1, six values of 15 positive class prevalence were used ranging from 1% to 50%. Three numbers of features were used in this experiment: the original 45 features, 10 features and 5 features. The features were selected using simple forward selection based on the linear discriminant performance with the entire set of 1005 examples. Although it has been clearly shown that feature selection should be done independently of training to avoid an optimistic bias (Sahiner et al., 2000), our study simulates the scenario where diagnostic significance of the particular features is previously known. Studying the impact of class prevalence on feature selection extends beyond the scope of this article. As with the simulated data, for each value of positive class prevalence and number of features, the data was split 50 times to account for the variability introduced by the data split and the stochastic nature of the neural network training.
5. Results
5.1. Experiment 1: simulated data
The discussion of the study findings is organized around the three main issues: (i) effect of class imbalance of classifier performance, (ii) comparison of neural network training methods and (iii) comparison of data imbalance compensation schemes. The combined effects of data parameters such as number of features and feature correlation are also addressed within the context of the three main issues.
The results of Experiment 1 for uncorrelated features are summarized in Figure 1 and Figure 2, each showing the neural network average test performance based on the size of the training dataset (1000 and 100 examples respectively). The error bars show the standard deviations in performance obtained for 50 neural networks. For each figure, there are 6 subplots. The subplots show average values of the two clinical FOMs (top row – AUC, bottom row – 0:9AUC) for two different methods of training (bars with no stripes – BP, bars with stripes – PSO) and three class imbalance handling schemes (dark grey – undersampling, medium grey – no compensation, light grey – oversampling). In each row, the three subplots show the results for different number of features: 5 (subplots A and D), 10 (subplots B and E) and 20 (subplots C and F). Selected results for correlated features are shown in Fig. 3 to highlight trends observed as with uncorrelated features.
Fig. 1.
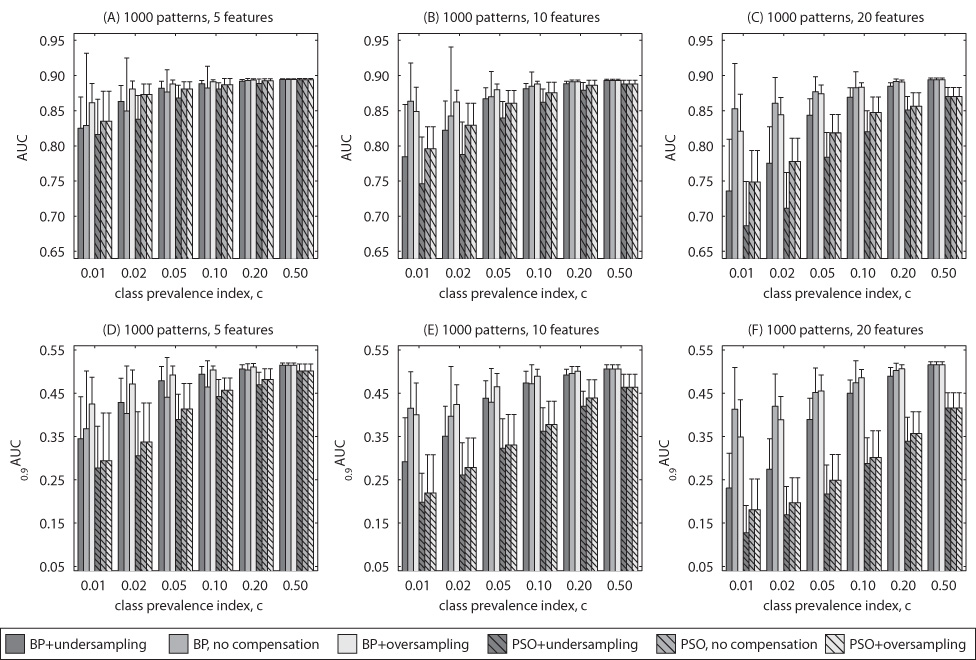
Simulated data with uncorrelated features: Average testing performance according to AUC and 0:9AUC for 1000 training examples.
Fig. 2.
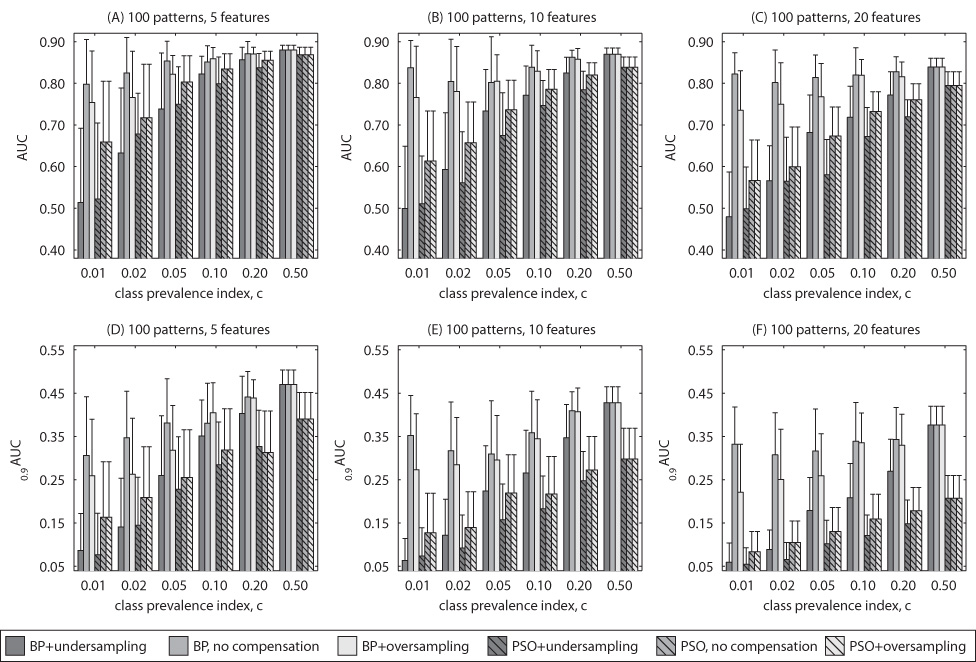
Simulated data with uncorrelated features: Average testing performance according to AUC and 0:9AUC for 100 training examples.
Fig. 3.
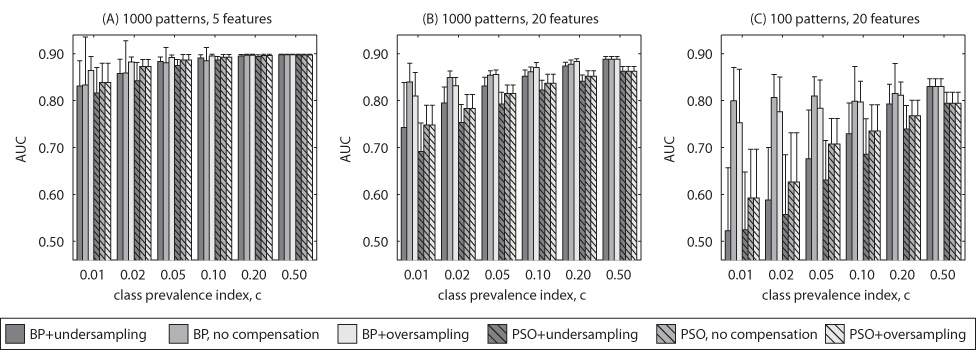
Simulated data with correlated features: Average testing performance for selected scenarios.
5.1‥1 Overall effect of class imbalance
Figure 1, Figure 2 and Figure 3 show that, in general, the increasing extent of class imbalance in the training data (i.e., reducing positive class prevalence) has an increasingly detrimental effect on the neural network classifier performance. In fact, for both BP and PSO training and no data imbalance compensation scheme, a statistically significant decline of AUC performance was observed (two-tailed p-value < 0:05) even for small imbalances (c ≤ 0:2) in vast majority of the cases. Note that the average performance of the neural networks trained for imbalanced datasets were compared to the performance obtained by the same training method when the data was balanced. This finding was consistent for both 100 and 1000 examples. Class imbalance appears to have even larger effect on the performance measured by 0:9AUC. For this FOM, a statistically significant decline was observed for class imbalance indices c ≤ 0:2, for all, except for one, analyzed choices of number of features and training sample size. Further, class imbalance appears to result in larger decline of the average performance when PSO is applied. All these findings were consistent for both correlated and uncorrelated data.
As expected, the decreasing positive class prevalence affected also the variability of the classifier’s final performance due to the random sampling of examples from the population and random factors present in the neural network training process. This was expressed in increasing standard deviation of the performance of 50 trained networks when c decreased. For example, for 5 uncorrelated features 1000 training examples and no correlation standard deviations of AUC estimates for BP with no compensation increased from 0.001 for c = 0:5 to 0.03 for c = 0:1 and to 0.1 for c = 0:01. With 100 training examples, the standard deviation of AUC increased from 0.01 for c = 0:5 to 0.04 for c = 0:1 and to 0.11 for c = 0:01.
5.1‥2 Effect of training method with no compensation
Comparison of the results for the two training methods leads to the following conclusions. For small number of features, PSO and MSE provide similar results for balanced datasets. It can be seen that the average performance for both training methods reaches values close to the population AUC of 0.9. When the number of features increases, average testing performance obtained by both training schemes decreases as well. The decrease in performance, however, is larger for the PSO-based training. Consistently with many previous studies, a low number of training examples has also detrimental effect for the average performance. Again, the drop in performance is larger for PSO training especially for 0:9AUC. Finally, as stated above the detrimental effect of low class prevalence was also higher for PSO. In conclusion, even though PSO neural network training was shown efficient for some tasks, in the scenarios analyzed in this study, BP is a preferable choice in terms of average performance. The results show no clear relation between the training method and performance variance.
5.1‥3 Effect of class imbalance compensation scheme
A clear conclusion from the obtained results is that undersampling is not a good choice of compensating for the imbalance in the training data. In fact, in most of the analyzed scenarios, undersampling provided worse performance than both no compensation and oversampling for any type of training and any FOM. This results was consistant for uncorrelated and correlated data.
As mentioned before, oversampling has no effect on the PSO training. Comparing oversampling for the BP training and no compensation does not lead to simple conclusions. It can be seen in Fig. 1, Fig. 2 and Fig. 3 that there are scenarios showing a beneficial effect of the oversampling and cases where oversampling has in fact a detrimental effect on the performance. Some regularities can be observed. Overall, for the examined distributions, oversampling is preferable when the ratio of number of training examples to number of features is high. For example, it can be seen that oversampling outperforms the no compensation approach for all c for the scenario with 5 features and 1000 training examples. On the other hand, in the case with 20 features and 100 examples, no compensation should be chosen for all c. This general observation holds for uncorrelated and correlated data and both examined FOMs. Comparison of the oversampling and no compensation approaches in terms of variance shows that generally the method providing a better average performance also results in lower performance variance.
5.2. Experiment 2: Breast cancer diagnosis data
Figure 4 shows the results of the second experiment based on the real clinical data. Most of the general conclusions drawn with experiment 1 hold for the clinical data study as well. Some minor differences, however, must be noted. The number of features has a smaller detrimental effect on the performance of PSO-trained classifiers. The general preference, however of choosing BP trained classifiers still holds.
Fig. 4.
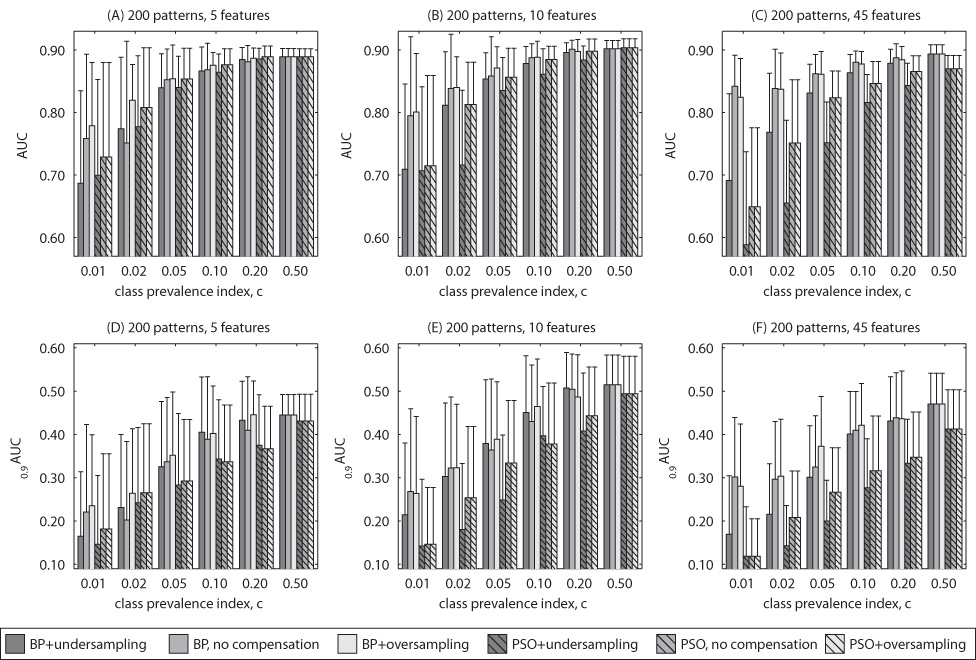
Results for clinical data. Average testing performance according to AUC and 0:9AUC for 200 training training examples.
In this experiment, a larger impact of class prevalence on the performance is observed. It can be explained by a more complex data distribution and larger number of examples needed to appropriately sample the feature space. Regarding compensation technique for the clinical data oversampling generally performed better than no compensation approach. However, there were still some cases where no compensation slightly outperformed oversampling. These results are consistent with the general conclusions drawn when using simulated data.
6. Conclusions
In this study the effect of a class imbalance in training data on the performance was evaluated for neural network based classifiers and the two-class classification problem. The confounding effects of other factors such as training sample size, number of features, and correlation between features were also considered. An extensive experimental study was performed based on simulated dataset and the conclusions were further validated with clinical data for breast cancer diagnosis.
The general conclusions drawn from this study are as follows. First, increasing class imbalance in the training dataset generally has a progressively detrimental effect on the classifier’s test performance measured by AUC and 0:9AUC. This is true for small and moderate size training datasets that contain either uncorrelated or correlated features. In the majority of the analyzed scenarios backpropagation provided better results as PSO training was more susceptible to factors such as class imbalance, small training sample size and large number of features. Again, this finding was true for both correlated and uncorrelated features.
Although undersampling was typically an inferior choice to compensate for class imbalance, there is no clear winner between oversampling and no compensation. The classifier designer should take into account factors such as class distribution, class prevalence, number of features and available training sample size when choosing a compensation strategy for training sets with class imbalances.
7. Acknowledgments
This work was supported in part by grants R01-CA-1901911, R01-CA-112437, and R01-CA-95061 from the National Cancer Institute.
The authors would like to thank the members of Computational Intelligence Laboratory at the University of Louisville and the members of Duke Advanced Imaging Laboratory at Duke University especially Dr. Robert Saunders for helpful discussions.
Footnotes
An abbreviated version of some parts of this article appeared in (Mazurowski et al., 2007).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aha DW, Kibler D, Albert MK. Instance-based learning algorithms. Machine Learning. 1991;6:37–66. [Google Scholar]
- Barnard E, Botha EC. Back-propagation uses prior information efficiently. IEEE Transactions on Neural Networks. 1993;4:794–802. doi: 10.1109/72.248457. [DOI] [PubMed] [Google Scholar]
- Beiden SV, Maloof MA, Wagner RF. A general model for finite-sample effects in training and testing of competing classifiers. IEEE Transaction on Pattern Analysis and Machine Intelligence. 2003;23:1561–1569. [Google Scholar]
- Boroczky L, Zhao L, Lee KP. Feature subset selection for improving the performance of false positive reduction in lung nodule CAD. IEEE Transactions Information Technology in Biomedicine. 2006;10:504–511. doi: 10.1109/titb.2006.872063. [DOI] [PubMed] [Google Scholar]
- Bradley AP. The use of the area uncer the roc curve in the evaluation of machine learning algorithms. Pattern Recognition. 1997;30:1145–1159. [Google Scholar]
- Chan H-P, Sahiner B, Hadjiiski L. Sample size and validation issues on the development of CAD systems; Proceedings of the 18th International Congress and Exhibition on Computer Assisted Radiology and Surgery; 2004. [Google Scholar]
- Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. Smote: synthetic minority over-sampling technique. Journal of Artificial Intelligence Research. 2002;16:321–357. [Google Scholar]
- Cheng H, Cai X, Chen X, Hu L, Lou X. Computer-aided detection and classification of microcalcifications in mammograms: a survey. Pattern Recognition. 2003;36:2967–2991. [Google Scholar]
- Clerc M, Kennedy J. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation. 2002;6:58–73. [Google Scholar]
- Doi K. Diagnostic imaging over the last 50 years: research and development in medical imaging science and technology. Physics in Medicine and Biology. 2006;51:R5–R27. doi: 10.1088/0031-9155/51/13/R02. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. Wiley-Interscience; 2000. [Google Scholar]
- Elazmeh W, Japkowicz N, Matwin S. Evaluating misclassifications in imbalanced data. Lecture Notes in Computer Science. 2006;4212:126–137. [Google Scholar]
- Fukunaga K, Hayes RR. Effect of sample size in classifier design. IEEE Transaction on Pattern Analysis and Machine Intelligence. 1989;11:873–885. [Google Scholar]
- Gur D, Wagner RF, Chan H-P. On the repeated use of databases for testing incremental improvement of computer-aided detection schemes. Academic Radiology. 2004;11:103–105. doi: 10.1016/s1076-6332(03)00511-7. [DOI] [PubMed] [Google Scholar]
- Habas PA, Zurada JM, Elmaghraby AS, Tourassi GD. Particle swarm optimization of neural network CAD systems with clinically relevant objectives; Proceedings of Medical Imaging 2007: Computer-Aided Diagnosis; 2007. 65140M pp. [Google Scholar]
- Hamamoto Y, Uchimura S, Tomita S. On the behavior of artificial neural network classifiers in high-dimensional spaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1996;18:571–574. [Google Scholar]
- Jain A, Zongker D. Feature selection: evaluation, application, and small sample performance. IEEE Transaction on Pattern Analysis and Machine Intelligence. 1997;19:153–158. [Google Scholar]
- Japkowicz N. Learning from imbalanced data sets: a comparison of various strategies. AAAI Workshop on Learning from Imbalanced Data Sets. 2000:00–05. [Google Scholar]
- Japkowicz N, Stephen S. The class imbalance problem: a systematic study. Intelligent Data Analysis Journal. 2002;6:429–450. [Google Scholar]
- Jesneck JL, Lo JY, Baker JA. Breast mass lesions: computer-aided diagnosis models with mammographic and sonographic descriptors. Radiology. 2007;244:390–398. doi: 10.1148/radiol.2442060712. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Metz CE, Nishikawa RM. A receiver operating characteristic partial area index for highly sensitive diagnostic tests. Radiology. 1996;201:745–750. doi: 10.1148/radiology.201.3.8939225. [DOI] [PubMed] [Google Scholar]
- Kawamoto K, Houlihan CA, Balas EA, Lobach DF. Improving clinical practice using clinical decision support systems: a systematic review of trials to identify features critical to success. British Medical Journal. 2005;330:765–772. doi: 10.1136/bmj.38398.500764.8F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy J, Eberhart R. Particle swarm optimization; Proceedings of IEEE International Conference on Neural Networks; 1995. pp. 1942–1948. [Google Scholar]
- Li Q, Doi K. Reduction of bias and variance for evaluation of computer-aided diagnostic schemes. Medical Physics. 2006;33:868–875. doi: 10.1118/1.2179750. [DOI] [PubMed] [Google Scholar]
- Li Q, Doi K. Comparison of typical evaluation methods for computer-aided diagnostic schemes: Monte Carlo simulation study. Medical Physics. 2007;34:871–876. doi: 10.1118/1.2437130. [DOI] [PubMed] [Google Scholar]
- Lisboa PJ. A review of evidence of health benefit from artificial neural networks in medical intervention. Neural Networks. 2002;15:11–39. doi: 10.1016/s0893-6080(01)00111-3. [DOI] [PubMed] [Google Scholar]
- Lisboa PJ, Taktak AFG. The use of artificial neural networks in decision support in cancer: a systematic review. Neural Networks. 2006;19:408–415. doi: 10.1016/j.neunet.2005.10.007. [DOI] [PubMed] [Google Scholar]
- Maloof MA. Learning when data sets are imbalanced and when costs are unequal and unknown; Proceedings of Workshop on Learning from Imbalanced Data Sets; 2003. [Google Scholar]
- Mazurowski MA, Habas PA, Zurada JM, Tourassi GD. Impact of low class prevalence on the performance evaluation of neural network based classifiers: Experimental study in the context of computer-assisted medical diagnosis; Proceedings of International Joint Conference on Neural Networks; 2007. pp. 2005–2009. To appear in Proceedings of 2007 Joint Conference on Neural Networks. [Google Scholar]
- Metz CE, Herman BA, Shen J-H. Maximum likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data. Statistics in Medicine. 1998;17:1033–1053. doi: 10.1002/(sici)1097-0258(19980515)17:9<1033::aid-sim784>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Mitchell T. Machine Learning. McGraw Hill; 1997. [Google Scholar]
- Obuchowski NA. Receiver operating characteristic curves and their use in radiology. Radiology. 2003;229:3–8. doi: 10.1148/radiol.2291010898. [DOI] [PubMed] [Google Scholar]
- Raudys S. On dimensionality, sample size, and classification error of nonparametric linear classification algorithms. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19:667–671. doi: 10.1109/tpami.1980.4767011. [DOI] [PubMed] [Google Scholar]
- Raudys SJ, Jain AK. Small sample size effects in statistical pattern recognition: recommendations for practitioners. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1991;13:252–264. [Google Scholar]
- Rumelhart DE, Hinton GE, Williams RJ. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. volume 1. MIT Press; 1986. chapter Learning internal representations by error propagation; pp. 318–362. [Google Scholar]
- Sahiner B, Chan HP, Petrick N, Wagner RF, Hadjiiski L. Feature selection and classifier performance in computer-aided diagnosis: the effect of finite sample size. Medical Physics. 2000;27:1509–1522. doi: 10.1118/1.599017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampat MP, Markey MK, Bovik AC. Handbook of Image and Video Processing. Academic Press; 2005. Computer-aided detection and diagnosis in mammography; pp. 1195–1217. [Google Scholar]
- van den Bergh F, Engelbrecht AP. A cooperative approach to particle swarm optimization. IEEE Transactions on Evolutionary Computation. 2004;8:225–239. [Google Scholar]
- Wagner RF, Chan H-P, Sahiner B, Petrick N. Finite-sample effects and resampling plans: applications to linear classifiers in computer-aided diagnosis; Proceedings of Medical Imaging 1997: Image Processing; 1997. pp. 467–477. [Google Scholar]
- Weiss GM, Provost F. The effect of class distribution on classifier learning: an empirical study. Department of Computer Science, Rutgers University; Technical report. 2001
- Wu Y, Giger ML, Doi K, Vyborny CJ, Schmidt RA, Metz CE. Artificial neural networks in mammography: application to decision making in the diagnosis of breast cancer. Radiology. 1993;187:81–87. doi: 10.1148/radiology.187.1.8451441. [DOI] [PubMed] [Google Scholar]
- Zhang GP. Neural networks for classification: a survey; IEEE Transactions on Systems, Man, and Cybernetics - Part C: Applications and Reviews; 2000. pp. 451–462. [Google Scholar]
- Zhou Z-H, Liu X-Y. Training cost-sensitive neural networks with methods addressing the class imbalance problem. IEEE Transactions on Knowledge and Data Engineering. 2006;18:63–77. [Google Scholar]


