Computational studies of the O₂-evolving complex of photosystem II and biomimetic oxomanganese complexes

Abstract

In recent years, there has been considerable interest in studies of catalytic metal clusters in metalloproteins based on Density Functional Theory (DFT) quantum mechanics/molecular mechanics (QM/MM) hybrid methods. These methods explicitly include the perturbational influence of the surrounding protein environment on the structural/functional properties of the catalytic centers. In conjunction with recent breakthroughs in X-ray crystallography and advances in spectroscopic and biophysical studies, computational chemists are trying to understand the structural and mechanistic properties of the oxygen-evolving complex (OEC) embedded in photosystem II (PSII). Recent studies include the development of DFT-QM/MM computational models of the Mn₄Ca cluster, responsible for photosynthetic water oxidation, and comparative quantum mechanical studies of biomimetic oxomanganese complexes. A number of computational models, varying in oxidation and protonation states and ligation of the catalytic center by amino acid residues, water, hydroxide and chloride have been characterized along the PSII catalytic cycle of water splitting. The resulting QM/MM models are consistent with available mechanistic data, Fourier-transform infrared (FTIR) spectroscopy, X-ray diffraction data and extended X-ray absorption fine structure (EXAFS) measurements. Here, we review these computational efforts focused towards understanding the catalytic mechanism of water oxidation at the detailed molecular level.

1. Introduction

Life on earth is sustained by the annual production of 260 Gigatons of atmospheric oxygen during photosynthesis [1, 2]. Oxygen evolution is driven by the absorption of solar light by the special chlorophyll species P680 and the subsequent oxidation of water by a catalytic oxomanganese cluster in the transmembrane protein complex called photosystem II (PSII). With the structure of the so-called O₂-evolving complex (OEC) in PSII not yet established, there have been extensive studies of the reaction mechanism, including biochemical and spectroscopic work aimed at elucidating fundamental structure/function relations in PSII [3-6]. Computational chemists use the models obtained by experimental studies as the starting point for the theoretical analysis of the active site of PSII [7-17]. With limited information regarding the structure, ligation and oxidation states of metal centers in the OEC of PSII, modeling the spectroscopy and mechanistic properties of the oxomanganese cluster is a challenge.

Quantum mechanics/molecular mechanics (QM/MM) modeling is an area of active research. In conjunction with density functional theory (DFT), QM/MM methods allow the explicit modeling of catalytic active sites in metalloproteins, including the influence of the surrounding protein environment. In particular, models of the oxomanganese cluster embedded in PSII have been developed, varying in the Mn oxidation states, protonation states of the ligands, the structure of oxo-bridges between Mn centers and the coordination of proteinaceous side chains [13, 15, 18, 19]. These studies of QM/MM structural models have also included simulations of extended X-ray absorption fine-structure spectra, the analysis of substrate water molecules and the vibrational analysis of ligands attached to the metal cluster, providing valuable insight on the interpretation of experimental data of the native enzyme. Therefore, there has been a productive integration of experimental and computational studies aimed at elucidating the overall oxidation and structural changes of the OEC as it evolves along the catalytic cycle.

In this paper, we review recent efforts towards understanding structure/function relations in PSII by developing and studying QM/MM computational structural models of the OEC embedded in PSII. The review is organized as follows. Section 2 introduces background information on the OEC in PSII and the process of oxygen evolution. The experimental information on the OEC metal-cluster architecture and the structure of the complete PSII transmembrane protein complex are essential for building realistic computational models of PSII. Section 3 is devoted to QM/MM models of the OEC in the dark stable S₁ state, including a description of the structure and ligation relevant to the native enzyme. Various models of the Mn₄Ca metal cluster have been developed, including structures with a ‘dangling’ Mn attached to a cuboidal tetramer complex directly, or via an oxo-bridge [20-22]. The properties of the models are directly compared to X-ray, EXAFS and FTIR data of the native OEC of PSII particles. This section also reviews the QM/MM vibrational analysis of the D1-A344 ligand and the underlying changes in vibrational properties induced by S-state transitions. It also addresses the QM/MM ligation of substrate water molecules, and discusses the effect of S-state transitions on the substrate-water binding to the metal cluster as revealed in light of time-resolved mass spectrometry measurements. For completeness, Section 3 also discusses the analysis of biomimetic oxomanganese clusters at the DFT level of theory, including the description of structural, electronic and magnetic properties as compared to readily available experimental data. Section 4 reviews QM/MM models of the OEC catalytic intermediates as the OEC cycles between different oxidation states and oxidizes water to dioxygen. Section 5 is focused on the potential mechanistic role of CP43-R357 suggested by QM/MM structural models. Finally, Section 6 summarizes and concludes.

2. Oxygen Evolution in Photosystem II

Atmospheric oxygen is produced during the light period of photosynthesis in the thylakoid membranes of green-plant chloroplasts and the internal membranes of cyanobacteria. The reaction involves photochemical water splitting into dioxygen, protons and electrons, as follows:

$$2{\mathrm{H}}_2\mathrm{O}\to {\mathrm{O}}_2+4{{\mathrm{H}}^{+}}_{\text{lumen}}+4{\mathrm{e}}^{-}$$ (1)

The process is catalyzed by a metal cluster containing four manganese ions and calcium at the so-called O₂-evolving complex (OEC) of photosystem II (PSII), shown in Figs. 1 and 2. A complete description of the overall photosynthetic light reaction in PSII has yet to be developed, although extensive work over many years of study has provided considerable insight [3, 5, 23-25].

Figure 1.

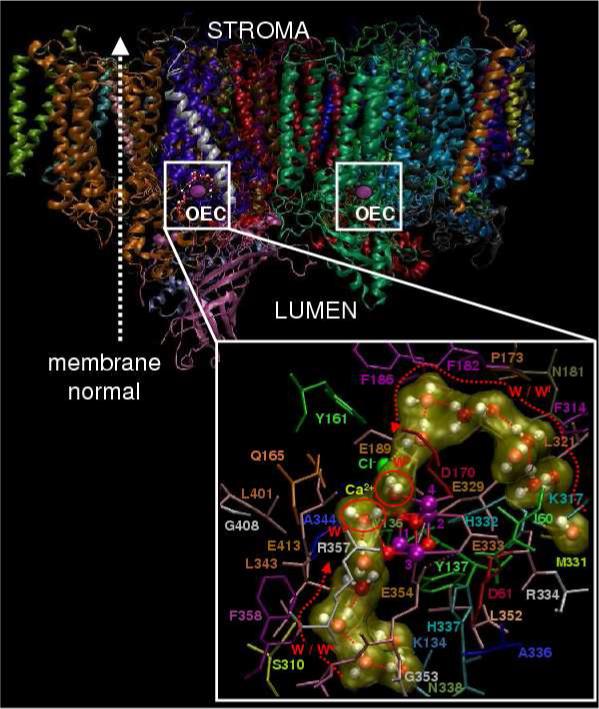
Molecular structure of the photosystem II dimer proposed by the 1S5L X-ray diffraction model from Thermosynechococcus elongatus [20] and inset QM/MM description of the oxygen-evolving complex (OEC) [13], including substrate water pathways from the lumen. Purple: Mn, Red: O; Yellow: Ca²⁺; and Green: Cl⁻.

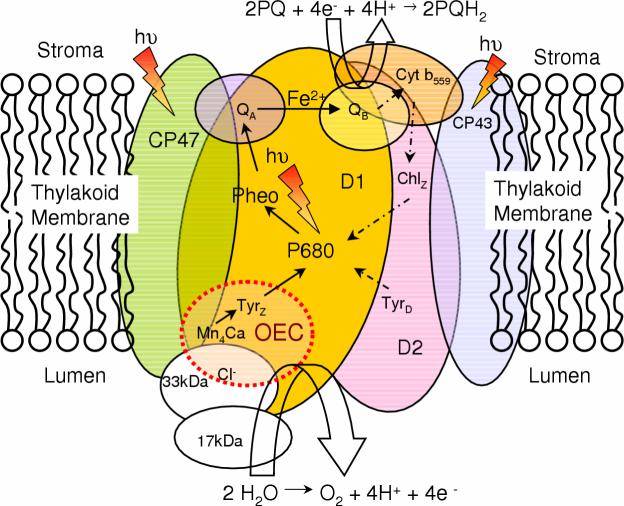
Figure 2.

Schematic representation of Photosystem II and its components embedded in the thylakoid membrane. The driving force for the Kok cycle is the repeated oxidation of P680 via successive absorption of photons. Note that the dashed and solid arrows indicate secondary and primary paths of electron transfer, respectively

Photoabsorption by the specialized chlorophyll a species, P680, triggers a chain of electron transfer (ET) reactions (see Fig. 2). The excited singlet state of P680 decays to the oxidized state P680⁺ by ET to a nearby pheophytin (Pheo), within approximately 2 ps after photoexcitation of P680. The charge separated state is stabilized by ET to a primary quinone electron acceptor (Q_A), which functions as a one-electron carrier. Subsequently, a secondary plastoquinone electron acceptor (PQ) functions as a two-electron carrier and forms plastohydroquinone (PQH₂) upon two-electron reduction and protonation with protons from the stromal side of the membrane [26]:

$$2\mathrm{PQ}+4{{\mathrm{H}}^{+}}_{\text{stroma}}+4{\mathrm{e}}^{-}\to 2{\mathrm{PQH}}_2$$ (2)

PQH₂ has low affinity for the PQ site and is released as neutral dihydroquinol into the stroma, displaced by a PQ from the membrane pool [3]. The photooxidized chlorophyll a species P680⁺ is reduced by a redox active tyrosine (Y_Z) [27-29] which is in turn reduced by the oxidation of water at the OEC, described in Eq. (1), releasing protons to the lumen. The combined redox reactions (1) and (2), effectively transfer protons from the stroma to the lumen, establishing a transmembrane pH (free-energy) gradient that is essential for ATP biosynthesis.

Advancing our understanding of the functional roles of the OEC components in the catalytic mechanism of oxygen evolution is an important challenge in Biology as well as in the design of biomimetic systems for artificial photosynthesis. In particular, the underlying mechanism is a paradigm for engineering direct solar fuel production systems, since it is based on a catalyst that involves inexpensive metals and has an overall efficiency that is yet to be matched by artificial processes [30]. However, progress in the field has been partially hindered by the lack of fundamental understanding of the key structural factors responsible for the efficient accumulation of oxidizing equivalents in the OEC. Here, we review recent advances in the development of structural models of the OEC of PSII, based on state-of-the-art quantum mechanics/molecular mechanics (QM/MM) hybrid methods applied in conjunction with recent breakthroughs in X-ray spectroscopy. The computational models address several aspects that have so far remained largely elusive to theoretical studies, including the nature of ligands attached to the catalytic center, such as amino acid residues, water, hydroxide and chloride, and the influence of the surrounding protein environment on the structural and electronic properties of the oxomanganese core.

According to the catalytic cycle proposed by Joliot and Kok [1, 2] (see Fig. 3), the photosynthetic dioxygen evolution involves multiple elementary steps. Starting from the dark stable S₁ state, the OEC is advanced by single-electron steps to a sufficiently high oxidation state that reacts with H₂O to form O₂. Each state along this so-called ‘Kok cycle’ is called a ‘storage-state’, or simply ‘S-state’, with S₀ representing the most reduced state of the OEC and S₄ the most oxidized state. In the dark, all S-states spontaneously convert into the S₁ resting state within minutes. Therefore, the S₁ state is commonly used as the point of departure for the elucidation of the molecular structure of catalytic intermediates.

Figure 3.

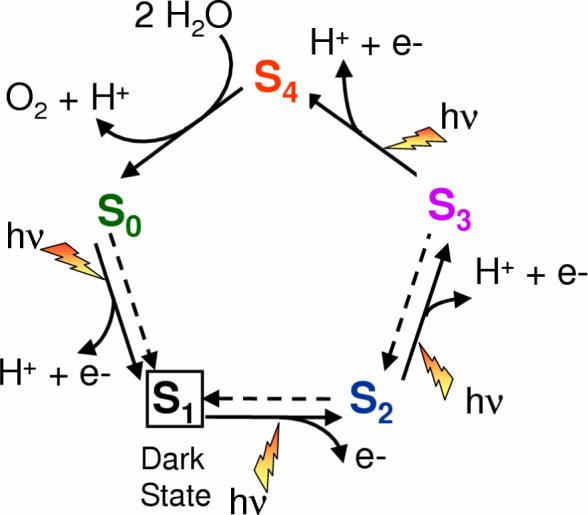
Catalytic cycle proposed by Joliot and Kok for water splitting into dioxygen, protons and electrons at the OEC in PSII [1,2]. Dashed arrows indicate spontaneous interconversion processes in the dark. The steps for substrate water attachment and proton release are only tentatively proposed and might change with pH.

A number of structural models of the OEC have been developed, including experimental [3, 5, 17, 25, 31-37] and theoretical [9, 38, 39] studies with mechanistic implications, in prolonged attempts to rationalize the catalytic cycle of water splitting at the detailed molecular level. However, many fundamental aspects of the reaction intermediates are the still the subject of current debate. In fact, unequivocal functional models of the S-states are yet to be established. Recent breakthroughs in X-ray crystallography yielded molecular structural models of PSII [20-22] resolving nearly all cofactors and most of the amino acid residues in the protein complex structure at 3.0—3.5 Å resolution (see Fig. 1). These X-ray models suggest that the core of the OEC consists of a pentanuclear metal cluster including four Mn ions and Ca linked by oxo-bridges. Figure 4 shows one of the suggested models [20].

Figure 4.

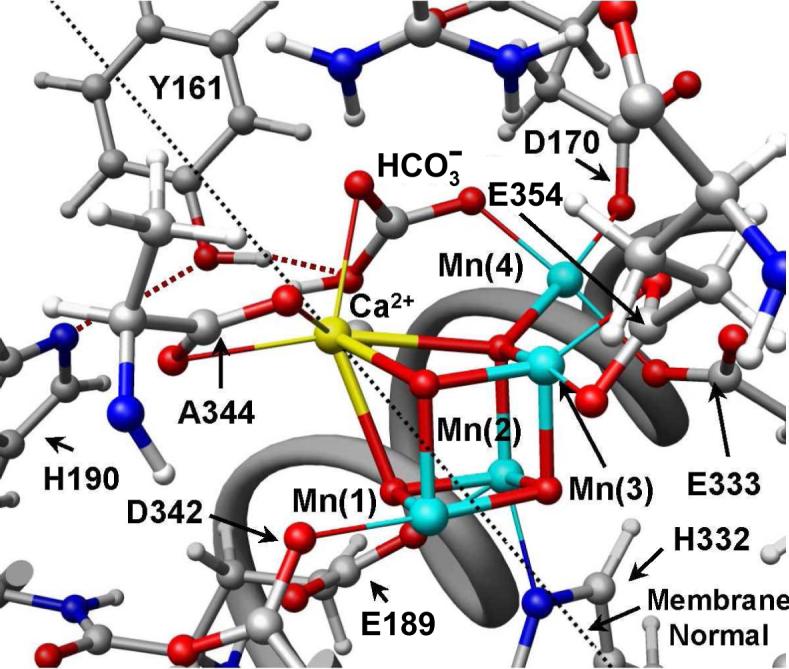
The OEC and its surrounding molecular environment proposed by the X-ray diffraction structure 1S5L [20], including the pentanuclear Mn₄Ca cluster and the redox active D1-Y161 (Y_Z).

Despite the new insight provided by the recent crystallographic structures, chemically sensible models of the OEC of PSII are yet to be established. In fact, many aspects of the recently reported X-ray diffraction structures of PSII [20-22] have met with criticism [13, 16, 17, 40-43], including both the geometric features of the Mn cluster [41, 42, 44] and the proposed proteinaceous ligation [40, 43, 45-48]. The fact that the usual coordination numbers of Ca²⁺ and high-valent Mn are 6−8, and 5−6, respectively, is a clear indication of the incomplete description of ligands in the reaction center. Furthermore, it is possible that several ligands (including vital substrate water molecules and Cl⁻, which are essential for O₂ evolution) could not be resolved even at the highest resolution. In addition to the moderate resolution and incomplete description of ligands in the reaction center, it is also possible that the high-doses of X-rays employed during data collection might have induced structural damage due to photoreduction of the Mn-cluster [49]. Nevertheless, the proposed X-ray models still constitute the most valuable starting point for the development of complete functional models of PSII. The resulting models are expected to provide valuable insight into a wide range of experimental observations that remain to be fully understood at the molecular level.

Recent computational models of the OEC have been based on the X-ray crystal structure of PSII from the cyanobacterium Thermosynechococcus elongatus [20]. Chemically sensible models were developed according to molecular mechanics methods [16, 17], quantum mechanical studies based on density functional theory (DFT) [14, 38], and state-of-the-art DFT quantum mechanics/molecular mechanics (DFT-QM/MM) hybrid methods [13, 15, 18, 19, 39]. In particular, the QM/MM structural models were consistent with available mechanistic data [25] and also compatible with X-ray diffraction models [20-22] and extended X-ray absorption fine structure measurements of PSII [41, 42, 44, 50].

3. Structure of the Oxygen Evolving Complex in the S₁ State

Most structural models of the OEC of PSII have been developed by use of spectroscopic and biochemical studies [51-54], including electron paramagnetic resonance (EPR) spectroscopy [36, 55-60], X-ray absorption spectroscopy (XAS) [41, 42, 44, 61-64], optical spectroscopy [65], Fourier transformed infrared spectroscopy (FTIR) [40, 43, 46, 48, 66] and site directed mutagenesis [40, 43, 45, 46, 67-75]. In addition, there have been significant advances in the development of X-ray diffraction models [20, 21, 76-78]. The first X-ray structure of PSII resolved the framework of the protein complex at 3.8 Ǻ resolution [76]. A subsequent refinement at 3.7 Ǻ resolution [77] assigned the extrinsic subunits. More recently, X-ray models have resolved nearly all amino acid residues and cofactors at 3.5—3.0 Ǻ resolution [20, 21, 78]. The X-ray diffraction data also provided the overall electronic density of the OEC metal cluster, suggesting possible structural models of the oxomanganese cluster and proteinaceous ligation schemes, including several amino-acid residues already thought to be ligands on the basis of site-directed mutagenesis and spectroscopic studies [67, 68].

The precise positions of the Mn ions and substrate water molecules are still uncertain in the current X-ray diffraction models, since the coordinate error in the density maps is usually as high as 1 Å [77] and the resolution of bridging ligands is typically out of reach [41]. Therefore, the X-ray models of the OEC metal centers have relied both on the overall electronic density maps and on Mn-Mn distances determined by XAS studies [79, 80].

The X-ray models of the metal cluster of the OEC partially agree with the “3 + 1 Mn tetramer” structure, previously suggested by EPR spectroscopic studies [36, 63]. The Mn-tetramer (see Fig. 3) takes the form of a Mn₄Ca cuboidal cluster, including three closely associated manganese ions linked to a single μ₄-oxo-ligated Mn ion, often called the “dangling manganese ion”. However, this cuboidal model is still the subject of debate [41, 44]. In particular, it is in disagreement with the most recent structures suggested by polarized EXAFS spectroscopic studies [41, 44] and also disagrees with previously proposed structures in which three Mn ions were placed roughly at three corners of an isosceles triangle, with the fourth Mn ion at the center of the triangle, either protruding toward the lumenal surface of the membrane [76, 77] or parallel to it [21].

Computational studies have investigated whether the proposed X-ray diffraction models of the OEC in PSII can lead to chemically sensible molecular structures that are structurally stable where the metal centers have complete coordination spheres [9, 10, 13-15, 38]. Recent theoretical work included rigorous DFT calculations of inorganic model complexes [9, 10, 14, 38] and more complete structural models with coordination of the OEC metal cluster by water, protein, ligands, hydroxide and Cl⁻ ions, including the perturbational influence of the surrounding protein environment [13, 15-17].

3.1. Biomimetic oxomanganese complexes

Earlier Studies

Recent DFT studies have assessed the capabilities and limitations of the B3LYP hybrid density functional as applied to studies of electronic, magnetic and structural properties of biomimetic oxomanganese inorganic complexes [14]. Previous theoretical studies have found that the DFT/B3LYP methodology typically overestimated Mn-Mn distances in model complexes with μ-oxo bridges as compared to X-ray diffraction data, with typical errors in the 0.10—0.15 Å range [38, 81]. Even more critical was the claim that B3LYP overestimated Mn-ligand distances along the Jahn-Teller axis of Mn³⁺ by as much as 0.23 Å [38, 81]. These problems seemed to be rather serious since the reported errors were comparable to typical structural rearrangements in the OEC metal cluster induced by oxidation of the constituent ions (i.e., changes of Mn-ligand bond-lengths in the 0.1−0.2 Å). In addition, it was known that hybrid functionals often overestimate the relative stability of high-spin over low-spin states of transition metal complexes [82, 83] a difficulty that could be critical in the process of identifying the nature of the ground electronic state, or in studies of spin-crossover phenomena in transition metal complexes [82, 84-89].

Benchmark Complexes

Recent studies [14] focused of well-characterized oxomanganese complexes [90-93], in an effort to assess the limitations of hybrid density functionals at the quantitative level. Calculations were based on the broken symmetry (BS) DFT method [94-97], since the complexes of interest have unpaired spins and therefore require spin-polarized calculations. The BS-DFT allowed for calculations of exchange magnetic coupling constants, that were in very good agreement with magnetic experimental data, and the ligand field analysis for metal d→d, charge transfer (ligand→metal, metal→ligand), and intervalence charge transfer (metal→metal or ligand→ligand) transitions [14].

Calculations on benchmark model compounds [14] included the synthetic di-μ-oxo Mn^IIIMn^IV complexes [Mn^IIIMn^IV(μ-O)₂(H₂O)₂(terpy)₂]³⁺ (terpy = 2,2’:6,2’’-terpyridine) and [Mn^IIIMn^IV(μ-O)₂(phen)₄]³⁺ (phen = 1,10-phenanthroline), the [Mn₃O₄(bpy)₄(H₂O)₂]⁴⁺ (bpy=2,2’-bipyridine) trimer, and the [Mn₄O₄L₆]⁺ tetramer, with L=Ph₂PO⁻². As a representative example of these model calculations Figure 5 shows the molecular structure of complex [Mn^IIIMn^IV(O)₂(phen)₄]³⁺ (phen = 1,10- phenanthroline) (a) and a simplified model system (b), optimized at the broken symmetry unrestricted B3LYP level with the following basis set: LACVP for manganese, 6−31G(d) for oxo-bridge oxygen atoms, 6−31G for water oxygen atoms and N, 3−21G for carbon and hydrogen. The agreement with experiments, for example in terms of structural parameters, was excellent so long as the μ-oxo bridges are modeled with sufficiently flexible basis sets. This was also the case for all characterized model complexes [14]. The analysis of the Mn trimer [Mn₃O₄(bpy)₄(OH₂)₂]⁴⁺, however, showed that the B3LYP functional can erroneously predict the relative stability of states of different spin multiplicity, usually overstabilizing high-spin states [14].

Figure 5.

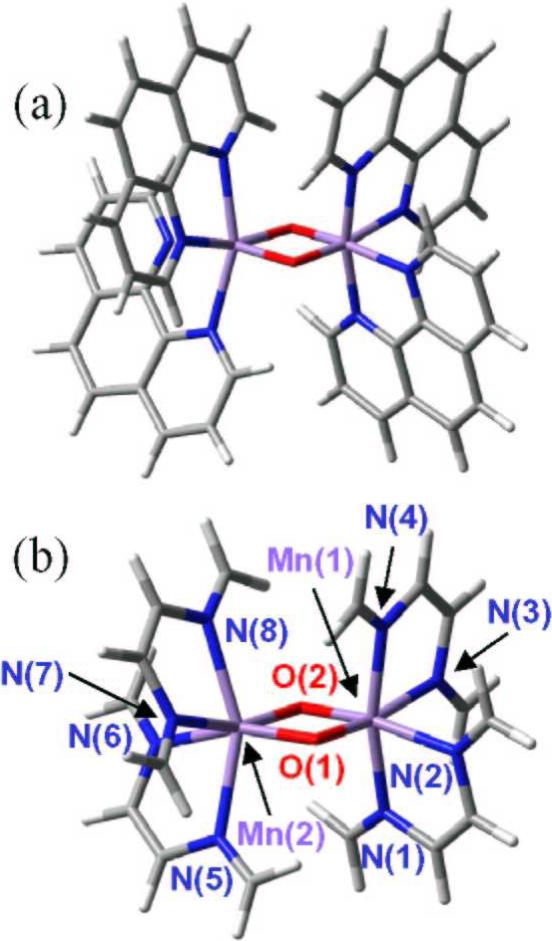
Molecular structure of complex [Mn^IIIMn^IV(O)₂(phen)₄]³⁺ (phen = 1,10-phenanthroline) (a) and simplified model system (b), optimized at the broken symmetry unrestricted B3LYP level with the following basis set: LACVP for manganese, 6−31G(d) for oxo-bridge oxygen atoms, 6−31G for water oxygen atoms and N, 3−21G for carbon and hydrogen [14].

These observations concluded that the hybrid B3LYP functional can predict equilibrium distances in Mn complexes (such as the OEC prepared in pre-selected spin-electronic states), in excellent agreement with X-ray diffraction data. Overestimations in Mn-Mn distances (by as much as 0.10−0.15 Å) and of Mn-ligand distances (along the Jahn-Teller axis of Mn³⁺ ions by as much as 0.23 Å) were significantly corrected simply by expanding the basis set of the ligands coordinated to the Mn ions with polarization functions. The description of the relative stability of low-lying spin-states associated with open-shell transition metal compounds, however, might be beyond the capabilities of the DFT/B3LYP level. Therefore, the assessment of DFT models must rely upon the analysis of a variety of structural and electronic properties, beyond the energetic analysis, as directly compared to experimental data.

OEC Model Complexes

Biomimetic models of the OEC of PSII have also been developed at the DFT/B3LYP level of theory [9, 10, 14]. These studies included models of the hydrated Mn₄Ca oxomanganese model complex, chelated only by water, hydroxyl ligands, and chloride, as well as models where the metal cluster was ligated by formates and imidazole ligands, mimicking the coordination of amino acid residues suggested by X-ray diffraction models. Even in the absence of the surrounding protein, the conformation of the hydrated Mn₄Ca cluster could be remarkably similar to the X-ray diffraction model of the oxomanganese cluster in PSII [20]. In addition, the predicted high-valent spin configuration of the ground electronic state was consistent with the S₁ state of the OEC of PSII, as indicated by EPR [98, 99] and X-ray spectroscopic evidence [80, 100]. These results suggested that the electronic and structural properties of the Mn₄Ca cluster, embedded in PSII, are intrinsic of the inorganic core. Therefore, the protein environment surrounding the Mn₄Ca cluster must have been adapted by natural selection to the electronic and structural properties of the Mn₄Ca cluster, in order to play a major catalytic role through the efficient supply of substrate (water) molecules and the removal of products (i.e., protons, electrons and dioxygen). Furthermore, on the basis of the similar structural and electronic properties of complexes with different ligands, it is natural to expect that a wide range of synthetic oxomanganese catalysts, based on the cuboidal ’3+1 Mn-tetramer’ and with different types of ligands, should be feasible.

3.2. QM/MM models

DFT models of PSII have been studied for many years, long before the crystal structures of PSII were available [7, 11]. These studies provided valuable insight into the intrinsic properties of the inorganic core, isolated from the protein environment. However, the influence of the surrounding protein could not be modeled since the protein structure was not known. Recent breakthroughs in X-ray diffraction spectroscopy [20, 21, 101], and XAS techniques [41, 42, 44, 49, 61, 80, 102-105] have motivated the development of QM/MM molecular models of PSII including not only the intrinsic properties of the oxomanganese cluster but also the perturbational influence of the surrounding protein environment [13, 15-19, 39]. The analysis of fully relaxed QM/MM configurations provided biologically relevant insight into the mechanisms of water splitting since room-temperature thermal fluctuations have negligible effects on the structure, protonation state, or charge localization effects of PSII, as indicated by XAS studies carried out at 20 K and room-temperature [42]. However, some deprotonation steps and structural rearrangements along the catalytic cycle occur only at room temperature, indicating that thermal nuclear fluctuations are essential for the activation mechanism. Figure 6 shows a QM/MM structural model of the OEC of PSII in the S₁ state, based on the 1S5L X-ray diffraction structure of PSII [20], explicitly considering about 2000 atoms of PSII.

Figure 6.

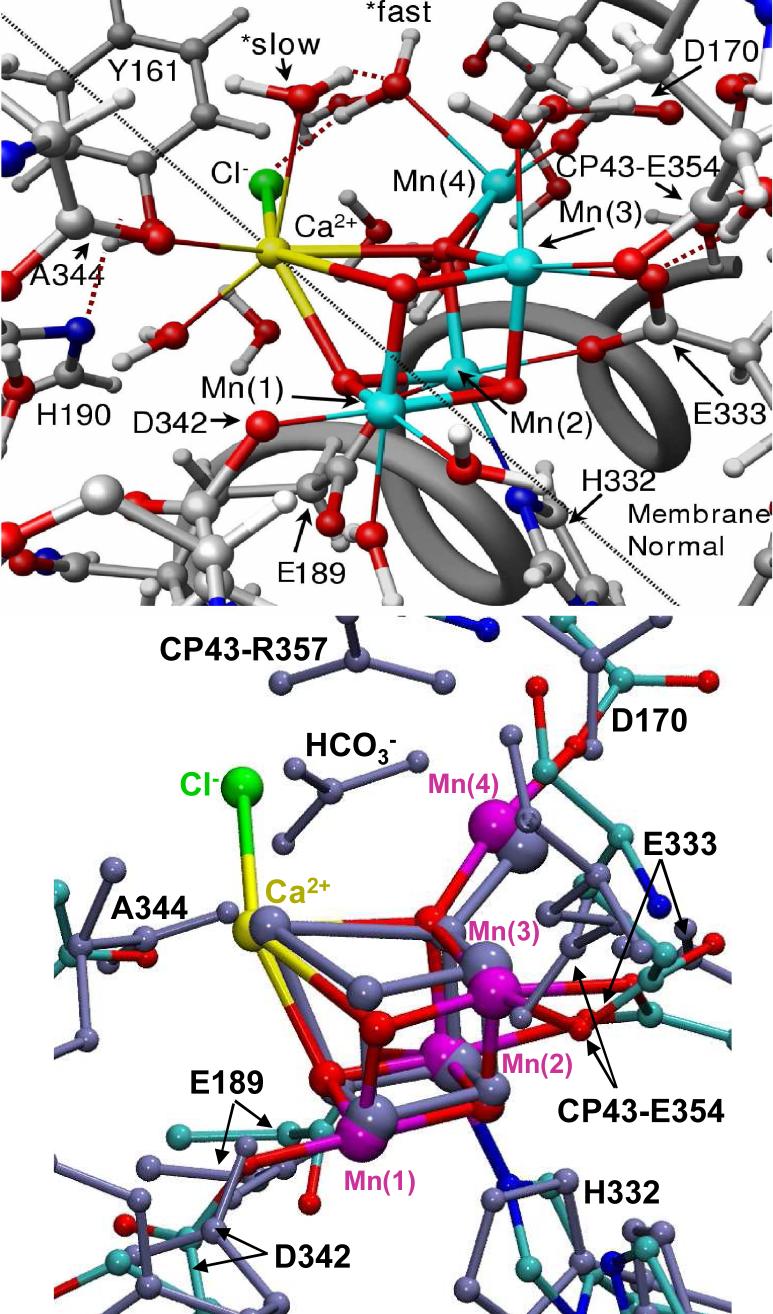
Proposed structural model of the OEC of PSII in the S₁ state (top), as described by the DFT QM/MM hybrid model obtained at the ONIOM-EE (UHF B3LYP/lacvp,6−31G(2df),6−31G:AMBER) level where the putative substrate waters labeled *fast and *slow are coordinated to Mn(4) and Ca²⁺, respectively [13], and superposition with the 1S5L X-ray diffraction model [20] (blue, bottom panel), shown in Figure 4. All amino acid residues correspond to the D1 protein subunit unless otherwise indicated.

Computational Approach

DFT-QM/MM molecular structures have been obtained by using the ONIOM (our own N-layered integrated molecular orbital plus molecular mechanics) method [106, 107] with electronic embedding (EE) at the (UHF B3LYP/lacvp,6−31G(2df),6−31G-AMBER) level of theory. The calculations are demanding but computationally tractable when combining the ONIOM-EE methodology, as implemented in Gaussian03 [108], with high-quality initial-guess spin-electronic states generated with Jaguar 5.5 [109]. The combined approach exploits important capabilities of ONIOM, including both the link-hydrogen atom scheme for efficient and flexible definitions of QM layers and the possibility of modeling open-shell systems by performing Unrestricted-DFT (e.g., UB3LYP) calculations. The molecular structure beyond the QM layer is described by the Amber MM force-field [110, 111]. Geometry relaxation of the complete structural model include the tetramanganesecluster and all amino-acid residues with α-carbon atoms within 15 Å from any atom in the OEC metal ion cluster and an additional buffer shell of amino-acid residues with α-carbon atoms within 15 to 20 Å from any atom in the OEC ion cluster with harmonic constraints to preserve the natural shape of the system [13, 16, 17].

Core Polarization

Under the DFT QM/MM approach, the system has been partitioned into a reduced system X, including the metal cluster, the proteinaceous ligands (E333, CP43-E354, D342, D170, E189 and H332), water and hydroxo ligated to metals and chloride. Region Y includes the rest of the system. The total energy E is obtained by using the two-layer ONIOM Electronic-Embedding (EE) link-hydrogen atom method from three independent calculations:

$$\mathrm{E}={\mathrm{E}}^{\mathrm{MM},\mathrm{X}+\mathrm{Y}}+{\mathrm{E}}^{\mathrm{QM},\mathrm{X}}-{\mathrm{E}}^{\mathrm{MM},\mathrm{X}},$$

where E^MM,X+Y is the energy of the complete system computed at the molecular mechanics level of theory, while E^QM,X and E^MM,X correspond to the energy of the reduced-system X computed at the QM and MM levels of theory, respectively. Electrostatic interactions between regions X and Y are included in the calculation of both E^QM,X and E^MM,X at the quantum mechanical and molecular mechanics levels, respectively. Thus, the electrostatic interactions computed at the MM level in E^MM,X and E^MM,full cancel and the resulting DFT QM/MM evaluation of the total energy involves a quantum mechanical description of the polarization of the reduced system, due to the electrostatic influence of the surrounding protein environment.

Protein Polarization

Polarization of the protein active sites induced by the distribution of charge in the QM layer has been introduced by correcting the atomic charges of amino-acid residues in close contact with the QM layer, according to the self-consistent polarization protocol MoD-QM/MM [13, 15, 39, 112]. The MoD-QM/MM method is a simple and rigorous method for the description of polarization effects whose accuracy and capabilities have been recently demonstrated in studies of high-valent metal complexes embedded in biological molecules as well as in applications to benchmark calculations of polypeptide-ligand model systems as well as in conjunction with the Poisson-Boltzmann equation in applications to the description of protein-protein electrostatic interactions [112].

Ligation

In contrast to the ligation scheme proposed by the X-ray diffraction structures, the QM/MM models involve metal ions with the usual number of ligands (i.e., 5 and 6 ligands coordinated to Mn ions with oxidation states III and IV, respectively, and 7−8 ligands attached to Ca²⁺ which usually ligates to 6−8 ligands (see Fig. 6). In the QM/MM models, the proteinaceous ligation includes η²-coordination of E333 to both Mn(3) and Mn(2) and hydrogen-bonding to the protonated CP43-E354 (neutral state); monodentate coordination of D342, CP43-E354 and D170 to Mn(1), Mn(3) and Mn(4), respectively; and ligation of E189 and H332 to Mn(2).

Hydration

The coordination spheres of calcium and Mn ions have been completed by hydration, assuming a minimum displacement of the ligating residues from their crystallographic positions. The usual coordination of 5 and 6 ligands was used for Mn ions with oxidation states III and IV, respectively. Furthermore, the variable coordination of calcium (typically with 6 to 8 ligands) was satisfied. The QM/MM models were hydrated by “soaking” the molecular structures in a large box containing a thermal distribution of water molecules and keeping those water molecules that did not sterically interfered with the protein residues or with existing water molecules in the model [13, 16]. Such a computational protocol resulted in the addition of water molecules attached to calcium and Mn ions in the cuboidal CaMn₄ cluster as well as water molecules approaching the cluster from the lumen. The resulting hydration of the cluster was roughly consistent with pulsed EPR experiments [36], revealing the presence of several exchangeable deuterons near the Mn cluster in the S₀, S₁, and S₂. However, the QM/MM model predicts more water/hydroxo ligands than suggested by EPR measurements, with about 6 such exchangeable protons.

Substrate Water

Two of the ligated waters bound to Ca²⁺ and Mn(4) were considered to be substrate water molecules, in agreement with earlier proposals [13, 16, 17, 35, 113-116], but in contrast to other models suggesting substrate water coordination as oxo-bridges between Mn ions [5, 35, 79, 117-119]. The two molecules accounted for the electronic density in the 1S5L X-ray diffraction structure that was initially assigned to bicarbonate [20]. The arrangement is consistent with mechanistic proposals that postulate O-O bond formation in the S₄ → S₀ transition [16, 17, 25, 116, 120], since the respective substrate oxygen atoms are 2.72 Å apart in the S₁ state, and become yet closer together in the S₄ state following deprotonation of the Mn-bound water.

The bicarbonate ion has not been included in the QM/MM hybrid models since the proposed docking site in the 1S5L structure was considered adventitious. In fact, bicarbonate has not been seen in the more recently published X-ray diffraction structure [21]. Consistently, recent studies by Siegbahn and co-workers have also discarded the feasibility of bicarbonate as a ligand to the OEC [10]. However, the substitution of ligated water molecules by bicarbonate elsewhere in the OEC [121] cannot be discounted.

Chloride binding

Considering that Cl⁻ is required for transitions beyond the S₂ state [122], the binding position was found by replacing each water molecule by Cl⁻ and selecting the lowest energy configuration [13, 16]. The minimum energy configuration placed Cl⁻ between the Mn cluster and Y_Z, similarly to acetate [13, 16]. These results are in line with EPR experiments showing that acetate competes with Cl⁻ and that acetate binds close to Y_Z [123]. In fact, acetate binding by substitution of Cl⁻ is predicted in excellent agreement with pulsed EPR data of the OEC [123], where chloride has been replaced by acetate and a distance of about 3.2 Å was measured between the acetate methyl group and Y_Z. Considering that the oxidation state of Y_Z might have a regulatory effect on the pKa of basic amino acid residues responsible for proton abstraction, the resulting binding site of Cl⁻ is also consistent with the proposal that chloride is part of a proton relay network [124].

The QM/MM structures thus predict that Cl⁻ is not directly bound to a Mn center but rather loosely bound to the metal cluster by electrostatic interactions, at approximately 5 Å from the nearest Mn. These predictions are partially consistent with recent experiments by Dau and co-workers indicating that Cl⁻ is not a first-sphere coordination ligand [125].

Oxidation states

Completing the coordination of the OEC metal centers with either water ligands, hydroxides, Cl⁻ and amino acid ligands necessarily leads to a large number of combinations of protonation and oxidation states. For instance, some water molecules ligated to metals could in principle be hydroxides, provided that the total charge is kept constant. A number of these combinations lead to reasonable models, as quantitatively judged by the resulting structure of the Mn cluster. Interestingly, some combinations of oxidation states on the Mn atoms do not necessarily maintain the integrity of the Mn cluster.

Only two combinations of spin states have comparable stability in the S₁ resting state. These include model (a) (shown in Fig. 6), where the dangling manganese Mn(4) is pentacoordinated and the oxidation states are Mn(1) = IV, Mn(2) = IV, Mn(3) = III, Mn(4) = III, also referred as Mn₄(IV,IV,III,III); and model (b) (not shown in Fig. 6) where the dangling manganese is hexacoordinated with an additional water and the oxidation states are Mn₄(IV,III,III,IV). The two DFT-QM/MM models are neutral in the S₁ state and predict anti-ferromagnetic coupling between Mn(1) and Mn(2), between Mn(2) and Mn(3), and between Mn(3) and Mn(4), but frustrated spin-coupling between Mn(1) and Mn(3) in the cuboidal structure. Both models include complete coordination of the high-valent Mn centers with oxidation numbers III and IV, with five or six ligands, respectively. The spin state of the two redox-isomers is determined by the number of ligands of Mn(4), which has oxidation state IV if it has six ligands, and oxidation state III if it has five ligands. Concurrently, the slightly strained coordination of H332 to the Mn cluster facilitates the hexacoordinated Mn(2) stabilizes the oxidation state IV when Mn(4) is pentacoordinated, while the oxidation state III (with a Jahn-Teller elongation along the Mn-H332 axis) is favored for Mn(2) when the coordination sphere of Mn(4) is complete. These results are consistent with EPR [98, 99] and X-ray spectroscopy [80, 100] as well as recent XANES [42] and ⁵⁵Mn ENDOR [126, 127] experiments, but disagree with low-valent Mn₄(III,III,III,III) proposals [128, 129].

Comparisons with X-ray diffraction Models

The quantitative analysis of interatomic bond lengths and bond orientation angles relative to the membrane normal in QM/MM models has allowed for rigorous comparisons with high-resolution EXAFS spectra and X-RAY DIFFRACTION models (see Table 1) [13, 15, 39]. The configuration of the cuboidal Mn₄Ca complex proposed by the QM/MM hybrid model shares common structural features with the X-ray diffraction model although with significant differences in the proposed ligation schemes (see Fig. 6). In addition, the two model QM/MM redox isomers of the OEC of PSII in the S₁ state (i.e., models (a) and (b)) have only minor structural differences, and the root mean squared displacement between the QM/MM structural models and the 1S5L X-ray diffraction structure is only 0.6 Å. Therefore, it is difficult to judge whether the oxomanganese cores in the QM/MM model and in the 3.5 Å resolution X-ray diffraction structure are truly identical or whether there are any significant differences. The agreement is truly remarkable, especially considering the limited resolution, incomplete ligation, and possible radiation damage [49] of the 3.5 Å resolution X-ray structure. Therefore, while the QM/MM models do not rule out other molecular structures, these results show that the QM/MM structural models are not only chemically sensible and consistent with available mechanistic data but also fully compatible with X-ray diffraction and EXAFS measurements.

Table 1.

Interionic distances and bond angles relative to the membrane normal in the DFT QM/MM structural models of the OEC of PSII in the S₀, S₁(a), S₂, S₃ and S₄ states, including comparisons to the 1S5L X-ray diffraction model [20].

	S0		S1 (a)		S2		S3		S4		X-Ray
Bond Vector	Length [Å]	Angle	Length [Å]	Angle	Length [Å]	Angle	Length [Å]	Angle	Length [Å]	Angle	Length [Å]	Angle
Mn(1)-Mn(2)	2.65	59°	2.76	57°	2.78	58°	2.69	57°	2.69	54°	2.65	59°
Mn(1)-Mn(3)	2.92	76°	2.76	85°	2.77	81°	2.81	73°	2.82	74°	2.67	79°
Mn(2)-Mn(3)	2.96	78°	2.82	63°	2.86	65°	2.82	77°	2.58	72°	2.72	71°
Mn(2)-Mn(4)	3.79	54°	3.34	54°	3.29	59°	3.84	58°	3.55	61°	3.25	58°
Mn(3)-Mn(4)	3.04	21°	3.72	29°	3.55	35°	2.81	21°	2.81	27°	3.26	38°
Ca-Mn(2)	3.59	63°	3.31	53°	3.78	57°	3.63	63°	3.61	71°	3.40	59°
Ca-Mn(3)	3.51	50°	3.95	35°	4.00	36°	3.74	53°	3.58	57°	3.38	39°

Simulations of EXAFS Spectra

Simulations of extended X-ray absorption fine structure (EXAFS) spectra allowed for the validation of the proposed DFT QM/MM structural models in terms of direct comparisons with high-resolution experimental data [41, 42, 49, 50, 61, 80, 130]. The simulations involved solving the multiscattering problem associated with the photoelectrons emitted by the Mn ions, upon X-ray absorption.

The quantum mechanical interference of outgoing photoelectrons with the scattered waves from atoms surrounding the Mn ions gives rise to local maxima and minima in the oscillations of EXAFS intensities. The Fourier transform of these oscillations determine the Mn-Mn distances, the coordination of Mn ions and changes in the Mn coordination determined by changes in the oxidation state of the OEC.

Calculations have been carried out according to the Real Space Green function approach as implemented in the program FEFF8 (version 8.2) [131, 132], which is based on the theory of the oscillatory structure due to multiple-scattering originally proposed by Kronig [133, 134] and worked out in detail by Sayers [135], Stern [136], Lee and Pendry [137], and by Ashley and Doniach [138]. The oscillatory part of the dipole transition matrix element, or EXAFS data, has been obtained with the module FEFF83, explicitly considering atoms within 10 Å from any metal in the OEC.

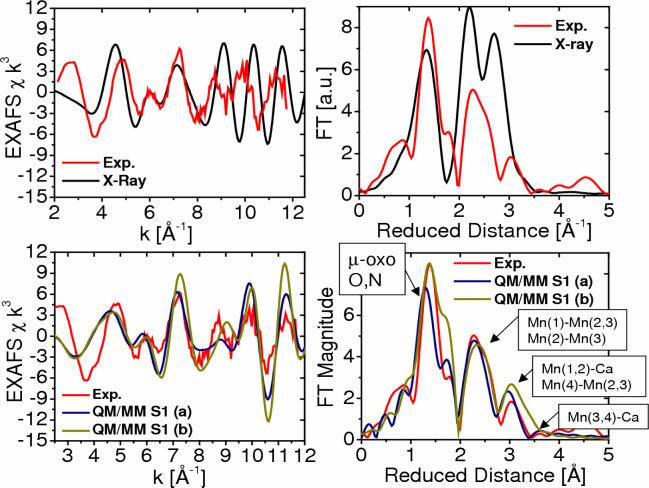
Figure 7 shows the comparison between experimental (red) and simulated EXAFS spectra of the OEC of PSII in the S₁ state, as described by the 1S5L X-ray diffraction model (black) and the two DFT-QM/MM structural models (blue (a) and green (b)). A detailed comparison of Mn-Mn and Mn-Ca distances for the OEC in the S₁ state is presented in Table 1, including metal-metal distances in the DFT-QM/MM and X-ray diffraction models. Figure 7 includes EXAFS spectra in momentum (k) space as well as the corresponding spectra in reduced distance (r) space obtained as the Fourier transform of the spectra in k-space (experimental data kindly provided by Prof. Holger Dau). These results show that the EXAFS spectra based on both QM/MM models are in very good agreement with experimental data, including the description of the peaks associated with multiscattering from the N and O Mn-ligand centers at 1.8 Å (reduced distances 1.41 Å), the short Mn-Mn distances at 2.7 Å (reduced distances 2.32 Å) characteristic of PSII, and backscattering due to the dangling Mn and Ca²⁺ at >3 Å. The main difference between the two simulated EXAFS spectra (see blue and green lines for the FT magnitude as a function of reduced distance) is the slightly different structure of the first prominent peak at reduced distances 1.6 Å where model (b) has a more pronounced shoulder due to the slightly shorter 2.1 Å coordination bond length between Mn(2) and the carboxylate oxygen atoms of E333, while the corresponding bond length in model (a) is 2.2 Å. In contrast, the simulated EXAFS spectrum obtained with the X-ray model structure (Fig. 7, top) shows less agreement with the experimental EXAFS spectrum, mainly due to the incomplete coordination of the metal centers. Also, the second and third peaks are shifted and with higher amplitude due to the slightly different geometry of the metal cluster.

Figure 7.

Comparison between experimental [41] (red) and calculated [13] (blue,green and black) EXAFS spectra in k-space (left) and Fourier transform of the EXAFS spectra in R-space (right) for the OEC of PSII, as described by the 1S5L X-ray diffraction model (top) and the DFT QM/MM models of the S₁ state, obtained at the ONIOM-EE (UHF B3LYP/lacvp,6−31G(2df),6−31G:AMBER) level, including model (a) where the dangling manganese is pentacoordinated and the oxidation states are Mn(1) = IV, Mn(2) = IV, Mn(3) = III, Mn(4) = III; and (b) where the dangling manganese is hexacoordinated with an additional water and the oxidation states are Mn(1)=IV, Mn(2)=III, Mn(3)=III, Mn(4)=IV.

Comparisons with Polarized EXAFS Models

The inorganic core of the DFT QM/MM models has also been compared to models of the Mn₄Ca cluster obtained from the analysis of polarized-EXAFS measurements, recently proposed by the Berkeley group [44], considering that multiple molecular models can render similar EXAFS spectra. The orientational dependent EXAFS amplitudes, obtained from 3-dimensionally ordered single crystals of PSII (∼0.3 × 0.3 × 0.9 mm), allowed extraction of the orientations of the Mn-Mn and Mn-Ca vectors. These studies reduced the original set of 11 possible empirical models [139], including the ‘dimer of dimers’ model extensively discussed in the past [5], to one although with four possible positions for Ca²⁺ (i.e., models I, II, IIa and III described in Ref. [44]).

The polarized-EXAFS models are considered to be the most reliable empirical models of the OEC metal cluster developed to date. However, EXAFS spectroscopy does not give any specific information on the arrangement of ligands and placing any of these polarized-EXAFS models into the X-ray diffraction structures results in unsatisfactory metal-ligand distances, coordination numbers and geometries [44]. In addition, model I is less likely to be correct since the Mn-Ca vectors do not lie along the membrane normal. In contrast, the inorganic core of the DFT-QM/MM model is fully consistent with the proteinaceous ligation proposed by the 2 independently developed X-ray diffraction structures [20, 21]. At this point it is also important to mention that, in contrast to the polarized-EXAFS models, the DFT-QM/MM structures are consistent with the original analysis of ⁵⁵Mn-ENDOR measurements on the S₂ state by Britt and co-workers [55]. The comparison between S₁ and S₂ states is meaningful because both states have almost identical geometry, as discussed in Sec. 4.2. The ⁵⁵Mn-ENDOR measurements allowed to extract reliable hyperfine interaction parameters that disfavor the ‘dimer of dimers’ model over models with a trinuclear-Mn core and a fourth Mn set off from the core by a longer Mn-Mn internuclear distance, or ‘dangler’ models.

Figure 8 shows the comparison of calculated EXAFS spectra for the models I, II, IIa and III, proposed by Yano et al. in Ref. [44], and the corresponding EXAFS spectrum of the DFT-QM/MM inorganic core (a) in the S₁ state isolated from the protein environment. These results show that the isotropic EXAFS spectra of these models are very similar. In fact, the observed differences among the polarized-EXAFS models give an estimate of the experimental error that is comparable to the observed deviations relative to the spectrum of the DFT-QM/MM model. Therefore, on the basis of the isotropic EXAFS spectra it is difficult to judge whether there are any significant spectroscopic differences. A more systematic comparative analysis would require comparisons of spectra for the oriented samples.

Figure 8.

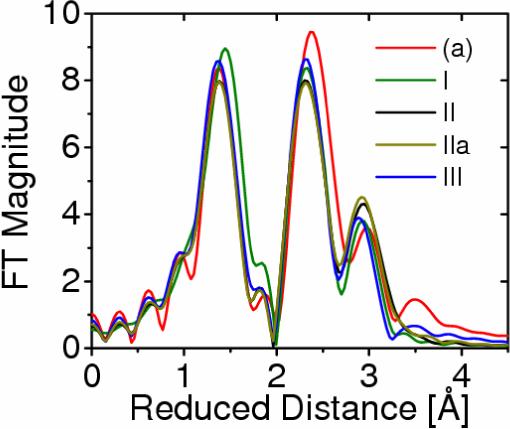
Comparison of calculated EXAFS spectra associated with the oxomanganese complex of PSII described by structures I, II, IIa, and III, proposed by Yano et al. [44] (green, black, dark yellow and blue, respectively), and model (a), obtained according to DFT QM/MM hybrid methods (red) [13,15,39].

Vibrational Analysis

The nature of the proteinaceous ligation has been extensively investigated by site directed mutagenesis in combination with FTIR and EPR [40, 43, 45, 46, 67, 71-75], in addition to X-ray diffraction studies [20, 21]. In particular, several FTIR studies indicated that the vibrational frequencies of carboxylate groups associated with amino acid residues D1-D170, D1-D342 and D1-E189 are not shifted as the OEC is oxidized from the S₀ to the S₃ states [43, 45]. The simplest possible interpretation of these experiments has been that none of these amino acid residues are ligated to the Mn ions oxidized during the S₀ —S₃ transitions, in marked disagreement with QM/MM and X-ray diffraction models. In addition, it has been observed that the vibrational frequencies of the carboxylate group of D1-A344 change during the S₁-S₂ transition but remain unaffected in Sr²⁺ reconstituted samples, although the ionic radius of Sr²⁺ is larger than the radius of Ca²⁺. These studies suggested that D1-A344 ligates to the Mn ion oxidized during the S₁-S₂ transition [46], also in disagreement with QM/MM and X-ray diffraction models. Unfortunately, more rigorous interpretations of these experiments have been hindered by the lack of systematic studies on the influence that the oxidation of Mn centers has on the vibrational frequencies of carboxylate ligands in high-valent oxomanganese complexes.

It is natural to expect that a change in the partial atomic charge of the oxidized metal center should at least produce an observable electrostatic influence on the vibrational frequencies of its ligands. However, any kind of correlation between the oxidation state of the metal center and its actual ionic charge is highly improbable due to charge delocalization among the metal centers in oxomanganese complexes [14, 140-144]. QM/MM studies have shown that the partial ionic charges of manganese centers are not significantly correlated with changes in oxidation states, as the system evolves along the catalytic cycle from the S₀ to the S₃ state (see Table 2) [13, 15, 39]. Therefore, no simple correlation is expected between the electrostatic influence of oxidation state transition and the vibrational frequencies of the ligands directly attached to the redox active metal centers. Changes in the overall charge of the oxomanganese cluster, however, can induce vibrational frequency shifts on the ligands involved in charge-transfer interactions. In addition, changes in vibrational modes are expected even for amino acid residues that do not necessarily ligate to the Mn-cluster but interact electrostatically or have side chains whose protonation states, or hydrogen-bonding interactions, change as the Mn-cluster is oxidized [145].

Table 2.

Mulliken spin population analysis and ESP atomic charges in the DFT QM/MM models of the OEC of PSII in the S0, S₁ (a), S₂, S₃ and S₄ states.

Ion Center	S0			S1			S2			S3			S4
	Spin Pop.	Ox. #	ESP Charge	Spin Pop.	Ox. #	ESP Charge	Spin Pop.	Ox. #	ESP Charge	Spin Pop.	Ox. #	ESP Charge	Spin Pop.	Ox. #	ESP Charge
Mn(1)	−2.88	+4	+1.30	−2.80	+4	+1.11	−2.79	+4	+1.14	−2.87	+4	+1.38	−2.85	+4	+1.32
Mn(2)	+3.83	+3	+1.20	+2.75	+4	+1.08	+2.92	+4	+1.02	+3.15	+4	+1.16	+3.19	+4	+1.72
Mn(3)	−3.87	+3	+1.27	−3.82	+3	+1.26	−2.74	+4	+1.59	−2.97	+4	+1.62	−2.84	+4	+1.72
Mn(4)	+3.80	+3	+1.15	+3.80	+3	+1.35	+3.79	+3	+1.49	+2.98	+4	+1.13	+3.10	+4	+0.97
O(5)	+0.00	−2	−0.75	+0.05	−2	−0.60	+0.09	−2	−0.53	+0.03	−2	−0.68	+0.03	−2	−0.76
O(6)	+0.05	−2	−0.92	+0.02	−2	−0.80	+0.02	−2	−0.81	+0.03	−2	−0.84	+0.01	−2	−0.99
O(7)	+0.00	−2	−0.74	+0.02	−2	−0.67	−0.03	−2	−0.78	+0.10	−2	−0.72	+0.07	−2	−0.72
O(8)	−0.03	−2	−0.95	−0.07	−2	−0.98	−0.09	−2	−0.86	−0.04	−2	−1.11	−0.05	−2	−1.49
Ca	−0.00	+2	+1.60	−0.01	+2	+1.77	−0.00	+2	+1.56	−0.00	+2	+1.65	−0.00	+2	+1.66
Cl	−0.04	−1	−0.54	−0.00	−1	−0.71	+0.00	−1	−0.67	−0.00	−1	−0.68	−0.27	−1	−0.48

A complete vibrational analysis of the ligated OEC remains to be reported. However, preliminary QM/MM studies have already addressed the vibrational properties of carboxylate ligands in close contact with the OEC. These studies have focused first on the D1-subunit carboxyl terminus D1-Ala344, which has long been thought to bind to one of the metal ions in the OEC [67, 71], in an effort to address the apparent contradictions between the FTIR and X-ray diffraction models with regards to D1-Ala344 ligation to the OEC.

As shown in Figs. 4 and 6, the X-ray diffraction structures of PSII suggest that D1-Ala344 is very close, or directly, ligated to Ca²⁺ in the OEC [20, 22], consistently with the QM/MM models of the OEC predicting unidentate ligation of the carboxylate group of D1-Ala344 to Ca²⁺. In contrast, results from several FTIR studies have been interpreted in terms of unidentate ligation of the C-terminus of D1-Ala344 to a Mn ion but not to calcium [43, 46, 48]. It was observed that the frequency of the symmetric stretching mode of the D1-Ala344 carboxylate changes from 1356 cm⁻¹, in the S₁ state, to either 1337 cm⁻¹ (a red shift of −19 cm⁻¹) or 1320 cm⁻¹ (a red shift of −36 cm⁻¹) in the S₂ state [43], likely due to a Mn³⁺ to Mn⁴⁺ transition [146]. Remarkably, the observed frequency shift was unchanged upon substitution of Ca²⁺ by Sr²⁺, suggesting that D1-Ala344 is not directly ligated to calcium [43] since the ionic radius increased from 0.99 Å to 1.12 Å and numerous unassigned vibrational modes changed in the ψ_sym(COO⁻) and ψ_asym(COO⁻) regions of the spectrum (1450—1280 cm⁻¹ and 1650—1510 cm⁻¹, respectively).

QM/MM studies showed that the symmetric-stretch vibrational frequency of the D1-Ala344 carboxylate, changes from 1381 cm⁻¹ to 1369 cm⁻¹ (a 12 cm⁻¹ red shift) upon S₁-S₂ oxidation. These results indicate that a red shift of the same order of magnitude as reported by FTIR studies can be produced simply by the underlying redistribution of charge in the S₁→S₂ transition, even when D1-Ala344 is coordinated to Ca²⁺. On the basis of the QM/MM vibrational analysis, it is thus concluded that ligation of the C-terminal carboxylate to calcium might be consistent with both X-ray diffraction and FTIR data. The apparent disagreement on this point, between FTIR and X-ray diffraction studies, must thus be due to the intrinsic difficulties associated with the interpretation of the FTIR frequency shifts as resulting from the electronic and structural rearrangements in the complex biomolecular environment, including changes in hydrogen bonding, protonation states of the ligands, and formation of oxo-bridges.

Preliminary studies of oxomanganese complexes have also addressed the effect of oxidation state transitions on the vibrational frequencies of carboxylate ligands directly attached to redox active Mn ions. These studies predict that vibrations of carboxylate ligands can often be quite insensitive to Mn oxidation, but the asymmetric stretch vibration is predicted to change upon Mn^III →Mn^IV oxidation when the carboxylate group is coordinated along the Jahn-Teller axis of a Mn^III. As discussed in Sec. 4, however, the QM/MM models suggest that neither D1-D170, nor D1-D342 or D1-E189 ligate along the Jahn-Teller axis of a Mn center when the OEC is in the S₀–S₃ states. Therefore, these results are consistent with negligible changes in the vibrational frequencies of carboxylate ligands even when they are directly ligated to Mn-centers that undergo oxidation state transitions as suggested by the DFT-QM/MM models. The only aminoacid residue ligated along the Jahn-Teller axis of a Mn^III ion is CP43-E354 for which there should be observable vibrational frequency shift as the OEC evolves from the S₀ to the S₃ state. This prediction, however, remains to be addressed by experiments.

Water Exchange

Direct scrutiny of substrate water molecules by time-resolved mass spectrometry (MS) has determined different exchange rates (k_ex) with bulk ¹⁸O-labeled water of the two substrate waters of the OEC in the S₀, S₁, S₂ and S₃ states [34, 51-53]. The more slowly exchanging water (W^slow) was associated with Ca²⁺, implying that the fast-exchanging water (W^fast) must be bound to a manganese ion. This has been rather surprising, especially considering that manganese ions are higher-valent (e.g., Mn³⁺ or Mn⁴⁺) than Ca²⁺ in the OEC. In addition, it has been observed that the exchange rate of W^slow (k_ex^slow) increases by two orders of magnitude upon S₁→S₂ oxidation, with k_ex(S₁) = 0.02 s⁻¹; and k_ex(S₂) = 2.0 s⁻¹ [53, 147]. These exchange rates correspond to activation energies of about 20 and 17 kcal mol⁻¹ in the S₁ and S₂ states, respectively. Considering that the S₁→S₂ transition involves oxidation of a manganese center, the observed acceleration of the exchange of W^slow was also intriguing since it implied that the oxidation of a manganese center must indirectly affect the exchange rate of a calcium-bound water molecule. While these observations were reproducible and unambiguous, it was not clear whether they could be rationalized by QM/MM, or mechanistic [25, 35, 120] models.

The observations of time-resolved mass spectrometry have been addressed through the QM/MM analysis of transition state energy barriers for water exchange in structural models of the OEC in the S₁ and S₂ states [18]. These calculations complemented earlier studies of water exchange in transition metal complexes [148-154], including theoretical studies of manganese complexes, based on Hartree–Fock and complete active-space self-consistent field theories [12, 149, 150, 155] as well as DFT studies of water exchange in other transition metal complexes [12, 156-159]. The specific QM/MM calculations focused on potential energy profiles associated with the minimum energy paths (MEPs), shown in Fig. 9, while progressively detaching substrate water molecules from Ca²⁺ and the dangling Mn(4). The resulting structural rearrangements provided insight on the water exchange mechanisms and the relative binding strengths, since elongation of the metal–oxygen bond is the primary step in water exchange and presumably rate-determining in this case [12, 149, 150]. The stretching the Ca²⁺–W^slow bond was energetically more demanding than stretching the Mn(4)–W^fast bond. This is due to the underlying redistribution of charge in the complex that partially neutralizes the net ionic charges of the metal centers, leaving a smaller positive charge on Mn(4) (q=+1.35) than on Ca²⁺ (q=+1.77). These results are consistent with W^slow attached to Ca²⁺, even when such a metal center has a smaller oxidation number than Mn(4), illustrating how charge transfer between manganese ions and ligand/oxo-bridges can affect the net ionic charges of metal centers, complicating the correlation with formal oxidation numbers [13-15]. The underlying charge delocalization is also common to synthetic oxomanganese complexes [14].

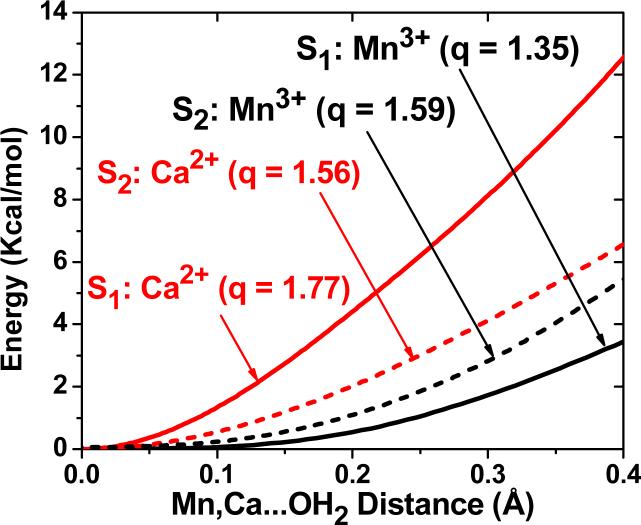
Figure 9.

DFT-QM/MM energy profiles, as a function of the coordination bond lengths between substrate water molecules attached to Ca²⁺ (red) and the dangling Mn³⁺ (black), for the OEC of PSII in the S₁ (dash) and S₂ (solid) states [18]. ESP ionic charges are indicated in parenthesis (q). The energy barriers are 21.2, 16.6, 8.4 and 7.9 kcal mol⁻¹, for water exchange from Ca²⁺(S₁), Ca²⁺(S₂), Mn³⁺(S₂) and Mn³⁺(S₁), respectively.

These opposite changes in the two water-exchange rates, induced by the S₁→S₂ transition, could also be traced to the corresponding changes in partial ionic charges modulated by charge transfer interactions. Figure 9 shows that the S₁→S₂ transition weakens the Ca²⁺–W^slow bond and strengthens the coordination of W^fast to Mn(4), as indicated by the potential energy profiles. This is mainly due to the redistribution of charge in the cluster when it becomes positively charged, strengthening charge transfer interactions between Ca²⁺ and D1-A344 and decreasing the partial ionic charge of calcium (Δq=–0.21) while increasing the charge of Mn(4) (Δq=+0.24). This QM/MM analysis of water exchange is consistent with the experimental observation that k_ex^slow increases and k_ex^fast decreases, upon S₁→S₂ oxidation [53].

Considering that the Mn₄Ca metal cluster involves carboxylate groups ligated to Ca²⁺ as well as carboxylate ligands coordinated to Mn³⁺ and Mn⁴⁺, it was important to address the origin of the preferential charge transfer between D1-A344 and Ca²⁺ upon S₁→S₂ oxidation of the OEC. To this end, a bond-order analysis based on natural atomic orbitals (NAO's) [160] has been performed. The results indicate that Mn–O bonds are predominantly covalent dative (Wiberg bond index = 1.05) while the Ca–O bonds are ionic (Wiberg bond index = 0.32). The difference is mainly due to charge delocalization from the p-orbitals of the oxo-ligands to vacant d-orbitals in manganese. Further, it was found that the delocalization mechanism involves both alpha and beta orbitals in similar amounts. Therefore, the total charges of the manganese ions are significantly reduced while the number of unpaired electrons (i.e., the oxidation state) remains almost unchanged.

The calculated DFT QM/MM energy barriers for water exchange from Mn(4) (7.9 and 8.4 kcal mol⁻¹, respectively) nicely agree with those for Mn complexes in solution, where the exchange of terminal water ligands requires only 8.6—9.6 kcal mol⁻¹ [12, 155]. However, the DFT QM/MM energy barriers for water exchange from Ca²⁺ (21.2 and 16.6 kcal mol⁻¹ in the S₁ and S₂ states, respectively) are significantly higher. The higher barriers are determined by the nature of hydrogen bonding interactions in the OEC binding pocket. The analysis of hydrogen bonds indicate that the exchanging water molecules have incomplete solvation shells and therefore make only 2−3 hydrogen bonds with the surrounding molecules or ions. Such an incomplete structure of hydrogen bonds stabilizes the coordination of water molecules to the metal cluster and correlates the relative orientation and displacement of the exchanging water molecules. These observations suggest that the molecular environment surrounding the OEC of PSII has been highly optimized by natural selection to stabilize the attachment of substrate water molecules to metal centers, reducing the number of interactions with surrounding amino acid residues. At the same time, the mostly hydrophobic protein environment stabilizes the coordination of Cl⁻ to the ionic cluster as well as the coordination of the oxomanganese cluster to carboxylate groups of proteinaceous ligands.

Water Channels

The DFT-QM/MM structural models suggest that the two substrate water molecules ligate to Ca²⁺ and the dangling Mn during different S-state transitions (see Sec. 4) and approach the metal cluster from the lumen along two distinct pathways (see Fig. 1), none of which correspond to the postulated proton exit channel (see Sec. 4) [13, 39]. Due to the low dielectric protein environment, water molecules form (on average) only 2−3 hydrogen bonds (i.e., each molecule is hydrogen bonded to the molecule in front and behind along the pathways but not to the surrounding amino acid residues). This hydrogen-bond structure establishes optimum conditions for water mobility, minimizing the number of competitive hydrogen bonding interactions with the surrounding amino acid residues, therefore, enhancing the attachment of water to the metal cluster. These results thus also support the idea that the protein environment surrounding the OEC has been optimized by natural selection to enhance water binding to the catalytic metal center with typical turnovers of up to 100 water molecules per second. Upon dioxygen evolution, the substrate water molecules attached to the cluster react and the next water molecules along the two channels are attached to the corresponding metal centers. As mentioned in Sec. 4, one substrate water molecule ligates to Ca²⁺ in the S₄→S₀ transition, promoting dioxygen formation. The other water molecule ligates to the dangling Mn, during the S₀→S₁ transition, opening a μ-oxo bridge between Mn(4) and Mn(3). Both of these events produce dramatic conformational changes in the cluster, as indicated by EXAFS spectroscopic measurements [42].

4. OEC Catalytic Cycle

The DFT-QM/MM models of the OEC of PSII in the S₁-state allowed for the investigation of structural changes induced by oxidation/reduction of the OEC and the effect of such electronic changes on the underlying coordination/protonation state of the ligands. The resulting models of the OEC catalytic intermediates have been validated in terms of simulations of EXAFS spectra and direct comparisons with experimental data. The quantitative analysis of metal-metal distances is presented in Table 1.

Figure 10 shows the comparison of experimental [42] and calculated EXAFS spectra of the OEC S-state intermediates S₀-S₃, as described by the DFT QM/MM structural models depicted in Fig. 11 [39]. Figure 10 (right panel) shows the evolution of the scattering EXAFS amplitudes, as determined by structural rearrangements in the metal cluster, including changes in the Mn-Mn and Mn-Ca distances and the Mn-ligand coordination bond lengths. The first prominent peak at reduced distance 1.41 Å (actual distance 1.8 Å) is determined by N and O centers directly ligated to Mn-ions. This first peak has a shoulder at reduced distance 1.6 Å (actual distance 2.1 Å) corresponding to scattering contributions from μ-oxo bridges and the ligated carboxylate group of E333 coordinated to Mn. The second prominent peak at reduced distance 2.32 Å (actual distance 2.7 Å) corresponds to the characteristic Mn-Mn distances in PSII. Finally, the third peak at reduced distance 3.0 Å and beyond corresponds to backscattering from the dangling-Mn and Ca²⁺ at distances >3.3 Å. The width of the second prominent peak at reduced distance 2.32 Å (actual distance 2.7 Å) indicates the distribution of short Mn-Mn distances in the manganese cuboidal core. In agreement with experimental data [42], the simulated spectra of the OEC in the S₁ and S₂ states indicate that such a distribution is consistent with a dangler cuboidal cluster where two Mn-Mn distances (Mn(1)–Mn(2) and Mn(1)–Mn(3)) are shorter than 2.75 Å while the third distance Mn(2)-Mn(3) is close to 2.8 Å. In contrast, in the S₀ state, the Mn(1)-Mn(3) distance becomes longer and the Mn(1)-Mn(2) shorter, splitting and broadening the second prominent peak of the FT-EXAFS spectrum into a bimodal distribution. In the S₃ state, three Mn-Mn distances become similar to each other and the corresponding scattering peak at reduced distance 2.32 Å becomes narrower. This is in agreement with the EXAFS data by Dau and co-workers [41] but in disagreement with data from the Berkeley group indicating that one of the Mn-Mn distances is significantly longer in the S₃ state [161, 162].

Figure 10.

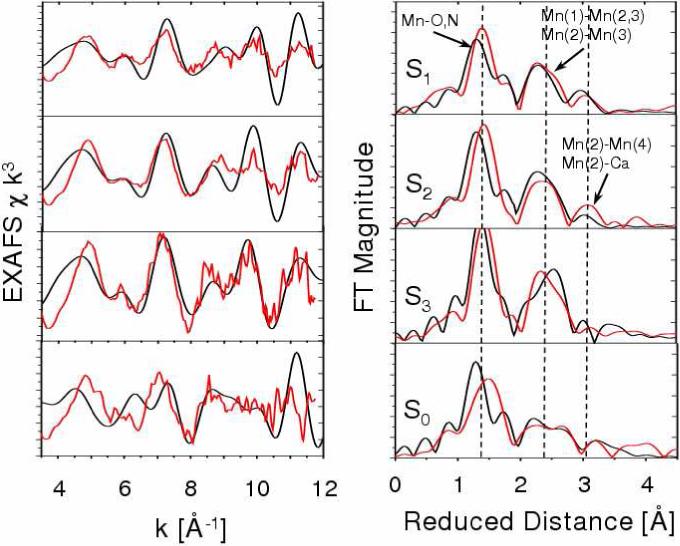
Comparison between experimental (red) [41] and calculated [39] (black) EXAFS spectra of OEC S-state intermediates of water splitting. Left: k-weighted EXAFS spectra. Right: Fourier-transformed spectra in r-space, showing three prominent peaks corresponding to scattering centers in the first (O,N), second (Mn in the core), and third (dangling Mn, Ca) coordination shells of Mn, respectively. Vertical dashed lines are included to facilitate the comparison.

Figure 11.

Catalytic cycle of water splitting suggested by DFT QM/MM models of the OEC of PSII [39]. Dashed arrows in dark yellow indicate transformations leading to the following S-state in the cycle. Changes caused by an S-state transition are highlighted in red. The blue circles highlight substrate water molecules (also shown in blue). Coordination bonds elongated by Jahn-Teller distortions are marked in green. The orientation of the metal cluster corresponds to Figure 6, where Mn(1), Mn(2), Mn(3) and Mn(4) are indicated.

The origin of some of the observed deviations between simulated and experimental spectra could be due to contributions from other redox isomers of comparable energy [13]. In fact, the first coordination sphere of Mn in the S₀ state is more structured in the simulated spectra than in the experimental data, suggesting the presence of other redox isomers or structural disorder. Nevertheless, the overall comparison between experimental and simulated EXAFS spectra partially validates the molecular models of S-state intermediates, indicating that the DFT QM/MM models are consistent with experimental data throughout the entire catalytic cycle.

A quantitative analysis of the structures and spin-electronic states associated with the structural models, depicted in Fig. 11, is presented in Tables 1 and 2. These results show that most oxidizing equivalents accumulate in the Mn ions, in accordance with experiments conducted on various PSII preparations and inorganic model compounds [25, 163]. In fact, the spin population analysis shows that Mn(2), Mn(3) and Mn(4) accumulate oxidizing equivalents, while Mn(1) remains redox inactive throughout the cycle and the fourth equivalent is accumulated as a terminal oxyl radical of the dangling manganese [7]. Note that the oxyl radical Mn^IV-O is an oxidized form of a substrate water molecule, deprotonated and ligated to Mn which is different from an oxo-Mn species Mn^V=O where the metal center is oxidized. Formation of the oxyl radical is predicted to be essential for O–O bond formation but disagrees with other proposals where the oxidation reaction involves species near the cluster [8, 164], or a manganese-bridging oxo group [79]. The overall reaction is also significantly different from other proposals where manganese-bridging oxo-ligands react with one another during the O–O bond forming step [5, 117], or where basic μ-oxo ligands deprotonate manganese-bound terminal water molecules [80].

4.1 The S₀→S₁ transition

The most reduced state of the OEC is advanced by oxidation of Mn(2), deprotonation of a water molecule ligated to the dangling Mn(4), and attachment of a substrate water molecule to Mn(4). The assumed deprotonation of the cluster is consistent with electrochromic measurements suggesting that there is no charge accumulation during this transition.

These changes in oxidation and protonation states open the protonated μ-oxo bridge between Mn(4) and Mn(3), stretching the Mn(4)-O distance and leaving the HO⁻ group ligated to Mn(3). Strengthening the coordination between Mn(3) and its axial ligand changes the Jahn-Teller distortion (elongated coordination bond) from axial to equatorial, shortening the Mn(1)-Mn(3) distance. These results are consistent with the EXAFS observation of a shortening a Mn-Mn distance by approximately 0.15 Å [64], with a single short (2.7 Å) Mn-Mn distance per Mn tetramer in the S₀ state and two short (2.72 Å) Mn-Mn distances in the S₁ state, with a third distance close to 2.8 Å. However, in contrast to the QM/MM model, the interpretation of EXAFS data has been based on deprotonation of one OH-bridge [42, 64].

Several significant differences can be noted, when comparing the QM/MM model for the S₀→S₁ transition to other recently suggested mechanisms [9, 35, 116], including the structure of oxo-bridges as well as the description of structural rearrangements and changes in oxidation and protonation states. In particular, a distinct feature of the QM/MM model in the S₀ state is the di-μ-oxo bridge structure linking the dangling Mn(4) to Mn(3) in the cuboidal cluster. One of these bridges is protonated from deprotonation of a substrate water, during dioxygen formation in the S₄→S₀ transition, while the other bridge is part of the cuboidal structure coordinated to Ca²⁺ and Mn(2). In addition, only the QM/MM mechanism predicts that ligation of a substrate water, during the S₀→S₁ transition, an event that opens the protonated μ–oxo bridge between Mn(3) and Mn(4) and produces significant conformational changes in the cluster, as indicated by EXAFS measurements.

4.2 The S₁→S₂ transition

The catalytic cycle depicted in Figure 11 indicates that the S₁→S₂ transition involves simply oxidation of Mn(3), without deprotonation [165-171] and with little structural rearrangements, or changes in Mn-Mn distances, consistently with EXAFS measurements [42]. The most significant change, associated with the S₁→S₂ oxidation, is that the cluster becomes positively charged due to the lack of deprotonation.

4.3 The S₂→S₃ transition

Following the catalytic cycle depicted in Figure 11, it is shown that the S₂→S₃ transition induces deprotonation of the substrate water molecule bound to Mn(4), consistently with electrochromism data [33, 115, 172-174], and advances the oxidation state of Mn(4) from III to IV. These changes strengthen the attractive interactions between Mn(4) and the HO⁻ ligand of Mn(3), inducing inter-ligand proton transfer from the HO⁻ ligand of Mn(3) to the hydrogen bonded HO⁻ ligand of Mn(4). This process transforms the HO⁻ ligand of Mn(4) into a water ligand and forms a μ-oxo bridge between Mn(3) and Mn(4). The HO⁻ proton acceptor is regenerated by deprotonation of the water ligand in the S₀→S₁ transition. These rearrangements are consistent with a pH-dependent rate constant [175], interpreted as a transition ’kinetically steered’ by proton movements. The rearrangements are also consistent with the observation of significantly conformational changes in the structure of the cluster upon formation of the S₃ state [42, 62], as manifested in the EXAFS spectra of S-state intermediates shown in Fig. 10 [39].

The formation of the μ-oxo bridge, between Mn(3) and Mn(4) by proton transfer between HO⁻ ligands is similar to transition proposed by Siegbahn [9] where, in contrast, the bridge is formed by double deprotonation of a water ligand attached to Mn(3) that releases a proton to the lumen and transfers the other proton to an HO⁻ ligand attached to the same Mn(3). However, the deprotonation of the cluster in the QM/MM model involves deprotonation of the substrate water molecule attached to the dangling Mn(4), as proposed by Messinger [35].

4.4 The S₃→S₄ transition

The QM/MM model indicates the S₃→S₄ transition further deprotonates the (already partially deprotonated) substrate water molecule bound to the dangling Mn(4) and hydrogen bonded to CP43-R357. This deprotonation releases another proton to the lumen via CP43-R357, changing the charge of the complex as suggested by electrochromic bandshift measurements [176]. The deprotonation forms the oxyl radical Mn^III–O· transient species that is subsequently oxidized by Y_Z^+• to form the Mn^IV –O^• species. Therefore, the QM/MM model suggests that the S₄ state accumulates the fourth oxidizing equivalent as an oxidized and deprotonated substrate water in the form of an oxyl radical, not as an oxidized Mn in the form of an Mn^V = O species. Formation of an oxyl radical has also been suggested by Siegbahn [9], and Messinger [35], although with different proposals for the reactivity of such an oxyl radical species. It is also consistent with the observation that S₄ formation might not involve manganese oxidation or reduction [104]. In addition, the formation of transient deprotonated species, prior to oxidation of the complex by the Y_Z^+. species, is consistent with the reported kinetically resolvable intermediate in the S₃→S₀ transition, within 200 μs after oxidation of Y_Z and prior to dioxygen formation [104].

4.5 The S₄→S₀ transition

The QM/MM mechanistic model involves dioxygen formation, during the S₄→S₀ transition, according to a nucleophilic attack of the calcium-bound water molecule on the electrophilic oxyl radical Mn^IV –O·. The reaction is promoted by substitution of the calcium bound water molecule by a water moiety in the second coordination sphere of calcium (see Fig. 11). Double deprotonation of the substrate water molecule, substituted from Ca²⁺, releases a proton to the lumen via CP43-R357 and transfers the other proton to the basic μ-oxo bridge linking Mn(4) and Mn(3).

The QM/MM reaction mechanism is, therefore, significantly different from the proposals by Siegbahn [9] and Messinger [35, 177], where oxyl radicals react with μ-oxo bridges instead of reacting with terminal Ca²⁺-bound water molecules. The reaction of a Ca²⁺-activated water molecule is similar to earlier proposals by Pecoraro [120] and Brudvig [25]. The main difference relative to these other nucleophilic-attack models is that in the QM/MM model the nucleophilic water attacks an oxyl radical, rather than attacking an oxo-Mn^V species. Another distinct aspect is that the reaction is promoted by water exchange in the coordination sphere of Ca²⁺ and that the nucleophilic water is activated not only by Ca²⁺ but also by two other basic species, including CP43-R357 and the basic μ-oxo bridge linking Mn(4) and Mn(3).

5. Proton Exit Channel

The advancement of the OEC of PSII through the S-state cycle, shown in Fig. 11, involves changes in oxidation states coupled to proton transfer events that balance the overall charge of the cluster and rearrange the protonation states of the ligands. The DFT-QM/MM hybrid models suggest that CP43-R357 is responsible for proton abstraction, functioning as a one-proton gate along the proton-exit channel to the lumen (see Fig. 12) [13, 116]. CP43-R357 is in close contact with the active face of the OEC and forms part of a hydrogen-bond network including both substrate water molecules, the side-chain of CP43-R357 and the calcium-bound chloride ion. Note that the guanidinium side-chain of CP43-R357 straddles the active face of the metal-oxo cluster, hydrogen bonding with the two putative substrate waters ligated to Ca²⁺ and Mn(4) and also with the putative non-substrate ligands (water or hydroxide) of Mn(3) and Mn(4). The ability to hydrogen-bond with both substrate and non-substrate ligands of Mn(3) and Mn(4) makes CP43-R357 particularly suitable to facilitate proton translocation. Nearby, two hydrogen-bonded nonligating water molecules (W_a and W_b in Fig. 12) fit easily into the structure between Mn(4) and D1-Asp61, which is the first residue of the putative proton-transfer channel leading to the lumenal surface of PSII. The CP43-R357 side-chain is thus expected to play a central role to facilitate the flow of protons from the OEC to the lumenal side of the membrane. This is consistent with its indispensability for O₂ evolution, as demonstrated by mutagenesis studies of PSII from Synechocystis sp. PCC 6803 where mutation of the homologous CP43 arginine (CP43-R342) to serine suppressed O₂ evolution [178]. In addition, the arginine side chain is a well-known component of hydrogen bonding networks in proteins [179, 180].

Figure 12.

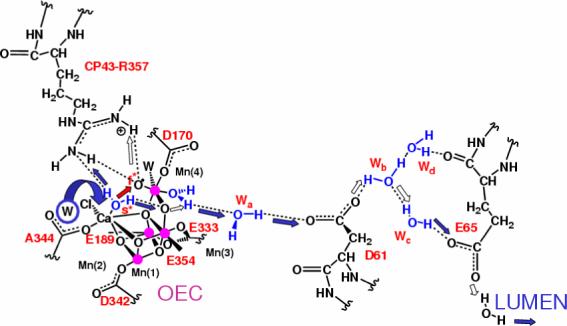
Proton exit channel suggested by the hydrated DFT QM/MM structural models, including a network of hydrogen bonds extended from substrate water molecules ’s’ (slow) and ’f’ (fast), via CP43-R357, to the first residue (D1-D61) leading to the lumenal side of the membrane [13,15,39]. Proton translocation events are indicated by blue and white arrows; the O=O bond formation event is indicated by a red arrow, as promoted by water exchange from Ca²⁺. Amino acid residues labeled with one-letter symbols correspond to the D1 protein subunit.

An important structural/functional aspect of the proposed proton exit channel is the OH⁻ ligand/(protonated) μ-oxo bridge of Mn(3). As mentioned in Sec. 4, the OH- ligated to Mn(3) deprotonates by proton transfer to an OH- ligand of Mn(4) during the S₂→S₃ transition, transforming such a ligand into a water and forming a μ-oxo bridge between Mn(3) and Mn(4). This event induces a rearrangement of hydrogen bonds: the hydrogen-bond between the two substrate water molecules is broken and two hydrogen bonds are formed, including a bond between W^slow and the μ-oxo bridge and another one between W^fast and CP43-R357. Upon further deprotonation of W^fast in the S₃→S₄ state, W^slow forms a hydrogen bond with CP43-R357 in addition to its hydrogen bond with the μ-oxo bridge, establishing two deprotonation pathways. During the S₄→S₀ transition, one proton transfers to the lumen via CP43-R357 while the other one translocates to the μ-oxo bridge and subsequently forms the OH⁻ ligand of Mn(3), upon opening of the bridge in the S₀→S₁ transition.

The QM/MM structural models of PSII are also consistent with the hypothesis that D1-Y161 (Y_Z) is an electron transport cofactor, especially judging by the proximity of Y_Z to the Mn cluster. D1-Y161 has long been viewed as an electron transport cofactor. The oxidized state P680⁺ is thought to be reduced by the redox-active tyrosine Y161 which in turn is reduced by an electron from water oxidation at the Mn cluster [28, 29]. Simple inspection of the QM/MM structural models also indicates that the phenoxy oxygen of Y_Z is typically close to the chloride ligand (3.4 Å apart) and Cl⁻ is positioned at 3.14 Å from Ca²⁺. Furthermore, the Y_Z phenol group is hydrogen bonded to the imidazole ε-N of the H190 side-chain. This hydrogen-bonding partnership is consistent with mutational and spectroscopic studies [70, 181, 182] as well as with earlier studies based on MM models [16, 17].

Considering the potential functional roles of CP43-R357 and D1-Y161, it is natural to expect that proton coupled electron transfer (PCET) might take place, as the catalytic cycle progresses, by passing electrons from the cluster to the oxidized Y_Z and protons to CP43-R357. These two charge-transfer processes might be coupled by long-range electrostatic modulation of the pKa of CP43-R357, induced by changes in the oxidation states of the cluster and Y_Z. The proposed PCET mechanism is consistent with a recent study of the energetics of a possible proton exit pathway for water oxidation in PSII [183], but disagrees with earlier proposals where Y_Z was thought to abstract hydrogen atoms from the OEC cluster in every one of the S-state transitions [163], or simultaneously oxidize and deprotonate the hydrated OEC [113]. The latter would require a mechanism where Y_Z abstracts hydrogen atoms and delivers protons to the protein surface via H190. However, based on the lack of a H-bonded pathway leading from H190 to the lumen, it is more likely that H190 accepts a proton from Y_Z during the oxidation and then returns the proton to Y_Z upon reduction.

Finally, the proposed charge transfer mechanism in the presence of Cl⁻ and Ca²⁺ ions is consistent with a considerable amount of experimental evidence suggesting that there is a discontinuity in the mechanism of S-state advancement beyond the S₂ state. It is known that only transitions beyond S₂ are blocked by the absence of calcium, or chloride, or by the presence of acetate [122, 184, 185]. In addition, electron transfer (ET) between the OEC and and the oxidized P680^+. is biphasic and significantly slower in the S-state transitions beyond S₂ than in the early S-states [186]. Furthermore, the reorganization energies of the two higher S-state transitions are significantly higher than those of the two previous transitions [187]. Finally, the sub-microsecond ET rates from the cluster to P680⁺ (via Y_Z) vary much more with temperature in post-S₂ transitions than earlier in the cycle [188]. These observations are consistent with the development of a positive charge in the OEC upon S₁–S₂ oxidation, with PCET, which is sequential during the S₀–S₁ transition and concerted in the transitions beyond S₂ [24, 189], a conclusion largely drawn on the basis of proton release measurements in the different S-states [190].

6. Conclusions

This review has outlined recent computational efforts in developing structural/functional models of the OEC of PSII by using state-of-the-art QM/MM hybrid methods. The QM/MM studies, in conjunction with benchmark DFT calculations on biomimetic model complexes, have clearly shown the capabilities of modern computational tools to investigate multinuclear high-valent metal clusters embedded in biological molecules.

Chemically sensible models of the OEC of PSII, including the catalytic metal cluster and the surrounding protein environment, with complete ligation by water, amino acid residues and chloride provide a detailed description of the catalytic water splitting mechanism at the molecular level, characterize possible water and proton channels and the potential role played by amino acid residues in close contact with the catalytic inorganic core as redox-coupled basic species. In addition, the models seem to reconcile an apparent contradiction between FTIR spectroscopy and X-ray diffraction models regarding ligation of amino acid residues to Mn ions and the C-terminus amino acid D1-Ala344 to calcium.

The proposed QM/MM structural models of S-state intermediates have been partially validated by direct comparisons between calculated and experimental EXAFS spectra. From the analysis of the QM/MM models, it is concluded that the electronic and structural properties of the OEC metal cluster are intrinsic to the ligated oxomanganese complex in the low-dielectric protein environment, while the surrounding macromolecular environment must have been optimized by natural selection for the efficient input of substrate molecules and removal of dioxygen, protons, and electrons with rapid turn over.

Abbreviations

EPR

electron paramagnetic resonance (spectroscopy)

ET

electron transfer

FTIR

Fourier-transform infrared (spectroscopy)

EXAFS

extended X-ray absorption fine-structure

PSII

photosystem II

P680

primary chlorophyll electron donor

UV/vis

ultraviolet and visible range spectroscopy

MM

molecular mechanics

PCET

proton-coupled electron transfer

QM

quantum mechanics

XANES

X-ray absorption near-edge structure

XAS

X-ray absorption spectroscopy

Y_Z

Tyr 160/161 of the D1 protein of PSII