Abstract
We consider a general class of purely inhibitory and excitatory-inhibitory neuronal networks, with a general class of network architectures, and characterize the complex firing patterns that emerge. Our strategy for studying these networks is to first reduce them to a discrete model. In the discrete model, each neuron is represented as a finite number of states and there are rules for how a neuron transitions from one state to another. In this paper, we rigorously demonstrate that the continuous neuronal model can be reduced to the discrete model if the intrinsic and synaptic properties of the cells are chosen appropriately. In a companion paper [1], we analyze the discrete model.
Keywords: Neuronal networks, discrete dynamics, singular perturbation, nonlinear oscillations
1 Introduction
Oscillatory behavior arises throughout the nervous system. Examples include the thalamocortical system responsible for the generation of sleep rhythms [2–5], networks within the basal ganlgia that have been implicated in the generation of Parkinsonian tremor [6,7], and networks within the olfactory bulb of mammals, or antennal lobe of insects [8–10]. Each of these systems has been modeled as an excitatory-inhibitory neuronal network and each model displays complex firing patterns. Thalamocortical models, for example, may generate clustered activity in which the network breaks up into subpopulations of cells, or clusters; neurons within each cluster fire in near synchrony, while cells within different clusters fire out-of-phase with each other. A recently proposed model for neuronal activity within the antennal lobe of insects [9] displays dynamic clustering: cells fire during distinct episodes and during each episode some subpopulation, or cluster, of cells fire in near synchrony. However, the membership of clusters may change so that two cells may fire together during one episode but they do not fire together during some other subsequent episode.
Several papers have used dynamical systems methods to analyze synchronous and clustered activity in excitatory-inhibitory networks [11–18]. However, very few papers have studied mechanisms underlying dynamic clustering. Moreover, previous papers have typically considered small networks with very simple architectures. It remains poorly understood how population rhythms depend on the network architecture.
Here we consider a general class of excitatory-inhibitory networks, with a general class of architectures, and characterize the complex firing patterns that emerge. Our strategy for studying these networks is to first rigorously reduce them to a discrete model. In the discrete model, each neuron is represented by a finite number of states and there are rules for how a neuron transitions from one state to another. In particular, the rules determine when a neuron fires and how this affects the state of other neurons.
The goal of this paper is to demonstrate that certain types of neuronal models can, in fact, be rigorously reduced to the discrete model. In a companion paper [1], we analyze the discrete model. By studying the discrete model, we are able to characterize properties of the dynamics of the original neuronal system. We demonstrate in [1], for example, that these networks typically exhibit a large number of stable oscillatory patterns. We also determine how properties of the attractors depend on network parameters, including the underlying architecture.
This paper is organized as follows. In the next section, we describe the neuronal model and introduce the two types of networks we are going to study: purely inhibitory and excitatory-inhibitory networks. In Section 3, we introduce the basic fast/slow analysis that will be used throughout the paper. We also consider some simple networks that will motivate the discrete dynamics. The discrete model is formally defined in Section 4. In Section 5, we briefly describe why it may not be possible, in general, to reduce a purely inhibitory network to the discrete model. The main analysis is given in Section 6 where we find conditions on parameters for when an excitatory-inhibitory network can be rigorously reduced to the discrete model. The results of numerical simulations are presented in Section 7 and there is a discussion of our results in the last section.
2 The neuronal model
A neuronal network consists of three components. These are: (1) the individual cells within the network; (2) the synaptic connections between cells; and (3) the network architecture. We now describe how each of these components is modeled. The models are written in a rather general form since the analysis does not depend on the specific forms of the equations. A concrete example is given in Section 7.
Individual Cells
We consider a general two-variable model neuron of the form
| (1) |
Here, v represents the membrane potential of the cell, w represents a channel gating variable and ε is a small, positive, singular perturbation parameter. We assume that the v-nullcline {f = 0} defines a cubic-shaped curve and the w-nullcline {g = 0} is a monotone increasing curve. Moreover, f > 0 (f < 0) below (above) the v-nullcline and g > 0 (< 0) below (above) the w nullcline.
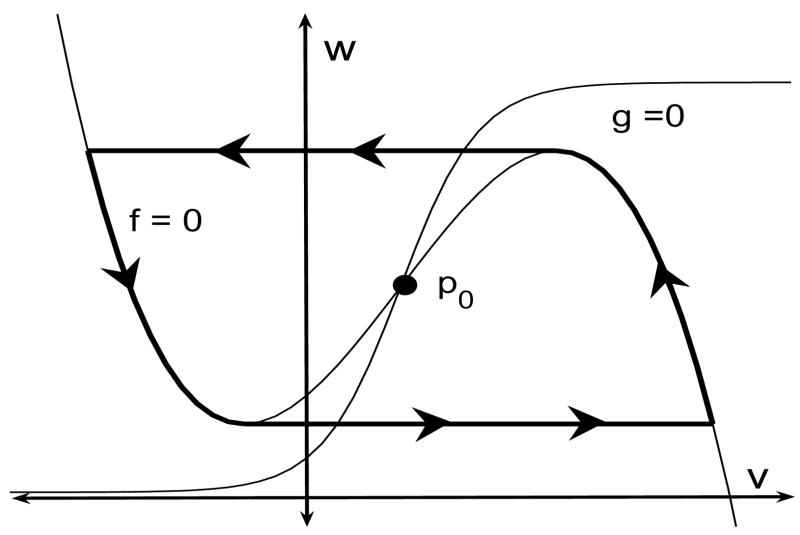
We further assume that the v- and w-nullclines intersect at a unique fixed point p0. If p0 lies along the left branch of the v-nullcline, then p0 is stable and the cell is said to be excitable. In the oscillatory case, p0 lies along the middle branch and, if ε is sufficiently small, then the cell exhibits stable oscillations. In the limit ε → 0, the limit cycle approaches the singular trajectory shown in Figure 1. For most of this paper, we will assume that individual cells, without any coupling, are excitable.
Figure 1.
Singular trajectory for an oscillatory cell. Note that the fixed point p0 lies along the middle branch of the cubic-shaped v-nullcline. During the silent and active phase, the singular trajectory lies on the left and right branch, respectively, of the v-nullcline. Transitions between the silent and active phase take place when the trajectory reaches a left or right knee of the v-nullcline. For most of the paper, we assume that the cell is excitable; that is, p0 lies along the left branch of the v-nullcline.
Synaptic Connections
A pair of mutually coupled neurons is modeled as:
| (2) |
where i and j are 1 or 2 with i ≠ j. Moreover, gsyn represents a constant maximal conductance, sj corresponds to the fraction of open synaptic channels, and α and β represent rates at which the synapse turns on and turns off. Note that sj depends on the presynaptic cell. To simplify the discussion, we will assume H(v) is the Heaviside step function.
Note that the coupling between cells is through the synaptic variables si. Suppose, for example, that cell 1 is the presynaptic cell. When cell 1 fires a spike, its membrane potential v1 crosses the threshold θ and this results in activation of the synaptic variable s1. More precisely, at the rate α + β This then turns on the synaptic current to cell 2. When cell 1 is silent, so that v1 < θ, then s1 turns off at the rate β.
Synapses may be either excitatory or inhibitory. This depends primarily on the synaptic reversal potential vsyn. We say that the synapse is inhibitory if vsyn < vi(t), i = 1, 2, along solutions of interest. In the excitatory case, vsyn > vi(t).
Synapses may also be either direct or indirect. In a direct synapse, the postsynaptic receptor contains both the transmitter binding site and the ion channel opened by the transmitter as part of the same receptor. In an indirect synapse, the transmitter binds to receptors that are not themselves ion channels. Direct synapses are typically much faster than indirect synapses. The synapses we have considered so far are direct since they activate as soon as a membrane crosses the threshold. We model indirect synapses as described in [13]. We introduce a new independent variable xi for each cell, and replace (2) with the following equations for each (xi, si):
| (3) |
The constants αx and βx are assumed to be independent of ε. The variable x corresponds to a secondary process that is activated when transmitters bind to the postsynaptic cell. The effect of the indirect synapses is to introduce a delay from the time one cell jumps up until the time the other cell feels the synaptic input. For example, if cell 1 fires, a secondary process is turned on when v1 crosses the threshold θ. The synapse s1 does not turn on until x1 crosses some threshold θx; this takes a finite amount of time since x1 evolves on the slow time scales, like the wi.
Network Architecture
We will be interested in two types of networks; these are purely inhibitory (I-) networks and excitatory-inhibitory (E-I-) networks. First we consider I-networks. Then the network architecture can be viewed as a directed graph D = <VD, AD>. The vertices correspond to the neurons; for convenience of notation, we assume that VD = [n] ≡ {1, …, n}. If there is an arc (or directed edge) e = <i, j>, then cell i sends inhibition to cell j. This network is modeled as:
| (4) |
We are assuming that the cells are homogeneous so that the nonlinear functions f and g do not depend on the cell i. The sum in (4) is over all presynaptic cells; that is, {j: <j, i> ∈ AD}. Here we assume that vsyn is chosen so that the synapses are inhibitory.
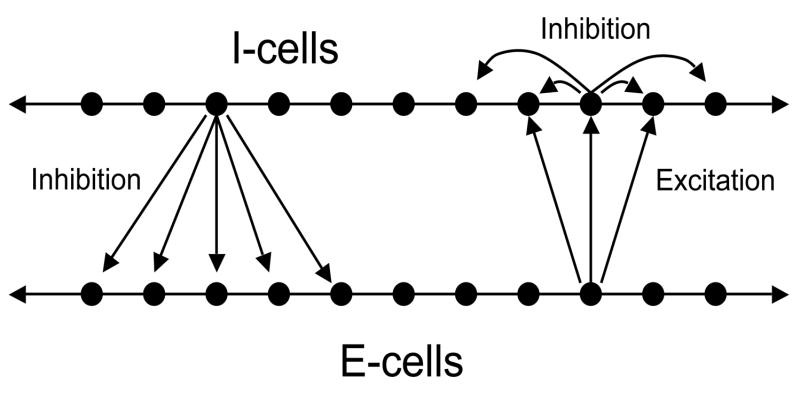
Now consider E-I-networks. We assume that there are two populations of cells. These are the excitatory (E-) cells and the inhibitory (I-) cells. The E-cells send excitation to some subset of I-cells. The I-cells send inhibition to some subset of E-cells as well as to I-cells. In the analysis which follows, We will need to assume that inhibitory synapses, corresponding to I →E and I →I connections, are indirect, while E →I connections are realized by direct synapses. Figure 2 shows the network. In Section 6.1, we write the equations.
Figure 2.
An excitatory-inhibitory network. Each I-cell sends inhibition to some subset of E-cells as well as to I-cells. Each E-cell sends excitation to some subset of I-cells.
3 Some example networks
We now consider some rather simple examples of inhibitory networks. These examples will be used to describe the sorts of solutions that we are interested in. The examples will also allow us to explain how the dynamics corresponding to the system of differential equations will be reduced to a discrete model. It will first be necessary to introduce some notation.
3.1 Some notation
Let Φ(v, w, s) ≡ f(v, w) − gsyns(v − vsyn). Then the right hand side of the first equation in (4) is Φ (vi, wi, Σsj) where the sum is over all cells presynaptic to cell i. If gsyn and s are not too large, then each defines a cubic-shaped curve. We will sometimes write to denote the cubic corresponding to synaptic input from K other active cells. We express the left branch of as {v = ΦL(w, K)} and the right branch of as {v = ΦR(w, K)}. Suppose that the left and right knees of are at w = wL(K) and w = wR(K), respectively.
Throughout this paper, we will use geometric singular perturbation methods to analyze solutions. That is, we construct singular trajectories for the limit when ε = 0. Recall, for example, the singular trajectory for the single oscillatory cell shown in Figure 1. While the cell is in either the silent or active phase, the singular trajectory lies on either the left or right branch of the cubic-shaped v-nullcline, respectively. The jump-up to the active phase or the jump-down to the silent phase occurs when the singular trajectory reaches the left or right knee of the v-nullcline.
In larger networks, the singular trajectory corresponding to each cell will also lie along either the left or right branch of a cubic-shaped v-nullcline during the silent or active phase. The jumps up and down between the silent and active phases occur when a singular trajectory reaches the left or right knee of some cubic. One can view the synaptic input as moving the cubic-shaped nullcline up or down, meaning that there is a family of cubic-shaped nullclines, depending on the synaptic inputs si. Which cubic a cell lies on depends on how many active cells it receives synaptic input from.
3.2 Post-inhibitory rebound
It is well known that two cells coupled through mutual inhibition can generate antiphase oscillations through the mechanism known as post-inhibitory rebound. This phenomenon arises in a variety of neuronal systems [19,20]. Along an antiphase solution, the cells take turns firing action potentials; when one cell jumps down, it releases the other cell from inhibition and that other cell then jumps up. This mechanism will play a central role in our analysis of larger networks. For this reason, we will briefly describe the geometric construction of a singular trajectory corresponding to the antiphase solution.
The singular trajectory is shown in Figure 3. There are two trajectories; these correspond to the projections of (v1, w1) and (v2, w2) onto the (v, w)- phase plane. Note that each cell, without any coupling, is excitable. The w-nullcline intersects both and along their left branches. Moreover, cells cannot fire unless they receive inhibitory input first.
Figure 3.
Post-inhibitory rebound. The cells take turns firing. When one cell jumps down, it releases the other cell from inhibition. If, at this time, the inhibited cell lies below the left knee of , then the inhibited cell will jump up to the active phase.
We now step through the construction of the singular trajectory corresponding to the antiphase solution. We begin with cell 1 at the right knee of ready to jump down. We further assume that cell 2 is silent and lies along the left branch of below the left knee of . When cell 1 jumps down, s1 → 0. Note that s1 → 0 instantaneously with respect to the slow time scale. Since (v2, w2) lies below the left knee of , cell 2 exhibits post-inhibitory rebound and jumps up to the right branch of .
Cell 2 then moves up the right branch of and cell 1 moves down the left branch of towards p1. Eventually, cell 2 reaches the right knee of and jumps down. If at this time, cell 1 lies below the left knee of , then it jumps up due to post-inhibitory rebound. The roles of cell 1 and cell 2 are now reversed. The cells continue to take turns firing when they are released from inhibition. Note that the time each cell spends in the active phase must be sufficiently long. This gives the silent cell enough time to evolve along the left branch of to below the left knee of so that it is ready to jump up when it is released from inhibition.
3.3 A larger inhibitory network
The next example network consists of seven cells and the network architecture is shown in Figure 4. All connections are assumed to be inhibitory with direct synapses. Two different responses, for the same parameter values but different initial conditions, are shown in the figure. Each response consists of discrete episodes in which some subset of the cells fire in near synchrony. These subsets change from one episode to the next; moreover, two different cells may belong to the same subset for one episode but belong to different subsets during other episodes. These solutions correspond to dynamic clustering. Note that cells fire due to post-inhibitory rebound.
Figure 4.
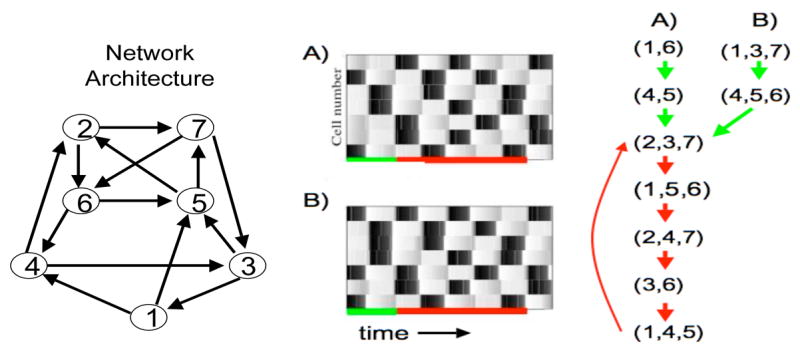
An example inhibitory network with seven cells. The left panel shows the graph of the network architecture. Cell 1, for example, sends inhibition to cells 4 and 5. Subsets or clusters of cells fire in distinct episodes. Each horizontal row in the middle panels represents the time course of a single cell. A black rectangle indicates when the cell is active. In the right panel, we keep track of which cells fire during each subsequent episode. The equations and parameters used are precisely those described in Section 7 except , αx = 1, βx = 4, I = 16 for the E-cells and I = 10 for the I-cells.
Consider, for example, the solution labeled (A). During the first episode, cells 1 and 6 fire action potentials and the cells that fire during the second episode are 4 and 5. After this transient period, the response becomes periodic. Note that the cells which fire during the third episode are cells 2, 3 and 7. These are precisely the same cells that fire during the eighth episode. This subset of cells continues to fire together every fifth episode.
Now consider the solution labeled (B). This solution has the same periodic attractor as the solution shown in the first panel, although the initial response is different. These two solutions demonstrate that two responses may have different initial transients but approach the same periodic attractor. There are, in fact, many periodic attractors. In the next section, we will demonstrate that this example exhibits seven periodic attractors.
4 The discrete model
As the examples presented in the previous section illustrate, solutions of the neuronal model may consist of discrete episodes. During each episode, some subset of cells fire in near synchrony; moreover, this subset changes from one episode to another. This suggests that we can reduce the neuronal model to discrete dynamics that keeps track of which cells fire during each discrete episode. In this section, we shall formally define the discrete dynamics. We then define what it means that the neuronal system can be reduced to the discrete model. We will then state the main result of this paper. In later sections, we shall describe conditions for when the neuronal model can be rigorously reduced to the discrete model. In [1], we embark upon a rigorous analysis of the discrete model.
4.1 Definition of the discrete model
First we consider a purely inhibitory network. In order to derive the discrete dynamics, we need to make two assumptions on solutions of the neuronal model. Later we will describe when parameters in the neuronal model can be chosen so that these assumptions are satisfied. The first assumption is that there is a positive integer p such that every cell has refractory period p. That is, if a cell fires during an episode then it cannot fire during the next p subsequent episodes. The second assumption is that a cell must fire during an episode if it received inhibitory input from an active cell during the previous episode and if it has not fired during the previous p episodes.
Consider, for example, the example shown in the first panel of Figure 4. Here, p = 1. Cells 1 and 6 fire during the first episode. Both of these cells send inhibition to cells 4 and 5 so, by the second assumption, both of these cells must fire during the second episode. During the third episode, cells 2, 3 and 7 fire. Note that cell 2 sends inhibition to cell 7; however, cell 7 cannot fire during the fourth episode because it fired during the third. Continuing in this manner, we can determine which subset of cells fire during each subsequent episode.
We now formally define the discrete model. Assume that we are given a directed graph D = <VD, AD> and a positive integer p. The vertices of D signify neurons and an arc <v1, v2> ∈ AD signifies a synaptic connection from neuron v1 to neuron v2. We associate a discrete-time, finite-state dynamical system SN with a network N = <D, p>. A state s→ of the system at the discrete time κ is a vector s→ (κ) = [P1(κ), …, Pn(κ)] where Pi(κ) ∈ {0, 1, …, p} for all i ∈ [n]. The state Pi(κ) = 0 of neuron i is interpreted as firing at time κ.
The dynamics on SN is defined as follows:
(D1) If Pi(κ) < p, then Pi(κ + 1) = Pi(κ) + 1.
(D2) If Pi(κ) = p, and there exists a j ∈ [n] with Pj(κ) = 0 and <j, i> ∈ AD, then Pi(κ + 1) = 0.
(D3) If Pi(κ) = p and there is no j ∈ [n] with Pj(κ) = 0 and <j,i> ∈ AD, then Pi(κ + 1) = p.
Recall that a cell ‘fires’ when Pi(κ) = 0. (D1) implies that after a cell fires, its state Pi increases by one unit each episode until Pi = p; at this time, the cell is ready to fire again. (D2) implies that if a cell is ready to fire at time κ, then it will do so at time κ + 1 if it receives input from some cell that has fired at time κ. Finally, (D3) states that even if a cell is ready to fire, it will not do so unless it receives input from some active cell.
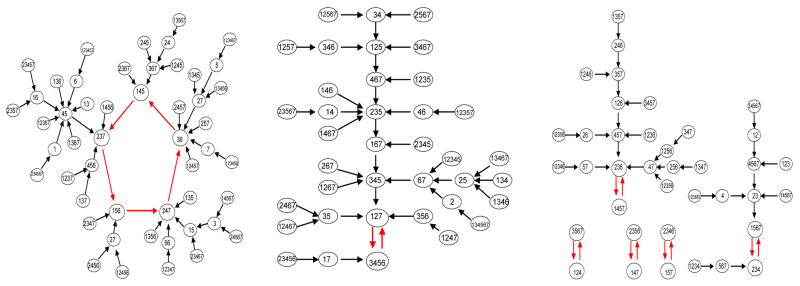
Note that the dynamical system SN can be viewed as a directed graph on its state space. This state transition digraph is different from D, the network connectivity graph. If there are n cells, then there are (p + 1)n states. For the example discussed in Section 3.3, there are seven cells and p = 1. Hence, there are 128 states. The entire directed graph corresponding to the discrete dynamics is shown in Figure 5. In the figure we have changed notation in order to simplify it. At each node, we list those cells which fire; these are the cells with Pi = 0.
Figure 5.
Discrete dynamics corresponding to the network shown in Figure 4
Now consider an E-I-network. We formally reduce this to an I-network by constructing a directed graph D whose nodes correspond to the E-cells. Suppose that there are n E-cells which we label as {Ei: i ∈ [n]}. For any i, j ∈ [n], we assume that there is an edge <i, j> ∈ D if there is an I-cell, say Ik, such that there exist both Ei → Ik and Ik → Ej connections. Now that we have the network connectivity graph D, we can consider the discrete-time dynamical system SN = <D, p> defined above.
The definition of the discrete dynamics for the E-I-network is based on two assumptions. Suppose that Ei and Ej are any E-cells and Ik is any I-cell such that there exist both Ei → Ik and Ik → Ej connections. The first assumption is that if Ei fires during an episode, then so will Ik. The second assumption is that if Ik fires during an episode, then Ej will fire during the next episode if and only if it has not fired during the previous p episodes.
4.2 Reduction from the neuronal model to the discrete model
Our goal is to find conditions on parameters for when the neuronal system generates dynamics that is consistent with a discrete model. Here we give a more precise definition for what it means that the neuronal system can be reduced to the discrete model. We only consider purely inhibitory networks in this subsection; a similar definition holds for E-I-networks.
Consider any network with any fixed architecture and fix p, the refractory period. We can then define both the continuous neuronal and discrete models, as was done in the preceding sections. Let s→ be any state of the discrete model. We then wish to show that there exists a solution of the neuronal system in which different subsets of cells take turns jumping up to the active phase. The active cells during each subsequent episode are precisely those determined by the discrete orbit s→(κ), and this exact correspondence to the discrete dynamics remains valid throughout the trajectory of the initial state. We will say that such a solution realizes the orbit predicted by the discrete model. This solution will be stable in the sense that there is a neighborhood of the initial state such that every trajectory that starts in this neighborhood realizes the same discrete orbit.
4.3 The main result
We now formally state our main result.
Theorem
Suppose we fix n, corresponding to the size of the network, and p, the refractory period. Consider any excitatory-inhibitory network such that both the number of E-cells and the number of I-cells are bounded by n. Assume that the E-cells and the I-cells are modeled by the equations that satisfy the assumptions spelled out in Subsection 6.4. We further assume that there is all-to-all coupling among the I-cells, the excitatory synapses are direct and the inhibitory synapses are indirect. Finally, we consider any architecture of E → I and I → E connections. We can then define both the continuous and the discrete models, as was done in the preceding sections. Then there are intervals for the choice of the intrinsic parameters of the cells and the synaptic parameters so that:
Every orbit of the discrete model is realized by a stable solution of the differential equations model.
Every solution of the differential equations model eventually realizes a periodic orbit of the discrete model. That is, if X(t) is any solution of the differential equations model, then there exists T > 0 such that the solution {X(t):t > T} realizes a periodic orbit or a steady state of the discrete model.
We remark that the intrinsic and synaptic parameters will not depend on the network architecture. Hence, every orbit of the discrete model, for any network architecture, can be realized by a solution of the neuronal model. Moreover, every attractor of the differential equations model corresponds to a periodic orbit of the discrete model.
In Section 7 we give a concrete example of equations that satisfy the assumptions spelled out in Subsection 6.4. As we shall see in the proof of the theorem, what is important are the positions of the left and right knees of the cubic-shaped nullclines, the rates at which the slow variables evolve during the silent and active phases and the strengths of the synaptic connections.
The proof of the Theorem is constructive in the sense that we give precise bounds on the parameters. In particular, the proof leads to an estimate for the time-duration corresponding to each episode of the discrete model (see inequality (16)).
5 A problem with inhibitory networks
We now discuss an example that illustrates difficulties that arise in I-networks. This example suggests that it is not possible, in general, to reduce the dynamics of an I-network to a discrete model. In the next section, we demonstrate that these difficulties can be overcome in E-I-networks.
Consider the inhibitory network shown in Figure 6. The discrete dynamics predicts that there is a solution in which the network breaks up into two clusters; Cluster A consists of cells 1 and 2 and cluster B consists of cells 3 and 4. There is actually no problem in demonstrating that such a solution exists. This solution is very similar to the antiphase solution described in the preceding section. The clusters take turns jumping up to the active phase when they are released from inhibition by the other cluster.
Figure 6.

An example network used to illustrate difficulties that arise with inhibitory networks.
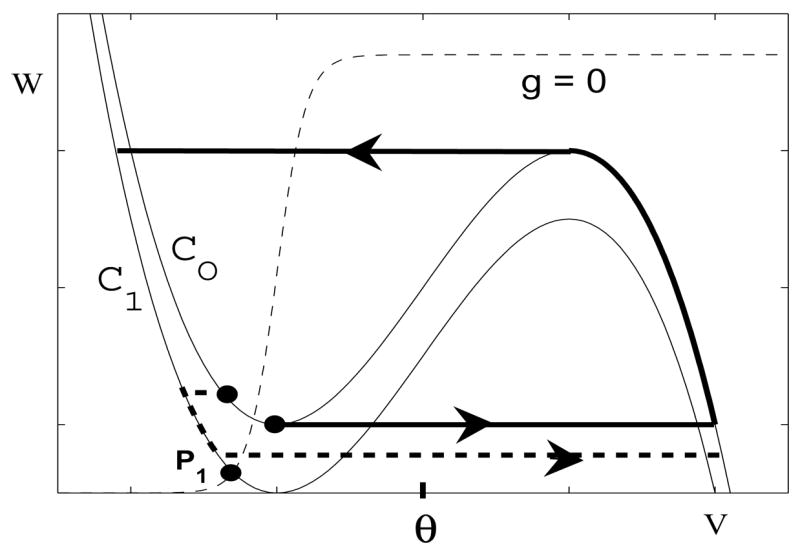
We next consider the stability of this solution. The following analysis will, in fact, suggest that this solution is not stable. In order to discuss stability, we need to define a notion of distance between two cells. Here, we define the distance between cells (v1, w1) and (v2, w2) to be simply |w1 − w2|.
Suppose we start so that cells within each cluster are very close to each other as shown in Figure 7. Note that Cluster A is active and lies along the right branch of . Cell 1 is at a right knee ready to jump down. Cluster B is silent and lies along the left branch of very close to the point p1 where intersects the w-nullcline. We now step through what happens once cell 1 jumps down. We will demonstrate that instabilities can arise in both the jumping-down and jumping-up processes.
Figure 7.
A singular trajectory corresponding to the network shown in Figure 6. (Left Panel) Cells 1 and 2 and cells 3 and 4 are initially close to each other with cell 1 at a right knee ready to jump down. (Right Panel) The trajectory until cell 2 reaches a right knee and jumps down.
When cell 1 jumps down, it stops sending inhibition to cells 2 and 3. Cell 3 responds by jumping up to the active phase. Cell 2, on the other hand, moves to the right branch of . During the next step, cells 2 and 3 move up the right branch of , while cell 1 moves down the left branch of and cell 4 move down the left branch of . During this time, both the distances between cells 1 and 2 and between cells 3 and 4 increase. This continues until cell 2 reaches the right knee of and jumps down. At this time, cell 4 jumps up. Then both cells 1 and 2 lie in the silent phase and cells 3 and 4 are active. However, cells within each cluster are further apart from each other than they were initially. This expansion in the distance between cells within each cluster may continue and destabilize the clustered solution.
Note that we have not rigorously demonstrated that the network shown in Figure 6 cannot reproduce the dynamics predicted by the discrete model for some choice of parameter values. The analysis shows that instabilities can arise in the singular limit as ε →0. On the other hand, numerical simulations indicate that it may be possible to choose parameters (with ε bounded away from zero) so that this network does reproduce the discrete dynamics. However, the dynamics is quite sensitive to changes in parameter values. In contrast, for the excitatory-inhibitory networks described in the next section, we are able to rigorously prove that under certain conditions the network will always reproduce the dynamics of the discrete model.
6 E-I-networks
We now consider E-I-networks and find conditions when they generate dynamics corresponding to that of the discrete model.
6.1 The equations
The architecture of E-I-network is shown in Figure 2. Recall that the E-cells send excitation to some subpopulation of I-cells, while the I-cells inhibit some subpopulation of E-cells. We will need to assume that each I-cell sends inhibition to every I-cell, including itself. The excitatory synapses are direct, while the inhibitory synapses are indirect.
The equations for the E-cells can then be written as:
| (5) |
and the equations for the I-cells can be written as:
| (6) |
Here,
where each sum is taken over the corresponding presynaptic cells. The reversal potentials and correspond to inhibitory and excitatory synapses, respectively. Note that we are assuming that all of the excitatory cells are the same, as well as all of the inhibitory cells; however, the excitatory cells need not be the same as the inhibitory cells.
6.2 Strategy
Suppose we are given an E-I-network as described in Section 6.1 and a positive integer p, corresponding to the refractory period. Let SN be the discrete-time dynamical system as defined in Section 4. Here we describe our strategy for showing that the neuronal model reproduces the dynamics of the discrete model. The analysis will be for singular solutions. Along the singular solution, all of the cells lie on either the left or right branch of some cubic during the silent and active phase, respectively, except when a cell is jumping up or down. In order to construct the singular solutions, we first introduce a slow time variable η = εt and then set ε = 0. This leads to reduced equations for just the slow variables. The reduced equations determine the evolution of the slow variables as a cell evolves along the left or right branch of some cubic. Once we construct the singular solutions, it is necessary to demonstrated that these singular solutions perturb to actual solutions of (5) and (6) with ε > 0. This analysis is straightforward but rather technical and we will not present the details here. A similar analysis can be found in [14].
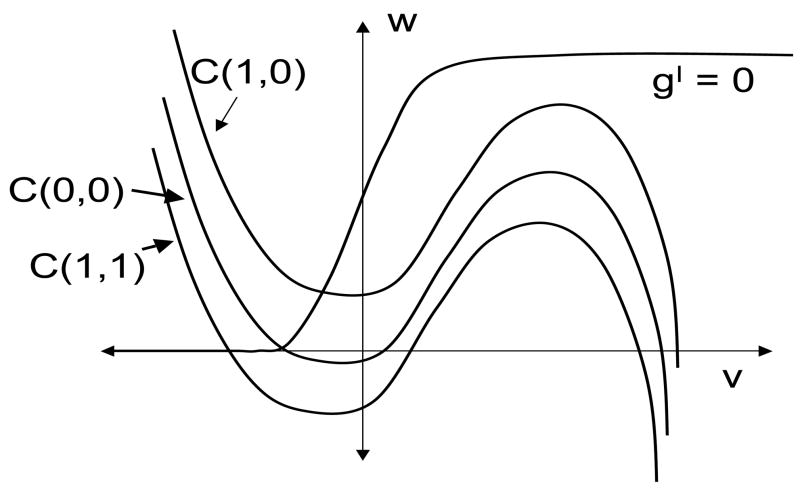
We will construct disjoint intervals , k = 1, …, p, and J0 = (0, W0) with the following properties. Let s→(0) = (P1, P2, …, Pn) be any state of the discrete model. Assume that when η = 0,
(A1) If Pi(0) = k, then wi(0) ∈ Jk.
(A2) If Pi(0) = 0, then Ei lies in the active phase.
(A3) If Pi(0) > 0, then Ei lies in the silent phase.
(A4) Every I-cell lies in the silent phase ready to jump up.
(A5) Each .
Then there exists T* > 0 such that when η = T*,
(B1) If Pi(1) = k, then wi(T*) ∈ Jk.
(B2) If Pi(1) = 0, then Ei lies in the active phase.
(B3) If Pi(1) > 0, then Ei lies in the silent phase.
(B4) Every I-cell lies in the silent phase ready to jump up.
(B5) Each .
(B6) The only E-cells that are both active and jump down in the interval [0, T*] are those with Pi(0) = 0.
In (A4) and (B4), we state that the I-cells are “ready to jump up.” By this we mean that each I-cell will jump up to the active phase if it receives excitatory input from some active E-cell. A more precise condition that the I-cells must satisfy will be given shortly, once we introduce some more notation.
Note that we can then keep repeating this argument to show that the solution of the neuronal model realizes the orbit predicted by the discrete model.
6.3 Slow equations and some notation
The first step in the analysis is to reduce the dynamics of each cell to equations for the slow variables. We introduce the slow variable η = εt and then let ε = 0 to obtain the reduced equations:
| (7) |
Differentiation is with respect to η.
We assume that αx is sufficiently large; in particular, αx ≫ βx. It follows that if , then , while if , then decays at the rate βx. Note that once an I-cell stops firing, there is a delay, which we denote as Δ, until it releases other cells from inhibition. This delay is determined by the slow variables, ; if αx is sufficiently large, then
| (8) |
The first and fourth equations in (7) state that the E- and I-cells lie on some cubic. Which cubic a cell lies on depends on the number of inputs it receives from active presynaptic cells. Note that if Ei is active, so that vi > θi, then si = α/(α + β) ≡ σE. If Ii is active, and , then . Suppose that Ei receives input from J active I-cells, and Ii receives input from K active E-cells and M active I-cells. Then
Let
Then the first and fourth equations in (7) can be written as
If gIE, gEI and gII are not too large, then these define cubic-shaped curves denoted by and , respectively. We express the left and right branches of as {v = ΦL(w, J)} and {v = ΦR(w, J)} and the left and right knees of as w = wL(J) and w = wR(J), respectively. The left and right branches, along with the left and right knees, of can be expressed as wL(K,M) and wR(K,M), respectively.
We can now write the second and fifth equations of (7) as
| (9) |
Here, ξ = L or R depending on whether the cell is silent or active. These are scalar equations for the evolution of the slow variables wi and .
6.4 Assumptions
In many neuronal models, the nonlinear function g(v, w) is of the form
| (10) |
where w∞(v) is nearly a step function. We assume that g(v, w) is of this form. Moreover, there exist V1 < V2 and constants τ1 and τ2 such that if v < V1, then w∞(v) = 0 and τ(v) = τ1; if v > V2, then w∞(v) = 1 and τ(v) = τ2.
We need to assume that the nullclines are such that E-cells can fire due to post-inhibitory rebound. We assume that intersects the w-nullcline at some point, pA = (vA, wA), where V1 < vA < V2. Moreover, the left knee of is at some point (vL(0), wL(0)) where wL(0) > 0.
We also assume that the left branches of the inhibited cubics lie in the region where v < V1. Finally, we assume that the right branches of each cubic for J ≥ 0 lie in the region v > V2.
These assumptions imply that the slow dynamics (9) do not depend on which cubic the cell lies on, unless the cell is on the uninhibited cubic . That is, if Ei lies in the silent phase, and this cell receives some inhibitory input, then wi satisfies the simple equation
| (11) |
We will assume that V2 − V1 is small. Hence, even if Ei does not receive any inhibitory input, then, except in some small neighborhood of the fixed point pA, wi also satisfies (11). If Ei is active, then wi satisfies
| (12) |
Similarly, we assume that gI(v, w) can be written as
Moreover, there exist constants and such that if , then and ; if , then and . For each cubic that is inhibited (M > 0) or does not receive excitation (K = 0), the part of the left branch above the v-axis lies in the region . The right branch of each cubic lies in the region .
Finally, we need to assume that an I-cell will fire only when it receives excitatory input from an E-cell and it does not receive inhibitory input from some other I-cell. This will be the case if the nullclines corresponding to the I-cells are as shown in Figure 9. Suppose that the left knee of is at ; recall that K and M are the number of excitatory and inhibitory inputs that the I-cell receives. We assume that if either K = 0 or M ≥ 1. Moreover, if K ≥ 1.
Figure 9.
Assumptions on the nullclines for the I-cells.
We can now give a more precise statement of (A4). We assume that when η = 0, every I-cell lies in the silent phase with . For the assumptions just given, this implies that each I-cell will jump up to the active phase if it receives input from an active E-cell. A more precise statement of (B4) is that when η = T*, every I-cell lies in the silent phase with .
6.5 Analysis
We now step through the solution keeping track of where cells are in phase space. We must keep track of where and when cells jump up and down and where they lie along the left branches of cubics in the silent phase. The sets Jk and the constant T* will be defined as they are needed in the analysis.
When do I-cells jump up?
We note that when one I-cell jumps up, it sends inhibition to every I-cell, including itself. However, because the inhibitory synapses are indirect, there is a delay from when one I-cell jumps up or down and other I-cells receive or are released from the resulting inhibition. These delays are modeled by the auxiliary variables xi. At time η = 0, the last of these variables crosses the threshold for releasing all I-cells from inhibition. For this reason, all of the I-cells are able to jump up when η = 0, as long as they receive excitatory input. Let I0 be those I-cells that receive input from at least one Ei with Pi(0) = 0. We have assumed in (A4) that each of these cells lies below the left knee of . It follows that every cell in I0 is induced to jump up precisely when η = 0.
We note that one potential problem is that when an I-cell, say , jumps up and crosses the threshold θI, then inhibition to all of the I-cells is turned back on. Hence, some of the I-cells that receive excitatory input may be induced to “turn around” and return to the silent phase. Note that it is the middle branch of the corresponding cubic that separates those I-cells that will return to the silent phase from those that will continue to jump up to the active phase: I-cells that lie to the left of the middle branch will return to the silent phase, while I-cells to the right of the middle branch will continue to jump up. For this reason, we need to choose θI so that it is to the right of the middle branch of the corresponding cubics. This will guarantee that inhibition is not turned back on until the I-cells are committed to fire.
When do I-cells jump down?
Note that active I-cells may lie on different cubics and jump down at different right knees. Choose constants so that when an I-cell jumps down, it does so with . Each I-cell in I0 jumps up at η = 0 with . Moreover, while in the active phase, wI(η) satisfies
It follows that every I-cell in I0 jumps down at some time Tijd that depends on the cell and always satisfies
| (13) |
where
| (14) |
We will need to assume that δI < Δ. Later we will find conditions on parameters for when this is the case. Let be the time when the last I-cell in I0 jumps down.
The set J0 and the constant T*
Let W0 = 1 + (wL(0) − 1)e−δI/τ2
| (15) |
It follows from (13) that
| (16) |
Note that T* corresponds to time-duration of an episode in the discrete model. Hence, (16), together with (14) and (8), gives a precise estimate on the lengths of these episodes.
When do E-cells jump down?
Consider those E-cells, Ei, with Pi(0) = 0. Recall that these E-cells are initially active. Here we estimate when these E-cells jump down. Suppose that the maximum number of I-cells that an E-cell receives input from is M. Then when an E-cell jumps down, it does so with wR(M) ≤ w ≤ wR(0). Moreover, when η = 0, each wi ∈ [0,W0] and, while in the active phase, the slow variables wi satisfy (12). It follows that the E-cells jump down at some time Tejd that satisfies
| (17) |
where
| (18) |
We will need to assume that E-cells that jump up remain active until time T* when all I-cells are released from inhibition. This will be the case if the following inequality holds.
| (19) |
We also need to assume that all E-cells that are active in a given episode jump down before the end of the episode, which translates into
| (20) |
Later, we find conditions on parameters for when this is the case.
The sets Jk
We now define the sets Jkfork > 0. To do this, we need to estimate the positions of the E-cells at time T*. Let .
First consider a cell Ei = (vi, wi) that initially lies in . Note that Ei jumps down at some Tejd and then lies in the silent phase for all times η with Tejd < η < T*. While in the silent phase, wi satisfies (11). Hence,
The position at which Ei jumps down satisfies wR(M) ≤ wi(Tejd) ≤ wR(0). Moreover, Tejd satisfies (17) and T* satisfies (16). Therefore,
where ,
Let . We have shown that if , then wi(T*) ∈ J1.
We now consider the other E-cells. For 1 ≤ k < p, let
Similarly, let
If k ≠ p, let . If k = p, let . Here, we assume that
| (21) |
(Recall that the fixed point along lies at pA = (vA, wA).) This assumption will be verified later (see inequality (23) or Step 4 of Section 6.7). We also assume that as long as , (vi,wi) lies in the region where wi satisfies (11); that is, vi < V1. The latter will be the case if V1 is sufficiently close to V2, as we assumed in Section 6.4.
Suppose that , 1 ≤ k < p, and wi(0) ∈ Jk. It follows from (21) that Ei lies in the silent phase for 0 ≤ η ≤ T*. Using (16) and the definition of Jk+1, we conclude that wi(T*) ∈ Jk+1.
It remains to consider those E-cells in . Suppose that wi(0) ∈ Jp. There are two cases to consider. First suppose that Ei does not receive inhibitory input from an I-cell in I0. Then, using (21), (vi, wi) approaches the fixed point pA and wi(η) remains in Jp.
Now suppose that Ei does receive inhibitory input from an I-cell in I0. We need to show that Ei jumps up at some time η < T* and then lies in J0 when η = T* To do this, we estimate the time at which Ei is released from inhibition. Recall that the I-cells in I0 jump down at some time Tijd that satisfies (13). Moreover the last I-cell in I0 jumps down at . Hence, E-cells are released from inhibition at some time Teju that satisfies
| (22) |
From the definitions, . It then follows from (21) that Ei jumps up at some η ∈ [TI + Δ, T*].
Finally, we need to show that wi(T*) ∈ J0. Note that when Ei jumps up, wi(Teju) < wL(0). Moreover, wi(η) satisfies (12) for Teju ≤ η T*. It follows from (22) and (16) that T* − Teju < δI. Hence,
Clearly, wi(T*) > 0. It now follows that wi(T*) ∈ J0.
Property (B2)
As remarked above, T* − Teju < δI, thus all E-cells that are induced to jump up between times 0 and T* do so in the interval (T* − δI, T*]. By (19), these cells will still be in the active phase at time T*, and Property (B2) follows.
Where are the I-cells when η = T*?
For the proof of (B4), recall that the last I-cell jumps down when . Hence, all of the I-cells are released from inhibition when . From the assumption of Section 6.4 it follows that since all I-cells still receive inhibitory input between times and , the I-cells cannot fire in this interval, and must remain in the silent phase, for . In order to guarantee that when η = T*, all the I-cells lie below the left knee of , we assume that the I-cells have fast refractory periods. In particular, the time it takes for the I-cells to evolve in the silent phase from their jump-down positions to below the left knee of is less than Δ. This will be the case if is sufficiently small.
Properties (B5) and (B6)
Property (B5) follows from our choice of as the time when the last I-cell jumps down and the assumption that αx ≫ βx. The latter implies that the xi for the last I-cell to jump down can be assumed to cross the threshold at time .
Property (B6) follows from the fact that the next E-cell to jump up after time η = 0 can do so only after the first I-cell that jumped up at time 0 has released its inhibition.
6.6 Choosing parameters
Here we demonstrate how to estimate the various constants needed in the analysis in terms of parameters in the model. These estimates will demonstrate how one needs to choose the positions of the left and right knees of the cubic-shaped nullclines, the time-constants τ1, τ2, and , and the delay Δ defined in (8).
First consider TE and δE, which are given in (18). We must choose parameters so that δI < TE < TE + δE < TI + Δ − δI and δI < Δ. We note that in many neuronal models, the right knees depend weakly on synaptic coupling. An example is given in the next section. If this is the case, then
If we further assume that wL(0) and are both close to 0, it follows that both δE and δI can be made to be as small as we please. In particular, δI < Δ. We can guarantee that TE + δE < TI by choosing the time constants τ2 and appropriately.
We next compute the and . After some calculation, we find that
We need to choose parameters so that
| (23) |
To get some idea when this is the case, we will consider, as above, the limiting case in which δE = δI = 0. In particular, all of the E-cells jump down at the same position, which we denote as wR, and all of the I-cells jump down at the same position, which we denote as . We further let wL(0) = wL. Then (23) becomes
This is satisfied if
or
| (24) |
Note that τ1ln(wR/wL) is the time it takes for a solution of (11) starting at wR to reach wL. Hence, one can interpret (24) as saying that p is roughly the ratio of the times that an E-cell spends in the silent phase and an I-cell spends in the active phase.
We have shown that in the limiting case when all right knees coincide and thus δE = δI = 0, we can have δI < TE < TE + δE < TI < TI + Δ − δI and δI < Δ. Since these numbers depend continuously on the positions of the knees, the inequalities will continue to hold if wR(0) ≈ wR(M) and .
Positions of the right knees
We have assumed that the positions of the right knees depend weakly on the synaptic inputs. This is often the case in neuronal models and here we demonstrate why. Consider an E-cell, (v,w). Recall that along a cubic-nullcline,
| (25) |
where S now represents the total synaptic input. If we let w = W(v, S) denote the cubic-nullcline, plug this into (25) and differentiate with respect to v, then we find that at (v, w) = (v, w(v, S)),
At the right knee, and, therefore,
| (26) |
We now write the position of the right knee as (vR(S), wR(S)). Plugging this into (25) and differentiating with respect to S, we find that
Together with (26), this implies that
We need to choose parameters so that is small. To do this, we need to estimate fw(vR, wR). To get a sense of how large fw is, we now consider the concrete example presented in the next section. For that example,
It follows that we can make as small as we please by choosing gsyn sufficiently small and choosing either gNa or gK, or both, sufficiently large. For the example presented in the next section, we find that at the right knees, w ≈ .5, v ≈ 0, and w∞(v) ≈ 1. It then follows that .
6.7 An alternative way of choosing parameters
Here we describe an alternative way of choosing suitable parameters. Rather than having nullclines with all right knees close together, we will only require that their positions are bounded away from 0 and 1. Specifically, we assume that there are positive numbers 0 < a < c and 0 < b so that for every ρ > 0 we can choose the nullclines for the E-cells in such a way that a < wR(0) < c, and 0 < wL(0) < ρ. Let . Note that our assumptions imply that d < wR(M) < c.
On the other hand, we may need very small values for the parameter βx, which is consistent with the rest of our argument, but places a restriction of a very slow release from inhibition on E-I-networks.
The construction focuses on the choice of five parameters: τ1, τ2, , , Δ. The parameter Δ does not depend on any of the other four parameters; according to equation (8), we can make Δ any positive number we want if we choose a suitably small βx for a given threshold θx. Moreover, the parameters τ1, τ2, , do not influence the shapes or relative positions of the nullclines and their knees.
We choose parameters in the following sequence of steps:
Step 1
Choose parameters so that the v- and w-nullclines for the I-cells have the desired shapes and are in the correct relative positions; in particular, so that the knees are in the required relative positions. This does not place constraints on τ1,τ2, , Δ.
Step 2
We will initially require that the nullclines for the E-cells satisfy our assumptions regarding the bounds a, b, c and are such that . Let τ2 = 1, and choose small enough so that . In particular, δI < −ln(1 − d/2). In view of the definition of W0, the latter implies that 1−W0 > 1−d/2. In view of (18) and the bounds on the knees this in turn implies that
| (27) |
and
| (28) |
Note that . Thus , and in view of the first inequality in (27), this will ensure that δI < TE. After this step, TI and δI are fixed.
Step 3
The refractory period p was fixed at the outset. Now fix τ1 sufficiently small so that . Eventually we will have −ln b > lnwR(0) − lnwR(M). This will ensure that for all k. Now choose a preliminary value of Δ that is sufficiently large so as to ensure that for all k < p and . Here Δ > 4p(TI + TE + δI + δE) will do for a quick and dirty estimate, where TE and δE can be replaced by the upper bounds in (27) and (28). Finally, let ρ be sufficiently small so that and after this initial choice of Δ. In order to assure the inequality , we can replace wR(0) by its lower bound a and TE by its upper bound −ln(1 − c).
Step 4
Choose the v-nullclines for the E-cells in such a way that , a < wR(0) < c, and 0 < wL(0) < Δ. This assures that and the endpoints of our intervals are in the correct relative position. If after this initial choice of Δ we are done; if not, increase the Δ a little bit more (which will move both and down without changing the strict order relation between the interval endpoints) until we have . Choose the w-nullclines for the E-cells in such a way that and V2 − V1 is sufficiently small.
Step 5
Fix “sufficiently small” as required in the last line of the proof of (B4) in Section 6.5.
6.8 Completion of the proof of the Theorem
We have so far shown that every orbit of the discrete model is realized by a stable solution of the differential equations model. In particular, the continuous dynamics realizes the discrete dynamics on trajectories that start in some open subset of the state space of the ODE model. This open subset is characterized by the conditions (A1)–(A6) given in Section 6.2. It is still not clear how solutions that start outside of this subset behave. We now prove that every solution of the differential equations model eventually realizes a periodic orbit of the discrete model. This then will complete the proof of the Theorem.
We start from any initial state at time η = 0 and define time η1 as follows: If no I-cell is active at time 0, let η1 = 0. If some I-cells are active at time 0, then all I-cells receive inhibition, and no additional I-cells can jump up until the last currently active I-cell jumps down. Let η1 be the time when the last I-cell that was active at time 0 jumps down. Now let η2 ≥ η1 be the earliest time when the last I-cell releases its inhibition. If at that time no E-cells are active or jump up exactly at η2, then no I-cells will jump up at time η2, and no E-cells will jump up subsequently to η2. In this case, there will be no subsequent firing, and the system will reach a state with all E-cells in the interval Jp, which corresponds to the steady state of the discrete system.
If at time η2 some E-cells are active or jump up, then those I-cells that are ready to fire and receive excitation will jump up at time η2. Let η2 < η3 <… < η2+p be the subsequent times when all I-cells are released from inhibition. If at any of these times no E-cells are active, then we are back to the situation described in the previous paragraph. Notice that for every i = 1, …, p we must have
This implies that at time η2+p all I-cells will have moved to the region where they are ready to fire if they are released from inhibition and receive excitation.
Now consider the E-cells at time η2+p. We distinguish two cases. If an E-cell has never been active between times [η2, η2+p] it will have had plenty of time to move to the interval Jp. The same is true for the E-cells that were active at time η2 and did not fire again before η2+p. If an E-cell did jump up at any time in the interval (η2, η2+p], it must have received inhibition from an I-cell that was active in this interval and whould have jumped up at some time in an interval (η2+i − δI, η2+i] for some i = 1, … p. Now our previous analysis applies to such cells and shows that at time η2+p this E-cell must be in the interval Jp−i. We have now shown that (A1) – (A6) given in Section 6.2 are satisfied at time η2+p. We can now use the analysis given in the previous sections to conclude that the continuous model realizes the discrete model for η > η2+p.
7 A concrete example
Here we give a concrete example of a neuronal model. Even though the connectivity of this network is much weaker than the connectivity assumed in proving the results of Section 6, numerical experiments indicate that this network still reliably generates firing patterns consistent with the predictionsof the discrete dynamics. The model consists of populations of both excitatory and inhibitory cells. The equations for each can be written as:
| (29) |
where gL = 2.25, gNa = 37.5, gK = 45, vL = −60, vNa = 55 and vK = −80 represent the maximal conductances and reversal potentials of a leak, sodium and potassium current, respectively. Moreover, ε = .04, I = 0, m∞(v) = 1/(1 + exp(− (v + 30)/15)) and w∞(v) = 1/(1 + exp(− (v + 45)/3)). The function τ(v) can be written as τ(v) = τ1 + τ2/(1 + exp(v/.1)) where τ1 = 4 and τ2 = 3 for each E-cell and τ1 = 4.5 and τ2 = 3.5 for each I-cell. The synaptic connections are modeled as in (3); however, in this model, we do not have the I-cells send inhibition to each other. We also assume that both the excitatory and inhibitory synapses are indirect. Here we take gsyn = .15, , vsyn = 0 and . Moreover, αx = 1.2 and βx = 4.8 for both the inhibitory and excitatory indirect synapses. To simplify the equations, we assume that the synaptic variables si and turn on and off instantaneously; that is, each si satisfies where H is the Heaviside step-function and θ = .1 is some threshold. A similar equation holds for each .
Figure 10 shows an example in which there are 100 excitatory and 100 inhibitory cells. Each E-cell has a refractory period of one and sends excitation to one I-cell and each I-cell sends inhibition to nine E-cells, chosen at random. We show solutions of both the neuronal model and the corresponding discrete model. Note that the cells that fire during each episode are exactly the same. After a transient of 2 cycles, there appears to be a stable attractor of 19 episodes.
Figure 10.
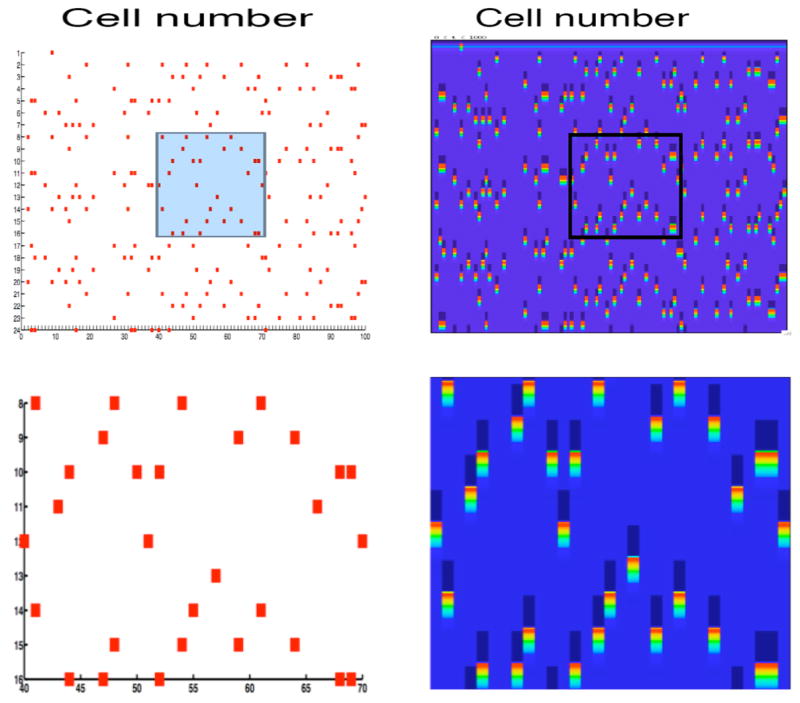
Solutions of the discrete model (left) and neuronal model (right) for a network of 100 excitatory and 100 inhibitory cells. Each E-cell effectively inhibits nine other E-cells chosen at random. In this example, the refractory period is one and the length of the attractor is nineteen. The top panels show the full network and the bottom panel shows a blow-up of the rectangular regions highlighted in the top panel. In the right panels, the bright areas indicate when a neuron fires; the dark areas indicate when a neuron receives inhibition.
8 Discussion
In this paper, we have demonstrated that it is possible to reduce a large class of excitatory-inhibitory networks to a discrete model. In a companion paper [1], we analyze the discrete dynamics and characterize when these networks exhibit a large number of stable firing patterns. Analysis of the discrete model also allows us to determine how the structure of firing patterns depend on the refractory period, the firing threshold, and the underlying network architecture.
The class of E-I-networks considered in this paper arises in many important applications. These include models for thalamocortical sleep rhythms [2–5], models for synchronous activity in the basal ganglia [6,7] and models for oscillations seen in a mammal’s olfactory bulb or an insect’s antennal lobe (AL) [8,9]. Each of these systems may exhibit rhythmic activity in which some subpopulation of cells fires in synchrony. Experimental recordings from neurons within the AL demonstrate that the network may exhibit dynamic clustering in which different subpopulations of cells take turn firing; moreover, the membership of these subpopulations may change from one episode to another. As the examples in Section 3.3 and Section 7 demonstrate, this sort of firing pattern arises naturally in the neuronal networks considered here. The analysis of the discrete model given in [1] examines how the tendency of the network to exhibit dynamic clustering depends on network architecture.
In order to reduce the neuronal model to the discrete model, we needed to make a number of assumptions on the network. In particular, we assumed that the inhibitory connections are indirect and the inhibitory cells have a very short refractory period. These assumptions are motivated by previous models for excitatory-inhibitory networks in the thalamus responsible for the generation of sleep rhythms [3]. In those models, the indirect synapses correspond to slow GABAB inhibition and the inhibitory cells do indeed have a very short refractory period. In fact, the concrete model presented in Section 7 is based on models for sleep rhythms generated by excitatory-inhibitory networks within the thalamus [3,4].
The analysis in Section 6 gives precise estimates on the parameter values so that the differential equations model reproduces the discrete dynamics. One may expect that it becomes increasingly more difficult to satisfy these estimates as the refractory period, p, or the size of the network, n, increases. This is true for p; however, the results are robust for a large class of arbitrarily large networks. For larger values of p, we must keep an increasing number of clusters separated along the left branch of the cubic-nullclines. Numerical simulations suggest that the largest value of p for which we can robustly reproduce the discrete dynamics is p = 5. Of course, the Theorem states that this is possible for any value of p. However, this result requires that the singular parameter ε be very small. If p is too large, then we may have to choose ε so small that it is impossible to generate the desired behavior.
The estimates given in Section 6 do not depend as crucially on the size of the network. Note that p is an intrinsic parameter of individual cells and does not depend on n. The only potential problem is if two cells within the same active cluster receive a significantly different amount of synaptic input from other active cells. The amount of synaptic input determines the right knee at which a cell jumps down; the estimates given in Section 6 depend on the maximum possible separation between these right knees. Therefore, as long as active cells receive approximately the same amount of synaptic input, our results do not depend on the size of the network.
Our analysis demonstrates that it may not be possible to rigorously reduce the continuous neuronal model to a discrete model in purely inhibitory networks, but this is possible in excitatory-inhibitory networks. A critical role of the additional layer of inhibitory cells in the E-I-network is to stabilize the timings of the firing of cells within each cluster. We note that the example discussed in Section 5 demonstrates that instabilities may arise during the jumping-up and jumping-down processes. That is, because cells within the same cluster may jump down at different times and at different right knees, the distances between these cells may increase. Moreover, these cells may release other cells from inhibition at different times and this may result in expansions in the distances between cells that jump up to the active phase. These types of expansions are in general also possible in E-I-networks because active cells within both the excitatory and inhibitory populations may also jump down at different right knees. It is, therefore, not obvious what advantages E-I-networks have over purely inhibitory networks. Note, however, that in our analysis of E-I-networks, all of the I-cells jump up at the same time. This follows from the assumption that the inhibitory synapses are indirect and there is all-to-all coupling between the inhibitory cells. Because all of the I-cells jump up at the same time, we were able to derive apriori bounds on when different I-cells jump down and then release E-cells from inhibition. (See inequalities (13)). This leads to an a priori bound on the possible expansion of the distances between cells during the jumping-down process and this, in turn, leads to an apriori bound on possible expansion during the jumping-up process. We remark that it is possible to weaken the assumption of all-to-all coupling among the I-cells in cases in which the underlying network architecture has some special structure; in particular, all-to-all coupling among simultaneously active I-cells is sufficient. It is likely that even this assumption can be further weakened. In the numerical simulation shown in Figure 10, for example, there is no coupling among the I-cells.
There have been numerous studies of clustering, dynamic clustering and transient synchrony in neuronal networks [12–18]. Previous work has typically considered smaller networks or larger networks with symmetries imposed on the network architecture; this includes all-to-all coupling. In these networks, dynamic clustering often emerges due to the presence of structurally stable heteroclinic cycles [10,15]. This is in contrast to the mechanism described in this paper which involves rebound properties of the excitatory cells. Our results hold for a more realistic neuronal model, we consider a completely general class of network architectures and the reduction to the discrete model leads to a complete characterization of the network behavior. We note that the clustering that may appear in the I-network considered in Section 4 appears to be unstable to perturbations of some clusters but not to others. This is similar to results presented in [15] where phase oscillator models were considered. Fast-slow analysis has been used in many studies of neuronal systems. This approach was used in [21], for example, where the analysis of the firing of a single excitable neuron, subject to stochastic input trains, was reduced to a discrete time Markov chain analysis. Finally, reproducible sequence generation in a class of excitatory-inhibitory network with random connections was studied in [16]. In that network, it was found that the highest likelihood for the existence of a stable limit cycle was close the regime of balanced excitatory-inhibitory input to each cluster; transient behavior was more likely far from the region of balanced input. The results presented in [1] demonstrate that for the network considered in the present paper, the existence of stable limit cycles or the existence of long or short transients, does not depend on a balance of excitatory and inhibitory input in the underlying E-I-network. Instead, long transients are more likely in networks with sparse connectivity, while short transients and a large number of stable limit cycles arise in networks with a dense connectivity. We note that the networks considered here and in [16] are quite different so that the different conclusions are not surprising.
Discrete models such as the one presented here have been proposed in numerous other studies of neuronal dynamics and other biological systems. If the refractory period of each neuron is one, then our model is an example of a Boolean dynamical system similar to the ones proposed as models for gene regulatory networks [22]. The relationship between network connectivity and “typical” network dynamics can be studied by investigating Random Boolean Networks (RBNs) [22], and a similar approach has been taken in [1]. We note, however, that the discrete model considered here is not random in the sense of RBNs. This is because once the architecture of the network is fixed, the dynamics of the discrete model is completely determined. The results in [1] demonstrate that the discrete model considered in this paper has properties that are in sharp contrast with those of RBNs. For example, in the study of Random Boolean Networks, a distinction is made between two types of behavior, called the ordered regime and the chaotic regime. Results on RBNs show that the network tends to become more chaotic, and hence less ordered, as the average number of inputs to the Boolean regulatory functions increases. Moreover, the attractors tend to be very few and very long in the chaotic regime. The results in [1] demonstrate that the dynamics of our discrete model becomes more ordered, as measured by the length and number of attractors, as the average degree of connectivity either decreases below or increases above a certain threshold.
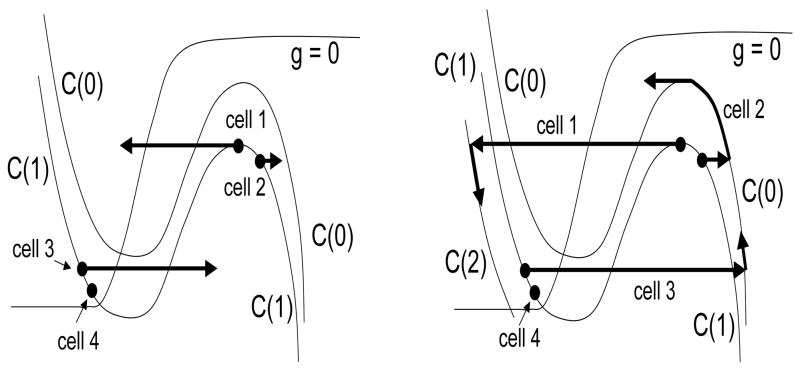
Figure 8.
The sets Jk used in the analysis. Here, p = 2. Cells in J0 evolve in the active phase until they jump down to lie in J1. During this time, cells in J1 move to J2. Note that only those cells in J2 that receive inhibition move to J0. The rest remain in J2.
Acknowledgments
This work was partially funded by the NSF under agreement 0112050 and by the NIH grant 1 R01 DC007997-01 and the NSF grant DMS 0514356 to DT.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errorsmaybe discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Just W, Ahn S, Terman D. Minimal attractors in digraph system models of neuronal networks. in progress. [Google Scholar]
- 2.Destexhe A, Sejnowski T. Synchronized oscillations in thalamic networks: insights from modeling studies. In: Steriade M, Jones E, McCormick D, editors. Thalamus. II. Elsevier; Amsterdam: 1997. pp. 331–372. [Google Scholar]
- 3.Golomb D, Wang XJ, Rinzel J. Synchronization properties of spindle oscillations in a thalamic reticular nucleus model. J Neurophysiology. 1994;72:1109–1126. doi: 10.1152/jn.1994.72.3.1109. [DOI] [PubMed] [Google Scholar]
- 4.Rinzel J, Terman D, Wang XJ, Ermentrout B. Propagating activity patterns in large-scale inhibitory neuronal networks. Science. 1998;279:1351–1355. doi: 10.1126/science.279.5355.1351. [DOI] [PubMed] [Google Scholar]
- 5.Terman D, Bose A, Kopell N. Functional reorganization in thalamocortical networks: Transition between spindling and delta sleep rhythms. Proc Natl Acad Sci USA. 1996;93:15417–15422. doi: 10.1073/pnas.93.26.15417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ. Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends in Neuroscience. 2002;25:523–531. doi: 10.1016/s0166-2236(02)02235-x. [DOI] [PubMed] [Google Scholar]
- 7.Terman D, Rubin J, Yew A, Wilson C. Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J Neurosci. 2002;22:2963–2976. doi: 10.1523/JNEUROSCI.22-07-02963.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Laurent G. Olfactory network dynamics and the coding of multidimensional signals. Nature Reviews, Neuroscience. 2002;3:884–895. doi: 10.1038/nrn964. [DOI] [PubMed] [Google Scholar]
- 9.Terman D, Borisyuk A, Ahn S, Wang X, Smith B. Excitation produces transient temporal dynamics in an olfactory network. submitted. [Google Scholar]
- 10.Rabinovich M, Volkovskii A, Lecanda P, Huerta R, Abarbanel HD, Laurent G. Dynamical encoding by network of competiing neuron groups: Winnerless competition. Physical Review Letters. 2001;87:068102. doi: 10.1103/PhysRevLett.87.068102. [DOI] [PubMed] [Google Scholar]
- 11.Kopell N, Ermentrout B. Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators. In: Fiedler B, Iooss G, Kopell N, editors. Handbook of Dynamical Systems II: Towards Applications. Elsevier; Amsterdam: 2002. [Google Scholar]
- 12.Rubin J, Terman D. Analysis of clustered firing patterns in synaptically coupled networks of oscillators. J Math Biol. 2000;41:513–545. doi: 10.1007/s002850000065. [DOI] [PubMed] [Google Scholar]
- 13.Rubin J, Terman D. Geometric singular perturbation analysis of neuronal dynamics. In: Fiedler B, Iooss G, editors. Handbook of Dynamical Systems II: Towards Applications. Elsevier; Amsterdam: 2002. pp. 93–146. [Google Scholar]
- 14.Terman D, Wang DL. Global competition and local cooperation in a network of neural oscillators. Physica D. 1995;81:148–176. [Google Scholar]
- 15.Ashwin P, Borresen J. Encoding via conjugate symmetries of slow oscillations for globally coupled oscillators. Physical Review E. 2004;70:06203. doi: 10.1103/PhysRevE.70.026203. [DOI] [PubMed] [Google Scholar]
- 16.Huerta R, Rabinovich M. Reproducible sequence generation in random neural ensembles. Physical Review Letters. 2004;93:238104. doi: 10.1103/PhysRevLett.93.238104. [DOI] [PubMed] [Google Scholar]
- 17.Chik TW, Coombes S, Mulloney B. Clustering through post inhibitory rebound in synaptically coupled neurons. Physical Review E. 1974;70:1011908. doi: 10.1103/PhysRevE.70.011908. [DOI] [PubMed] [Google Scholar]
- 18.Hansel D, Mato G, Meunier C. Clustering and slow switching in globally coupled phase oscillators. Phys Rev E. 1993;48:3470. doi: 10.1103/physreve.48.3470. [DOI] [PubMed] [Google Scholar]
- 19.Brown TB. On the nature of the fundamental activity of the nervous centers; together with an analysis of the conditioning of rhythmic activity in progression, and a theory of the evolution of function in the nervous system. Journal of Physiology. 1914;48:18–46. doi: 10.1113/jphysiol.1914.sp001646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Perkel DH, Mulloney B. Motor pattern production in reciprocally inhibitory neurons exhibiting postinhibitory rebound. Science. 1974;185:181–182. doi: 10.1126/science.185.4146.181. [DOI] [PubMed] [Google Scholar]
- 21.Rubin J, Josic K. The firing of an excitable neuron in the presence of stochastic trains of strong synaptic inputs. Neural computation. 2007;19:1251–1294. doi: 10.1162/neco.2007.19.5.1251. [DOI] [PubMed] [Google Scholar]
- 22.Kauffman S. Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press; New York: 1993. [Google Scholar]