Use of intrinsic modes in biology: Examples of indicial response of pulmonary blood pressure to ± step hypoxia

Abstract

Recently, a new method to analyze biological nonstationary stochastic variables has been presented. The method is especially suitable to analyze the variation of one biological variable with respect to changes of another variable. Here, it is illustrated by the change of the pulmonary blood pressure in response to a step change of oxygen concentration in the gas that an animal breathes. The pressure signal is resolved into the sum of a set of oscillatory intrinsic mode functions, which have zero “local mean,” and a final nonoscillatory mode. With this device, we obtain a set of “mean trends,” each of which represents a “mean” in a definitive sense, and together they represent the mean trend systematically with different degrees of oscillatory content. Correspondingly, the oscillatory content of the signal about any mean trend can be represented by a set of partial sums of intrinsic mode functions. When the concept of “indicial response function” is used to describe the change of one variable in response to a step change of another variable, we now have a set of indicial response functions of the mean trends and another set of indicial response functions to describe the energy or intensity of oscillations about each mean trend. Each of these can be represented by an analytic function whose coefficients can be determined by a least-squares curve-fitting procedure. In this way, experimental results are stated sharply by analytic functions.

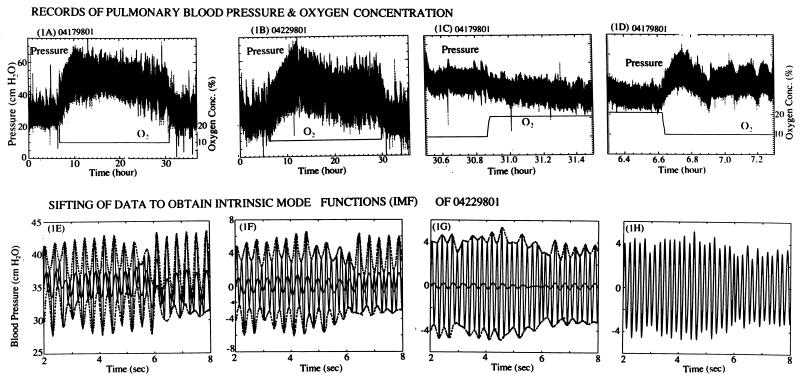
One often studies a biological system by changing one variable as a step function of time and recording the changes of other variables that are sometimes oscillatory, stochastic, and nonstationary. The question is how to analyze such stochastic data to obtain crystal clear results describing the effects of that step change of one variable on the other measured variables. For example, in ref. 1, we have shown that the pulmonary blood pressure in a rat in a presumably constant environment is stochastic. Now, let us consider the pulmonary blood pressure in response to step change of oxygen concentration in the gas that an animal breathes. The general feature of the results of such an experiment is shown in Fig. 1A. The upper, oscillatory trace shows a 36-h record of the pulmonary blood pressure in the arterial trunk of a rat breathing normal air at sea level for 6 h, breathing a gas with 10% oxygen at sea level for the next 24 h, and returning to normal air (20.9% oxygen) for 6 h. The lower, smooth line shows the history of oxygen concentration as a function of two steps. One can see certain trends of change of the pulmonary blood pressure in the record, but we need a definitive way to handle this overwhelmingly complex data to reveal the underlying physiological variations. Fourier analysis does not work for such nonstationary signals. The intrinsic mode method (1, 2), however, applies naturally to the present situation. The present article shows how it works and what physiological responses it reveals.

Figure 1.

Records of the blood pressure at the rat pulmonary arterial trunk in response to step changes of oxygen concentration in the breathing gas at sea level (upper row) and the method of sifting the signals to obtain the IMFs (lower row). (A and B) Thirty-six-hour records of two rats breathing gas with 20.9% O₂ from 0 h to 6, 10% O₂ from 6 to 30 h, and 20.9% O₂ from 30 to 36 h (the balance being N₂ and trace of CO₂), showing differences among individuals. (C) A 1-h strip from 29.7 to 30.7 h. The O₂ level increased from 10 to 20.9% in 29.97 to 29.99 h. (D) A 1-h record from 5.7 to 6.7 h. The O₂ level changed from 20.9 to 10% in a time interval from 6.04 to 6.06 h. In the lower row, E is a 6-s strip of data X(t) with the upper and lower envelopes shown in dotted lines and the first mean of the envelopes, m₁(t), plotted in heavy solid line. (F) The difference of data X(t) and the first mean m₁(t) was plotted. The envelopes of maxima and minima and the second mean m₂(t) were plotted. (G) Two iterations later, the mean was still not zero. (H) By iteration, one obtains the first IMF, C₁(t), whose local mean is zero.

Pulmonary hypoxic hypertension has been studied by many authors (3–25). Tissue changes and cellular aspects are discussed in refs. 3–12. Molecular aspects are discussed in refs. 13–19. Our own preliminary results on the arterial tissue remodeling and change of mechanical properties caused by the altered mechanical stresses are presented in refs. 20–25. A method of analysis of the blood pressure to derive the indicial response function is not available. In this paper, we use a rational approach to deduce the indicial response of the pulmonary blood pressure to ± step hypoxia.

METHODS

Experimental Procedures.

Sprague–Dawley rats (Harlan–Sprague–Dawley), male, ≈3 months old, were used in the study. The protocol was approved by the University of California, San Diego Committee on Animal Research. Each rat was implanted with an indwelling catheter in the pulmonary arterial trunk while breathing a gaseous anesthesia of isoflurane (1). After the catheter implantation, the awakened free-ranging rat was housed in a cage that was put in a chamber circulated with a gas of controlled composition (1, 24). The pulmonary blood pressure was measured continuously through the catheter while the animal moved freely or slept. The oxygen concentration in the breathing gas was controlled. The animal room was maintained at ≈70°F, was illuminated by fluorescent lighting from 6 a.m. to 6 p.m., and remained dark from 6 p.m. to 6 a.m. The tubing connected to the catheter was connected to an infusion pump and a Statham P23ID transducer (Statham, Hato Rey, PR) through a “T” tube, and the catheter was irrigated with a heparinized (20 units/ml) saline at a rate of 0.6 ml/h pumped by a Syringe Pump (Razel, Stamford, CT). Data were collected by a computer while the pressure waveform and the oxygen concentration signal also were recorded on a recorder (Astro-Med, West Warwick, RI). The analog-to-digital conversion was accomplished by a board (DT31-EZ, Data Translation, Marlboro, MA). The pressure wave was sampled 100 points per second.

The size of the modified commercial animal chamber (Snyder, Denver) was 0.28 m³ (0.66 × 0.56 × 0.75). The change of oxygen concentration level from 20.9 to 10% was accomplished in 1.5 ± 0.5 min by an infusion of pure N₂ at a selected rate and was well mixed with the air with a fan. A feedback-control system of O₂ sensor and a flow meter for N₂ was used. CO₂ in the hypoxic chamber was absorbed by soda lime (Fisher Scientific), and ammonia was absorbed by activated carbon (Fisher Scientific). The change of the breathing gas back to fresh air by opening the door of the chamber also was accomplished in 1.5 ± 0.5 min. For the measurement of oxygen, we used a portable oxygen analyzer (Model 320A, Teledyne Analytical Instruments, City of Industry, CA) with a flow-through adapter in the animal cage. The oxygen analyzer was calibrated in the normal air.

Data Analysis Methodology.

The method of intrinsic mode functions (IMFs) presented in refs. 1 and 2 is used here. Let us first explain what an intrinsic mode is. A signal as shown in Fig. 1E is designated as X(t), t being time. In Fig. 1E, the successive peaks of the signal are connected by a cubic spline dot-dashed smooth upper envelope; the successive valleys are connected similarly by a lower envelope. The mean of these two envelopes is shown in Fig. 1E by a thick solid curve and is denoted by the symbol m₁(t). The difference X(t) − m₁(t) is designated as h₁(t). A plot of h₁(t) is shown in Fig. 1F. It is seen that h₁(t) has a few negative local maxima and positive minima, suggesting an imperfection in the quality of h₁(t) as a representation of an “oscillation about the mean.” To improve the situation, we impose two definitive requirements for a function that represents the “oscillations about the mean”: (i) in the whole data set, the number of extrema and the number of zero-crossings must either be equal or differ at most by one, and (ii) at any time, the mean value of the envelop of the local maxima and the envelop of the local minima must be zero. An oscillatory function that satisfies these two conditions is called an intrinsic mode function (IMF). The function h₁(t) shown in Fig. 1F does not meet the requirement of an intrinsic mode. To improve, we treat h₁(t) as a new set of data, determine its upper and lower envelops, and compute their new mean m₁₁(t). The difference h₁ − m₁₁ is designated as h₁₁(t). This h₁₁(t) again is treated as new data, and the process is repeated a number of times (Fig. 1 G and H) until it converges. The convergent result, Fig. 1H, is designated by C₁(t) and is called the first intrinsic mode, which has a zero local mean.

The difference between X(t) and C₁(t) is a function of time representing a “mean trend” after the first round of intrinsic mode identification. It is designated as the “first residue” R₁(t):

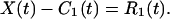1

R₁(t) is again oscillatory and can be analyzed as new data by the same method, yielding the second intrinsic mode C₂(t) and the “second residue” R₂(t). The process can be continued until either the residue or the intrinsic mode becomes less than a predetermined small number or the residue becomes nonoscillatory. If the process takes n steps, then we have

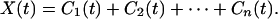2

The last term C_n(t) represents the nonoscillatory trend of the signal. The other terms C_n-1, C_n-2, and ⋅⋅⋅ represent the oscillatory part of the mean trend. A low-frequency representation of the mean trend of the signal X(t) is

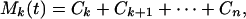3

where 2 < k < n. The lower the k, the more oscillations M_k(t) contains. Thus, our algorithm resolves the signal X(t) into a set of oscillations with zero local mean and a set of mean trends with various degrees of oscillations.

Analytic Representation of Indicial Response.

When we look for the indicial functions that represent the changes of the signal X(t) in response to step changes of the oxygen concentration, we look for the changes in the mean trends M_n(t), M_n-1(t), and ⋅⋅⋅ with respect to changes in O₂ level. We may fit the experimental result on M_k(t) with an analytic function. For example, if we take the origin of time t = 0 at the time of imposing a step change of oxygen tension, we may write the course of change of the mean blood pressure in response to a step change for t > 0 as

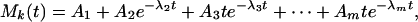4

where the constants A₁, ⋅⋅⋅, A_m, and λ₂, ⋅⋅⋅, λ_m are to be determined by the method of least-squares errors. Depending on the choice of the values of k and m, we may present different degrees of details.

In reality, we can only approximate a step function of O₂ as shown in Fig. 1 A–D. Furthermore, a dropping step of O₂ (Fig. 1D) and a rising step of O₂ (Fig. 1C) cause different changes in blood pressure. Hence, we use two different empirical functions. For the first case the equation is

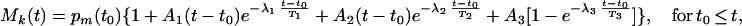5

where t₀ is the instant of time when O₂ concentration drops suddenly, and p_m(t₀) is the measured value of M_k(t₀). For the second case the following equation appears good enough:

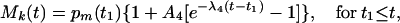6

where t₁ is the time when O₂ concentration increases suddenly. A₁, A₂, A₃, and A₄ are dimensionless.

Spectral Representation of Pulse Waves.

The Hilbert transform of X(t) is Y(t) defined by the reciprocal relationship given by Eq. 4 of ref. 1. Hilbert has shown that the complex variable Z(t) = X(t) + iY(t) is an analytic function of t (26) and can be written in polar coordinates as a(t)exp[iθ(t)], thus defining the amplitude a(t) and phase angle θ(t). Huang et al. (2) defined the instantaneous frequency ω(t) as the derivative of θ(t) with respect to time t. (See Eqs. 5–8 of ref. 1). Knowing the amplitude a(t) and the frequency ω(t) as functions of time t, we can plot contour maps as shown in Fig. 4D. The contour maps of the amplitude as functions of frequency and time is called the Hilbert amplitude spectrum, H(ω,t).

Figure 4.

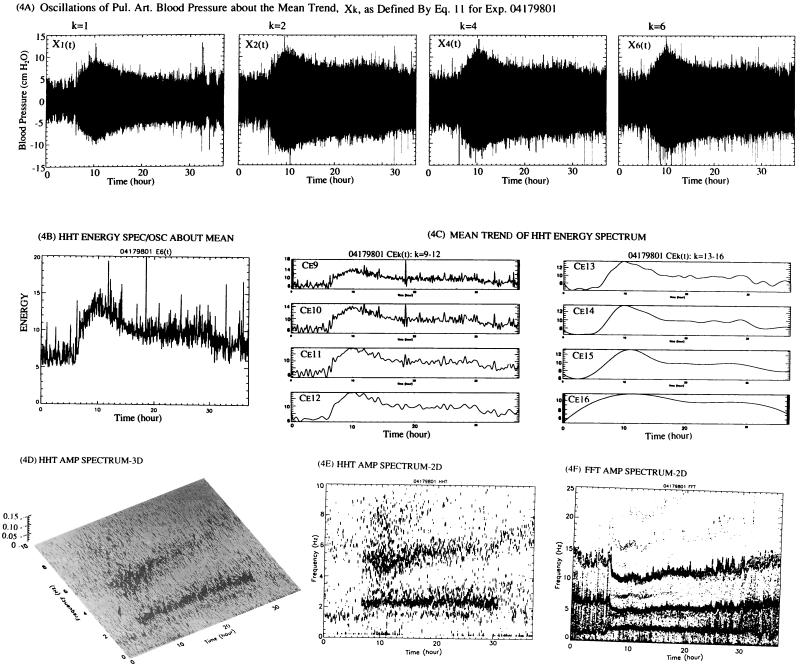
Oscillations about the mean trend M_k(t), their energy spectrum, IMF, and plots of Hilbert and Fourier spectra. (A) A set of oscillations of the pulmonary arterial blood pressure about the mean, defined by X_k in Eq. 7, is shown for k = 1, 2, 4, and 6. (B) The instantaneous amplitude spectrum of the oscillations about the mean, X_k(t), defined by Eq. 7, is denoted by H_k(ω, t). The integral of the square of H_k(ω, t) that covers the range of frequencies ω is the Energy spectrum E_k(t), which is plotted as a function of time. (C) A complete set of the IMF of E_k(t) was obtained. The last mode, n = 16, was nonoscillatory. Using Eq. 3, we obtained the mean trend of E_k(t), which is plotted here as Cek, with k specified as shown. (D) The three-dimensional (amplitude-frequency-time) plot of the Hilbert spectrum (HHT). (E) A two-dimensional (contour of amplitude on the frequency-time plane) plot of the Hilbert Spectrum (HHT). (F) Fourier Spectrum (FFT) over successive minutes is plotted two-dimensionally. See Discussion.

The vanishing of the local means of the IMFs C₁, ⋅⋅⋅, and C_n-1 is a very important fact because the amplitude a(t), and phase angle θ(t) of the Hilbert spectrum are sensitive to the local means. This is discussed in ref. 1. However, we take this opportunity to make a correction of a misprint in ref. 1: p. 4818, line 10 from the bottom in the left column, the term “+ icos t ” should be deleted from X(t).

We have defined M_k(t) in Eq. 3 to represent the mean trend. We may define the corresponding sum

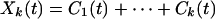7

as representing the oscillations about the mean trend M_k+1(t). The Hilbert amplitude spectrum of X_k(t) may be designated as H_k(ω,t). The square of H_k(ω,t) represents an oscillatory energy density. We can define the oscillatory energy about the mean, E_k(t), by an integration over all frequencies:

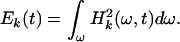8

The variations of E_k(t) and M_k(t) with oxygen level O₂(t) yield the desired summary of information about the transient response of X(t) to O₂(t).

RESULTS

The experimental results are displayed in Fig. 1 A–D. In each record, the oscillatory trace is the recorded blood pressure, and the straight line segments are the oxygen concentration in the gas that the animal breathes. In Fig. 1 A and B, two 36-h records of two rats breathing gas at sea level with 20.9% O₂ from 0 to 6 h, 10% O₂ from 6 to 30 h, and 20.9% O₂ from 30 to 36 h are presented. One sees the oscillations of the blood pressure, the general rise of blood pressure when the oxygen concentration in the breathing gas is lowered, and the general drop of blood pressure when the oxygen tension was raised. The ranges of the systolic and diastolic pressures were large for each animal, and there were considerable differences between animals. Without mathematical analysis, it is not possible to describe the blood pressure history concisely and with precision.

Fig. 1 C and D show some parts of a record in an expanded time scale. Fig. 1D shows how the blood pressure oscillates before and after a rapid change of oxygen concentration, which was dropped from 20.9 to 10% in 1.5 ± 0.5 min. In the scale of 1 day, we consider this a “step” decrease; and, henceforth, we say that the oxygen concentration changed as a step function. Fig. 1C shows the pressure change around a step increase of O₂ concentration.

Fig. 1 E–H show how the intrinsic modes (1, 2) are determined. Take the case 04229801 as an example (Fig. 1B). A 6-sec segment of the signal was plotted in Fig. 1E. The successive maxima (systolic pressure) were connected by a smooth curve (shown dotted in Fig. 1E) by the method of cubic spline. Then, the minima were connected by cubic spline. The mean of these two envelopes was computed and plotted (heavy solid line). It is seen that the mean was not zero. Let the signal be denoted by X(t) and the mean be denoted by m₁(t). The difference X(t) − m₁(t) was computed and plotted in Fig. 1F. Again the upper and lower envelopes of the maxima and minima were computed respectively, and the mean, m₂(t), was plotted. Again it was seen that m₂(t) was nonzero. The difference, X(t) − m₂(t), was computed and was treated the same way. Two iterations later, the result was shown in Fig. 1G. The iteration continued until the mean become sufficiently small to be called zero. The converged result now satisfies the definition of “intrinsic mode function” (IMF) and is designated C₁(t), shown in Fig. 1H. Thus, we obtain the first IMF.

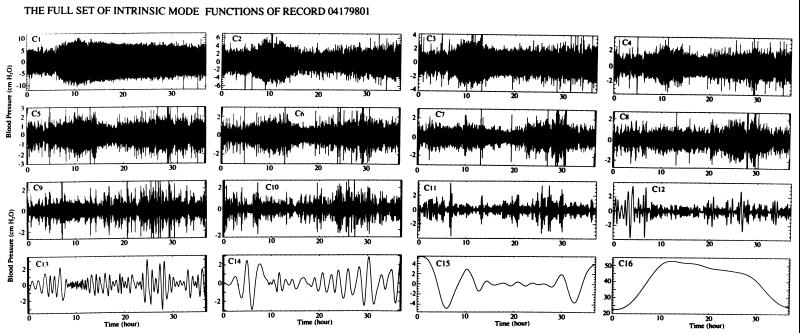
The signal X(t) minus the first IMF C₁(t) is called the first residue R₁(t) (Eq. 1). R₁(t) was treated the same way as X(t) shown in Fig. 1E, yielding the second IMF with zero local mean. The process was continued until finally a mode became either zero (insignificantly small) or nonoscillatory. The whole set of IMFs for the signal of the case 04179801 is shown in Fig. 2.

Figure 2.

The whole set of IMFs of the record of rat 04179801. The 16th mode is nonoscillatory.

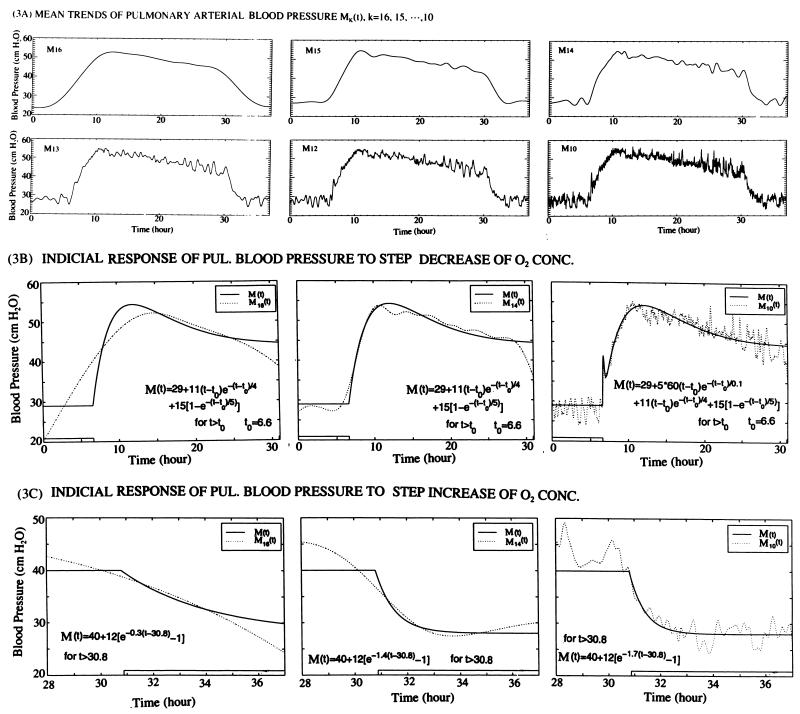
From the results of Fig. 2, we can compute the mean trend functions M_k defined by (Eq. 3). Typical results for the case 04179801 are shown in Fig. 3A, which are the main results to be used for the indicial response determination.

Figure 3.

The mean trends and their analytic representation. (A) A set of mean trends of pulmonary arterial blood pressure changes mathematically defined by Eq. 3. M₁₆ is the last IMF that is nonoscillatory for the rat 04179801. The other M_k with k < 16 contains various levels of oscillations. (B) Analytic representation of the indicial response of pulmonary arterial blood pressure to step decrease of O₂ concentration from 20.9 to 10.0% at 6.00 h. The mean trends M_k(t), k = 16, 14, and 10, as defined by Eq. 3, are fitted by analytic functions as shown in each panel. (C) Indicial response of pulmonary blood pressure to a step increase of O₂ concentration from 10.0 to 20.9% at 30.00 h. The mean trends M_k(t), for k = 16, 14, and 10 are representable by analytic functions show in each panel.

The analytic representation of the indicial response functions of Fig. 3A by Eqs. 4, 5, and 6 was done by the least-squares error method. Typical results are shown in Fig. 3 B and C. These are the main results that we are searching for, to be used in tissue engineering analysis and design.

The results shown in Figs. 3B and 3C give us the indicial response functions of the mean pulmonary blood pressure at the arterial trunk in response to a step decrease or a step increase of oxygen concentration. A similar quest can be directed toward the oscillational modes defined by Eq. 7. A direct look at the oscillation modes is shown in Fig. 4A. These curves contain a lot of information that needs to be extracted into simple, understandable terms. This is done by Hilbert transform and Hilbert spectrum. The results are shown in Fig. 4 B–F. Fig. 4B is a plot of the oscillatory energy defined by Eq. 7 as a function of time. When this spectrum is analyzed as a nonstationary random signal, we can resolve it into oscillatory IMF modes and mean trend functions M_k(t), with associated analytic functional representation. This is illustrated in Fig. 4C for k = 9, 10, ⋅⋅⋅, and 16.

Finally, the results of calculations of the instantaneous frequency and amplitude of oscillations of the pressure signal X(t), made possible by means of Hilbert transformation (1), can be plotted against time in a three-dimensional manner as in Fig. 4D. The same can be plotted two-dimensionally on the plane of time and frequency by contour lines of equal amplitudes, as shown in Fig. 4E. These results may be compared with the spectra computed by Fourier transforms of the pressure signal in 1-min segments under the assumption that the process is stationary in each segment. The Fourier spectrum is shown in Fig. 4F.

DISCUSSION

Fourier analysis is based on the hypothesis of segmental stationary random oscillation, the principle of linear superposition of sine waves, and global average of waveform convolution over each time segment. The HHT is based on the hypothesis of nonstationary process, the principle of linear superposition of nonlinear IMFs, and local determinations of amplitude and frequency (through differentiation rather than convolution) of each IMF. In terms of the IMF, the first k modes can be added together to represent the oscillations about the mean trend M_k+1(t). The Fourier series cannot represent time variation in the nonstationary signal, and it does not have such a property to separate a signal into two parts, one part representing a mean trend while the other part represents oscillations about the mean. The number of the intrinsic modes, n, is finite. In general, the n < log₂N, where N is the total number of data points. The number of harmonics in Fourier analysis is N/2. Comparison of the Hilbert and Fourier spectra shown in Fig. 4 E and F shows that both spectra display a major frequency at ≈5 Hz where the energy is concentrated. This is close to the heart rate of the rat. This rate decreases when the oxygen concentration decreased. These two spectra are in different vertical scales. The Hilbert spectrum contains no energy with frequency >10 Hz, and it also has fewer yet more diffused frequency bands than the Fourier spectrum. This is because the Hilbert spectrum presents the transient variation of the frequency from one instant to the next whereas the Fourier spectrum gives only the global mean. The mean values certainly will show less variations. The Fourier spectrum contains more frequency bands because any deviation of waveform from the basic harmonic will result in strong higher harmonics whereas the Hilbert spectrum allows variation of instantaneous frequencies, hence the fuzzy spread in frequencies, calling attention to the fact that the heart rate is also a stochastic variable, which could be studied by the same intrinsic mode method. The strong higher harmonic band with frequency >10 Hz in the Fourier spectrum is probably spurious. The clarity of the set of mean trends and the corresponding set of the oscillations is a unique contribution of the IMF method.

ABBREVIATION

IMF

intrinsic mode function