A computational model of adipose tissue metabolism: Evidence for intracellular compartmentation and differential activation of lipases

Abstract

Regulation of lipolysis in adipose tissue is critical to whole body fuel homeostasis and to the development of insulin resistance. Due to the challenging nature of laboratory investigations of regulatory mechanisms in adipose tissue, mathematical models could provide a valuable adjunct to such experimental work. We have developed a computational model to analyze key components of adipose tissue metabolism in vivo in human in the fasting state. The various key components included triglyceride-fatty acid cycling, regulation of lipolytic reactions, and glyceroneogenesis. The model, consisting of spatially lumped blood and cellular compartments, included essential transport processes and biochemical reactions. Concentration dynamics for major substrates were described by mass balance equations. Model equations were solved numerically to simulate dynamic responses to intravenous epinephrine infusion. Model simulations were compared with the corresponding experimental measurements of the arteriovenous difference across the abdominal subcutaneous fat bed in humans. The model can simulate physiological responses arising from the different expression levels of lipases. Key findings of this study are as follows: (1) Distinguishing the active metabolic subdomain (~3% of total tissue volume) is critical for simulating data. (2) During epinephrine infusion, lipases are differentially activated such that diglyceride breakdown is ~4 times faster than triglyceride breakdown. (3) Glyceroneogenesis contributes more to glycerol-3-phosphate synthesis during epinephrine infusion when pyruvate oxidation is inhibited by a high acetyl-CoA/free-CoA ratio.

Introduction

Adipose tissue is no longer considered a metabolically quiescent storage depot of lipids, but an active organ that regulates plasma fatty acid (FA) levels (Frayn, 2002; Frayn et al., 2003) and secretes various cytokines and hormones such as leptin, adiponectin, resistin, tumor necrosis factor (TNF)-α etc. (Trayhurn and Beattie, 2001; Frayn et al., 2003). The understanding of adipose tissue metabolism and its regulation is underscored by the demonstration of its role in the development of insulin resistance, regulation of satiety, and other metabolic functions (Kahn et al., 2006;Frayn, 2001).

Since adipose tissue does not have a unique artery (inflow) and vein (outflow), reliable in vivo data across this tissue are limited. In fact, the only location available for arteriovenous difference measurement in human is the subcutaneous fat bed in the abdominal wall (Samra et al., 1996;Frayn et al., 1994; Coppack et al., 1990). Based on data from this single depot, generalizations cannot be made about all metabolically heterogeneous depots (subcutaneous vs. visceral) of adipose tissue (Jensen, 2002). As an alternative, in vivo microdialysis has been applied to study adipose tissue metabolism in human, but it provides only qualitative data of several metabolites in the interstitium. In vitro studies of tissue explants or isolated cells do not provide comparable physiological data with respect to in vivo conditions (Frayn et al., 2003). Mathematical models and simulations of adipose tissue metabolism in vivo offer a method for quantitative analysis of control mechanisms for lipid mobilization and for prediction of physiological responses.

Adipose tissue comprises about 20% of body weight but its rate of utilizing oxygen in the basal state is less than 2% of whole body rate of oxygen consumption (Frayn et al., 1995). Despite its negligible contribution to energetics, it actively participates in the whole body fuel homeostasis by modulating lipid metabolism. Regulation of breakdown (lipolysis) and synthesis (esterification) of triglycerides (TG) in adipose tissue controls lipid flux into circulation. Since adipose tissue via lipolysis releases more FA into circulation than required for oxidation, a significant part of the released FA are re-esterified in adipose tissue and in other organs. This triglyceride- fatty acid (TG-FA) cycle, is composed of an intra-adipose tissue cycle and an extra-adipose tissue cycle. FA released into plasma are taken up by the liver, re-esterified, and secreted as very large density lipoprotein (VLDL)-TG, which are then transported to the periphery to be reincorporated into adipose tissue TG (Newsholme and Crabtree, 1976; Klein and Wolfe, 1990; Frayn et al., 1994). As proposed by Newsholme et al. (Newsholme and Crabtree, 1976), the existence of TG-FA cycle provides for increased sensitivity and flexibility in controlling lipid mobilization.

Hormone sensitive lipase (HSL) was considered the only rate limiting enzyme for lipolysis of TG in adipose tissue (Large et al., 1998). However, recently, it has been shown that the HSL deficient mice retain the basal lipolysis rate and respond to the beta-adrenergic stimulation, although the response was quantitatively less than in the wild type (Okazaki et al., 2002;Zechner et al., 2005; Haemmerle et al., 2002). The accumulation of diglycerides (DG) in the adipose tissue of HSL knockout mice suggests that HSL is the rate limiting enzyme for the hydrolysis of DG and not TG (Haemmerle et al., 2002). Adipose TG lipase (ATGL) has been suggested to be the key enzyme involved in TG hydrolysis in the adipose tissue (Schweiger et al., 2006;Haemmerle et al., 2006;Zimmermann et al., 2004). TG lipolysis was shown to be severely impaired in ATGL-deficient mice accumulating large amount of fat in major organs and leading to premature death (Haemmerle et al., 2006). The integrated response of these lipase reactions is essential to understand the metabolic regulation of lipolysis in the adipose tissue.

Re-esterification of fatty acids requires a source of glycerol-3-phasphate (G3P). Since the activity of glycerol kinase is very low in the adipose tissue (Edens et al., 1990b), it cannot form G3P from glycerol in significant quantities. Instead, glucose and/or pyruvate are utilized to produce G3P. The use of pyruvate to form G3P has been termed glyceroneogenesis (Reshef et al., 2003). Quantitative estimation of glyceroneogenesis has not been performed in human in vivo. Animal studies using isotopic tracers have shown that glyceroneogenesis is the dominant pathway in different physiological and nutritional conditions (Tordjman et al., 2003;Brito et al., 2006) (C. K. Nye, R. W. Hanson, and S. C. Kalhan, unpublished data). These data underscore the need to examine the metabolism of the precursors for G3P by the adipose tissue.

In the present study, we have developed a mathematical model of adipose tissue metabolism in vivo in human in the fasting state and investigated the integrated response to increased lipolysis induced by epinephrine. The intravenous epinephrine infusion study in human inguinal fat bed was used to validate the model simulations (Samra et al., 1996). We assessed the capability of the model to reproduce and predict the physiological responses to enzymatic modulation in steady state by altering the expression levels of ATGL and HSL. We hypothesized that a metabolic subdomain exists in the adipose tissue due to the large volume fraction of lipid droplets and most of metabolic reactions occur in a small region of adipose tissue. In addition, we postulated that the individual lipase reactions are differentially activated during epinephrine infusion resulting in the distinctive dynamics of lipolytic intermediates (i.e., DG, MG). Finally, we used this model to predict the source of G3P. We hypothesized that the increase in FA levels during epinephrine infusion inhibits pyruvate oxidation and increases glyceroneogenesis.

METHODS

A mathematical model of adipose tissue metabolism was developed that incorporates essential transport and reaction processes. The model is composed of spatially lumped cellular and blood compartments. Exchange of substrates occurs between the two compartments via simple diffusion or carrier-mediated transport. For a minimal representation of the consequences of glucose and fatty acid metabolism, individual metabolic pathways are lumped to include at least one irreversible reaction step favoring the formation of product (Figure 1). The reversible reactions catalyzed by lactate dehydrogenase (LDH) and G3P dehydrogenase have forward and reverse rate coefficients that are related by the thermodynamic constraint (Appendix I). Pathways associated with TG breakdown and synthesis include various lipolytic intermediates (i.e., DG, MG) and regulatory enzymes, i.e., ATGL, HSL, MGL (monoglyceride lipase) as shown in Figure 1.

Figure 1.

Metabolic pathways involved in triglycerides synthesis and breakdown in the adipose tissue. As shown, glucose is taken up from, and pyruvate, lactate, free fatty acids, glycerol, and alanine are released, into the blood compartment. Alanine is considered to represent all amino acids released by protein breakdown. Glycerol-3-phosphate, used for the esterification of fatty acids, is formed either from glucose via glycolysis or from pyruvate via glyceroneogenesis. The various steps in the esterification and hydrolysis of triglycerides are shown. ATP-ADP and/or NADH-NAD⁺ are used as co-substrates in the model, but are not shown except for the oxidative phosphorylation. The arrow with both ends indicates a reversible reaction step. GLC, glucose; PYR, pyruvate; LAC, lactate; ALA, alanine; GLR, glycerol; FA, fatty acids; G6P, glucose-6-phosphate; GAP, glyceraldehyde-3-phasphate; G3P, glycerol-3-phosphate; ACoA, acetyl CoA; FAC, fatty acyl CoA; TG, triglycerides; DG, diglycerides; MG, monoglycerides; LPL, Lipoprotein Lipase; ATGL, Adipose Triglyceride Lipase; HSL, Hormone Sensitive Lipase; MGL, Monoglyceride Lipase.

Chemical species

The major metabolic species related to glucose and fatty acid metabolism were incorporated into the model. Glycolytic species included glucose (GLC), glucose-6-phosphate (G6P), glycerol-3-phosphate (G3P), glyceraldehydes-3-phosphate (GAP), pyruvate (PYR), and lactate (LAC). Chemical species for lipid metabolism included FA, TG, DG, MG, fatty acyl-CoA (FAC), free CoA, and glycerol (GLR). Palmitate with 16 carbons was considered to represent all FAs. TG, DG, and MG were considered esterified products of G3P and palmitate. Acetyl-CoA (ACoA) and oxygen were included for substrate oxidation. ATP, ADP, inorganic phosphate (Pi), NADH, and NAD⁺ were incorporated into the reaction steps where they were required as co-substrates. Finally, alanine (ALA) was used as the representative amino acid.

Model Specifications and Assumptions

The basal condition for model simulations was the overnight fasted human at rest. Data from arteriovenous balance studies of the subcutaneous adipose tissue bed (Frayn et al., 1991; Frayn et al., 1995; Frayn et al., 1994;Coppack et al., 1990) and biochemical data of enzyme activity (Zechner et al., 2005;Shen et al., 1998; Large et al., 1998), were utilized to develop the framework of metabolic fluxes. Various assumptions were required in the absence of experimental data.

Carbohydrate and energy metabolism

Glucose and FA are the major fuels for adipose tissue. Approximately 50% of the glucose taken up by the adipose tissue is used for oxidative metabolism and about 40% is released as lactate (Frayn et al., 1995; Coppack et al., 1990). FA oxidation accounted for the remaining oxygen consumption. The relative contribution of glucose and FA to oxidative metabolism is consistent with reported respiratory quotient (RQ) of 0.91 (Coppack et al., 1990). Synthesis and breakdown of glycogen were considered to be negligible (Jurczak et al., 2007). We assumed that less than 10% of glucose uptake was converted to G3P, which can also be formed from pyruvate via glyceroneogenesis (Reshef et al., 2003). Uptake of glucose and release of lactate by the adipose tissue of humans indicates a significant glycolytic contribution to G3P (Coppack et al., 1990). In contrast, animal studies using isotopic tracers have shown glyceroneogenesis to be the major pathway for G3P synthesis under different physiological and nutritional conditions (Tordjman et al., 2003;Brito et al., 2006). Therefore, we assumed equal contribution of glycolysis and glyceroneogenesis in the basal state. However, we investigated the effects of different weightings of the two pathways during epinephrine infusion.

Lipid metabolism

The contribution of lipolysis in the blood compartment by lipoprotein lipase (LPL) was determined from the arteriovenous difference (AVD) of TG in adipose tissue bed (Samra et al., 1996). The intracellular rates of lipolysis by ATGL, HSL, and MGL were estimated from the difference between AVDs of glycerol and TG such that ~15% of the produced FA are re-utilized inside adipose tissue (Frayn et al., 1994;Coppack et al., 1990). Finally, fluxes through individual lipase reaction were estimated based on the 10-fold higher activity that HSL has for DG than for TG and MG (Shen et al., 1998;Haemmerle et al., 2002). Thus, the flux rate for DG breakdown by HSL was calculated first and then those for TG and MG breakdown by HSL. The maximum rate coefficient of HSL (V_max,k) for TG and MG breakdown were 10-times lower than that for DG breakdown.

Although FA can be transported by both simple diffusion and carrier-mediated transport (Bradbury, 2006), the simple diffusion of FA was assumed in this model.

Amino acid metabolism

A net release of amino acids into plasma from adipose tissue occurs in the fasting state (Patterson et al., 2002). Alanine and glutamine are released in significant quantities and there is a net uptake of glutamate by the adipose tissue (Frayn et al., 1991). The net release of amino acids by the adipose tissue and the rate of proteolysis in the adipose tissue were used to calculate the mass transport and the rates of appearance of amino acids as represented by alanine (Patterson et al., 2002;Coppack et al., 1996).

Reaction Kinetics

Kinetic expressions based on in vitro data for each elementary enzymatic reaction were not feasible for this in vivo study. Instead, we used a phenomenological Michaelis-Menten (M-M) equation constrained by the physiological conditions. We assumed that all metabolic reactions are expressed by a general bi-bi M-M form. The kinetic parameters such as the phenomenological M-M constants (i.e., K_m,k, K_i,k, K_f,k and K_b,k) were set to the initial tissue concentrations of the corresponding substrates. Since we used a top-down approach to relate the responses of different scales (i.e., cellular and tissue levels), several reaction steps are lumped. Palmitate and alanine represent the entire family of fatty acids and amino acids. The efficacy of this approach has been demonstrated in other studies (Kim et al., 2007;Zhou et al., 2005). Since the maximum rate coefficients are determined from in vivo flux data and the phenomenological M-M constants, the metabolic fluxes described by this method can be bounded within physiological limits.

Intracellular compartmentation

Due to the large volume fraction of lipid droplets in adipocyte, we postulated that the most of metabolites are localized in a small sub-cellular domain. The effect of cellular localization of chemical species was examined by modulating the volume fraction of adipose cellular compartment (v_cf). The cellular volume fraction assuming localization was optimally estimated using data from the literature. For comparison, simulation without localization assumed the physical volume fraction of adipose tissue cells (v_cf = 0.8). TG, DG, and MG, whose concentrations are high compared with other substrates, were not assumed localized in the subdomain.

Activation of lipolytic reactions

HSL can break down all lipolytic intermediates (i.e., TG, DG and MG), while ATGL is responsible for hydrolyzing TG only (Large et al., 2004; Langin and Arner, 2006; Zechner et al., 2005). The breakdown of MG is not subject to the beta-adrenergic stimulation (Large et al., 2004;Zechner et al., 2005). We assumed that the following three lipolytic reactions are subject to the beta-adrenergic stimulation: 1) TG breakdown to DG by ATGL, 2) TG breakdown to DG by HSL, and 3) DG breakdown to MG by HSL. We compared two different schemes for activating lipolytic reactions. We tested the hypothesis that individual lipolytic reactions were differentially activated during epinephrine infusion as quantified by different degree of activation (λ_k). Thus, the rates of TG and DG breakdowns could be increased to different extents. Simulations of differential activation for lipase reactions were compared with simulations of uniform activation (λ_k) values so that TG and DG breakdowns have the same stimulation.

Beta-adrenergic stimulation

Cyclic-AMP (cAMP) dependent protein kinase A (PKA) phosphorylates HSL and other proteins including perilipin upon beta-adrenergic stimulation (Brasaemle et al., 2000). The time scale of increase in cAMP levels and activation of PKA is reported to be less than 1 min (Honnor et al., 1985). In contrast, the response to the intravenous epinephrine infusion showed that the peak concentration of venous epinephrine was reached after ~30min (Samra et al., 1996). The time scales of fatty acids and glycerol releases were more comparable to that of venous epinephrine levels (Samra et al., 1996). Consequently, the effect of instantaneous changes in cAMP levels on the simulated responses would be negligible in the time frame of our model simulation (~60min). Therefore, we have lumped all the cascade controls of the molecular level regulatory mechanisms into the action of epinephrine by introducing a phenomenological equation relating the activation of lipolytic reactions to the venous epinephrine levels. With this algorithm, the modulation of maximum rate constants (V_max) by epinephrine represents not only the activation of lipase, but also concomitant activation of other proteins including perilipin.

Dynamic mass balance equations

The dynamic mass balance equations describe changes in substrate concentration in blood and adipose cells in tissue. The blood compartment represents plasma in equilibrium with interstitial fluid. The concentration of substrate i in the blood compartment is determined by:

$$V_b\cdot \frac{d{C}_{b,i}}{dt}=Q\cdot (C_{a,i}-C_{b,i})+R_{b,i}-J_{b\leftrightarrow c,i}$$ (1)

where C_a,i is the arterial concentration; C_b,i is the capillary blood concentration (equal to the adipose venous concentration C_v,i); Q is the blood flow in adipose tissue; J_b↔c,i is the net mass transport flux across the blood-cell exchange barrier; R_b,i is the net metabolic reaction rate of substrate i in the blood compartment; V_b is the volume of blood compartment, which is equal to the physical volume of capillary blood and interstitial fluid comprising 20% of total tissue volume (V_tissue). Since oxygen and carbon dioxide are transported as free and bound forms in the blood, the effective volume of the blood compartment is different from the physical volume as shown in Appendix II.

In the adipose cellular compartment, the dynamic mass equation of substrate i is

$$V_c\cdot \frac{d{C}_{c,i}}{dt}=R_{c,i}+J_{b\leftrightarrow c}$$ (2)

where C_c,i is the cellular concentration; R_c,i is the net metabolic reaction rate of substrate i; V_c is the volume of the cellular compartment.

For convenience in simulation, the compartment volumes in Eq. (1) and (2) were replaced with the volume fractions (v_bf =V_b/V_tissue or v_cf =V_c/V_tissue). Consequently, blood flow and rate coefficients in this model are specified per unit volume of tissue. For comparison to experimental data, the blood flow, AVD, and metabolic reaction rates from the model equations were converted from a tissue volume basis to a tissue wet weight basis by division with mass density.

Mass transport flux between blood and tissue

The substrates involved in blood-tissue transport are glucose, lactate, pyruvate, alanine, glycerol, FA, carbon dioxide, and oxygen. They are transported via either simple diffusion or carrier-mediated (facilitated) transport. The mass transport flux of glycerol, FA, oxygen and carbon dioxide between blood and cell (J_b↔c,i) occurs by passive diffusion:

$$J_{b\leftrightarrow c,i}={\gamma }_i\cdot (C_{b,i}-C_{c,i})$$ (3a)

where γ_i is the mass transport coefficient of substrate i. The mass transport flux of glucose, pyruvate, lactate and alanine occurs by facilitated transport:

$$J_{b\leftrightarrow c,i}=T_{max,i}\left(\frac{C_{b,i}}{M_{m,i}+C_{b,i}}+\frac{C_{c,i}}{M_{m,i}+C_{c,i}}\right)$$ (3b)

where T_max,i is the maximum mass transport coefficient of substrate i and M_m,i is the M-M constant of substrate i.

Metabolic flux

The metabolic reaction rates (R_x,i, x = b or c) are the net result of metabolic reactions producing and utilizing the corresponding substrate:

$$R_{x,i}=\sum _k{\alpha }_{i,k}{\phi }_{x,k},x=b\text{ or }c$$ (4)

where φ_x,k is the flux rate of the metabolic reaction k including substrate i; α_i,k is the corresponding stoichiometric coefficient, which is either positive (product) or negative (reactant). The net reaction rate for each substrate is shown in Table 1.

TABLE 1.

Net reaction rate (R_b,i or R_c,i) for each substrate in blood and cellular compartments

Substrate	Net Reaction Rate, Rb,i or Rc,i
Blood
GLR	φTG → GLR,LPL
FA	3φTG →GLR,LPL
TG	−φTG →GLR,LPL
Cells
GLC	−φGLC → G6P
PYR	φGAP→PYR + φALA →PYR − φPYR↔LAC − φPYR→G3P − φPYR → ACoA
LAC	φPYR ↔ LAC
ALA	− φALA → PYR + φProteolysis
GLR	φMG →GLR,MGL + φMG → GLR,HSL + 0.5φMG-MG→DG + φDG→TG −φMG-GLR →G3P
FA	φTG →DG,ATGL + φTG →DG,HSL + φDG→MG,HSL + φMG→GLR,HSL + φMG→GLR,MGL − φFA →FAC
TG	φDG →FAC + 0.5φDG-DG→TG + φDG-MG→TG − φTG →DG,ATGL −φTG → DG,HSL
O2	−φO2→ H2O
CO2	φPYR →AcoA + 2φACoA→CO2
G6P	φGLC→G6P − φG6P → GAP
GAP	2φG6P→GAP − φGAP→PYR − φGAP ↔G3P
G3P	φGAP ↔ G3P + φPYR →G3P + φGLR→G3P − φG3P-FAC→DG
ACoA	φPYR →AcoA + 8φFAC→AcoA −φACoA→CO2
FAC	φFA→FAC − 8φFAC→AcoA − 2φG3P→DG −φDG→TG
CoA	2φG3P→DG + φDG →TG + φACoA→CO2 − φPYR →AcoA − φFA→FAC − 7φFAC→ACoA
DG	φTG →DG,ATGL + φTG →DG,HSL + φG3P→DG+ 0.5φMG-MG →DG − φDG →MG,HSL − φDG →TG − φMG-DG→TG − φDG-DG →TG
MG	φDG →MG,HSL + 0.5φDG-DG →TG − φMG →GLR,HSL − φMG→GLR,MGL − φMG-DG→TG − φMG-MG →DG
ATP	2φGAP→PYR + φACoA →CO2 + 6φO2→H2O − φGLC→G6P − φG6P→GAP − 3φPYR →G3P − 2φFA→FAC − φGLR→G3P − φATP→ADP
ADP	−Rc,ATP
Pi	2φPYR →G3P + 2φFA→FAC + φG3P→DG + φATP→ADP − φGAP→PYR − φACoA →CO2 − 6φO2→H2O
NAD+	φPYR ↔LAC + φGAP↔G3P + 2φPYR →G3P + 2φO2→H2O − φGAP→PYR − φPYR →ACoA − 14φFAC→AcoA −4φACoA→CO2
NADH	−Rc,NAD+

GLC, glucose; PYR, pyruvate; LAC, lactate; ALA, alanine; GLR, glycerol; FA, fatty acids; G6P, glucose-6-phosphate; GAP, glyceraldehyde-3-phasphate; G3P, glycerol-3-phosphate; ACoA, acetyl CoA; FAC, fatty acyl CoA; CoA, free CoA; Pi, inorganic phosphate. φ_A→B is the flux rate of the metabolic reaction

Metabolic fluxes are expressed with a general irreversible bi-bi substrate to product enzymatic reaction coupled with controller energy metabolite pairs (Kim et al., 2007).

where E₁ and E₂ are ATP and ADP or vice-versa, and/or NADH and NAD⁺ or vice-versa. The corresponding reaction flux equation for flux k can be expressed as:

$${\phi }_{\text{k}}=V_{max,\text{k}}\left(\frac{P{S}^{\pm }}{{\mu }^{\pm }+P{S}^{\pm }}\right)\left(\frac{R{S}^{\pm }}{{\nu }^{\pm }+R{S}^{\pm }}\right)\left(\frac{C_{\text{X}}\cdot C_{\text{Y}}}{K_{\text{m},\text{k}}+C_{\text{V}}\cdot C_{\text{W}}\cdot K_{\text{m},\text{k}}/K_{\text{i},\text{k}}+C_{\text{X}}\cdot C_{\text{Y}}}\right)$$ (5)

where C_X, C_Y, C_V, and C_W are reactant and product concentrations; V_max,k is the maximum rate coefficient in flux k; K_m,k is the phenomenological M-M constant for the reactants; K_i,k is the constant for the product inhibition. Product inhibition occurs only in reactions specified in Appendix I. PS⁺ (= C_ATP/C_ADP) and RS⁺ (= C_NADH/C_NAD+) indicate cellular phosphorylation and redox states. For some reactions, the effect of these controllers can be in the opposite direction. In this case, PS⁻=1/PS⁺ and RS⁻=1/RS⁺. In addition, μ^± and ν^± are parameters for the metabolic controllers.

Fluxes of lactate dehydrogenase and G3P dehydrogenase reactions, which can be close to thermodynamic equilibrium, are described as reversible reactions:

$${\phi }_{\text{k}}=\left(\frac{V_{\text{f},\text{k}}\frac{C_{\text{X}}\cdot C_{\text{Y}}}{K_{\text{f},\text{k}}}-V_{\text{b},\text{k}}\frac{C_{\text{V}}\cdot C_{\text{W}}}{K_{\text{b},\text{k}}}}{1+\frac{C_{\text{X}}\cdot C_{\text{Y}}}{K_{\text{f},\text{k}}}+\frac{C_{\text{V}}\cdot C_{\text{W}}}{K_{\text{b},\text{k}}}}\right)$$ (6)

where V_f,k and V_b,k are the forward and reverse rate coefficients; K_f,k and K_b,k are the phenomenological M-M constants for reactants and products; K_eq is the equilibrium constant calculated from the Gibbs free energy of reaction. The reaction rate coefficients are related by a thermodynamic constraint (or Haldane relationship):

$$V_{\text{f},\text{k}}=V_{\text{b},\text{k}}\frac{K_{eq}\cdot K_{\text{f},\text{k}}}{K_{\text{b},\text{k}}}$$ (7)

In the blood compartment, the breakdown of TG to FAs and glycerol is the only reaction that is catalyzed by LPL. Since some LPL is carried by blood (Karpe et al., 1998), the activity of LPL reaction depends on adipose blood flow:

$${\phi }_{\text{TG}\to \text{GLR},\text{LPL}}=V_{\text{max},\text{LPL}}\left(\frac{C_{\text{b},\text{TG}}}{K_{\text{m},\text{LPL}}+C_{\text{b},\text{TG}}}\right)\left(\frac{Q}{K_{\text{m},\text{Q}}+Q}\right)$$ (8)

where K_m,LPL and K_m,Q are phenomenological M-M constants for the LPL reaction.

In addition to the metabolic control by the cellular phosphorylation and redox state, epinephrine provides further regulation by stimulating lipolysis reactions governed by ATGL and HSL. The maximum rate coefficients for these three reactions undergo the further modulation by epinephrine according to an empirical relation (Kim et al., 2007):

$$V_{max,k}=V_{max,k}^0\cdot \left(1.0+{\lambda }_k\frac{{(C_E(t)-C_E(0))}^2}{\alpha +{(C_E(t)-C_E(0))}^2}\right)$$ (9)

where C_E(t) is the epinephrine concentration in adipose venous at time t; $V_{max,k}^0$ is the basal state maximum rate coefficient; λ_k and α are parameters. Here, λ_k indicates the degree of activation for a corresponding lipolytic reaction.

Parameter determination at basal state

Starting with the mass transport fluxes (Table 2), the unknown flux rates were determined with appropriate assumptions on fuel metabolism as described above. Once all the metabolic fluxes were estimated (Table 3 and 4), then parameter values at basal state were determined together with the metabolite concentrations in blood and tissue (Table 5 and 6). Since 60~85% of adipose tissue is lipids with 90~99% being TG (Albright and Stern, 1998), the concentrations of non-lipid substrates in total tissue volume are difficult to quantify. However, their levels in the intracellular water of adipocyte have been shown to be comparable to those in other tissues (Denton et al., 1966). When data of adipose tissue were not available, we used the concentrations in skeletal muscle (Table 6). The phenomenological M-M parameters, K_m,k, K_i,k, K_f,k and K_b,k were set to the initial tissue concentrations of the corresponding substrates. The maximum metabolic rate coefficients for irreversible reactions, V_max,k were calculated from basal flux, tissue concentration, and K_m,k (Table 3). The equilibrium constant was also utilized to calculate the forward and reverse rate coefficients (V_f,k and V_b,k) for reversible reactions (Table 4). Mass transport coefficients (T_max,i and γ_i) were computed from arteriovenous differences, blood flow rate, and concentrations in arterial blood and tissue. The parameter λ_k must be optimally estimated using data from in vivo epinephrine infusion studies in humans. Other model parameters are listed in Table 7.

TABLE 2.

Basal mass transfer flux rates between blood and cells, and associated parameters

Substrate	Jb→c,i*	Tmax,i†	Mm,i‡	γi§
GLC	1.88	11.73	4939
PYR	−0.13	0.48	72
LAC	−1.55	9.84	750
ALA	−0.57**	1.73	268
GLR	−3.42			0.171
FA	−8.59			0.030
O2	19.82			0.615
CO2	−18.03			0.072

^*J_b↔c,i, net mass transport flux across the blood-cell exchange barrier (μmol·min⁻¹·kg wet tissue⁻¹). Negative values mean the release of corresponding substrate from tissue and vice versa. Data are from in vivo human studies (Coppack et al., 1990;Frayn et al., 1994) except for the marked with **, which is from the references (Coppack et al., 1996;Patterson et al., 2002).

^†T_max,i, maximum mass transport coefficient of substrate i (μmol·min⁻¹·kg wet tissue⁻¹).

^‡M_m,i, Michaelis-Menten (M-M) constant of substrate i (μM).

^§γi, mass transport coefficient of substrate i (l·min⁻¹·kg wet tissue⁻¹).

TABLE 3.

Basal reaction flux rates and associated parameters for irreversible reaction fluxes

Fluxes	Flux Rate*	VX→V*	Km†	Ki†	챧	ν±§
φGLC→G6P	1.88	4.06	460000‡	570
φG6P→GAP	1.88	7.53	570		0.72 (−)
φGAP→PYR	3.56	28.44	216000‡		0.72 (−)	9 (−)
φPYR→G3P	0.21	1.66	250		1.39 (+)	0.11 (+)
φGLR →G3P	0.01	0.02	1012000‡
φALA →PYR	2.08	4.16	1300
φProteolysis	2.65**	2.65
φPYR →ACoA	3.74	22.46	50000‡	25		9 (−)
φFA→FAC	1.70	6.82	200000‡		1.39 (+)
φFAC→ACoA	0.42	2.55	16000‡	25		9 (−)
φTG→DG,ATGL	3.35	3.38	10
φTG→DG,HSL	0.65	0.66	10
φDG→MG,HSL	3.29	6.58	2000
φMG→GLR,HSL	0.33	0.66	200
φMG→GLR,MGL	2.67	29.37	2000
φG3P-FAC→DG	0.43	0.85	104000‡
φDG-FAC→TG	0.43	0.85	160000‡
φDG-DG →TG	0.60	1.20	2000
φMG-MG→DG	0.32	0.64	200
φMG-DG→TG	0.27	0.54	400000‡
φACoA→CO2	7.14	57.15	67500‡		0.72 (−)	9 (−)
φO2→H2O	19.82	79.32	27‡		0.72 (−)	0.11 (+)
φATP→ADP	125.40	376.19	4600	15180000‡
φTG→GLR,LPL	0.61	0.62	10

^*Values are in μmol·min⁻¹·kg wet tissue⁻¹. V_max,k, maximum rate coefficient.

^**Data is from the references (Coppack et al., 1996;Patterson et al., 2002).

^†Values are in μmol·kg wet tissue⁻¹ except for the marked (^‡), which are in (μmol·kg wet tissue⁻¹)². K_m,k, phenomenological M-M constant for the reactants; K_i,k, phenomenological M-M constant for the product inhibition

^§Values are dimensionless. (+) represents μ⁺ or ν⁺ while (−) represents μ⁻ or ν⁻. μ^± and ν^±, parameters for the metabolic controllers.

TABLE 4.

Basal reaction flux rates and associated parameters for reversible reaction fluxes

Fluxes	Flux Rate*	Vf, X↔V†	Vb, X↔V†	Kf, X↔V‡	Kb, X↔V‡	Keq, X↔V§
φPYR ↔LAC	1.55**	4.67	0.023	12500	648000	1.06 × 104
φGAP↔G3P	0.21	0.62	3.3 × 10−7	4000	585000	2.77 × 108

^*Values are in μmol·min⁻¹·kg wet tissue⁻¹. Data marked with ** is from the reference (Coppack et al., 1990).

^†V_f,k and V_b,k, forward and reverse rate coefficients (μmol·min⁻¹·kg wet tissue⁻¹).

^‡K_f,k and K_b,k, phenomenological M-M constants for reactants and products (μmol·kg wet tissue⁻¹)².

^§K_eq, equilibrium constant calculated from the Gibbs free energy of reaction (dimensionless), which is from the reference (Alberty, 2003).

TABLE 5.

Arterial and venous substrate concentrations

Substrate	Arterial Concentration*†	Venous Concentration*§
GLC	5000	4939
PYR	68	72
LAC	700	750
ALA	192	282
GLR	70	200
FA	660	719
TG	990	970
O2 (Total)	8000	7360
O2 (Free)	84‡	66‡
CO2 (Total)	21700	22218
CO2 (Free)	1124‡	1151‡

^*Values are in μM.

^†Data are from the reference (Kim et al., 2007).

^‡Free concentrations of O2 and CO2 are calculated from the equations given in Appendix II.

^§Venous concentrations are calculated from the corresponding arteriovenous difference and arterial concentration data.

TABLE 6.

Substrate concentration in the cellular compartment

Substrate	Concentration*	Reference
GLC	2540	(Tiessen et al., 2002)
PYR	250	(Denton et al., 1966)
LAC	1440	(Jansson et al., 1994)
ALA	1300‡	(Kim et al., 2007)
GLR	220	(Jansson et al., 1994;Stumvoll et al., 2000)
FA	1000
TG	990000†	(Albright and Stern, 1998)
O2	34‡	(Dash and Bassingthwaighte, 2006; Popel, 1989)
CO2 (Total)	15427‡	(Dash and Bassingthwaighte, 2006; Geers and Gros, 2000)
CO2 (Free)	1403‡	(Dash and Bassingthwaighte, 2006; Geers and Gros, 2000)
G6P	570	(Denton et al., 1966)
GAP	80‡	(Kim et al., 2007)
G3P	1300	(Denton et al., 1966)
ACoA	25	(Denton and Halperin, 1968)
FAC	80	(Denton and Halperin, 1968)
CoA	200	(Denton and Halperin, 1968)
DG	2000†	(Arner and Ostman, 1974)
MG	200†	(Arner and Ostman, 1974)
ATP	4600	(Denton et al., 1966)
ADP	3300	(Denton et al., 1966)
Pi	2700‡	(Kim et al., 2007)
NAD+	450‡	(Kim et al., 2007)
NADH	50‡	(Kim et al., 2007)

^*Values are in μM and based on the volume of intracellular water except for those marked with ^† which are based on the total cellular volume. Values marked with ^‡ are from skeletal muscle studies.

Table 7.

Miscellaneous model parameters and the input functions^*

	Values	Units
Km,Q	31	ml·min−1·kg−1
α	0.04	nM2
Q0	0.031†	ml·min−1·kg−1
Cv,Epi,0	0.1†	nM

^*K_m,Q, phenomenological M-M constants for LPL reaction; α, parameter for epinephrine action; Q₀, adipose tissue blood flow at basal state; C_v,Epi,0, epinephrine concentration in adipose tissue vein at basal state. Data marked with ^† are from the references (Samra et al., 1996;Jansson et al., 1994).

Model simulation for epinephrine infusion

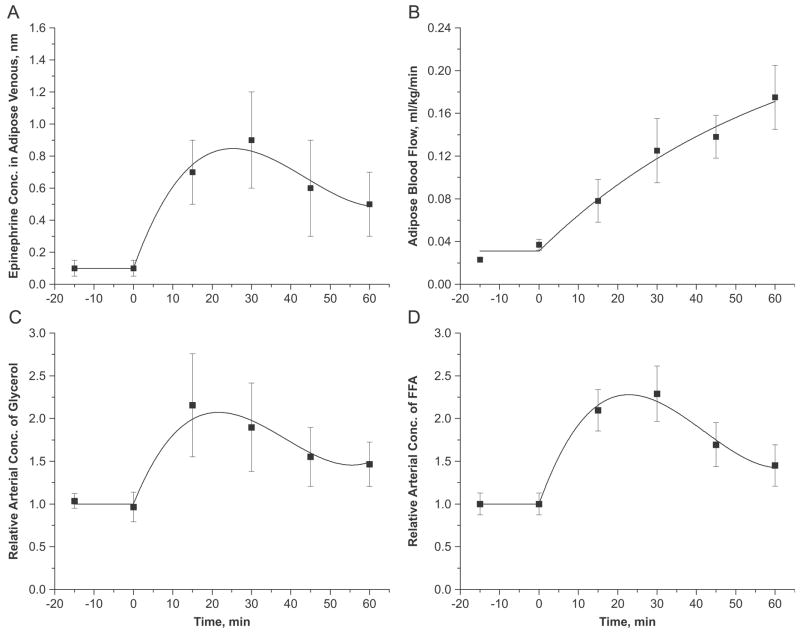
Corresponding to in vivo studies (Samra et al., 1996), the epinephrine infusion was simulated with a constant rate infusion for 60min (Samra et al., 1996). Since the tissue responds to the epinephrine levels in the interstitial fluid, the epinephrine levels in adipose venous outflow were used to stimulate the cellular metabolic reactions. The epinephrine levels in the adipose tissue vein and in the adipose tissue were assumed to be in equilibrium. However, epinephrine infusion modulated the blood flow to adipose tissue as well as the arterial glycerol and FA concentrations, while the arterial levels of other metabolites were kept constant (Samra et al., 1996). Thus, venous epinephrine concentration (C_v,Epi), adipose tissue blood flow (Q), and arterial substrate concentrations for glycerol and FA (C_a,GLR, C_a,FA) were the only input functions for model simulation (Figure 2). These empirical relations are shown in Table 8.

Figure 2.

Dynamic changes in (A) epinephrine concentration in adipose tissue vein, (B) adipose tissue blood flow, and (C, D) relative arterial concentrations of glycerol and FA following the intravenous infusion of epinephrine at time=0. Relative arterial concentration is the ratio of arterial concentrations at any time t>0 to t=0. Squares represent the experimental data (mean±SEM) of Samra et al. (Samra et al., 1996). Solid lines are the model simulations.

Table 8.

Model input functions^*

Time (min)	Input Functions
t ≤15	Q = Q0, Cv,Epi = Cv,Epi,0, Ca,GLR, = Ca,GLR,0, Ca, FFA = Ca, FFA,0
	Q = Q0 · (1+7.32 · (1 − e−(t-15)/62.317)))
t >15	Cv, Epi = Cv, Epi,0 + 6.837× 10−2 · (t − 15) − 1.903 × 10−3 · (t − 15)2 + 1.453× 10−5 · (t − 15)3 Ca,GLR = Ca, GLR, 0 + 7.979 · (t − 15) − 0.256 · (t − 15)2 + 0.002 · (t − 15)3 Ca, FA = Ca,FA,0 + 84.486· (t − 15) − 2.544 · (t − 15)2 + 0.02 · (t − 15)3

^*Parameters for the input functions were optimally estimated based on the data from the human in vivo study (Samra et al., 1996). Q: Blood flow to the adipose tissue; C_v,Epi: Epinephrine concentration in the vein; C_a,GLR, C_a,FA: Arterial glycerol and FA concentrations. Time courses of these input functions are shown in Figure 2.

Simulation strategies

The effect of intracellular compartmentation of chemical species was examined by modulating the cellular volume fraction (v_cf). As a comparative reference, simulations were conducted of ‘localized’ (i.e., optimally estimated v_cf) and of ‘non-localized’ responses (i.e., v_cf=0.8). Also, the effects of activation with different values of λ_k (i.e., differential activation) and with equal values of λ_k (i.e., uniform activation) were compared. The effects of different ratios of glycolysis and glyceroneogenesis on the synthesis of G3P were simulated during epinephrine infusion. An equal ratio (1:1) of these processes was assumed for the basal state.

Parameter estimation and numerical solution

Values of the volume fraction of cellular compartment (v_cf), hormonal control (λ_k) and parameters of the model input functions were estimated by minimizing the sum of squared errors between the experimental data and the corresponding simulated outputs in response to epinephrine infusion. The experimental data from studies in humans, included AVDs of glycerol, FA and TG across the inguinal fat bed in vivo and the concentration dynamics of glycerol and FA in the venous blood draining the inguinal fat bed (Samra et al., 1996). The model equations were numerically solved using a stiff ordinary differential equation solver, ‘ode15s’ (MATLAB^®, The MathWorks Inc.). Optimal estimates of the model and input parameters were obtained using ‘lsqcurvefit’ (MATLAB^®, The MathWorks Inc.) with ‘ode15s’.

Sensitivity Analysis

The sensitivity of the model parameters was quantified by the change in the sum of squared differences between simulated model outputs with different parameter values. Since a thorough statistical analysis of all the model parameters is not feasible, parameter sensitivity directly related to the lipid mobilization was investigated by perturbing parameter individually. A sensitivity index for i th parameter, θ_i can be computed as done previously (Beard, 2005):

$$S_i=max\left(\frac{\left|E({\theta }_i^{\ast }+0.1{\theta }_i^{\ast })-E({\theta }_i^{\ast })\right|}{0.1E({\theta }_i^{\ast })}\right)$$ (11)

where S_i is a sensitivity index; E is the sum of squared residuals for a model output; θ_i* is the ith parameter at its optimum. This equation represents the changes in the model output in response to 10% change in a specific parameter from its optimum.

RESULTS

Basal state analysis

The metabolic flux rates during basal state were estimated using the dynamic mass balance equations at steady state (Table 3 and 4). Approximately 45% (0.8 μmol·min⁻¹·kg⁻¹) of glucose taken up by adipose tissue was released as lactate and pyruvate ((J_PYR,b↔c+J_LAC,b↔c, Table 2), ~5% was utilized to synthesize G3P for re-esterfication of fatty acids (φ_{GAP ↔G3P}, Table 4), and ~50% was oxidized (φ_{PYR ↔ACoA}, Table 3). When the activities of HSL for TG and MG breakdown were based on that of DG breakdown, it showed that ~84% of TG breakdown was catalyzed by ATGL (φ_{TG →DG,ATGL}/(φ_{TG →DG,ATGL}+φ_{TG →DG,HSL}))and ~89% of MG breakdown was catalyzed by MGL (φ_{MG →GLR,MGL} /(φ_{MG →GLR,HSL} +φ_{MG →GLR,MGL})) with an insignificant contribution by HSL (Table 3). VLDL-TG breakdown by LPL in the blood compartment comprised 13% of total TG breakdown in adipose tissue bed (φ_{TG →GLR,LPL}/(φ_{TG →DG,ATGL} + φ_{TG →DG,HSL} + φ_{TG →GLR,LPL}), Table 3). The total production of FA by lipolysis in the tissue was 10.3 μmol·min⁻¹·kg⁻¹ (φ_{TG →DG,ATGL} + φ_{TG →DG,HSL} + φ_{DG →MG,HSL}, Table 3): ~84% of FA were released into the circulation (J_FA,b↔c, Table 2), ~12% was re-esterified (φ_G3P-FAC→DG + φ_DG-FAC→TG) and ~4% was oxidized (φ_FAC→ACoA ) (Table 3). In contrast, ~99.7% of glycerol produced was released into the circulation (J_FA,b↔c, Table 2) with insignificant re-utilization within the tissue (φ_{GLR →G3P}, Table 3).

Effect of change in lipase activity

Beginning with the basal model parameters, the basal maximum rate constants (V_max) for HSL and ATGL were modulated to simulate the effect of change in lipase activity. V_max for HSL reactions (V_{max,HSL,TG→DG}, V_{max,HSL,DG→MG}, V_{max,HSL,MG→GLR}) were modulated in order to examine the effect of over- and under-expression of the enzyme. Multiplying the V_max with a factor smaller than one represents knockdown of the expression of the corresponding enzyme, while multiplying with a factor larger than one represents over-expression. The new steady-state flux rates were determined after the model parameters were perturbed. Similarly, the steady-state fluxes for the reaction catalyzed by ATGL (V_{max,ATGL,TG→DG}) were determined.

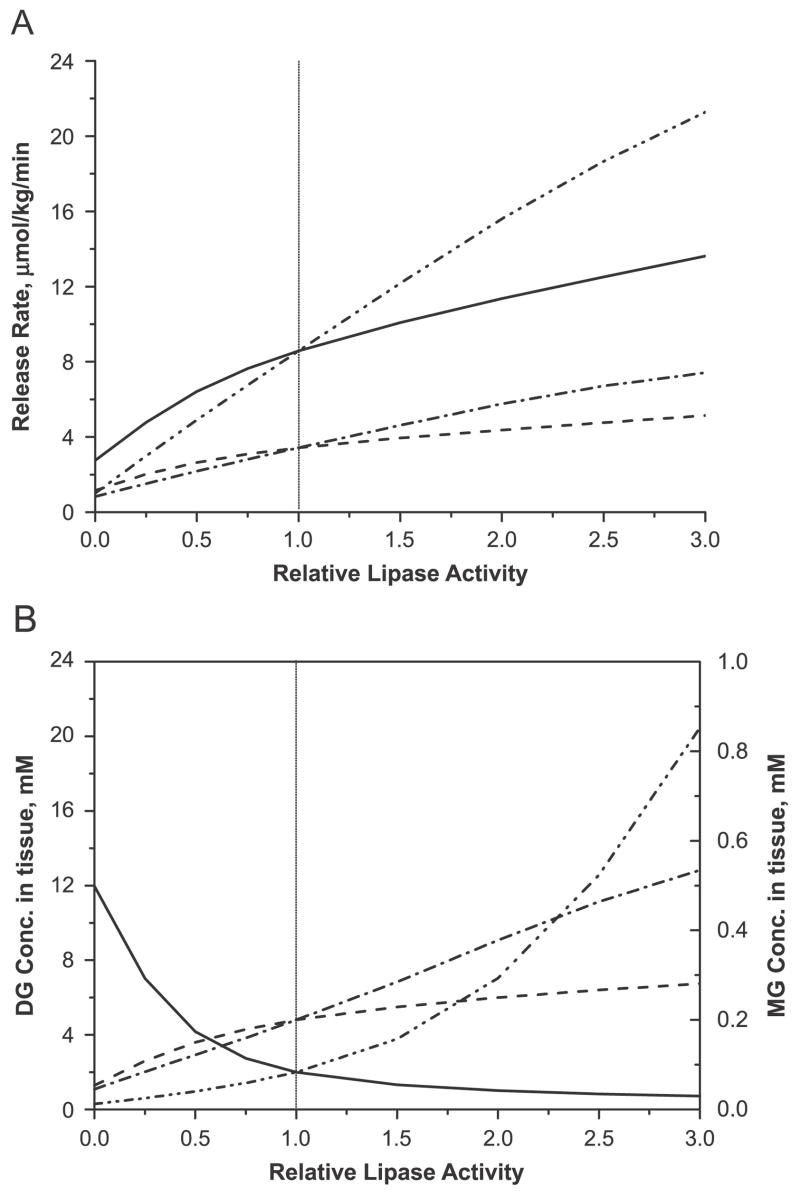
Figure 3.A shows rates of release of FA and glycerol at the steady state in relation to the change in activities of HSL and ATGL relative to control value (=1). A decrease in the activity of ATGL to zero lowered the rate of release of FA by 88%, while a decrease in the activity of HSL caused a 68% reduction in the release rate of FA. The rate of release of glycerol decreased by 76% associated with HSL and 66% associated with ATGL. As shown in Figure 3.B, the model simulations showed a 6-fold increase in concentration of DG (relative to control) with decreasing HSL activity. In contrast, DG concentration decreased by ~85% with decreasing ATGL activity because of the lower production of DG from TG hydrolysis by ATGL. There was no significant difference in the tissue concentration of MG as a result of varying enzyme activities.

Figure 3.

Effect of varying levels of lipase expression in the basal state on (A) the rates of releases of FA (Solid: HSL, Dash double dotted: ATGL) and glycerol (Dashed: HSL, Dash dotted: ATGL) and (B) the tissue concentrations of DG (Solid: HSL, Dash double dotted: ATGL) and MG (Dashed: HSL, Dash dotted: ATGL). Relative lipase activity is the enzyme activity of ATGL or HSL relative to the control value.

Over-expressing ATGL increased the rates of release of both FA and glycerol more than those with the over-expression of HSL (~150% in ATGL vs. ~50% in HSL). The magnitude of increase was higher for FA (150% increase) than for glycerol (120% increase). The higher production of DG as a result of TG hydrolysis by ATGL resulted in the accumulation of DG. In contrast, the over-expression of HSL resulted in a higher rate of breakdown of DG relative to TG hydrolysis and, consequently, lower tissue levels of DG. The levels of MG were increased by higher activities of both ATGL and HSL.

Model validation and intracellular compartmentation

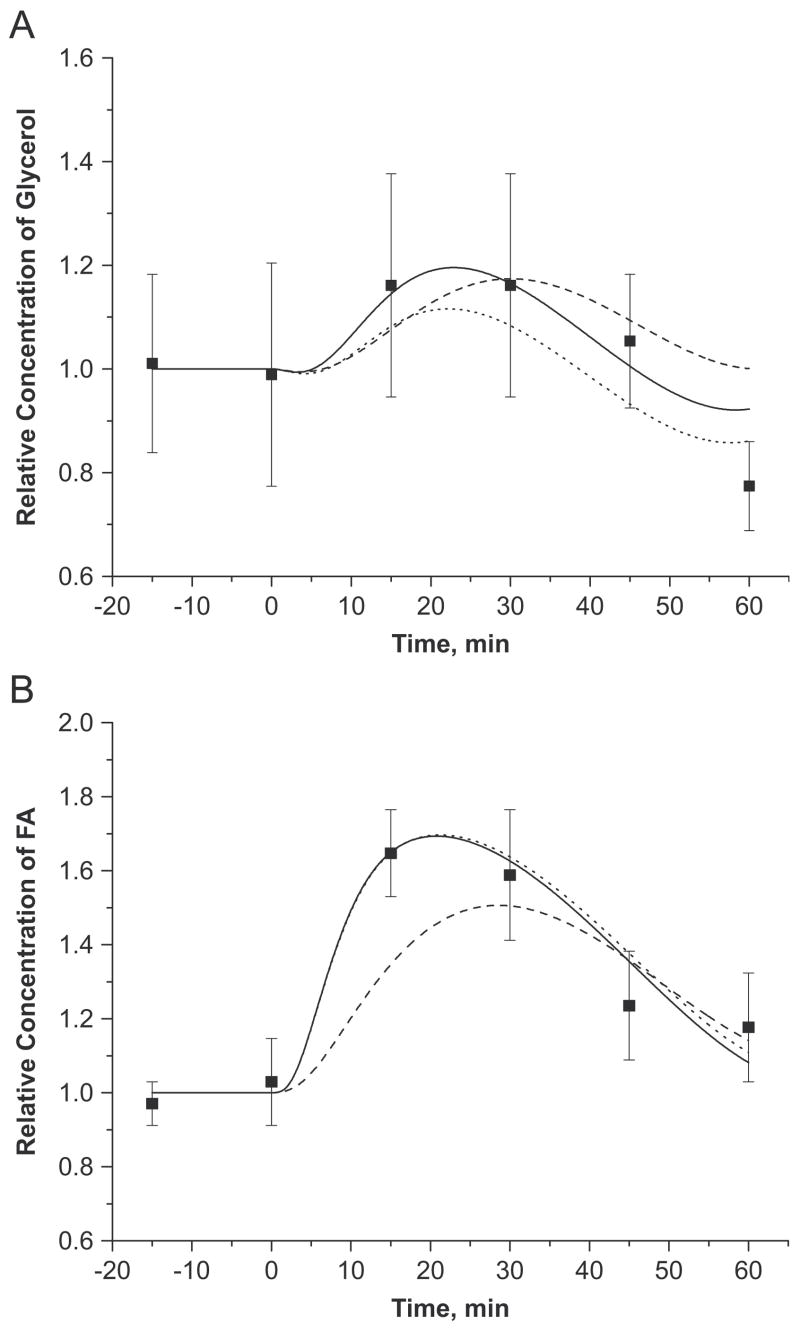
Model simulations showed that epinephrine infusion increased glycerol (~3 fold) and FA (~4 fold) release rates (i.e., AVD) from adipose tissue into the circulation (Figure 4A, 4B). Simulated AVD responses are in agreement with the experimental data assuming localized metabolism (v_cf=0.031) and differential activation of lipases (i.e., λ_k) with parameter values in Table 9 The effect of v_cf on glycerol AVD was much less than that on FA AVD. When the lipase reactions were not localized (v_cf=0.8), the initial increase in FA release rate was slower and 30~50% smaller than that found experimentally (Figure 4A, 4B). Model simulation showed that the breakdown of plasma TG by LPL, as indicated by AVD, gradually increased by a factor of 5 (Figure 4C). Both glycerol and FA concentrations in the venous blood reached maximal values around ~25min with 20% and 70% increases, but returned to basal values at the end of epinephrine infusion (Figure 5). The localization of lipase reactions had minimal effect on the response of glycerol in the venous blood (Figure 5A). However, the initial dynamics of FA (up to 30min) were much slower without localization (v_f=0.8) resulting in 10~20% lower venous levels (Figure 5B).

Figure 4.

(A, B) Effect of intracellular compartmentation and differential activation of lipases on dynamic exchanges of glycerol and FA across adipose tissue bed in response to the intravenous infusion of epinephrine. Relative AVD = AVD(t)/AVD(0), is the ratio of arteriovenous differences (AVD) at any time t>0 to t=0. Squares represent the experimental data (mean±SEM) of Samra et al. (Samra et al., 1996). Solid (localized, differential), dotted (localized, uniform) and dashed (unlocalized, differential) lines are the model simulations according to the localized (V_cf=0.031) or unlocalized (V_cf=0.8) metabolic subdomain and the uniform (same λ_k) or differential (different λ_k) activation of intracellular lipases.

(C) Dynamic exchanges of TG across adipose tissue bed in response to the intravenous infusion of epinephrine. Squares represent the experimental data (mean±SEM) of Samra et al. (Samra et al., 1996). Solid line is the model simulation.

Table 9.

Estimated model parameters^*

Parameters	Differential Activation	Uniform Activation
λTG→DG,ATGL	0.72	3.18
λTG→DG,HSL	0.91	3.18
λDG→MG,HSL	6.19	3.18

^*Values are dimensionless.

Figure 5.

Effect of intracellular compartmentation and differential activation of lipases on changes in relative concentration of glycerol (A) and FA (B) in adipose venous blood during the intravenous infusion of epinephrine. Relative concentration is the ratio of concentrations at any time t>0 to t=0. Squares represent the experimental data (mean±SEM) of Samra et al. (Samra et al., 1996). Solid (localized, differential), dotted (localized, uniform) and dashed (unlocalized, differential) lines are the model simulations according to the localized (V_cf=0.031) or unlocalized (V_cf=0.8) metabolic subdomain and the uniform (same λ_k) or differential (different λ_k) activation of intracellular lipases.

Regulation of lipase activities

The parameter values for which the model simulations produced the best fit to experimental data are listed in Table 9 for differential and uniform activation (λ_k). In the former, the optimal estimates for λ_k indicate that the activation of lipolytic reactions catalyzed by HSL and ATGL increased by 1.7~7.2 fold. The activation required to convert DG to MG by HSL (λ_k = 6.2) was approximately 4 times larger (λ_k = 0.7~0.9) than for other reactions. With uniform activation (λ_k = 3.18), all lipase reactions were increased by the 4.18 fold. Figure 3 and 4 show the effect of different lipase regulations in response to epinephrine infusion. When the metabolic reactions were localized (v_f=0.031), the AVD and the venous concentration dynamics of FA were in good agreement with experimental data with both activation schemes. In contrast, the AVD of glycerol during the first 30 min was 15~20% lower with uniform activation than with differential activation. This produced lower glycerol concentration in the venous outflow (Figure 4.A and 5.A).

MG and DG dynamics

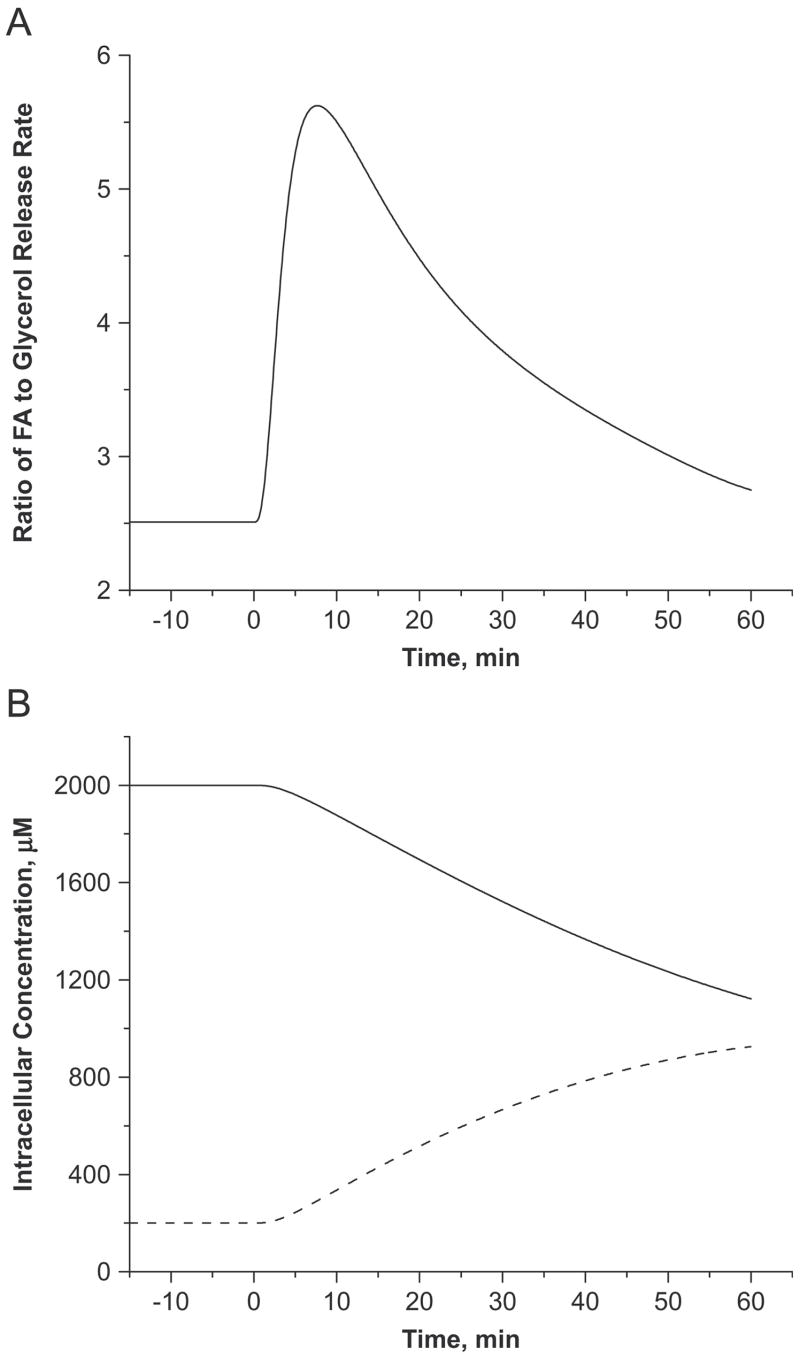
Due to the intracellular TG-FA cycle, the simulated ratio of FA to glycerol released from adipose tissue cells into the blood circulation at basal state, J_FA,b↔c/J_GLR,b↔c ~2.5 (Figure 6A) was lower than the theoretical maximum ratio of 3. However, this ratio increased above the theoretical maximum of 5.6 at 8min and then gradually decreased to 2.8 at 60min. A ratio above 3 indicates an accumulation of the glycerol moiety in adipose tissue as DG and/or MG. Therefore, the model can be used to predict the major contributors to the accumulation of glycerol by simulating the tissue dynamics of lipolytic intermediates (DG and MG). Model simulations showed that MG continuously accumulated in tissue during epinephrine infusion (0.2mM to 0.93mM), while DG levels decreased from 2mM to 1.1mM (Figure 6B).

Figure 6.

Model-simulated ratio of FA to glycerol released by the adipose cellular compartment (i.e., J_{FA,b↔ c}/J_GLR,b↔c) (A) and changes in intracellular lipolytic intermediates (i.e., DG: solid line, MG: dashed line) (B) in response to the intravenous infusion of epinephrine.

Re-esterification dynamics

Increased FA availability as a result of TG breakdown in the adipose tissue resulted in a higher intracellular re-esterification rate (Figure 7A). Model simulations showed that the re-esterification rate reached its maximum (1.45 μmol/kg/min) at 10min and gradually decreased toward the basal value. An increased re-esterification rate was associated with an increased rate of G3P synthesis. The relative contribution of glyceroneogenesis to G3P synthesis increased 3~14% during epinephrine infusion regardless of its fractional contribution at the basal state (Figure 7B).

Figure 7.

(A) Model-simulated dynamic responses of FAC dependent re-esterification rate (solid line), ACoA synthesis from pyruvate (dashed line) and FAC (dotted line). (B) Relative fractional glyceroneogenesis with different contributions at the basal state. The fractional glyceroneogenesis, F_GRNG(t) =φ_{PYR →G3P}/(φ_{GAP ↔G3P} + φ_{PYR →G3P}) and the relative F_GRNG is the ratio of F_GRNG(t) at any time t>0 to t=0. The solid line represents the equal contribution of glycolysis and glyceroneogenesis (F_GRNG(0)=0.5) while the dashed and dotted lines represent higher (F_GRNG(0)=0.8) and lower (F_GRNG(0)=0.2) contribution of glyceroneogenesis.

Sensitivity Analysis

The sensitivity of the model parameters was quantified by the change in the sum of squared differences between simulated model outputs with different parameter values. In addition to the parameters (V_c, λ_ATGL,TG→DG, λ_HSL,TG→DG, and λ_HSL,DG→MG) optimally estimated from the experimental data, V_max and K_m for the reactions involved in lipolysis and transacylation were investigated as well. The sensitivity indices of the various model parameters are listed in Table 10. The high sensitivity indices of the parameters involved in breakdown of DG by HSL and MG by MGL (e.g., λ_HSL,DG→MG, V_{max,HSL,DG→MG} and V_{max,MGL,MG→GLR}) suggest that the model output is more responsive to the changes in these parameters. In contrast, the low sensitivity indices of the parameters involved in breakdown of TG by HSL and ATGL (e.g., λ_HSL,TG→DG, V_{max,HSL,TG→DG}, K_{m,ATGL,TG→DG} and K_{m,HSL,TG→DG}) suggest a minimal effect of these parameters on the model output.

Table 10.

Sensitivity indices of the model parameters related to the lipid mobilization

Parameters	Sensitivity Index (Si)*
vcf	0.298
λATGL,TG→DG	0.202
λHSL,TG→DG	0.045
λHSL,DG→MG	1.925
Vmax,ATGL,TG→DG	0.386
Vmax,HSL,TG→DG	0.054
Vmax,HSL,DG→MG	2.310
Vmax,HSL,MG→GLR	0.102
Vmax,MGL,MG→GLR	2.473
Km,ATGL,TG→DG	0
Km,HSL,TG→DG	0
Km,HSL,DG→MG	0.098
Km,MGL,MG→GLR	0.251
Km,HSL,MG→GLR	0.281
Km,FAC-G3P→DG	0.282
Km,DG→TG	0.281
Km,DG-DG→TG- MG	0.280
Km,MG-MG→DG-GLR	0.288
Km,MG-DG→TG-GLR	0.298

^*Values are dimensionless.

Discussion

Even though adipose tissue plays a significant role in regulating whole body fuel metabolism, it has been difficult to get reliable quantitative data (e.g., exchange of substrates) due to the heterogeneity of fat depots. Furthermore, data from various kinds of experimental studies must be integrated to get a coherent understanding of adipose tissue metabolism. Therefore, we developed a physiologically based mechanistic model of adipose tissue metabolism that includes key metabolites and regulatory enzymes in the metabolic pathways. With this model, we integrated available information on mass transport mechanisms for the tissue-blood substrate exchange, cellular metabolic pathways and their control mechanisms, as well as specific physiological characteristics of adipose tissue. Estimated parameters and dynamic responses by the model simulations were similar to those in literature and provided insight into those that cannot be estimated in vivo.

Effect of altered expression levels of lipases

LPL catalyzes hydrolysis of VLDL-TG in the capillary bed of the adipose tissue. Until recently, HSL was considered the only lipase responsible for hydrolyzing intracellular TG stores. However, the existence of another intracellular lipase was proposed since it was reported that HSL deficient mice retain the basal lipolytic rate (Okazaki et al., 2002;Zechner et al., 2005;Haemmerle et al., 2002). The critical roles of this new lipase, ATGL have been shown in various studies with transgenic mice (Haemmerle et al., 2006). Due to the experimental difficulties, however, the comprehensive analysis on physiological responses in these transgenic mice could not be done, and in vitro studies had to be resorted for the indirect measurement. Therefore, we used the model to reproduce and predict the physiological responses arising from the genetic modulation.

As shown in Figure 3A, the simulations confirm the important role of ATGL in regulating the basal lipolytic rate. The greater decrease of FA release by knocking down ATGL expression than that of HSL is consistent with experimental observations with transgenic mice, where ATGL-deficient mice have substantially lower levels of plasma FA (60% lower than the control) in association with massive accumulation of lipid (Haemmerle et al., 2006). In contrast, HSL- deficient mice have moderate reduction (10~20%) in the plasma FA levels without significant decrease in the basal lipolytic rate (Wang et al., 2001). As expected from the fact that DG can be hydrolyzed only by HSL, it was shown that DG accumulated in the adipose tissue of HSL-deficient mice (Haemmerle et al., 2002).

The model simulations, which were in good agreement with experimental observations, provided additional information on the lipolytic intermediate levels in other alterations. However, the reduction in the rate of release of FA with decreasing HSL activity seems to be higher in the model simulation because the basal lipolytic rate was unaltered in HSL-deficient mice. This discrepancy could be associated with a concomitant increase in ATGL expression of HSL- deficient mice to compensate for the decreased lipolytic rate due to the reduction in HSL activity. Indeed, when the expression of HSL was knocked out, the model was able to simulate a 3-fold increase in ATGL activity that maintained the rate of release of FA from the adipose tissue (data not shown).

Intracellular compartmentation

The localized metabolism in a subdomain volume of adipose tissue cells had significant impact on simulated responses. A smaller subdomain volume produced faster dynamic responses for the substrate exchange and adipose venous concentration of glycerol and FA (Figure 4 and 5). Furthermore, the higher concentrations increased the blood-tissue concentration gradient to produce the required mass transport rate for sufficient metabolism. This effect was magnified by the initial acceleration in the rate of lipolysis in the tissue that increased intracellular concentrations of glycerol and FA. The localized metabolic subdomain is consistent with a small cytosolic volume due to large lipid droplet in adipocyte (Moore et al., 2005;Denton et al., 1966). Furthermore, the volume fraction of this metabolic subdomain estimated by the model corresponds to the volume fraction of intracellular water space (1~4% of total tissue volume) measured from in vitro studies of adipose fat pad (Denton et al., 1966; Crofford and Renold, 1965)

Recent in vitro studies of adipocyte lipid mobilization showed that major lipolytic enzymes and proteins are co-localized in a subcellular domain during beta-adrenergic stimulation (Granneman et al., 2007;Moore et al., 2005;Clifford et al., 2000). The localization of enzyme complexes reduces the transit time of metabolites which allows faster cellular dynamics (Welch and Easterby, 1994). To simulate cellular dynamic responses observed experimentally, cellular metabolites and enzymes should be localized to a metabolic subdomain of ~3% of total adipose tissue volume. Under this condition, model simulations can relate the intracellular mechanisms to the physiological response of the adipose tissue bed.

Differential regulation of lipases

Regulation of lipase reaction during beta-adrenergic stimulation involves complex cellular mechanisms (Langin and Arner, 2006; Large et al., 2004). While HSL is highly regulated via reversible phosphorylation by protein kinase A (PKA), the breakdown of TG by HSL requires co-activation of another protein called perilipin, which coats lipid droplets and prevent HSL and ATGL from hydrolyzing TG (Clifford et al., 2000). Consequently, the lipolysis of TG is an integrated process involving differential regulation of major lipases and other proteins. Only with differential activation for regulating lipase reactions did model simulations compare well with experimental data.

After 30 min of epinephrine infusion, glycerol AVD reached ~60% and FA AVD reached ~80% of their steady-state values. The faster dynamic response and higher FA production from adipose tissue (Figure 4) is required to generate the sufficient concentration gradient for blood-tissue transport. The estimated parameter values (Table 9) show that DG breakdown by HSL required four times higher activation during beta-adrenergic stimulation than TG breakdown by ATGL and HSL. To simulate experimental data, the first and the second steps in lipid mobilization were stimulated to different extents. These data are consistent with the suggested role of perilipin in TG hydrolysis (Sztalryd et al., 2003;Londos et al., 1995)

The model was formulated using the biochemical data that MG breakdown by HSL and MGL are not subject to the activity change via phosphorylation with constant maximum rate coefficients (Large et al., 2004;Zechner et al., 2005). As a consequence, while MG levels in adipose tissue increased, DG levels in adipose tissue decreased over time due to the greater increase in HSL activity for DG breakdown. The accumulation of either MG or DG can be expected from a ratio of glycerol to FA release rate higher than 3. However, model simulations predicted that accumulation of MG and not DG occurs (Figure 6B). In vitro study of human adipose tissue showed 46~53% reduction in the DG levels during the increased lipolysis (Edens et al., 1990a), which is close to our model simulations (45% reduction). Measurement of dynamic changes of lipolytic intermediates (e.g., DG, MG) during epinephrine infusion in vivo will be required to confirm the model predictions of differential activation of lipase reactions.

Source of G3P for re-esterification

Glyceroneogenesis, an abbreviated version of gluconeogenesis, involves the formation of G3P from precursors other than glucose or glycerol (Reshef et al., 2003). Since the adipose tissue lacks glycerol kinase, it cannot directly utilize glycerol for TG synthesis (Reshef et al., 2003). Therefore, G3P for the intracellular re-esterification of FA is formed from either glucose or pyruvate. We used the model to predict the relative contribution of glucose and pyruvate to G3P synthesis during the intravenous epinephrine infusion. In the absence of available in vivo human data, we assumed that glucose via glycolysis and pyruvate via glyceroneogenesis contribute equally in the basal state. Model simulations showed the effect of varying these contributions. Intracellular re-esterification increased by up to 13% during epinephrine infusion (Figure 7A). In the absence of changes in other hormone levels during epinephrine infusion (Samra et al., 1996), the re-esterification rate was primarily regulated by the availability of substrates. Model simulation showed that the increased rate of G3P synthesis occurred with a greater contribution of glyceroneogenesis regardless of its relative contribution at the basal state. FAC levels increased ~80% (data not shown), which increased re-esterification during epinephrine infusion. Increase in FAC levels due to lipolysis resulted in an increased ratio of acetyl CoA to free CoA (~20%, data not shown), which inhibited the oxidation of pyruvate by decreasing the activity of pyruvate dehydrogenase (PDH). Indeed, Figure 7A showed that ACoA synthesis from pyruvate decreased 12%, while that from FAC increased 13%. These responses suggest that the increased flux of glyceroneogenesis comes from reduction in pyruvate oxidation. Noting that the experimental epinephrine infusion rate did not alter the arterial glucose and insulin levels (Samra et al., 1996), an increase in the glucose uptake during epinephrine infusion is unlikely. Correspondingly, model simulation predicted a relatively small contribution of glycolysis. Overall, our model provided quantitative understanding of the change in in vivo metabolic flux rate induced by a physiological perturbation.

Sensitivity Analysis

There are 4 parameters (e.g., λ_HSL,TG→DG, V_{max,HSL,TG→DG}, K_{m,ATGL,TG→DG} and K_{m,HSL,TG→DG}) whose sensitivity indices are smaller than 0.1 indicating that these parameters were poorly estimated. Since two enzymes (ATGL and HSL) can hydrolyze TG, the one with the dominant contribution to the TG breakdown in the basal state (i.e., ATGL reaction) will have the higher sensitivity unless additional intracellular data are added to examine the differential effect of individual enzyme. Thus, the model parameters related to TG breakdown by HSL have low sensitivity indices. For these parameters to be estimated precisely, changes in activities of these enzymes must be measured.

The low sensitivity of Km parameters, whose values were taken from the literature, may have resulted from the very high TG concentration in the adipose tissue. With a smaller Km value than the substrate level, the reactions breaking down TG are of zero order (i.e., independent of concentration). Therefore, the sensitivity indices for these Km values were computed as zero. Note that there are three parameters whose sensitivity indices are greater than one. Two parameters relate to DG breakdown by HSL and one relates to MG breakdown by MGL. Therefore, reactions involving DG and MG breakdown have a more significant effect on the model simulations in response to the intravenous epinephrine infusion.

Model limitations

This model was developed from the experimental data obtained from a local subcutaneous adipose tissue bed (Coppack et al., 1990;Frayn et al., 1994;Frayn et al., 1991;Frayn et al., 1989;Samra et al., 1996). Therefore, it may not simulate the whole-body kinetic responses as measured by isotopic tracer studies. In addition, we did not incorporate the heterogeneity of various adipose depots in the body. To investigate the role of adipose tissue in relation to metabolic disorders, a model that incorporates different types of adipose depots will be required to predict the integrated response of adipose tissue in the whole body.

The effect of beta-adrenergic stimulation on the rates of lipolytic reactions was simulated by changing the maximum rate coefficient (V_max) of Michaelis-Menten metabolic flux equations. With these equations, activation of enzymatic reactions can also be achieved with lower K_m values that lead to increased substrate affinity. Although some K_m values were available from the literature, we had to assume others equal to the tissue levels of corresponding substrates. Because of the uncertainty of many K_m values, we did not simulate how variations of these would affect lipolytic reactions rates. An alternative strategy for future studies would be to incorporate detailed enzyme kinetics related to various lipase reactions, but this would introduce even more unknown parameters. To make such an analysis worthwhile, many more experiments must be performed to obtain appropriate data.

Due to the lack of experimental data for adipose tissue, we had to use intracellular concentration data for GAP, NADH, NAD+, Pi, O₂ and CO₂ from those in the skeletal muscle. It could introduce some miscomputations. However, this is unlikely to cause significant problem since the concentrations of these metabolites do not change significantly during experimental perturbations.

Conclusions

A physiologically based mathematical model of adipose tissue metabolism was developed to simulate dynamic responses to intravenous infusion of epinephrine. The model not only simulated the exchange of substrates across the tissue bed and the concentration dynamics in the venous blood for FA and glycerol, but also provided quantitative predictions on the metabolic regulation in the adipose tissue. A key finding in our study is the recognition of a metabolic subdomain in adipose tissue where most of enzymes and metabolic substrates were localized. By incorporating the mechanisms for regulating various lipase reactions to mobilize TG, the model showed that these lipase reactions were differentially activated during epinephrine infusion resulting in the distinctive dynamic responses of lipolytic intermediates. Critical experiments are needed to test model predictions of metabolic regulation in adipose tissue.