Modeling transient collapsed states of an unfolded protein to provide insights into early folding events

Abstract

The primary driving force for protein folding is the sequestration of hydrophobic side chains from solvent water, but the means whereby the amino acid sequence directs the folding process to form the correct final folded state is not well understood. Measurements of NMR line broadening in spin-labeled samples of unfolded apomyoglobin at pH 2.3 have been used to derive a quantitative model for transient hydrophobic interactions between various sites in the polypeptide chain, as would occur during the initiation of protein folding. Local clusters of residues with high values for the parameter “average area buried upon folding” (AABUF) form foci not only for local contacts but for long-range interactions, the relative frequencies of which can be understood in terms of differences in the extent of reduction in chain configurational entropy that occurs upon formation of nonlocal contacts. These results complement the striking correlation previously observed between the kinetic folding process of apomyoglobin and the AABUF of its amino acid sequence [Nishimura C, Lietzow MA, Dyson HJ, Wright PE (2005) J Mol Biol 351:383–392]. For the acid-unfolded states of apomyoglobin, our approach identifies multiple distinct hydrophobic clusters of differing thermodynamic stability. The most structured of these clusters, although sparsely populated, have both native-like and nonnative character; the specificity of the transient long-range contacts observed in these states suggests that they play a key role in initiating chain collapse and folding.

Characterization of transient structures in disordered states of proteins and understanding their role in initiating and directing protein folding remain two of the most fundamental challenges in structural biology. With the recognition that intrinsically disordered proteins are widespread throughout all genomes and play a central role in a diverse range of cellular processes and disease states, the urgency of surmounting these challenges is growing. The dynamic heterogeneity of disordered protein ensembles remains the major obstacle impeding their structural characterization. Still, significant progress has been made in characterizing residual structure and potential folding nuclei at atomic resolution, notably with various NMR techniques. Site-directed spin labeling (SDSL), in which a paramagnetic moiety is introduced into the polypeptide chain by cysteine mutagenesis and chemical linkage, is particularly useful for identifying long-range contacts (1). The measured enhancement of amide proton transverse relaxation rates by the paramagnetic tag reports directly on intrachain distances and contact probabilities.

Unfolded apomyoglobin (apoMb) was one of the first disordered states in which long-range interactions were detected by using SDSL (2) and has been thoroughly characterized by other NMR spectroscopic approaches (3, 4). Residual dipolar couplings of apoMb in 8 M urea (5) are consistent with statistical coil models of the unfolded state (6, 7), whereas the acid-unfolded state at pH 2.3 contains small amounts of residual helix in the A, D/E, and H regions of the protein (4, 8, 9), which align independently in anisotropic media (5). The dynamics of the acid-unfolded state in 8 M urea suggest formation of local hydrophobic clusters separated by highly flexible glycine- and alanine-rich “hinge” regions (10).

Here, we introduce a simple model for interpreting SDSL paramagnetic relaxation enhancement (PRE) in highly unfolded protein states. The model is based on the observation that long-range PRE occurs in chain segments with above-average values of the parameter “average area buried upon folding” (AABUF), defined for each amino acid as the difference in accessible surface area between a solvent-exposed standard state and the mean solvent accessibility of the amino acid in a database of folded proteins (11). Two major energetic contributions are evaluated: contact free energies between interaction sites and the reduction in chain configurational entropy that occurs upon formation of nonlocal contacts. The model is validated for the acid-unfolded states of apoMb through quantitative comparison with PRE data from 14 distinct spin-label sites.

Results

Spin-Labeled apoMb Mutants: Design and Characterization.

A set of 14 proteins was prepared, each with a single site mutated to cysteine for coupling of spin label. The labeling sites were chosen for their high degree of solvent exposure in the holomyoglobin structure (12) and/or their relevance to the ABGH folding core of the molten globule intermediate. The locations of the spin-labeled residues are shown in Fig. 1a. ¹H-¹⁵N HSQC NMR spectra were recorded with the spin label oxidized (paramagnetic) and again after reduction with ascorbic acid (the diamagnetic reference). All spectra faithfully reproduced wild-type chemical shifts under the conditions investigated, with the exception of residues in the immediate vicinity of the spin-label sites in the primary sequence, indicating that wild-type conformational propensities remain essentially unperturbed in the mutant proteins.

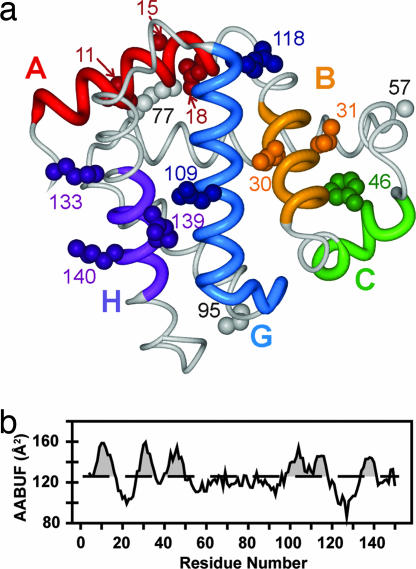
Fig. 1.

Structure and AABUF of myoglobin. (a) Backbone structure of sperm whale holomyoglobin (PDB entry 1MBC) (12). apoMb adopts a similar structure except that the F helix is disordered (29). The side chains of residues that were substituted with spin labels are shown as spheres. Local clusters (interaction sites) are colored red (A region; residues 4–16), orange (B region; residues 27–35), green (C region; residues 40–49), blue (G region; residues 98–117), and purple (H region; residues 134–141). (b) Sequence variation of AABUF, plotted by using a seven-residue moving average. The dashed line is the mean value of AABUF for the entire chain; intersections of the moving average with this value define the local cluster boundaries given above.

Intrachain Distance Distribution Functions for Disordered Chain Segments.

Introduction of a paramagnetic spin label enhances the transverse relaxation rate of amide protons in a manner that can be quantified experimentally as the ratio of ¹H-¹⁵N HSQC peak intensities with the spin label in paramagnetic and diamagnetic states (13):

where R_2,0 is the transverse relaxation rate in the absence of paramagnetic broadening, R_2P,ave is the ensemble-averaged paramagnetic contribution to R₂, t is the total INEPT delay in the ¹H-¹⁵N HSQC pulse sequence, and I_para and I_dia are the amide cross peak intensities for the paramagnetic and diamagnetic protein samples. Whereas in general R_2P,ave is a complex function of the intrinsic R_2P of individual conformers and the chain relaxation kinetics, in the case of an unfolded protein with rapidly interconverting conformers, R_2P,ave reduces to a population-weighted average over all ensemble members. If we describe the intrachain distances through a potential of mean force U = −k_BT ln(P(r;|i − j|)), where P(r;|i − j|) is the distance distribution function for a sequence separation of |i − j|, k_B is the Boltzmann constant, and T is the absolute temperature, this average becomes an integral over the amide-spin-label separation r:

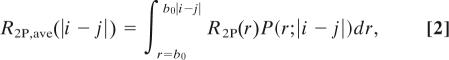where b₀ = 3.8 Å, the average i, i + 1 C^α distance. We neglect the contribution of the nitroxide side chain at this resolution. The dependence of R_2P(r) on r is given explicitly as (14)

where K = 1.23 × 10⁻³² cm⁶·s⁻² for the proton–electron interaction (15), ω_H is the proton resonance frequency, and τ_c is the correlation time for the electron-nuclear dipole–dipole interaction, taken to be 4 ns for disordered proteins (1).

To evaluate various aspects of the model presented below, we require a set of reference distribution functions P(r;|i − j|) that describe the unfolded chain in the absence of residual interactions. Such distribution functions should reproduce the PRE in disordered regions of the protein and give a radius of gyration (R_G) comparable with that measured by SAXS (35.8 Å) for the fully unfolded protein (16). While acknowledging that other expressions likely exist that yield reasonable results, we use the mean field approximation to the unperturbed wormlike chain model (17) with an empirical logistical correction,

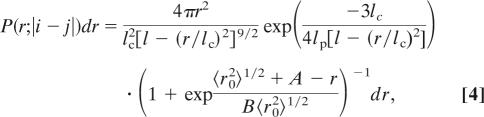where l_p is the chain persistence length, l_c = b₀|i − j|, 〈r₀²〉^1/2 is the root mean square end-to-end distance for the unperturbed chain (i.e., without the logistical correction), and A and B are fitting parameters.

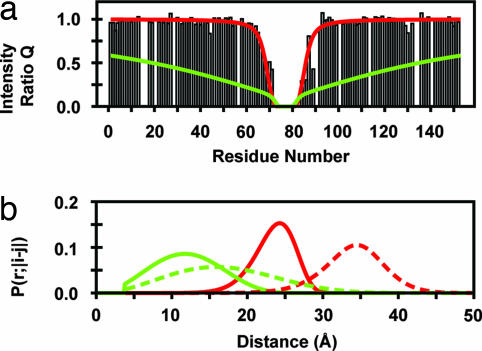
For completely disordered polypeptide segments, plots of Q versus residue (hereafter referred to as PRE profiles) exhibit a characteristic inverted bell-shaped depression (2), exemplified by the K77C* spin-label data plotted in Fig. 2a. (The asterisk is used to emphasize that the cysteine mutants are chemically conjugated to the nitroxide spin label.) The set of P(r;|i − j|) described by Eq. 4, when combined with Eqs. 1–3, are able to quantitatively reproduce this behavior (red line) while maintaining the SAXS R_G. Representative P(r;|i − j|) corresponding to sequence separations of 10 and 20 residues are plotted in Fig. 2b as solid and dashed red lines, respectively. The logistical correction acts to both narrow and shift the unperturbed distribution functions. In its absence, the significant short-range tails of the unperturbed wormlike chain distribution functions result in near universal overprediction of the paramagnetic line broadening, even for large l_p values where short-range probabilities are significantly reduced. An example of this behavior with l_p = 20 representing a quite stiff chain is shown for comparison in Fig. 2 (green lines).

Fig. 2.

Logistical corrections to distribution function of disordered regions. (a) Paramagnetic enhancement to nuclear spin relaxation at pH 2.3 for an apoMb variant with a nitroxide spin label at position 77. The histogram shows the experimental intensity ratios (Q = I_para/I_dia) for each residue with an adequately resolved cross peak in the ¹H-¹⁵N HSQC spectrum. An intensity ratio of 1 indicates no effect of the spin label on an amide proton. The superimposed curves show Q values calculated from Eqs. 1–4 with l_p = 20 (green) or fitted to the logistically corrected Eq. 4 (red) with parameters l_p = 2.64 ± 0.04, A = 16.6 ± 0.4, and B = 0.108 ± 0.001. Note that the logistical correction contributes to chain stiffness that removes the direct correspondence between the parameter l_p and the chain's actual persistence length. (b) P(r;|i − j|) calculated by using Eq. 4 with (red lines) and without (green lines) its logistical correction for sequence separations |i − j| of 10 residues (l_c = 38 Å; solid lines) and 20 residues (l_c = 56 Å; dashed lines). Data for overlapping resonances are omitted from the PRE profiles and analysis.

Deviations from Statistical Coil Behavior in Acid-Unfolded apoMb.

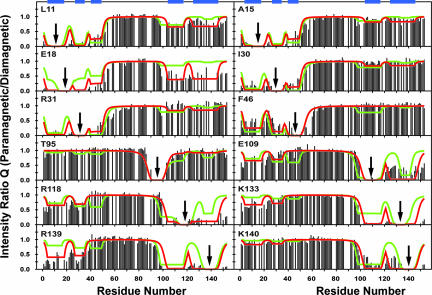
In contrast to the complete disorder of the chain interior, apoMbs with spin labels attached nearer either terminus show PRE well beyond the ≈15 residues expected for a statistical coil (2), indicative of extensive intrachain contacts. The PRE profiles of the acid-unfolded state (Fig. 3) exhibit five distinct local minima, which we designate A–C, G, and H because they coincide closely with the high-AABUF sequences in the A and B helices, the CD loop, and the G and H helices, respectively (Fig. 1b). Individual minima are generally more pronounced in a given PRE profile when close to the site of spin-label insertion, regardless of whether the corresponding interaction is native-like. Whereas one of the most obvious interactions (between G and H) corresponds to a helical hairpin in the folded structure, another (between A and B) is entirely nonnative.

Fig. 3.

Paramagnetic enhancement to nuclear spin relaxation for unfolded apoMb at pH 2.3 in the absence of urea for 12 apoMb variants. Each panel is labeled with the residue for which the spin-labeled cysteine was substituted; arrows indicate the sites of substitution. As in Fig. 2a, the histograms show the experimental intensity ratios. The fitted curves correspond to the initial (green) and corrected (red) models described in the text. The analysis includes previously published data for the E18, K77, and K133 mutants (2). The locations of the local clusters (regions of high AABUF) are indicated by blue bars at the top of the figure. Data for overlapping resonances are omitted from the PRE profiles and analysis (see Table S4 for all measurable Q values under these conditions). Fits for A57 and K77 mutants, the PRE profiles of which exhibit minimal deviations from statistical coil behavior, are included as Fig. S3.

For intrachain contacts involving only one of the chain termini, the PRE of amides at the site of interaction are largely independent of the specific position of a spin-label probe within the site. It follows that such interactions must be highly nonspecific, with rapid dynamic and structural averaging. In contrast, when contacts involve both termini, the sensitivity to the spin-label insertion site is more apparent, suggesting greater specificity in these long-range interactions. For example, adjacent spin labels R139C* and K140C* induce strikingly different extents of PRE in N-terminal amides. Additionally, while many of the G- and H-region spin-label probes enhance the relaxation of the amides in the B region, spin labels conjugated at this latter site (I30C*, R31C*) induce minimal or no PRE at the C terminus.

Modeling PRE as AABUF-Driven Loop Closure.

To develop a quantitative model of the PRE, we treat the five high-AABUF regions in the chain as a set of local clusters whose boundaries are defined by the points at which the AABUF profile drops below its mean value (Fig. 1b). Nonlocal clusters are then defined as combinatorial associations of two or more local clusters. In this framework, the acid-unfolded ensemble separates into a set of 52 macrostates defined by the nonlocal clusters each possesses.

We model the free energy of each macrostate (relative to the completely unfolded reference state) in terms of two opposing energetic contributions: (i) a favorable contact energy for formation of nonlocal clusters, ΔG_O, and (ii) the reduction in configurational entropy required to form these contacts, ΔG_L. Contact free energies ΔG_TR for the n individual coalescence events (transitions) required to reach a given macrostate from the unfolded reference are taken to contribute additively to ΔG_O (i.e., ΔG_O = Σ_nΔG_TR). In the simplest scenario applied below, we use a single value of ΔG_TR to describe all such coalescence events.

In general, ΔG_L for a particular macrostate may be decomposed into a set of conditional free energies that describe the sequential introduction of the individual topological restraints into the chain via a series of loop-closure events. We therefore need to first calculate the conditional entropy loss ΔG′ for a pairwise coalescence event (e.g., between the A and H regions) that starts from a macrostate with an arbitrary set of preformed contacts (e.g., a BG cluster). The concept of effective contact order (ECO) provides a convenient way of expressing this type of conditional dependence; for two clusters centered at residues i and j in a given macrostate, ECO is defined as the number of monomeric links along the shortest path between i and j traced either covalently or topologically (18). (Note that in the absence of any nonlocal clusters, ECO is identical to the sequence separation |i − j|.) In the above example, the ECO between the A and H clusters is considerably less than the corresponding sequence separation because it is calculated by shortcutting across the BG cluster. In effect, ECO provides an estimate of the effective loop length that must be closed to form the additional contact. One may calculate a ΔG′ that corresponds to closure of such a loop via (19)

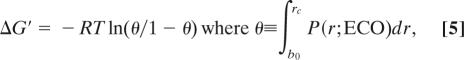where the capture radius r_c, defined as the average distance to which the central residues of the two clusters must approach before coalescence occurs, is calculated by using the spherical approximation of the diffusion-collision model (20), and ECO now replaces |i − j| in the set of distribution functions. Because the use of ECO in this manner is imperfect, summations of ΔG′ along different sequential pathways leading to the same macrostate exhibit some degree of variability. We therefore define ΔG_L for any macrostate whose formation requires multiple loop closure events as the largest such sum; only such a choice ensures that conformational entropy decreases monotonically along all coalescence pathways. Example calculations for ΔG_L are included in supporting information (SI) Text and Tables S1 and S2.

The R_2P value for an amide proton–spin label pair in a given macrostate will also depend largely on the ECO between the two corresponding residues. In the case where the ECO path is composed of linker residues and/or dissociated local clusters, we obtain R_2P for the macrostate through Eq. 2 by using the appropriate disordered-region distribution function determined above (again, replacing |i − j| with ECO). We model the collapsed nature of nonlocal clusters by setting the maximal contribution to the ECO of such clusters to a value of 4, which corresponds to the maximal separation consistent with complete line broadening within experimental uncertainty for a fully populated contact. Further discussion and example calculations are included in SI Text. Note that our model does not provide a realistic representation of the distance distributions within these collapsed structures but models the average root mean square distance for the spin label–amide proton pair.

To account for the observation that the PRE in clusters involving interactions between the two chain termini depends significantly on the spin-label insertion site, we introduce the concept of a spin-label solvation factor. The more highly solvated a particular spin-label side chain is throughout the lifetime of a long-range cluster in which it is involved, the further the paramagnetic moiety will be on average from amide protons within the cluster, and thus the less it will enhance the relaxation of these protons. Each spin label is assigned a solvation factor f_S between zero and two. The value of f_S is added to any ECO where the spin label is involved in a cluster involving simultaneous interaction of both chain termini (e.g., clusters ABH or AG but not clusters ABC or GH) before calculating the R_2P for the interaction. When f_S is zero, the spin-label side chain is, on average, buried within the cluster; the close proximity of the paramagnetic side chain to amide protons in the cluster induces maximal relaxation enhancement. When f_S is greater than zero, the side chain can be considered partially (f_S = 1) or fully (f_S = 2) exposed to solvent and thus the relaxation enhancement will be correspondingly smaller.

Given the above framework, model-dependent R_2P,ave values are calculated by summing over contributions from individual macrostates weighted by their fractional populations p_i (R_2P,ave = Σ_ip_iR_2P,i). The set of f_S and ΔG_TR may then be determined by fitting the set of Q values through nonlinear regression. The resulting fit of the acid-unfolded state PRE (green lines in Fig. 3) yields a contact free energy for cluster formation ΔG_TR = −3.1 kcal·mol⁻¹. Solvation factors deviate from zero for a significant number of residues (Table 1).

Table 1.

Spin-label solvation factors f_S

Spin-label position	Solvation factor, fS
11	1
15	1
18	0
30	2
31	2
109	1
133	1
139	0
140	2
46/118	N/D

f_S values were not determined for F46C* and R118C* because the C cluster that contains F46C* does not measurably interact with the C terminus of the chain (as required by the definition of f_S) and R118C* lies outside all local clusters. N/D, not determined.

The model is able to reproduce many features in the experimental PRE profiles but is quantitatively deficient on two different levels. First, the single-value ΔG_TR model requires C region interactions to be among the most heavily populated because of its central position in the chain (and correspondingly low energetic penalties for loop closure events initiating at this site). In contrast to this prediction, the experimental data show no evidence of either CG or CH contacts but do exhibit other, more entropically unfavorable contacts between the N terminus and C terminus of the chain. The single-value ΔG_TR model also overpredicts PRE between the C region and A/B regions (most readily observed in the I30C* and F46C* panels of Fig. 3), but to a lesser extent. We necessarily conclude that nonlocal clusters involving the C region are inherently less stable than those involving other high-AABUF regions. The second level at which this simple model appears to be deficient is in the precise prediction of local cluster boundaries. The model underpredicts PRE for spin label E18C* (region A appears to include this residue), overpredicts PRE for spin label T95C* (where better agreement requires shifting the N-terminal boundary of the G region to residue 104), and does not account for much of the PRE at the C terminus of the protein chain. This latter discrepancy, though possibly due to a separate hydrophobic cluster at residues 149–150 that was not included in our analysis (Fig. 1b), is more likely to be due to the H region's taking on dynamic helical structure while interacting with other sites. This conjecture is consistent with both the amphipathicity and strong helical propensity of this chain segment (4) and accounts for the strikingly different solvation factors for R139C* and K140C* (Table 1) if the resulting helix takes a native-like orientation. H region interaction site boundaries can be estimated from secondary chemical shift data (4).

If we incorporate the above considerations into the model by slight adjustments of the local cluster boundaries and by adding energetic penalties of ΔG_C-A/B and ΔG_C-G/H to macrostates in which the C region is coalesced with the A/B and G/H regions, respectively, the model reproduces the data remarkably well (red line in Fig. 3) giving ΔG_TR = −3.4 kcal·mol⁻¹, ΔG_C-A/B = +1.5 kcal·mol⁻¹, and ΔG_C-G/H > ≈+3 kcal·mol⁻¹. The major species in the ensemble generated by fitting this improved model to the experimental data are listed in Table 2 along with their fractional populations. By summing over all species in which a particular contact exists, one obtains the contact probabilities for the 10 possible pairwise interactions (Table S3). Nearly 70% of all molecules in the unfolded apoMb ensemble at pH 2.3 contain nonlocal contacts, most of which are restricted to within ≈50 residues of a chain terminus. Only a small subset of the calculated ensemble contains interactions between the two termini (≈6%). To verify that the network of interactions in the acid-unfolded state of apoMb identified by this analysis is consistent with the SAXS-determined radius of gyration, we model the radius of gyration from the distance distribution functions via R_G² = 1/153²Σ_{1≤i<j≤153}∫r²P(r;ECO)dr (21), where 153 is the number of residues in the apoMb chain. The resulting radius of gyration, 32.6 Å, is in reasonable agreement with the 30.2 ± 2.5 Å determined from SAXS experiments (16).

Table 2.

Most highly populated macrostates in the pH 2.3 acid-unfolded apoMb ensemble

Species	Population
A-B-C-G-H	0.305
A-B-C-GH	0.194
AB-C-G-H	0.159
AB-C-GH	0.101
A-BC-G-H	0.061
ABC-G-H	0.041
A-BC-GH	0.039
ABC-GH	0.026
ABGH-C	0.011
A-BGH-C	0.010
AGH-B-C	0.009
ABG-C-H	0.007
ABH-C-G	0.006

Grouped letters (not separated by hyphens) correspond to nonlocal clusters.

Upon addition of 8 M urea to the acid-unfolded apoMb at pH 2.3, the PRE profiles change significantly (Fig. S1) and long-range interactions between the chain termini are no longer observed. Fitting of the PRE profiles reveals only short- and medium-range interactions: the unfolded ensemble contains only two minor subspecies—one in which the A and B regions coalesce (comprising 4.4% of the total ensemble) and one in which the G and H regions coalesce (comprising 2.4% of the total ensemble). All other macrostates containing nonlocal clusters are populated at ≤0.5%. In contrast to the acid-unfolded state, the urea PRE data can be fitted well without the need to invoke a solvation factor f_S, indicating that any native-like interactions (or H region helicity) are disrupted and only highly dynamic, nonspecific interactions remain.

Discussion

Paramagnetic relaxation enhancement is increasingly being used to characterize biological macromolecules in situations where traditional approaches (e.g., measurement of NOEs) have proven inadequate. Here, we demonstrate that PRE studies can be used to detect and characterize very small populations of collapsed states or equilibrium intermediates within an otherwise highly unfolded background. In both the acid- and urea-unfolded states of apoMb, PRE reveals the presence of collapsed states comprising <5% of the total ensemble. Such states contribute disproportionately to the measured PRE but only modestly perturb the global properties of the chain. For apoMb in 8 M urea, for example, the transient A/B and G/H contacts detected by PRE are present at such low levels in the ensemble that they do not cause residual dipolar couplings to deviate measurably from statistical coil models (5–7). PRE profiles obtained for protein variants with different spin-label conjugation sites provide a surprising amount of insight into the structural features of these weakly populated species. In the case of acid unfolded apoMb, these results indicate the highly heterogeneous nature of the clusters in 8 M urea and the formation of long-range clusters with native-like tertiary packing in the absence of urea (see below).

The Role of AABUF in Initiating Hydrophobic Collapse.

Based on the correlation between AABUF and a number of measured properties of acid-unfolded apoMb that report on hydrophobic cluster formation, it has been proposed that chain segments that score highly on the AABUF scale are likely sites of initiation in protein folding (22). Here, we have demonstrated that a simple model in which AABUF plays the role of the major driving force for chain compaction and hydrophobic cluster association can reproduce the PRE profiles in both urea- and acid-unfolded states of apoMb remarkably well. All five regions in the apoMb sequence corresponding to AABUF maxima are involved in transient contacts in the acid-unfolded state. Moreover, there are no detectable contacts involving any chain segment outside of these five maxima. Scales such as the Kyte–Doolittle hydrophobicity scale (23) fail to exhibit a similar correspondence. In particular, the Kyte–Doolittle profile (Fig. S2) fails to identify the C region as a site of potential interaction and exhibits maxima in several regions, including the C terminus of the E helix and the F helix, which do not exhibit discernable interactions in the PRE profiles (Fig. 3 and Fig. S3). The significantly better correspondence between experimental interaction sites and AABUF maxima suggests that the aliphatic portions of charged/polar side chains contribute more to stabilization of transient long-range contacts than do small aliphatic side chains that score higher on the Kyte–Doolittle scale (24).

The role of AABUF was recently examined for the kinetic folding pathway of apoMb (22) with striking results. A quadruple mutant of myoglobin was generated in which the AABUF values of two helices were interchanged while largely maintaining the overall integrity of the packing interactions in the natively folded hydrophobic core. In both the wild-type and mutant proteins, only regions with above-average values of AABUF exhibited significant protection from amide exchange in the burst phase intermediate (22), thus clearly demonstrating the role of AABUF in governing the temporal order of events along the kinetic folding pathway.

Conformational Sampling in the Acid-Unfolded Ensemble.

Although AABUF works well in identifying which regions along the chain tend to initiate the collapse process, the magnitude does not appear to predict the relative strengths of various interactions. Our results indicate that differences in intrinsic stabilities of nonlocal contacts are overwhelmed by the relative energetic barriers to loop closure required to create them. Consequently, localized interactions tend to be more highly populated than longer range contacts, despite having similar or lower intrinsic stabilities. Indeed, at the level of resolution of our analysis, we are unable to detect any significant differences in the intrinsic association propensities for four of the five interaction sites in acid-unfolded apoMb. This is not overly surprising because the different segments are similar in length (8–15 residues) and amino acid composition. The two regions that exhibit weaker than average association propensities, the C region and the N terminus of the G region, both have above-average local positive charge density and above-average residue-to-residue variations in AABUF, with more frequent interspersion of low AABUF residues. These characteristics would work together to disfavor both local chain compaction and long range cluster formation.

Native-Like Interactions in a Sparsely Populated Substate.

PRE data in themselves cannot easily establish the cooperativity of interactions. However, while acknowledging that coincidence of population levels does not necessarily indicate simultaneity of interactions, the fact that the probabilities of A/G, A/H, B/G, and B/H contacts are all similar (in the range of 3.30–3.7%; Table S3) strongly suggests that all contacts involving both chain termini report on a single, coalesced substate. This conjecture is further supported by the solvation factors f_S for each of the 14 spin labels (Table 1). The f_S values are only weakly correlated with the degree of solvation of the relevant side chains in the native structure (Fig. 1a) but can be fully explained if the hydrophobic core in the transiently interacting species observed by PRE is rearranged relative to the native apoMb structure to more effectively bury the highest AABUF residues. In particular, the f_S of zero for R139C* indicates that this side chain interacts strongly with the A and B regions, whereas it is distant from these regions in the native structure. The contrasting f_S values for R139C* and K140C* further indicate that this region is at least partially ordered and likely helical in a significant fraction of the collapsed substates. In contrast, the N terminus of the native H helix, which contains several residues critical to formation of the native core (most notably M131) but is otherwise poorly hydrophobic (Fig. 1b), exhibits some of the weakest PRE of any C-terminal residues in the acid-unfolded state. Indeed, our model suggests that these residues are disordered and only exhibit PRE because of covalent linkage to nearby interaction sites. The identical f_S values of E109C* and R118C* are also not consistent with tight, native-like packing—because the two residues are located on opposite sides of the native helix (Fig. 1a)—but instead support significant dynamic heterogeneity in the G region within the compact substate(s) observed herein. The moderate solvation of the L11C* and A15C* spin labels is consistent with an approximately native-like and possibly helical orientation and packing of the A region, dominated by burial of W14 and its neighboring residues. In the holoprotein structure, the side chain of R31 is packed against the G helix whereas the PRE data indicates that this side chain remains solvated in the compact substate(s) observed here; the difference can be explained by a modest rotation of the B region to more effectively bury the side chains of L29 and L32. Thus, the most compact species observed in the acid-unfolded state appears to retain a relatively native-like core that has “collapsed” in on itself to better bury the hydrophobic surface that would pack against the C-E regions in the native structure. That these transient compact states retain such a large extent of native-like contacts is of particular interest because it suggests that the specificity of contacts within the initial collapsed state, rather than its intrinsic stability, may be key in facilitating progression toward a cooperatively folded molten globule intermediate.

Materials and Methods

Preparation of Proteins.

Site-directed cysteine mutants of sperm whale myoglobin were constructed and spin labels attached as described in ref. 2. Uniformly labeled ¹⁵N and ¹⁵N/¹³C protein samples were prepared by expression in E. coli BL21-DE3 cells in M9 minimal media and purified by methods published in refs. 2 and 4. NMR samples typically contained 200 μM apoMb at pH 2.3 in 90% ¹H₂O/10% ²H₂O. The final chloride concentration was ≈200 mM in the 8 M urea samples (10) and <5 mM in the samples at pH 2.3 without urea. Reduction of the spin label to its diamagnetic state was achieved by addition of a 5-fold molar excess of ascorbic acid and incubation overnight.

NMR Measurements.

NMR experiments were carried out on a Bruker DMX750 spectrometer at 20°C (urea-unfolded) or 25°C (acid-unfolded), calibrated by using methanol (25). For measurements of paramagnetic relaxation enhancement, ¹H-¹⁵N HSQC spectra were recorded in the presence and absence of ascorbic acid. Backbone assignments were transferred from those for the wild-type protein (4, 10) and verified by using triple resonance (HCA)CO(CA)NH experiments (26). Spectra were processed by using NMRPipe (27) and analyzed with NMRView (28).