On the electronic nature of low-barrier hydrogen bonds in enzymatic reactions

Abstract

The electronic nature of low-barrier hydrogen bonds (LBHBs) in enzymatic reactions is discussed based on combined low temperature neutron and x-ray diffraction experiments and on high level ab initio calculations by using the model substrate benzoylacetone. This molecule has a LBHB, as the intramolecular hydrogen bond is described by a double-well potential with a small barrier for hydrogen transfer. From an “atoms in molecules” analysis of the electron density, it is found that the hydrogen atom is stabilized by covalent bonds to both oxygens. Large atomic partial charges on the hydrogen-bonded atoms are found experimentally and theoretically. Therefore, the hydrogen bond gains stabilization from both covalency and from the normal electrostatic interactions found for long, weak hydrogen bonds. Based on comparisons with other systems having short-strong hydrogen bonds or LBHBs, it is proposed that all short-strong and LBHB systems possess similar electronic features of the hydrogen-bonded region, namely polar covalent bonds between the hydrogen atom and both heteroatoms in question.

It has been suggested that formation of “short-strong” hydrogen bonds (SSHB) or “low-barrier” hydrogen bonds (LBHB) can stabilize intermediates and/or transition states of enzymatic reactions (1–13). Originally, the involvement of LBHB in enzymatic reactions was suggested by Cleland (1) based on the observation of unusually low hydrogen fractionation factors for certain enzymes. He realized that this physicochemical property can be understood if the potential energy surface of the hydrogen bond in question is a double well potential with a low barrier (≈2 kcal/mol) toward hydrogen transfer, thus the name “low-barrier hydrogen bond.” This description was adapted from Kreevoy and Liang (15). The idea of having a special type of hydrogen bond in certain enzymatic systems also was invoked by Gerlt and Gassman (2, 3) to explain the stabilization of various enolic intermediates of enzyme catalyzed proton abstraction from carbon acids. They proposed a bonding scenario in which the hydrogen resides midway between the oxygen of the enolic intermediate and the conjugate base of the active site catalyst (2). Cleland and Kreevoy (4) extended the proposal of LBHB as important in enzymatic systems to cover systems with enolate-types of intermediate invoked in the catalytic mechanism. They noted that, when known, these enzymes all display the unusually short heteroatom distance characterizing SSHB. Furthermore, they suggested that the bonding energy related to formation of an LBHB could be as high as 10–20 kcal/mol and that the LBHB will be essentially covalent (4). Frey et al. (5–7) found evidence, in the form of very high δ_H, for the likelihood of having an LBHB forming in the catalytic triad of a serine protease between aspartate and histidinium, which is present in the tetrahedral intermediate. They suggested that in the Asp-His LBHB, formal charges of <−1 and +1 should be assigned to Asp and His (5), hereby resulting in a more disperse charge distribution in the LBHB structure relative to a localized Asp^−… . H–His⁺ form. This lead Warshel et al. (17) to disregard LBHBs as being important in enzymatic reactions, as they proposed that electrostatic interactions alone can explain the catalytic power of the enzymatic reactions (18). It should be noted that the current generally accepted idea of “smeared” charges associated with LBHBs has so far been based purely on speculations. Kreevoy and Cleland (4) and Frey et al. (5–7) suggested that a large degree of covalency will be associated with an enzymatic LBHB, similar to what Gilli et al. (19–24) have proposed for a series of β-keto-enols.

In this paper, we discuss the electronic nature of LBHBs, as exemplified by a comparative study of the electron distribution of benzoylacetone, which is based on a very low-temperature x-ray diffraction study and on a high level ab initio theoretical study.

MODEL AND METHODOLOGY

Benzoylacetone is a β-diketone that upon enolization forms a cis-β-keto-enol structure with an intramolecular hydrogen bond, which potentially can be either asymmetrical as in 1a and 1b or symmetrical as in 1c (Reaction 1).

This molecule is a good model substrate for studying the electronic nature of a SSHB, as (i) it has a short O· · · · ·O separation of 2.502(4) Å (14), (ii) it resembles the enzymatic enolates where LBHBs have been proposed to form (2–4), and (iii) in the solid phase, the hydrogen bonded moiety is not involved in other hydrogen bonds (14). The exact position of the hydrogen atom of the intramolecular hydrogen bond was determined by low temperature neutron diffraction (14). From these measurements, it was found that the hydrogen is positioned slightly asymmetric between the two oxygen centers, closest to the phenyl-substituted carbonyl group (14), hereby establishing the nuclear environment expected for the formation of an LBHB (2, 4). High level ab initio studies at the B3LYP/6–311G(d, p) (26, 27) level of theory confirmed that the intramolecular hydrogen bond is indeed associated with a double-well potential having a low barrier toward hydrogen transfer¶ (1.7 kcal/mol from 1b to 1a, and 2.4 kcal going in the opposite direction) (25), and for example, not a single-well potential as was found theoretically for the formate–formic acid interaction (28–31). Structure 1c represents the transition state for the movement of the hydrogen atom from one oxygen center to the other in benzoylacetone. It was found that, upon inclusion of the zero-point vibrational energies, 1c became the lowest energy structure among 1a, 1b, and 1c, and thus it represents the theoretical prediction for the bonding in benzoylacetone (25). The theoretical structure is in fine agreement with the low temperature neutron structure (14).

Two methods based on analyses of the experimental and theoretical electron distributions were applied to study the electronic nature of the LBHB in benzoylacetone. First, an evaluation of the atomic partial charges of the hydrogen-bonded atoms was carried out. Secondly, Bader’s (32) topological analyses by using the atoms in molecules (AIM) theory were undertaken. The AIM theory is a quantum mechanical theory in which all topological species (atoms, bonds, rings, and cages) that constitute a structure are uniquely defined from the electron density of the molecular system. The structural elements are identified at the critical points of the electron density (▿ρ = 0), with atoms being associated to maxima, bonds and rings associated to saddle points, and cages associated to local minima in the electron distribution (32). Bader (32) has shown that the sign of the Laplacian of the electron density at a bond critical point reveals whether charge is concentrated (▿²ρ < 0) as in a covalent bonds or depleted (▿²ρ > 0) as in electrostatic bonds. Thus, the AIM theory provides a tool for characterizing the specific types of bonds present in benzoylacetone.

Experimentally, the electron density is obtained from a low temperature (8 K) x-ray diffraction experiment (14). When using the multipole method (33, 34) for description of the experimental electron density, atomic partial charges can be estimated from the monopole populations (14). Theoretically, atomic partial charges are calculated by using the Brenneman et al. (35) scheme for fitting charges to the electrostatic potential at the B3LYP/6–311G(d, p) level of theory (25). The AIM analysis was carried out by using the XD-suite of programs (36) for the experimental electron distribution; whereas for the theoretical analysis, the critical-point option of the AIM-keyword (37–44) as implemented in gaussian 94 (45) was used. For further details on the analyses, the following papers should be consulted (see refs. 14 and 25).

RESULTS

The computed theoretical net charges for the hydrogen-bonded moiety of benzoylacetone are listed in Table 1 for 1a, 1b, and 1c. To be able to make comparisons, we have included computed charges for the imaginary non-hydrogen bonded trans-β-keto-enols, 2a and 2b. These two sets of charges serve as reference points for judging the charge redistribution upon formation of the intramolecular hydrogen bond. Both experimental and theoretical atomic partial charges are found in the table for the neutron structure, 3, as measured at 20 K (14).

Table 1.

Atomic charges calculated at the B3LYP/6-311G(d, p) level of theory using Brenneman’s et al. scheme for fitting atomic charges from the electrostatic potential

Charge	H−	O2	O6
1a	0.453	−0.573	−0.573
1b	0.477	−0.571	−0.611
1c	0.490	−0.589	−0.608
2a	0.406	−0.483	−0.522
2b	0.327	−0.403	−0.527
3	0.451	−0.559	−0.593
Experiment	0.40  (3)	−0.51  (5)	−0.45 (4)

Experimental charges are included for comparison (14). The atom numbering scheme corresponds to 1a. 

The results of the AIM-analyses are listed in Table 2 and Table 3 for the electron density, ρ, and the Laplacian, ▿²ρ, respectively. Entries for the asymmetric cis-β-keto-enols (1a and 1b), for the trans-β-keto-enols (2a and 2b), the transition state (1c), and for the experimental structure (3), with both theoretical and experimental values, are listed.

Table 2.

Electron density at bond critical points found in the keto-enol fragment of molecules 1a, 1b, 1c, 2a, 2b, and 3

ρ (eÅ−3)	H1–O2	O2–C3	C3–C4	C4–C5	C5–O6	O6–H1
1a	0.419	2.530	1.930	2.171	2.137	2.136
2a	n/a	2.700	1.834	2.236	1.988	2.485
1b	2.102	2.130	2.149	1.946	2.545	0.446
2b	2.475	1.983	2.226	1.823	2.728	n/a
1c	1.240	2.324	2.050	2.062	2.360	1.160
3	1.084	2.132	2.057	2.026	2.354	0.861
Experiment	0.89  (3)	2.44  (8)	2.17  (4)	2.04  (4)	2.54  (8)	0.76  (3)

The experimental value is included for comparison (14). The atom numbering scheme corresponds to 1a. 

Table 3.

The Laplacian of the electron density at bond critical points for all hydrogen–oxygen interactions in molecules 1a, 1b, 1c, 2a, 2b, and 3

∇2Q (eÅ−5)	H1–O2	O6–H1
1a	+3.69	−5.15
2a	n/a	−6.12
1b	−5.01	+3.72
2b	−6.13	n/a
1c	−8.45	−5.65
3	−6.34	−10.91
Experiment	−9.1  (2)	−4.5  (2)

The experimental values are included for comparison (14). The atom numbering scheme corresponds to 1a. 

Electronic Nature of an LBHB.

The atomic partial charges reveal that the LBHB in benzoylacetone is a very polar bond because large partial charges are found (14). Furthermore, it can be seen in Table 1 that the theoretical and experimental methods of calculating atomic partial charges give almost quantitative agreement for the three hydrogen-bonded atoms of the neutron structure, 3, with the theoretical values being numerically slightly higher. The theoretical charges indicate that the atomic partial charges of the hydrogen bonded moiety are unaffected by the position of the hydrogen atom between the two oxygens as essentially identical charges are computed for 1a, 1b, and 1c; all of which compare well with the charges of the neutron structure, 3. However, it is interesting to note that the formation of the hydrogen bond leads to increased charges (compare 1a with 2a and 1b with 2b). A consequence of these observations is that LBHBs should not be considered as having more disperse (18) charge distributions than normal hydrogen bonds. Therefore, this generally accepted assumption is not correct.

To learn more about the type of bonds found in the hydrogen bonded portion of benzoylacetone, an AIM analysis was carried out. From the electron densities at the bond critical points of the pseudo 6-membered ring (Table 2), it is again seen that there is essentially quantitative agreement between theory and experiment as very similar numbers are found for 3 (see entry 6 and 7 in Table 2). The theoretically calculated values of the electron densities at the bond critical points all correlate well with the measured bond distances (25); the shorter the bond, the greater the electron density in the bond. This is especially true for all the oxygen–hydrogen interactions present in the analyzed molecules. An ordinary O—H bond not engaged in hydrogen bonding has a density of 2.5 e/ų (2a and 2b), whereas an O—H bond engaged in an intramolecular hydrogen bond (1a and 1b) has a decreased density of ≈2.1 e/ų. At the other extreme, normal long hydrogen bonds have densities of ≈0.1 e/ų (46). In between these extremes are the LBHB in 1c and 3 with densities of 0.8–1.2 e/ų s and the short asymmetric hydrogen bonds in 1a and 1b with densities of 0.42–0.45 e/ų. The observed changes in ρ upon formation of an asymmetric bond or an LBHB shows that charge redistribution takes place in the hydrogen-bonded moiety, but as outlined above, this redistribution does not influence the atomic partial charges of the involved atoms. Therefore, although it may be possible to account for the catalytic power of enzymes from purely electrostatic considerations (17, 18), it is probably not a realistic model due to the observed large degree of charge redistribution in the system (47, 48).

As stated above, the sign of the Laplacian at a bond critical point is a descriptor of the type of bond. The values in Table 3 show that covalent bonds are found between the central hydrogen atom and both oxygens in an LBHB, confirming the Gilli et al. (19–24) predictions for β-keto-enol systems and Kreevoy and Cleland (4) and Frey et al. (5–7) proposal of LBHB as being covalent in enzymatic reactions. The two cis-β-keto-enol isomers, 1a and 1b, both have one covalent and one electrostatic bond, as expected. The emerging description of the electronic nature of the LBHB in benzoylacetone is thus a very polar covalent bond as indicated in 4 (25). The strength of the short-strong resonance-assisted hydrogen bond is estimated to be ≈16 kcal/mol.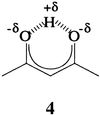

Benzoylacetone represents a globally neutral molecule, as does the proposed LBHB between aspartate and histidinium in the catalytic triad of serine proteases. Garcia-Viloca et al. (49) have calculated the electron density and the Laplacian at the two bond critical points found in the transition state for hydrogen transfer from 1-methyl imidazolium to 2,2-dichloropropionate at the HF/6–31 + G(d) level of theory, for which an LBHB is proposed to form (6). They find numbers very similar to what we find in this study for benzoylacetone [ρ: 1.147 e/ų (O||||||H)³ and 0.945 e/ų (H||||||N); ▿²ρ: −9.881 e/Å⁵ (O||||||H) and −4.338 e/Å⁵ (H||||||N)], which indicates that the type of bonds in the two systems are very similar. For a globally charged system, the LBHB in the maleate ion, Garcia-Viloca et al. (50) found properties of the electron density at the bond critical points of the symmetrically hydrogen-bonded moiety that are very similar to the globally neutral molecules (ρ = 1.215 e/ų and ▿²ρ = −10.6 e/Å⁵). This suggests that the electronic nature of a SSHB may be independent of how charges are formally assigned for the system—a conclusion that also was reached by Gilli et al. (21) based on a completely different type of analysis. An x-ray diffraction study of the succinate anion, which has a short-strong intermolecular hydrogen bond, confirms this statement because properties similar to those of the above molecules (ρ = 1.058 e/ų and ▿²ρ = −6.81 e/Å⁵) were found (51). Thus, four chemically different molecular systems, all possessing a SSHB, show very similar properties of the electron density at the bond critical points of the hydrogen-bonded fragment.

Implications for Enzymatic LBHB.

The above analysis provides evidence for the observation that all SSHB and LBHB may have very similar characteristics of the electron distribution of the hydrogen-bonded area. Therefore the findings in the present study may be extrapolated to enzymatic systems were LBHBs have been suggested. This means that an LBHB in an enzymatic active site can be expected to have covalent-bonding contributions between the hydrogen and both heteroatoms involved, as was originally suggested by Cleland and Kreevoy (4) and by Frey et al. (5–7). Our study of benzoylacetone furthermore shows that the hydrogen bonded atoms of SSHB, whether being an asymmetric or close-to-symmetric hydrogen bond, do have large atomic partial charges. It can thus be expected that enzymatic LBHBs will consist of largely charged atoms.

According to the description of LBHB as being polar covalent bonds, the large hydrogen bond energy for SSHBs and LBHBs (in benzoylacetone 16 kcal/mol) is a sum of the normal electrostatic interaction energy of a weak hydrogen bond and an additional covalent interaction energy. Warshel et al. (17, 18) have claimed, that electrostatic interactions alone can explain the catalytic power of enzymes. The present study reveals that the electrostatic contribution plays a significant role in LBHBs because the involved atoms have large partial charges, but the analysis of the charge distributions also shows that the fundamental electronic character of the two hydrogen bonds has changed to include a covalent component as well. Therefore, one should include the possibility for studying nonelectrostatic changes, such as charge-transfer and structural changes when modeling systems with SSHBs or LBHBs.

The formation of two covalent bonds to the bridging hydrogen center results in a very deshielded proton and the observed large partial charges on the hydrogen-bonded atoms. This is in agreement with the very high ¹H chemical shifts measured by NMR for protons proposed to be involved in LBHB formation (5–12). The emerging picture of LBHBs as having covalent bonds between charged atoms is thus in good agreement with this special spectroscopic characteristic of the LBHB systems. Further investigations focusing on the electronic character and energetics of SSHBs and LBHBs are in progress in our laboratories.

ABBREVIATIONS

SSHB

short-strong hydrogen bond

LBHB

low-barrier hydrogen bond

AIM

atoms in molecules