Calculation of protein–ligand binding free energy by using a polarizable potential

Abstract

The binding of charged ligands benzamidine and diazamidine to trypsin was investigated by using a polarizable potential energy function and explicit-water molecular dynamics simulations. The binding free energies were computed from the difference between the free energies of decoupling the ligand from water and protein environments. Both the absolute and the relative free energies from the perturbation simulations agree with experimental measurements to within 0.5 kcal·mol⁻¹. Comparison of free-energy components sampled from different thermodynamic paths indicates that electrostatics is the main driving force behind benzamidine recognition of trypsin. The contribution of electronic polarization to binding appears to be crucial. By computing the free-energy contribution caused by the polarization between the ligand and its surroundings, we found that polarization has the opposite effect in dissimilar environments. Although polarization favors ligand solvation in water, it weakens the protein–ligand attraction by screening the electrostatic interaction between trypsin and benzamidine. We also examined the relative binding free energies of a benzamidine analog diazamidine to trypsin. The changes in free energy on benzamidine-diazamidine substitution were tens of kilocalories in both water and trypsin environments; however, the change in the total binding free energy is <2 kcal·mol⁻¹ because of cancellation, consistent with the experimental results. Overall, our results suggest that the use of a polarizable force field, given adequate sampling, is capable of achieving chemical accuracy in molecular simulations of protein–ligand recognition.

Specific recognition of ligands by proteins is at the core of many crucial biological functions and systems such as enzyme catalysis and intracellular signaling. Binding affinity characterizes the strength of such recognition. With the recent advancements in computing, prediction of the binding affinity based on physical principles of molecular interaction has come to the forefront of active research and has been the subject of regular reviews (1–5). All-atom molecular dynamics (MD) simulation with explicit solvent, coupled with efficient free-energy sampling algorithms, can potentially offer accurate prediction of binding free energies of ligands to proteins (5). Common free-energy simulation algorithms include the double-decoupling method (DDM) and potential of mean force approach (PMF). Free-energy perturbation (FEP), thermodynamic integration (TI), or umbrella sampling can be used to compute free-energy differences in either DDM or PMF. It has been argued that DDM is problematic for charged systems, because the binding free energy is computed as a small difference between two large solvation energies in water and in protein (6). However, the PMF approach does not quantify absolute solvation energies of ligand, which makes it difficult to detect potential problems in treatment of long-range effect and boundary conditions (7, 8). A comparison of PMF and FEP in ion channel study indicated the former suffered more seriously from hysteresis (9). Alternatives to free-energy pathway calculations include linear response analysis (LRA) (10) and linear interaction energy (LIE) (11), where only the ligand-bound and unbound states are simulated. A semimacroscopic approach based on Protein Dipoles Langevin Dipole (PDLD/S) was applied previously in LRA to further reduce the computational cost (12). Recent reviews have summarized some of the advantages and drawbacks of LRA and LIE (5, 13).

MD/FEP methods have been used to calculate the absolute binding free energies of different protein–ligand systems, such as L99A mutant of T4 lysozyme with benzene (14–16), tyrosyl-tRNA-synthetase with tyrosine (14), FKBP with several ligands (17, 18), and human Lck SH2 domain with phosphotyrosine peptide (6), to name a few. Strong correlation between computed binding free energies and experimental values has been reported for a series of ligands binding to FKBP and lysozyme. Nonetheless, the calculated absolute binding free energies can still deviate from experimental measurement by several kilocalories. There has been a limited number of simulation studies of highly charged systems. Recently, the PMF approach was used successfully in calculating the binding free energies of a charged peptide binding to the SH2 domain (6).

It has been recognized that the bottlenecks to achieving chemical accuracy in molecular simulations are the underlying physical models and the sampling convergence (5). The current-generation common force fields employ fixed atomic charges and therefore lack the ability to respond to the actual local electrostatic environment. Explicit treatment of polarization to provide realistic electrostatic representation dates back to Warshel and Levitt's use of atomic induced dipoles in the enzyme reaction study (19). Polarized force field (PFF) was later applied to estimating binding free energies in systems such as trypsin, antibody–antigen, and DNA polymerase (10, 20, 21). History and development of PFF have been covered in recent reviews (13, 22). Aside from the physical potential, sampling convergence remains an enormous challenge in binding simulations with atomic force fields, especially when a large number of conformational and other degrees of freedom are involved (23).

In this study, we report the calculation of the absolute and relative binding free energies of trypsin with two charged ligands from molecular dynamics simulations with a polarizable force field, in which the electrostatics was represented by atomic multipoles and induced dipoles. Trypsin is a serine protease that has been well studied, both experimentally and computationally. Benzamidine and its derivatives are well characterized inhibitors of trypsin that form a salt bridge with the D189 aspartic acid in the S1 site. Benzamidines carry net charges and are relatively small and rigid. This allows us to achieve adequate sampling and focus on the application of the polarizable potential in the calculation of binding free energies. Besides comparing calculated free energy with experimental literature, we also examined the role of electrostatics and polarization in ligand–protein binding.

Results and Discussion

Absolute Binding Free Energy.

To evaluate the absolute binding free energy of benzamidine to trypsin, the free energies of decoupling benzamidine from water and trypsin-water were computed from MD simulations, respectively. The decoupling free energies were evaluated from a path in which the electrostatic and then the van der Waals (vdW) interactions between benzamidine and its environment were turned off in steps. A soft-core version of buffered-14-7 potential with n = 5/α = 0.7 (see Eq. 2) was used in the vdW decoupling. A harmonic potential (k = 20 kcal·mol⁻¹·Å⁻²) was used to restrain the benzamidine to the trypsin.

Figs. 1 and 2 show the decoupling free energies of the ligand–water system and the ligand–protein system, respectively. The first 100 ps of MD trajectories in all simulations were considered as system equilibration and subsequently ignored in the free-energy analysis. In addition to calculating cumulative averages, running averages were computed from 100-ps blocks of trajectories to illustrate the fluctuation. Note that the running averages do not reflect the statistical error in the final free energy. The free energies of the ligand–water system are reasonably converged in 1 ns (Fig. 1), whereas the ligand–protein free energy took longer to settle down, even with a restraining bond between the ligand and protein (Fig. 2b). This is expected because trypsin–water is much more complex than bulk water and thus requires longer simulations. For both ligand–water and ligand–protein, the electrostatic free energy fluctuates much less than the vdW component. This is because full van der Waals interactions are present during electrostatic decoupling, which confines benzamidine to the pocket with low mobility. In contrast, as the vdW interactions between benzamidine and its environment were gradually decoupled, the benzamidine molecule sampled greater and greater regions of space, coming in close contact with and eventually penetrating the surrounding water and protein atoms. Additionally, water molecules were found to occupy the pocket after ≈500 ps as benzamidine was annihilated from the S1 pocket of trypsin. All of these factors may contribute to the wild fluctuations in the vdW free energy.

Fig. 1.

Electrostatic (a) and van der Waals (b) decoupling free energies (kcal·mol⁻¹) of ligand–water system. The dashed line with cross markers is the running average of every 100-ps block. The solid line with square markers is the cumulative average. Time is in picoseconds.

Fig. 2.

Electrostatic (a) and van der Waals (b) decoupling free energies of ligand–protein system (kcal·mol⁻¹). The dashed lines with cross markers are the running average of every 100-ps block. The solid lines with square markers are the cumulative average. Time is in picoseconds.

The electrostatic and the van der Waals decoupling free energies were determined to be 1.27 ± 0.2 kcal·mol⁻¹ and −2.42 ± 0.4 kcal·mol⁻¹, respectively, for benzamidine–water, and 7.78 ± 0.2 kcal·mol⁻¹ and 3.72 ± 0.3 kcal·mol⁻¹ for benzamidine–trypsin (Table 1). Thus, the free energy of benzamidine binding to trypsin is −6.78 kcal·mol⁻¹ (see Eq. 4), which includes a correction of 5.87 kcal·mol⁻¹ for the bias due to the restraint. Several experimental binding free energies were reported, ranging from 6.3 to 7.3 kcal·mol⁻¹ (24–27, 53). It is not uncommon for the experimental binding affinity to vary up to a factor of 10 (1.3 kcal·mol⁻¹), depending on the assay conditions (27), or the specific experimental method such as spectrophotometry (27) or crystallography (53).

Table 1.

Absolute free energy of benzamidine binding to trypsin computed by using different force constants and soft-core coefficients

Restraint constant, kcal·mol−1·Å−2	Soft core	ΔAwat(L→0)*		ΔApro (L→0)*		Restraint correction	ΔAcalc	ΔAexp
		ΔAele	ΔAvdw	ΔAele	ΔAvdw
20	0.5/4	1.27 (0.2)	−2.27 (0.4)	7.78 (0.2)	3.42 (0.3)	5.87	−6.33	−6.3†
								−7.3‡
								−6.4§
								−6.7¶
20	0.7/5	1.27‖	−2.42 (0.4)	7.78‖	3.72 (0.3)	5.87	−6.78	–
40	0.7/5	1.27‖	−2.35**	7.57 (0.2)	4.56 (0.2)	6.48	−6.73

*The numbers in parentheses are the standard errors.

^†ref. 27.

^‡ref. 25.

^§ref. 53.

^¶ref. 26.

^‖The value is taken from the row above.

**Averaged from the two ligand–water vdW decoupling free energies in the rows above.

The free energy of decoupling benzamidine from water appears to be much lower than the expected solvation free energy of a charged molecule, which is typically several tens of kilocalories per mole. As noted in Methods, we decoupled the electrostatic interaction by zeroing out the atomic multipoles and polarizabilities of the benzamidine; and the end states of the ligand–water and ligand–protein simulations feature a “ghost” benzamidine molecule without intramolecular electrostatic interactions. We have determined that the recharging free energy of benzamidine in vacuum is 46.92 kcal·mol⁻¹. Combining this value with the decoupling energy above, the electrostatic solvation free energy of benzamidine in water becomes −48.19 kcal·mol⁻¹ (Table 2). Thus, a large portion of solvation free energy of charged benzamidine (both in water and trypsin environments) is actually not responsible for driving its binding to trypsin.

Table 2.

Absolute solvation free energies of benzamidine and diazamidine in water and trypsin

	Protein		Water		Binding
	ele*	vdw†	ele*	vdw	ele	vdw	Total
Benzamidine	−54.60‡	2.17‡	−48.19	2.35‡	−6.41	−0.18	−6.59
Diazamidine§	−75.56	−2.17	−69.38	−2.97	−6.18	0.80	−5.38

*Intramolecular contribution of −46.92 kcal·mol⁻¹ is included.

^†Restraint correction is included in the vdW component.

^‡Averaged from values in Table 1.

^§Computed based on the relative binding free energy.

Effect of Soft-Core vdW Potential.

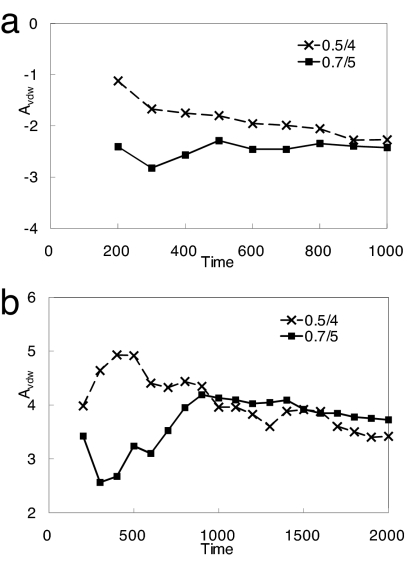
Free energy is a state function, and therefore independent of the sampling path. We investigated two soft-core modifications of the buffered-14-7 function (see Eq. 2), n = 5 and α = 0.7, in the calculation of vdW decoupling free energy in ligand–water and ligand–protein. As shown in Fig. 3, the free energies computed by using the two potentials converge toward each other after ≈1 ns of simulation. By using n = 4/α = 0.5_, the van der Waals decoupling free energies were found to be −2.27 ± 0.4 and 3.42 ± 0.3 kcal·mol⁻¹ for ligand–protein and ligand–water, respectively, compared with −2.42 ± 0.4 and 3.72 ± 0.3 kcal·mol⁻¹ from simulations with n = 5/α = 0.7 (Table 1). The differences between the two sets of values are comparable to the statistical error.

Fig. 3.

Comparison of vdW decoupling free energies (kcal·mol⁻¹) of ligand–water (a) and ligand–protein (b) systems with different soft-core pathways. All lines are cumulative averages. The dashed lines with cross markers are from n = 4/α = 0.5 simulations. The solid lines with square markers are from n = 5/α = 0.7 simulations (the same data as in Fig. 2b). Time is in picoseconds.

Free Energy as Driving Force for Binding.

It is possible to decode the physical driving force behind benzamidine binding to trypsin because our calculations offer detailed information on atomic interactions that are not easily measurable by experimental procedures. However, this is complicated because of the presence of the restraint between benzamidine and trypsin. We overcame this complication by comparing simulation results from different restraints.

Besides using a force constant of 20 kcal·mol⁻¹·Å⁻² for the restraint, we performed another set of simulations of trypsin–benzamidine with doubled restraint strength (k = 40 kcal·mol⁻¹·Å⁻²). The electrostatic and the vdW decoupling free energies from the two sets of simulations were compared in Fig. 4. The electrostatic decoupling free energy is 7.57 ± 0.2 kcal·mol⁻¹ from the simulation with k = 40, compared with 7.78 ± 0.2 kcal·mol⁻¹ when using the weaker restraint (Table 1). This similarity indicates that the restraint strength has little effect on the electrostatic decoupling. This is not surprising because benzamidine is likely to be confined within the trypsin-binding pocket by vdW interactions at this stage. The restraint does not truly come into effect until the vdW interactions are turned off. Indeed, the van der Waals free energies differ by 0.8 kcal·mol⁻¹ depending on the restraint strength. However, the correction to the binding free energy caused by the restraint also varies as the restraint strength increases from 20 to 40 by a similar amount (0.6 kcal·mol⁻¹). Based on the preceding observation, we argue that the restraint affects mostly the vdW decoupling such that the correction should be applied mainly to the vdW decoupling free energy of benzamidine–trypsin. After taking these corrections into account, the van der Waals free energies of decoupling benzamidine from trypsin become −2.3 kcal·mol⁻¹ (averaged over values from two soft-core vdW potential at k = 20) and −1.9 kcal·mol⁻¹ (k = 40). These quantities are fairly close to the vdW decoupling free energy of ligand–water (−2.27 and −2.42 kcal·mol⁻¹, depending on the soft-core potential). In contrast, the electrostatic decoupling free energy of ligand–water and ligand–protein differ by −6.4 kcal·mol⁻¹ on average, which amounts to almost all of the binding free energy. Thus, we conclude that the electrostatic interaction is responsible for the binding of benzamidine to trypsin.

Fig. 4.

Comparison of electrostatic (a) and van der Waals (b) decoupling free energies (kcal·mol⁻¹) of benzamidine–trypsin system by using different force constants for the restraint that confines the benzamidine to trypsin. The dashed lines with cross markers are the cumulative averages from a force constant k = 20 kcal·mol⁻¹·Å⁻², whereas the solid lines with square markers are from a force constant k = 40 kcal·mol⁻¹·Å⁻². Time is in picoseconds.

As shown in Fig. 4b, the vdW decoupling free energy with stronger restraint (k = 40) seems to stabilize much quicker than that with k = 20. Nonetheless, it still drifts slightly over the 2-ns simulation timeframe. We extended the simulation to 3 ns, during which the free-energy value changed by −0.31 kcal·mol⁻¹. Therefore, the stronger force constant may offer a quicker estimation of the binding free energy, although long simulations (≈3 ns) are still necessary to obtain accurate results.

In Table 1, we summarized the three sets of the binding free energies computed by using different soft-core vdW and restraint strengths. Consistency among the simulation results supports the premise that the sampling is adequate and the results are well converged, owing to the presence of the restraint and to the fact that benzamidine is small and rigid. Our best estimate of the absolute binding free energy of benzamidine–trypsin is therefore 6.6 kcal·mol⁻¹, averaged over all simulation results. The agreement between the calculated and experimental values is well within chemical accuracy.

Polarization Effect.

A unique feature of the present model is the explicit treatment of dipole polarization, which allows the electrostatics to respond to the environment, be it water or protein. It was suggested that accounting for polarization improves the transferability of a force field (28), which would be critical for transferring ligand from bulk water into the protein. It is therefore of interest to examine the effect of polarization on the thermodynamics of benzamidine binding to trypsin. We turned off the dipole induction between benzamidine and its environment by using free-energy perturbation to compute the “polarization free-energy” in both bulk water and trypsin. Note that there is still polarization present between water–water and trypsin–water, although both water and trypsin are unable to feel the electric field due to benzamidine and vice versa. The free-energy change caused by the removal of the polarization between benzamidine and water is 4.49 kcal·mol⁻¹, and −22.37 kcal·mol⁻¹ between benzamidine and trypsin. Not only are the magnitudes dramatically different, the sign is also opposite. Although polarization seems to enhance the solvation of benzamidine in water, it weakens the association between benzamidine and trypsin. Overall, the polarization works to diminish the effect of permanent electrostatics in driving the binding of benzamidine to trypsin.

Turning on polarization leading to an increase in the energy of the protein–ligand complex may appear counterintuitive. Indeed, polarization energy always lowers the “total” system energy by making a negative contribution. However, the polarization energy of the complex became less negative when the polarization between benzamidine and trypsin–water was present. In other words, the gain in electrostatic energy because of permanent electrostatic interactions, e.g., salt bridges, is counterbalanced by the loss in the polarization energy. The local polarization response to the association of two charged entities is to screen the electrostatic interactions, similar to the dielectric effect of water screening charge interactions. To verify this phenomenon, we computed the total dipole moment of the carboxyl group (CO₂⁻) of trypsin's aspartic acid D189, which forms a salt bridge with benzamidine, before and after polarization was turned on. Consistent with our observation of energy, the dipole moment did decrease by 0.1 D when polarization was present.

In our model, polarization energy between benzamidine–water and benzamidine–trypsin differs by 27 kcal·mol⁻¹. Our results agree with earlier findings that electrostatics is sensitive to local environment. Calculations by Lee et al. (10) showed that the polarization energy in water and antibody–antigen complex varied by as much as 8 kcal·mol⁻¹. A quantum mechanics/molecular mechanics (QM/MM) study of HIV-1 protease-inhibitor binding (29) suggested that polarization contributed to approximately one-third of the total electrostatic interaction energy.

However, the artificial model we created by turning off polarization is not equivalent to fixed-charge-based force fields. Previous LIE studies of trypsin–benzamidine using fixed-charge potentials reported electrostatic contribution to the binding free energy to be between −4.9 and −6.4 kcal·mol⁻¹ (30–32). The values are close to −6.5 kcal·mol⁻¹ obtained in this study, although the electrostatic solvation energies of benzamidine in water differ from our values by −4 to −17 kcal·mol⁻¹ (Table 2). This suggests that it is possible for fixed-charge models to implicitly include the overall polarization effect in the binding equilibrium. Direct comparisons of polarizable and nonpolarizable force fields in the free-energy pathway calculations will perhaps offer further insight. It has also been discussed previously that unless divalent ions are involved (13) or binding occurs at the protein interior (19), polarization plays a secondary role and may be absorbed by effective parameterization of fixed charges.

Relative Binding Free Energy.

In addition to simulating benzamidine, we also calculated the relative binding free energy of another ligand, diazamidine (Fig. 5). Diazamidine is a benzamidine derivative with the phenyl ring replaced by a 1,3-diazine (pyrimidine). In benzamidine, there is essentially one internal rotatable bond linking the aromatic ring and the amidine group (C_a–C_i). In Fig. 6, the gas-phase QM (MP2/6–311++G(2d,2p)) conformational energy profiles about this bond have been plotted for both benzamidine and diazamidine. The minimum energy occurs at 45° for benzamidine and at 0° for diazamidine. Most interestingly, the rotational barrier increases by a factor of 4 from benzamidine to diazamidine, implying a double-bond nature of the C_a–C_i bond in the latter. Although the conformational flexibilities of the two ligands are dramatically different, we have adopted a generic torsional energy parameter, E_tor = 2.7*(1 − cos 2ϕ) kcal·mol⁻¹, for both molecules. The same parameter is also used for the C_ε–C_ζ–O–H torsion in AMOEBA tyrosine. As shown in Fig. 6, the conformational energies computed by AMOEBA are consistent with the QM results. The locations of minima and maxima are well reproduced. The rotational energy barrier of diazamidine is replicated almost exactly, whereas the barrier for benzamidine is lower in our model. In AMOEBA energy profile, the torsion potential contributes to <30% of the rotational barrier in diazamidine. The majority of the conformational energy arises from electrostatic and vdW interactions. This illustrates that transferability of torsion potentials requires a physical treatment of intramolecular nonbonded interactions.

Fig. 5.

Chemical structure of two charged ligands of trypsin: benzamidine (Left) and diazamidine (Right).

Fig. 6.

AMOEBA and QM potential energy (kcal·mol⁻¹) with respect to the rotation about the C_a–C_i bond (degrees) for the two ligands of trypsin: benzamidine (Benz) and diazamidine (Diaz). The C_a–C_i bond connects the aromatic ring and the amidine group.

We calculated the binding free energy of diazamidine by perturbation from benzamidine. Two sets of MD simulations were performed in ligand–water and ligand–protein systems where benzamidine was mutated into diazamidine. No restraint was used between trypsin and ligands. The perturbation was done by changing the parameters involved in the C→N mutation in several steps (electrostatic, vdW, two bonds, and one angle). A new set of atomic multipoles was derived for diazamidine from QM. The hydrogen atoms bonded to the mutated phenyl carbon atoms were turned into dummies (no nonbonded interactions with all other atoms). The free-energy change on mutating benzamidine into diazamidine in bulk water was −26.51 ± 0.5 kcal·mol⁻¹, whereas the free-energy change in trypsin was computed to be −25.30 ± 0.3 kcal·mol⁻¹. Approximately 80% of the free-energy changes are due to electrostatics. We repeated the calculation where polarization between ligand and its environment was turned off. We observed a similar difference in the diazamidine polarization free energies in water (5.56) and trypsin (−19.80), compared with 4.49 and −22.37 kcal·mol⁻¹ obtained for benzamidine. In addition, the molecular polarizability of benzamidine, 13.8 ų, is only slightly greater than that of diazamidine, 12.6 ų. These results imply that it is primarily the permanent electrostatics that differentiates between benzamidine and diazamidine in binding to trypsin.

The calculated binding energy of diazamidine is thus weaker than that of benzamidine by 1.21 kcal·mol⁻¹, compared with the experimental value of 1.59 kcal·mol⁻¹ (33). Note that diazamidine was solvated much more favorably than benzamidine in both water and trypsin. The total solvation free energy of diazamidine in water is −72.35 kcal·mol⁻¹ (Table 2), similar to that of a potassium ion (34). The 1.21 kcal·mol⁻¹ difference was further decomposed into its electrostatic (0.11 kcal·mol⁻¹), vdW (0.98 kcal·mol⁻¹), and geometric (0.12 kcal·mol⁻¹) components. These results indicate that vdW is actually the main cause for the drop in the binding affinity, because the large free-energy changes due to electrostatics cancel out between water and trypsin–water environments.

Conclusion

A polarizable force field was applied to compute the binding affinity of a positively charged ligand and its analog to protein. Parameters were either directly derived from QM or transferred from the protein force field without modification or recalibration. Molecular dynamics simulations were performed with double decoupling of benzamidine from both water and trypsin binding site with free-energy perturbation. Different thermodynamic sampling paths were used by varying the softness of vdW potential and the restraint strength, and the resulting free energies were consistent. The computed absolute binding free energy is well within experimental accuracy.

Our results indicate that the electrostatics is the driving force for benzamidine binding to trypsin. We have further evaluated the role of polarization in binding by “turning off” the dipole induction between the ligand and its environment. It was found that polarization response varies drastically depending on the nature of the environment, and its contribution to the decoupling free energy does not simply cancel between water and protein. As a result of this finding, we believe that it is critical to treat polarization explicitly to achieve chemical accuracy in predicting the binding affinity of charged systems.

We also evaluated the relative binding free energy of a second ligand, diazamidine, with a pyrimidine group in place of the phenyl ring of benzamidine. On mutation from benzamidine to diazamidine, the binding weakens by 1.21 kcal·mol⁻¹, consistent with 1.59 kcal·mol⁻¹ measured by experiment. Nevertheless, our calculations show that the changes in the solvation free energy in both water and trypsin complex are actually tens of kilocalories. It is the cancellation between the water and trypsin that leads to the subtle change in the binding energy.

In summary, electrostatics and polarization play important roles in molecular recognition and need to be accounted for in quantitative modeling. Our study demonstrates that chemical accuracy in predicting protein–ligand binding free energy can be achieved with a polarizable potential energy function when adequate sampling is possible.

Methods

Potential Energy Model and Ligand Parameterization.

The potential energy of the system (protein, water, and ligand) is given by

The electrostatic contribution consists of permanent and polarized (by atomic-induced dipole) components (22, 35, 36). The van der Waals interaction is described by a buffered-14-7 function (37). The valence terms consist of typical harmonic function for bond stretching, angle bending, three-term Fourier torsional potential, and out-of-plane term for trigonal centers, as in the MM3 potential by Allinger and coworkers (38).

Previously, a potential, AMOEBA, based on this model has been developed for water (36, 39), ions (34, 40, 41), and organic molecules and peptides (22, 35). Independent studies using AMOEBA have also been reported (42–45). Parameters for proteins are available with the TINKER modeling package (46). In the current work, the AMOEBA potential was used for trypsin without modification. For the ligand, the electrostatic parameters were derived from QM, whereas vdW and other parameters were transferred from AMOEBA protein potential. The details of parameterization and ligands parameters are provided in the supporting information (SI) Dataset S1.

Absolute Binding Free Energy from Double-Decoupling Simulations.

The absolute free energy of benzamidine binding to trypsin was calculated by using the double-decoupling method by “disappearing” the ligand in both water and solvated protein complex in two sets of simulations. The electrostatic interactions were decoupled in 10 steps by scaling down ligand atomic multipoles and polarizabilities linearly. Similar thermodynamic cycles were adopted in previous studies where atomic charges were zeroed out (10, 21). It is worth noting that scaling the ligand electrostatic parameters turns off electrostatic interactions between the ligand and its environment, and within the ligand, resulting in seemingly small decoupling energies (Table 1). To evaluate the complete ligand solvation energy (Table 2), the ligand was recharged in vacuum after being decoupled from its environment. However, the recharging energy is identical for both ligand–water and ligand–protein, and hence makes no contribution to the binding free energy. The recharging in vacuum was done by scaling the multipoles and atomic polarizabilities back to their full values in six steps linearly. A time step of 0.1 fs was used, with polarization convergence set to 1 × 10⁻⁵ D per atom.

VdW interactions between the ligand and environment were decoupled by directly modifying the pairwise interactions. To avoid singularity at small-vdW interaction distances, a situation where ligand atoms are in close contact and vdW energy approaches infinity, we replaced the buffered-14-7 vdW function with a soft-core modification (47):

At λ = 1, Eq. 2 reduces to the original buffered-14-7 function. By varying λ from 1.0 to 0.0, vdW interactions between ligand and its environment were turned off linearly in 10 uniform steps.

MD simulations were performed in parallel for all steps along the decoupling pathway. The SANDER executable from the AMBER package (v. 9) was used (48). The benzamidine–trypsin complex (1BTY) was placed in a periodic octahedral water box of 2,222 water molecules. The initial dimensions of the cube that encloses the octahedron were 50 Å on each side. Particle Mesh Ewald (49) was used to compute electrostatic interactions, with a real-space cutoff of 7.0 Å. Further details of MD simulation are given in the SI Text.

A harmonic virtual bond was used to restrain the ligand to the protein pocket during the decoupling process (14, 50):

where k is the force constant. The positional fluctuation of benzamidine in the binding pocket of trypsin was measured from 100-ps MD simulations without restraint. A force constant of 20 kcal·mol⁻¹·Å⁻² was subsequently obtained from k = 3RT/〈δr²〉, where δr is the atomic position fluctuation.

The final binding free energy was calculated from the difference between the decoupling free energies in both water and protein–water environments (50, 51):

A correction was made to the final binding free energy to remove the bias introduced by the harmonic restraint, −RT ln(C°V) where C° is the standard concentration and V is the sampling volume of the ligand under the restraint. The correction term amounts to 5.87 kcal·mol⁻¹ for k = 20 kcal·mol⁻¹·Å⁻², and 6.48 kcal·mol⁻¹ for k = 40 kcal·mol⁻¹·Å⁻².

Free-Energy Analysis.

The free-energy changes between adjacent steps were computed by using the Bennett acceptance ratio method (BAR) (52). The free-energy change between simulations λ_i and λ_i+1 was computed iteratively by using equation 12 from ref. 52. The statistical error of estimated free energy between successive steps was computed from equation 10 in ref. 52. The total statistical error in decoupling free energy is computed as the sum of the errors from individual steps.

Polarization Free Energy.

We computed the free energy caused by the induction between the ligand and its environment. The polarization between ligand and surrounding atoms was turned off by scaling the damping coefficient from the original 0.39 (36) to 0 in 5 steps (0.39, 0.039, 0.0039, 0.00039, 0). The polarization within water or protein–water remained unchanged. A 500-ps MD simulation run was carried out at each step. Because dipole induction is short-ranged, a cutoff of 14 Å and 8 Å was used for damping in protein and in bulk water, respectively.