Explaining a complex living system: dynamics, multi-scaling and emergence

Abstract

Complex living systems are difficult to understand. They obey the laws of physics and chemistry, but these basic laws do not explain their behaviour; each component part of a complex system participates in many different interactions and these interactions generate unforeseeable, emergent properties. For example, microscopic interactions between non-living molecules, at the macroscopic level, produce a living cell. Here we discuss how to explain such complexity in the format of a dynamic model that is mathematically precise, yet understandable. Precise, computer-aided modelling will make it easier to formulate novel experiments and attain understanding and control of key biological processes.

1. Explanation

Science seeks explanations. To explain, according to the dictionary, is to relieve an idea, event or object of its obscurity, complexity or difficulty. In other words, to explain is to make the thing simple. The root meaning of explanation derives from the Latin planus, which denotes a plane, a flat and even surface (Oxford English Dictionary 1989). Thus, one might say that the idea of an explanation is to connote the plain and simple, the uncomplicated two-dimensional. The English word plan also derives from the same Latin planus. Plans need to be dependable, unchanging and plain—free of unnecessary complications. Classically, an ideal scientific explanation reduces the apparent complexity of nature to a smooth plane of immutable natural laws (Popper 2000).

The living organism, however, resists smooth explanations (Fleck 1979; Efroni & Cohen 2002). Biology has done well in its plan to carve living systems into their component parts, but the reductionist program has not uncovered the fundamental laws from which we can deduce how a particular living system actually works. A cell cannot be reduced to a few formative principles, in the way, for example, the behaviour of the Solar System can be reduced to the laws of gravity and motion (Cohen 2000). We even find it difficult to assemble the great amounts of experimental data into an understandable whole. Most would agree that computer-assisted computational tools are needed to deal with the data in hand (Harel 2003). One's choice of informatic approach, however, depends on one's view of the organism.

2. Transformation

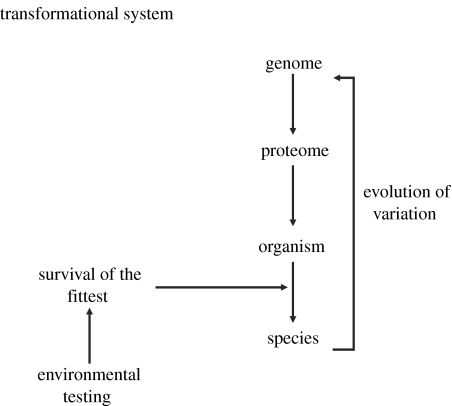
The discovery that DNA embodies the genetic code has drawn attention to DNA both as the cell's primary reservoir of information and as the informatic vehicle for evolutionary change (Mayr 1961). Biologic explanations often start with DNA: biological information is seen to originate in the genome, and this genomic DNA information is translated, by the way of RNA transcripts, into the diversity of expressed proteins—the proteome. The proteome then fashions the phenotype that defines the functioning organism. The genome, from such a viewpoint, appears as the master plan—the explanation—that encodes the organism (Mayr 1961). This view has motivated many to develop bioinformatic algorithmic methods: first, to read the genetic program; second, to decipher how genetic information is transformed into a phenotype; and third, to discover how natural selection of the more fit phenotypes, in turn, feeds back to influence the frequencies of particular genotypes, and thus drive evolution; for example, see Mossel & Vigoda (2005). The final incarnation of DNA information is the transformation of biological processes into ideas by human minds (exemplified by the way scientists do experiments, derive conclusions and write papers; Cohen 2006). In the parlance of system design, DNA-based informatics sees the organism as a transformational system (Harel & Pnueli 1985): the organism transforms DNA sequence information, the genetic ‘program’, into its phenotype, in a series of sub-transformations. Figure 1 depicts this cyclical transformation of DNA information. The explanation of the living system, from this viewpoint, is obtained not by reducing its complexity to a simple underlying ‘one-dimensional’ genetic code, but rather by reducing its complexity to an orderly, sequential transformation of information from genes to phenotypes (Mayr 1961). This transformational plan is not static, but homeostatic—the transformation of information from genome to phenotype, with the help of controlling feedback loops, generates the evolution of a stable, balanced adaptation of the living system to its changing environment (Segel & Bar-Or 1999).

Figure 1.

Life as a transformational system. In this scheme, the information encoded in the genome—the DNA—is transformed into the proteome—functional proteins—that, in turn, generate the organism and the species. The fitness of the organism and the species in the environment feed back to select better-adapted genomes and evolution results.

3. Reaction

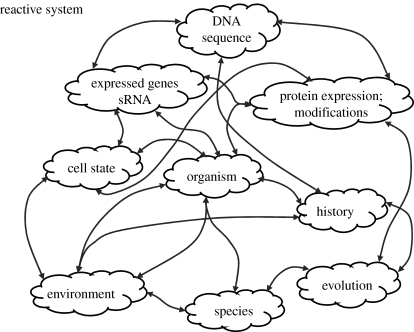
But there is another way of explaining the living system; not as a hierarchical, sequential transformational system, but as a highly concurrent reactive system (Harel & Pnueli 1985; Harel 2003). A reactive system, in contrast to a transformational system, does not behave according to a pre-programmed chain of linked instructions. Rather, such a system reacts in parallel to many concurrent inputs, and its behaviours, outputs and effects, are not just a function of the values of its inputs but also of their variety, of the order in which they arrive, of their timing, of their arrival speeds and so forth. A reactive system expresses a dynamic narrative in which the DNA code is one of the many formative inputs (figure 2). Structural proteins, enzymes, carbohydrates, lipids, intracellular signals, hormones and other molecules play key roles in forming and informing the system. The environment of the living system is a most critical source of information (Cohen 2006). True, DNA serves as a special repository of information because it is replicated and transmitted across generations, but DNA is meaningless without the proteins and other molecules that selectively activate segments of the DNA sequence in variable and alternative ways to create genes. The activation of specific genes emerges from the dynamic state of the cell. One could argue that DNA is just as much a servant of the cell's state as it is the cell's master; there is no hierarchical master plan (Cohen & Atlan 2006).

Figure 2.

The living organism as a reactive system. According to this view, the cell, the organism and the species are not mere sequential transformations of information encoded in the genome—a DNA master program. Living cells, organisms and species emerge from a web of ongoing concurrent interactions of various entities and processes; DNA is only one of the many participating informational entities.

Note that, unlike a transformational system, a reactive system does not seek equilibrium, has no set point and no state of rest (Cohen 2000). A reactive system holds itself together as a system just by reacting. A reactive system succeeds not by reaching homeostasis; a brain in homeostasis is clinically dead. A reactive system succeeds by being both robust and resilient. The reactive system responds to simultaneous perturbations and continues to survive; thanks to its reactive dynamics. It is true that organisms feature sub-systems that can be described nicely by homeostatic principles; some examples are the thermoregulatory system that maintains your internal temperature at 37°C, your water balance system and blood glucose regulation. But these systems act only like the transformational systems when viewed as a whole; internally, each of these systems is fashioned by collectives of concurrently reactive, never-resting cells.

4. Emergence across scales

Reactive systems call our attention to their emergent properties. An emergent property of a system is a behaviour of the system, taken as whole, that is not expressed by any one of the lower-scale components that comprise it. Life, for example, is an emergent property; none of the component molecules of a cell are alive, only a whole cell lives. Emergence is difficult to define in biological terms. A recent survey lists five different definitions of emergence (Deguet et al. 2006). The notion of ‘levels’, however, is shared by all the five definitions (Deguet et al. 2006). Emergence, in other words, is a matter of scale.

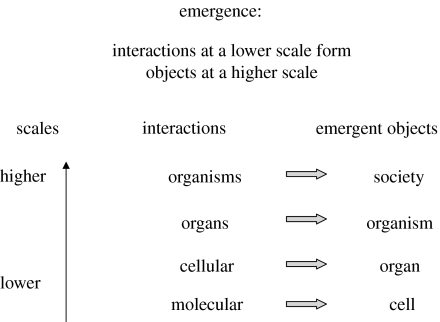
A cell emerges from the structured interactions of the molecules that comprise the cell. But the cell is orders of magnitude larger than its component molecular interactions. Obviously, you cannot see a cell from the inside at the molecular scale. The cell emerges only when you step back—zoom out—and look at the cellular system at a scale appropriate to seeing an entire cell. The cell emerges from its component interactions at the scale at which the cell functions as an object with its own interactions with other cells and molecules. In other words, interactions at one scale create objects at a higher scale; that is, transition from interaction to object is the essence of emergence (figure 3). Molecular interactions create higher-scale cells, cellular interactions create higher-scale organs, and so on from organisms to societies. The microscopic activities of your neurons, for example, give rise to the macroscopic behaviour of your brain only when we view the brain; at lower scales of observation we see only cells or molecules. Indeed, reading this article emerges at the scale of a whole human (who has learned to read) from underlying interactions at the cellular scale of eye and brain. Obviously, the capacity to read cannot be deduced merely by cataloguing all the neurons and their connections in your eye and brain. A human brain at the neuronal scale looks pretty much like the brain of a chimpanzee, and the DNA of chimpanzees and humans differ by only a few per cent (Olson & Varki 2003). But still only humans will read this article; reading emerges from human cultures that have used human brains to invent reading.

Figure 3.

The emergence of objects. Objects emerge at higher scales from interactions at lower scales. Molecular interactions at one scale give rise to a cell at a higher scale: interactions between cells generate an organ; interactions between organs generate an organism; and interactions between organisms generate a society.

A major goal of systems biology is to learn how the concurrent reactions and interactions of the lower-scale components of a cell, organism or society generate emergent properties visible at higher scales and higher layers of reality. In particular, we want to know about the factors responsible for a system's robustness (which genes, for example, can be knocked out without changing the phenotype and which cannot) and for a system's resilience (which molecules are critical in controlling the system's behaviour). We would like to know, for example, which neuronal interactions generate reading.

The larger-scale system we need for observing whole cells, for example, can be varied according to the objective of the study; we can observe cells through an electron microscope, through their secretions, shape or movement, through their interactions in tissue culture, in an organism, and so forth. Likewise, the organism emerges when we observe collections of cells at a scale at which the collective—the organism—performs collective interactions with other organisms (Cohen 2006). Biologic entities, like Russian Babushka dolls, are formed by embedded interactions at various scales and various layers. Interactions at a lower scale emerge as objects expressing their own properties at a higher scale. Scaling is the key to emergence; emergent properties arise as new objects from one scale to the next (figure 3).

To see emergence and study it, one has to be able to observe and manipulate the system at more than one scale. One has to cross scales to see how lower-scale molecular interactions create and affect higher-scale cellular interactions; one would like to know the effects of molecular experiments (lower-scale manipulations) on cellular behaviours (higher-scale outcomes). Thus, a computer methodology that would allow us to zoom back and forth between lower-scale data and higher-scale behaviour while experimenting in silico is an ideal way—possibly the only way—to study emergence computationally.

5. Reactive animation

One of the techniques we have used in our own study of emergence in reactive systems is what we call reactive animation (RA; Efroni et al. 2003, 2005). RA is a precise representation of a complex system, but it does not search for orderly organizing principles imposed by the informed biologist top-down. Rather, RA begins bottom-up by translating the actual database generated by experiments and observations into a precise dynamic notation legible to computers and executable by computers. RA then proceeds to exhibit the executed simulations transformed into a realistically animated front end, easily recognized and comprehended by biologists. RA is thus fashioned in two tiers: specification and animation.

We have achieved precise specification of experimental data using the visual computer language of Statecharts as an example of choice (Harel 1987; Harel & Gery 1997).1 The Statecharts language was initially developed to create and study reactive systems designed by human brains, such as aerospace and automotive systems, telecommunication and control applications, interactive software and so forth. We have discovered, however, that Statecharts suits natural systems too (Kam et al. 2001).

The object-oriented version of Statecharts is embedded in a structural definition of classes of objects and the connections between them; a statechart is constructed for each object class, to specify the precise state-based behaviour and the behavioural manifestations of the connections of any object in that class (see top portion of figure 4). This notation, composed of object class, states and connections, is most suitable for biology, which deals with many classes of objects (molecules, cells, organisms, societies, etc.) and with the connections between them (interactions, inheritance, causal influences, etc.). Also, biologists think experimentally in terms of the states of molecules, cells and populations. So Statecharts is a well-suited medium for dealing with living systems.

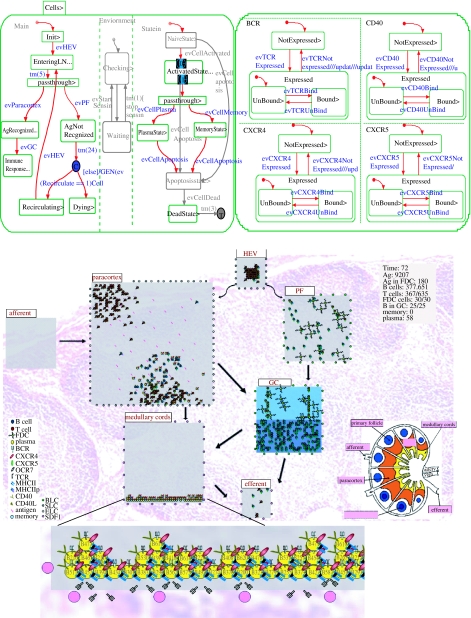
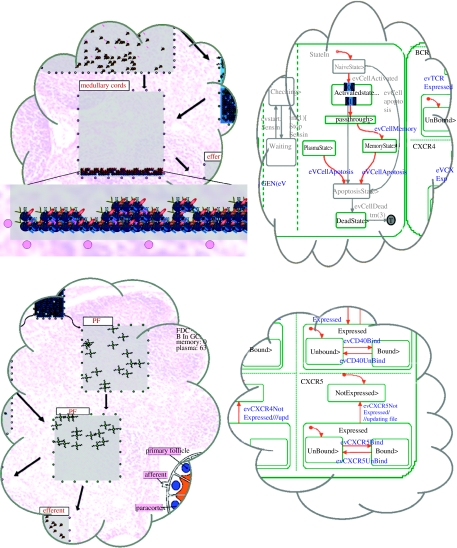
Figure 4.

From a model of the lymph node [SCH06]. Snapshots of a Statechart simulation in Rhapsody, carried out under standard conditions, together with the animated outcomes presented in Flash. The left-hand statechart describes part of the behaviour of a B cell, which undergoes many changes as the organ evolves; the right-hand statechart describes four of the many cell receptors that play an important role in the immune response. Below the statecharts is a snapshot of the resulting animation in Flash showing the various elements in the various parts of the lymph node; see [SCH06].

Statecharts are modular and hierarchical, and so is the underlying structure of the objects; you can add or remove objects, connections, states and transitions at any level. There are ample means to specify rich kinds of behaviour such as concurrency, stochasticity, chain reactions and time-dependent or time-constrained actions. The multi-level, hierarchical nature of Statecharts is most important to emergence: you can build any object (a cell, for example) from the lower-scale objects (molecules or organelles, for example) that create it, and you can view behaviour on any level you choose—molecular or cellular. The Statecharts language comes complete with a mathematically precise dynamic semantics legible to computers, rendering it amenable to execution/simulation.

The Statecharts visual language is itself multi-scalar, but the part of RA that makes scale crossing both more vivid and more revealing is the connection between the Statecharts simulations (tier one) and true animation (tier two). Technically, RA involves connecting the Statecharts simulation tool (in our case, Rhapsody from I-Logix) to an animation tool through an interface that empowers the simulation to construct an animated representation (see figures 4 and 5, which illustrate RA using a recent model of the lymph node; Swerdlin et al. submitted). We initially developed RA to study the differentiation of stem cells into mature T cells in the thymus, a critical process in the development of the immune system (Efroni et al. 2003). For that study, we primed the Flash animation tool2 with visual motifs representing the cells and parts of cells (receptors and markers) relevant to the thymus. Animation motifs, however, can be fashioned to reflect any dynamic system of interest: a traffic system; an operating army; an economic system; a political system; and so forth. RA embodies two defining features: the simulation tool instructs the animation tool to deploy its motifs according to the actual simulation and one can interact with the model and experiment with it, by the way of either the underlying statecharts or the front-end animation. In our RA study of the thymus, the resulting Flash animation expressed the properties of cells that emerged from the molecular-scale interactions fed into the Statecharts simulation tool (Efroni et al. 2003, 2005). However, the animated representation can be constructed to suit any imaginable scale crossing, from atoms or less (less than 10⁻¹² m) to galaxies and beyond (greater than 10⁺²⁵ m). It is only necessary that lower-scale reactions produce and direct a moving picture of higher-scale objects and their behaviours (figures 4 and 5). Emergent properties are disclosed in the animated transition from one scale to another.

Figure 5.

Illustrating reactive animation in the lymph node model [SCH06]. In the top portion of the figure, the statechart transition from figure 4 that allows a B cell to differentiate to a plasma cell has been removed (top right) and as a result no plasma cells can be created. This can be seen in the animation snapshot (top left), which shows that B cells that were fated to become plasma cells (represented in the animation as yellow circles, secreting antibodies) stay undifferentiated (blue circles). In the bottom portion, the transition that allows receptor CXCR5 to be expressed has been removed (bottom right), thus preventing cells from expressing it. CXCR5 is necessary for cell migration as it responds to the chemokine signal BLC, which is secreted from the PF regions (primary follicles) and attracts cells to these regions. The animation snapshot shows that no cells are present in these areas (bottom left).

We did not intend to study emergence when we built RA, but we realized that RA created a new platform for emergence when we noticed that the RA animation disclosed cell behaviours that were not overtly pre-programmed in the molecular data we included in the Statecharts simulation. Unexpectedly, RA revealed fine details of cell movements in defined anatomic compartments in both the lymph node (Swerdlin et al. submitted) and the thymus (Efroni et al. in press), and competition between individual T cells for critical stimulatory interactions with other cell types, selection of T cells for their velocity, and other high-scale behaviours hidden in the molecular data of T-cell development in the thymus (Efroni et al. in press). These emergent properties became noticeable only through the transition of simulation to animation (figure 5); the Statechart representation alone did not disclose them. The role of competition in the physiology of T-cell development in the thymus was not previously studied, or even discussed, by immunologists; the animation of T-cell behaviour in the thymus in fact simulated by RA alerted us to study the phenomenon (Efroni et al. in press). RA has thus served to catalyse novel thinking and, ultimately, experimentation.

RA not only alerts, but also empowers the observer. We built the RA interface in a way that allows the observer to become an experimenter in silico and knockout, add or modify cells, molecules or whatever else on the fly. The animation tool communicates the modification to the simulation tool, and the simulation generates a modified animation (Efroni et al. in press; Swerdlin et al. submitted). Emergent properties thus can be studied as well as revealed computationally by RA (figure 5). RA made it possible both to investigate the role of competition and to predict the outcome of experimentation (Efroni et al. in press). RA combines modelling for explanation with modelling for prediction.

Others have developed or employed visualization techniques for modelling complex systems: Petri nets (Reisig 1998) are one example and the compound UML set of languages is another (UML). These approaches differ from RA in that they are either stand-alone languages (in the case of the former) or a multitude of loosely connected languages (in the latter); they do not, in and of themselves, feature the ability to both specify and model visually and see the system in operation in a visual fully animated fashion. However, a detailed discussion of these other visual simulation technologies is beyond the scope of the present paper. Indeed, any technology or combination of technologies that would support bottom-up specification linked to an interactive animated front end would serve.

6. Dynamics

The animation tool in RA should not be viewed merely as an amusement or computational virtuosity. RA conveys dynamics—the capacity to change with time—and dynamics is the essence of a reactive system. Consider, for example, the distinction between a living cell and a dead cell: at a single instant, a living cell and a dead cell may contain precisely the same catalogue of component molecules in the same concentrations; the parts catalogue is the same for both the living and the dead. It is not the parts themselves, but the dynamics of their interactions that distinguish the living from the dead (Cohen 2000). The living cell goes on interacting as a reactive system and the dead cell decays into disintegration.

A computer is a tool for realizing dynamics, and living systems, as dynamic systems, are aptly described by computer simulation of their dynamics. Many kinds of mathematical-looking formulations are static statements, even though (as in the case of differential equations, for example) they often describe change over time. However, a formulation such as RA, whose very nature is to give rise to moving and realistic computer simulations, is dynamic in its essence; just like a living cell, a computer simulation has no existence but for its variation in time.

7. Live modelling

Reduction alone is not an explanation in biology; the complex living system cannot be explained merely by digging deeper into the system; the essence of the system includes its higher-scale emergent properties as well as its fundamental component parts (Cohen 2000). Explanation requires combining classical scientific reduction (to a lower scale) with extension (to a higher scale), which we have illustrated in developing RA. Extension, in addition to reduction, is needed because a complex system, such as a living organism, reveals different features at different scales of observation (Cohen 2006).

Even the non-living physical world is sensitive to scale and frame of reference. Different scales of physical observation clearly reveal material realities that fit radically different physical descriptions—witness the varied worldviews of classical mechanics, relativity and quantum mechanics (Feynman 1988). Fortunately for the physicist, however, each of these physical views of material reality can usually be fixed at one scale of observation; hence, most physical explanations can be adequately reduced to the laws of nature that pertain to a particular scale. Physicists can deal with one scale at a time. Hence, physics is served well by immutable mathematics. The math for the physicist is the explanation.

The complexity of living systems, however, is such that biologists are obliged to attend simultaneously to more than one scale of observation. Higher-scale extension must complement lower-scale reduction. Most importantly, living systems are essentially dynamic, and so are best represented by methods that, from the very start, are geared towards realistic, multi-scale computer simulations.

In summary, we might say that RA redefines the concept of a model as used by biologists. A biological model traditionally functions as a representation of a biological theory (or proto-theory); one's model represents the way one understands the real system. Classically, we build a biological model to test the validity of our understanding by seeing how well the model accounts for the known behaviour of the real system, or how accurately the model predicts the results of new experiments. Tradition says, first understand, and then make a model to explain what you understand. RA, at least for complex living systems, turns the process around: first make a dynamic model that integrates the data, then you will understand. A model that represents faithfully the dynamic crossing of scales and layers is itself an explanation of the living system's emergent properties (Efoni et al. 2005).