Abstract
We study the mechanical properties of fin rays, which are a fundamental component of fish fin structure. We derive a linear elasticity model that predicts the shape of fin rays, given the input muscle actuation and external loading. We then test the model using experiments that measure (i) the ray deflection for a given actuation at the muscular interface, and (ii) the force–displacement response under conditions of actuation and non-actuation. The model agrees well with the experiment; both show a concentration of curvature at the ray base or at the point of an externally applied force, and a variation in ray stiffness over more than an order of magnitude depending on actuation at the bases of the fin rays.
Keywords: fishes, elasticity, locomotion, fin ray, curvature
1. Introduction
Ray-finned fishes are a group of over 28 000 species, comprising more than half of all vertebrates, that have diversified into a wide variety of aquatic habitats and are known for their diversity of locomotory styles. One of the key characteristics of ray-finned fishes is the presence of fins that extend into the water and act as control surfaces during locomotion (Lauder & Drucker 2004; Lauder 2006). Ray-finned fishes possess both median (midline) and paired fins (figure 1), which allow fishes to control body position and to generate force during locomotion. Fish fins are important for steady rectilinear locomotion, and also for manoeuvring during which fishes can vector forces through control of fin shape and orientation (e.g. Drucker & Lauder 2003).
Figure 1.
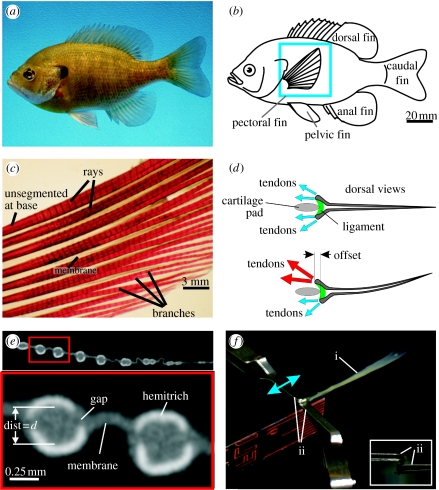
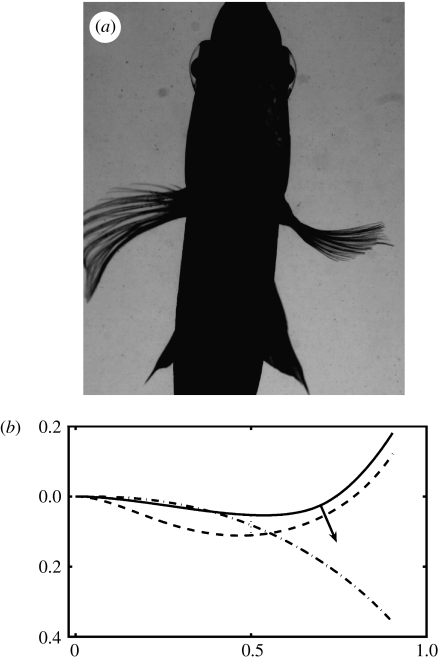
(a) A photograph of a bluegill sunfish. (b) Schematic showing the location of the fish fins. The pectoral fin is highlighted with the blue box. (c) A photograph of a cleared and stained pectoral fin. The short segments can be seen along the length of the rays. (d) Schematic showing dorsal views of a fin ray with two hemitrichs. Muscles (not shown) exert forces on the tendons attached to the head of each hemitrich. (e) Single cross-section slice from a microCT scan of a pectoral fin. The upper panel shows multiple rays and the lower panel shows an expanded cross-section of two rays. Each of the two rays is composed of two hemitrichs. The bright white regions are bony areas and the grey is softer tissues (fin membrane and connective tissues). The separation between the two hemitrichs of the left ray is labelled ‘dist=d’. (f) Apparatus for holding ray hemitrichs. The ray (label ‘i’) is held by two clips (label ‘ii’). The upper clip can move to apply an offset between the hemitrichs. The inset image shows the end-on view. The upper clip holds one hemitrich and the lower clip holds the other hemitrich.
The structure of ray-finned fish fins is generally characterized as being composed of individual ray-like components made of small segmented bony elements, connected to each other through a collagenous membrane (figure 1). This basic fan-like design allows fishes to change fin area during locomotion, and this architecture provides a balance between stiffness and flexibility, which potentially allows for finely tuned hydrodynamic interaction. Since fins provide the structural interface between the fin muscles and the fluid environment, understanding the mechanics of fin function is an essential component of a complete analysis of how locomotor forces are transmitted by fishes to the aquatic environment.
The fins of ray-finned fishes possess one remarkable design feature not present in other swimmers, i.e. fishes can actively control the curvature of individual fin rays, and hence the curvature of the whole fin surface (McCutchen 1970; Geerlink & Videler 1987; Lauder 2006). Fish fin rays are bilaminar in structure (figure 1) and the two halves of each ray can slide past each other when actuated at the base by fin muscles (figure 1d). As the base of one-half ray is pulled past the other, the fin ray will curve or resist the imposed hydrodynamic loading. While the anatomy of fish fin rays has been previously characterized in the literature, there is only limited information on how fin rays function and on the mechanical properties of this anatomical design.
In this paper, we study fin-ray function using a simple mechanical model intended to abstract the essential physiological features. We address the following questions. What is the relationship between input and output forces and displacements as a function of the fin-ray geometry and material properties? In particular, how does the tapering of the ray and stiffness of its components influence its operation? In §2, we describe the experimental techniques used to study these mechanical properties. We then derive an equation for the fin ray using linear elasticity (§3), and present solutions that are evaluated by comparing their predictions of ray shapes and force–displacement behaviour with results from real fin rays (§§4 and 5). We find that the fin-ray mechanism allows the fish to actively vary fin-ray stiffness over more than an order of magnitude. The ability of the fish to dramatically stiffen fins compared with a passive flexible body may be instrumental to understanding fin-based swimming behaviour.
1.1 Previous models
To our knowledge, the only previous model using equations for the fin ray was proposed by McCutchen (1970). He found an expression relating the axial shift along the ray to its curvature and intraray spacing, and a further expression for the balance between the moment on the ray due to tension and compression in the two ray halves and the moment due to hydrodynamical forces. Using this expression, he deduced that the fin ray can support only a single load distribution, up to an overall multiplicative constant. However, it is clear from experiments that a fin ray can in fact support many different load distributions, including a point-force load and a distributed load (as occurs in hydrodynamic interaction).
Here, we derive a new model based on linear elasticity. We first show how McCutchen's (1970) geometrical equation may be derived more systematically, and then introduce internal mechanics. The internal forces arise through bending rigidity and the elastic properties of the collagenous intraray material, which are seen to be essential to understanding the shape of the ray in our experiments. This is accomplished by starting with the picture of the fin-ray mechanism proposed by Geerlink & Videler (1987), and writing down the corresponding linear elasticity equations.
2. Experimental methods
Bluegill sunfish (Lepomis macrochirus) were obtained from White's Pond in Concord, MA. Six fishes with fins of similar size (maximum ray length =40.3±0.8 mm, mean±s.e.) were euthanized with tricaine methanesulphonate (MS-222), and their fins were removed. Individual fin rays were dissected for testing and a three-dimensional micro-computed tomography (microCT) scan was made from one of the fins. The microCT specimen was preserved in formaldehyde and ethanol for transport to the imaging facility (University of Texas High-Resolution X-ray CT). The remaining experiments were performed with the rays submersed in water within 48 h of euthanizing the fish. Fins and fin rays were stored in water at 4°C between the time of dissection and experiments.
Slices from the microCT scan show a good contrast between the bone, the soft tissue and the background (figure 1e). Image slices were thresholded to isolate the bony regions after which the area, centroids and area moments of inertia were calculated for the ray halves (called ‘hemitrichs’) and for whole rays as a function of length s along the ray. The distance d between the hemitrichs was calculated as the separation between the hemitrich centroids.
Experiments to measure mechanical properties were done on 24 separate rays. Fish pectoral fin musculature can activate to offset the hemitrichs at the ray base. To reproduce the motion, an apparatus was built to hold each of the two hemitrichs with small clips (figure 1f). Moving one of the clips relative to the other offsets the hemitrichs and the ray will then curve. Both the base offset distance and the tension or compression force are measured. A set of two experiments measures the relationships between the hemitrich base offset and the ray curvature and between the hemitrich base force and the ray curvature. During these experiments, some rays were snipped at the distal end to see if the offset- and force-to-curvature relationships change.
Two further experiments measure the force needed to prevent the rays from curving when either an offset or a force is applied to the hemitrich base (see §5.1). The force that resists the ray curvature is applied at a single point about two-thirds of the way along the ray.
Experiments were also done comparing the stiffness (force per unit deflection) of the fin ray when both hemitrich bases are fixed to prevent sliding to the stiffness when one hemitrich base is fixed and the second is free to slide (see §5.2). The cantilevered ray was deflected by applying a point force about two-thirds of the way along the ray.
3. Linear elasticity model
Our fin-ray model consists of two identical, inextensible beams represented by the elastica theory (Antman 2005). Between the beams is a thin, incompressible layer of material with varying shear modulus, the distribution of which determines the shapes the fin ray may assume. Our modelling begins with a one-dimensional approximation to the deformation of this layer.
In the unstressed state, the central axes of each beam are assumed to be a mirror image of the other, reflected about the centre line between them (figure 2b). The actual rays show a slight asymmetry, which is typically small relative to the spacing between the rays. The distance between the corresponding points at arc length s on each beam in the unstressed state is denoted by d(s). The material between the beams (predominantly a collagenous gel network; Videler 1993) is approximated as an incompressible linearly elastic material, for the sake of simplicity. Real collagen behaves nonlinearly for large shear strains (stiffening as the collagen fibres stretch; Sacks & Sun 2003), but in this first analysis of the fin-ray mechanism, we will mainly use a linear resistance to shear for simplicity.
Figure 2.
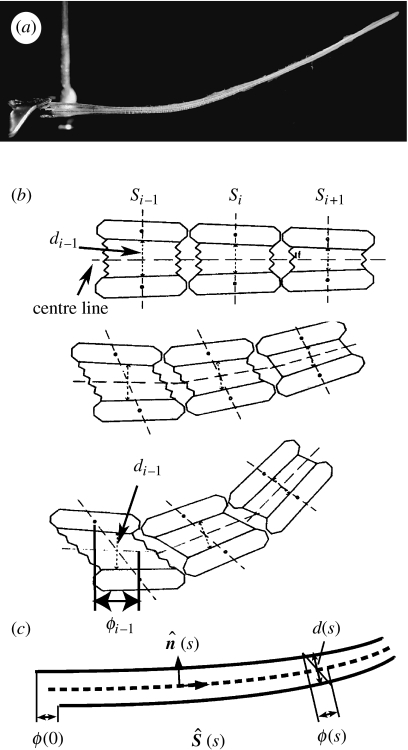
(a) A photograph of a single fin ray (ray 4 out of 13 in the pectoral fin of a bluegill sunfish) held by force calipers in the experimental set-up. The upper hemitrich base is displaced to the left relative to the lower hemitrich base, leading to an upward deflection. (b) A schematic of the physical mechanism of fin-ray bending proposed by Geerlink & Videler (figure adapted from the original figure in Geerlink & Videler 1987). We introduce here the notation s for the arc length along the ‘centre line’—the line at the average position of the initially opposite hemitrichia; d for the distance between midpoints of opposing segments; ϕ for the displacement of the segment in the direction tangent to the centre line. Subscripts denotes segment number i. (c) The model we consider in this work, which is the continuum limit of the diagram in (b).
Our model expresses all geometrical and material quantities as functions of distance along the centre line of the two-beam system, where the centre line is defined as the average of the two beams' trajectories (figure 2c, dashed line). After assuming linear elasticity and symmetry of the beams, our next assumption is incompressibility of the intraray material at leading order, because the collagen gel is mainly fluid by volume. Incompressibility can be expressed in terms of the relative motion of opposite points on the beams with respect to the centre line. For an incompressible material confined to a thin layer, this motion at leading order is ‘simple shear’ (Segel 1987), i.e. material in planes aligned with the centre line slide over each other, but do not change their distance normal to the centre line. In our model, the central axes of the two beams are two lines, with the two-dimensional area between them as the intraray material. The actual rays have a finite thickness, which is small relative to length, allowing the use of the beam model. In the actual rays, the cross-section of the intraray material is roughly cylindrical (figure 1e). Nonetheless, the two-dimensional model captures the basic mechanics of a single-ray bending in a plane.
In two dimensions, incompressibility means that the x- and y-components of displacements u and v obey ∂xu+∂yv=0. Now consider a thin layer of height d in the y-direction (figure 2c). For a given shift ϕ0 applied at the bases, ∂xu∼ϕ0/L and ∂yv∼Δd/d, where Δd is the local change in layer thickness. Incompressibility in the thin layer thus implies that Δd∼dϕ0/L. Thus, two points initially opposite undergo a displacement normal to the centre line that scales as the tangential shift ϕ0 times the aspect ratio d/L≪1. Taking the limit that Δd goes to zero simplifies our two-dimensional model to an essentially one-dimensional problem. A similar approximation occurs in the lubrication theory of fluid flow in thin layers (Batchelor 1967).
In the actual fin rays, the hemitrichia consist of one continuous bony region at the base, followed by smaller bony segments connected by collagen in the main, flexible part of the ray (figures 1c and 2a). The separation between the ray heads is somewhat larger than that between the smaller bony segments. There are four muscle attachments onto the ray heads of all but the first ray in each fin (figure 1d; Videler 1993). These muscles apply a combination of forces and moments to the rays both within and out of the plane of the fin. As our model is two-dimensional, and is intended to model only the fully segmented portion of the ray, we assume that the forces from muscle attachments are transmitted to the ‘base’ of the ray (defined as the point beyond which the rays are fully segmented) as simply a net force and net bending moment on each hemitrich, which are the only boundary conditions needed in our beam theory.
After giving the equations and boundary conditions, we will consider the relative magnitudes of the physical and non-dimensional parameters, and their distribution along the ray.
3.1 Equations
We begin with the equations for two inextensible beams, each described by the elastica equation (Antman 2005)
| (3.1) |
Here, the force per unit length resisting bending is defined in terms of the product of B(s), the bending rigidity, with the difference between beam i's curvature κi and its rest curvature κeq. Note that κeq has opposite signs for the two mirror-image beams. Since d(s)/2 is the distance from the undeformed hemitrich to the centre line, . Here, and are the unit vectors tangent and normal to the two beams.
The tension force in beam i is Ti, an axial force maintaining inextensibility. Additional loads are the following: fn, a normal force per unit length that maintains constant normal distance of the beams with respect to the centre line; fs, a tangential force per unit length that resists a relative tangential motion of the beams (due to shearing of the intraray material); and fi ext, the force per unit length on beam i due to external forces, such as a hydrodynamic pressure.
Hence, each beam in our model experiences four different internal forces—two forces from internal beam mechanics and two from beam–beam interactions through the intraray material. Inextensibility is a good approximation to the fin ray, which undergoes negligible axial stretching in experiments.
The normal force per unit length from the intraray material is fn, which preserves d(s), the component of the distance between the beams normal to the centre line. It may be expressed as a spring force,
| (3.2) |
where is the unit normal to the centre line between the two beams. We then take the modulus of compression k1→∞, hence
| (3.3) |
The quantity acts as a Lagrange multiplier, which preserves the constraint of fixed normal distance.
The shear force per unit length fs is a spring force due to the shearing of the intraray material. It may be expressed in two different ways. First, in terms of the shear modulus G of an isotropic elastic material, in which case
| (3.4) |
where
| (3.5) |
is the shift, or the relative tangential displacement of initially opposite points on the two beams.
Second, we may consider the elasticity of the intraray material as arising from stretching of collagen fibres with ends anchored in opposite segments of the hemitrichia. The undeformed length of these fibres is d, while the stretched length is (figure 2c). In this case,
| (3.6) |
with spring constant k2. We shall mainly use expression (3.4) for fs in terms of G, for simplicity, though many analogous results hold for the second nonlinear case.
3.1.1 Centre-line equation
Having introduced the mechanics of the two beam system, we now use the thin-layer approximation to replace the two beam equations with a single equation for the position of the centre line of the layer.
We can express ϕ in terms of the already-introduced intraray spacing d(s) and the curvature of the centre line κavg as follows. First, we note from equations (3.3) and (3.5) that d and ϕ are the components of X1−X2 in the centre-line frame,
| (3.7) |
Differentiating equation (3.5) with respect to s yields
| (3.8) |
We restate our thin-layer assumption that d/L≪1. Since κavg may be as large as O(1/L), the first term on the right-hand side is O(d/L). Each of the three factors in the second term on the right-hand side is O(d/L), as may be seen by differentiating equation (3.7) to obtain κ1−κ2 and . Hence, the second term in equation (3.8) is O((d/L)3), so we may drop it with a relative error of (d/L)2.
Hence to a very good approximation,
| (3.9) |
| (3.10) |
where ϕ0 is a free parameter set directly using clamps or indirectly by muscle action, in terms of the boundary conditions discussed in §3.2. Equation (3.10) shows that a shift between the beams ϕ can be reduced by increased centre-line curvature, in proportion to the intraray spacing d.
We derive the single centre-line equation from the internal elastic energy of the two-beam system,
| (3.11) |
| (3.12) |
which expresses that the fin shape is a trade-off between the bending energy and the shear energy of the intraray material. We take the variation with respect to ϕ and integrate by parts to obtain
| (3.13) |
Using equation (3.9), we see that the expression multiplying δϕ in the integral is the derivative of the internal bending moment of the two-beam system divided by d. In the absence of the shear term Gϕ/d2, this would be 2∂s(Bκ/d), the value for the two beams. When the ray is in equilibrium, we may put this expression for the internal bending moment of the system in balance with the moment due to external forces,
| (3.14) |
Here, Mext is the hydrodynamical moment of the external forces on the ray, whether from point forces in the experiments below, or from fluid-pressure loading. Equation (3.14) is a second-order differential equation for ϕ, which we term the ‘centre-line equation’. If we model the resistance to shear as that due to collagen fibres modelled as linear springs (equation (3.6)), the corresponding equation is
| (3.15) |
This completes our derivation of the centre-line equation, which depends only on the elastic parameters B and G and the geometrical parameter d. We now discuss the appropriate boundary conditions.
3.2 Boundary conditions
We employ different boundary conditions corresponding to each of the experiments with which we compare the model. The boundary term in equation (3.13) implies one boundary condition on ϕ at each end of the ray. Either ϕ is fixed, or free, in which case
| (3.16) |
In the first set of experiments (§4.2), the shift at the base of the ray is set to ϕ0. If instead a tension/compression force T0 is specified at the bases, we may relate T0 to ϕ0 by taking the variation of the energy with respect to ϕ0 : T0=δU/δϕ0.
In a second experiment (§5.2), the ray is deflected by a point force with zero relative force applied between the bases, in which case equation (3.16) is applied there.
At s=1, we assume that the ray ends are either ‘fused’ or ‘free’. We have performed CT scans, as shown in figure 1e, at the tips of the rays, which find that the two hemitrichia appear to be fused there. The tips are also the location of the actinotrichia, which are involved in ray growth (Videler 1993). However, it is unclear whether the hemitrichia tips are always fused, so we also consider the hemitrichia being free at the tips, which also occurs when we remove a portion of the ray in the first set of experiments (§4.2). Allowing the tips to be free also allows us to separate the mechanical effect due to shearing of the collagen gel from that of the tips being fused.
We impose the boundary condition that the rays are fused at s=1 by setting ϕ(1)=0. Alternatively, if the ray tips are not fused, we apply the boundary condition in equation (3.16).
Having solved for ϕ with the two boundary conditions, we obtain the ray curvature κ using equation (3.9). We assume that the mean position of the ray base is set to 0, so that x=y=0 at s=0, and that the mean tangent angle θ0 at s=0 is given. We use θ0=0 throughout this paper. Using these boundary conditions, one obtains the trajectory of the ray as
| (3.17) |
| (3.18) |
3.3 Non-dimensionalization
We now non-dimensionalize equation (3.14), i.e. we non-dimensionalize all lengths d, ϕ, 1/κ by the ray length L, the bending rigidity B by its value B0 at s=0, and G (or k2) by B0/L2. We note that the dimensional G has dimensions of three-dimensional shear modulus times area, because by its definition in equation (3.11), it is the three-dimensional shear modulus times the cross-sectional area of the intraray material. We henceforth use the same notation for the non-dimensional quantities with the assumption that they have been non-dimensionalized.
We study the behaviour of ray shape κ or alternatively ϕ in terms of the parameters d, B, G (or k2).
3.4 Physical scalings
A beam is a familiar mechanical structure, but the mechanics particular to the two-beam fin ray containing a material with moderate shear modulus G confined to a thin layer d is less well known. Here, we give some simple estimates for the order of magnitude of the three important parameters, B, G and d, with respect to their use in bluegill pectoral fin swimming.
First, the order of magnitude of the bending rigidity B can be predicted from the simple observation that fins bend in normal swimming conditions. One way to quantify this property is to say that under peak hydrodynamic loading in steady swimming, a fin ray should bend significantly—i.e. the fin radius of curvature 1/κ would be of the same order of magnitude as its length L. Hence, there is a balance of stored elastic energy (within the beam model) with the kinetic energy of the fluid with which the ray interacts. We take this amount of kinetic energy to be that contained in a volume of fluid swept out by the fin ray. Because there are about a dozen rays per pectoral fin, this quantity of volume is assumed to be 1/12 the volume swept out by the whole fin. The fluid kinetic energy in a three-dimensional potential flow past a square fin of side length L broadside-on to the flow scales as ρU2L3, so we use L3/12 for the volume of the fluid whose kinetic energy undergoes an order-one change due to the bending of a single fin ray. We put this fluid kinetic energy in balance with the stored bending energy in the two beams,
| (3.19) |
where the quantity on the left-hand side is the stored elastic energy per unit length of the two hemitrichia, Bκ2, times the length of the ray L. Using the density of water, L=4 cm for the length of a typical bluegill fin ray, U=6 cm s−1 for a typical bluegill swimming speed and we obtain B≈10−6 J m. In our experiment, we have found using three-point bending tests that the ‘composite’ Young's modulus corresponding to the whole structure is E≈108–109 N m−2, with the average area moment of inertia I≈10−6 cm4. Hence, the measured B=EI≈10−6–10−5 J m. The most plausible reason for our underestimate of B from the scaling argument is an underestimate of the flow speed U needed to induce order-one bending.
In subsequent sections we will determine a value for G by fitting the model and experiment, but here we give a simple estimate for the order of magnitude of G using physical considerations. From equation (3.14), we estimate G≈B0/L2. Using L=4 cm again, we have G≈6×10−4 N. This gives a shear modulus of the intraray fish collagen of roughly 103 Pa. For comparison, type 1 collagen found in mammal skin has a shear modulus of 10–102 Pa (Velegol & Lanni 2001).
The size of d is related to the function of the ray as a force transducer. A large axial force T is applied at the ray base (figure 1d) over a distance of the base shift ϕ0, resulting in a deflection of the ray y against a normal fluid force per unit length f. Thus, Tϕ0∼fyL. As we assumed in the estimate of G, to induce an order-one curvature in equation (3.11), we require d∼ϕ0. If the deflection is of the order of the ray length, d∼fyL/T∼fL2/T. Using our estimate of f∼ρU2L/12 above, we find d/L∼(ρU2L2/12)/T. This has the interpretation that the ray aspect ratio is simply the ‘mechanical advantage’, i.e. the ratio of typical fluid force to muscle force.
4. Unloaded ray
4.1 Simple solutions
We present some simple exact solutions to equation (3.14), which show the effect of varying the parameters d(s), B(s) and G(s), with fin tip both fused and free.
4.1.1 Fused ends
First, we consider the basic case where the shear stiffness G is zero, but the tips are fused. A ray with fused ends also arises as the limit of very large shear modulus concentrated at the tip. We solve for the ray trajectory directly by integrating equation (3.14) with the boundary conditions ϕ(0)=ϕ0 and ϕ(1)=0. We obtain
| (4.1) |
for the ray curvature. We see that the curvature equals ϕ0/d when d and B are uniform. Hence, decreasing the intraray spacing with the base shift held constant results in a more curved ray.
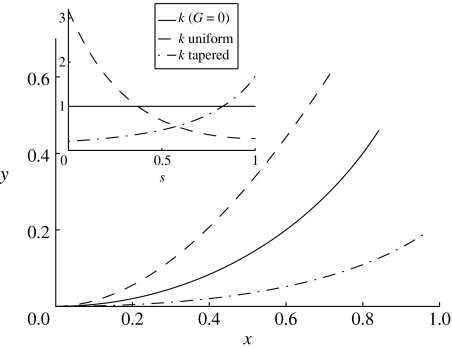
Considering now a tapered ray, for which d decreases as s increases, we consider the physically relevant cases where B(s) is proportional to dα, α>1. The actual rays are somewhere between a ray that tapers with constant out-of-plane width W (in which case α=3) and a ray that tapers with constant cross-section (α=4). In both the cases, the right-hand side of equation (4.1) increases towards the tip, so the curvature increases towards the tip for a tapered ray (figure 3, dashed-dotted line). Hence, having a fused tip (or concentrating shear stiffness at the tip) with tapering is a way of concentrating curvature at the tip.
Figure 3.
Three representative trajectories of the fin-ray model with a base shift of ϕ0=0.01, where the undeflected ray (ϕ0=0) lies along the x-axis: 1, a ray with zero shear modulus and fused end (equation (4.1); solid line); 2, a uniform ray (equation (4.3); dashed line); and 3, a ray with G increasing towards the end as 11s10, d linearly tapered as 0.02(1.5−s), and B=d3 (dashed-dotted line), intended to simulate the case of a tapered ray with shear modulus weighted towards the tip (see §4.1.3). Inset, the curvature as a function of arc length for the three cases. The curvature either decreases (dashed line), remains constant (solid line) or increases (dashed-dotted line) towards the end.
4.1.2 Uniform ray
The next simple case is where B, d and G are all uniform, with the ends not fused. Then, with the boundary conditions ϕ(s=0)=ϕ0 and ∂sϕ(s=1)=0, equation (3.14) has the solution
| (4.2) |
We have indicated here that ϕ and κ asymptote to decaying exponentials for . The inset to figure 4 shows that for large , solutions are essentially the same when the distance from the base is scaled by . Hence, in contrast to the previous case with fused tips (i.e. with G concentrated at the tip), if G is spread out uniformly over the ray, and much larger than B, curvature is concentrated at the base, increasingly so as G increases. There is a simple physical interpretation that the ray curves enough at the base to take up nearly all the shift, leaving little bending or shear in the remainder of the ray. This concentration of curvature is consistent with the bending energy and shear energies in equation (3.11) being comparable, since G≫B in this limit.
Figure 4.
Solutions to the centre-line equation (3.14) for rays with uniform G varying over five orders of magnitude (102, 103, 104, 105, 106), and uniform intraray spacing (d=0.01), bending modulus (B=1) and base shift ϕ0=0.01. Deflection increases with G. Inset, the five rays plotted with distances multiplied by , so the vertical axis shows and the horizontal axis shows . The curves overlap closely. For large , L0 is the size of the region at the base of the ray where bending is concentrated.
The solution above assumes free ends. To obtain the solution with fused ends, we use the boundary condition ϕ(s=1)=0 instead of ∂sϕ(s=1)=0. The solution with fused ends—and uniform G, B and d—is
| (4.3) |
(figure 3, dashed line), which has the same asymptotic behaviour as the free-end solution for large . The free- and fused-end solutions are exponentially close, because the dominant, exponentially decaying solution nearly obeys both the free- and fused-end boundary conditions, with an exponentially small error. We shall see that the experimental rays compare well with models at sufficiently large G/B that the two s=1 boundary conditions give similar ray trajectories, so we will henceforth use the fused-tip boundary condition unless otherwise stated.
4.1.3 The effect of tapering
The first simple solution showed that with zero shear modulus but fused ends, the uniform ray has a uniform curvature. The second simple solution, with uniform shear modulus, showed the curvature becomes concentrated near the base of the ray. One may therefore infer that by varying the distribution of shear modulus, one may vary the distribution of curvature along the ray. The extreme case of distributing most of the shear modulus at the tip of the ray approaches, in the limit, the case of zero shear modulus but fused ends, leading to a uniform curvature. At the other extreme, distributing most of the shear modulus at the base of the ray is similar to a uniform distribution of shear modulus, because the bending occurs in the nearest location to the base that has G≈B, which is at the base in both the cases.
The bending rigidity B and the intraray spacing d are correlated in the real rays, as the thickness of the bony segments is positively correlated with the intraray spacing. In the case of linear proportionality, we would expect B∼d3W, where W is the width of the ray in the direction out of the plane of bending. W may be constant, or scale as d for a ray of constant cross-sectional shape, or scale as 1/d for a ray of constant cross-sectional area. In our measurements of actual rays using CT scans, the width typically scales like d to a power between 0 and 1. The rays may bifurcate towards the ends, in which case the width may increase as d decreases.
We shall now consider the effect of non-uniform B and d for a ray, in which G increases towards the tip (if G is uniform or decreases with axial distance, the ray assumes the shape with bending concentrated at the base as in figure 4, regardless of tapering). First, from equation (3.14), we see that if d decreases towards the tip, the ratio G/d2 increases towards the tip, effectively increasing the shear modulus term towards the tip. The ratio B/d2 still decreases towards the tip in this case, since B decreases faster than d2 by the comments above. Consequently, if there is a region in which B≫G near the base of the ray, the curvature actually increases towards the tip there. An example with G increasing sharply towards the tip as 11s10, and B and d tapered similarly to actual rays—d=0.02(1.5−s), B=d3—is shown by the dashed-dotted line in figure 3. Hence, a simple way for a ray to distribute curvature away from the base is by (i) tapering and (ii) increasing the shear modulus G towards the tip.
We now present some comparisons of the centre-line trajectory of the shifted fin ray in the experiment and model, to check whether the two are generally in agreement, and to quantify the distribution of shear modulus along the experimental rays.
4.2 Comparison with experiment: estimate of shear modulus of intraray material
Our model is determined by one geometrical parameter—the intraray spacing—and two material parameters—the single-hemitrich bending modulus and the shear modulus of the intraray material. We now describe how we can use the model with the first two of these parameters—the spacing and bending modulus—as inputs in order to predict the third, the shear modulus. To our knowledge, there have not yet been direct measurements of the shear modulus of the intraray fish collagen.
Using CT scans, we have measured directly the intraray spacing d for five representative rays of the 13 in the bluegill pectoral fin. We have estimated the distribution of bending rigidity of a single hemitrich from measurements of its cross-sectional area. The bending rigidity B is the product of Young's modulus and the second moment of area of a cross-section of a hemitrich with respect to the centre line of the ray. In a fin ray, the role of Young's modulus is played by the resistance to stretching of collagen fibres linking adjacent (not opposite) bony segments (shown schematically in figure 2b; see also Videler 1993). The simplest assumption is that the elastic properties of these fibres, and therefore also the effective Young's modulus in our beam model, are uniform along the ray. Second, we extract the second moment of area using CT scans at six nearly equally spaced locations in the region being modelled, for ray 3 in a specimen, which is similar to ray 4 in geometrical and mechanical properties. We now use ray 4 of a single specimen for the comparison between model and experiment, and the determination of the shear modulus G.
The shear modulus of the intraray material cannot be deduced simply from geometrical properties. Here, we attempt to estimate its value along the fin ray as one of the primary uses of the mechanical model. We consider one specimen's fin ray 4, typically one of the longest rays in the pectoral fin, though all the rays beyond the first two have similar muscle attachments and lengthwise distributions of material properties (Videler 1993). Hence, we take this ray to be a ‘typical’ fin ray for estimating bending and shear modulus.
In figure 5a, we compare 10 actual fin-ray trajectories from an experiment (dashed-dotted lines) with model fin-ray trajectories. The 10 experimental trajectories consist of the whole ray 4 specimen clamped at three different base shifts, and the same specimen cut-off at two locations, and again clamped at three to four different base shifts. By cutting off the ray ends, we test two properties of the rays: (i) the lengthwise distribution of the intraray shear modulus, and (ii) the importance of the intraray shear modulus relative to that of the fused ends (in the whole ray only) in bending.
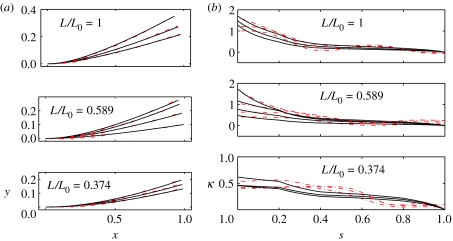
Figure 5.
(a) A comparison between model (solid lines) and experimental (dashed-dotted lines) fin-ray trajectories. For each of the three ray fractions given in table 1, three to four trajectories are shown, each for a different base shift ϕ0. The shear moduli used for the model are those which minimize the mean-square distance between the trajectories and are given in the third column of table 1. (b) Experimental and model fin-ray curvatures (κ) versus arc length (s) for the same datasets. The shear moduli used for the model are those which minimize the mean-square difference between the curvatures and are given in the fourth column of table 1.
By measuring the base shift and centre-line trajectories of the ray from photographs, and the distribution of the intraray spacing from CT scans on separate specimens, we have all the data needed for input to the centre-line model, except for the shear modulus. In appendix A, we describe how shifts and centre-line trajectories are extracted from the fin-ray photographs.
For each experimental trajectory, we determine the model trajectory that minimizes least-square distance from it, using uniform shear modulus G as a single fitting parameter. Here, we assume a uniform shear modulus for simplicity, though a shear modulus that varies along the length can also be considered for better agreement. The approximation of uniform shear modulus could be expected to apply to the extent that the intraray material has uniform density and anisotropicity of collagenous fibres. The available microscopic images of the fibres (Videler 1993) show at least that these properties are not very obviously non-uniform. The model trajectories in figure 5a fit the experimental trajectories to within a mean-square error of 0.8–4.1% in position relative to specimen length over the 10 trajectory comparisons. Each comparison is listed in a row of table 1, with the shear moduli of the best-fit rays in the third column.
Table 1.
Non-dimensional shear modulus G estimated from experimental ray trajectories.
| ray fraction (L/L0) | base shift (ϕ0/L) | trajectory-fit log2G | curvature-fit log2G |
|---|---|---|---|
| 1 | 4.51×10−3 | 8.25 | 8 |
| 1 | 5.85×10−3 | 7.25 | 7 |
| 1 | 7.64×10−3 | 6.5 | 6 |
| 0.589 | 4.51×10−3 | 7.5 | 8 |
| 0.589 | 8.40×10−3 | 5.75 | 6 |
| 0.589 | 1.23×10−2 | 4.25 | 5.25 |
| 0.589 | 1.38×10−2 | 5.25 | 6.5 |
| 0.374 | 1.57×10−2 | 2.5 | 3.5 |
| 0.374 | 1.81×10−2 | 2.5 | 2.75 |
| 0.374 | 2.05×10−2 | 2.5 | 3 |
In figure 5b, we repeat the comparison with a different metric for the best-fit rays, to validate our prediction of G. Here, instead of trajectories, we compare the distributions of curvature. Because curvature is a second derivative of the trajectory with respect to the arc length, this comparison is more sensitive to deviations in position than the bare trajectory comparison. The method of obtaining the curvature distribution from the experiment is described in appendix A. For each of the 10 photographs, the shear moduli of the best-fit rays from the curvature comparison are listed in the fourth column of table 1.
The values of G listed in table 1 are given on a logarithmic (base 2), not linear scale, in order to cover a range of several orders of magnitude with relatively few evaluations of the model. Also, the values of G are only given in steps of 20.25, or about 10% precision. However, this increment in G corresponds to a difference of less than 1% in trajectory, in terms of mean-square deviation.
The values of G we obtain range up to 300. At this value of G, curvature is relatively concentrated near the fin-ray base (as we have shown in figure 4 for a uniform ray). Thus, in the unloaded case, we see a concentration of curvature at the ray base. In §5, we consider how loading may distribute curvature farther from the base, which is of importance in the hydrodynamic situations in which the ray evolved. We see also in comparing the cut-off ray (lower two panels, figure 5a) with the intact ray (top panel, figure 5a) that the ray bends similarly even after the tip is cut-off, which is further evidence for the importance of the intraray material to ray bending. In table 1, we see that the best-fit values of G obtained by the two methods of fitting are within a factor of 2.2 in the third and fourth columns, which gives an estimate of the precision with which we have determined G through our curve-extraction and curve-fitting procedures. In spite of this variation, we find a systematic decrease of G as the ray is cut shorter. This provides evidence that G is actually non-uniform, so these best-fit values should be interpreted as weighted averages of the true distribution of G over the ray. In this interpretation, we find a significant decrease in shear stiffness towards the base of the ray. Along with the tapering, the effect of which is described in §4.1.3, this distribution of shear stiffness can distribute more curvature towards the tip of the ray, relative to a ray with uniform shear modulus. However, curvature is still concentrated near the base for the rays in the experiment in this test.
In this comparison of the unloaded ray, we have found that our simple model can help us understand the concentration of curvature at the base for an unloaded ray actuated by shifting at the base. We now consider the behaviour of a fin ray under different types of loading, in order to test our model further and understand the fin-ray mechanics in situations closer to its use in swimming.
5. Loaded ray
5.1 Bending against a point force
For the case of a point force Q applied normally to a uniform ray at s0, the external moment in equation (3.14) is Mext=Q(s0−s) for s<s0 and zero for s>s0.
The solution to equation (3.14) in this case is
| (5.1) |
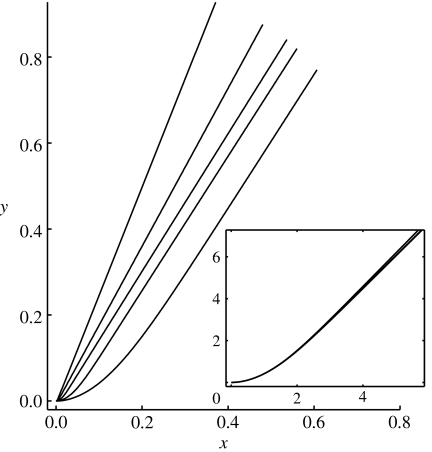
In figure 8b, we show the solution for ϕ0=0.01, Q=220, d=0.01, G=200, B=1 and s0=2/3. Here, the relevant dimensionless point-force parameter Qd/Gϕ0≈1, so the upward deflection due to the shift at the base alone is comparable to the downward deflection from the point force alone.
Figure 8.
(a) Ventral view of a bluegill turning to the right. The fin to the right is actively cupped into the flow, increasing the drag force. (b) Shapes of a model fin ray under three loading situations: 1, a concentrated normal point load (solid line, equation (5.1) with ϕ0=0.01=0.01, Q=220, d=0.01, G=200, B=1 and s0=2/3); 2, a uniform force per unit length (dashed line, equation (5.1) with ϕ0=0.01, p=200, d=0.01, G=200 and B=1); 3, a ‘passive’ ray under the same uniform loading (dashed-dotted line), with a free base (∂sϕ=0 at s=0). The difference between 2 and 3 shows the effect of changing the base shift ϕ0 from its passive value.
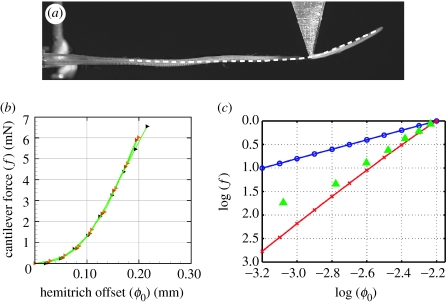
We now compare this solution with the actual fin ray under a simple case of loading under a point force. One hemitrich base is fixed in position and orientation (clamped) and the second hemitrich is clamped to a micrometer. As the micrometer is turned, the second hemitrich base slides axially relative to the first, setting ϕ0. A probe pushes down on the fin ray near the tip, measuring the force needed to hold vertical deflection to zero at this point as ϕ0 is increased.
Figure 6a shows ray 4 of a specimen for one value of ϕ0. The corresponding model ray, depicted as a white dashed line, is shown for comparison. The model ray has the same value of ϕ0, distributions of B and d taken from imaging of ray 6 in a different specimen, and a constant value of G=128, the mean of G values for the fully intact ray in table 1, which is the same specimen. We see that both the model and the experiment show a sharp upturning beyond the point where the force is applied. The experimental ray shows an additional inflection point nearer to the base while the model ray is relatively flat. This discrepancy may result from the nonlinear elastic properties of the actual fin ray.
Figure 6.
(a) A comparison between the model (dashed line) and the experimental trajectory (photograph), when a point force is applied (aluminium triangle in the photograph) at two-thirds the distance from the base to the tip of the ray. The point s=0 for the model is defined as the point where both hemitrichs appear fully segmented in the photo, though here the agreement is relatively insensitive to where s=0 is defined, since the bending occurs mainly beyond the point force. (b) Experimental measurements of the force versus base shift, for a point force which holds a point two-thirds along the ray fixed as in (a). (c) The data in (b) replotted on a log–log scale (green triangles), together with the corresponding data for the two models: equation (3.14), a uniform-shear-modulus material (blue circles) showing a linear growth of force with shift, and equation (3.15), collagen springs (red crosses) showing a cubic growth of force with shift. Forces f have been normalized to the value 1 at ϕ0=10−2.2, and only the slopes of the lines are to be compared.
The ray shape under this point force has a simple physical interpretation. The point force prevents the ray from bending upward sharply near the base, as in the unforced solution shown in figure 4. Thus, the ray is constrained to be relatively flat with shear approximately ϕ0/d in this region. Just beyond the point of application of the point force, the ray bends sharply to relieve most of the shear energy in the collagenous gel in the remainder of the ray, between the point force and the tip.
In figure 6b, we plot the point force versus ϕ0 measured in the experiment. The force grows nonlinearly, which also occurs in a model with a nonlinear shear behaviour—such as that provided by collagen fibres as springs. In figure 6c, we replot the experimental data from figure 6b (triangles) with the behaviour of the models, with linear shear material with rigidity G (circles) and with the collagen springs with stiffness k2 (crosses). For the linear shear material, there is a linear force–shift relationship, whereas the collagen spring model shows a cubic growth. This cubic behaviour arises because the second term in equation (3.15) grows cubically with ϕ0 for small ϕ0. For both models, all material properties are uniform; for simplicity we do not consider the effect of tapering in this comparison. We adjust the (uniform) values of G and k2 here, and compare only the slopes of the curves. We see that the experimental data show a dependence that grows more rapidly than a linear growth and slightly less rapidly than a cubic growth. However, cubic behaviour seems to be a reasonable approximation to the nonlinear behaviour of the actual intraray material, with its more complex material properties.
5.2 Cantilever
In figure 7, we examine a complementary situation that highlights the ‘stiffening’ function of the fin-ray mechanism. Here, the two bases of the ray are either clamped, with both clips held fixed at the same longitudinal position, or else free to slide axially, with only one of the fin-ray bases held by a clip. In our model, the two corresponding boundary conditions are (i) ϕ0=0 or (ii) the free-base boundary condition in equation (3.16).
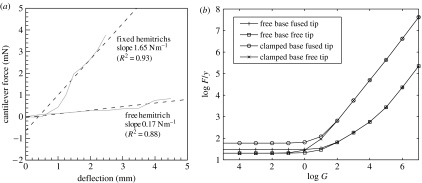
Figure 7.
(a) The ability of the ray-shifting mechanism to resist a point force is quantified in the experiment by measuring the deflection of the ray versus an applied point force, for two different conditions at the base of the ray. The ray is clamped horizontally at the base, and a vertical point force is applied at two-thirds of the distance from the ray base to the tip, as in figure 6a. When only one of the bases is clamped, the ray deflects much more than when both bases are clamped. In the latter case, the force–displacement curve may be fit with a slope of 1.98 N m−1, about 12 times the value when one hemitrich is free. Dashed lines show linear fits to the data. (b) In the corresponding model, only slopes of the corresponding curves in the linear (small-deflection) regime are shown, versus the non-dimensional shear modulus G (introduced in equation (3.11)). Four boundary conditions are tested—two at the base (both bases clamped versus one free) and two at the tip (hemitrichs fused or free at the tip). When G≪1, G drops out of the problem and the bending modulus B alone resists the force as a classical cantilever. In this limit, if the tip is fused, the resistance is increased. By contrast, for G≫1, the slope increases linearly with G in all cases, as the shear modulus provides the primary resistance. As G increases through 1, the ratio of force–displacement with both bases clamped versus one free transitions from 3 to 100; the experimental ratio of 12 occurs for G≈102, which is close to the values of G found by ray-shape fitting in table 1.
Meanwhile, a probe pushes down on the fin ray at approximately two-thirds of the distance from the base to the tip, and the force on the probe is measured as a function of tip deflection of the ray. The experimental data are shown in figure 7a. We see an approximately linear relation between force and deflection for the case of one hemitrich base free, and an approximately linear relation with an offset—and much larger slope or stiffness—for the case of both bases fixed.
In figure 7b, we present the corresponding data for uniform rays in the model with two different boundary conditions at each of the base and tip—resulting in four curves in total. Here, a downward point force F (non-dimensionalized by B0/L2) is applied at s=2/3, resulting in an external bending moment for 0<s<2/3 in equation (3.14). Unlike in the experiment, for these idealized rays with flat equilibrium shapes, there is an asymptotically linear relation between deflections y and forces F for small forces. Thus, each data point corresponds to the slope of a line like those in figure 7a but perfectly linear. Therefore, we plot only the slope (or stiffness) dF/dy in this linear regime and study its dependence on the intraray shear modulus G. There are two main results to emphasize, which hold also for rays with d tapered as in the experiment. First, when G>3—when shear energy is comparable to bending energy—the rays with clamped bases give stiffnesses that exceed those of the rays with free bases by a factor of 4 (for G=3) to 100 (for G>105). In the experiment, the factor is 12, which occurs when G≈100 in the model, similar to the value of G found by curve fitting the whole ray in table 1. Second, for clamped bases and G>10, the stiffness scales linearly with G. This indicates that in this regime, the shear energy provides the dominant resistance to the point force when both bases are clamped. Here, G is large enough to give a shear energy comparable to bending energy for all deflections of the ray by the point force. For free bases, by contrast, dF/dy grows more slowly. In this case, the bending rigidity of each hemitrich is of greater importance in resisting the point load over a wider range of G.
We have noted that figure 7a shows a relation between force and deflection which is linear with an offset for both bases clamped. One possible explanation for the offset is that the unstressed shape of the real ray is not flat, so some amount of deflection at the tip is possible without much change of position at the bases. Another explanation follows directly from the model with a shear force given by collagen fibres modelled as linear springs (equation (3.15)). Here, the force grows as deflection cubed instead of linearly, for small forces, because the second term on the left-hand side of equation (3.15) scales as for small ϕ0.
5.3 Uniform force distribution
So far, we have considered a point force applied to the ray. In the case of a distributed normal force per unit length p applied to the ray, such as a hydrodynamic force, there are also solutions with inflection points, but the sharp change in the derivative of curvature implied by a point-force loading in equation (3.14) is now spread out over the ray. For a uniform p, the external moment in equation (3.14) is .
The solution to equation (3.14) for uniform loading is
| (5.2) |
In figure 8b, we show the solution for ϕ0=0.01, p=200, d=0.01, G=200 and B=1. Here, the relevant dimensionless point-force parameter pd/Gϕ0=1. As for the case of the point-force load, the resistance to bending is a combined effect of the shear modulus of the intraray material and the fused-end boundary condition at s=1. For comparison, we show in figure 8b a ‘passive’ ray under the same loading, but with a free-base boundary condition. This is the shape of the ray when no force is applied at the base to resist loading. For these parameters, we see that the base shift creates an S-shaped ray and a reversal of the ray-tip deflection.
6. Synthesis and future directions
Using experiments and a mathematical model, we have examined the mechanical properties of fin rays that allow the control of fin shape and fin stiffness in response to external forces. Our mechanical model approximates the two-ray halves as thin beams, and the intraray material as incompressible and with shear modulus that is constant with respect to shear (i.e. the intraray material is linearly elastic), or representative of collagenous fibre springs. Under these assumptions, the model involves just three parameters (each functions of axial position along the ray): (i) the bending rigidity of each ray half, (ii) the intraray spacing, and (iii) the intraray shear modulus. In uniform rays, we have found that curvature is localized near the base, so as to relieve shear strain over the remainder of the ray. We have found that tapering is a way of distributing curvature more evenly over the ray. Furthermore, we have shown that forcing at the fin-ray base can dramatically increase the stiffness of the ray under loading.
Our model is sufficiently general to study a wide range of mechanical properties of fin rays. It was proposed by McCutchen (1970) that flexibility has a hydrodynamical benefit through lift-based propulsion of the tail, by creating a curved (or ‘cambered’) surface. A classical result from airfoil theory is that the lift on a slender wing increases linearly with the amount of curvature (Batchelor 1967). However, there has been relatively little work on the hydrodynamical role of flexibility of fin rays. Nonetheless, the fin ray, with its complex structure that confers flexibility, is widespread among fish species, so we hypothesize that flexibility confers advantages in applying forces to the fluid. We note that the tapering of a ray, by allowing the distribution of curvature away from the ray base, allows a closer approximation to the nearly constant curvature of a classical cambered airfoil. Future work will consider more specifically the design and function of the fin ray with respect to its dynamical interaction with a fluid environment.
The fin ray uses a material with bending rigidity confining an incompressible material to transduce motion. Our one-dimensional model may be extended to other confined incompressible materials, which arise in other motion-transduction systems. By making the shear modulus G large, and changing the walls to be extensible with negligible bending rigidity, we may model the tensile stresses in skin containing an internally driven muscle that resists shearing. Jordan gave a qualitative picture of a similar model for swimming leeches (Jordan 1996), and such a model could be a simple way to quantify Wainwright's (2000) models of fully coupled skin, muscle and backbone mechanics. This model may be used to quantify the forces and stresses acting on bodies of incompressible muscle with an internal backbone and exterior tension-bearing skin, of which fishes and the soft appendages including tongues and tentacles are examples (Kier & Smith 1985).
Despite the fact that ray-finned fishes are a highly successful group that have been the subject of numerous studies of locomotor anatomy and mechanics, very little attention has been paid to one of their key characteristics, i.e. the fin rays that give the group its name. The fin rays of ray-finned fishes possess a novel bilaminar structure capable of active curvature control, which is distinct from the rod-like fin ray supports in other major fish groups, such as sharks and lungfishes. This endows ray-finned fishes with the potential of modulating fluid dynamic forces in a way not possible in other major groups of fishes, or in other animals with oscillating appendage-based propulsion, such as insects. And it is probable that there is considerable diversity of fin-ray design and function within ray-finned fishes themselves, although this diversity has yet to be investigated. In this paper, we test the model of fin-ray mechanics with data from one taxon, the bluegill sunfish, but this model could easily be extended to other species, with the goal of understanding the diversity of fin function. One of the more obvious areas to expect diversity across ray-finned fishes is the location of maximal bending on fin rays. Ray-finned fishes that use fins for propulsion on the substrate may possess fin rays that generate the greatest bending near the tips. Fishes such as mudskippers that use their pectoral fins for terrestrial locomotion may possess stiffer rays for support, or may use the bilaminar actuation mechanism to produce thrust against the substrate. The extent of variation in fin-ray structure and mechanical properties among different fins, during growth, or across different species with distinct habits such as burrowing or different swimming styles is entirely unknown. The development of a mathematical model of fin-ray properties provides a starting framework for exploring the diversity of propulsive surface mechanics across a broad range of fish species, and lays the quantitative structure for future comparative biological study.
Acknowledgments
We acknowledge useful conversations with Michael Brenner, L. Mahadevan and Eric Lauga. This work was supported by an NSF Mathematical Sciences Postdoctoral Fellowship to S.A., an ONR-MURI grant no. N00014-03-1-0897 on fish pectoral fin function, monitored by Dr Thomas McKenna and initiated by Dr Promode Bandyopadhyay, and by an NSF grant IBN0316675 to G.V.L.
Appendix A. Fitting experimental and model curvatures and trajectories
Here, we describe the method for obtaining the best-fit values of log2G, shown in table 1.
A.1 Extracting experimental geometry
We consider a single fin-ray specimen (fin ray 4 from a bluegill sunfish), which has been cut out of a fin. The fin ray is held in clips, which apply an axial shift (ϕ0 in the above model) at the base of the ray. The actual fin rays have an unsegmented section starting from the base, and segmenting begins some distance along the ray—usually 10–30% of the ray length. We define the base of the fin ray (s=0 in the model) as the position where complete segmenting begins. Complete segmenting is essential to our application of a beam model to the ray.
Given a photo such as figure 2a, we define the ray as the region where pixels are above a threshold in lightness. We then use the boundary-tracking software included in Matlab v. 7.0 to extract the boundary of this region. We identify the base (s=0) as the horizontal location where segmenting begins. We identify the tip (s=1) as the point in the region farthest from the base. We then perform a Fourier filter on the boundary (which is a closed loop), setting to zero the amplitudes for wavenumbers higher than k=20. The Fourier filter removes jagged edges from the region due to pieces of interray fin membrane. To find the centre-line trajectory of the ray, we take the average of the two halves of the boundary connecting the base to the tip.
We can also estimate the other geometrical parameters d/L and ϕ0/L directly from the photographs. The length of the centre-line trajectory above is L. In a photo of the unforced ray, we note the relative axial position of the fin ray halves (approximately aligned) at the base. We then directly measure the change in axial position at the base in photos with non-zero deflection. This change is the shift ϕ0, corresponding to shifts in the ray heads applied by the clips. The spacing between the ray halves (d) is measured in CT scans. From axial CT scans, we estimate that the bony segments take up about 30% of this thickness. The remaining thickness, composed of the collagenous intraray material, has an approximately cylindrical geometry. To obtain the average thickness, we therefore multiply this thickness by the factor π/4, which is the average height of a semicircle of radius 1.
A.2 Extracting experimental curvature
Differences in trajectories are amplified when the trajectories are differentiated twice to find curvatures. Therefore, a potentially more accurate way of finding the best theoretical-curve fit to a curve extracted from noisy data is to compare distributions of curvature instead of trajectories.
Another reason why comparing curvatures is advantageous in our case is that the range of theoretical rays has a simple classification in terms of curvature. As the shear modulus G is increased, the centroid of curvature in an unforced ray moves towards the base, monotonely.
We extract the curvatures of the experimental rays by fitting the trajectory data to quintic smoothing splines. A widely used method for choosing the smoothing parameter was given by Craven & Wahba (1979). Quintic splines find the piecewise quintic polynomial p(s), which best fits a set of data points f(si) in the sense that it minimizes the function
| (A1) |
where ρ is a smoothing parameter. Hence, the best-fit quintic spline strikes a balance between fitting the data and preserving smoothness (here measured by minimization of the third derivative), a balance set by the smoothing parameter ρ. When ρ is large, the spline matches the data exactly—and is as noisy as the data. When ρ is small, the spline has zero third derivative, and is thus the best constant-curvature fit to the data. To find the ‘best’ value of ρ, we use the fact that for ρ too large, and for ρ too small, the absolute value of the curvature is spread out almost uniformly over the ray. However, our model predicts (and inspection of photographs confirm) that the curvature is largest near the base of the ray. Hence, we choose that value of ρ which minimizes the distance of the centroid of the absolute value of the curvature from the base of the ray. As we have noted, the location of the centroid of curvature also parametrizes the theoretical curves—as the shear modulus G is increased, the centroid of curvature moves towards the base, monotonely.
A.3 Fitting to experimental trajectory
In the third column of table 1, we list the value of G that gives a theoretical ray corresponding to the least-square distance from the centre-line trajectory extracted above.
A.4 Fitting to experimental curvature
Increasing the parameter G concentrates the curvature near the base of the ray. Decreasing it spreads the curvature out along the ray. In the fourth column of table 1, we list the value of G that gives the best match between the theoretical and experimental curves in the location of the centroid of the curvature.
References
- Antman S.S. 2nd edn. Springer; New York, NY: 2005. Nonlinear problems of elasticity. [Google Scholar]
- Batchelor G.K. 1st edn. Cambridge University Press; Cambridge, UK: 1967. An introduction to fluid dynamics. [Google Scholar]
- Craven P, Wahba G. Smoothing noisy data with spline functions—estimating the correct degree of smoothing by the method of generalized cross-validation. Numerische Mathematik. 1979;31:377–403. doi: 10.1007/BF01404567. [DOI] [Google Scholar]
- Drucker E.G, Lauder G.V. Function of pectoral fins in rainbow trout: behavioral repertoire and hydrodynamic forces. J. Exp. Biol. 2003;206:813–826. doi: 10.1242/jeb.00139. [DOI] [PubMed] [Google Scholar]
- Geerlink P.J, Videler J.J. The relation between structure and bending properties of teleost fin rays. Neth. J. Zool. 1987;37:5980. [Google Scholar]
- Jordan C.E. Coupling internal and external mechanics to predict swimming behavior: a general approach? Am. Zool. 1996;36:710–722. [Google Scholar]
- Kier W.M, Smith K.K. Tongues, tentacles and trunks—the biomechanics of movement in muscular-hydrostats. Zool. J. Linn. Soc. 1985;83:307–324. [Google Scholar]
- Lauder G.V. Locomotion. In: Evans D.H, Claiborne J.B, editors. The physiology of fishes. 3rd edn. CRC Press; Boca Raton, FL: 2006. pp. 3–46. [Google Scholar]
- Lauder G.V, Drucker E.G. Morphology and experimental hydrodynamics of fish fin control surfaces. IEEE J. Oceanic Eng. 2004;29:556–571. doi: 10.1109/JOE.2004.833219. [DOI] [Google Scholar]
- McCutchen C.W. The trout tail fin: a self-cambering hydrofoil. J. Biomech. 1970;3:271–281. doi: 10.1016/0021-9290(70)90029-1. [DOI] [PubMed] [Google Scholar]
- Sacks M.S, Sun W. Multiaxial mechanical behavior of biological materials. Annu. Rev. Biomed. Eng. 2003;5:251–285. doi: 10.1146/annurev.bioeng.5.011303.120714. [DOI] [PubMed] [Google Scholar]
- Segel L.A. 1st edn. Dover Publications; New York, NY: 1987. Mathematics applied to continuum mechanics. [Google Scholar]
- Velegol D, Lanni F. Cell traction forces on soft biomaterials I: Microrheology of type I collagen gels. Biophys. J. 2001;81:1786–1792. doi: 10.1016/S0006-3495(01)75829-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Videler J.J. 1st edn. Chapman & Hall; London, UK: 1993. Fish swimming. [Google Scholar]
- Wainwright S.A. The animal axis. Am. Zool. 2000;40:19–27. doi: 10.1668/0003-1569(2000)040%5B0019:TAA%5D2.0.CO;2. [DOI] [Google Scholar]