Abstract
There has been much uncertainty as to whether metastasis requires mutation at the time of spread. Here, we use clinical data to calculate the probability of the spread of melanoma and breast cancer cells. These calculations reveal that the probability of the spread of cancer cells is relatively high for small tumours (∼1 event of spread for every 500 cells for melanomas of 0.1 mm) and declines as tumours increase in size (∼1 event of spread for every 108 cells for melanomas of 12 mm). The probability of spread of breast cancer cells from the lymph nodes to the periphery is ∼1 event of spread for every 108 cells in the nodal masses, which have a mean diameter of 5 mm, while the probability of spread of cancer cells from the breast to the periphery when the primary masses are 5 mm is also ∼1 event of spread for every 108 cells. Thus, the occurrence of an event of spread from the breast to the lymph nodes appears not to increase the propensity of the progeny of those cells to spread from the lymph nodes to the periphery. These values indicate that the spread of human breast cancer and melanoma cells is unlikely to occur by a mechanism requiring mutation at the time of spread.
Keywords: metastasis, probability, mutation
There has been much uncertainty as to whether metastasis requires mutation at the time of spread (Cifone and Fidler, 1981; Fidler, 1983; Sobel, 1990; Welch et al, 2000; Yokota, 2000; Bernards and Weinberg, 2002; Couzin, 2003; Bernards, 2003; Van't Veer and Weigelt, 2003; Yang et al, 2004). Mutations have a number of characteristic features, in terms of the rates of their occurrence and other qualities, which are diagnostic: mutations are rare, a phenotype conferred on a cell by mutation is inherited by the progeny of the cell, and the rates of the appearance of phenotypes caused by mutations either remains constant over time for those phenotypes requiring only a single mutation, or increase in frequency for those phenotypes requiring the accumulation of multiple mutations. We have recently shown that from clinical data it is possible to measure the rates of metastatic spread, expressed in terms of the probability of spread per cell (Michaelson, 1999; Michaelson et al, 2002, 2003). Here we use this methology to measure the probability of spread per cell for human breast cancer and melanoma. The values of these probabilities are inconsistent with metastasis occurring by a process of mutation.
METHODS
Data
Data on the relationship between tumour size and breast cancer survival is from the USC/Van Nuys population (Silverstein, 2000; Michaelson et al, 2002, 2003), from Tabar et al (2000) and Tubiana and colleagues (Koscielny et al, 1984; Tubiana and Koscielny, 1990, 1991). For details and the general equivalence of these survival values (based on the 15-year Kaplan–Meier survival rate, based upon Karrison et al (1999) finding that it is not until this point in time that the survival rate become clear), see Michaelson et al (2002, 2003). Data on the relationship between tumour thickness and melanoma survival are 10-year Kaplan–Meier disease survival values from Balch et al, 2001).
Tumour diameters (breast cancer) and thickness (melanoma) were taken at pathological analysis. Since we shall be interested in tumour size in terms of the number of cells that they contain, N, we can generate rough estimates of the value of N that are quite satisfactory for our purposes here by converting values of tumour diameter or thickness, D, into values of cell number, N, assuming spherical geometry and a density of s (here we shall use 108 cells/cm3 as a biologically plausible estimate of, s, as outlined in Boon et al, 1982; Pesce and Colacino, 1986; Van der Linden et al, 1986; and Michaelson et al, 2002). While this estimate of the value of s is biologically reasonable, for the purposes of the calculations made here, it need not be precise, as any error in the estimation of s by an order of magnitude or more will not change the general lessons drawn here on the nature of cancer spread, although it will affect the precise values of the probability of spread.
Node-positive patients are defined as those patients with one or more lymph nodes found to have cancer upon pathological analysis. The range of nodes examined among women in the USC/Van Nuys populations varied from 1 to 47; however, only 10% of women had fewer than 10 nodes examined, while only 2% of women had fewer than five nodes examined. The mean and median number of nodes examined was 16.8 and 17, with a s.d. of 7.2.
Information on the size of the cancer metastases in the lymph nodes was collected from microscope slides from 16 node-positive patients, chosen at random, among MGH patients with invasive breast cancer diagnosed in 1993, among which there were 49 positive lymph nodes. Microscopic imagines of each node were captured with a Nikon Eclipse E400 microscope equipped with an Insight digital camera (Diagnostic Instruments Inc., Sterling Heights, MI, USA), used to capture high-resolution noninterpolated image with a × 10 objective. The image measurements were calibrated by comparison to an image of the 1 mm grating on a haemocytometer. The longest dimension of the metastasis was measured from prints made of the images. All slides were reviewed by a qualified breast pathologist (DS). In some nodal metastases, noncancerous cells were apparent within the mass of cancer, and the sizes of these cancerous and noncancerous areas were measured. Thus, the values labelled ‘Diameter (corrected)’ (Table 3) were corrected with respect to the cancerous component of each metastasis, and thus were representative of the size that a mass of cancer would have had, had it shown the same number of cells but no noncancerous component.
Table 3. Sizes of the invasive breast cancer metastases seen in the lymph nodes.
| Node number | Patient number | Diameter (mm) | Fraction of the metastatic area containing cancer (%) | Diameter (corrected) |
|---|---|---|---|---|
| 49 | 16 | 0.3 | 100 | 0.3 |
| 32 | 9 | 1 | 100 | 1 |
| 20 | 3 | 1 | 100 | 1 |
| 31 | 8 | 1.1 | 100 | 1.1 |
| 43 | 14 | 1.4 | 100 | 1.4 |
| 41 | 14 | 1.9 | 65 | 1.5 |
| 17 | 2 | 2 | 100 | 2 |
| 21 | 4 | 2 | 95 | 2 |
| 39 | 12 | 2.1 | 100 | 2.1 |
| 13 | 2 | 2.5 | 93 | 2.4 |
| 29 | 7 | 2.7 | 95 | 2.6 |
| 15 | 2 | 3 | 95 | 2.9 |
| 30 | 7 | 3 | 100 | 3 |
| 36 | 12 | 3 | 95 | 3 |
| 2 | 1 | 3.2 | 10 | 3.2 |
| 22 | 5 | 3.4 | 95 | 3.3 |
| 5 | 1 | 3.4 | 93 | 3.3 |
| 34 | 10 | 3.7 | 95 | 3.7 |
| 37 | 12 | 3.9 | 100 | 3.9 |
| 4 | 1 | 3.9 | 86 | 3.6 |
| 47 | 15 | 4.3 | 95 | 4.2 |
| 35 | 11 | 4.5 | 95 | 4.4 |
| 40 | 13 | 5.4 | 95 | 5.2 |
| 6 | 1 | 5.4 | 86 | 5 |
| 16 | 2 | 5.4 | 100 | 5.4 |
| 23 | 5 | 5.5 | 76 | 4.8 |
| 33 | 10 | 5.5 | 78 | 4.9 |
| 24 | 5 | 6 | 80 | 5.4 |
| 48 | 15 | 6 | 90 | 5.7 |
| 42 | 14 | 6.4 | 10 | 6.4 |
| 45 | 14 | 7.1 | 60 | 5.5 |
| 10 | 2 | 7.1 | 100 | 7.1 |
| 11 | 2 | 7.1 | 100 | 7.1 |
| 12 | 2 | 7.7 | 95 | 7.5 |
| 18 | 2 | 8 | 43 | 5.2 |
| 19 | 2 | 9 | 72 | 7.6 |
| 46 | 14 | 9 | 90 | 8.5 |
| 28 | 6 | 9 | 80 | 8 |
| 1 | 1 | 9.8 | 84 | 9 |
| 44 | 14 | 10 | 49 | 7 |
| 9 | 2 | 10 | 65 | 8.1 |
| 3 | 1 | 10 | 86 | 9.3 |
| 14 | 2 | 10 | 95 | 9.7 |
| 7 | 1 | 10.7 | 55 | 7.9 |
| 26 | 6 | 11 | 35 | 6.5 |
| 8 | 2 | 11 | 95 | 10.7 |
| 25 | 6 | 12.5 | 45 | 8.4 |
| 27 | 6 | 14.5 | 85 | 13.4 |
| 38 | 12 | 15 | 100 | 15 |
| Average | 5.95 | 86 | 5.31 |
Mathematical methods
Following the line of thinking outlined previously (Michaelson et al, 2002), let us define p as the probability of a single successful event of metastatic spread prior to surgery per unit of tumour volume, s. When the value of s is chosen so as to be to be equivalent to the volume of a cell, then p, from a practical standpoint, is also the probability of spread per cell, N. Note that by defining p on a per volume or per-cell basis, we are not assuming that every cell in the tumour has the potential to spread. For example, if we find that in a specific context, p=1-in-ten-billion, then we shall not mean that every cell in the tumour mass will have such a chance of spread. Rather, this simply means that for every ten billion cells in a tumour, there will be about one event of metastatic spread. Note also that we have defined p as the probability of an event of spread, which can be either the spread of a single cell or a cluster of cells. Additionally, since we are defining p in terms of successful events of spread, that is events of spread that go on to give rise to evident cancer in the local nodes, or to give rise to distant metastatic disease, we are not concerned with those events of spread that do not result in such manifestations of metastasis. Let us define L as the fraction of patients displaying the occurrence of such an event of spread. If we are interested in examining the probability of the lethal spread of cells to the periphery, resulting in metastatic disease, then L will be the fraction of patients dying of the cancers; while if we are interested in measuring the nonlethal spread of cancer cells to the lymph nodes, then L will be the fraction of patients with cancer found in the nodes upon pathological analysis. It follows that (1-L) will be the fraction of the fraction of patients not displaying the occurrence of spread Similarly, as p is the per-cell probability of an event of spread, the probability that there will not be an event of spread will be (1-p), and the overall probability that a tumour of N cells has not given rise to one or more such metastases will be (1-p)N. It has long been appreciated that for small values of p, (1-p)N can very well be approximated by e-Np, and thus:
 |
Rearranging provides a way to estimate the probability of spread (p) per cell (N):
RESULTS
From clinical data, we are able to observe the consequences of several examples of the spread of cancer cells, and their probabilities: the lethal spread of breast cancer and melanoma cells from the primary site to the periphery (pBC-overall and pMEL-overall); and the nonlethal spread of breast cancer cells from the primary site to the local nodes (pBC-to-nodes), and the lethal spread of breast cancer cells from the lymph nodes to the periphery (pBC-from-nodes) (Tables 1 and 2). To see the general approach for estimating the values of these probabilities, consider the simple example of a group of patients with tumours containing a billion cells (N=109 cells, ∼3 cm), of whom 10% have died of metastatic disease (L=0.1). If we assume, for explanatory purposes, that each death was the result of the spread of a single cell from the primary site to the periphery (an assumption not made in the math outlined in equations (1) and (2) above) then it follows that the probability (p) of lethal spread is approximately 1 event of spread for every ten billion cells in the primary mass (p≈L/N=0.1/109). Similarly, if about 1% patients with a different type of tumour, but of the same size (N=109 cells), have died of metastatic disease (L=0.01), then it follows that the probability of lethal spread (p) is about 1 event of spread for every hundred billion cells (p≈L/N=0.01/109).
Table 1. Data and calculations of the probability of the spread of cancer cells.
| Cancer | Population | Size range | Nominal tumour size (mm) | Cell number (N) | Manifestation of metasatasis | Fraction of patients with a manifestation of metastasis (L) (%) | Probability of spread (p=−ln(1−L)/N) |
|---|---|---|---|---|---|---|---|
| Breast cancer | Tabar et al | 10–14 | 12 | 9.05E+07 | Cancer death | 13 | 1/6.5 × 108 |
| Breast cancer | Tabar et al | 15–19 | 17 | 2.57E+08 | Cancer death | 20 | 1/1.2 × 109 |
| Breast cancer | Tabar et al | 20–29 | 25 | 8.18E+08 | Cancer death | 45 | 1/1.4 × 109 |
| Breast cancer | Tabar et al | 30–49 | 39 | 3.11E+09 | Cancer death | 56 | 1/3.9 × 109 |
| Breast cancer | Tubiana et al | 10–25 | 17 | 2.57E+08 | Cancer death | 27 | 1/8.2 × 108 |
| Breast cancer | Tubiana et al | 26–35 | 30 | 1.41E+09 | Cancer death | 42 | 1/2.6 × 109 |
| Breast cancer | Tubiana et al | 36–45 | 40 | 3.35E+09 | Cancer death | 55 | 1/4.1 × 109 |
| Breast cancer | Tubiana et al | 46–55 | 50 | 6.54E+09 | Cancer death | 66 | 1/6.1 × 109 |
| Breast cancer | Tubiana et al | 56–65 | 60 | 1.13E+10 | Cancer death | 78 | 1/7.4 × 109 |
| Breast cancer | Tubiana et al | 66–75 | 70 | 1.80E+10 | Cancer death | 83 | 1/1.0 × 1010 |
| Breast cancer | Tubiana et al | 76–85 | 80 | 2.68E+10 | Cancer death | 81 | 1/1.6 × 1010 |
| Breast cancer | Tubiana et al | 86–95 | 90 | 3.82E+10 | Cancer death | 92 | 1/1.5 × 1010 |
| Breast cancer | Van nuys | 10–14 | 12 | 9.05E+07 | Cancer death | 14 | 1/6.0 × 108 |
| Breast cancer | Van nuys | 15–19 | 17 | 2.57E+08 | Cancer death | 28 | 1/7.8 × 108 |
| Breast cancer | Van nuys | 20–29 | 25 | 8.18E+08 | Cancer death | 33 | 1/2.0 × 109 |
| Breast cancer | Van nuys | 30–49 | 39 | 3.11E+09 | Cancer death | 46 | 1/4.0 × 109 |
| Breast cancer | Van nuys | 15–19 | 17 | 2.57E+08 | Cancer in nodes | 32 | 1/6.7 × 108 |
| Breast cancer | Van nuys | 20–24 | 22 | 5.58E+08 | Cancer in nodes | 39 | 1/1.1 × 109 |
| Breast cancer | Van nuys | 25–29 | 27 | 1.03E+09 | Cancer in nodes | 39 | 1/2.1 × 109 |
| Breast cancer | Van nuys | 30–34 | 32 | 1.72E+09 | Cancer in nodes | 50 | 1/2.5 × 109 |
| Breast cancer | Van nuys | 35–39 | 37 | 2.65E+09 | Cancer in nodes | 54 | 1/3.4 × 109 |
| Breast cancer | Van nuys | 40–44 | 42 | 3.88E+09 | Cancer in nodes | 63 | 1/3.9 × 109 |
| Breast cancer | Van nuys | 45–50 | 47 | 5.44E+09 | Cancer in nodes | 54 | 1/7.1 × 109 |
| Breast cancer | Van nuys | 50–54 | 52 | 7.36E+09 | Cancer in nodes | 59 | 1/8.3 × 109 |
| Melanoma | Balch et al | — | 0.10 | 5.3E+01 | Cancer death | 11 | 1/480 |
| Melanoma | Balch et al | — | 0.23 | 6.8E+02 | Cancer death | 9 | 1/7100 |
| Melanoma | Balch et al | — | 0.37 | 2.6E+03 | Cancer death | 10 | 1/2.4 × 104 |
| Melanoma | Balch et al | — | 0.44 | 4.3E+03 | Cancer death | 14 | 1/2.9 × 104 |
| Melanoma | Balch et al | — | 0.50 | 6.7E+03 | Cancer death | 18 | 1/3.4 × 104 |
| Melanoma | Balch et al | — | 0.60 | 1.2E+04 | Cancer death | 22 | 1/4.5 × 104 |
| Melanoma | Balch et al | — | 0.70 | 1.8E+04 | Cancer death | 18 | 1/9.1 × 104 |
| Melanoma | Balch et al | — | 0.84 | 3.1E+04 | Cancer death | 20 | 1/1.4 × 105 |
| Melanoma | Balch et al | — | 0.91 | 3.9E+04 | Cancer death | 23 | 1/1.5 × 105 |
| Melanoma | Balch et al | — | 0.97 | 4.8E+04 | Cancer death | 21 | 1/2.0 × 105 |
| Melanoma | Balch et al | — | 1.11 | 7.1E+04 | Cancer death | 20 | 1/3.1 × 105 |
| Melanoma | Balch et al | — | 1.17 | 8.5E+04 | Cancer death | 27 | 1/2.7 × 105 |
| Melanoma | Balch et al | — | 1.31 | 1.2E+05 | Cancer death | 30 | 1/3.3 × 105 |
| Melanoma | Balch et al | — | 1.38 | 1.4E+05 | Cancer death | 25 | 1/4.8 × 105 |
| Melanoma | Balch et al | — | 1.51 | 1.8E+05 | Cancer death | 30 | 1/5.0 × 105 |
| Melanoma | Balch et al | — | 1.58 | 2.1E+05 | Cancer death | 25 | 1/7.1 × 105 |
| Melanoma | Balch et al | — | 1.71 | 2.6E+05 | Cancer death | 30 | 1/7.1 × 105 |
| Melanoma | Balch et al | — | 1.85 | 3.3E+05 | Cancer death | 32 | 1/8.3 × 105 |
| Melanoma | Balch et al | — | 1.88 | 3.5E+05 | Cancer death | 38 | 1/7.1 × 105 |
| Melanoma | Balch et al | — | 1.98 | 4.1E+05 | Cancer death | 44 | 1/7.1 × 105 |
| Melanoma | Balch et al | — | 2.11 | 4.9E+05 | Cancer death | 40 | 1/1.0 × 106 |
| Melanoma | Balch et al | — | 2.25 | 6.0E+05 | Cancer death | 45 | 1/1.0 × 106 |
| Melanoma | Balch et al | — | 2.52 | 8.3E+05 | Cancer death | 36 | 1/1.9 × 106 |
| Melanoma | Balch et al | — | 2.72 | 1.1E+06 | Cancer death | 45 | 1/1.8 × 106 |
| Melanoma | Balch et al | — | 3.02 | 1.4E+06 | Cancer death | 47 | 1/2.3 × 106 |
| Melanoma | Balch et al | — | 3.39 | 2.0E+06 | Cancer death | 50 | 1/2.9 × 106 |
| Melanoma | Balch et al | — | 3.72 | 2.7E+06 | Cancer death | 54 | 1/3.4 × 106 |
| Melanoma | Balch et al | — | 4.26 | 4.1E+06 | Cancer death | 54 | 1/5.3 × 106 |
| Melanoma | Balch et al | — | 4.73 | 5.5E+06 | Cancer death | 55 | 1/7.1 × 106 |
| Melanoma | Balch et al | — | 5.27 | 7.7E+06 | Cancer death | 59 | 1/8.3 × 106 |
| Melanoma | Balch et al | — | 5.77 | 1.0E+07 | Cancer death | 57 | 1/1.2 × 107 |
| Melanoma | Balch et al | — | 6.74 | 1.6E+07 | Cancer death | 63 | 1/1.6 × 107 |
| Melanoma | Balch et al | — | 7.75 | 2.4E+07 | Cancer death | 65 | 1/2.3 × 107 |
| Melanoma | Balch et al | — | 12.32 | 9.8E+07 | Cancer death | 76 | 1/6.7 × 107 |
Table 2. The values of the probabilities of various events of cancer spread.
| Metastatic event | Probability of spread per cell p=-ln(1-L)/N | Source of information for the value of L | Value of p the probability of spread per cell for tumour masses of ∼5 mm | Nature of relationship between the value of p and tumour size |
|---|---|---|---|---|
| Lethal spread of breast cancer from the primary site in the breast to periphery, pathway unknown | p BC-overall | LBC-overall=the fraction of breast cancer deaths among all patients | 8.27 × 10−9 | p=aNb aBC-overall≈0.000056 bBC-overall≈-0.56203 |
| Lethal spread of melanoma from the primary site in the skin to periphery, pathway unknown | p MEL-overall | LMEL-overall=the fraction of melanoma deaths among all patients | 1.23 × 10−7 | p=aNb aMEL-overall≈0.027 bMEL-overall≈-0.7836 |
| Nonlethal spread of breast cancer from the primary site in the breast to the lymph nodes | p BC-to-nodes | LBC-to-nodes=the fraction of node positive patients among all patients | 1.75 × 10−8 | p=aNb aBC-to-nodes≈0.000092 bBC-to-nodes≈-0.69251 |
| Lethal spread of breast cancer from the lymph nodes to the periphery | p BC-from-nodes | LBC-from-nodes=6.08%, the lethal contribution per positive lymph node | 7.96 × 10−9a | Undefined |
The size of nodal metastases was found to have a mean value of 5.3 mm (Table 3). The value shown here for pBC-overall is for a mass of 5 mm; for 5.3 mm, pBC-overall=7.49 × 10−09.
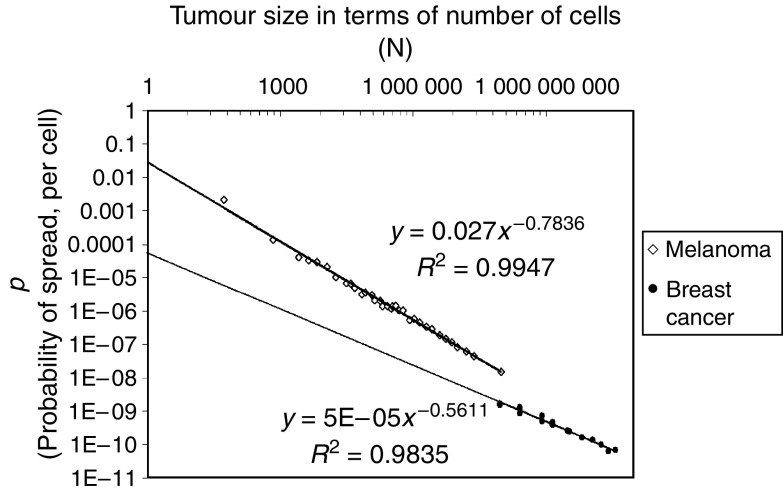
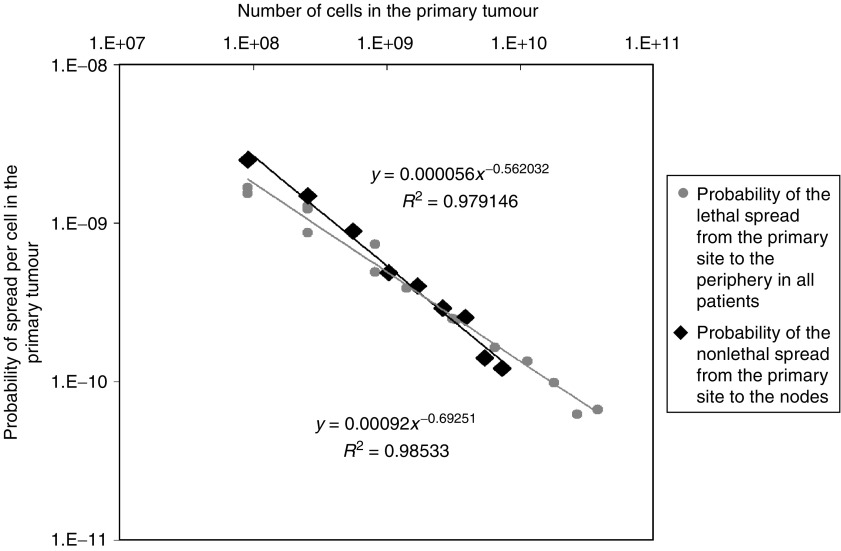
Equation (2) provides the technique for accurately quantifying the probabilities of these types of cancer spread. In three instances (pBC-overall, pMEL-overall and pBC-to-nodes, Tables 1 and 2), data are available on spread from tumours of various sizes, revealing that the probability values do not remain constant as tumours grow, but declines as tumours increase in size (Figures 1 and 2). For example, the probability of lethal spread of melanoma cells from the primary site in the skin to the periphery (pMEL-overall) is ∼1 event of spread for every 500 cells for melanomas of 0.1 mm, but 100,000-fold lower (∼1 event of spread for every 108 cells) for 12 mm tumours (Figure 1). As we have reported previously (Michaelson et al, 2002), a similar decline in the probability of spread per cell is also seen as tumours become larger for the overall probability of lethal spread of breast cancer cells from the primary site in the breast to the periphery (pBC-overall, Figure 1). As can also be seen in Figure 1, a similar decline in the probability of spread per cell occurs for the nonlethal spread of breast cancer cells from the primary site in the breast to the lymph nodes (pBC-to-nodes, Figure 2) (Tables 1 and 2). Furthermore, in each of the three contexts this decline occurs in a highly predictable fashion with N, such that it is well fit (Figures 1 and 2) to a power function of the form:
 |
Figure 1.
Calculations of the probability of lethal spread of breast cancer and melanoma cells, as a function of tumour size, and the close fit of the data to equation (2). (R2=0.98 for breast cancer, (R2=0.9 for melanoma). Shown here are the overall values for the probability of lethal spread of cancer cells from the primary site to the periphery for breast cancer (pBC-overall) and melanoma (pMEL-overall) using tumour size/survival data for all patients (Table 1). Note the close fit to the power function, equation (3).
Figure 2.
Calculations of the probability of lethal spread of breast cancer from the primary site to the periphery (pBC-overall) by equation (2) and using tumour size/survival data for all patients (Table 1), and the probability of nonlethal spread of breast cancer from the primary site to the lymph nodes (pBC-to-nodes) by equation (2) and using tumour size/nodal status data (Table 1). Note that in both cases the relationship between the probability of spread and tumour size is well fit by a power function, equation (3).
Values for a and b for each of these three types of metastatic spread are shown in Table 2. b has a negative value of approximately −0.5 to −0.8, reflecting the fact that the value of p declines as tumours increase in size. a can be thought of as the probability of spread for the very first cell in the tumour, because p=a when N=1. Note that the parameter a is approximately 500-fold higher for melanoma than for breast cancer, reflecting the long-appreciated greater propensity of melanoma to give rise to metastases.
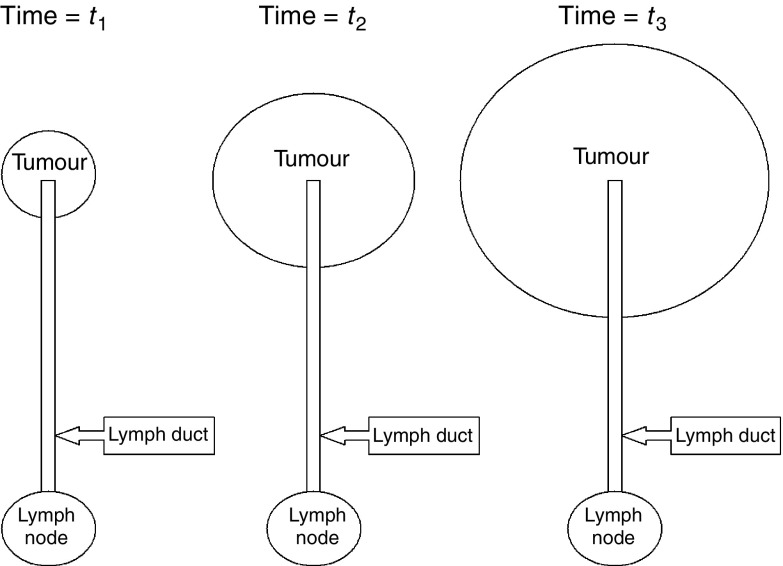
There are a number of possible explanations for why the probability of spread per cell, p, declines as tumours become larger. It could be that only a subpopulation of tumour cells are capable of metastasising, and that the relative abundance of these cells decline as tumours grow. Another possibility is that the decline in the per-cell probability of spread is the result of the simple geometrical constraints posed to the escape of cells from the primary mass (Padera et al, 2002), which become more formidable as tumours increase in size. As shown in the Supplementary material, such possibilities are mathematically possible, and are testable in experimental systems (Figure 3).
Figure 3.
Schematic of Geometrical Model #1. Shown is a highly idealised image of a tumour mass and a lymph duct leading to a local lymph node.
The spread of cancer cells can occur in single steps, such as the spread of a cell directly from the primary site to the periphery, or in multiple steps, such as the initial spread of a cell from the primary site to a local lymph nodes followed by the subsequent spread of one of the progeny of that cell away from the node to the periphery. By measuring the breast cancer death rate among subpopulations of patients sorted by both the size of the primary mass and the number of such positive lymph nodes, we have recently found that the presence of each positive node is associated with an extra 6.08% chance of death (Michaelson et al, 2003). It is possible to use this information with equation (2) to measure the probability of the spread of breast cancer cells from the nodes to the periphery (pBC-from-nodes). To carry out this calculation, we set the value of L=0.0608, and to determine the value of N, we collected data on the sizes of metastases in lymph nodes, revealing a mean size of 5.3 mm, which is equivalent to N=7.84 × 106 cells (Table 3). It follows with equation (2) that the probability of the spread of cancer cells from lymph nodes pBC-from-nodes=7.96 × 10−09≈1 event of spread for every 108 cells. This value is remarkably close to the value for the probability of the lethal spread of breast cancer cells from the primary mass in the breast when the primary mass is also 5.3 mm (pBC-overall=7.49 × 10−09), as calculated by extrapolation of equation (3). This reveals that the occurrence of an event of spread of cancer cells from the primary site in the breast to the local lymph nodes does not appreciably change the tendency of the progeny of those cancer cells to make yet a second event of spread from the lymph nodes to the periphery.
DISCUSSION
It has often been wondered whether mutation at the time of spread is a requirement for metastasis (Cifone and Fidler, 1981; Fidler, 1983; Sobel, 1990; Welch et al, 2000; Yokota, 2000; Bernards and Weinberg, 2002; Couzin, 2003; Bernards, 2003), but the values of the probabilities of metastatic spread of breast cancer and melanoma cells revealed by equation (2) are difficult to reconcile with such genetic changes due to several reasons: First, the value of the probability of spread for the smallest melanomas (0.1 mm), at ∼1 event of spread for every 500 cells, is many orders of magnitude greater than that expected for a genetic change. Second, the occurrence of one event of spread (the spread of breast cancer cells from the breast to the local lymph nodes) does not appear to increase the chance of a second event of spread (the spread of breast cancer cells from the local lymph nodes to the periphery). In other words, the occurrence of the initial event of spread does not lead to a cell-heritable change in the tendency of the progeny of that cell to spread. Third, the data shown here reveal that the probability of metastatic spread per cell declines as tumours increase in size. While this decline is consistent with a number of explanations that are mechanical, (using this term in the sense in which it is used in physics: ‘pertaining to the relations of force and matter’), such as the effect of tumour geometry on the ease of the escape of cells from the primary mass (see Supplementary material), it is not what would be expected for genetic events. Indeed, the probability of genetic events over time should be expected either to remain constant (if only a single genetic event is required) or to increase with time (if the accumulation of multiple genetic events is required). Taken together, these findings would appear to be in agreement with the viewpoint put forward by Bernards and Weinberg ‘that the tendency to metastasise is largely determined by the identities of mutant alleles that are acquired relatively early during multistep tumorigenesis’, and that ‘genes and genetic changes specifically and exclusively involved in orchestrating the process of metastasis do not exist’ (Bernards and Weinberg, 2002).
Footnotes
Supplementary Information accompanies the paper on British Journal of Cancer website (http://www.nature.com/bjc)
Supplementary Material
References
- Balch CM, Soong SJ, Gershenwald JE, Thompson JF, Reintgen DS, Cascinelli N, Urist M, McMasters KM, Ross MI, Kirkwood JM, Atkins MB, Thompson JA, Coit DG, Byrd D, Desmond R, Zhang Y, Liu PY, Lyman GH, Morabito A (2001) Prognostic factors analysis of 17,600 melanoma patients: validation of the American Joint Committee on Cancer melanoma staging system. J Clin Oncol 19: 3622–3634 [DOI] [PubMed] [Google Scholar]
- Bernards R (2003) Clues for migration. Nature 425: 247–248 [DOI] [PubMed] [Google Scholar]
- Bernards R, Weinberg RA (2002) A progression puzzle. Nature 418: 823. [DOI] [PubMed] [Google Scholar]
- Boon ME, Trott PA, van Kaam H, Kurver PJ, Leach A, Baak JP (1982) Morphometry and cytodiagnosis of breast lesions. Virchows Arch [Pathol Anat] 396: 9–18 [DOI] [PubMed] [Google Scholar]
- Cifone MA, Fidler IJ (1981) Increasing metastatic potential is associated with increasing genetic instability of clones isolated from murine neoplasms. Proc Natl Acad Sci USA 78: 6949–6952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couzin J (2003) A clash over genes that foretell metastasis. Science 299: 1005. [DOI] [PubMed] [Google Scholar]
- Fidler IJ (1983) The Ernst W. Bertner Memorial Award lecture: the evolution of biological heterogeneity in metastatic neoplasms. Symp Fundam Cancer Res 36: 5–26 [PubMed] [Google Scholar]
- Karrison TG, Ferguson DJ, Meier P (1999) Dormancy of mammary carcinoma after mastectomy. J Natl Cancer Inst 91: 80–85 [DOI] [PubMed] [Google Scholar]
- Koscielny S, Tubiana M, Le MG, Valleron AJ, Mouriesse H, Contesso G, Sarrazin D (1984) Breast cancer: relationship between the size of the primary tumor and the probability of metastatic dissemination. Br J Cancer 49: 709–715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelson J (1999) The role of molecular discreteness in normal and cancerous growth. Anticancer Res 19: 4853–4867 [PubMed] [Google Scholar]
- Michaelson JS, Silverstein M, Sgroi D, Cheongsiatmoy JA, Taghian A, Powell S, Hughes K, Comegno A, Tanabe KK, Smith B (2003) The effect of tumor size and nodal status on the lethality of breast cancer. Cancer 98: 2133–2143 [DOI] [PubMed] [Google Scholar]
- Michaelson JS, Silverstein M, Wyatt J, Weber G, Moore R, Halpern E, Kopans DB, Hughes K (2002) The prediction of breast cancer survival from tumor size. Cancer 95: 713–723 [DOI] [PubMed] [Google Scholar]
- Padera TP, Kadambi A, di Tomaso E, Carreira CM, Brown EB, Boucher Y, Choi NC, Mathisen D, Wain J, Mark EJ, Munn LL, Jain RK (2002) Lymphatic metastasis in the absence of functional intratumor lymphatics. Science 296: 1883–1886 [DOI] [PubMed] [Google Scholar]
- Pesce C, Colacino R (1986) Morphometry of the breast fibroadenoma. Pathol Res Pract 181: 718–720 [DOI] [PubMed] [Google Scholar]
- Silverstein MJ (2000) The Van Nuys Breast Center: the first free-standing multidisciplinary breast center. Surg Oncol Clin North Am 9: 159–175 [PubMed] [Google Scholar]
- Sobel ME (1990) Metastasis suppressor genes. J Natl Cancer Inst 82: 267–276 [DOI] [PubMed] [Google Scholar]
- Tabar L, Vitak B, Chen HH, Duffy SW, Yen MF, Chiang CF, Krusemo UB, Tot T, Smith RA (2000) The Swedish two-county trial twenty years later. Updated mortality results and new insights from long-term follow-up. Radiol Clin North Am 38: 625–651 [DOI] [PubMed] [Google Scholar]
- Tubiana M, Koscielny S (1990) The natural history of human breast cancer: implications for a screening stratergy. Int J Radiation Oncol Biol Phys 19: 1117–1120 [DOI] [PubMed] [Google Scholar]
- Tubiana M, Koscielny S (1991) Natural history of human breast cancer: recent data and clinical implications. Breast Cancer Res Treatment 18: 125–140 [DOI] [PubMed] [Google Scholar]
- Van der Linden HC, Baak JP, Smeulders AW, Lindeman J, Meyer CJ (1986) Morphometry of breast cancer. I. Comparison of the primary tumours and the axillary lymph node metastases. Pathol Res Pract 181: 236–242 [DOI] [PubMed] [Google Scholar]
- Van't Veer LJ, Weigelt B (2003) Road map to metastasis. Nat Med 8: 999–1000 [DOI] [PubMed] [Google Scholar]
- Welch DR, Steeg PS, Rinker-Schaeffer CW (2000) Molecular biology of breast cancer metastasis. Genetic regulation of human breast carcinoma metastasis. Breast Cancer Res 2: 408–416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Mani SA, Donaher JL, Ramaswamy S, Itzykson RA, Come C, Savagner P, Gitelman I, Richardson A, Weinberg RA (2004) Twist, a master regulator of morphogenesis, plays an essential role in tumor metastasis. Cell 117: 927–939 [DOI] [PubMed] [Google Scholar]
- Yokota J (2000) Tumor progression and metastasis. Carcinogenesis 21: 487–503 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.