Consequences of patient position in the radiographic measurement of artificial disc replacement angles

Abstract

Accurate clinical measurement of spinal range of motion (ROM) is essential in the evaluation of artificial disc performance. The effect of patient placement with respect to the X-ray beam source is yet to be reported and may be an influencing factor in radiographic artificial disc angle measurements. This study aims to evaluate how radiographic patient placement influences artificial disc angle measurements. An anatomically accurate synthetic L4–L5 motion segment was instrumented with an artificial disc and two pins. The instrumented motion segment was mounted onto a frame allowing for independent rotation and elevation while holding the artificial disc angle and anatomical position between L4 and L5 fixed. Analyses included descriptive statistics, evaluation of uncertainty, intra- and inter-observer, and a 2-way analysis of variance (ANOVA). The mean angle measurement range at the various positions was 1.26° for the pin, and 2.74° for the artificial disc endplates. The centered patient position had the highest inter- and intra-observer reliability. ANOVA results showed elevation effects to be statistically significant (P = 0.021), and rotational effects to be extremely statistically significant (P < 0.0001) for the pin angles. In terms of the mean artificial disc angle, however, the ANOVA showed a highly statistically significant interaction term (P = 0.002). A significant difference was found in the angle measurements of a fixed artificial disc prosthesis based on a sample of patient radiographic placement positions. Since it is important to assess the success of an artificial disc replacement by evaluating the relatively small ROM present, it is crucial to aim at minimizing the error by placing the patient parallel to the plate with the beam centered not at the mid lumbar spine, but at the level of the arthroplasty, for both flexion and extension views.

Introduction

Artificial disc replacements are considered as an alternative to interbody fusion in the treatment of degenerative disc disease. Such replacements have been designed to provide the advantage of kinematic preservation at the operated and adjacent intervertebral disc levels when compared to fusion [2]. Furthermore, with considerable (>5°) segmental flexion–extension range of motion (ROM), artificial disc replacements have been correlated to better clinical outcomes [4], and suggested to have reduced long-term risk in the development of radiographic adjacent level degeneration [5, 13].

Accurate clinical measurement of ROM is essential in the diagnosis and treatment of spinal disorders as well as in the evaluation of artificial disc replacement performance. The Cobb method is commonly used in clinical practice to measure deformity and spinal ROM using flexion–extension radiographs [14]. Inter- and intra-observer reliability for spinal deformity assessment have been shown to be consistent using the Cobb method [6, 14]. In assessing kyphosis using the Oxford Cobbometer for example, a 2° absolute mean difference between the readings with a 95% limit of agreement of ±5.8° has been reported [14].

In relation to ROM measurements of an artificial disc, a threshold as low as 2° between flexion–extension radiographs has been used to establish motion [3]. More recent studies have reported artificial disc flexion–extension ROM values even below this 2° threshold [7, 10]. To help define this critical threshold angle, in which differences in flexion–extension radiographs truly represent artificial disc motion, investigators have looked at inter- and intra-observer measurement variability [1, 8, 9], measurement precision using different radiographic landmarks (e.g. keel, endplate) [8], and different radiological assessment methods (e.g. Cobb method, superposition method) [1]. Studies have reported intra- and inter-observer accuracy values as low as ±2.0° and ±3.0°, respectively [1], or as high as ±4.6° and ±5.2°, respectively [9]. Conclusions from the higher end results suggest a threshold angle between flexion–extension radiographs of at least 4.6° (i.e., intra-observer value) is needed to be certain that the ROM of the artificial disc replacement is not zero [9].

In addition to the measurement error results presented in the aforementioned studies, patient placement with respect to X-ray beam source may influence radiographic angle measurements. In general, when flexion–extension radiographs are acquired, the beam is directed at the mid-lumbar spine and not specifically centered on the operated level. This oblique X-ray source may introduce distortions in the recorded radiograph reducing measurement precision. This study aims to evaluate how patient positioning influences artificial disc radiographic angle measurements. To achieve this objective, a fixed reference angle created using Steinmann pins and a fixed artificial disc endplate angle are evaluated using standard digital radiographs taken at seven rotations and four elevations representing a sample of possible patient placement positions.

Methods

An anatomically accurate synthetic L4–L5 motion segment was instrumented with a CHARITE artificial disc (DePuy Spine, Raynham, MA, USA). The CHARITE endplates are available in multiple sizes and degrees of angulation for restoring spinal lordosis [10]. A size 4-footprint geometry with a 5° angulation, and a size 4-footprint with a 7.5° angulation, were used in this study for the inferior vertebral endplate of L4 and superior endplate of L5, respectively. Two stainless steel Steinmann pins were used to develop a reference allowing for higher precision measurements. The first pin was driven through the L4 vertebra while the second was driven through the L5 vertebra, both along the mid-sagittal plane.

The instrumented motion segment was mounted onto a frame allowing for independent rotation and elevation of the motion segment while holding the artificial disc angle and anatomical position between L4 and L5 fixed. The frame was initially placed with the motion segment, 25 cm from the detecting plate and centrally located with respect to the X-ray beam. The X-ray source was located 1.5 m away from the detecting plate.

The centered motion segment position, situated as described above, was noted to be 0 cm for elevation and 0° for rotation. The angle formed by the two Steinmann pins and the angle of the artificial disc was evaluated using standard digital radiographs (model PL-SX80, Siemens Medical Solutions, Erlangen, Germany) of the instrumented motion segment at seven rotations (−15°, −10°, −5°, 0°, 5°, 10°, and 15°) and four elevations (0, −5, −10 and −15 cm), giving a total of 28 radiographs. The negative and positive rotations correspond to turning and facing the anterior part of the motion segment towards the detecting plate or X-ray source, respectively. All radiographs were directly imported to a computer and analyzed using the ImageJ public domain software (version 1.36b, National Institutes of Health, Bethesda, MD, USA). Using this software, X- and Y-coordinates were recorded for the endpoints of each Steinmann pin (4 points, 8 coordinates) and for the external corners of the inferior and superior artificial disc endplates (4 points, 8 coordinates), by a single observer, from each radiograph (Fig. 1). The same observer repeated this measurement procedure ten times resulting in 280 separate data sets containing 8,960 total points. In addition, two separate independent observers, blinded to the measurement already made, recorded the same points for the centered position (0 cm, 0°) and for each extreme (−15 cm 15°, and −15 cm −15°). A single equation using the eight measured coordinates, derived from the scalar dot product of two vectors, was used to separately calculate the angle between the Steinmann pins, and the angle between the artificial disc endplates:

1

where x_n and y_n are corresponding coordinates for the same point (see Fig. 1).

Fig. 1.

Digital radiograph of the instrumented motion segment model at the centered (0 cm, 0°) position displaying the landmark points and respective coordinates chosen for calculation of the pin (P) angle and the artificial disc endplate (E) angle

The angle between the Steinmann pins and the angle of the artificial disc endplates at each position, repeatedly calculated from the multiple readings of the coordinate measurements, were summarized using descriptive statistics such as the arithmetic mean, min, and max. Measurement uncertainty was calculated as the standard deviation of each measured coordinate Since the angles were determined from the eight measured coordinates (Eq. 1), errors in each independent coordinate combine to produce an error in the final calculated angle. This uncertainty or error in the calculated angles is thus a function of the coordinate standard deviations, and the equation relating the coordinates to the angle (Eq. 1). To determine the angle uncertainty (σ_θ), a multivariate equation including these aforementioned error contributions was applied [11]:

2

To assess the inter- and intra-observer agreement, single measure intraclass correlation coefficients (ICC) were calculated [15]. A two-way random approach was employed looking at both the absolute agreement between observers/readings and data correlation. Agreement strength was defined as highly reliable (0.90 ≤ ICC), moderately reliable (0.80 ≤ ICC ≤ 0.89), and questionably reliable (0.70 ≤ ICC ≤ 0.79) [16].

A two-way repeated measures analysis of variance (ANOVA) was utilized to study the interactions and average effects of rotation and elevation on the angle means. Significance levels were categorized as extremely statistical significant (α = 0.001), highly statistical significant (α = 0.01), and statistically significant (α = 0.05).

Results

The range for the Steinmann pin mean angle (i.e., the reference offering higher precision) at the various positions was 1.26° (Fig. 2). Specifically, the maximum and minimum mean angles were found to be 7.78° (−15 cm, 15° position) and 6.51° (−10 cm, −15° position), respectively. The mean Steinmann pin uncertainty was calculated to be 0.06° (max = 0.07°, min = 0.04°). A maximum angle of 7.83° (−15 cm, 15°) and minimum angle of 6.42° (−5 cm, −15°) were determined from the complete data set prior to averaging the repeated trials at each position (range = 1.41°). At the centered position (0 cm, 0°) a maximum pin angle of 6.92° and minimum angle of 6.68° were found from the 10 repeated readings (mean = 6.82°).

Fig. 2.

Mean pin angles with uncertainty bars for the seven rotations and four elevations studied

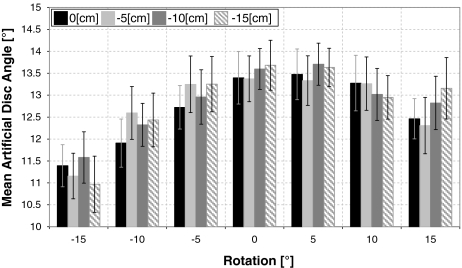
The range of mean artificial disc angle at various positions was 2.74° (Fig. 3). The maximum and minimum mean angles were found to be 13.71° (−10 cm, 5°) and 10.97° (−15 cm, −15°), respectively. The mean artificial disc angle uncertainty was calculated to be 0.57° (max = 0.70°, min = 0.44°). A maximum angle of 15.08° (0 cm, 5°) and minimum angle of 9.74° (−15 cm, −15°) were determined from the complete data set prior to averaging the repeated trials at each position (range = 5.34°). At the centered position (0 cm, 0°) a maximum artificial disc endplate angle of 14.24° and minimum angle of 12.18° were found from the ten repeated readings (mean = 13.40°).

Fig. 3.

Mean artificial disc endplate angles with uncertainty bars for the seven rotations and four elevations studied

Inter-observer agreement (comparing readings between observers) was highly reliable in all but one case (Table 1). This case, found when testing absolute agreement between observers at the extreme −15 cm, −15° position, resulted in moderate reliability (ICC = 0.896). Intra-observer agreement (comparing readings of a single observer) was highly reliable in all cases. The centered position (0 cm, 0°) had the highest inter- and intra-observer ICC, both in absolute agreement and consistency of readings, and was thus always the most reliable.

Table 1.

Inter- and intra- observer single measure intraclass correlation coefficient (ICC) results at the ideal and extreme positions

	Inter-observer		Intra-observer
	Absolute	Consistency	Absolute	Consistency
0 cm, 0°	0.987	0.990	0.990	0.989
−15 cm, −15°	0.896	0.911	0.963	0.959
−15 cm, 15°	0.941	0.965	0.949	0.951

Both rotation and elevation of the motion segment were studied as treatment factors using a balanced design repeated measures two-way ANOVA. Elevation effects were found to be statistically significant (P = 0.021) when testing the null hypothesis that the mean Steinmann pin angles are equal. In addition, extreme statistical significance (P < 0.0001) was found when testing rotational effects for the pin angles. No statistical significance was found for the interaction term (P = 0.068) leading to the conclusion that rotation and elevation of the motion segment can independently affect the value of the observed Steinmann pin angle. In terms of the mean artificial disc angle, however, the ANOVA additive model was rejected due to a highly statistical significant interaction term (P = 0.002). Thus, interactions exist leading to the conclusion that the observed artificial disc angle is dependent on some combination of both rotation and elevation.

Discussion

This study adds to the spine literature by presenting the consequences of patient positioning in the radiographic measurement of artificial disc replacement angles using two fixed angles. The first fixed angle (i.e., between the pins) allows for higher precision measurements while the second angle (i.e., between artificial disc endplates) was the main topic of interest. A sample of possible patient placement positions was evaluated using seven different rotations and four different elevations within the imaging field. Results from studying the pins suggest that positioning itself significantly influences the radiographic projection of a fixed angle, and can be independently identified with precision at different rotations and elevations (range observed 1.26°). Compared to the pins, an increased uncertainty and range was observed in the mean artificial disc angle measurements using the endplates. Furthermore, from the increased error observed in the angular measurements using the endplates, the main effects of rotation and elevation could not be independently identified. Since experimental conditions remained unchanged and both the intra- and inter-observer readings were highly reliable, the added errors may be explained by an increased difficulty in finding the same endplate landmarks on the radiographic projections taken at different elevations and rotations. The observer was able to consistently identify the external corners of the inferior and superior artificial disc endplates, but these identified corners may have been biased due to a projection shadow from the elliptical artificial disc endplates caused by the decentralized X-ray beam.

The use of a motion segment model, without the surrounding tissue and body mass, presents a limitation to our study. The aim of this experiment, however, was to produce high accuracy and precision results, far greater than with an in vivo or cadaveric model, to capture the intricate errors that may be present during radiographic imaging. In addition, the repeated radiation required to perform this analysis in vivo would present safety concerns. Furthermore, when compared to the measurement methods used in average clinical practice, the use of digitized radiographs and imaging software further enhanced this objective to produce high accuracy and precision in the measurements. The results therefore present a lower end error compared to what can be expected in practice.

The results of this study are based on a single artificial disc model without keels. It has been suggested that using artificial disc keels as references may result in increased measurement accuracy [8]. Although the findings from this study cannot be directly associated to other artificial disc geometries without validation using a similar experimental model, especially since keel geometries vary from model to model, an implication can be made that even the increased accuracy suggested from measurements using the keel approach would not exceed what was found here for the pins. Therefore, measurements using such implants would not be free of patient positioning deviations within the radiographic field of view (e.g. rotation and elevation).

Even with the higher precision offered by the methods used in this study, a mean difference as high as 2.74° was found in a fixed artificial disc prosthesis based on a sample of patient radiographic placement positions. Subtracting the artificial disc extreme max and min angle results from all the positions evaluated, prior to averaging, presents the error range for the worse case scenario observed (5.34°).

In conclusion, since it is important to assess the success of an artificial disc replacement by evaluating the relatively small ROM present (≈10.8 ± 1.2° flexion–extension [12]), it is crucial to aim at minimizing the error by placing the patient parallel to the plate with the beam centered not at the mid lumbar spine, but at the level of the arthroplasty, for both flexion and extension views. This however, will not completely eliminate imaging errors as an inherent difference of at least 2.06° (range at the 0 cm, 0° position) could still be found in the absence of movement on each separate view. Clinicians and researchers should therefore keep these imaging limitations in mind when reporting on existing artificial disc ROM and its relation to clinical outcome.