Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Jan 1.
Published in final edited form as: J Biomech. 2008 Jan 28;41(4):762–769. doi: 10.1016/j.jbiomech.2007.11.027

Combined Effects of Microtopography and Cyclic Strain on Vascular Smooth Muscle Cell Orientation

Graham R Houtchens 1,¥, Michael D Foster 1,¥, Tejal A Desai 1,¥, Elise F Morgan 1,2, Joyce Y Wong 1,*
PMCID: PMC2365919  NIHMSID: NIHMS43190  PMID: 18222460

Abstract

Cellular alignment studies have shown that cell orientation has a large effect on the expression and behavior of cells. Cyclic strain and substrate microtopography have each been shown to regulate cellular alignment. This study examined the combined effects of these two stimuli on the alignment of bovine vascular smooth muscle cells (VSMCs). Cells were cultured on substrates with microgrooves of varying widths oriented either parallel or perpendicular the direction of an applied cyclic tensile strain. We found that microgrooves oriented parallel to the direction of the applied strain limited the orientation response of VSMCs to the mechanical stimulus, while grooves perpendicular to the applied strain enhanced cellular alignment. Further, the extent to which parallel grooves limited cell alignment was found to be dependent on the groove width. It was found that for both a small (15 μm) and a large (70 μm) groove width, cells were better able to reorient in response to the applied strain than for an intermediate groove width (40 μm). This study indicates that microtopographical cues modulate the orientation response of VSMCs to cyclic strain. The results suggest that there is a range of microgroove dimensions that is most effective at maintaining the orientation of the cells in the presence of an opposing stimulus induced by cyclic strain.

Introduction

It has been well established that cellular alignment through various modalities influences cell behavior. The ability to align cells thus enables one to modulate cell behavior. One method for achieving cellular alignment is through contact guidance, or culturing cells on substrates with microstructures to help guide the cells into the desired configuration. A common topographical pattern used for cellular alignment is microgrooves, which act as channels to affect cell morphology (Brunette et al., 1999, Glass-Brudzinski et al., 2002, Glawe et al., 2005, Hsu et al., 2005). Cells cultured on untextured substrates have randomly distributed orientation angles, whereas in the presence of microgrooves show significant orientation along the mircrogrooves (Sarkar et al., 2005). Studies into the efficacy and of these channels have shown that cellular alignment is sensitive to the width, depth, and spacing of microgrooves, and that for a wide range of these dimensions, microgrooves are effective at maintaining alignment within the grooves (Glass-Brudzinski et al., 2002, Glawe et al., 2005). The ability of cells to align as a result of microgrooves is well established, and cell response to microgrooves has been predicted using control theory (Kemkemer et al., 2006). The microgrooves cause changes in cell behavior and further promotes aligned ECM deposition (den Braber et al. 1998; Glass-Brudzinski et al., 2002).

A second method for aligning cells is by means of a mechanical stimulus, commonly by an applied strain to the substrate containing the cell culture. Numerous studies have shown that cells plated on a substrate subjected to cyclic strain orient themselves perpendicular to the applied strain (Kim et al., 2000, Standley et al., 2006). Again, as a result of the alignment of the cells by the stimulus, the cells exhibit different behavior than when cultured on static substrates. Experiments by Kim et al. (2000) demonstrated that the application of cyclic strain was also associated with upregulation elastin and collagen. This in turn led to significantly higher Young’s modulus and ultimate stress values. Isenberg and Tranquillo (2003) also found increases in the ultimate tensile strength and modulus of smooth muscle cells when exposed to a cyclic strain stimulus over a period of time.

Few studies have been conducted to examine the interplay between different cellular alignment modalities. The interplay between fluid shear forces and cyclic strain has been shown to be algebraically equal, with each of the stimuli able to cancel the effect of the other in cultures subjected to both (Owatverot et al., 2005). A study examining the interplay between cyclic strain and microgrooves showed that contact guidance via microgrooves was a stronger driving influence than cyclic strain (Wang et al., 2000). An applied cyclic strain stimulus intended to orient the cells away from the microgrooves was ineffective for all microgroove dimensions investigated.

Because the ability of microgrooves to orient cells is sensitive to all three dimensions of the groove, the current study aims to further investigate the interplay between cyclic strain and microtopography in aligning vascular smooth muscle cells. In the previously mentioned study of cyclic strain paired with microgrooves, the dimensions of the grooves were 10 μm wide by 3 μm deep, with 10 μm spacing. The range for which microgrooves can effectively align cells in culture is much wider, with efficacy having been shown with up to 60 μm wide grooves (Glawe et al., 2005). In the current study, three different groove widths were investigated, 15, 40, and 70 μm, at a depth of 5 μm and with 14 μm spacing.

Materials and Methods

Thin Polydimethylsiloxane (PDMS) Films

Micropatterned films were created using previously established microfabrication and soft lithography techniques (Deutsch et al., 2000). Silicon wafers were patterned using SU-8 photoresist spin coated to a thickness of 5 μm.

Micropatterned thin films of PDMS were created by pouring a 10:1 (w/w) mixture of Sylgard 186 (Dow Corning) and the crosslinking agent onto the patterned silicon wafer. The wafer was then placed on a spin coater (Specialty Coating Systems, Inc., Indianapolis, IN) and spun at 1000 rpm for 90 sec. This process yielded thin films of PDMS approximately 150μm thick.

In preparation for cell culture, thin PDMS films were treated with a layer-by-layer process to deposit alternating charged polyelectrolyte layers of polyethyleneimine and polystyrene sulfate to reduce hydrophobicity and promote cell adhesion. First, the films were incubated in poly(ethyleneimine) (PEI) (1 mg/mL) in phosphate buffered saline (PBS) for 30 min. The films were then rinsed once with PBS. This was followed by a 30 min incubation in poly (styrenesulfonate) sodium salt (PSS) (Alfa Aesar, Ward Hill, MA) (3 mg/mL) in PBS. The films were then rinsed once with PBS. These steps were repeated two more times to complete the process. After the layer-by-layer treatment, thin films were incubated with human plasma fibronectin (Gibco, Grand Island, NY) (5 μg/ml in PBS) for 1.5 hr at room temperature. Films were then rinsed with sterile PBS directly before seeding. Three or four films were used for each stretching condition (groove width and orientation combinations).

Cell Culture

Bovine vascular smooth muscle cells (AG08504, Coriell Cell Repositories) (VSMCs) were cultured on micropatterned and unpatterned thin PDMS films. VSMCs were maintained in Dulbecco’s Modified Eagle Medium (Gibco) supplemented with 10% bovine calf serum (Hyclone, Logan,UT),1% penicillin-streptomycin (Gibco) and 1% L-glutamine (Gibco). Prior to being seeded, VSMCs were serum-starved for a minimum of 12 hr to ensure that all cells were synchronized such that cell cycle variability was removed from the experiments. Cells were seeded onto the fibronectin-coated thin films at a seeding density of 5000 cells per cm2 and allowed to attach for approximately 24 hr. Thin films were then subjected to cyclic strain, or were cultured unstrained, for 24 hr.

Cyclic Strain Apparatus

To achieve a dynamic cell culture environment a cyclic strain apparatus similar to one previously described (Kim et al., 2000) was constructed (Figure 2). Briefly, each end of an elastic substrate was placed between two aluminum clamp pieces and secured with stainless steel screws. The film with its clamped ends was placed onto a moveable stage. One end of the film was secured to the moveable stage while the other end was secured to a stationary platform below. Cyclic motion of the stage was actuated by an enclosed gear motor outfitted with an eccentric hub. A stainless steel link connected the hub to the moveable stage. A strain rate of 1 Hz was chosen as a physiological relevant rate. We chose a strain magnitude of 10% to match the range that is experienced by native blood vessels in vivo: values of cyclic strain in the range of 5–10% have been shown to upregulate collagen and elastin expression by VSMCs (Kim et al., 1999) as well as increase the Young’s modulus and ultimate strength of collagen constructs populated with VSMCs in studies ranging from 5 to 20 weeks (Kim et al., 1999; Isenberg et al., 2003; Seliktar et al., 2003).

Figure 2. Custom-made cyclic strain apparatus designed to accommodate four samples and fit into a standard cell culture incubator.

Figure 2

Open in a new tab

Aluminum clamps attach each end of the elastic substrate to the apparatus. To increase the uniformity of the strain field on the film, a dowel pin is placed between the top clamp and the PDMS film. Additionally, a jig is used to ensure the PDMS is centered on the apparatus and to ensure a uniform applied strain for each of the samples. On one end, the film is secured to a movable stage and the other end, to a stationary platform. An enclosed gear motor outfitted with an eccentric hub actuates the cyclic motion of the stage, and a stainless steel link connects the hub to the movable stage. The apparatus is designed to enable an application of strain rate ranging from 0 to 2 HZ and a strain magnitude of 10%.

Strain Characterization

The actual strain field produced on the PDMS thin films was characterized using image analysis of the stretched films. To quantify the strain, thin films from each pattern and orientation group were made using the procedure described above. A marker was used to make 25 dots in a five-by-five pattern on each film. The films were then loaded into the cyclic strain apparatus and placed under a Zeiss Stemi SV11 stereo microscope (Carl Zeiss) with a camera attachment linked to a personal computer. Images were then taken at the minimum and maximum strain positions. The pairs of images were then analyzed using a cross-correlation algorithm written in Matlab (Mathworks, Natick, MA). Each image was divided into a regular array neighboring blocks of equal size such that each block contained one dot. The average displacement vector for each block, which was almost completely dominated by the displacement of the dot, was calculated.

These displacements, together with the strained and unstrained Cartesian coordinates of the dots were used to calculate the strain field in the film by first discretizing the film into an array of triangles, each defined by a group of neighboring three dots (Figure 4). The two-dimensional strain components for each triangle were then calculated as

Figure 4. Strain distribution created by cyclic strain apparatus.

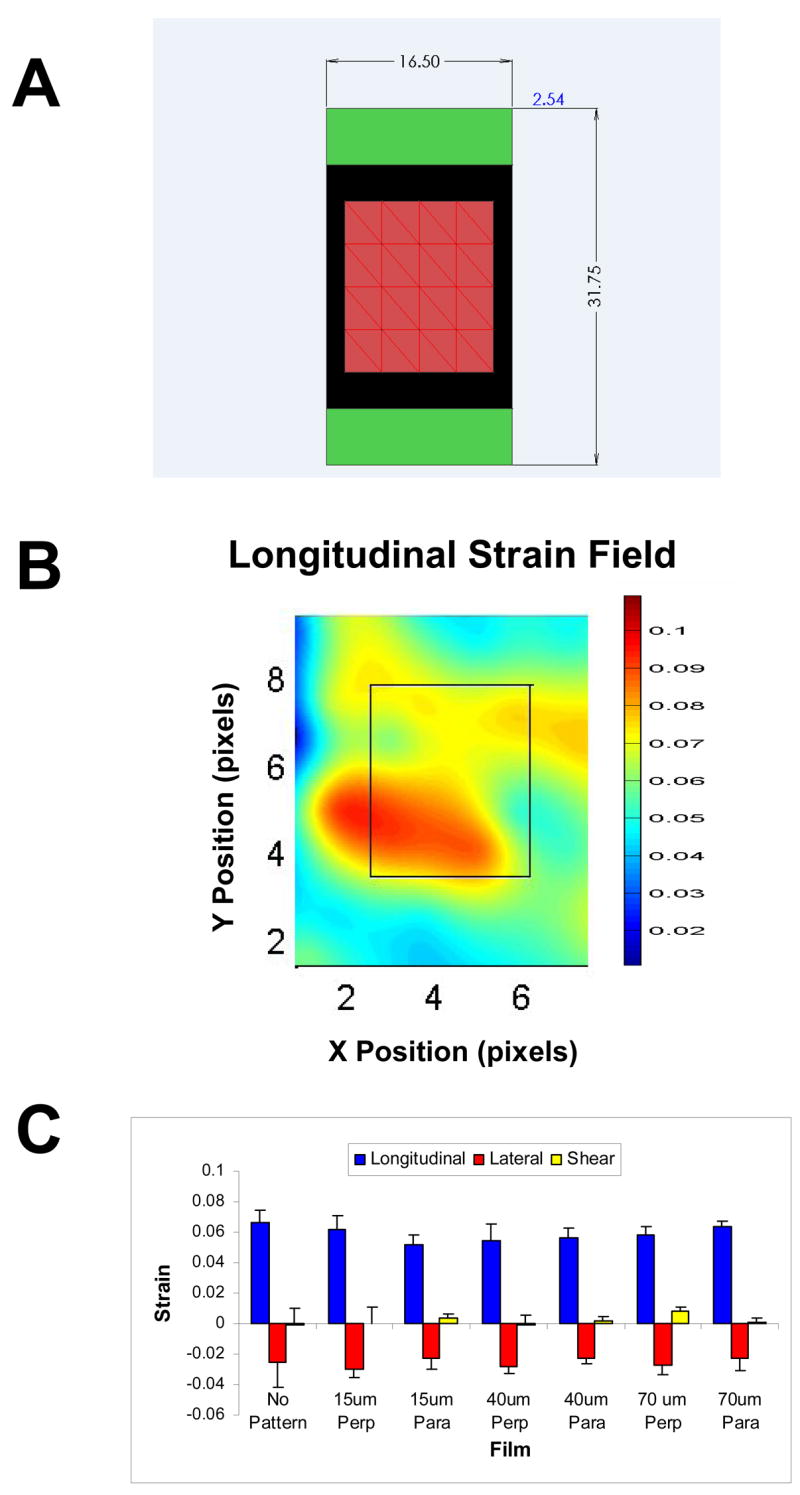
Figure 4

Open in a new tab

(A) The red region represents the area for which strain is measured. The green regions are areas of the film that are obscured by the clamps. The Y-direction is defined in the direction of the applied cyclic tensile strain. Strain in this direction is referred to as the longitudinal strain. Strain in the X-direction that develops due to the Poisson effect is referred to as lateral strain. (B) Representative longitudinal strain map measured for a control sample which did not contain any grooves. (C) Average longitudinal, lateral and shear strain values for the central eight triangles defined for the strain calculations. No pattern = control. “Perp” and “Para” indicate that the pattern was perpendicular or parallel to the strain, respectively.

ds2−dS2=dX•EdX (1)

where ds and dS are the strained and unstrained magnitudes of the side-lengths of the triangle, respectively, E is the Green-Lagrange strain tensor, and dX is the Cartesian components of the unstrained side-lengths of the triangle. We note that this method necessarily treats the strain field as uniform within a given triangular region and that the resulting strain components represent average values for each region.

Cell Staining

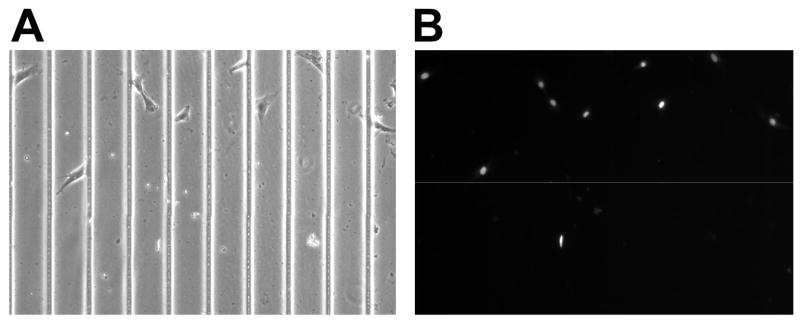
After cell culture, VSMCs on thin films were fixed using 4% glutaraldehyde (Polysciences, Inc, Warrington, PA) in PBS for approximately 15 min at room temperature. The cells were then treated for 5 min in 0.5 μg/ml of potassium borohydride (Sigma) in PBS to remove auto-fluorescence. Cells were then incubated in Hoechst 33342 (Molecular Probes), 1 μM in PBS, for 30 min at room temperature to stain the nuclei (Figure 5).

Figure 5. Representative image of Hoechst straining on films.

Figure 5

Open in a new tab

Cells in images were seeded onto a film with 70 μm grooves, with images taken using bright-field (A) and DAPI (B). DAPI images were then used to determine the major axes of the cells and the corresponding angle in relation to the applied strain.

Microscopy and Image Analysis

The samples were imaged with a Zeiss Axiovert S100 Microscope (Carl Zeiss) equipped with fluorescence and a digital camera, and images were processed using Metamorph Data Acquisition software (Universal Imaging, Downington, PA). Image-Pro Plus (Media Cybernetics, Silver Spring, MD) was used to obtain cell metrics from cell images. To determine cell orientation on smooth and microtextured PDMS films the cell nucleus orientation was measured (Dunn 1982) using ImageJ (NIH freeware). Cells were outlined by hand and a software plug-in was used to determine the major and minor axes of each cell. The angle of the cell nucleus was then determined using the major axis of the cell. For all films the cell angle was measured with respect to the direction of the applied tensile strain with a cell angle of 0° signifying perfect alignment with the tensile strain axis. Three or four films were used for each combination of grooves and strain direction, and for each film 16–28 images were taken, with each image containing between 1 and 129 cells. This led to ~700–1400 measured cell orientation angles for each combination of groove width and strain direction.

Statistical Analysis

For each groove width and pattern orientation, the cell orientation data was fit to a von Mises probability distribution, which describes the distribution of random variable with period 2π. The probability density function for this distribution is

f(x|μ,κ)=eκcos(x−μ)2πI0(κ) (2)

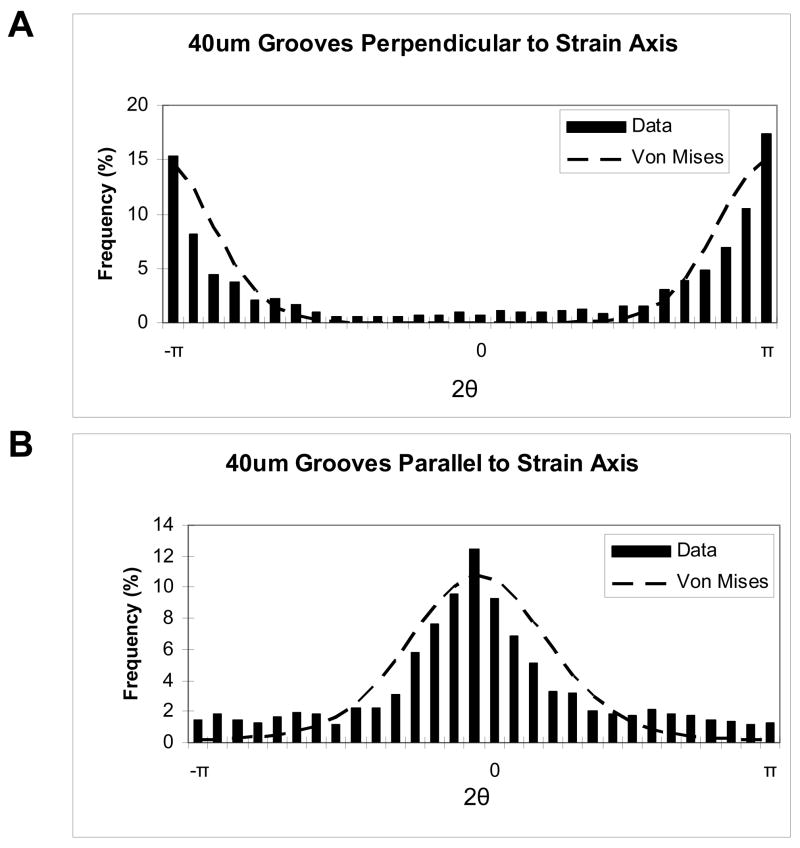
where μ is the mean cell orientation angle, k is the inverse of the variance of the angle, and I0(k) is the zeroth order Bessel function evaluated for the calculated value of k. Fitting Equation (2) to the data requires that the data possess a maximum theoretical range of 0–2π (or − π to π). However, because measurements were taken as the angle between the long axis of the cell and the strain axis, the measured angles (θ) range only from 0–π. Thus, these angles were multiplied by 2 prior to the curve fit such that x in Equation (2) represents 2π. Figure 3 shows von Mises fits for data collected from films with 40 μm grooves oriented either parallel or perpendicular to the applied strain. For all of the groove width and groove orientation combinations, the data were represented well by a von Mises distribution.

Figure 3. Von Mises distributions for films with 40μm grooves oriented (A) perpendicular to applied strain and (B) parallel to applied strain.

Figure 3

Open in a new tab

For both figures, the frequency of each angle is plotted for 2θ, with θ being the angle of the cell nucleus with respect to the axis of applied strain.

To determine the separate and combined effects of groove width and groove orientation on cell alignment, values of μ and Κ were compared across combinations of groove width and orientation using analysis of variance (ANOVA). Values of P < 0.05 were considered to be significant. Values of Κ and μ determined from the experiments are shown in Table 1.

Table 1. Fitted von Mises distribution parameters.

Κ is the inverse of the variance (1/degrees2) and μ is the mean of each set of cell angles (degrees). “US” and “S” refer to unstrained and strained films, respectively, “perp” refers to microgrooves oriented perpendicular to applied strain and “para” refers to microgrooves oriented parallel to the applied strain. For all data, the angle is measured from strain axis. Values are average fitted parameters over all films used for the given combination of orientation and groove width (n = 3 or 4).

Κ (1/degrees2) μ (degrees)
UP/US 7.57 −38.97515924
UP/S 45.25 85.38248408
15/Perp 301.49 89.01859873
15/Para 119.52 15.73949045
40/Perp 213.65 85.97178344
40/Para 113.21 −3.871719745
70/Perp 117.72 87.67404459
70/Para 40.31 29.82468153
Open in a new tab

Results

Strain Field Characterization

The plot shown in Figure 4 demonstrates that the central region of the film experienced tensile strains ranging between 5.15 and 6.67%. In our cell alignment studies, only VSMCs seeded in the central region of the film were evaluated.

Cyclic Strain Studies

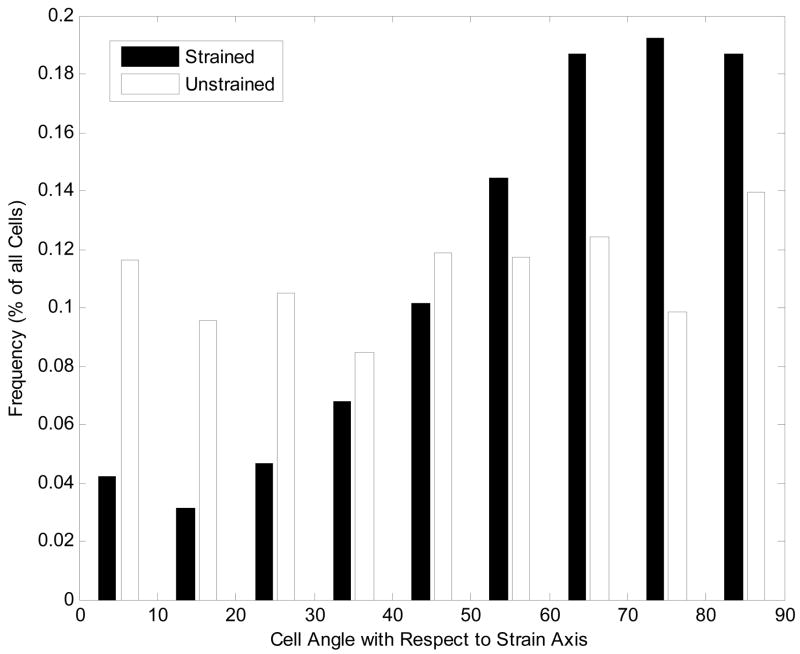
The average cell orientation angle (μ) and standard deviation of VSMCs on unpatterned PDMS films was determined to be 47.5 ± 26.3º on unstrained films. On unpatterned, cyclically-strained films the average cell orientation angle was determined to be significantly higher at 59.3 ± 21.8º (p < 0.05). The histogram in Figure 6 reveals that for these unpatterned films, approximately 57% of the cells were oriented at angle 60º or greater with respect to the applied tensile strain whereas cells had a more uniform distribution of orientation angles in the absence of strain.

Figure 6. Orientation angles of vascular smooth muscle cells (VSMCs) on unpatterned substrata.

Figure 6

Open in a new tab

Angles are measured from the axis along which the tensile strain would be applied. For strained substrata, the average maximum strain was approximately 6% strained at 1 Hz.

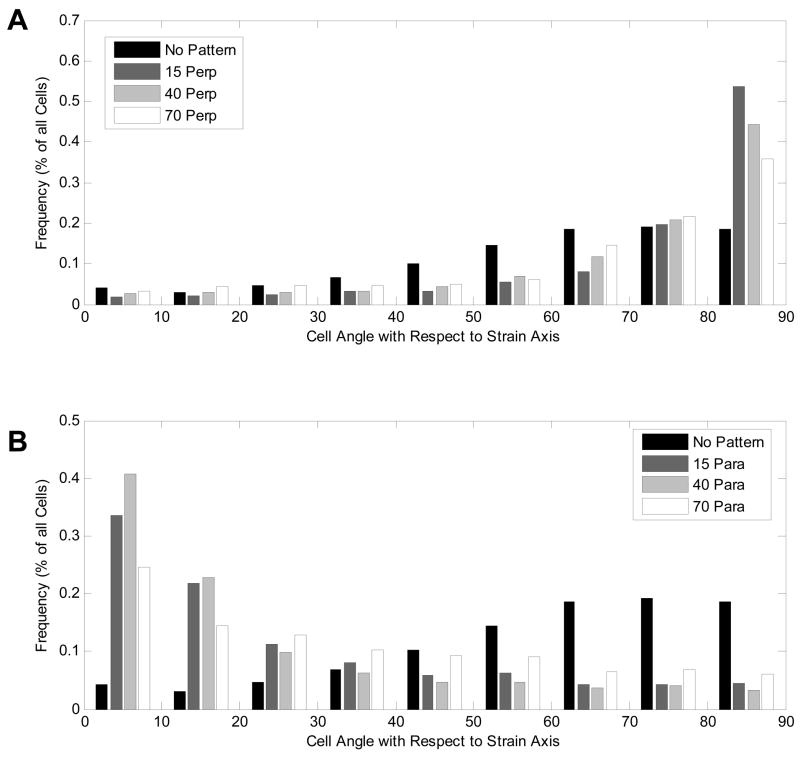
The cell orientation angle distributions for VSMCs on films with grooves perpendicular to the direction of the applied cyclic strain are shown in Figure 7a. Average cell orientation angles and standard deviations were measured to be 72.1º ± 20.7º, 69.7º ± 21.5º and 65.8º ± 23.2º on 15, 40 and 70 μm grooved films, respectively. For all three groove widths, the average cell orientation angles were significantly higher than those on unpatterned, strained films (p < 0.05 for all cases). In addition, as the groove width decreased, the proportion of cells aligned nearly perpendicular (80–90º) to the strain increased steadily from 36 to 44 to 54% for 70, 40, and 15 μm grooved films, respectively.

Figure 7. Orientation angles for patterned films subjected to cyclic strain with grooves oriented (A) perpendicular to strain and (B) parallel to strain.

Figure 7

Open in a new tab

For all cases the angle is measured from the axis of the applied tensile strain, and films were subjected to approximately 6% strain at 1 Hz.

The cell orientation angle distributions for VSMCs on films with grooves parallel to the direction of the applied cyclic strain are shown in Figure 7b. The average orientation angles for cells on films with grooves oriented parallel to the cyclic strain were found to be significantly lower than the 59.3º found for unpatterned films. Cell orientation angles for VSMCs were measured as 26.2º ± 24.3º, 22.6º ± 23.4º and on 34.5º ± 26.2º for 15, 40, and 70 μm grooved films, respectively. On all patterned films, the largest fraction of cells were oriented parallel (0–10°) to the applied strain. VSMCs on 40 μm grooved films had the highest percentage of parallel aligned cells (41%). For cells on 15 and 70 μm grooved films, 34 and 25% of cells were aligned parallel to the strain axis, respectively.

Discussion

Our experiments with unpatterned substrata confirmed previous findings that cyclic strain leads to cellular alignment perpendicular to the strain axis. On unpatterned substrata subjected to cyclic strain, the distribution of cell angles clearly showed a trend towards perpendicular alignment to the direction of applied strain. A higher percentage of cells were found in a smaller range of bins, with over 50% of cells having an angle greater than 60 degrees on strained films as opposed to 30% for unstrained films, which is indicative of an even distribution. This is in agreement with findings previously reported (Kanda et al., 1992; Wang et al., 2000). The unstrained films had an even distribution of cell angles across the 90 degree span, implying no preferred orientation in the absence of mechanical and microtopographical cues.

However, when we combined cyclic mechanical strain with microgrooved substrata, we found that cell orientation depends on the orientation of the grooves with respect to the direction of applied cyclic, tensile strain. For cells on substrata with grooves perpendicular to the direction of applied strain we observed that the strength of cellular alignment in the direction perpendicular to the strain axis increased significantly as compared to unpatterned substrata (p < 0.05). In contrast, when the microgrooves were parallel to the direction of cyclic strain, we found that cells tended to be aligned in the groove direction, rather than perpendicular to the strain axis. Together, these results suggest that the arrangement of microgrooves parallel to direction of applied strain is a barrier to the tendency of cells to reorient perpendicular to the strain axis.

This antagonistic effect of groove orientation on cell alignment was weakest for the 70 μm grooves. One possible reason for this finding is that the wide grooves provide the most room for the cells to maneuver and orient themselves as they respond to the cyclic strain. Interestingly, cell alignment on 15 μm groove films is significantly lower than on 40 μm groove films (p < 0.05). This in contrast to previous findings, which show that for decreasing groove width the frequency of alignment in the grooves is greater (Glawe et al., 2005). However, in the mentioned study, the groove separation was 10 μm while in the current study the spacing is 14 μm. Consequently, while the space provided for cell movement by 40 μm grooves is greater than for the 15 μm grooves, cells on 15 μm grooved films mainly attached to the ridges as opposed to aligning within the grooves. Thus, the cells in this case were not restrained within grooves and were able to reorient above the plane of the pattern. This suggests that the walls of the grooves provide additional restraint to the cyclic strain orientation response of the cells. Thus, for different groove spacing at narrower microgrooves, the trend toward greater alignment in the grooves for narrower channels does not hold. The results illustrate a lower limit of microgroove width where making the grooves narrower becomes less effective at constraining cells in the presence of cyclic strain. This phenomenon has not previously been observed for microgroove topography without a secondary stimulus, and was also not observed in previous studies combining both alignment stimuli. This shows the importance of the groove spacing towards cell behavior for multiple stimuli when using microgrooves.

Applying cyclic strain to a substrate within an aqueous medium will inevitably cause some swirling of the solution and resulting fluid shear stress (FSS) on the attached cells. Studies have shown that FSS of 10 dyn/cm2 resulted in significant reorientation of VSMCs, whereas FSS of 1 dyn/cm2 did not lead to reorientation (Lee et al., 2002). Moreover, other studies have shown that for 10% strain in culture (above what was used in this study), the induced FSS is in the range of 0 +/− 0.2 dyn/cm2 (Sung et al., 2007), which is well below the reported range needed for VSMC reorientation. As a result, effects due to FSS in the current study were not considered in analysis.

The data suggest that there is a range of microgroove widths for which the effect of cyclic strain can be attenuated for the groove spacing investigated. With small groove widths, such as the 15μm grooves, the cells tend to remain on the top surface and can better reorganize as influenced by the cyclic strain. However, with large groove widths the cells have more freedom to move within the grooves, again lending themselves to reorganization as a result of the cyclic strain. Our conclusion is that there is an effective range of groove widths which will effectively limit the ability of VSMCs to reorganize in the presence of an applied cyclic strain oriented parallel to the grooves for a given groove spacing. Because of the sensitivity of alignment behavior to all three of the dimensions of microgroove topography, future work should be done to better characterize the interplay between cyclic strain and microgrooves by using more combinations of groove widths, depth and spacing to better understand the effective range of maintaining cellular alignment in the presence of an antagonistic mechanical stimulus for varying dimensions of microgrooves.

In order to understand the underlying mechanisms for realignment, it would be beneficial to carry out studies investigating the cell signaling pathway and the effects of cytoskeletal rearrangement induced by the combined effects of the stimuli. Previous studies have suggested the involvement of nitric oxide signaling for VSMCs subjected to cyclic strain (Standley et al., 2002), though there are likely multiple alternate pathways in the combined system. Studies regarding cytoskeletal changes induced by the two stimuli have been conducted independently on fibroblasts, and suggest different mechanisms for cytoskeletal rearrangement. A study involving cyclic strain found that the effects of the stimulus led to increased f-actin production and subsequent changes in cell structure (Pender et al., 1991). On the other hand, contact guidance studies of fibroblasts using different cytoskeletal inhibitors found that the most influential component of cytoskeletal rearrangement was microtubules (Oakley et al., 1997). The interplay between the two components of the cytoskeleton (actin and microtubules) in the presence of the two different stimuli has yet to be investigated. Future studies into the effects on the cytoskeleton in a combined system would be beneficial for understanding the pathways and hierarchy for cellular alignment.

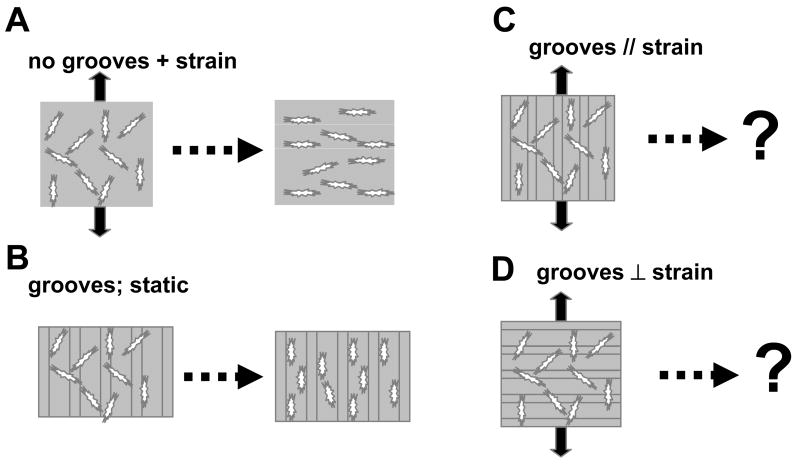
Figure 1. Schematic of interplay between microtopography and applied cyclic strain.

Figure 1

Open in a new tab

(A) Previous studies have shown that applied cyclic strain orients cells perpendicular to the strain axis. (B) Previous studies have shown that microtopography under static conditions lead to orientation of the cells along the groove direction. (C,D) Focus of this study: determination of cell orientation in the presences of grooves oriented parallel or perpendicular to the applied strain axis.

Acknowledgments

This work was supported by a grant from NASA (NNJ04HC73G) and NIH (R01 HL72900). We thank P. DiMilla and X. Brown for insightful discussions and B. Isenberg for critical reading of the manuscript. We thank the Scientific Instrument Facility in the Physics Dept. at BU for manufacturing the device and the cleanroom in Photonics for use of the microfabrication facilities.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Brunette DM, Chehroudi B. The effects of the surface topography of micromachined titanium substrata on cell behavior in vitro and in vivo. J Biomech Eng. 1999;121:49–57. doi: 10.1115/1.2798042. [DOI] [PubMed] [Google Scholar]
  2. Deutsch J, Motlagh D, Russell B, Desai TA. Fabrication of microtextured membranes for cardiac myocyte attachment and orientation. J Biomed Mater Res. 2000;53:267–275. doi: 10.1002/(sici)1097-4636(2000)53:3<267::aid-jbm12>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
  3. Dunn GA. Contact guidance of cultured tissue cells: a survey of potentially relevant properties of the substratum. In: Ruth Bellairs AC, Dunn Graham, editors. Cell Behaviour. Cambridge: Cambridge University Press; 1982. pp. 247–280. [Google Scholar]
  4. Glass-Brudzinski J, Perizzolo D, Brunette DM. Effects of substratum surface topography on the organization of cells and collagen fibers in collagen gel cultures. J Biomed Mater Res. 2002;61:608–618. doi: 10.1002/jbm.10243. [DOI] [PubMed] [Google Scholar]
  5. Glawe JD, Hill JB, Mills DK, Mc Shane MJ. Influence of channel width on alignment of smooth muscle cells by high aspect-ratio microfabricated elastomeric cell culture scaffolds. J Biomed Mater Res A. 2005;75:106–114. doi: 10.1002/jbm.a.30403. [DOI] [PubMed] [Google Scholar]
  6. Hsu S, et al. Oriented Schwann Cell Growth on Microgrooved Surfaces. Biotechnology and Bioengineering. 2005;92(5):579–88. doi: 10.1002/bit.20634. [DOI] [PubMed] [Google Scholar]
  7. Isenberg BC, Tranquillo RT. Long-term cyclic distention enhances the mechanical properties of collagen-based media-equivalents. Ann Biomed Eng. 2003;31:937–949. doi: 10.1114/1.1590662. [DOI] [PubMed] [Google Scholar]
  8. Kanda K, Matsuda T, Oka T. Two-dimensional orientational response of smooth muscle cells to cyclic stretching. Asaio J. 1992;38:M382–385. doi: 10.1097/00002480-199207000-00060. [DOI] [PubMed] [Google Scholar]
  9. Kemkemer R, et al. Cell Orientation by a Microgrooved Substrate Can Be Predicted by Automatic Control Theory. Biophysical Journal. 2006;90(12):4701–4711. doi: 10.1529/biophysj.105.067967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kim BS, Mooney DJ. Scaffolds for engineering smooth muscle under cyclic mechanical strain conditions. J Biomech Eng. 2000;122:210–215. doi: 10.1115/1.429651. [DOI] [PubMed] [Google Scholar]
  11. Kim BS, Nikolovski J, Bonadio J, Mooney DJ. Cyclic mechanical strain regulates the development of engineered smooth muscle tissue. Nat Biotechnol. 1999;17:979–983. doi: 10.1038/13671. [DOI] [PubMed] [Google Scholar]
  12. Lee AA, et al. Fluid Shear Stress-Induced Alignment of Cultured Vascular Smooth Muscle Cells. J Biomech Eng. 2002;124:37–43. doi: 10.1115/1.1427697. [DOI] [PubMed] [Google Scholar]
  13. Oakley C, et al. Sensitivity of Fibroblasts and Their Cytoskeletons to Substrate Topographies: Topographic Guidance and Topographic Compensation by Micromachined Grooves of Different Dimensions. Experimental Cell Research. 1997;234:413–424. doi: 10.1006/excr.1997.3625. [DOI] [PubMed] [Google Scholar]
  14. Owatverot TB, et al. Effect of Combined Cyclic Stretch and Fluid Shear Stress on Endothelial Morphological Responses. J Biomech Eng. 2005;127 doi: 10.1115/1.1894180. [DOI] [PubMed] [Google Scholar]
  15. Pender N, McCulloch CAG. Quantation of actin polymerization in two human fibroblast sub-types responding to mechanical stretching. Journal of Cell Science. :187–193. doi: 10.1242/jcs.100.1.187. [DOI] [PubMed] [Google Scholar]
  16. Sarkar S, et al. Vascular tissue engineering: microtextured scaffold templates to control organization of vascular smooth muscle cells and extracellular matrix. Acta Biomaterialia. 2005:93–100. doi: 10.1016/j.actbio.2004.08.003. [DOI] [PubMed] [Google Scholar]
  17. Seliktar D, Nerem RM, Galis ZS. Mechanical strain-stimulated remodeling of tissue-engineered blood vessel constructs. Tissue Eng. 2003;9:657–666. doi: 10.1089/107632703768247359. [DOI] [PubMed] [Google Scholar]
  18. Standley PR, et al. Cyclic stretch induces vascular smooth muscle cell alignment via NO signaling. AJP-Heart Circ Physiolol. 2002;283:H1907–14. doi: 10.1152/ajpheart.01043.2001. [DOI] [PubMed] [Google Scholar]
  19. Sung HJ, et al. Cyclic strain and motion control produce opposite oxidative responses in two human endothelial cell types. Am J Physiol Cell Physiol. 2007;293:87–94. doi: 10.1152/ajpcell.00585.2006. [DOI] [PubMed] [Google Scholar]
  20. Wang JH, Grood ES. The strain magnitude and contact guidance determine orientation response of fibroblasts to cyclic substrate strains. Connect Tissue Res. 2000;41:29–36. doi: 10.3109/03008200009005639. [DOI] [PubMed] [Google Scholar]

RESOURCES