Mechanical separation of the complementary strands of DNA

Abstract

We describe the mechanical separation of the two complementary strands of a single molecule of bacteriophage λ DNA. The 3′ and 5′ extremities on one end of the molecule are pulled progressively apart, and this leads to the opening of the double helix. The typical forces along the opening are in the range of 10–15 pN. The separation force signal is shown to be related to the local GC vs. AT content along the molecule. Variations of this content on a typical scale of 100–500 bases are presently detected.

Mechanical force at the molecular level is involved in the action of many enzymes. This is the case for the processes of replication or transcription in which enzymes translocate processively with respect to DNA. Such translocation occurs unidirectionally over long segments of DNA, and the enzymatic machinery has to develop a force against a number of impediments: the disruption of complementary base pairs, the possible attachments of the DNA or the enzymes to cellular components, structural proteins that coat DNA and have to be displaced, topological constraint, and viscous friction. The force necessary to stop a transcribing Escherichia coli polymerase recently has been measured (1). In the case of replication (2), the DNA double helix is opened, and two daughter strands are formed. The opening may be associated to the translocation mechanism of the polymerase itself or may be assisted by accessory proteins like helicases or single-strand binding proteins. Moreover, because the strands are intertwined, strand separation is coupled to a local rotation. Topological constraints are resolved by topoisomerases (3, 4).

Long before the enzymes associated to replication were known, a simple model had been considered (5) in which the mechanism of unwinding the strands during replication is coupled to rotation of the whole molecule. A molecular configuration with a Y shape had been proposed in which the vertical part is the parent helix, and the two arms are the separated strands that get replicated. As replication proceeds, a “speedometer cable” rotation motion was proposed for all three branches of the Y.

We have set up an experiment to measure directly the forces involved in the elementary process of mechanical strand separation, with no enzyme present. The experiment presented here is approaching the Levinthal and Crane (5) configuration.

Force measurement on single molecules of DNA is an emerging field (6–13). For typical molecular interactions involving biomolecules, the forces involved are small (sub-picoNewton to 10s of picoNewtons [pN = 10⁻¹² N]). For this reason, sensitive measuring devices (14–17) such as optical tweezers, soft micro-needles, or levers of atomic force microscopes have been used.

METHODS

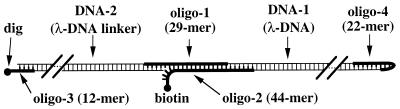
To achieve mechanical unzippering of DNA, the small interstrand spacing (nanometer) has to be adapted to the micrometer size of a micromechanical device that will separate the strands. To solve this problem, a specific molecular construction has been designed in which (i) one strand of the DNA to be opened is prolonged by a linker arm and (ii) two specific functionalizations are introduced to obtain the desired attachments of the construction to the micromechanical device. The design of the construction used in the experiment appears in Fig. 1 and includes two molecules of double stranded λ-phage DNA, each comprising 48.5 kb. The DNA to be opened is DNA-1, and the linker arm is DNA-2. Oligonucleotides are used to connect DNA-1 and DNA-2 and to introduce attachment points via a digoxigenin group and a biotin group. The other extremity of DNA-1 is capped with an oligonucleotide forming a hairpin (18) (oligo-4), which prevents the separation of the two strands when reaching the end of the opening process. This allows repeated cycles of opening and closing.

Figure 1.

The molecular construction. The DNA to be opened (DNA-1) and the linker arm (DNA-2) are comprised of double-stranded λ-phage DNA (or occasionally of multimers of double-stranded λ-phage DNA). Oligonucleotides (thick lines) are used to introduce the biotine and dig attachments and to connect covalently DNA-1 and DNA-2.

Preparation of the Molecular Construction.

The preparation is done sequentially, using λ-DNA from Pharmacia and oligonucleotides from Pharmacia or Genset (Paris). The 12-base single-strand segments (Cos end) that protrude at the 5′ ends of linearized λ DNA are used to assemble the construction.

The Cos sequence are: 5′-Agg TCg CCg CCC-3′ and 5′-ggg Cgg CgA CCT-3′ We have chosen the following sequences for the oligonucleotides:

Oligo1, 5′-Agg TCg CCg CCC AAg ggA CTA CgA gAT Tg-3′ (29 mer); Oligo2, 5′-Agg TCg CCg CCC CAA TCT CgT AgT CCC AAA AAA TCA gCA gTA AC Biotine-3′ (3′ biotinylated 44 mer); Oligo3, 5′-ggg Cgg CgA CCT digoxigenin-3′ (3′ digoxigenin 12 mer); and Oligo4, 5′-ggg Cgg CgA CCT AgC gAA AgC T-3′ (22 mer).

DNA-2 (10 μg) and oligo-3 (preparation A, 1:10 molar ratio, 20 μl) as well as DNA-1 (10 μg) and oligo-4 (preparation B, 1:10 molar ratio, 20 μl) were hybridized (55°C, 1 h) and then ligated (0.2 Weiss units of T4 ligase, T = 16°C, 1 h). Then, preparation A and oligo-1 (preparation C), as well as preparation B and oligo-2 (preparation D), were hybridized (55°C, 1:10 molar ratio, 1 h), then ligated (0.2 Weiss units of T4 ligase, T = 16°C, 1 h), and then purified (Amicon 100 column). Finally, preparations C and D with 15% added polyethylene glycol (preparation E, 1:1 molar ratio of C and D, molecular weight of polyethylene glycol = 8000) were hybridized (40°C, 1 h, then cooled slowly), then ligated (0.2 Weiss units of T4 ligase, T = 16°C, 2 h), and purified (Amicon 100 column). The end mixture E was diluted for final use. Occasionally, constructs may incorporate multimers of λ-DNA (in the linker arm or in the DNA to be opened).

Experimental Configuration.

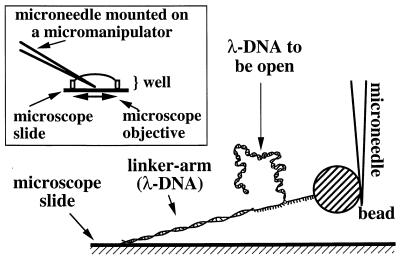
The experiments were performed in a liquid buffer (PBS, pH 7.0/10 mM phosphate/150 mM NaCl, at room temperature), which was retained by a ring glued with paraffin on top of a microscope slide. This assembly formed a “well” (see Fig. 2, Inset) and was placed on an inverted video microscope. The face of the microscope slide in contact with the buffer was coated with an antibody against digoxigenin. The digoxigenin functionalized extremity of the construction was attached to this face, and the biotinylated extremity was anchored to a microscopic bead coated with streptavidin (Dyna beads, ∅ = 2.9 μm; Dynal, Oslo). The experimental set-up for the mechanical unzippering of DNA is presented schematically in Fig. 2. The bead was attached to a glass microneedle (19) (treated with biotin), which was introduced through the free meniscus and was positioned by an xyz micromanipulator. The microneedle served as a force sensor, i.e., the deflection of the tip of the microneedle was monitored under a microscope as a function of the lateral displacement of the surface. The microscope was custom-built (objective Zeiss Achroplan, oil immersion × 100, N.A. 1.25), and images were collected by a black and white CCD camera [Cohu (San Diego) model 4912–5100] attached to the microscope. The images were recorded on an S-VHS VCR [Panasonic (Secaucus, NJ) model AG-7355]. Using a digital image acquisition board, the tip deflection of the microneedle was extracted either on-line from the live video images or off-line at higher resolution from the video tape, which will be described later. A custom-built translation stage, based on a combination of a motor and a piezo unit (Physik-Instrumente, Waldbronn, Germany, 50-μm range) allowed coarse and fine lateral motion of the well. This motion was measured with submicron resolution by an inductive gauge connected to a 6.5-digit voltmeter. Data were transferred via a general purpose interface bus to a PC.

Figure 2.

Principle of the force measurement in which a double-stranded λ-DNA is forced open as the surface is displaced to the left. (Inset) A plastic ring is glued to the microscope slide that is coated with antidig. This well was placed on an inverted microscope. The microneedle was introduced through the free meniscus.

Preparation and Use of a Microneedle.

Using a commercial pipette puller, we prepared tapered glass microneedles (typical dimensions: shank diameter 1 mm, tip diameter 1 μm, and tapered length 1 cm). The stiffness varied from needle to needle and was calibrated (as described in the next section). The needles were chemically biotinylated [silanization with N-(β-aminoethyl)-γ-amino-propyltrimethoxysilane (Pierce) followed by reaction with succinimidyl-6-(biotinamido)hexanoate]. The tip of a treated microneedle stuck readily to the streptavidin-coated microbeads upon touching them with the tip. After a measurement, the beads could be removed by a mechanical shock on the microneedle or by using a meniscus effect (simply taking the microneedle out and then putting it back into the liquid).

Calibration of the Microneedle Stiffness.

Using the previously described microscope set-up, a paramagnetic bead (Dyna) was attached to the end of the microneedle within a well (without DNA). A magnet was approached, and the deflection of the tip of the microneedle vs. the magnet-to-bead distance was measured. The magnet was removed to a position that corresponded to a small deflection. The bead was then detached mechanically from the soft microneedle using a second, stiff microneedle controlled by micromanipulation. The bead then moved quickly toward the magnet.

Using stroboscopic illumination, the time-dependent position of the bead was recorded on video during the acceleration toward the magnet. The velocity of the bead as a function of the bead-magnet distance was derived from these data. The local velocity v was proportional to the force on the bead (by Stokes’ formula: F = 6πηRv where η is the viscosity of the buffer and R is the radius of the bead). From both sets of measurement (microneedle deflection vs. bead-to-magnet distance and bead velocity vs. bead-to-magnet distance), we derived the force-deflection curve and hence the stiffness of the microneedle. A single microneedle (with a stiffness of 1.7 pN/μm ± 20%) was used throughout all experiments presented here.

An independent confirmation of the calibration follows: Sometimes, when the opening does not occur (this may be due to partial adsorption of the construction to the bead), the force rises as a function of the displacement until the characteristic plateau in the force vs. extension curve of the double helix (12, 13) is observed. This corresponds to the overstretching of the linker arm. Using the above force calibration, force values of ≈70 pN obtained for that plateau are consistent with the values reported in the literature.

Incubation of the Construction in the Well.

In the preparation steps in which a small volume of reaction was preferred, we used a small circular disc of thin glass that fit inside the ring of the well. Reactions took place in a thin layer of fluid limited by the microscope slide and the disc. The microscope slide was coated (6, 11) with antibodies against digoxigenin (anti- digoxigenin, Boehringer Mannheim). Then, a dilution of the construction (10 μl of a dilution of typically 1 ng/μl) first was added to the well, and a disk was dropped onto it. Incubation typically was done in this covered well for 30 min. Excess buffer was then added to the well, and the glass disk was removed. The beads (Dynal, paramagnetic beads, ∅ = 2.9 μm, streptavidin-coated) were introduced, sedimented, and reacted with the biotinylated extremity of the molecular constructions. After 1 h of incubation, a large part of the unattached beads was removed by dipping transiently a small rare earth magnet. Dilutions and incubation times were adjusted so that tethering events were rare, and tethering of a bead with two constructions was negligible. Typically, 10–30 beads were observed within the field of view under the microscope with a ×20 objective after removing the free beads. A variable fraction of the beads was stuck to the surface, and a fraction was tethered (as seen by imposing a weak flow in the well; they displaced by ≈16 μm and then stop). The characteristic tether length (16 μm) was understood as corresponding to the length of the linker arm, and this implied that DNA-1 was not opened by the forces associated to the flow.

Preparing a Force Measurement.

The tip of the microneedle was first attached to a chosen bead. Then a translation stage displaced laterally the well while the base of the microneedle was maintained at a fixed position. The deflection of the tip of the microneedle under microscope was measured on the video image as a function of this displacement.

Before the attachment of the microneedle on a tethered bead, no external force was present, and the linker arm was compacted by the action of the entropic forces. The beads were thus situated at a close distance (<1 μm) from the attachment point on the bottom surface. Just after attaching the bead to the microneedle, it was raised by a few micrometers above the bottom surface to avoid solid friction between bead and surface. The sample was displaced laterally at a constant velocity in a given direction, and a sizable deflection appeared when the displacement approached the contour length of the DNA linker. The experiment also can be done by displacing the sample in the reverse direction; a symmetrical measurement results. This symmetry was used to localize the “zero” point for the displacement. The range of translation velocities explored spanned from 20 to 400 nm/s although the data presented in this paper were obtained in the low velocity range of 20 to 40 nm/s.

During a measurement, the bead-to-surface distance was small compared with the lateral displacement (because of the long linker arm). Therefore, the trigonometric corrections were neglected.

RESULTS

A First Analysis at Low Resolution.

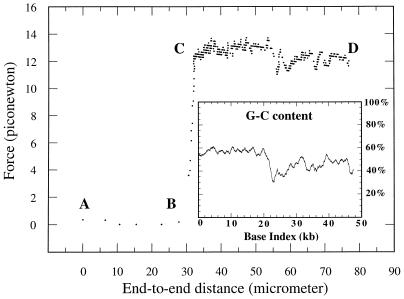
In Fig. 3, an example of an on-line (0.2–0.3 pN resolution) force measurement obtained at a translation velocity of 40 nm/s is presented. For this particular measurement, the linker arm was a dimer of λ DNA with a length of 32 μm. The horizontal axis of Fig. 3 is the displacement minus the deflection; this is intended to correspond to the “end-to-end distance” between the two anchor points of the molecular construction. Point A corresponds to the initial attachment at zero force and zero displacement. The segment A–B–C corresponds to the extension of the linker arm against the entropic forces; the regime described by Smith et al. (6, 7) on the stretching of a single DNA double helix is qualitatively recovered.

Figure 3.

Force (deflection of the calibrated microneedle) as a function of the end-to-end distance while displacing the well at an average velocity of 40 nm/s. The end-to-end distance is defined as the displacement of the well minus the deflection of the microneedle. The linker arm is a dimer in this particular measurement, and the rise of force thus occurs ≈32 μm, i.e., twice the crystallographic length of λ-DNA. The quasi-plateau C to D corresponds to the opening of the double helix. Going back from D to A (not shown), the two single strands reannealed, and a new measurement cycle could be engaged. (Inset) GC content (GC%) averaged over 1000 bp along the sequence of λ phage DNA from 1 to 48,502 bp.

At point C, a sudden change in the force vs. end-to-end distance dependence occurs. A quasi-plateau C–D is observed at a typical force of ≈13 pN with variations of approximately ±1 pN and extending over a total length of ≈50 μm. This quasi-plateau differs from the observed transition (12, 13) of dsDNA under mechanical stretching because the latter (i) occurs at a typical force level of 60–70 pN and (ii) extends only over ≈10 μm (for a λ DNA), followed by a steep rise in force. In our experiment, a fine structure was visible in the quasi-plateau and was reproducibly obtained. Typically, for the first 20 μm (from ≈32 to 53 μm in Fig. 3), the average force was 13 pN with fluctuations of ±0.5 pN. For the last 20 μm of the quasi-plateau (from ≈60 to 80 μm), the average force was 12 pN with fluctuations of ±0.5 pN. In between (from 53 to 60 μm), a marked dip was observed.

Going back from D to A (not shown), the two single strands reannealed, and a new measurement cycle could be engaged. The force signal acquired during this return phase may have differed from the signal obtained during the opening, with instabilities and partial nonreproducibility. However, upon opening again, the force signal gives the same signature again. Measurements may be interrupted by the breakage of the anchoring or of the molecule, e.g., nicks. Typically, ≈90% of the tested molecules in a given sample begin to open.

Connection to the Sequence: A First Example.

The full sequence of bacteriophage λ-DNA (20) was taken from the European Molecular Biology Laboratory database. An averaged GC content curve (GC%), as a function of base index, is presented in the inset of Fig. 3. The characteristic gross features of the GC% curve (average over 1000 bases) are a high GC% of ≈60% in the first 20,000 bases, followed by a central notch and then a second part (28,000–48,000) with a lower GC% of ≈40%.

By a scaling adjustment of the horizontal axis of the GC content curve, it was possible to approximately match the above gross features with the experimental force curve vs. end-to-end distance. This suggested the following empirical relation: a displacement of 1 μm of the well corresponds to a progression of 1000 bp in the sequence (corresponding to a total of 2000 bases of ssDNA). During an opening experiment, the single strands were stretched by an approximately constant force value of f₀ = 13 pN. The total length of a ssDNA of 2000 bases subjected to a force of 13 pN is ≈1 μm (in a TE buffer at 150 mM NaCl) (12), a value consistent with the empirical relation determined above.

A Measurement on an Inverted Construction.

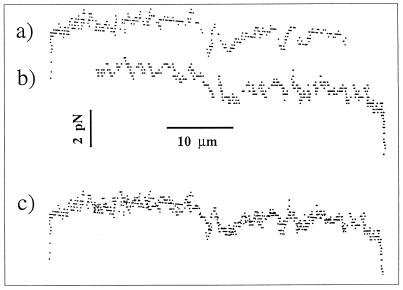
To experimentally substantiate that a displacement corresponded to a progression in the sequence, we prepared a different molecular construction; in this new construction (called “Λ⁻¹” in opposition to the preceding construction called “Λ”), the DNA-1 molecule has been reversed, i.e., the opening is expected to occur from base index 48,502 to 1, rather than 1 to 48,502 in Λ. This was obtained with a different set of oligonucleotides in which oligos 2 and 4 have their Cos ends exchanged. A force measurement on this construction (with a similar low resolution) gave a signal with the same features but in reverse order (Fig. 4). This underlines the idea that the forces we measured were indeed associated to the mechanical opening of the double helix and that the signal (at least at this level of resolution) was connected to the sequence.

Figure 4.

Force vs. end-to-end distance obtained for λ DNA. Only the part corresponding to the opening has been plotted (a) and measured with the construction Λ (same as Fig. 3). (b) Signal obtained with the construction Λ⁻¹, in which the opening starts at index 48,502 rather than 1; the plot has been reversed (opening occurs from the right to the left on the figure) so that the signals obtained at a given location of the sequence are superimposable. In c, the direct superimposition of a and b is presented.

Force Signal at High Resolution.

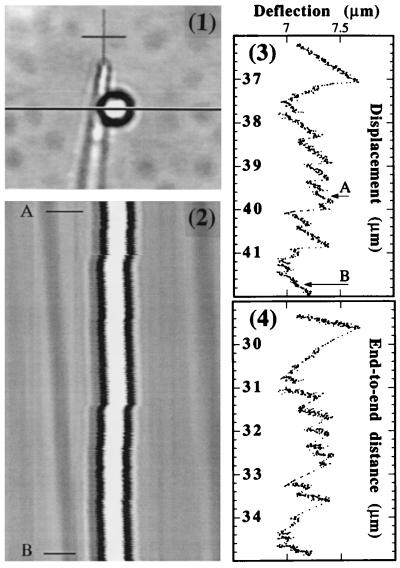
We carried out an analysis of the sequence dependence of the force signal with a high resolution mode of data extraction, performed off-line from the video-taped movie of the bead and the microneedle under the microscope. Fig. 5.1 is a typical video frame. A single video line per frame, shown as a dark horizontal line, is sampled at a constant rate of 5 or 12 times/s; it carries the information of the instantaneous deflection of the microneedle. Each line is converted to a computer file consisting of 640 pixels with 256 gray levels. From this, a spatio temporal image (5.2) is constructed (time linearly increasing from top to bottom). In this example, the well is being displaced to the right, and the microneedle bends accordingly. The scanned region corresponds approximately to the region spanning the 17,000- to 19,000-bp index in the sequence of λ DNA. The signal, i.e., the two parallel black strips (corresponding to the bead position as a function of time) presents a line-to-line variation on a short time scale corresponding to noise and a variation on a longer time scale corresponding to the time-dependent force signal. The major source of noise in the experiment is not Brownian motion but mechanical vibrations arising from seismic or acoustic perturbations. The noise is partially removed by low-pass filtering, and the signal is extracted by a thresholding procedure on the black/white contrast of the bead. Presently, a resolution of about 50 nm is obtained for the deflection.

Figure 5.

(1) Typical video image of the bead and the microneedle under the microscope during the DNA opening. The bead diameter is 2.9 μm. Some surface defects of the glass-slide appear as scattered gray spots in the background. The well is being displaced to the right, and the microneedle is bent to the right by the molecule being opened. A single video line per frame, shown as dark horizontal line, is sampled at a constant rate of 5 times per second. From this, a spatio temporal image (2) is constructed. The total time interval represented in 2 is 96 s and corresponds to a displacement of the well of 1.9 μm (time increasing linearly from top to bottom). The two parallel black stripes rising from the bead image contain the information on the time-dependent deflection. The displacement of the well appears in the inclined faint gray stripes arising from the surface defects. The faint lines that are vertical corresponds to fixed spots (dust/defects in the optics and camera). In 3, we present the extracted force signal corresponding to 2. In 4, the deflection vs. end-to-end distance is plotted for the same region as in 3.

Fig. 5.3 shows the corresponding high resolution force signal vs. displacement of an opening from a base index of ≈14,000–19,000. The segment A–B corresponds to the Fig. 5.2. The signal presents a succession of saw teeth with a distribution of amplitudes and sizes. Those features are reproducible, e.g., when opening again, a signal with about the same features at the same positions and amplitudes is obtained. This reproducibility is better at low speed (20 nm/s) and is presently not perfect, particularly for the smallest details. We believe that the mechanical vibrations of the set-up are responsible for those imperfections. In a given sawtooth, the signal is raising slowly at an approximately constant rate and then drops suddenly. Because of this difference in time-scale, a rise appears more “noisy” to the eye than a drop in force. To represent the force as a function of the end-to-end distance, the displacement has to be turned into displacement minus deflection. In the coordinates (deflection vs. end-to-end) shown in Fig. 5.4, a slow rise is turned to a steeper slope, and a fast drop is turned into a trajectory following approximately a line with a negative slope of −1 (because a large deflection is associated to only a small displacement).

High Resolution Comparison Between Force and Sequence.

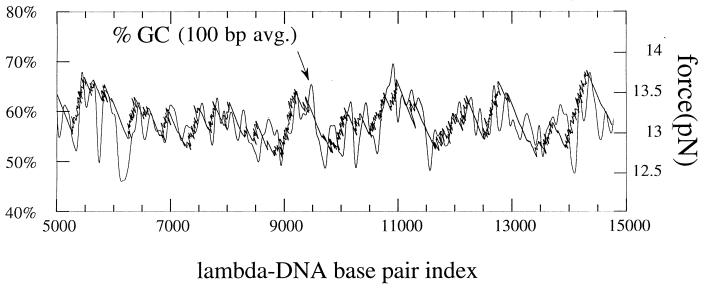
A direct comparison between a high resolution force signal and the sequence of λ DNA appears in Fig. 6. The sequence is presented through the GC content averaged over 100 bases (thin, continuous, smooth line corresponding to a Gaussian weight with a full width of 100 bases at 1/e of the maximum). The correspondence that we determined (1000 bases = 1 μm end-to-end distance) allows to present the curves with a common horizontal axis. The sequence is presented from 5,000 to 15,000 in base index. It is shown clearly that the signal is related to the sequence; most of the steep rises in the force signal correspond to peaks in the GC% curve. We described earlier in this article that the sizable segments of negative slope correspond to fast motions. Peaks in the GC% thus appeared to block transiently the opening until the force reached a level where the opening occurs quickly over a long segment in the base index. When trying to adjust the width of the averaging, a 50-base average gave more information than the signal reflected; on the contrary, information contained in the measured signal was lacking on a 200-base average. Thus, the 100-base average appeared to be a reasonable size to reveal the triggering events; this does not mean, however, that the resolution was 100 bases because the signal after a trigger appeared to “surf over,” and some details of the sequence are ignored. As a different way to define the sequence resolution given by the force signal, the number of events in a total opening gave a typical density of one event per 500 bases.

Figure 6.

Comparison between the force signal and the average GC content along a segment from 5000–15,000 bp of the sequence of λ DNA. Two curves are superimposed: (i) The smooth curve is the GC% averaged over 100 bases (Gaussian weight with a total width of 100 bases at 1/e of the maximum height) for the sequence of λ-DNA. (ii) The second curve is the force measurement (force vs. end-to-end distance) obtained by mechanical opening (experimental points have been connected by lines).

The comparison presented in Fig. 6 shows that a constant speed displacement is turned into a nonhomogeneous speed of opening. When reconsidering the deflection vs. displacement curve (Fig. 5.3), the slow rise in force corresponding to a sawtooth is associated to a nearly blocked progression in the sequence. The slope of the force rise vs. displacement was thus due to the total elasticity of the mechanical configuration in which the displacement was imposed through elastic components (i.e., the microneedle, the single strands, and the linker arm). When the opening fork did not progress as fast as the mechanical displacement, elastic energy was stored and subsequently released when the opening fork progressed more quickly. This “molecular stick-slip” has been analyzed in more detail elsewhere (39).

We found that the force level necessary to trigger the opening (maximum amplitude of a given sawtooth) along the sequence increases with the GC content of the peak that blocks the progression. These triggering events were observed here in the 40–60% range; a linear fit in that domain of the force vs. GC% gave a rough estimate of 15 pN for opening a 100% GC sequence and 10 pN for a 100% AT sequence.

DISCUSSION

We report in this work a direct measurement on the forces involved in the unzippering of a long segment of DNA. The mechanical forces involved in the strand separation were in the range of 10–15 pN and were shown to be sequence-dependent. The opening was shown to proceed in a nonhomogeneous manner, and this effect was related to the sequence and the elastic nature of the mechanical configuration. This unzippering occurred away (≥1 μm) from solid surfaces, hence there was no disturbing influence due to solid molecule interaction.

Speed of Opening.

The experiments reported here were performed in the range of 20–40 nm/s, which correspond to an average speed of opening of ≈20–40 bp/s. This is to be compared with typical translocation velocities of 50–2000 bp/s observed with processive replication or transcription enzymes. Mechanical opening experiments at higher speeds were possible (up to hundreds of base pairs per second) but were limited by the response bandwidth of the microneedle. As mentioned before, the force data were obtained during the opening phase. Upon closing, we observed that the signal presented a degree of nonreproducibility. Because the two single strands had to reanneal in exact register, any local disturbance might have hindered transiently the process. Such a hindrance might have been a local out-of-phase reannealing, the formation of possible secondary structures in the opened single strands, or the possible trapping of an unattached DNA construction between the two branches of the Y of the closing fork. Also, the reannealing to form the double helix imposed a rotation of the double-stranded part of the molecule; this possibly would be associated to a complex dynamics. Upon opening again, however, a reproducible signal was obtained.

Related Studies.

A previous study with Atomic Force Microscopy was directed toward the measurement of the force necessary to break a base pairing (21). An Atomic Force Microscopy tip was coated with a type of nucleotide (A or C), and a surface was coated with A, T, G, or C. A separation force of 54 pN was reported for a single AT base pair. Our results were much smaller (≈10 pN for an AT base pair). It is possible that the values obtained by Boland and Ratner (21) were strongly affected by the close presence of the solid surfaces. Also, the rate of separation was much higher in the AFM experiment, and this is expected to have influenced the measurement (22).

Force separation of DNA oligomers have been measured also with Atomic Force Microscopy by shearing apart opposite extremities (23). Using repetitive sequences (ACTG)n of variable length hybridized to complementary oligonucleotides, breaking forces of ≈800 pN (for 12-base long oligonucleotides), 1200 pN (for 16 bases), and 1500 pN (for 20 bases) have been reported. Again, our results showed much smaller forces, and the results of Lee et al. (23) (i) may include a strong coupling between bases because of the shearing motion and (ii) were produced at a higher rate. The mechanical opening of a long segment of dsDNA has been considered only theoretically (5, 24, 25). In Viovy et al. (25), an analysis was carried out assuming no thermal fluctuations. The estimated force level of opening was 500 pN. In Thompson and Siggia (24), the thermal fluctuations were taken into account, but the sequence considered comprised only a succession of a unique base, e.g., poly A on one strand and poly T on the other.

Melting vs. Mechanical Separation.

Strand separation may be obtained in vitro through melting. This well known helix-coil transition (26, 27) may be obtained by destabilizing the double helix with respect to the single strands. This may be obtained by raising the temperature or by using denaturing agents or low levels of salt or other methods. For the reassociation of separated single strands of nucleic acid to form a double-stranded structure, the dynamics are simple for short length and more complex for long segments. Once a nucleus of 3–4 bases has been formed, rates of zippering have been estimated (28, 29) to be in the typical range of 10⁶-2.10⁷ bp/s for short oligoribonucleotides. This rate was found to be temperature and length-dependent. For larger molecules, it is known that melting occurs through the formation of bubbles (30–32). As the destabilization parameter is raised, bubbles form in specific sites of the sequence and invade progressively the more stable regions. Using phage T2 or T7 DNA, a complex dynamic is observed to reach equilibrium (33), and this effect has been associated with the rotation of the molecule that has to occur as melting progresses. The experiment described in the present paper may be considered a “directional melting” of the helix. In this latter case, the opening was performed at ionic and temperature ranges at which no melted bubble was present. An interesting open question, from both experimental and theoretical points of view, is whether there is a simple relation between the formation of bubbles at higher temperature (i.e., collective phenomena of melting at zero force) and the zones of sudden mechanical unzippering.

Order of Magnitude of Energies Involved.

From our results, the opening of 1 bp results in an average length l₀ liberated of order 1 nm. An estimation of the characteristic energy ɛ₀ associated with the opening process of 1 bp is thus: ɛ₀ = f₀ × l₀ = 1.9 kcal/mol. This compares reasonably with the unpairing/unstacking free energies as deduced from melting studies (34, 35) (≈1.5 kcal/mol for an AT pair and 3 kcal/mol for a GC pair).

Induced Rotation of the Double Strand.

Opening the double helix by pulling on the single strands generates rotation in the strands. This was already noted by Levinthal and Crane (5). In our case, one expects that the single strands either do not transmit rotation or will be able to rotate on their axis with little resistance. The double-stranded tail of the molecule had to rotate to relax the torsion imposed by the separation process. The opening of the 48,502 bp of λ-DNA corresponded to more than 4000 turns (assuming 10.5 pairs per double helix turn). For a typical opening time of 20 min, this meant approximately four turns per second on the average. The progression in the sequence, however, was nonuniform, and it was expected that the large jumps would suddenly generate a lot of torsion, probably inducing a transient coiling wave through the unopened part of the molecule. In the preliminary analysis, when performing the experiment at a speed of 20–40 nm/s, the characteristic time associated to a sudden force drop (≈1 s for 1 pN) was longer than the time associated to the hydrodynamic friction of the microneedle (≈70 ms for a force drop of 1 pN from the initial level of 13 pN). This may be associated to hydrodynamic drag of the double-stranded tail that limited the rotational dynamics. An estimation of friction induced by rotation had been considered in by Levinthal and Crane (5) but only for the case of “speedometer cable” motion, i.e., when rotation is not coupled to translation of any section of the molecule.

Characteristic Force Levels Associated with DNA.

The following picture emerges for the characteristic forces involved with dsDNA: Breaking of the double strands has been reported to occur at a force level (36, 37) of ≈480 pN ± 20%; the structural transition of uncoiling upon stretching (12, 13) has been reported to occur ≈60–80 pN; this transition has been compared with the similar effect of DNA elongation induced by recA binding. Strand separation (room temperature, 150 mM NaCl) is in the 10–15 pN range and is sequence-specific (this work); nucleosome formation is estimated (38) to be associated with forces in the range of a few picoNewtons; the characteristic entropic force (6, 7) (as obtained by dividing the characteristic thermal energy kT by the persistence length of DNA) is a fraction of 1 pN. The experimental determination of the order of magnitude of the forces involved in the mechanical unzippering of DNA is a step toward a better understanding of forces involved in replication, particularly for the action of helicases.

Potential Applications to Genomics.

Genomic DNA analysis is presently an indirect and laborious process. At the level of single base resolution, sequencing involves stretches of ≈500 bases and entails segmentation, cloning, and alignment of the contigs. In this context, this work suggests that mechanical measurements could complement enzymatic sequence analysis of DNA, giving an intermediate scale information on long pieces of DNA.