Revisiting the Ramachandran plot: Hard-sphere repulsion, electrostatics, and H-bonding in the α-helix

Abstract

What determines the shape of the allowed regions in the Ramachandran plot? Although Ramachandran explained these regions in terms of 1–4 hard-sphere repulsions, there are discrepancies with the data where, in particular, the α_R, α_L, and β-strand regions are diagonal. The α_R-region also varies along the α-helix where it is constrained at the center and the amino terminus but diffuse at the carboxyl terminus. By analyzing a high-resolution database of protein structures, we find that certain 1–4 hard-sphere repulsions in the standard steric map of Ramachandran do not affect the statistical distributions. By ignoring these steric clashes (N···H_i+1 and O_i−1···C), we identify a revised set of steric clashes (C^β···O, O_i−1···N_i+1, C^β···N_i+1, O_i−1···C^β, and O_i−1···O) that produce a better match with the data. We also find that the strictly forbidden region in the Ramachandran plot is excluded by multiple steric clashes, whereas the outlier region is excluded by only one significant steric clash. However, steric clashes alone do not account for the diagonal regions. Using electrostatics to analyze the conformational dependence of specific interatomic interactions, we find that the diagonal shape of the α_R and α_L-regions also depends on the optimization of the N···H_i+1 and O_i−1···C interactions, and the diagonal β-strand region is due to the alignment of the CO and NH dipoles. Finally, we reproduce the variation of the Ramachandran plot along the α-helix in a simple model that uses only H-bonding constraints. This allows us to rationalize the difference between the amino terminus and the carboxyl terminus of the α-helix in terms of backbone entropy.

In 1963, Ramachandran et al. introduced the ϕ–ξ angles (Fig. 1A ▶) as a parameterization of the protein backbone. The plot of these angles, the Ramachandran plot, has become a standard tool used in determining protein structure (Morris et al. 1992; Kleywegt and Jones 1996) and in defining secondary structure (Chou and Fasman 1974; Muñoz and Serrano 1994). Using an analysis of local hard-sphere repulsions between atoms that are at least third neighbors (1–4 interactions), Ramachandran et al. (1963) constructed a steric map of the Ramachandran plot that predicted the commonly allowed regions: the α_R, α_L, and β-regions. This steric map (Fig. 1B ▶) has become the standard interpretation of the Ramachandran plot (Richardson 1981) where Mandel et al. (1977) identified the specific steric clashes that define the boundaries of the standard steric map.

Figure 1.

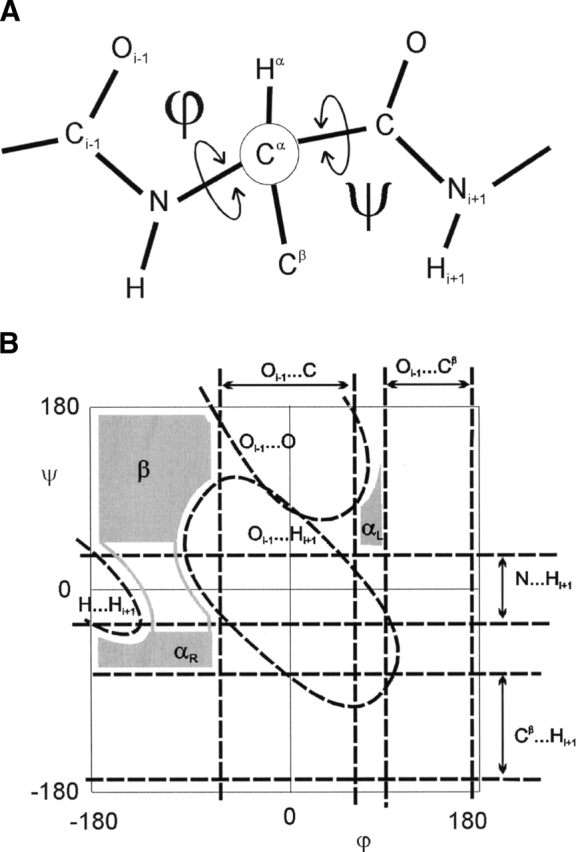
Schematic of the ϕ–ψ angles. (A) The schematic of the alanine dipeptide that represents the protein backbone parameterized by the ϕ = C-N-C-C^α-C and ψ = N-C^α-C-N dihedral angles. (B) The original Ramachandran steric map (Ramachandran et al. 1963) where the specific hard-sphere repulsions (dashed line) identified by Mandel et al. (1977) define the allowed regions (gray): α_L, α_R, and β regions.

However, there are differences with the data. Using a high-resolution (<1.8 Å) database of structures with a sample size of nearly 100,000 residues (Lovell et al. 2003), we can see differences between the observed Ramachandran plot (Fig. 2A ▶) and the standard steric map (see Fig. 1B ▶). The α_R and α_L regions are diagonal (Garnier and Robson 1990; Hovmöller et al. 2002). The β-region partitions into two diagonal lobes: the β-strand region (left) and the polyproline II region (right; Kleywegt and Jones 1996^; Hovmöller et al. 2002). There also exists sparsely populated regions that are forbidden in the standard steric map such as the γ and γ‘ regions (Milner-White 1990), the type II turn region (Sibanda and Thornton 1985), and the pre-Pro region (Macarthur and Thornton 1991).

Figure 2.

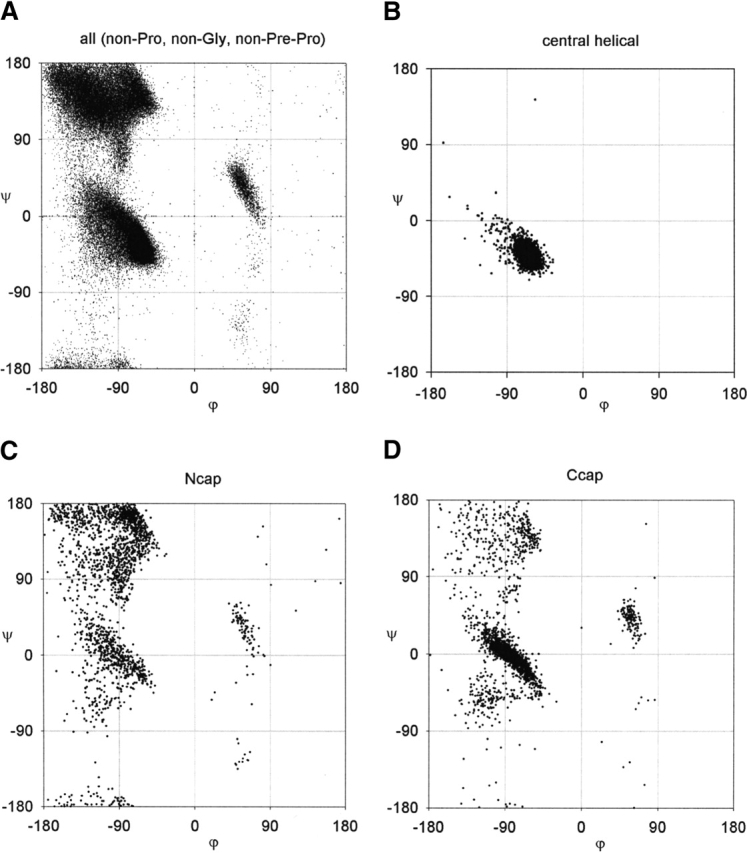
Ramachandran plots. (A) All residues excluding Pro, Gly, and pre-Pro; (B) residues in the center of the α-helix, which are more constrained than for all residues; (C) the Ncap residue; and (D) the Ccap residue in the α-helix, which are scattered throughout the entire allowed region.

Various studies have refined the calculation of the Ramachandran plot by using Lennard-Jones potentials and electrostatics (for a review, see Ramachandran and Sasisekharan 1968). Nevertheless, electrostatics fail to adequately reproduce the Ramacahandran plot (Lovell et al. 2003). In particular, the origin of the diagonal shape of the α_R, α_L, and β-strand regions is not well understood. Furthermore, Hu et al. (2003) showed that typical molecular mechanics (MM) force fields generate unrealistic Ramachandran plots. In contrast, they modeled the alanine dipeptide using quantum mechanics (QM), which they placed in an explicit solvent modeled with MM. They reproduced the observed Ramachandran plot, showing that the Ramachandran plot arises from local backbone interactions.

Is there a simple way to account for the boundaries of the observed Ramachandran plot? To this end, we have analyzed the statistical distributions of the interatomic distances parameterized by the ϕ–ξ angles. We found that certain 1–4 steric clashes in the standard steric map have no discernible effect on the statistical distributions. By ignoring these clashes, we can analyze the contributions of the remaining steric clashes. We thus obtain a revised steric map that produces a better match to the observed Ramachandran plot.

However, steric clashes do not account for the diagonal shape of the α_R-region. The standard steric map predicted a smaller α_R-region (see Fig. 1B ▶) than the observed α_R-region (Fig. 2A ▶). However, the predicted α_R-region is also elongated horizontally into regions where there is no observed density. Another problem is why the Ramachandran plot of residues in α-helices is constrained to the lower half of the general α_R-region (Fig. 2B ▶). It is often stated (Karplus 1996) that the α_R-region consists of two discrete regions: the helical α_R-region and the δ_R-region. In this study, we attempt to clarify the relationship between the general α_R-region and the helical α_R-region.

Given that the strong diagonal shape of the observed α_R-region has been reproduced by QM calculations (Hu et al. 2003), the shape of the α_R-region must be due to local backbone interactions. Lovell et al. (2003) argued that the diagonal α_R-region is due to the disfavoring of the conformations near (−150°, −60°) where the H and H_i+1 atoms are close together. However, we find that crowded H and H_i+1 atoms are also found in favored conformations of the α_R-region, for example (−110°, 0°). As the crowding of H atoms produces different results in different parts of the Ramachandran plot, something else must induce the diagonal shape of the α_R-region.

We use electrostatics to analyze the conformational dependence in the Ramachandran plot of specific interatomic interactions. We find that various dipole–dipole interactions, when combined with the revised steric map, conformationally induce diagonal α_R, α_L, and β-strand regions. Although, in general, electrostatics cannot account for the Ramachandran plot (Lovell et al. 2003), the conformational dependence of individual interatomic interactions in the Ramachandran plot cannot differ greatly between electrostatics and QM. After all, only atoms with opposite partial charges attract and like charges repel. However, as the strength of individual interactions can vary greatly in the QM calculation, the electrostatic approximation fails when all the individual minima are summed together.

Recent studies have found that the shape of the helical α_R-region varies depending on the position of the residue in the α-helix. In the central residues and in the amino terminus, the helical α_R-region is constrained to the lower half of the general α_R-region. However, Petukhov et al. (2002) found that the Ramachandran plot at the carboxyl terminus is much more diffuse than the rest of the α-helix. This flexibility in the carboxyl terminus has also been observed in peptide studies (Miick et al. 1993). In simulations, there is an asymmetry between the amino terminus and the carboxyl terminus in both folding (Sung 1994; Voegler-Smith and Hall 2001) and unfolding (Soman et al. 1991) studies. The origin of this asymmetry has not yet been resolved.

Ramachandran and Sasisekharan (1968) showed that H-bonding constraints induce the constrained helical α_R-region. They analyzed α-helices where all residues were parameterized with the same ϕ–ξ angles. They identified the ϕ–ξ angles where d(O_i···H_i+4) ∼2.0 Å for all CO···HN H-bonds along the α-helix. These ϕ–ξ angles correspond to the constrained helical α_R-region in central helical residues. However, as the analysis of Ramachandran and Sasisekharan (1968) used α-helices that had identical ϕ–ξ angles, this only accounts for central helical residues. What then causes the differences between the amino terminus and the carboxyl terminus? We first analyzed the Ramachandran plots along different positions of the α-helix in the structural database. Then, using an extension of the model of Ramachandran and Sasisekharan (1968), we studied the constraints of the backbone H-bonding along the α-helix. As our model reproduced the observed variation along the α-helix, we can use backbone H-bonding to explain the observed differences between the amino terminus and the carboxyl terminus of the α-helix.

Materials and methods

Data set

We used the data set of 500 nonhomologous proteins (Lovell et al. 2003) from the PDB (Bernstein et al. 1977) with resolution better than 1.8 Å. In this data set, all hydrogen atoms have been projected from the backbone and optimized. Due to their specialized Ramachandran plots, we excluded Gly, Pro, and pre-Pro residues (MacArthur and Thornton 1991) from our analysis. In the steric clash analysis, we used the van der Waals (vdW) radii given by the Richardson lab (Word et al. 1999) (H^α = 1.17 Å, H = 1.00 Å, C = 1.65 Å, C^α and C^β = 1.75 Å, O = 1.40 Å, and N = 1.55 Å). We used DSSP (Kabsch and Sander 1983) to define α-helical residues.

Local conformations of the ϕ–ξ map

To calculate the ideal curves of the interatomic distances as a function of the ϕ-ξ angles, we modeled the alanine dipeptide (see Fig. 1A ▶). Covalent bond lengths and angles were fixed to standard Engh and Huber (1991) values, which only allows the ϕ–ξ angles to vary. The ϕ–ξ angles of the central residue were incremented in 5° steps and the corresponding distance parameters were calculated. Then, we generated the energy map of the Ramachandran plot by calculating, for each value of ϕ–ξ, the energy of various interatomic interactions. We used two types of interactions: partial charge electrostatics

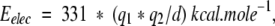and Lennard-Jones 12–6 potentials

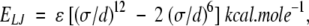where the parameters were taken from CHARMM22 (MacKerell Jr. et al. 1998).

Model of α-helix

We modeled the α-helix with a chain of 7 Ala residues. Covalent bond lengths and angles were fixed to standard Engh and Huber (1991) values where the ϕ–ξ angles are the only degrees of freedom. As the ϕ–ξ angles of the Ncap and Ccap do not affect the geometry of the H-bonds within the α-helix, they were ignored.

The simplest requirement to form CO···HN H-bonds is that d(O···H) ∼2.0 Å. Thus, to impose a given CO···HN H-bond, we used a harmonic distance constraint to minimize the O···H distance:

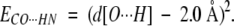The minimum of this constraint is zero when d[O···H] = 2.0 Å. We also used E_CO···_HN to measure the deviation from the ideal CO···HN H-bond geometry when the given conformation cannot form the CO···HN H-bond. To avoid steric clashes, we applied Lennard-Jones 12–6 potentials:

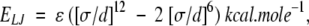where the parameters were taken from CHARMM22 (MacKerrell Jr. et al. 1998).

To analyze the H-bonding constraints in the amino terminal residues (N1, N2, and N3; red in Fig. 8B ▶, below), we fixed the ϕ–ξ angles of N4, N5, and N6 to the average helical values (−63°, −42°), which assumes that the α-helix from N4 to the carboxy-terminal is fixed in the α-helical conformation. We then minimized the energy function:

Figure 8.

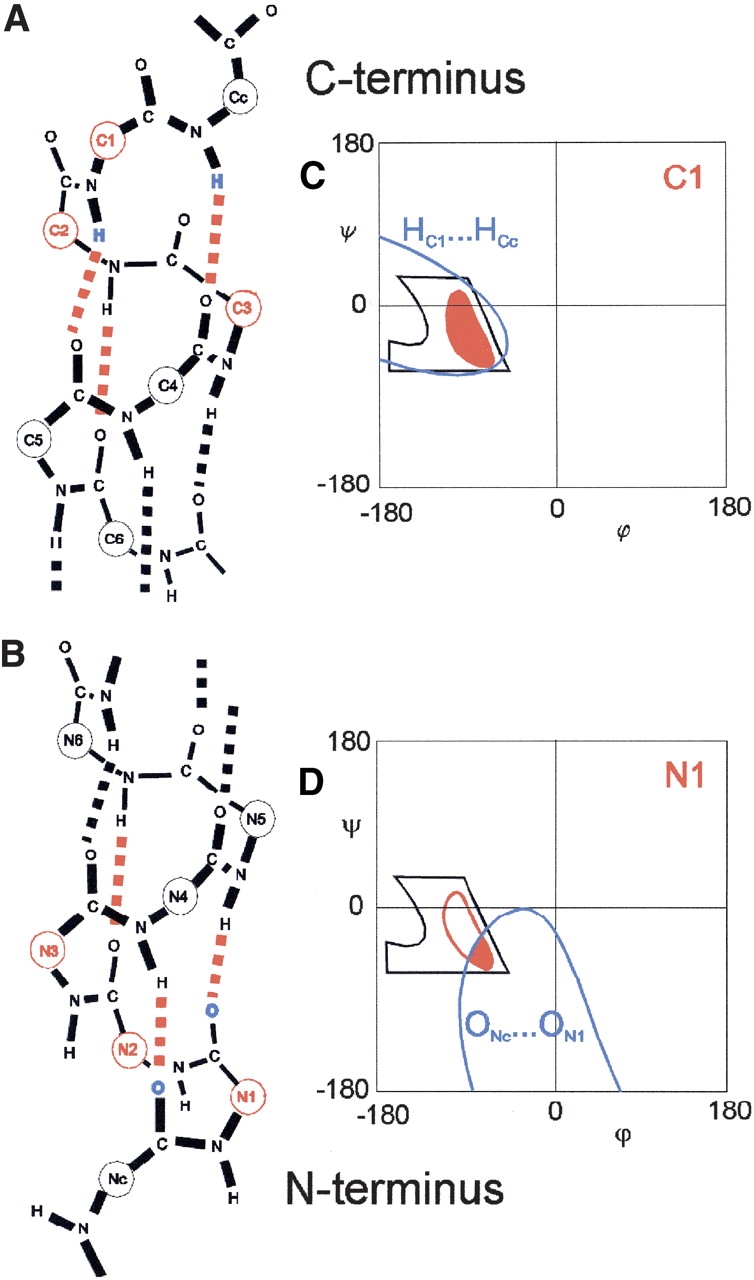
H-bonding in the amino terminus and carboxyl terminus of the α-helix. (A) Carboxyl terminus showing the carboxy-terminal residues (red) and the H-bonds (red) used in the model. (B) The amino terminus showing the amino-terminal residues (red). (C) The schematic of the allowed region in C1 residue (solid red), which is due to steric constraints (black), electrostatics (red outline), and formation of H-bonds that bring the two H atoms together (blue; see also A). (D) The schematic of the H-bonding constraints on the N1 residue (see also B).

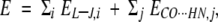where the first term refers to the Lennard-Jones potential, which models the steric clashes, and the second term refers to the harmonic potentials that minimizes the CO_Nc···HN_N4, CO_N1···HN_N5, and CO_N2···HN_N6 H-bonds (red in Fig. 8B ▶, below).

1. For N1, we divided the Ramachandran plot into a grid of points separated by 5° intervals. For each grid point, we used Powell minimization (Press et al. 1986) to minimize E by varying the ϕ–ξ angles of the N2 and N3 residues. We repeated the process for all grid points of N1 to generate an energy profile of N1.

2. For the grid points of N2, we allow the ϕ–ξ angles of N1 and N3 to vary.

3. For the grid points of N3, we allow the ϕ–ξ angles of N1 and N2 to vary.

To analyze the H-bonding constraints in the carboxy-terminal residues (C1, C2, and C3; red in Fig. 8A ▶, below), we fixed the ϕ–ξ angles of C4, C5, and C6 to the average helical values of (−63°, −42°), which assumes that the α-helix from C4 to the amino terminus is fixed in α-helical conformation. In the energy minimization, we modeled the CO_C4···HN_Cc, CO_C5···HN_C1, and CO_C6···HN_C2 H-bonds (red in Fig. 8A ▶, below).

1. For the grid points of C3, we allow the ϕ–ξ angles of C2 and C1 to vary.

2. For the grid points of C2, we allow the ϕ–ξ angles of C1 and C3 to vary.

3. For the grid points of C1, we allow the ϕ–ξ angles of C2 and C3 to vary.

Results and Discussion

Because the database of protein structures contains a large number of residues (97,368), we can compare the statistical distributions directly to the ideal geometry of the protein backbone. The local interatomic distances that are directly parameterized by the ϕ–ξ angles can be divided into three categories: ϕ dependent, ξ dependent, and ϕ-ξ codependent distances. In Table 1, we list the parameters of these interatomic distances. By comparing the value of the 5% minimum (5th percentile band) with the vdW diameter, we can see which atoms are in contact and can interact. We focus on the steric clashes of the standard steric map (Ramachandran and Sasisekharan 1968). As described in Mandel et al. (1977), they are: O_i−1···C and O_i−1···C^β, which restricts ϕ; N···H_i+1 and C^β···H_i+1, which restricts ξ; and O···H_i+1, H···H_i+1 and O_i-1···O, which shaves off the corners of the allowed regions (see Fig. 1B ▶).

Table 1.

Range of the interatomic distances [Å] parameterized by the ϕ–ξ angles

	vdW	5%	95%	αL	αR	β
ϕ dependent parameters
H···Hα	2.17	2.74	2.98	2.20 ± 0.09	2.84 ± 0.06	2.92 ± 0.06
H···Cβ	2.75	2.43	3.01	3.13 ± 0.09	2.52 ± 0.10	2.69 ± 0.18
H···C	2.65	2.53	3.22	3.18 ± 0.12	3.09 ± 0.14	2.79 ± 0.22
Oi−1···Hα	2.57	2.26	2.85	3.83 ± 0.12	2.60 ± 0.18	2.45 ± 0.15
Oi−1···Cβ	3.15	3.32	4.30	3.09 ± 0.17	4.19 ± 0.15	3.92 ± 0.30
Oi−1···C	3.05	2.85	4.11	3.01 ± 0.25	3.14 ± 0.31	3.66 ± 0.40
Ci−1···C	3.30	2.96	3.62	3.07 ± 0.13	3.12 ± 0.17	3.36 ± 0.21
Ci−1···Cβ	3.40	3.20	3.75	3.08 ± 0.09	3.68 ± 0.09	3.53 ± 0.17
ξ dependent parameters
Hα···O	2.57	2.47	3.30	2.93 ± 0.16	2.57 ± 0.11	3.24 ± 0.06
Cβ···O	3.15	2.82	3.40	2.86 ± 0.25	3.21 ± 0.17	3.12 ± 0.16
N···O	2.95	2.67	3.63	3.49 ± 0.21	3.53 ± 0.13	2.82 ± 0.14
Hα···Hi+1	2.17	2.20	3.69	2.92 ± 0.28	3.55 ± 0.18	2.33 ± 0.13
Cβ···Hi+1	2.75	2.96	3.97	3.89 ± 0.43	3.33 ± 0.29	3.45 ± 0.29
N···Hi+1	2.55	2.34	3.99	2.67 ± 0.39	2.55 ± 0.23	3.78 ± 0.22
Hα···Ni+1	2.72	2.46	3.33	2.85 ± 0.17	3.24 ± 0.12	2.54 ± 0.08
Cβ···Ni+1	3.30	3.03	3.66	3.61 ± 0.25	3.25 ± 0.17	3.32 ± 0.19
N···Ni+1	3.10	2.70	3.64	2.89 ± 0.22	2.81 ± 0.13	3.50 ± 0.15
ϕ-ξ co-dependent parameters
Oi−1···O	2.80	3.27	4.85	3.61 ± 0.42	3.73 ± 0.46	4.34 ± 0.51
Ci−1···O	3.05	3.31	4.50	3.93 ± 0.30	4.02 ± 0.27	3.80 ± 0.32
H···Hi+1	2.17	2.40	4.64	3.03 ± 0.50	2.72 ± 0.29	4.42 ± 0.22
H···Ni+1	2.55	2.91	4.30	3.43 ± 0.29	3.21 ± 0.21	4.00 ± 0.23
Ci−1···Hi+1	2.65	2.70	4.82	3.09 ± 0.50	3.11 ± 0.35	4.31 ± 0.43
Ci−1···Ni+1	3.15	3.11	4.63	3.31 ± 0.31	3.35 ± 0.25	4.19 ± 0.34
Oi−1···Hi+1	2.40	3.00	4.82	3.37 ± 0.50	3.59 ± 0.39	4.05 ± 0.59
Oi−1···Ni+1	2.95	3.13	4.87	3.33 ± 0.36	3.54 ± 0.37	4.16 ± 0.54
O···H	2.40	2.38	4.34	4.20 ± 0.32	4.20 ± 0.24	2.81 ± 0.36

Minimum–maximum values are defined by the 5th–95th percentile bands. The criteria to define the regions in the Ramachandran plot are α_L: ϕ > 0°; α_R: ϕ < 0° and ξ < 50°; and β: ϕ < 0° and ξ > 50°. The average and standard deviation for the interatomic distances are also given for each region. The average (ϕ, ξ) for each region are α_L = (61°, 26°); α_R = (−73°, −33°); and β = (−108°, 136°). Comparing the 5% minimum of the distances with the corresponding vdW radius indicates possible steric clashes.

The ϕ dependent and ξ dependent steric constraints

The ϕ-dependent distances

We first consider the restrictions from the standard steric map that restrict ϕ: O_i−1···C^β and O_i−1···C (see Fig. 1B ▶). To evaluate the effect of each steric clash on the observed distribution, we can make two comparisons. First, we can compare the ϕ frequency distributions to the ideal curve. The idea is that if a hard-sphere repulsion restricts ϕ, then, in regions of ϕ where the ideal curve is below the vdW diameter, the ϕ frequency distribution should drop correspondingly. Distributions that are found below the vdW radius indicates a steric overlap that could be due to some kind of interaction. For example, Ho and Curmi (2002) showed that in the allowed regions of ϕ in β-sheet residues, there is an O_i−1···H^α nonbonded electrostatic interaction where most of the observed values are found below the vdW diameter (Fig. 3A ▶). We plot the observed frequency distribution of ϕ at the bottom of Figure 3 ▶. For the ideal curves of both d(O_i−1···C^β) versus ϕ (Fig. 3D ▶) and d(O_i−1···C) versus ϕ (Fig. 3B ▶), we see that as the interatomic distance decreases below the vdW diameter, the ϕ frequency distribution drops correspondingly. This is consistent with the O_i−1···C^β and O_i−1···C steric clashes restricting the ϕ angle.

Figure 3.

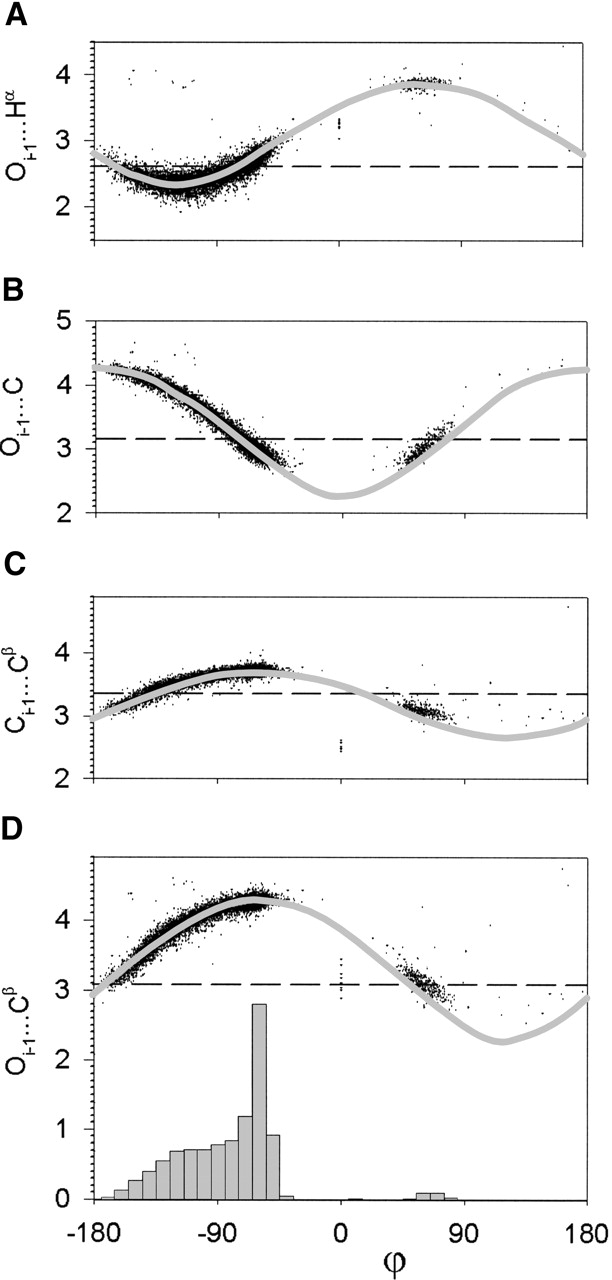
Distributions of interatomic distances [Å] parameterized by ϕ [°]. The ideal curves (gray) are calculated using Engh and Huber (1991) geometry. The vdW diameters (dashed line) are taken from Word et al. (1999). (A) O_i−1···H^α versus ϕ; (B) O_i−1···C versus ϕ; (C) C_i−1···C^β versus ϕ; and (D) O_i−1···C^β versus ϕ. The ϕ frequency distribution is shown at the bottom of D.

Second, we can compare the observed distributions against the ideal curves based on standard geometry (see Materials and Methods). Deviation of the observed distribution from the ideal curve indicates possible steric strain. The observed distributions of d(O_i−1···C) versus ϕ (Fig. 3B ▶) and d(O_i−1···C^β) versus ϕ (Fig. 3D ▶) fit the ideal curves well, showing that there are no significant deviations from standard geometry.

The ξ-dependent distances

In the standard steric map, it is the N···H_i+1 steric clash that restricts ξ in the region 0° < ξ < 90° (see Fig. 1B ▶). Comparing the ideal curve of d(N···H_i+1) versus ξ to the ξ frequency distribution (bottom of Fig. 4 ▶), we see that there is no corresponding drop in the ξ frequency distribution as d(N···H_i+1) descends below its vdW diameter (Fig. 4C ▶). The N···H_i+1 steric clash has no effect on the ξ angle. Furthermore, the observed distribution of d(N···H_i+1) versus ξ is distorted from the ideal curve for the region where d(N···H_i+1) is below the vdW diameter. Karplus (1996) has shown that this deviation accommodates the close approach of the N···H_i+1 interaction. On the other hand, we find that the ideal curve of d(C^β···O) versus ξ corresponds quite well to the variation of the ξ frequency distribution (Fig. 4D ▶). This suggests that in the region 0° < ξ < 90°, we can ignore the effects of the N···H_i+1 steric clash and instead, use the C^β···O steric clash. Indeed, given that the N···H_i+1 interaction deviates from the ideal geometry, the position of the H_i+1 atom is somewhat flexible.

Figure 4.

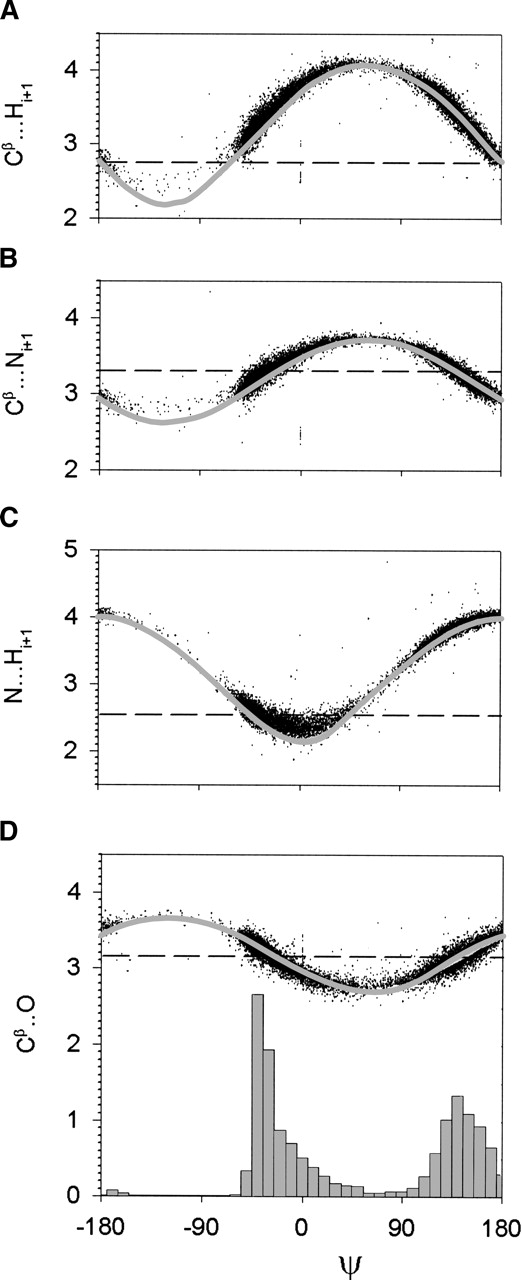
Distributions of interatomic distances [Å] parameterized by ψ [°]. The ideal curves (gray) are calculated using Engh and Huber (1991) geometry. The vdW diameter (dashed line) are taken from Word et al. (1999). (A) C^β···H_i+1 versus ξ; (B) C^β···N_i+1 versus ξ; (C) N···H_i+1 versus ξ; and (D) C^β···O versus ξ. The ξ frequency distribution is shown at the bottom of D.

In the standard steric map, it is the C^β···H_i+1 steric clash that restricts ξ in the region −180° < ξ < −50° (see Fig. 1B ▶). In the comparison of the ξ frequency distribution (bottom of Fig. 4 ▶) to the ideal curve of d(C^β···H_i+1) versus ξ, the C^β···H_i+1 steric clash appears to restrict ξ (Fig. 4A ▶). However, the observed 5% minimum value of d(C^β···H_i+1) is 0.21 Å higher than the vdW diameter (Table 1), suggesting that the C^β···H_i+1 steric clash is not responsible for the restriction on ξ. Is there any other interaction that could be responsible? The ideal curve of d(C^β···N_i+1) versus ξ also corresponds to the drop-off in the ξ distribution (Fig. 4B ▶). However, the observed 5% minimum value of C^β···N_i+1 is below the vdW diameter (Table 1), which is a clear steric contact. Hence, we should ignore the C^β···H_i+1 steric clash and replace it with the C^β···N_i+1 steric clash. Furthermore, as the H atom is more flexible than the other backbone atoms and the H atom has a negligible vdW interaction, we expect that the C^β···H_i+1 interaction will be soft and not behave as a hard steric clash.

The ϕ–ξ codependent distances

However, if we look at interatomic distances as a function only of ϕ, or as a function only of ξ, then we will miss steric clashes that are ϕ–ξ codependent. For example, in the standard steric map, the O_i−1···C steric clash excludes the middle of the Ramachandran plot, resulting in vertical boundaries in the α, α_L, and β regions (see Fig. 1B ▶). However, these vertical boundaries are not found in the observed distribution, where the corresponding boundaries are diagonal (see Fig. 2A ▶). Because the ϕ–ξ codependent steric clashes induce diagonal boundaries, if we ignore the O_i−1···C steric clash, then we can identify the steric clashes that induce diagonal boundaries (Fig. 5A ▶).

Figure 5.

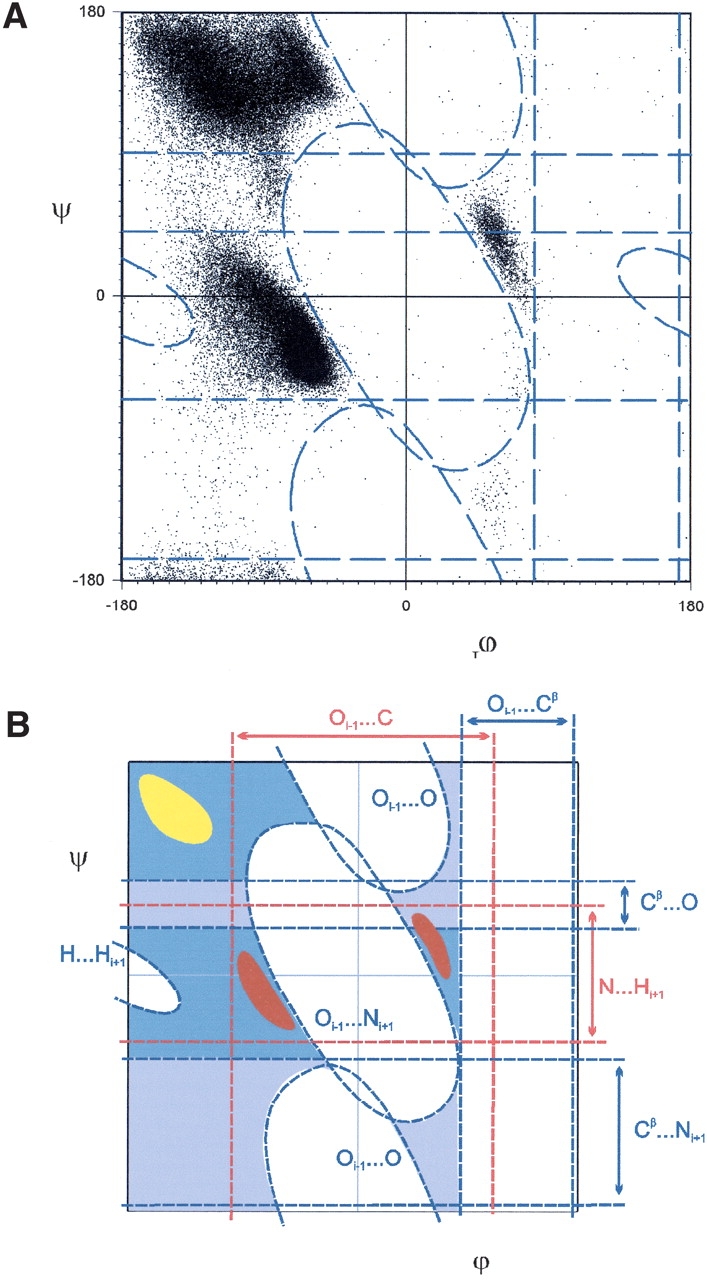
Revised steric map. (A) The steric clashes (dashed blue lines) that best match the data. d(O_i−1···O) = 2.7Å, d(O_i−1···N_i+1) = 2.7 Å, and d(H···H_i+1) = 1.6 Å. (B) Schematic of the revised steric map showing steric restrictions (dashed blue lines) and sterically allowed regions (dark blue). The revised steric map gives diagonal boundaries for the α_R, α_L, and β regions and defines a more realistic upper boundary for the α_R-region. Diagonal α_R and α_L regions (red region) from the dipole–dipole analysis (Fig. 7G ▶) are defined mainly by the attractive O_i−1···C and N···H_i+1 interactions (red lines). The diagonal β-strand region (yellow) is induced by aligning the CO···HN dipole–dipole interaction. Regions that are only excluded by a single steric clash (light blue) accounts for the outlier region in Lovell et al. (2003).

To make the comparison with the data, we generate all the contour plots of constant distance for the ϕ–ξ codependent interactions. We show these contour plots in Figure 6 ▶ mainly as a reference. We then define the steric boundaries of each contour plot by considering the regions where the distances are smaller than the corresponding vdW diameter (Table 1). In Figure 5A ▶, we identify the steric clashes that best match the diagonal boundaries of the observed distribution. These diagonal boundaries exclude a region in the Ramachandran plot that runs down the middle of the plot. This excluded region can be divided into two. The first region, excluded by the O_i−1···O steric clash, consists of both the upper-central and lower-central regions, which are symmetric due to the inversion symmetry found in all the contour maps (Fig. 6 ▶). The second region, excluded by the O_i−1···N_i+1 steric clash, is in the center of the Ramachandran plot.

Figure 6.

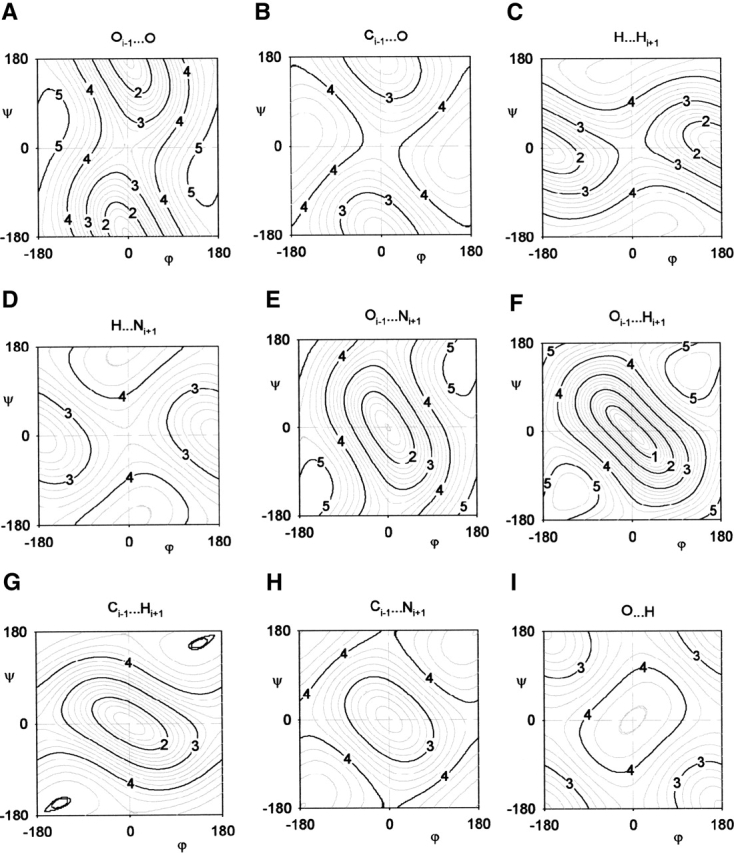
Contour plots of the ϕ–ξ codependent interactions. The contours of constant distance [Å] are shown as functions of the ϕ–ξ angles [°]. These interactions can be grouped in terms of dipole–dipole interactions in the alanine dipeptide (see Fig. 1A ▶) where the contour plots within each group are geometrically similar. In terms of the CO_i−1···CO dipole–dipole interaction, they are (A) O_i−1···O, (B) C_i−1···O. In terms of the NH···NH_i+1 interaction, they are (C) H···H_i+1 and (D) H···N_i+1. In terms of the CO_i−1···NH_i+1 interaction, they are (E) O_i−1···N_i+1, (F) O_i−1···H_i+1, (G) C_i−1···H_i+1, and (H) C_i−1···N_i+1. In terms of the CO···HN interaction, the only ϕ–ξ codependent distance is (I) O···H. All contour plots possess a twofold inversion symmetry through the point ϕ = ξ = 0°. The sterically excluded regions are defined as the regions where the interatomic distance is smaller than the corresponding vdW diameter (see Table 1).

The revised steric map of the Ramachandran plot

From the analysis above, we find that the N···H_i+1 steric clash does not affect the frequency distributions of ξ and that ignoring the O_i−1···C steric clash results in well-defined diagonal boundaries in the Ramachandran plot. Thus, we obtain a revised set of steric clashes where (1) the O_i−1···C^β steric clash restricts ϕ; (2) the C^β···O and C^β···N_i+1 steric clashes restrict ξ; and (3) the O_i−1···O and O···N_i+1 steric clashes restrict ϕ–ξ. Compared to the standard steric map (see Fig. 1B ▶), the revised steric map (dark blue regions in Fig. 5B ▶) matches the data better. The revised steric map gives a better upper bound to the α_R-region and defines diagonal boundaries in the β, α_R, and α_L region (Fig. 5A ▶).

In their analysis of the ϕ–ξ distribution, Lovell et al. (2003) defined regions in the observed Ramachandran plot in terms of favored (98%), outlier (between 98% and 99.5%), and strictly forbidden regions. In the outlier region, observed conformations are rare but nevertheless allowed if there exists a compensating interaction. The outlier regions include the plateau region below the α_R region, the region between the α_R and β-regions, and a sinuous, sparsely populated stripe at ϕ ∼70° (Fig. 5A ▶). The outlier region includes the rare type II‘ turn, γ and γ‘ conformations. In contrast, conformations near ϕ = 0° are strictly forbidden.

What is the difference between the outlier and strictly forbidden regions? We find that (1) the strictly forbidden region corresponds to the region excluded by the O_i−1···C^β, O_i−1···O, and O···N_i+1 steric clashes; and (2) the outlier region is excluded by the C^β···O and C^β···N_i+1 steric clashes. Although we have identified only a single steric clash that is induced by diagonal boundaries in Figure 5B ▶, some of the boundaries are in fact induced by multiple steric clashes. The existence of multiple hard steric clashes accounts for the difference between the strictly forbidden and outlier regions. The multiple steric clashes exist because we can group the ϕ–ξ codependent distances in terms of the dipole–dipole interactions in the alanine dipeptide (see Fig. 1A ▶). The contour plots that belong to each dipole–dipole interaction are geometrically similar (Fig. 6 ▶).

In the strictly forbidden region of the Ramachandran plot (white in Fig. 5B ▶), both the O_i−1···O (Fig. 6A ▶) and C_i−1···O (Fig. 6B ▶) steric clashes exclude the same ϕ–ξ region. We find that all the interatomic interactions that are grouped within the CO_i−1···NH_i+1 interaction dipole–dipole interactions (O_i−1···N_i+1, O_i−1···H_i+1, C_i−1···H_i+1, and C_i−1···N_i+1) exclude the same central region in the Ramachandran plot (Fig. 6E ▶–H). We also find that both the O_i−1···C^β steric clash (see Fig. 3D ▶) and C_i−1···C^β steric clash (see Fig. 3C ▶) exclude the same region of ϕ where the C_i−1···C^β interaction is in a particularly serious steric overlap. This steric overlap could be an indication that the vdW radius of C (Word et al. 1999) is overestimated or that the electron shell of C is not entirely spherical.

In contrast, the outlier region corresponds to the region restricted by a single steric clash (light blue in Fig. 5B ▶). For the region 0° < ξ < 90°, only the C^β···O steric clash restricts ξ (see Fig. 4D ▶). It is not reinforced by N···H_i+1 (see Fig. 4C ▶) as the N···H_i+1 interaction is not a hard steric clash. In the other region −180° < ξ < −50°, as C^β···H_i+1 is probably not a hard steric clash (see Fig. 4A ▶), only the C^β···N_i+1 steric clash (Fig. 4B ▶) restricts ξ.

Local electrostatic interactions in the Ramachandran plot

However, not all the features of the observed Ramachandran plot can be explained by local steric clashes. In this section, we focus on the diagonal shapes of the α_R, α_L, and β-strand region. In previous studies, the γ and γ‘ regions were explained in terms of a C7 H-bond (Milner-White 1990). The polyproline II region within the β-region was explained in terms of both a favorable CO_i−1···CO interaction (Maccallum et al. 1995) and as the most entropically favored conformation (Pappu and Rose 2002). Ho and Curmi (2002) showed that restrictions due to hydrogen bonds in β-sheet formation induce a diagonal β-strand region. However, the diagonal shape of the β-strand region is also induced for residues not in β-sheets. Therefore, the diagonal β-strand region must also arise from local backbone interactions.

Lovell et al. (2003) argued that the diagonal α_R-region is due to the disfavoring of the conformations near (−150°, −60°) (Fig. 5A ▶), where the H and H_i+1 atoms are close together. They postulated that the crowding of the H atoms is disfavored because this prevents the formation of one H-bond with the solvent. However, comparing the contour distance plot of H···H_i+1 (Fig. 6C ▶) with the observed α_R-region (see Fig. 2A ▶), we can see that favored conformations in the observed plot, such as (−110°, 0°), also has crowded H and H_i+1 atoms. As the crowding of H atoms produces different results in different parts of the Ramachandran plot, something else must induce the diagonal shape of the α_R-region.

Following Maccallum et al. (1995), we analyze the electrostatic interactions of the alanine peptide in terms of the dipole–dipole interactions: the CO_i−1···CO, NH···NH_i+1, CO_i−1···NH_i+1, and CO···NH interactions. The difference with the study of Maccallum et al. (1995) is that in our calculation, we have included the Lennard-Jones potentials of our revised set of steric clashes (Fig. 7A ▶).

Figure 7.

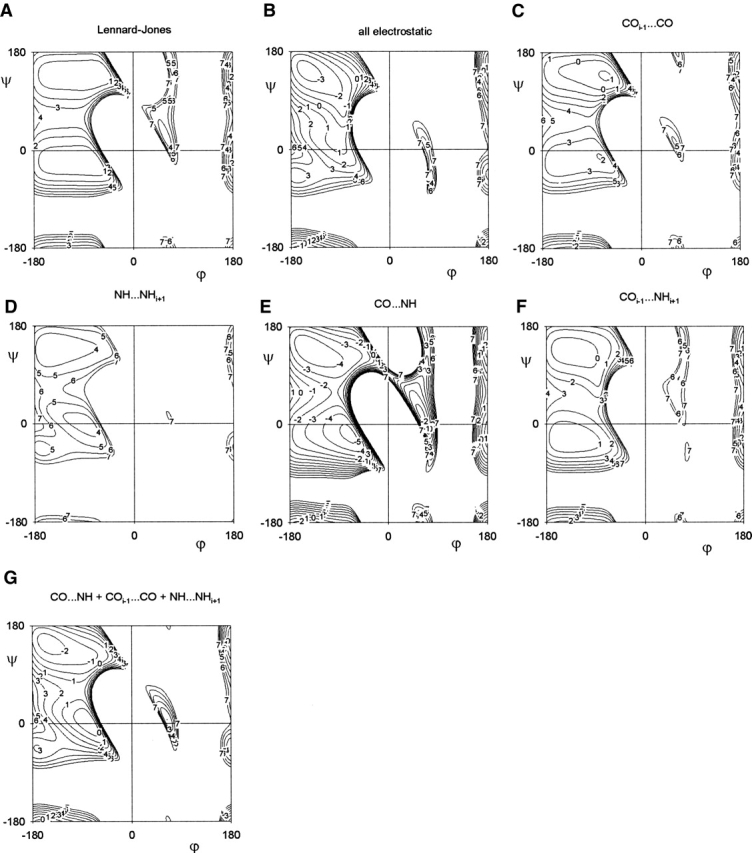
Contour plots of the dipole–dipole interactions [kcal/mole] as a function of the ϕ–ξ angles [°]. Energy plots of (A) the Lennard-Jones 12–6 potentials of the revised set of steric clashes; (B) all electrostatic interactions; the individual dipole–dipole interactions of (C) CO_i−1···CO; (D) NH···NH_i+1; (E) CO···NH; and (F) CO_i−1···NH_i+1. (G) The combination of the CO_i−1···CO, NH···NH_i+1 and CO···NH dipole–dipole interactions produces clear diagonal minima in the α_R, α_L, and β regions.

The combined electrostatic map (Fig. 7B ▶) does not produce a minimum in the α_R-region. However, when considered individually, we find that, of the four dipole–dipole interactions, the CO_i−1···CO (Fig. 7C ▶), NH···NH_i+1 (Fig. 7D ▶), and CO···NH (Fig. 7E ▶) interactions induce diagonal shapes in the α_R and α_L regions. Consequently, the energy map that combines the CO_i−1···CO, NH···NH_i+1, and CO···NH interactions (Fig. 7G ▶) produces well-defined diagonal minima in the α_R and α_L regions. In the backbone conformation of these regions (the diagram in Fig. 1A ▶ corresponds to such a conformation), (1) the CO_i−1 dipole points toward the CO dipole such that O_i−1 is in contact with C; (2) the NH_i+1 dipole points toward the NH dipole such that the N atom is in contact with the H_i+1 atom; and (3) the CO and NH groups are aligned in an antiparallel conformation such that O is as far away from H as possible. A simple description of this conformation is that the O_i−1···C and N···H_i+1 attraction are simultaneously optimized. Optimizing the O_i−1···C interaction will restrict |ϕ| < 100°, and optimizing the N···H_i+1 interaction will restrict |ϕ| < 80° (see Fig. 5B ▶). The optimization of the N··· H_i+1 interaction in the α_R-region was also observed by Karplus (1996).

Maccallum et al. (1995) showed that the polyproline II region corresponds to a minimum in the electrostatic CO_i−1···CO interaction. We can see this in Figure 7C ▶. Similarly, we find that the diagonal β-strand region can also be explained in terms of an electrostatic dipole–dipole interaction. A diagonal minimum of the CO···NH is induced (Fig. 7E ▶), which corresponds to the observed β-strand region (see Fig. 5A ▶). In this minimum, the CO and NH groups in the backbone are essentially aligned and co-planar. This CO···HN electrostatic minimum is so deep that the diagonal β-strand region is still found in the combined electrostatic interaction (Fig. 7B ▶).

Although it has been shown that the CO_i−1···NH_i+1 interaction induces the γ and γ‘ region (Milner-White 1990), the electrostatic approximation of the CO_i−1···NH_i+1 interaction does not induce a minimum in the γ region (Fig. 7F ▶). However, it does induce a weak minimum in the γ‘ region. Compared to the QM calculcations (Hu et al. 2003), the electrostatic approximation of the CO_i−1···NH_i+1 interaction is poor, which is probably the reason why the combined electrostatic map (Fig. 7B ▶) does not give the diagonal α_R-region.

Ramachandran plots of the α-helix

Although the Ramachandran plot of residues in α-helices is found within the α_R-region (Ramachandran and Sasisekharan 1968), there are subtle but significant differences. The Ramachandran plot of residues in the center of the α-helix is smaller than the α_R-region and the Ramachandran plot varies at different positions of the α-helix termini (Petukhov et al. 2002). We use the Richardson and Richardson terminology (1988) to describe the different positions of the α-helical residues. The residues at the amino terminus are labeled Ncap-N1-N2-N3-N4–··· (Fig. 8B ▶) where the amino-terminal residues (N1, N2, N3) only contribute CO groups to H-bonds. The residues at the carboxyl terminus are labeled ···C4-C3-C2-C1-Cap (Fig. 8A ▶) where the carboxy-terminal residues (C1, C2, C3) only contribute NH groups to H-bonds. Ccap and Ncap are boundary residues, which are not considered part of the α-helix.

Here, we plot the Ramachandran plots of the α-helical residues: Ncap (see Fig. 2C ▶), N1, N2, N3 (Fig. 9 ▶), central (see Fig. 2B ▶), C3, C2, C1 (Fig. 10 ▶), and Ccap (see Fig. 2D ▶). The statistical parameters of these distributions are listed in Table 2. There appear to be no systematic restraints on the capping residues as the Ramachandran plot of the Ncap and Ccap residues are found all over the Ramachandran plot (see Fig. 2C,D ▶). This is understandable given the plurality of capping interactions in the α-helix (for review, see Aurora and Rose 1998). The central (see Fig. 2B ▶), N1, N2, N3 (Fig. 9 ▶), and C3 (bottom of Fig. 10 ▶) residues all have similar Ramachandran plots, which are constrained to the lower half of the general α-region of the Ramachandran plot. The C2 residue (center of Fig. 10 ▶) is slightly more diffuse than the central residues, whereas the C1 residue (top of Fig. 10 ▶) is identical to the general α_R-region.

Figure 9.

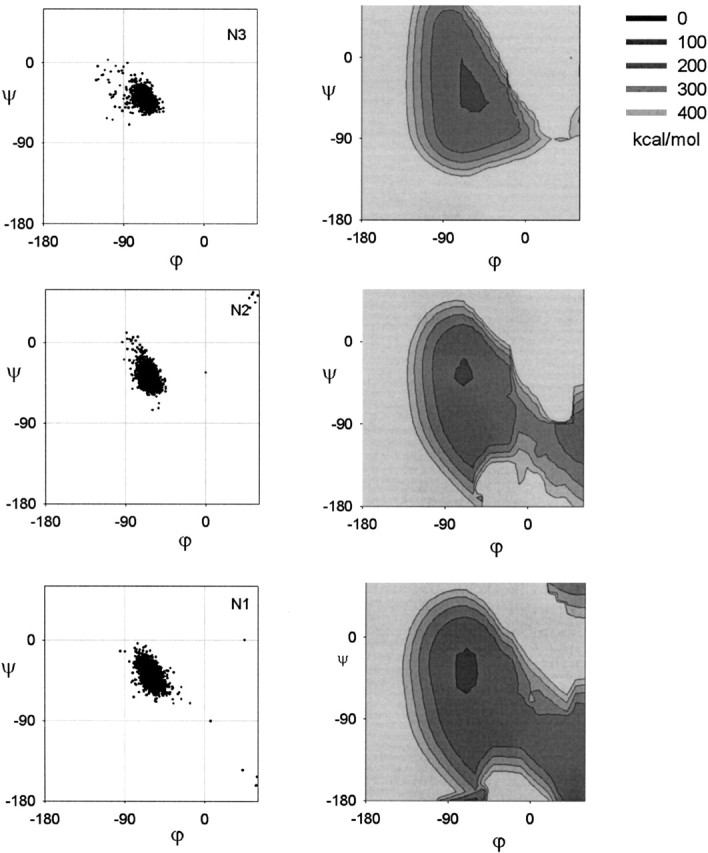
The Ramachandran plot of the amino-terminal residues. The left column gives the observed distribution. The right column gives the energy map of the H-bonding constraints and Lennard-Jones potential. The Ramachandran plot has been truncated for clarity.

Figure 10.

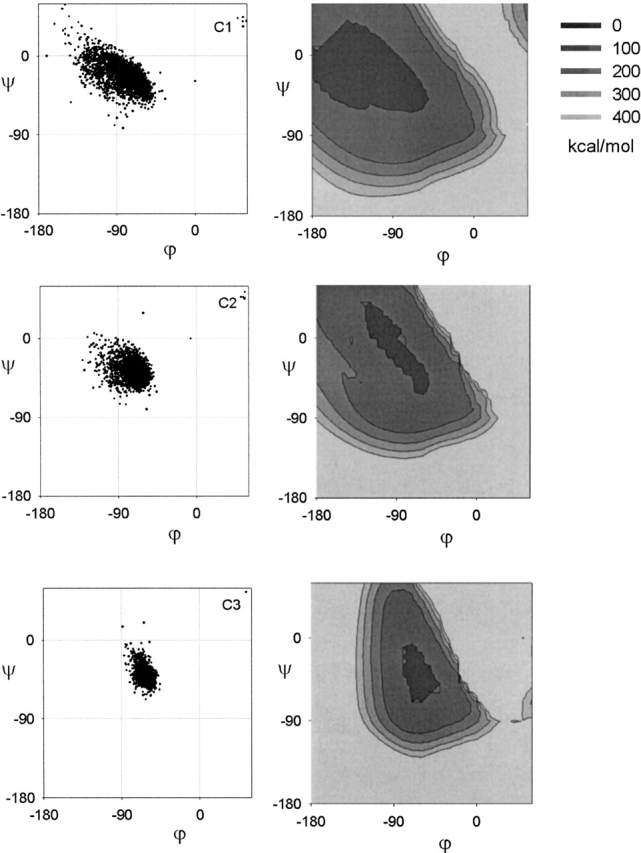
The Ramachandran plot of the carboxyl-terminal residues. The left column gives the observed distribution. The right column gives the energy map of the H-bonding constraints and Lennard-Jones potential. The Ramachandran plot has been truncated for clarity.

Table 2.

Parameters of the ϕ–ξ distributions in the α-helix

		ϕ			ξ
Position	Counts	5%	Avg ± std	95%	5%	Avg ± std	95%
Nc	2179	−151	−89 ± 44	−42	−59	83 ± 86	173
N1	2332	−71	−59 ± 10	−48	−55	−39 ± 14	−24
N2	2375	−73	−63 ± 9	−54	−51	−39 ± 10	−23
N3	2484	−77	−66 ± 8	−57	−51	−41 ± 7	−30
central	15343	−72	−63 ± 6	−56	−51	−42 ± 6	−32
C3	2533	−72	−63 ± 6	−56	−51	−40 ± 8	−26
C2	3084	−94	−71 ± 13	−58	−52	−37 ± 11	−20
C1	3101	−118	−79 ± 21	−56	−44	−24 ± 15	1
Cc	2265	−126	−77 ± 43	55	−52	22 ± 61	148

Minimum–maximum values are defined by the 5th–95th percentile band.

We also examined the Ramachandran plots of N1, N2, N3, C3, C2, and C1 for different amino acids but did not find any significant differences between the amino acids. This is consistent with previous studies (Chakrabarti and Pal 2001; Lovell et al. 2003), which found that the contours of the Ramachandran plot are relatively stable although the frequencies of occurrence differ for the different amino acids. Given that the contours for each α-helical positions are the same for different amino acids, the shape of the contours must be due to backbone interactions.

H-bonds in the α-helix

What kind of backbone interactions can induce different constraints along the α-helix? The obvious interaction is the backbone H-bond. To analyze the H-bonding constraints, we extend the analysis of Ramachandran and Sasisekharan (1968) where, instead of modeling identical ϕ–ξ angles along the α-helix, we treat the ϕ–ξ angles of different residues independently (see Materials and Methods). We modeled the amino terminus by allowing the ϕ–ξ angles of the N1, N2, and N3 residues to vary independently to form the first three CO···HN H-bonds (red in Fig. 8B ▶). Similarly, we model the carboxyl terminus by allowing the ϕ–ξ angles of the C1, C2, and C3 residues (red in Fig. 8A ▶) to vary independently to form the last three CO···HN H-bonds (red in Fig. 8A ▶). This induces different restrictions on the N1, N2, N3, C3, C2, and C1 residues.

To model the CO···HN H-bonds, we use harmonic distance constraints (see Materials and Methods). Although we also considered electrostatics and Lennard-Jones potentials, we found that the harmonic distance constraint was sufficient to induce well-formed H-bonds and that using electrostatics to align the CO and NH dipoles did not make a significant difference. Furthermore, the harmonic distance constraint easily converged to a unique solution. We also imposed Lennard-Jones 12–6 potentials of the revised set of steric clashes to avoid local steric clashes. Subsequently, we obtain energy maps of the Ramachandran plot that show regions where the H-bonds are allowed to form and where there are no significant steric clashes. The restricted regions are reproduced for N1, N2, N3 (Fig. 9 ▶) and C3 (bottom of Fig. 10 ▶). A more diffuse region is obtained for C2 (center of Fig. 10 ▶) and a very diffuse region is obtained for C1 (top of Fig. 10 ▶). H-bonding constraints thus explain the variation in the Ramachandran plots along the α-helix.

How can we understand the big difference between the Ramachandran plots of the N1 (bottom of Fig. 9 ▶) and C1 (top of Fig. 10 ▶) residues? The H-bonding constraints can be understood as the problem of simultaneously forming two neighboring CO···HN H-bonds in the α-helix. When these two CO···HN H-bonds are formed, they will be parallel and close together. The N1 residue is found between the CO_Nc···HN_N4 and CO_N1···HN_N5 H-bonds. Forming these two H-bonds simultaneously will minimize the O_Nc···O_N1 distance (colored blue in Fig. 8B ▶). Consequently, from the contour plot of d(O_i−1···O) versus ϕ–ξ (see Fig. 6A ▶), we extract the region d(O_i−1···O) < 3.00 Å. This produces an allowed region (blue in Fig. 8D ▶) that encompasses the allowed N1 residue Ramachandran plot (red in Fig. 8D ▶). If we also eliminate the region with local steric clashes (black in Fig. 8D ▶), then we obtain the constrained region corresponding to the N1 residue.

In the carboxyl terminus, the C1 residue sits between the CO_C5···HN_C1 and CO_C4···HN_Cc H-bonds. Forming these two H-bonds will minimize the H_C1···H_Cc distance. Hence, from the contour plot of d(H···H_i+1) versus ϕ–ξ (see Fig. 6C ▶), we extract the region d(H···H_i+1) < 3.00 Å. This produces an allowed region (blue outline in Fig. 8C ▶) that encompasses the allowed region of C1 (red in Fig. 8C ▶). However, unlike the N1 residue, the local steric clashes in the C1 residue (black in Fig. 8C ▶) do not eliminate any part of the α_R-region, resulting in the larger C1 Ramachandran plot.

Conclusion

Interactions that determine the Ramachandran plot

We have analyzed the statistical distributions of the protein backbone and find that certain 1–4 interactions in the standard steric map can be ignored (N···H_i+1, O_i−1···C, and C^β···H_i+1). This allows us to identify a revised steric map (C^β···O, O_i−1···N_i+1, C^β···N_i+1, O_i−1···C^β, and O_i−1···O) that matches the observed Ramachandran plot better than the standard steric map (see Fig. 5A ▶). We also find that the rare, but allowed, outlier region in the Lovell et al. (2003) study can be defined as the regions that are only restricted by a single steric clash. In the strictly forbidden regions, the backbone geometry brings more than one pair of atoms into a steric clash. Our analysis follows the hard-sphere model pioneered by Ramachandran et al. (1963) and supports the view of Baldwin and Rose (1999) that, to quote Richards (1977), ". . . the use of the hard-sphere model has a venerable history and an enviable record in explaining a variety of different observable properties." For simple models of the protein, the revised steric map represents an efficient way to improve the match with the data. Furthermore, the revised steric map consists of steric clashes between heavy atoms, which should be useful for models that ignore H atoms. Indeed, we find that the H. . .H_i+1 steric clash in the standard steric map (see Fig. 1B ▶) has no significant effects on the revised Ramachandran plot (see Fig. 5B ▶).

However, other features of the Ramachandran plot must be explained in terms of electrostatic interatomic interactions. The β-strand region corresponds to conformations where the CO and NH dipoles are aligned, which optimizes the dipole–dipole interaction (yellow region in Fig. 5B ▶). The diagonal shape of the α_R and α_L regions depends on the optimization of the N···H_i+1 and O_i−1···C interactions (red region in Fig. 5B ▶). The N···H_i+1 and O_i−1···C interactions are also found to have no steric effect on the statistical ϕ–ξ distributions. Although these electrostatic interactions should only be viewed as useful approximations, we can use these results to understand the QM calculation (Hu et al. 2003). The effect of applying QM is to induce a strong N···H_i+1 and O_i−1···C attraction that neutralizes the hard-sphere repulsion. Consequently, diagonal α_R and α_L regions are induced.

Along the α-helix

We have also shown that the variation in the Ramachandran plots along the α-helix is induced by backbone H-bonding constraints. This severely restricts the residues in the middle and amino terminus of the α-helix but not in the carboxyl terminus. The larger size of the Ramachandran plot in C1 (Fig. 8C ▶) compared to N1 (Fig. 8D ▶) can be interpreted as a larger backbone entropy in the carboxyl terminus than in the amino terminus. This would make the carboxyl terminus more flexible than the amino terminus, which has been experimentally observed (Miick et al. 1993). In simulations of the folding of α-helices, H-bond formation proceeds faster in the N to C direction than in the opposite C to N direction (Sung 1994; Voegler-Smith and Hall 2001). Because the backbone entropy of the carboxyl terminus is larger, the change in free-energy required to form the carboxyl terminus [ΔG = ΔH_H-bond − T(S_coil − S_helix)] is smaller, and hence it is more probable for the α-helix to form in the N to C direction. Other simulations find that α-helix unfolding proceeds faster in the opposite C to N direction (Soman et al. 1991). The smaller backbone entropy in the amino terminus makes it more likely for H-bonds to break at the amino terminus, which corresponds to unfolding in the C to N direction.