Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2003 Nov;12(11):2542–2548. doi: 10.1110/ps.03143803

Free-energy landscape of a chameleon sequence in explicit water and its inherent α/β bifacial property

Kazuyoshi Ikeda 1,2,3, Junichi Higo 2,3
PMCID: PMC2366969  PMID: 14573865

Abstract

A sequence in yeast MATα2/MCM1/DNA complex that folds into α-helix or β-hairpin depending on the surroundings has been known as "chameleon" sequence. We obtained the free-energy landscape of this sequence by using a generalized-ensemble method, multicanonical molecular dynamics simulation, to sample the conformational space. The system was expressed with an all-atom model in explicit water, and the initial conformation for the simulation was a random one. The free-energy landscape demonstrated that this sequence inherently has an ability to form either α or β structure: The conformational distribution in the landscape consisted of two α-helical clusters with different packing patterns of hydrophobic residues, and four β-hairpin clusters with different strand–strand interaction patterns. Narrow pathways connecting the clusters were found, and analysis on the pathways showed that a compact structure formed at the N-terminal root of the chameleon sequence controls the cluster-cluster transitions. The free-energy landscape indicates that a small conditional change induces α-β transitions. Additional unfolding simulations done with replacing amino acids showed that the chameleon sequence has an advantage to form an α-helix. Current study may be useful to understand the mechanism of diseases resulting from abnormal chain folding, such as amyloid disease.

Keywords: All-atom model, multicanonical molecular dynamics, generalized-ensemble method, α-β transition, amyloid

The structure and folding pathway of a protein are determined as one by its primary structure (i.e., amino acid sequence). Resent studies, however, have shown that a unique sequence can take different secondary structures depending on its context, such as chameleon sequence (Abel et al. 1996; Minor Jr. and Kim 1996; Tan and Richmond 1998; Yang et al. 1998; Smith et al. 2000; Whisstock et al. 2000). This property may provide a key to understanding the protein local folding or the cause of amyloid diseases.

Mezei (1998) searched amino acid sequences that took different secondary structures in Protein Data Bank (PDB) and reported that the maximum sequence length was seven, although no clear sequence pattern was found in the sequences. Mutation, Pro26Ala, of Fis induced a β-to-α conformational change of a segment, where the mutation site located at the hinge of the segment (Yang et al. 1998). A designed 11-residue sequence was introduced at different positions of the IgG-binding domain of protein G and showed different secondary structures, without changing the native structure of the protein (Minor Jr. and Kim 1996).

An X-ray crystallography provided two copies for the complex MATα2/MCM1/DNA. The chameleon sequence, located at the linker part between MATα2 and MCM1, took α-helix in a copy and β-strand in the other copy (Tan and Richmond 1998). The chameleon sequence is unstructured in the free protein (Sauer et al. 1988). The conformational change at the linker part in the complex is thought to be important to regulate DNA-binding when binding to DNA (Vershon and Johnson 1993).

Molecular dynamics (MD) simulation is a useful tool to study protein folding. Folding pathways of villin headpiece in explicit water were traced in a 1-μsec MD simulation (Duan and Kollman 1998). Folding processes of a mini-protein BBA5 (a 23-residue β-hairpin/turn/α-helix motif inspired by the zinc finger fold) in implicit water were picked up out of a large number of independent MD runs (Snow et al. 2002). MD runs, each of which covered different areas of the conformational space, were integrated to generate a free-energy landscape of proteins in explicit water (Boczko and Brooks III 1995; Shea et al. 2002).

The free-energy landscape is essentially important to understand the protein folding. However, a large number of energy barriers in the conformational space make the sampled area small, resulting in the energy trapping. Thus, it is still difficult to obtain a statistically reliable landscape for a large system from a simulation of an all-atom protein model in explicit water; however, it has become possible for peptides ∼10 residues long by using generalized-ensemble methods (Garcia and Sanbonmatsu 2001; Higo et al. 2001a,b; Kamiya et al. 2002). A multicanonical algorithm, used in the current study, was originally introduced to enhance the sampling of a spin system (Berg and Neuhaus 1992) and applied to biological systems (Hansmann and Okamoto 1993; Kidera 1995). Recent development in the generalized-ensemble methods was summarized well in a review (Mitsutake et al. 2001).

In the present work, we obtained the free-energy landscape of a 16-residue peptide taken from MATα2 by using the multicanonical MD simulation, for which the sequence is 1Ace-2Val-3Phe-4Asn-5Val-6Val-7Thr-8Gln-9Asp-10Met-11Ile-12Asn-13Lys-14Ser-15Thr-16Nme, where Ace and Nme are, respectively, N-terminal acetyl and C-terminal N-methyl groups introduced to block the peptide termini. The region [8Gln–15Thr] is the chameleon sequence, and the region [2Val–7Thr] is hydrogen-bonding to the chameleon sequence in the β-strand form. We restrained [2Val–7Thr] around the crystal structure in the complex, because the conformation of this region does not change in either α or β conformation of the chameleon sequence in the crystal structure (Tan and Richmond 1998). We report that this peptide inherently folds into either α or β structure, and we discuss the mechanism of this local folding.

Results and Discussion

Conformational clusters in free-energy landscape

The free-energy landscape was obtained from the multicanonical MD simulation of the 16-residue peptide taken from MATα2. Here, we briefly describe the computational method (for details, see Materials and Methods). The chameleon sequence (i.e., [8Gln–15Thr] denoted by Scham) is flexible in the simulation. The N-terminal half [2Val–7Thr] was denoted by SN-term and restrained around the crystal structure, as described above. The peptide was surrounded by explicit water.

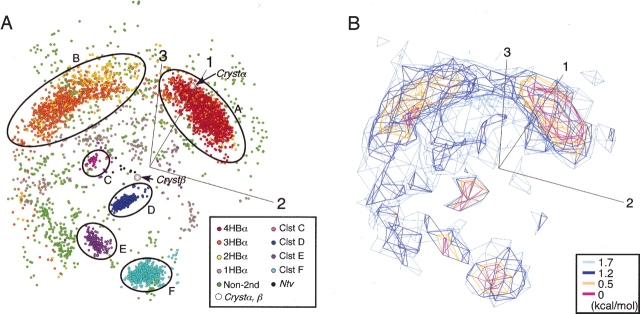
Figure 1A ▶ is the conformational distribution of the peptide at 300 K in the three-dimensional principal component analysis (PCA) space constructed by v1, v2, and v3 (for details of PCA, see Materials and Methods). Low free energy is assigned to high-density regions with crowded points in the figure. Thus, this distribution is regarded as a free-energy landscape. The contribution of the conformational distribution along each PCA axis to the whole distribution is assessed by a value λi / Σk λk, where the summation was taken over all eigen-values: The value was 55% (for i = 1), 20% (for i = 2), 17% (for i = 3), and 2% (for i = 4). Therefore, the first three PCA axes determined the distribution by 92%. This means that the three-dimensional PCA space is a good approximation to express the free-energy landscape. Figure 1B ▶ is an iso-density map expressed in terms of potential of mean force (PMF): PMF = −RT ln ρ(r), where R is the gas constant, T = 300 K, and ρ(r) is the density at position r in the PCA space. The α-helical conformations were assigned to clusters A and B. Cluster A was the longest helix, involving four intra main-chain hydrogen bonds (H-bonds): 7O–11HN (designated as HBα1), 8O–12HN (HBα2), 9O–13HN (HBα3), and 10O–14HN (HBα4). The H-bond 11O–15HN (HBα5) was not always formed in clusters A and B. Cluster B was a shorter helix, the majority of which involved three H-bonds, HBα2, HBα3, and HBα4. A hydrophobic core, formed by the side chains of 6Val and 11Ile and the hydrophobic part of 10Met, was found only in cluster A. Because both the hydrophobic core and HBα1 were located at the root of Scham, this compact structure was called Scham-root structure. The majority of helices with two HBα were scattered in cluster B (Fig. 1A ▶).

Figure 1.

Figure 1.

Open in a new tab

Free-energy landscape at 300 K. (A) Conformational distribution of Q(300 K) in three-dimensional PCA space by v1, v2, and v3. Axis numbers 1, 2, and 3 represent eigen-value numbers. nHBα represents conformation with n HBα; ClstX, cluster X (X = A to F). Circles roughly cover the cluster location. Crystβ and Crystα are, respectively, crystallographic β and α conformations. Ntv is β-hairpin with the same strand–strand H-bond pattern as that in Crystβ. Non-2nd is assigned to conformations of nonsecondary structures. (B) Iso-density map from the same orientation as Figure 1A ▶, expressed in terms of PMF.

The conformations in clusters C, D, E, and F were various β-hairpins with different strand–strand ladder patterns of H-bonds. Cluster D included three or more of five H-bonds: 7HN–10O, 5O–12HN, 5HN–12O, 3O–14HN, and 3HN–14O. Cluster E, which involved type I β-turn (ξ10 = −52 degrees, φ11 = −113, and 9Cα − 12Cα = 5.4 Å), had two or more of four H-bonds: 9HN–13O, 9O–12HN, 6O–15HN, and 6HN–15O. Most of cluster-F conformations included four H-bonds: 8HN–11O, 6O–13HN, 6HN–13O, and 4O–15HN. Cluster C included an H-bond, 5O–15HN. A small number of conformations (Ntv in Fig. 1A ▶) with the same H-bond pattern as that in Crystβ were found.

Crystα was located in cluster A (Fig. 1A ▶). Comparison of a cluster-A conformation with Crystα is shown in Figure 2A ▶ (best main-chain root mean square deviation [RMSD] = 0.4 Å). Crystβ, which has type 1 β-turn, is characterized by the five H-bonds: 3O–15HN, 5HN–13O, 5O–13HN, 7HN–10O, and 7O–10HN. A conformation (Crmsd in Fig. 2B ▶) in Ntv gave the best main-chain RMSD (1.4 Å) to Crystβ, although the Ntv conformations did not form a β-turn. Figure 2B ▶ also displays a cluster-D conformation with a well-ordered strand–strand H-bonds.

Figure 2.

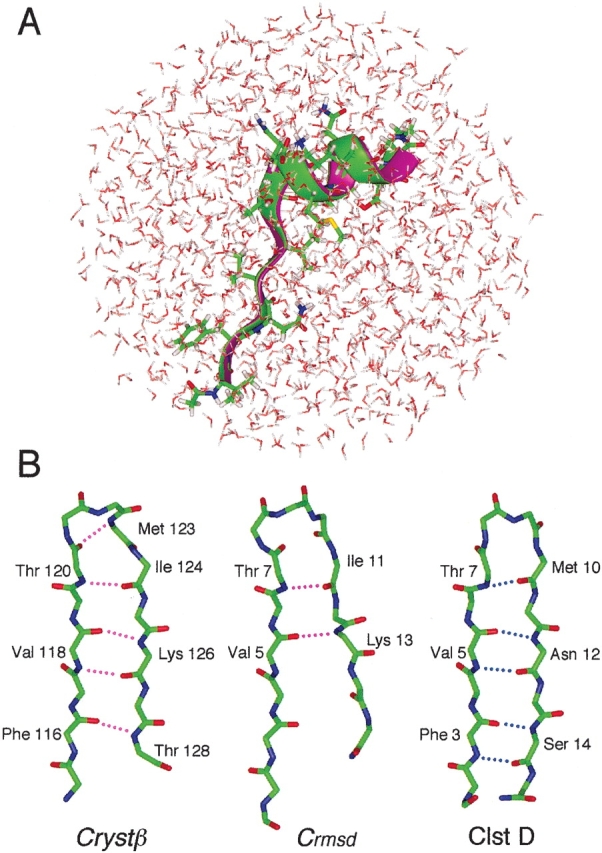
Figure 2.

Open in a new tab

Comparison of simulation conformations with Crystα or Crystβ. (A) Ribbon representation of a cluster-A conformation (green) and Crystα (magenta). Side chain of the cluster-A conformation is shown. Water molecules in simulation are also displayed to show how peptide is surrounded by water. (B) Main-chain conformations of Crystβ, Crmsd (the closest conformation to Crystβ in Ntv), and of cluster D. Broken lines indicate intra main-chain H-bonds involved in Crystβ (magenta) and in cluster-D conformation (blue).

The separation of conformations into clusters, as shown in Figure 1 ▶, indicates the free-energy barriers among the clusters. The probabilities of existence assigned to helices, hairpins, and nonsecondary structures were listed in Table 1: In total, 52.6% was assigned to α-helices; 31.5%, to β-hairpins. The conformations with only one HBα were not counted as helix in Table 1. The probability for the remaining (i.e., nonsecondary structures) was 11.5%. Thus, Scham inherently exhibited the bifacial feature of the chameleon sequence in solution with the restraint on SN-term. The largest probability was assigned to the helices, which means that Scham has a strong propensity to form helix in water. Our result agrees with the result that Scham is helix when exposed to solvent in crystal structure (Tan and Richmond 1998).

Table 1.

Probabilities of existence for each conformation

Conformation Probability of existence (%)
4HBα 29.78
3HBα 17.45
2HBα 5.30
1HBα 4.49
C1stC 0.61
C1stD 17.29
C1stE 2.82
C1stF 10.62
Ntv 0.15
non-2nd 11.50
Open in a new tab

See text for definition of nHBα and caption of Fig. 1 ▶ for definition of other conformations.

Pathways among clusters

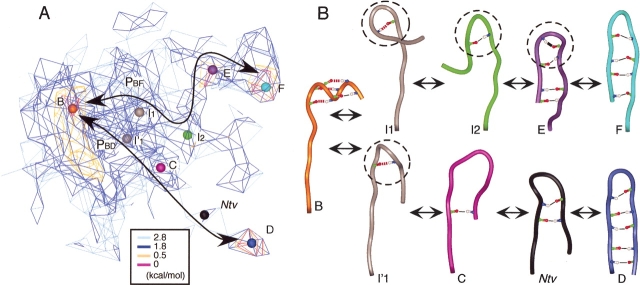
Figure 3 ▶ focuses on the intermediate regions between clusters A and B. This figure illustrates two narrow pathways connecting the clusters. The difference between the pathways was found in the conformation of the C-terminal of Scham (see ribbon representations in Fig. 3 ▶). The Scham-root structure was broken on both pathways and in cluster B. This break provides flexibility to Scham. In contrast, Cluster-A conformations maintained the backbone structure by the presence of the Scham-root structure, even when HBα1 was broken.

Figure 3.

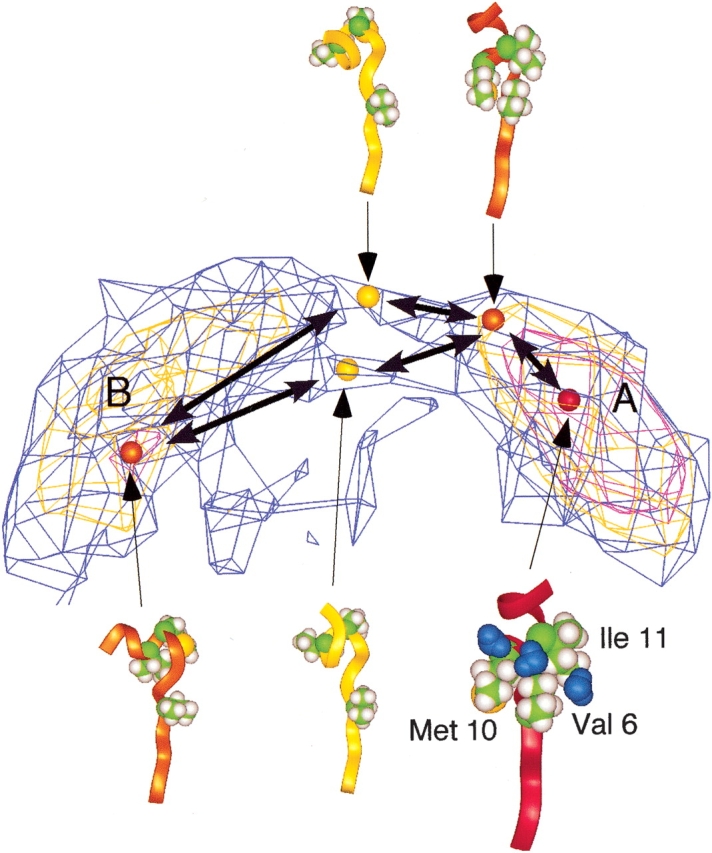
Figure 3.

Open in a new tab

Pathways between α-helical clusters expressed by iso-density map. Density levels are the same as those of Figure 1B ▶. Ribbon representations are conformations (colored spheres) picked from the map. Coloring of ribbons and of spheres in the map is the same as that in Figure 1A ▶. Three side chains—6Val, 10Met, and 11Ile, constructing a hydrophobic core—are displayed in CPK model with the ribbon model. Three water molecules (blue) in the vicinity of the hydrophobic core are displayed.

Figure 4 ▶, A and B, focus on the intermediate regions for the α-β transition pathways and conformational changes along the pathways. We found two pathways: PBF connecting clusters B and F; PBD, clusters B and D. The Scham-root structure, which was found in cluster A, did not exist on the pathways. However, along pathway PBF, other compact structures (Fig. 4B ▶, circles) were formed around the root of Scham, although atoms participating to the compactness changed. The β-turn appeared only in cluster E. On the other hand, a significant feature of pathway PBD was strand–strand H-bond rearrangements without forming the compact structure, except for I’1 conformation. Crystβ-like conformations (Ntv) existed on PBD. PBF is a lower free-energy pathway than is PBD. The formation of the compact structure may reduce the free-energy barrier along the pathway.

Figure 4.

Figure 4.

Open in a new tab

Pathways between α-helix and β-hairpin conformations. (A) Iso-density map around clusters B, C, D, E, and F. Pathways PBF and PBD are shown by solid lines with arrows. Coloring of spheres is the same as that of Figure 1B ▶. (B) Tube representations of conformations picked from the map. I1, I2, and I′ are conformations from intermediate regions. Circles of broken lines are mentioned in the text. Thick black line in conformation E represents a β-turn H-bond; red broken lines, α-helical H-bonds formed in Crystα. Other intra main-chain H-bonds are shown by thin solid lines. Coloring of the tubes is the same as that of Figure 1A ▶.

The multicanonical MD simulation is an enhanced sampling method, in which the conformation can overcome high-energy regions. Thus, the obtained trajectory should not be regarded as one at a constant temperature but be done as a conformational ensemble to obtain the free-energy landscape. The cluster A-B pathways (Fig. 3 ▶) and pathway PBF (Fig. 4A ▶) were well characterized by contour lines. This means that the transitions among the clusters can happen along the pathways at room temperature. On the other hand, pathway PBD was not clearly characterized by contour lines. This means that the transition along PBD is considerably rare at the room temperature. Ono et al. (1999) showed that the sampling of high-energy regions is sparse, even with the multicanonical method. Thus, to more clearly evaluate pathway PBD, sampling should be done with focusing on the high-energy regions.

No substantial cluster was found around Crystβ. This is probably because the studied sequence was treated as isolated in solution: In the crystal structure of the complex, the C-terminal of Scham was connected to MATα2, and 8Gln was hydrogen bonding to Ser 51 of MCM1. We presume that the lack of the conformational restriction allowed the peptide the variety of β-hairpins with different H-bond patterns.

In addition, this artificial treatment of the system affected the conformational fluctuations of Scham: The conformational fluctuation in the helical form was relatively large in our computation (data not shown), although it was reported that the fluctuation in the helical form was small in the crystal structure (Tan and Richmond 1998). This is because the C-terminal of Scham was free in our simulation, although the terminal was restrained in the crystal structure. The current study, however, showed that the sequence could inherently reproduce the bifacial property of Scham. The surroundings of the sequence may determine which conformation, α or β, is selected to regulate the protein–DNA binding, and slight changes in the surroundings may cause the conformational change of Scham.

Determinant factors for the bifacial property

The restraint applied on SN-term is essentially important for the β form of Scham. We have reported the free-energy landscape of three peptides (Higo et al. 2001a, b; Kamiya et al. 2002; Ikeda et al. 2003), in which no restraint was applied on the peptides. There, the random state was the most stable at 300 K, and the secondary structures were semi-stable on the free-energy landscape. These results imply that if there is no restraint, the probability that both SN-term and Scham take extended conformations is considerably small. Contrary, in the current work, the β structure had a large probability. The strand shape of SN-term provides a suitable framework to fold Scham into the β conformation.

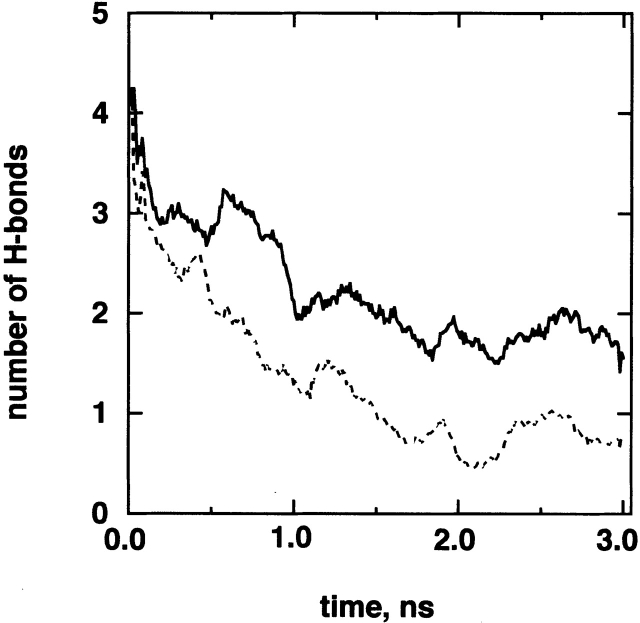
On the other hand, the α-helix does not require the strong interaction between Scham and SN-term. To understand the structural determinant for the α-helix, we did unfolding MD simulations of a different amino acid sequence with applying the same restraint on SN-term as follows. First, we randomly picked up a conformation from cluster A and did an unfolding MD simulation for 3 nsec at 500 K starting from the picked conformation. Next, we replaced two amino acids 10Met and 11Ile by 10Ser and 11Ser, respectively, on the picked conformation. Remember that 10Met and 11Ile contributed to the Scham-root structure in cluster A. The Ser has a small hydrophilic side chain. The amino acid replacement did not introduce atomic overlapping. Then, we did an unfolding simulation of this mutated system for 3 nsec at 500 K with the same restraint on SN-term. Finally, we repeated this procedure 12 times with randomly picking up conformations from cluster A (i.e., number of runs is 12 for both the original and mutated sequences). Figure 5 ▶ demonstrates that the number of H-bonds in the mutated sequence decreases more quickly than the original one. The unfolding MD simulations showed that the original sequence has an advantage to from α-helix.

Figure 5.

Figure 5.

Open in a new tab

Process of H-bond breaking at 500 K. Numbers of H-bonds is the average over 12 unfolding runs, for which the initial conformations were randomly picked up from cluster A. Possible maximum number of H-bonds is five: HBα1 through HBα5. Solid line is from the original chameleon sequence; broken line, mutated sequence (see text).

Recently, computer power and simulation techniques for protein-folding study have remarkably developed. For example, Snow et al. (2002) have succeeded in comparing simulated and experimental folding-dynamics within biologically appropriate time scales by using a distributed-computing method. One of the goals in the simulations is to elucidate the mechanism by which protein misfold causes serious disease, such as Alzheimer’s or bovine spongiform encephalopathy (BSE). To investigate the complicated folding mechanism, however, more precise and realistic sampling method is demanded. The precise sampling method is also useful to assess the accuracy of the forcefield. Recent multicanonical study has shown that AMBER Parm 96 provides results that are more statistically reliable than Parm 94 (Ono et al. 2000;Higo et al. 2001b). Current work may provide a clue to understand the abnormal chain folding. We observed the α-β structure transition in detail by analyzing the energy landscape obtained from the multicanonical sampling using the all-atom model in the explicit water. When a peptide has the inherent property to fold into either the α or β conformation, conditional change may induce different folding, and the differently folded conformation may enhance the protein aggregation or fibrillation (Sticht et al. 1995; Zhang et al. 2000). The current study showed that the balance of probability for the α or β clusters is subtle, and slight conditional changes induce the transition.

Materials and methods

Materials

The peptide sequence studied was given in the last paragraph of the introduction. This sequence was taken from MATα2 (115th to 128th residues in the original PDB file of MATα2/MCM1/DNA complex; PDB entry is 1MNM; Tan and Richmond 1998): The sequence [2Val–7Thr], designated as SN-term, is the N-terminal of MATα2, and the sequence [8Gln–15Thr], designated as Scham, is the chameleon sequence. The SN-term forms a β-strand with hydrogen bonding to a β-sheet in MCM1 in the complex (Tan and Richmond 1998). The crystal structure tells us that Scham folds into a β-hairpin when it interacts with SN-term, and takes an α-helix when exposed to solvent. The β-strand conformation of SN-term is well maintained in both the α-helix and β-hairpin conformations of Scham (main-chain RMSD for SN-term = 0.39 Å). Thus, we restrained the main-chain atoms of [2Val–7Thr] in SN-term around the crystal structure with applying a harmonic potential on SN-term during the simulation.

System of the simulation

The peptide was put in a sphere of 42 Å diameter, setting the geometrical center of SN-term on the sphere center. The remaining volume in the sphere was filled with water molecules with 1 g/cm3 density. A harmonic potential was applied to a water molecule only when the molecule flew outside the sphere, to confine the molecule in the sphere. Similarly, atoms in Scham were also confined in a 36 Å-diameter sphere, for which the center was put on that of the 42 Å sphere. Thus, the flexible parts were Scham, the side chains of SN-term, and water molecules. The initial conformation of Scham for simulation was a random one. The system consisted of 234 peptide atoms and 1193 water molecules.

Multicanonical MD

We used a generalized-ensemble method, multicanonical MD simulation (Nakajima et al. 1997), for the conformational sampling. The conformation can overcome energy barriers during the simulation by the introduction of an additional force term, in which the density of state of the system is effectively included. A canonical ensemble, Q(T), at an arbitrary temperature, T, is derived from the sampled conformations. Iteration of multicanonical runs is required to accurately obtain the density of state in a wide energy range, and the last run is used as the sampling run to generate Q(T). The initial MD conformation of Scham for the first run was a random conformation, in which no intrapeptide hydrogen bonds were formed. The initial conformation for the ith run was the last conformation of the (i − 1) th run. The runs were repeated 24 times, and the sampling run of 162 × 106 MD steps produced a flat energy distribution (data not shown) in a temperature range of 290 to 650 K.

We used the computer program PRESTO (Morikami et al. 1992) modified for multicanonical MD. A cell-multipole expansion (Ding et al. 1992) was used for the electrostatic computation, SHAKE algorithm (Ryckaert et al. 1977), to constrain covalent bonds between hydrogen and heavy atoms. The MD time step was 1 fsec, and temperature was controlled by the constant-temperature method (Evans and Morriss 1983). The forcefield used was AMBER parm 96 (Kollman et al. 1997) for peptide and the flexible TIP3P potential (Jorgensen et al. 1987) for water.

Principal component analysis

The Q(T) was analyzed with a PCA (Kamiya et al. 2002). A peptide conformation was denoted as q = [r1, r2,…, rn] = [q1,q2, …, q3n], where the ith atomic position ri = [xi, yi, zi] = [q3i − 2, q3i − 1, q3i], and n is the number of peptide atoms. If Q(T) consists of N conformations, a variant–covariant matrix is defined as Cij = 〈qiqj〉 − 〈qi〉〈qj〉, where Cij is the (i,j)th matrix element, and ≤…> is the ensemble average over the N conformations. Placing the matrix on a diagonal, eigen-vectors {v1, v2, …, v3N}, where vi × vj = δij, and eigen-values {λ1, λ2, …, λ3N} are obtained. The eigen-vectors construct a multidimensional conformational space, in which the N conformations are distributed. The λi represents the standard deviation of the distribution along vi. We arranged the eigen-values in the descending order. In the conformational space, q is expressed by [c1, c2, …, c3N], where ck = q × vk. The distribution in the conformational space gives the free-energy landscape (Nakajima et al 2000; Ono et al. 2000; Higo et al. 2001a, b; Kamiya et al. 2002).

Acknowledgments

We are grateful to Dr. H. Nakamura from Osaka University for helpful discussions.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03143803.

References

  1. Abel, K., Yoder M.D., Hilgenfeld, R., and Jurnak, F. 1996. An α to β conformational switch in EF-Tu. Structure 4 1153–1159. [DOI] [PubMed] [Google Scholar]
  2. Berg, B.A. and Neuhaus, T. 1992. Multicanonical ensemble: A new approach to simulate first-order phase transitions. Phys. Rev. Lett. 68 9–12. [DOI] [PubMed] [Google Scholar]
  3. Boczko, E.M. and Brooks III, C.L. 1995. First-principles calculation of the folding free energy of a three-helix bundle protein. Science 269 393–396. [DOI] [PubMed] [Google Scholar]
  4. Ding, H.-Q., Karasawa, N., and Goddard III, W.A. 1992. Atomic level simulations on a million particles: The cell multipole method for Coulomb and London nonbond interactions. J. Chem. Phys. 97 4309–4315. [Google Scholar]
  5. Duan, Y. and Kollman, P.A. 1998. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 282 740–744. [DOI] [PubMed] [Google Scholar]
  6. Evans, D.J. and Morriss, G.P. 1983. The isothermal/isobaric molecular dynamics ensemble. Phys. Lett. A 98 433–436. [Google Scholar]
  7. Garcia, A.E. and Sanbonmatsu, K.Y. 2001. Exploring the energy landscape of a β hairpin in explicit solvent. Proteins 42 345–354. [DOI] [PubMed] [Google Scholar]
  8. Hansmann, U.H.E. and Okamoto, Y. 1993. Prediction of peptide conformation by multicanonical algorithm: New approach to the multiple-minima problem. J. Comp. Chem. 14 1333–1338. [Google Scholar]
  9. Higo, J., Galzitskaya, O.V., Ono, S., and Nakamura, H. 2001a. Energy landscape of a β-hairpin peptide in explicit water studied by multicanonical molecular dynamics. Chem. Phys. Lett. 337 169–175. [Google Scholar]
  10. Higo, J., Ito, N., Kuroda, M., Ono, S., Nakajima, N., and Nakamura, H. 2001b. Energy landscape of a peptide consisting of α-helix, 310-helix, β-turn, β-hairpin, and other disordered conformations. Protein Sci. 10 1160–1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ikeda, K., Galzitskaya, O.V., Nakamura, H., and Higo, J. 2003. β-Hairpins, α-helices, and the intermediates among the secondary structures in the energy landscape of a peptide from a distal β-hairpin of SH3 domain. J. Comp. Chem. 24 310–318. [DOI] [PubMed] [Google Scholar]
  12. Jorgensen, W.L., Chandrasekher, J., Madura, J.D., Impey, R.W., and Klein, M.L. 1987. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79 926–935. [Google Scholar]
  13. Kamiya, N., Higo, J., and Nakamura, H. 2002. Conformational transition states of a β-hairpin peptide between the ordered and disordered conformations in explicit water. Protein Sci. 11 2297–2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kidera, A. 1995. Enhanced conformational sampling in Monte Carlo simulations of proteins: Application to a constrained peptide. Proc. Natl. Acad. Sci. 92 9886–9889. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kollman, P.A., Dixon, R.W., Cornell, W.D., Chipot, C., and Pohorille, A. 1997. The development/application of a "minimalist" organic/biochemical molecular mechanic forcefield using a combination of ab initio calculations and experimental data. In Computer simulations of biological systems (eds. W.F. van Gunsteren et al.), Vol. 3, pp. 83–96. KLUWER/ESCOM, The Netherlands.
  16. Mezei, M. 1998. Chameleon sequences in the PDB. Protein Eng. 11 411–414. [DOI] [PubMed] [Google Scholar]
  17. Minor Jr., D.L. and Kim, P. S. 1996. Context-dependent secondary structure formation of a designed protein sequence. Nature 380 730–734. [DOI] [PubMed] [Google Scholar]
  18. Mitsutake, A., Sugita, Y., and Okamoto, Y. 2001. Generalized-ensemble algorithms for molecular simulations of biopolymers. Biopolymers 60 96–123. [DOI] [PubMed] [Google Scholar]
  19. Morikami, K., Nakai, T., Kidera, A., Saito, M., and Nakamura, H. 1992. PRESTO: A vectorized molecular mechanics program for biopolymers. Comp. Chem. 16 243–248. [Google Scholar]
  20. Nakajima, N., Nakamura, H., and Kidera, A. 1997. Multicanonical ensemble generated by molecular dynamics simulation for enhanced conformational sampling of peptides. J. Phys. Chem. B 101 817–824. [Google Scholar]
  21. Nakajima, N., Higo, J., Kidera, A., and Nakamura, H. 2000. Free energy landscapes of peptides by enhanced conformational sampling. J. Mol. Biol. 296 197–216. [DOI] [PubMed] [Google Scholar]
  22. Ono, S., Nakajima, N., Higo, J., and Nakamura, H. 1999. The multicanonical weighted histogram analysis method for the free-energy landscape along structural transition paths. Chem. Phys. Lett. 312 247–254. [Google Scholar]
  23. ———. 2000. Peptide free energy profile is strongly dependent on the force field: Comparison of C96 and AMBER95. J. Comp. Chem. 21 748–762. [Google Scholar]
  24. Ryckaert, J.-P., Ciccotti, G., and Berendsen, H.J.C. 1977. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comp. Phys. 23 327–341. [Google Scholar]
  25. Sauer, R.T., Smith, D.L., and Johnson, A.D. 1988. Flexibility of the yeast α2 repressor enables it to occupy the ends of its operator, leaving the center free. Genes & Dev. 2 807–816. [DOI] [PubMed] [Google Scholar]
  26. Shea, J.E., Onuchic, J.N., and Brooks III, C.L. 2002. Probing the folding free energy landscape of the Src-SH3 protein domain. Proc. Natl. Acad. Sci. 99 16064–16068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Smith, C.A., Calabro, V., and Frankel, A.D. 2000. An RNA-binding chameleon. Mol. Cell 6 1067–1076. [DOI] [PubMed] [Google Scholar]
  28. Snow, C.D., Nguyen, H., Pande, V.S., and Gruebele, M. 2002. Absolute comparison of simulated and experimental protein-folding dynamics. Nature 420 102–106. [DOI] [PubMed] [Google Scholar]
  29. Sticht, H., Bayer, P., Willbold, D., Dames, S., Hilbich, C., Beyreuther, K., Frank, R.W., and Rosch, P. 1995. Structure of amyloid A4-(1-40)-peptide of Alzheimer’s disease. Eur. J. Biochem. 233 293–298. [DOI] [PubMed] [Google Scholar]
  30. Tan, S. and Richmond, T.J. 1998. Crystal structure of the yeast MATα2/MCM1/DNA ternary complex. Nature 391 660–666. [DOI] [PubMed] [Google Scholar]
  31. Vershon, A.K. and Johnson, A.D. 1993. A short, disordered protein region mediates interactions between the homeodomain of the yeast α2 protein and the MCM1 protein. Cell 72 105–112. [DOI] [PubMed] [Google Scholar]
  32. Whisstock, J.A., Skinner, R., Carrell, R.W., and Lesk, A.M. 2000. Conformational changes in serpins, I: The native and cleaved conformations of α1-antitrypsin. J. Mol. Biol. 296 685–699. [DOI] [PubMed] [Google Scholar]
  33. Yang, W.Z., Ko, T.P., Corselli, L., Johnson, R.C., and Yuan, H.S. 1998. Conversion of a β-strand to an α-helix induced by a single-site mutation observed in the crystal structure of Fis mutant Pro26Ala. Protein Sci. 7 1875–1883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhang, S., Iwata, K., Lachenmann, M.J., Peng, J.W., Li, S., Stimson, E.R., Lu, Y., Felix, A.M., Maggio, J.E., and Lee, J.P. 2000. The Alzheimer’s peptide a β adopts a collapsed coil structure in water. J. Struct. Biol. 130 130–141. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES