Abstract
The heat-induced denaturation kinetics of two different sources of ovalbumin at pH 7 was studied by chromatography and differential scanning calorimetry. The kinetics was found to be independent of protein concentration and salt concentration, but was strongly dependent on temperature. For highly pure ovalbumin, the decrease in nondenatured native protein showed first-order dependence. The activation energy obtained with different techniques varied between 430 and 490 kJ•mole−1. First-order behavior was studied in detail using differential scanning calorimetry. The calorimetric traces were irreversible and highly scan rate-dependent. The shape of the thermograms as well as the scan rate dependence can be explained by assuming that the thermal denaturation takes place according to a simplified kinetic process 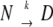 where N is the native state, D is denatured (or another final state) and k a first-order kinetic constant that changes with temperature, according to the Arrhenius equation. A kinetic model for the temperature-induced denaturation and aggregation of ovalbumin is presented. Commercially obtained ovalbumin was found to contain an intermediate-stable fraction (IS) of about 20% that was unable to form aggregates. The denaturation of this fraction did not satisfy first-order kinetics.
where N is the native state, D is denatured (or another final state) and k a first-order kinetic constant that changes with temperature, according to the Arrhenius equation. A kinetic model for the temperature-induced denaturation and aggregation of ovalbumin is presented. Commercially obtained ovalbumin was found to contain an intermediate-stable fraction (IS) of about 20% that was unable to form aggregates. The denaturation of this fraction did not satisfy first-order kinetics.
Keywords: Irreversible transitions, scan-rate dependence, scanning calorimetry, chromatography, protein denaturation, aggregation, globular proteins, ovalbumin
Aggregation of proteins is an important process in many biological systems and industrial processes. In biological systems it is required for the assembly of structures with specific functions such as microtubules, blood clots, and viral coatings. The formation of plaques is also related to aggregation of specific proteins that have somehow been modified. The aggregation of proteins is, in general, triggered by a conformational change of the protein induced by heat, enzymatic cleavage, or other processes that affect the folded structure. After this change of structure a series of reactions takes place that lead to the formation of aggregates. In many cases it is not clear what drives the formation of specific structures in these aggregates or the formation of fibrils (Thirumalai et al. 2003). Here we present a study of the heat-induced aggregation of chicken egg white ovalbumin. Ovalbumin is known to form fibrillar types of aggregates upon aggregation and, at high enough protein concentrations, a gel can be formed (Weijers et al. 2002b). It is our aim to use ovalbumin as a model system to study how fibrillar aggregates can be formed and what conditions affect the properties of these aggregates. The results are relevant both to understanding the biological function of protein aggregation and for the industrial applications of proteins in food and nonfood systems.
Egg white ovalbumin is a member of the serine protease inhibitor (serpin) superfamily, but shows no recognized protease-inhibitory activity (Stein et al. 1991). Egg white proteins are applied in a wide range of food products. The ability of egg white proteins to form a gel upon heating and their water-binding and emulsifying capacity are important functional properties (Mine 1995). Typical applications are in the meat industry (emulsifier), in foams, in the confectionery industry, and in bakery products (Forsythe 1960; Kiss et al. 1988). For most functional applications, denaturation and aggregation is required. Ovalbumin is the major protein in egg albumin, and much work has been conducted on its thermal aggregation and gelation (Clark et al. 1981; Doi and Kitabatake 1989; Arntfield et al. 1990a,b; Harte et al. 1992; Kitabatake and Kinekawa 1995; Van der Linden and Sagis 2001; Weijers et al. 2002a). It was found by Smith and Back (Smith and Back 1962) that ovalbumin behaves as a mixture of two proteins, where the amount of S-ovalbumin depends on the storage time and pH of the eggs. In the literature, different terminologies are used for ovalbumin. Native (N-) ovalbumin can be converted into Stable (S-) ovalbumin through the formation of an Intermediate (I-). All these species are able to aggregate. The ovalbumin used in this study (SIGMA) contains N-ovalbumin (N1) and a fraction native ovalbumin (N2), which can denature, but not aggregate. The DSC profile shows this intermediate fraction, and this fraction is therefore referred as Stable Intermediate (SI-) ovalbumin.
To study the heat-induced denaturation of ovalbumin, we used the model proposed by Lumry and Eyring (1954) for the irreversible denaturation.
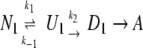 |
(1) |
Here, N, U, D, and A are native, unfolded, denatured, and aggregated protein forms, respectively, and k1, k−1, and k2 are the rate constants for the corresponding reactions. We assume that only D can form aggregates. A commonly used method to study the transition from the native to the denatured state is differential scanning calorimetry (DSC). Equilibrium analysis (N↔U) of DSC thermograms corresponding to reversible unfolding of proteins provides information about the thermodynamics and mechanisms of the reversible unfolding (Privalov 1979, 1982, 1989). However, there are many proteins whose denaturation is irreversible (Donovan and Beardslee 1975; Sanchez-Ruiz et al. 1988; Davoodi et al. 1998; Grinberg et al. 2000; La Rosa et al. 2002), probably due to the occurrence of “side” processes such as aggregation (Klibanov and Ahern 1987). Due to denaturation, hydrophobic interaction can occur, and exposed thiol groups can form disulfide bonds, which results in irreversible behavior (Hoffmann et al. 1996; Alting et al. 2000). Unfolding in the absence of denaturation has been studied using different denaturants (Zemser et al. 1994), but is of less importance in this study, because no kinetic parameters (Ea) can be obtained. Here, thermodynamic parameters such as K will be obtained. Analysis of DSC data for the irreversible denaturation has been reported by several authors (LePock et al. 1992; Kurganov et al. 1997; Lyubarev and Kurganov 2000). In these cases, theoretical equations describing the dependence of the excess heat capacity on temperature were fitted to experimental DSC curves.
Irreversible protein denaturation, as shown in equation 1, involves at least two steps: reversible unfolding of the native protein, followed by the irreversible alteration of the unfolded state to a denatured state, and possibly to another final state. If k2 ≫ k1, most of the U molecules will be converted to D (or another final state). The concentration of U will be very low and the amount of U converted into D is restricted to k1. This results in a simple first-order reaction, the DSC analysis of which has been worked out by Sanchez-Ruiz (Sanchez-Ruiz et al. 1988) using a practical two-state model is represented by:
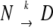 |
(2) |
Gel permeation chromatography is a suitable method to study aggregation kinetics. The aggregation process can be quenched by rapidly cooling the sample to room temperature. Structural properties of the aggregates formed can then be studied. Recently, we reported a detailed study of the heat-induced aggregation and gelation of ovalbumin at low and high ionic strength at neutral pH (Weijers et al. 2002b). As mentioned above, heat-induced aggregation of ovalbumin has been studied intensively by several workers, but none of the earlier investigations on ovalbumin clearly showed the effect of concentration or demonstrated that first-order kinetics applies. Koseki et al. (1989b) found that when a 5-g/L ovalbumin solution in 20 mM potassium-phosphate buffer of pH 7 was heated, the process satisfied first-order kinetics.
In the present study, we investigated the rate of protein conversion for many conditions by varying temperature, protein concentration, and salt concentration. Samples were analyzed by gel-permeation chromatography (GPC). From these results the reaction order, energy of activation (Ea), and the overall rate constants were determined. Subsequently, the kinetic parameters determined by GPC were combined with the kinetic parameters found with DSC, and we propose a new model for the heat-induced denaturation and aggregation of ovalbumin. This model (an extension of the Lumry and Eyring model), which incorporates a heat-stable fraction, is used to describe both sets of experimental data (protein conversion upon heating and DSC data).
Results
Conversion of monomers into aggregates induced by heating
The heat-induced conversion of ovalbumin monomers to aggregates at neutral pH was measured using two slightly different chromatographic techniques: HPSEC and SEC-MALLS. Temperature, ovalbumin concentration, NaCl concentration, and protein source (WCFS and SIGMA) were varied. The heat-induced aggregates are stable under cooling and dilution, and can thus be characterized at room temperature. As described in Materials and Methods, with HPSEC the samples were acidified to their isoelectric point prior to elution, the denatured and aggregated protein precipitated and the amount of nondenatured monomeric protein left after heating was determined. With SEC-MALLS, the heated protein samples, which were cooled to room temperature, were injected on the column without further treatment. In this case, denatured as well as nondenatured monomers will elute at the same volume, and consequently, no discrimination between denatured and nondenatured monomers can be made. Combining the results determined with both techniques allowed us to properly discriminate nondenatured, denatured monomers, and the aggregated fractions.
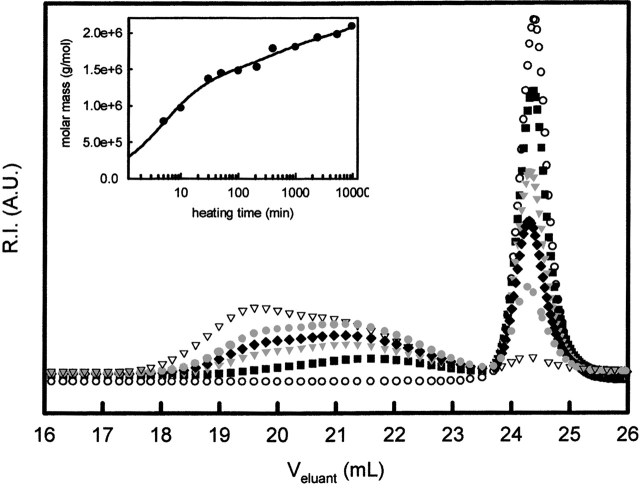
Figure 1 ▶ shows a chromatogram of heated ovalbumin (WCFS) that was not acidified prior to elution. The ovalbumin solutions were heated at 72°C for different times ranging from 0 to 5000 min. Ovalbumin aggregates elute at volumes between 18 and 23 mL. With increasing heating time, the relatively broad aggregate peak shifts to smaller volumes and the scattered intensity of the aggregate peak increases; this means that the size and amount of the aggregates formed increases. The inset in Figure 1 ▶ shows the weight average molar mass of the aggregate peak as calculated from the MALLS data. The molar mass increased from 47 103 Da (M of a monomer) for the shortest heating times to 2•106 Da (corresponding to aggregates consisting of approximately 45 monomers) for a heating time of 1 104 min. The ovalbumin aggregates were always large enough to be clearly distinguished from native proteins. This indicates that under these conditions no or very few stable oligomers (dimers, trimers, etc.) are formed. The size of the aggregates depends on the initial protein concentration and salt concentration during heating, as reported earlier (Weijers et al. 2002b). The polydispersity (Mw/Mn) of the ovalbumin aggregates was approximately 1.5, and did not change significantly as a function of heating time.
Figure 1.
Chromatograms of ovalbumin (WCFS) solutions at pH 7, C = 27.1 gL−1, and 200 ppm NaN3 at different heating times at 72°C. Heating times: (Open circles) Not heated, (filled squares) 10 min, (filled triangles) 30 min, (filled diamonds) 50 min, (filled circles) 100 min, (open triangles) 5338 min. The inset shows the molar mass of the aggregates formed corresponding to the aggregate peaks in the chromatogram.
The narrow peak at volumes between 24 and 25 mL corresponds to nonaggregated monomers. With increasing heating time, the fraction of monomers decreases and stabilizes at about 6% monomers for heating times longer than 1000 min. The size distribution of this fraction was narrow; the polydispersity was about 1.0, and did not increase upon heating.
Comparison of the acidifying and nonacidifying method
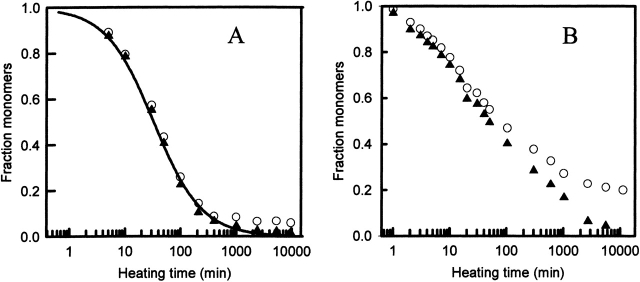
The fraction of monomers as a function of heating time, for the acidifying and nonacidifying methods, is shown in Figure 2 ▶ for two protein samples (WCFS and SIGMA). Data from acidified and nonacidified heated samples gave significantly different results at long heating times. When SIGMA ovalbumin samples had been subjected to long heating times and subsequently acidified, we found precipitation of all of the monomers, whereas the same samples without acid treatment showed a stable intermediate fraction (SI-ovalbumin) of monomers of approximately 20%. The abundance of this stable fraction did not depend on temperature in the range 72°C to 85°C (data not shown). From the nature of the techniques used, we therefore conclude that this SI-fraction is due to monomers that are denatured but not aggregated. These SI-fractions do not aggregate, and therefore cannot participate in the formation of a network. Consequently, this SI-fraction does not contribute to the structure and gelling functionality. Similar results were obtained for WCFS ovalbumin, but the SI-fraction was smaller, namely approximately 6%.
Figure 2.
Heating time dependence of the fraction of monomers using the nonacidifying (open circles) and acidifying (filled triangles) method. (A) WCFS ovalbumin (pH 7, C = 27 gL−1, T = 72°C), (B) SIGMA ovalbumin (pH 7, C = 27 gL−1, T = 78°C). Solid line in A represents a fit with reaction order 1.
Dependence of temperature and protein concentration on the denaturation rate
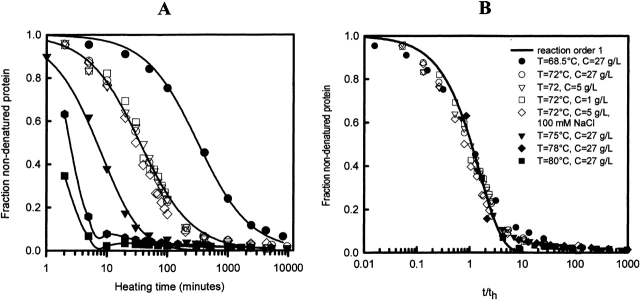
To present a kinetic model for the temperature-induced denaturation and aggregation, a detailed study of the influence of temperature and protein concentration on the denaturation rate was carried out. The relative concentration of nondenatured ovalbumin in the supernatant as a function of heating time, at five temperatures and three initial protein concentrations, is shown in Figure 3A ▶. Table 1 gives an overview of all conditions investigated, for WCFS ovalbumin as well as for SIGMA ovalbumin, and the half time of these reactions. From Figure 3 ▶ and Table 1, three interesting observations can be made:
Figure 3.
(A) Heating time dependence of the fraction of nondenatured ovalbumin (WCFS) under different conditions. (B) Same data as in A plotted as a function of heating time, normalized by the time needed to denature and aggregate half of the proteins (th). Solid lines in A are guides to the eye.
Table 1.
Heating conditions of WCFS and SIGMA ovalbumin and the half times (th) in which 50% of the protein was denatured and/or aggregated
| Ovalbumin (WCFS) | Ovalbumin (SIGMA) | |||||||
| Temp. (°C) | Conc. (g/L), added salt | th (min)a | Temp. (°C) | Conc. (g/L), added salt | th (min)a | Temp. (°C) | Conc. (g/L), added salt | th (min)a |
| 80 | 27, 0 mM | 1.2 | 80 | 27, 0 mM | 1 | 72 | 27, 0 mM | 126 |
| 78 | 27, 0 mM | 2.3 (2.6) | 78 | 27, 0 mM | 72 | 10, 20 mM | 125 | |
| 75 | 27, 0 mM | 7.2 (7.9) | 76.5 | 27, 0 mM | 6.7 | 72 | 10, 50 mM | 127 |
| 72 | 27, 0 mM | 37 (39) | 76.5 | 10, 0 mM | 5.8 | 72 | 10, 100 mM | 126 |
| 72 | 5, 0 mM | 37 (35) | 76.5 | 5, 0 mM | 6.8 | 70 | 27, 0 mM | 500 |
| 72 | 5, 100 mM | 37 (37) | 76.5 | 1, 0 mM | 6.4 | |||
| 72 | 1, 0 mM | 37 (43) | 74.8 | 27, 0 mM | 48 | |||
| 68.5 | 27, 0 mM | 320 (306) | 72 | 60, 0 mM | 126 | |||
A strong temperature dependence on the reaction rate was observed. At 80°C, half of the protein was denatured and aggregated in less than 2 min (half-time, th), while at 68.5°C this took approximately 6 h. For SIGMA ovalbumin the effect was even bigger. The rate at which the proteins denatured was strongly temperature dependent, but the shape of the conversion–time curves was the same for all conditions. This is illustrated in Figure 3B ▶, where the data are plotted as a function of time normalized by th. Clearly, all data superimpose within experimental error. The data satisfy a denaturation rate with order 1 (solid curve in Fig. 3B ▶). The temperature dependence of the denaturation rate is shown to satisfy Arrhenius’ relation (Fig. 4B ▶). An activation energy of about 480 kJ•mole−1 was found. This is comparable to the activation energy found for other proteins, such as β-lactoglobulin (Le Bon et al. 1999), actin, carboxypeptidase, creatine kinase, etc. (Lyubarev and Kurganov 2000). The large value of Ea might be expected, because the highly cooperative nature of the protein implies a large Δh between the folded and denatured protein, and Ea always larger than Δh (see also Le Bon et al. 1999).
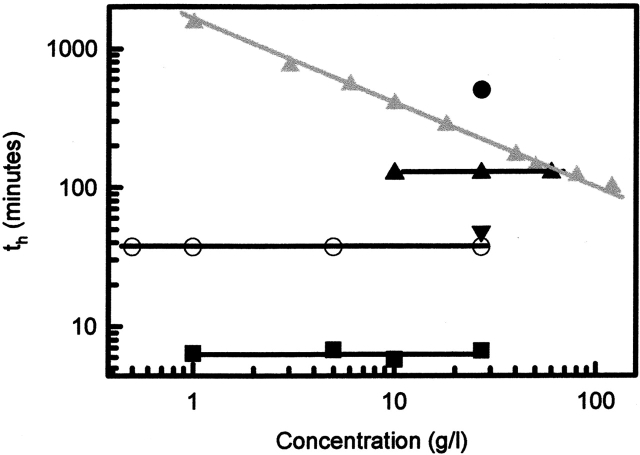
The half-time of the reaction, as described in Table 1, did not depend on initial protein concentration (within the experimental range of 0.1–60 g/L; Fig. 5 ▶). Also, no dependence of the ionic strength on the half time was found (in the range of 3–100 mM). This is different from results found for β-lactoglobulin; here, the decrease in concentration of native β-lactoglobulin during heating was fitted by a reaction order of 1.5 (Roefs and De Kruif 1994; Le Bon et al. 1999). For comparison, the concentration dependence of the half-time of β-lactoglobulin is also plotted in Figure 5 ▶ (data taken from Le Bon et al. 1999). From the data presented in Figure 5 ▶, they found for β-lactoglobulin a total reaction order of 1.5. From the results so far, it is clear that the decrease of nondenatured protein as a function of heating time only depends on temperature and neither on protein concentration nor on NaCl concentration, which suggests that a unimolecular process like denaturation is the rate-limiting step in this process.
Finally, remarkable differences in denaturation rates were observed between the two sources of ovalbumin. SIGMA ovalbumin denatures much more slowly than WCFS ovalbumin. This may be due to the storage time of the eggs before purification or to the purification itself, and will be discussed in the general discussion section.
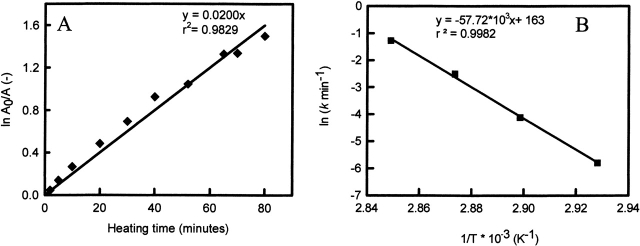
Figure 4.
(A) The fraction of nondenatured ovalbumin (WCFS) (A0 = 5 g/L, [NaCl] = 100 mM, T = 72°C) as a function of heating time shows a first-order dependence. The half-time (th) is calculated from ln 2/k, where k is a temperature-dependent rate constant, obtained from the slope. (B) Arrhenius plot obtained from data from Figure 3A ▶, which are analyzed as in Figure 4A ▶.
Figure 5.
Concentration dependence of the half-time for ovalbumin and β-lactoglobulin (data β-lactoglobulin taken from Le Bon et al. 1999). Black symbols represent SIGMA ovalbumin. Open symbols represent WCFS ovalbumin, and gray symbols represent β-lactoglobulin. Heating conditions: (Black circles) T = 70°C, (black triangles) T = 72°C, (black upside-down triangles) T = 75°C, (black squares) T = 76.5°C, (open circles) T = 72°C, (gray triangles) T = 67°C.
Differential scanning calorimetry of ovalbumin under irreversible conditions
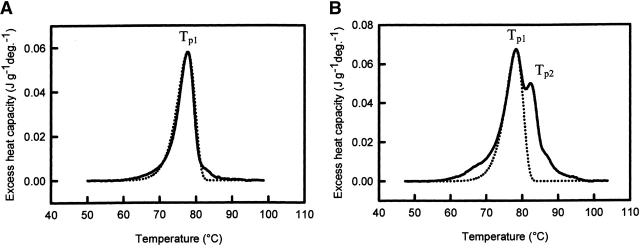
Differences between WCFS and SIGMA ovalbumin were also observed with DSC. Figure 6 ▶ shows the DSC thermograms of both ovalbumin sources, at a scan rate of 0.5°C min−1. For both ovalbumin sources the calorimetric transitions were apparently irreversible. After cooling from the first run, no transition could be detected in the second heating run. The ovalbumin obtained from SIGMA shows two overlapping endothermic peaks centered at 78.4°C (Tp1) and 82.45°C (Tp2), respectively. The second peak represents a stable intermediate (SI), which is an intermediate in the conversion of native ovalbumin (N) into stable ovalbumin (S). The presence of this intermediate has been reported by others (Huntington et al. 1995; Hagolle et al. 1997). The appearance of two distinct peaks in the thermogram of SIGMA ovalbumin indicates that no rapid conversion between the two native states is possible, and therefore, both fractions denature independently. A fast equilibrium between the two fractions (N1 and N2) would imply a fixed ratio between N1 and N2. Therefore, the ratio between dD1/dt and dD2/dt would also be fixed, and no calorimetric distinction could be made between the two fractions. Barbut and Findlay have shown that when ovalbumin and its stable form (S-ovalbumin) are both present in a solution, they undergo denaturation independently.
Figure 6.
Differential scanning calorimetry thermograms and the best fit of the two-state irreversible denaturation model (χ2 of 4•10−6) of WCFS ovalbumin (A) and SIGMA ovalbumin (B) solutions at a scan rate of 0.5°C/min (solid lines) and pH 7.0, protein concentrations of 20 g/L and 35 g/L, respectively. Dashed lines represent irreversible first-order fits.
From DSC experiments (Fig. 6 ▶), the presence of an SI- fraction of about 20%, as observed with SEC-MALLS, is confirmed. We suggest that the decrease in denaturation rate of SIGMA ovalbumin is probably due to the interference of a 20% SI-fraction (intermediate between N-ovalbumin and S-ovalbumin), which can denature but cannot aggregate. Lumrey and Eyring (1954) originally proposed the two-state kinetic model. Based on our findings, we propose an irreversible two-state kinetic model for the denaturation and aggregation of ovalbumin in general.
N1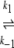 U1 U1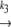 D1 → A D1 → Ak−5 N2 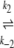 U2 U2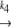 D2 D2
|
(3) |
In our model, we assume two different native states in the starting material; both native states denature independently upon heating. There is no fast equilibrium between N1 and N2. Denaturation is the rate-limiting step in this process, which means that when the protein unfolds (and denatures), one of the denatured states (D1) aggregates immediately, while the other one cannot aggregate and is therefore referred to as the stable fraction (D2).
As we show below, our irreversible two-state kinetic model, based on a mixture of two different ovalbumin fractions, is supported by DSC measurements.
From detailed DSC experiments we attempted to get answers to the following questions: (1) What is the activation energy of both sources of ovalbumin, and are these values comparable with the values found for Ea with other techniques as described above? (2) Can we describe experimental DSC thermograms of WCFS and SIGMA ovalbumin with irreversible first-order kinetics? (3) Is it possible to describe experimental data for the conversion of nondenatured monomers into aggregates with two first-order rate constants, as we assume in our model?
Activation energy of ovalbumin
The activation energy for the denaturation of ovalbumin can be obtained from the scan rate dependence of the peak temperature from a DSC thermogram. Table 2 gives the temperatures corresponding to the maximum in heat capacity (Tp) at different scan rates for both ovalbumin sources. The results presented in Table 2 clearly show a strong dependence on the scan rate, which indicates the absence of equilibrium between native and the denatured state, during scanning.
Table 2.
Effect of scan rate on peak temperatures (Tp) for WCFS ovalbumin (C = 10 g/L) and SIGMA ovalbumin solutions (C = 20 g/L)
| Ovalbumin (WCFS) | Ovalbumin (SIGMA) | |||
| Scan rate (°C/min) | Tp1 (°C) | Scan rate (°C/min) | Tp1 (°C) | Tp2 (°C) |
| 0.10 | 74.81 | 0.05 | X | 78.22 |
| 0.20 | 75.40 | 0.10 | 75.72 | 79.41 |
| 0.30 | 76.66 | 0.20 | 76.62 | 80.78 |
| 0.50 | 77.72 | 0.50 | 78.38 | 82.45 |
| 1.00 | 79.04 | 1.00 | 79.86 | 83.46 |
| 1.50 | 79.71 | 1.50 | 80.66 | 83.31 |
| 2.00 | 80.82 | 2.00 | 81.34 | 83.95 |
To check whether the results are in agreement with the proposed first-order reactions, we used the model developed by Sanshez-Ruiz et al. (1988). Briefly, the two-state model can be represented as 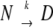 , where N is the native state, D is the unfolded state or, more probably, a final state, with k being a first-order rate constant. From the following equation the energy of activation can be calculated from DSC data.
, where N is the native state, D is the unfolded state or, more probably, a final state, with k being a first-order rate constant. From the following equation the energy of activation can be calculated from DSC data.
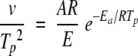 |
(4) |
where v is the scan rate, Ea the energy of activation, A the frequency factor of the Arrhenius equation, and R the gas constant.
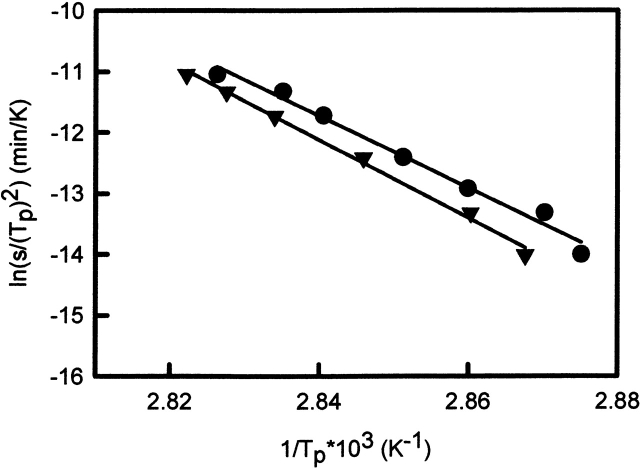
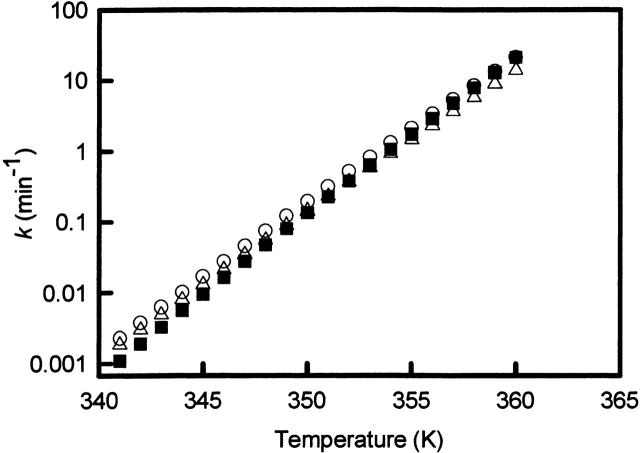
If the proposed model is correct, equation 4 requires a linear dependence of ln (v/Tp2) versus 1/Tp. Indeed, a linear dependence is observed (see Fig. 7 ▶). The Ea calculated from the scan rate dependence was found to be 490 kJ•mole−1 for WCFS ovalbumin, which is in very good agreement with values found with other techniques as reported in Table 3. The energy of activation obtained from the scan rate dependence for SIGMA ovalbumin is obtained for the main fraction. The scan rate dependence of the main peak is almost identical to the WCFS one with an Ea of 530 kJ•mole−1. The Ea of the additional fraction (Tp2) has not been calculated, because it is doubtful from HPSEC and DSC analysis whether this fraction shows first-order behavior. Using the Ea and A obtained from experimental data of WCFS and SIGMA (Tp1) ovalbumin, the rate constants are calculated at different temperatures (Fig. 8 ▶). From Figure 8 ▶ it is clear that the rate constants for WCFS and the main fraction of SIGMA ovalbumin are almost identical. This indicates that the main fraction of SIGMA is probably the same as the WCFS ovalbumin and that both can be described with first-order kinetics.
Figure 7.
Plots of ln (v/Tp2) versus 1/Tp for WCFS (filled circles) and SIGMA (filled triangles) ovalbumin corresponding to equation 2 in the text. Each data point corresponds to a scan rate given in Table 2.
Table 3.
Activation energy (Ea) and frequency factor (A) of the Arrhenius equation determined from experimental DSC and HPGPC data and the best fit (thermograms) for WCFS and SIGMA ovalbumin
| HPGPC | DSC | DSC FIT | |||
| Ea (kJ • mole−1) | A (−) | Ea (kJ • mole−1) | A (−) | Ea (kJ • mole−1) | |
| WCFS | 480 | 6.17 × 1070 | 492 | 5.17 × 1072 | 430 |
| SIGMA (Tp1) | 530 | 1.67 × 1078 | 430 | ||
Figure 8.
Rate constant (k) for WCFS and SIGMA ovalbumin as a function of temperature. First-order rate constant changes with temperature as described in the Arrhenius equation; frequency factor and energy of activation are obtained from Table 3. Rate constants calculated for (open circles) WCFS (DSC), (open triangles) WCFS (HPGPC), (filled squares) SIGMA (Tp1).
Fitting thermograms of ovalbumin with irreversible first-order kinetics
Figure 6 ▶ shows the best fit of the experimental DSC profile (including a baseline correction, resulting in ΔCp = 0 Jg−1K−1) recorded at 0.5°C/min, for WCFS and SIGMA ovalbumin. It is evident that the two-state irreversible denaturation (N→D) model reproduces the experimental data well in the whole temperature range for WCFS ovalbumin. The parameters obtained from the best fit are: Ea = 430 kJ•mole−1; Tp1 = 77.68°C using the condition that the surface area under the peak is the same: Δh ≈ 800 kJ•mole−1. Note that DSC measures the Δh of the overall process, while kinetics deals only with the rate-determining step. This result is an additional indication of a multistep reaction. Attempts were also made to fit the experimental data for SIGMA ovalbumin by the two-state irreversible denaturation model. The main peak is successfully generated with almost the same parameters as for WCFS ovalbumin: Ea = 430 kJ•mole−1; Tp1 = 78.28°C and Δh ≈ 800 kJ•mole−1, where the fraction participating in the main peak was 81% (SI-fraction 19%). We neglected the minor shift of the peak due to the additional fraction. However, the best fit of the additional peak was less successful. A too high Ea had to be used to fit the peak height, and this resulted in a too small peak. From this result we conclude that the denaturation of the additional fraction cannot be described with irreversible first-order kinetics.
Experimental data described with two first-order rate constants
For the determination of the rate of decrease of the nondenatured ovalbumin concentration upon heating, chromatography experiments were carried out. From Figure 4A ▶, it is clear that experimental data for WCFS ovalbumin show first-order behavior. Experimental data of SIGMA ovalbumin could not be described with first-order dependence because this ovalbumin contained two fractions. Therefore, we attempted to describe the experimental data with two first-order rate constants (equation 5)
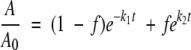 |
(5) |
where A/A0 is the fraction of denatured protein, and f the fraction of denatured but not aggregated protein (f = 20%). Fitting the experimental data assuming two first-order rate constants was not successful, because, again, the additional fraction probably does not denature by a first-order process.
Discussion
We investigated the effect of temperature, protein concentration, and salt concentration on the protein consumption of ovalbumin. From the experimental results a kinetic model for the temperature-induced denaturation and aggregation of ovalbumin is presented.
We observed that th was not dependent on protein concentration, nor on salt concentration. For WCFS ovalbumin, first-order kinetics was observed as shown in Figure 4A ▶. Note that for long heating times interference of the 6% SI-ovalbumin occurs. This results at long heating times in a deviation from first-order kinetics. For SIGMA ovalbumin first-order dependence could not be obtained because of an additional fraction of 20% SI-ovalbumin. Combining the acidifying and nonacidifying techniques, we found that this additional SI-fraction is able to denature, but cannot aggregate. Two different ways to obtain heat-stable ovalbumin have been suggested (see thermograms, Fig. 6 ▶). (1) The amount of S-ovalbumin is related to the storage time and pH of the eggs. Increased storage time results in a growth of the intermediate fraction (Smith and Back 1962). We found that ovalbumin prepared from different batches of eggs resulted in different amounts of SI-ovalbumin, and therefore, different kinetic behavior was observed (data not shown). (2) The formation of I-ovalbumin could be induced by the incubation of purified ovalbumin at basic pH (9.9) and elevated temperature (55°). It has been demonstrated that by varying the incubation time, ovalbumin is converted in time into more heat-stable forms like I- and S-ovalbumin. (J. De Groot and H. H. J. De Jongh, private commun). In the latter case, I- and S-ovalbumin can form aggregates, whereas we find here that it is not possible for our 20% fraction SI-ovalbumin to form aggregates. Therefore, it is most likely that the fraction SI-ovalbumin, present in the SIGMA batch, is formed in the egg as mentioned under (1).
The presence of 20% SI-ovalbumin was also confirmed by DSC, where we clearly observed that SIGMA ovalbumin behaved as a mixture of two proteins with different rates of denaturation. The thermograms for the thermal denaturation of ovalbumin can be interpreted in terms of a kinetic process 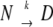 , where k is a first-order kinetic constant that changes with temperature as described by the Arrhenius equation. This model predicts that the peak positions should be dependent on the scan rate, as is the case for ovalbumin. For SIGMA ovalbumin the scan rate dependence is used for the main peak, where we neglected the minor shift of the peak due to the additional fraction. The above-mentioned simple two-state model appears to imply that the denatured state is thermodynamically more stable than the native one. A more realistic representation of the irreversible thermal denaturation of ovalbumin, which results in the same first-order kinetic process, is probably given by:
, where k is a first-order kinetic constant that changes with temperature as described by the Arrhenius equation. This model predicts that the peak positions should be dependent on the scan rate, as is the case for ovalbumin. For SIGMA ovalbumin the scan rate dependence is used for the main peak, where we neglected the minor shift of the peak due to the additional fraction. The above-mentioned simple two-state model appears to imply that the denatured state is thermodynamically more stable than the native one. A more realistic representation of the irreversible thermal denaturation of ovalbumin, which results in the same first-order kinetic process, is probably given by:
N1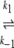 U1 U1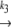 D1 → A D1 → Ak−5 N2 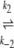 U2 U2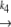 D2 D2
|
(3) |
where N1 and N2 are the native states, U1 and U2 the unfolded states, D1 and D2 the denatured states, and A a final state, which is in this case an aggregated form. If we assume that the conversions of N to U are first-order processes and k3,4 ≫ k1,2, most of the U molecules will be converted into A instead of returning to N through the process U→N. As a result no equilibrium between N and U will be established, so that the denaturation may be considered as being an irreversible process N→A, kinetically controlled by a slow conversion of N→U. This is valid for WCFS ovalbumin; indeed, the DSC traces could be well described with this model resulting in a χ2 of 4•10−6. Calculations on the same DSC traces (given concentration, Δh and Tp) using a reversible process resulted in a χ2 of 5•10−5. The authors interpret the results of the fit as extra support for the proposed model.
For SIGMA ovalbumin the situation is more complex. If we assume two native fractions (as was confirmed by DSC and chromatography) and k5,−5 ≫ k1,2, then a fast equilibrium between N1 and N2 is established. This would imply a fixed ratio between N1 and N2, and therefore, no calorimetric distinction between the two can be made. However, this is not applicable to SIGMA ovalbumin, because two peaks are observed. If k5,−5 ≪ k1,2, N1 and N2 denature independently, and this will result in a calorimetric distinction between the two. The DSC traces should be consistent with two first-order reactions. For SIGMA ovalbumin it was clear that N1 could be fitted with the same parameters as for WCFS ovalbumin, while N2 could not be fitted with irreversible first-order kinetics at all. Therefore, we conclude that N2 probably does not denature by a first-order process. A possibility is that k5,−5 ~ k1 (k1 ~ 0.3 min−1). For that case, and under specific conditions, numerical calculations showed that N1 could be described with irreversible first-order kinetics, whereas N2 could not. We must emphasize that the latter ideas are rather speculative.
Conclusions
The rate of decrease of nondenatured native WCFS ovalbumin when heating solutions of ovalbumin at pH 7 can be described with first-order kinetics, which means that denaturation is the rate-limiting step. The temperature dependence obeys Arrhenius law and is controlled by an activation energy of about 490 kJ•mole−1. From analyzing the shape of the thermograms as well as the scan rate dependence, activation energies of respectively 430 and 490 kJ•mole−1 are found. In contrast to WCFS ovalbumin, SIGMA ovalbumin showed two distinct peaks. The main peak could be successfully described with the same parameters as for WCFS ovalbumin, and assuming 81% of the protein participating in the main peak. Analyzing the scan rate dependence of the main fraction, an activation energy of 530 kJ•mole−1 was found, in good agreement with values found for WCFS ovalbumin. However, experimental results cannot be sufficiently described by implementing a second first-order process (equation 5) corresponding to the additional fraction in SIGMA ovalbumin. Therefore, we conclude that the denaturation of the additional fraction (SI-ovalbumin) does not behave as a first-order process.
Materials and methods
Ovalbumin
Two different sources of hen egg ovalbumin were used in this study. Ovalbumin was purified from egg white of freshly laid hens; eggs (less than 2 h) based on the procedure of Vachier et al. (1995). In the text, this source of pure ovalbumin is referred to “WCFS-ovalbumin”. Another source of hen egg ovalbumin was purchased from Sigma (grade V, >99% pure by agarose electrophoresis, crystallized and lyophilized, Lot # 19H7002). This type of ovalbumin is referred in the text as SIGMA ovalbumin. The purity of both sources was checked with mass spectrometry and SDS PAGE. The latter showed for WCFS ovalbumin one clear spot at 45 kD and for Sigma ovalbumin an additional very small spot was observed at about 80 kD (data not shown). Mass spectrometry was not possible for ovalbumin because it showed many envelopes since it contains 2, 1, and 0 phosphate groups per molecule and is usually glycosylated.
For kinetic experiments, ovalbumin (both WCFS and SIGMA) was dissolved in double-distilled water with 3 mM NaN3 added to avoid bacterial growth. Final protein concentrations were varied between 0.1 and 60 g/L and NaCl concentrations between 0 and 100 mM. The solutions were subsequently stirred for at least 2 h at ambient temperature to allow the protein to dissolve. The pH of the solution was adjusted to 7.0 and the solution was subsequently centrifuged and filtered (0.45 μm; Millex-SV, Millipore Corp., Bedford, MA) to remove a small fraction of insoluble material. The protein solutions were heated in screw-cap vials containing ca. 5 mL of ovalbumin solution in a temperature-controlled water bath at temperatures varying between 68.5 and 80°C. After heating, the solutions were rapidly cooled by placing the tubes in ice-water. The amount of nondenatured native proteins after heat treatment was determined with a standard assay involving acid precipitation and high-performance size-exclusion chromatography (HPSEC; Hoffmann and Mil 1997). The total amount of monomeric protein (nondenatured as well as denatured) after heat treatment was determined with a standard assay without acidification step, employing size-exclusion chromatography in combination with multiangle laser light scattering (SECMALLS).
For differential scanning calorimetry (DSC) experiments, ovalbumin solutions (WCFS) of 1, 5, 10, and 20 g/L without added NaCl were prepared as described above. For ovalbumin solutions (SIGMA), concentrations of 20 and 35 g/L without added NaCl were used.
HPSEC
For the determination of the rate of decrease in concentration of nondenatured ovalbumin upon heating, different series of screw-cap vials containing ca. 5 mL of ovalbumin solution with different initial concentrations were heated at 80, 78, 75, 72, and 68.5°C for WCFS ovalbumin, and 80, 78, 76.5 75, 72, and 70°C for SIGMA ovalbumin. The vials were cooled in ice-water and the protein solutions were diluted to a final concentration of nondenatured protein in the range of 0.1 to 5 g/L, to be within the calibration range. Then, the pH was adjusted to 4.7 ± 0.1 with 0.1 M HCl, which causes the denatured and aggregated ovalbumin to precipitate. After centrifugation at 20,000g for 5 min at ambient temperature, the concentration of nondenatured ovalbumin in the supernatant was determined by HPSEC (Phenomenex BioSep-SEC-S2000 column, 300 × 7.5 mm) with UV detection at 280 nm. In this report, this technique is referred to the “acidification” method, and is assumed to measure the amount of nondenatured native protein left after heating.
SECMALLS
Heated ovalbumin solutions (without acid treatment) were injected after cooling into a high-performance gel chromatography system consisting of a PL-GFC 300, PL-GFC 1000, and PL-GFC 4000 column (300 × 7.5 mm) in series (Polymer Laboratories Ltd.). The specified exclusion limits of these three columns are 1•105, 2•106, and 1•107 Daltons, respectively. The eluant was a 25 mM TRIS/Tricine buffer, pH 8.0, the flow rate was 1.0 mL/min. Heated ovalbumin samples were diluted with double-distilled water to a protein concentration of approximately 10 g/L. These samples were subsequently diluted with twofold concentrated eluant (50 mM TRIS/Tricine), after which 200-μL aliquots were injected into the chromatographic system. This technique is referred in this report as the “nonacidification” method; it determines the total amount of monomeric protein (both native and denatured).
For on-line light-scattering detection a DAWN-F MALLS photometer (Wyatt Technology) was used, equipped with a K5 flow cell and a linearly polarized He-Ne laser light source (5 mW) with a wavelength of 632.8 nm. The DAWN contains 18 detectors, but the four smallest scattering angles (θ) were excluded, as the signal-to-noise ratio of these detectors was too low for an accurate measurement. The concentration of the eluting material was determined with a UV spectrophotometer (Jasco CD-1595, Japan) at 280 nm and a differential refractometer (ERC-7510 ERMA Optical Works Ltd). The data were accumulated and processed using Astra for Windows, version 4.0. The molar mass Mi of the ovalbumin monomers and aggregates in each fraction i was calculated with a first-order Debye fit, using a specific refractive index increment (dn/dc) of 0.172 cm3/g for ovalbumin in TRIS/Tricine buffer.
DSC
DSC scans were carried out with a SETARAM micro-DSC III with stainless steel 1-mL sample cells. Calibration was done with naphthalene. The DSC has two measuring cells: one is used for the sample, and the other, for the reference. Samples were prepared at ovalbumin (WCFS) concentrations of 5, 10, and 20 g/L, pH 7.0, without added salt. For ovalbumin (SIGMA) concentrations of 20 and 35 g/L were used. The same solution without the protein was used in the reference cell. The temperature was scanned from 25 to 120°C at scanning rates of 0.05, 0.10, 0.20, 0.30, 0.50, 1.00, 1.50, 2.00, and 3.00°C min−1. To obtain the Cpeff curves, reference–reference baselines were obtained at the same scanning rate and subtracted from the sample curves.
For DSC scans at an ovalbumin (WCFS) concentration of 1 g/L, a Microcal MC-2 calorimeter was used. Experiments with varying protein concentrations in the range of 1–10 gL have shown that DSC transitions do not depend on protein concentration (data not shown).
The statistics of the fit are calculated using the following equation:
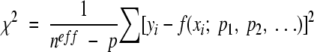 |
(6) |
where neff are the number of data points and p the number of parameters.
Acknowledgments
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.03242803.
References
- Alting, A.C., Hamer, R.J., de Kruif, C.G., and Visschers, R.W. 2000. Formation of disulfide bonds in acid-induced gels of preheated whey protein. J. Agric. Food Chem. 48 5001–5007. [DOI] [PubMed] [Google Scholar]
- Arntfield, S.D., Murray, E.D., and Ismond, M.A.H. 1990a. Influence of salts on the microstructure and rheological properties of heat-induced protein networks from ovalbumin and vicilin. J. Agric. Food Chem. 38 1335–1343. [Google Scholar]
- ———. 1990b. Dependence of thermal properties as well as network microstructure and rheology on protein concentration for ovalbumin and vicilin. J. Texture Stud. 21 191–212. [Google Scholar]
- Clark, A.H., Judge, F.J., Richards, J.B., Stubbs, J.M., and Suggett, A. 1981. Electron microscopy of network structures in thermally induced globular protein gels. Int. J. Pept. Protein Res. 17 380–392. [DOI] [PubMed] [Google Scholar]
- Davoodi, J., Wakarchuk, W.W., Surewicz, W.K., and Carey, P.R. 1998. Scan rate dependence in protein calorimetry: The reversible transitions of Bascillus circulans xylanase and a disulfide-bridge mutant. Protein Sci. 7 1538–1544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi, E. and Kitabatake, N. 1989. Structure of glycinin and ovalbumin gels. Food Hydrocolloids 3 327–337. [Google Scholar]
- Donovan, J.W. and Beardslee, R.A. 1975. Heat stabilization produced by protein–protein association. J. Biol. Chem. 250 1966–1971. [PubMed] [Google Scholar]
- Forsythe, R.H. 1960. The materials of baking eggs. In Bakery technology and engineering (ed. S.A. Matz), pp. 188–220. AVI Publishing Co. Inc., Westport, CT.
- Grinberg, V.Ya., Burova, T.V., Haertlé, T., and Tolstoguzov, V.B. 2000. Interpretation of DSC data on protein denaturation complicated by kinetic and irreversible effects. J. Biotechnol. 79 269–280. [DOI] [PubMed] [Google Scholar]
- Hagolle, N., Relkin, P., Dalgleish, D.G., and Launay, B. 1997. Transition temperatures of heat-induced structural changes in ovalbumin solutions at acid and neutral pH. Food Hydrocolloids 11 311–317. [Google Scholar]
- Harte, J.B., Zabik, M.E., Ofoli, R.Y., and Morgan, R.G. 1992. Ovalbumin thermal gelation prediction by application of temperature-time history. J. Food Sci. 57 1093–1098. [Google Scholar]
- Hoffmann, M.A.M. and Mil, P.J.J.M.v. 1997. Heat-induced aggregation of β-lactoglobulin: Role of the free thiol group and disulphide bonds. J. Agric. Food Chem. 45 2942–2948. [Google Scholar]
- Hoffmann, M.A.M., Roefs, S.P.F.M., Verheul, M., Mil, P.J.J.M.v., and Kruif, K.G.d. 1996. Aggregation of β-lactoglobulin studied by in situ light scattering. J. Dairy Res. 63 423–440. [Google Scholar]
- Huntington, J.A., Patson, P.A., and Gettins, P.G.W. 1995. S-ovalbumin, an ovalbumin conformer with properties analogous to those of loop-inserted serpins. Protein Sci. 4 613–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss, E., Nádudvari, V., Hoschke, Á., and Biacs, P. 1988. Enzyme hydrolyzed egg white protein and its application. In Functional properties of food proteins: Proceedings of international seminar held in Budapest on 7–9 September 1988 (eds. R. Lásztity and M. Ember-Karpati), p. 290. Budapest Technical University, Budapest.
- Kitabatake, N. and Kinekawa, Y. 1995. Turbidity measurement of heated egg proteins using a microplate system. Food Chem. 54 201–203. [Google Scholar]
- Klibanov, A.M. and Ahern, T.J. 1987. Thermal stability of proteins. In Protein engineering (eds. D.L. Oxender and C.F. Fox), pp. 213–218. Alan R. Liss, New York.
- Koseki, T., Fukuda, T., Kitabatake, N., and Doi, E. 1989a. Characterization of linear polymers induced by thermal denaturation of ovalbumin. Food Hydrocolloids 3 135–148. [Google Scholar]
- Koseki, T., Kitabatake, N., and Doi, E. 1989b. Irreversible thermal denaturation and formation of linear aggregates of ovalbumin. Food Hydrocolloids 3 123–134. [Google Scholar]
- Kurganov, B.I., Lyubarev, A.E., Sanchez-Ruiz, J.M., and Shnyrov, V.L. 1997. Analysis of differential scanning calorimetry data for proteins criteria of validity of one-step mechanism of irreversible protein denaturation. Biophys. Chem. 69 125–135. [DOI] [PubMed] [Google Scholar]
- La Rosa, C., Milardi, D., Grasso, D.M., Verbeet, M.P., Canters, G.W., Sportelli, L., and Guzzi, R. 2002. A model for the thermal unfolding of amicyanin. Eur. Biophys. J. 30 229–570. [DOI] [PubMed] [Google Scholar]
- Le Bon, C., Nicolai, T., and Durand, D. 1999. Kinetics of aggregation and gelation of globular proteins after heat-induced denaturation. Macromolecules 32 6120–6127. [Google Scholar]
- Lepock, J.R., Ritchie, K.P., Kolios, M.C., Rodahl, A.M., Heinz, K.A., and Kruuv, J. 1992. Influence of transition rates and scan rate on kinetic simulations of differential scanning calorimetry profiles of reversible and irreversible protein denaturation. Biochemistry 31 12706–12712. [DOI] [PubMed] [Google Scholar]
- Lumry, R. and Eyring, H. 1954. Conformation changes of proteins. J. Phys. Chem. 58 110–120. [Google Scholar]
- Lyubarev, A.E. and Kurganov, B.I. 2000. Analysis of DSC data relating to proteins undergoing irreversible thermal denaturation. J. Therm. Anal. Cal. 62 51–62. [Google Scholar]
- Mine, Y. 1995. Recent advances in the understanding of egg white protein functionality. Trends Food Sci. Technol. 6 225–232. [Google Scholar]
- Privalov, P.L. 1979. Stability of proteins. Small globular proteins. Adv. Protein Chem. 33 167–241. [DOI] [PubMed] [Google Scholar]
- ———. 1982. Stability of proteins. Proteins which do not present a single cooperative system. Adv. Protein Chem. 35 1–104. [PubMed] [Google Scholar]
- ———. 1989. Thermodynamic problems of protein structure. Annu. Rev. Biophys. Biophys. Chem. 18 47–69. [DOI] [PubMed] [Google Scholar]
- Roefs, S.P.F.M. and De Kruif, K.G. 1994. A model for the denaturation and aggregation of β-lactoglobulin. Eur. J. Biochem. 226 883–889. [DOI] [PubMed] [Google Scholar]
- Sanchez-Ruiz, J.M., Lopez-Lacomba, J.L., Cortijo, M., and Mateo, P.L. 1988. Differential scanning calorimetry of the irreversible thermal denaturation of thermolysin. Biochemistry 27 1648–1652. [DOI] [PubMed] [Google Scholar]
- Smith, M.B. and Back, J.F. 1962. Modification of ovalbumin in stored eggs detected by heat denaturation. Nature 193 878–879. [DOI] [PubMed] [Google Scholar]
- Stein, P.E., Leslie, A.G.W., Finch, J.T., and Carrell, R.W. 1991. Crystal structure of uncleaved ovalbumin at 1.95 Å resolution. J. Mol. Biol. 1991 941–959. [DOI] [PubMed] [Google Scholar]
- Thirumalai, D., Klimov, D.K., and Dima, R.I. 2003. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr. Opin. Struct. Biol. 2003 146–159. [DOI] [PubMed] [Google Scholar]
- Vachier, M.C., Piot M., and Awedé, A.C. 1995. Isolation of hen egg white lysozym, ovotransferrin and ovalbumin, using a quaternary ammonium bound a highly crosslinked agarose matrix. J. Chromatogr. B 66 201–210. [DOI] [PubMed] [Google Scholar]
- Van der Linden, E. and Sagis, L.M.C. 2001. Isotropic force percolation in protein gels. Langmuir 17 5821–5824. [Google Scholar]
- Weijers, M., Sagis, L.M.C., Veerman, C., Sperber, B., and Linden, E.v.d. 2002a. Rheology and structure of ovalbumin gels at low pH and low ionic strength. Food Hydrocolloids 16 269–276. [Google Scholar]
- Weijers, M., Visschers, R.W., and Nicolai, T. 2002b. Light scattering study of heat-induced aggregation and gelation of ovalbumin. Macromolecules 35 4753–4762. [Google Scholar]
- Zemser, M., Friedman, M., Katzhendler, J., Greene, L.L., Minsky, A., and Gorinstein, S. 1994. Relationship between functional properties and structure of ovalbumin. J. Protein Chem. 13 261–274. [DOI] [PubMed] [Google Scholar]