Abstract
Methods for the analysis of brain morphology, including voxel-based morphology and surface-based morphometries, have been used to detect associations between brain structure and covariates of interest, such as diagnosis, severity of disease, age, IQ, and genotype. The statistical analysis of morphometric measures usually involves two statistical procedures: 1) invoking a statistical model at each voxel (or point) on the surface of the brain or brain subregion, followed by mapping test statistics (e.g., t test) or their associated p values at each of those voxels; 2) correction for the multiple statistical tests conducted across all voxels on the surface of the brain region under investigation. We propose the use of new statistical methods for each of these procedures. We first use a heteroscedastic linear model to test the associations between the morphological measures at each voxel on the surface of the specified subregion (e.g., cortical or subcortical surfaces) and the covariates of interest. Moreover, we develop a robust test procedure that is based on a resampling method, called wild bootstrapping. This procedure assesses the statistical significance of the associations between a measure of given brain structure and the covariates of interest. The value of this robust test procedure lies in its computationally simplicity and in its applicability to a wide range of imaging data, including data from both anatomical and functional magnetic resonance imaging (fMRI). Simulation studies demonstrate that this robust test procedure can accurately control the family-wise error rate. We demonstrate the application of this robust test procedure to the detection of statistically significant differences in the morphology of the hippocampus over time across gender groups in a large sample of healthy subjects.
Index Terms: Heteroscedastic linear model, hippocampus, multiple hypothesis test, permutation test, robust test procedure
I. Introduction
Various methods for modeling the morphology of the brain, including voxel-based, surface-based, and tensor-based morphometries, provide invaluable tools for understanding neuroanatomical differences in brain structure across subjects [1]-[7]. Statistical analysis of these morphometric measures can subsequently be used to understand normal brain development, the neural bases of neuropsychiatric disorders, and how environmental and genetic factors interact to determine brain structure and function. For instance, a joint analysis of brain morphometry and genotype may reveal brain regions with strong heritability in healthy subjects [8], [9]. Moreover, some measures of brain structure may be used as an endophenotypic marker for a disease if statistical analyses show that they are associated with behavioral, cognitive, or clinical outcomes [6], [10]-[14]. Studies of brain morphology have been conducted widely to characterize differences in brain structure across differing populations, such as patients with schizophrenia and healthy subjects [7], [15]-[19].
The statistical analysis of morphometric measures usually involves two procedures executed in sequence. The first procedure entails fitting a general linear model (LM) to the morphometric data from all subjects at each voxel and generating a statistical parametric map that contains a statistic (or a p value) at each voxel [20]. The second procedure entails using various statistical methods (e.g., random field theory, false discovery rate, permutation method) to calculate adjusted p values that account for the multiple statistical tests that are conducted across the many voxels of the brain region [21], [22]. All these statistical methods are implemented in existing neuroimaging software platforms, such as SPM, FSL, and SnPM.
The existing methods for these two procedures, however, have at least three limitations. First, the general linear model used in the neuroimaging literature usually involves two key assumptions: that the variance of the imaging data are homogeneous across subjects and that the data conform to a Gaussian distribution at each voxel. These two assumptions are critically important for the valid calculation of parametric distributions (e.g., t, F, and T) in conventional tests (e.g., t test) that assess the statistical significance of parameter estimates in the general linear model [3], [23]. Diagnostic procedures have been proposed to test these assumptions of the general linear model [24], [25], yet few statistical methods have been developed to analyze imaging data when these two assumptions are not satisfied. Second, the methods of random field theory that account for multiple statistical comparisons depend strongly on these assumptions of the general linear model, as well as several additional assumptions (e.g., smoothness of autocorrelation function) [21]. Third, permutation methods require the so-called “complete exchangeability” [26]-[28]. Complete exchangeability, however, is in fact a very strong assumption. For instance, consider two diagnostic groups (healthy controls and a disease group) and suppose that the null hypothesis is that the morphometric measures in all voxels from the two groups have the same mean. A permutation null distribution actually enforces equal distributions in the two groups in all voxels, which is a much stronger assumption than that of equal means across groups [26], [28].
The aim of this paper is to use new statistical methods to address these three limitations of extant methods for morphometric analyses. Specifically, we propose to apply two statistical techniques to the analysis of brain morphology: a heteroscedastic linear model, which avoids the two key assumptions of the general linear model, and a robust test procedure to correct for multiple statistical tests.
First, we use a heteroscedastic linear model together with a Wald-type statistical test to test linear hypotheses of brain morphology. The heteroscedastic linear model does not assume the presence of homogeneous variance across subjects, and it allows for a large class of distributions in the imaging data. These extensions are desirable for the analysis of real-world imaging data (e.g., anatomical and functional magnetic resonance imaging (fMRI) data, positron emission tomography measures), because between-subject and between-voxel variability in the imaging measures can be substantial [29]-[31]. Moreover, the distribution of the imaging data often deviates from the Gaussian distribution (see example in Sections III and IV) [2], [6], [23]. Under the heteroscedastic linear model, we calculate the ordinary least squares (OLS) estimator (denoted by β̂) to estimate the associations (denoted by β) between the measures of a brain region and the covariates of interest. We then use a Wald-type test statistic based on a consistent estimator of the covariance matrix (CECM) for β̂ under the null hypothesis [32], [33]. Although the Wald-type test statistic does not have a simple parametric distribution, we can use a wild bootstrap method to improve the finite performance of the Wald-type test statistic. The wild bootstrap method has been shown to have good theoretical properties and excellent performance in practice [34], [35].
To test multiple hypotheses across all voxels of a brain region, we propose a robust test procedure to control the family-wise error rate. Specially, we perform the Wald-type test statistic using the wild bootstrap method simultaneously at all voxels of the brain region, while preserving the dependence structure among the test statistics. In addition, the wild bootstrap method does not involve repeated analyses of simulated datasets and therefore is not computationally intensive. Specifically, the wild bootstrap method requires neither complete exchangeability nor a Gaussian distribution for the imaging data. The robust test procedure is, thus, widely applicable to other imaging modalities, including fMRI and positron emission tomography (PET) data.
II. Methods
Here, we formally introduce the heteroscedastic linear model and use a Wald-type test statistic for testing linear hypotheses of β. We then present a robust test procedure based on the wild bootstrap as a method for correcting p values for multiple statistical comparisons.
A. Heteroscedastic Linear Model and a Wald-Type Test Statistic
In a particular voxel d on the brain structure, we consider the following heteroscedastic linear model:
| (1) |
for t = 1, … , n, where t represents the tth subject, yt represents a measure of brain morphology (e.g., signed Euclidean distance, grey matter density), Xt is an exogenous k × 1 vector (e.g., age, gender, and genotype), β is a k × 1 vector of unknown parameters, and εt is a random error term. Let Y = (y1, … , yn)T, X = (X1, … , Xn)T, ε = (ε1, … , εn)T, and , where the superscript T represents transpose. Then, (1) can be rewritten as
| (2) |
Here, without loss of generality, we assume that X is a column full rank matrix, i.e. rank(X) = k. The ordinary least squares estimate of parameter β, given by β̂ = (XT X)−1 XT Y, has been implemented in SPM1 and widely used in many neuroimaging studies, because of its computational simplicity. In contrast, if Ω were known, we could use the generalized least squares estimate of β, which is more efficient than β̂ [36]. However, except for a few special cases (e.g., fMRI), we rarely have prior information to consistently estimate Ω [32], [34].
Let In be an n × n identity matrix, PX = X(XT X)−1 XT, and for t = 1, … , n. The covariance matrix of β̂ is given by
while a consistent estimator of the covariance matrix (CECM) of β̂ in model (2) has the following form:
| (3) |
where , at = 1/(1−ht), and ε̂t is the tth component of ε̂ = Y − Xβ̂ = (In − PX)Y [34]. It should be noted that Ω̂ is not a consistent estimate of Ω, whereas because n−1XT(Ω̂−Ω)X converges to zero, is a CECM [32].
Ignoring heteroscedasticity in model (1) leads to using σ̂2(XT X)−1 as an estimate of the covariance matrix for the OLS estimator β̂, where σ̂2 = YT(I − PX)Y/(n − k). However, failure to account for interindividual variance can lead to the following consequences: 1) σ̂2(XT X)−1 may be inconsistent; 2) conventional statistics for testing linear hypotheses of β do not follow t and F distributions; 3) invalid inferences based on σ̂2(XT X)−1 lead to large Type I and/or Type II error rates for testing linear hypotheses of β [32], [34], [37].
We consider testing the linear hypotheses
| (4) |
where R is an r × k matrix of full row rank and b0 is an r × 1 specified vector. We test the null hypothesis H0 : Rβ = b0 using a Wald-type test statistic
| (5) |
where ΣΩ̃ is a consistent estimate of the covariance matrix of Rβ̂ − b0 under H0. Explicitly, ΣΩ̃ is given by
| (6) |
where and ε̃t is the tth component of ε̃ as given in (8). Various simulation studies have shown that the use of ε̃ leads to a better control of Type I error rates [34], [38].
Under H0, a restricted least squares (RLS) estimate of β, denoted by β̃, is given by (Appendix I)
| (7) |
and a restricted residual vector ε̃ = Y − Xβ̃ is calculated to be
| (8) |
Because Wn is asymptotically distributed as χ2(r), a chi-square distribution with r degrees-of-freedom, under the null hypothesis H0, an asymptotically valid test can be obtained by comparing sample values of test statistic with the critical value of the right-hand tail of χ2(r) distribution at a prespecified significance level α [32]. That is, we reject H0 if , and do not reject H0 otherwise, where is the upper α-percentile of the χ2(r) distribution. However, for small n, numerical results have shown that Wn may yield misleading results (large Type I and/or Type II error rates) [34], [35], [37], [39].
B. Wild Bootstrap
We present a wild bootstrap method to improve the finite performance of Wn in testing the null hypothesis H0. This wild bootstrap method has been extensively studied in the literature [34], [35]. To use wild bootstrapping to test H0 : Rβ = b0 we generates bootstrap samples that conform to the null hypothesis. Thus, we estimate the unknown parameters of β under the constraint Rβ = b0, which is exactly the RLS estimator of β, β̃. Then, a p value can be calculated based on the generated bootstrap samples.
To produce a bootstrap sample , we use the following data-generating process (DGP):
| (9) |
where β̃ and ε̃ are, respectively, defined in (7) and (8), and are independently and identically distributed as a distribution F. Following Flachaire [34], F is chosen as
| (10) |
Thus, a bootstrap sample can be obtained using the data-generating process (9). Let , and . Equation (9) can be rewritten as
| (11) |
We now calculate the Wald-type test statistic for the bootstrap sample. It follows from (11) that the ordinary and restricted least squares estimates of β are, respectively, given by
| (12) |
Thus, the ordinary residual vector of model (11) is given by
Furthermore, the restricted residual vector of model (11), denoted by ε̃*, is given by
| (13) |
where RX = X(XT X)−1 RT. Let , where is the tth element of ε̃*. Since Rβ̂* − b0 = R(XT X)−1 XT Ω̃1/2 ε*, the Wald-type test statistic based on the bootstrap sample is given by
| (14) |
where ΣΩ̃* = R(XT X)−1 XT Ω̃* X(XT X)−1 RT.
We can approximate the p value of Wn as follows:
Step 1) Independently generate S bootstrap samples for s = 1, … , S using the bootstrap DGP (11).
Step 2) Calculate for each bootstrap sample.
-
Step 3) Approximate the p value of Wn by
where I (·) is an indicator function.
We may consider other bootstrap methods, such as the pairs bootstrap, and other distributions F, such as the two-point distribution of Mammen [34], [40], [41]. For instance, we may use the pairs bootstrap method, but bootstrap samples generated by the pairs bootstrap method may not come from model (2) conforming to the null hypothesis Rβ = b0. Thus, some appropriate modifications of the pair bootstrap are needed and these modifications lead to the use of the wild boostrap [34]. In addition, the use of the pair bootstrap can lead to a loss of power [34]. Various simulation studies have clearly shown that the wild bootstrap outperforms the pairs bootstrap in the literature [34], [42], [43]. The noise distribution (10) is justified by theoretical underpinnings and numerical simulations [34], [35].
The above heteroscedastic linear model and the wild bootstrap method can be used to analyze {(yt, Xt) : t = 1, … , n} in each voxel d of the brain region. Henceforth, we use d in our notation if necessary, such as .
C. Robust Test Procedure
To test whether H0 : Rβ = b0 holds in all voxels of the brain region under investigation, we consider a maximum statistic, the maximum of the Wald-type test statistics, as
| (15) |
The maximum statistic WD plays a crucial role in controlling the family-wise error rate. In order to use WD as a test statistic, we need to approximate the distribution of WD under the null hypotheses in all voxels of the brain structure. We may apply random field theory for χ2 processes to approximate the upper tail of WD, because Wn(d) converges to a χ2(r) distribution under certain conditions as the number of subject n is sufficiently large [44]-[46]. However, the random field theory for χ2 processes may be conservative because the asymptotic test of Wn(d) leads to large Type I (and/or Type II) error rates in a single voxel d[37].
We propose a robust test procedure based on the wild bootstrap method to approximate the distribution of WD. This procedure is implemented as follows.
Step 1) In each voxel d of the brain structure, calculate the Wald-type test statistic Wn(d) given in (5) based on the observed data {(yt(d), Xt) : t = 1, … , n}. Compute WD = maxd Wn(d).
Step 2) Generate a random sample from the distribution F. In all voxels d, generate observations from model (11) using the same sample .
Step 3) Calculate the Wald-type test statistic based on the bootstrap sample and .
-
Step 4) Repeated Steps 2–3 S times and calculate . Finally, the p value is approximated by
(16) We reject that the null hypothesis H0 : Rβ = b0 is true in all voxels of the brain structure if pD is smaller than a prespecified value α.
-
Step 5) Calculate adjusted p value in each voxel d according to
(17)
We note here at least four important advantages of this test procedure compared with existing procedures:
-
i)
the wild bootstrap method performs well at each point d even for relatively small n (e.g., n ≤ 40);
-
ii)
the above test procedure asymptotically preserves the dependence structure among the Wn(d);
-
iii)
the above test procedure is not computationally intensive, because it does not involve the repeated analysis of simulated datasets;
-
iv)
the above test procedure does not require complete exchangeability.
We can show that the robust test procedure asymptotically preserves the dependence structure among the Wn(d). According to in (14), the correlation between and is primarily determined by the correlation between and . We can show that
holds for any two points d and d′. Similarly, the correlation between Wn(d) and Wn(d′) is primarily determined by the correlation between and , which is given by
Thus, under some conditions [32]
converges to zero in probability, and thus we have proved the advantage (ii).
III. Simulation Studies and Real-World Studies
We conducted two sets of Monte Carlo simulations. The first examined the finite performance of the wild bootstrap method for Wn at the single-voxel level. In particular, we compared its performance to the F test, the asymptotic test for Wn, and the permutation method based on the t test statistic. The second set of Monte Carlo simulations was to evaluate the family-wise error rate and power of the robust test procedure at the level of the whole surface (or brain). Then, we compared its performance to the permutation method based on the t test statistic and random field theory for F and χ2 fields.
A. Monte Carlo Simulations: Set I
1) Design
For the first set of Monte Carlo simulations, we simulated data from the heteroscedastic linear model
| (18) |
for t = 1, … , n, where ∈t is a random error with zero mean, β is a k × 1 vector of unknown parameters, and Xt is a k × 1 vector of covariates of interest. Because of prior extensive simulations reported in the literature [34], [35], [37], [39], we chose a simple Xt as follows: Xt = (1, 0)T for t = 1, … , [n/2] and Xt = (1,1)T for t = [n/2] + 1, … , n, where [n/2], denotes the largest integer smaller than n/2. We set n = 10, 20, and 40.
2) Random Errors
We considered the effects of three differing distributions of ∈t to examine the effects of these distributions on the finite performance of the four test statistics at the single-voxel level, including the wild bootstrap method for Wn, the F test, the asymptotic test for Wn, and the permutation method based on the t test statistic, at the single-voxel level. First, ∈t is a Gaussian error from N(0,1), where N(μ, σ2) denotes a Gaussian distribution having a mean μ and standard deviation σ. The Gaussian errors with unit variance were generated to meet the assumptions of the general linear model. Second, we assumed ∈t = χ2(2) − 2, in which χ2(2) represents a chi-squared random variable with 2 degrees-of-freedom. The skewed distribution χ2(2) − 2 differs substantially from any Gaussian distribution. Third, we assumed that ∈t = σtz and z were independently generated from a N(0,1) distribution. Moreover, σ(t) = exp(u) when Xt,2 = 0 and σ(t) = exp(u + 1) when Xt,2 = 1, where u were independently generated from a N(0,1) distribution. Conditional on u, the variances of ∈t were highly heterogeneous.
3) Hypothesis
We assumed β = (β0, β1)T = (1, 0)T and set the null hypothesis H0 : β1 = 0 to assess the Type I error rates for the four test statistics. Furthermore, we assumed β = (β0, β1)T = (1, 2)T and test the hypothesis H0 : β1 = 0 against H1 : β1 ≠ 0. Then, we examined the Type II errors for the four test statistics (e.g., F test). In both cases, R = (0,1) and b0 = (0).
For each simulation, the significance level was set at α = 5%, and 20 000 replications were used to estimate the rejection rates. For a fixed α, if the Type I rejection rate is smaller than α, then the test is conservative, whereas if the Type I rejection rate is greater than α, then the test is anticonservative, or liberal [57].
B. Monte Carlo Simulations: Set II
1) Basic Design
We used a heteroscedastic linear model to generate data in all m = 2064 points on the surface of a reference sphere for all n subjects (or objects) (Fig. 1). For the tth subject, Y(t) denotes an m × 1 vector that contains all morphometric measures (e.g., signed Euclidean distance, grey matter density) in all m points, B denotes an m × k matrix of unknown parameters, and x(t) is a k × 1 vector of covariates of interest. The heteroscedastic linear model can be written as
Fig. 1.
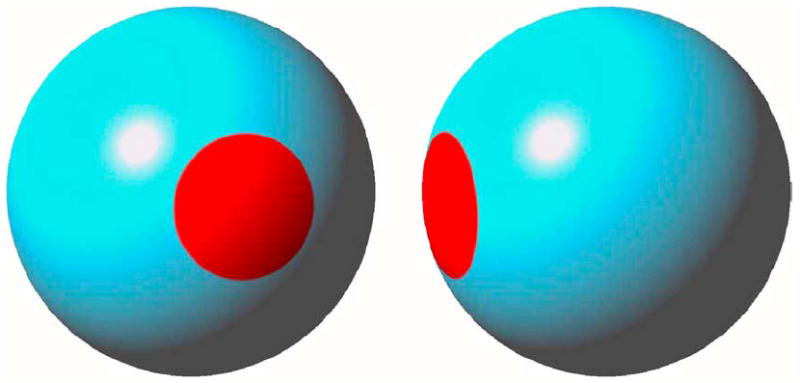
Simulation study ROI. ROI is highlighted in red on the surface of a reference sphere: (a) anterior and (b) right lateral views.
| (19) |
for t = 1, … , n, where e(t) is an m × 1 vector of independent Gaussian errors with zero mean and unit variance and C is an m × m correlation matrix. In addition, x(t), C, and σ2(t) are specified below.
2) Covariates of Interest
Our choice of statistical covariates was motivated by two scientific aims. The first was to compare brain structure across diagnostic groups (e.g., healthy controls (HC) and persons with schizophrenia) [8], [50]. To compare the performance of our robust test procedure with that of the permutation test, we choose a simple x(t) given by
| (20) |
where HC denotes the healthy control group. Moreover, the first [n/2] subjects were assumed to be healthy controls, and the rest were assumed to be patients.
The second scientific aim was to understand differences in brain structure across genders in the sample of healthy controls [19]. We choose x(t) as
| (21) |
where Gender equals 0 for males and 1 for females. We assumed that the first [n/2] subjects were males, and the rest were females. The Age variable was uniformly generated from the interval [1, n].
3) Variance Structure
We considered two types of variance structures: a homogeneous case and a heterogeneous case. For the homogeneous case, we assumed that σ(t) ≡ 1 for all t = 1, … , n. However, for the heterogeneous case, we assumed that we observed larger variability from the male group as compared with the female group. Thus, for the covariates of interest in (20) and (21), we set σ(t) = exp(z) and generate z from a N(0,1) distribution for each man, and from a N(1,1) distribution for woman.
4) Correlation Structure
We considered a stationary and exponential correlation matrix C, in which the correlation between any two points d and d′ on the surface was given by ρ‖d–d′‖, where ρ ∈ [0, 1] and ‖d–d′‖ represents Euclidean distance between d and d′ [51]. We denote such an exponential correlation matrix by C(ρ). We simulated images based on C(ρ) using, ρ = 0, 0.25, 0.5, and 0.75 in order to mimic the differing degrees of smoothness in the simulated images [52].
5) Hypotheses
For x(t) in (20), we first assumed β = (β0, β1)T = (1, 0)T in all points on the reference sphere to assess the family-wise error rate. In addition, to assess both the power and family-wise error rate, we selected a region-of-interest(ROI) with 64 points on the reference sphere and set β1 = 5 for any point d in ROI [Fig. 1(a) and (b)]. In this case, k, the dimension of β, was 2. We were interested in testing the null hypothesis H0 : β1 = 0 at all points on the surface of the reference sphere. In this case, R = (0, 1) and b0 = (0).
For x(t) in (21), we first assumed β = (β0, β1, β2)T = (1, 0, 0)T in all points on the surface of the reference sphere to assess the family-wise error rate. Furthermore, we used the same ROI on the reference sphere and set β2 = 5 for any point d in ROI [Fig. 1(a) and (b)]. In this case, the dimension of β was 3. We were interested in testing whether any differences of morphology changes existed across gender groups, that is, H0 : β3 = 0. In this case, R = (0, 0, 1) and b0 = (0).
6) Type I Error Rate and Average Power
For each simulation study, we calculated the family-wise error rate (FWER = P(V ≥ 1) for the Type I error rates [26], [55]. The significance level was set at α = 5%, and 1000 replications were used to estimate the FWER. For a fixed α, if the FWER is smaller than α, then the test is conservative, whereas if the FWER is greater than α, then the test is anticonservative, or liberal [57]. We also calculated an average power, that is, the average of the probabilities of rejecting each of the 64 vertices in ROI.
7) Test Procedures
We evaluated the family-wise error rate of the four test procedures as follows. First, we considered the robust test procedure based on the maximum statistic WD (Section II-C), in which S = 699 boostrap samples were generated to calculate the adjusted p value. Second, we also used the Wald-type test statistics Wn(d) and WD, but we calculated the p value of WD and the corrected p values of Wn(d) using the theoretical results of χ2(1) field [21], [22], [56]. Third, we calculated the F statistic for the general linear model at each voxel and the maximum of the F statistics across those voxels. Then, we approximated the adjusted p values of all F statistics using the results of the F field [22], [56]. Finally, we only applied the permutation test based on the maximum of absolute values of the t statistics with 699 permutations to model (19) with x(t) given in (20), because the permutation method based on the t statistic may not be applicable when x(t) given in (21) has multiple covariates.
8) Random Field Theory
We applied the results for the χ2 and F fields to the calculation of the corrected p value of the local maxima of the F statistics (or Wn(d)) and the adjusted p value in each point of the reference sphere. Explicitly, for the second test procedure, the corrected p value of WD in a 2-D search region D is well approximated by
| (22) |
where Reselsc and ECc, respectively, represent the resels of the search region and the Euler characteristic density of the χ2(1) field in c dimension. Equation (22) can be used to calculated the adjusted p value for large Wn(d) in each vertex of the reference sphere. For the triangular mesh on the reference sphere (2-D), we have Resels0 = 2, Resels1 = 0, and
| (23) |
Moreover, let u0, u1, and u2 be three n × 1 vectors of the normalized residuals at each vertex of a triangular of the reference sphere, we define Δu = (u1 − u0, u2 − u0) [56]. Expressions of the Euler characteristic densities for the χ2 field and d ≤ 2 can be found in [22]. Similarly, we used (23) to calculate the resels of the search region D and then applied the expected Euler characteristic for the F field to calculate the corrected p value of the local maxima of the F statistics [22], [56].
C. Real-World Example
The robust test procedure was used to model morphological changes in the hippocampus over time across gender groups.
1) Subjects
All 123 healthy subjects were recruited from a telemarketing list of families in southern Connecticut. The ages of all subjects range from 7 to 62 years (mean 20.14, SD: 13.2 years). The sample was similarly distributed across gender (males: 67; female: 56). Subjects were predominantly right handed (93.5%).
2) Image Acquisition Protocol
Head positioning in the head coil of the magnetic resonance imaging (MRI) scanner was standardized using cantho-meatal landmarks. We acquired high-resolution T1-weighted MRIs on a single 1.5-T scanner (GE Signa; General Electric, Milwaukee, WI) using a sagittal 3-D volume spoiled gradient echo sequence. Parameters included repetition time = 24 msec, echo time = 5 msec, 45° flip angle, frequency encoding superior/inferior, no wrap, 256 × 192 matrix, FOV = 30 cm, 2 excitations, slice thickness = 1.2 mm, and 124 contiguous slices encoded for sagittal slice reconstruction, voxel dimensions 1.17 × 1.17 × 1.2 mm3.
3) Selection of the Reference Structure
We first selected a preliminary brain of one subject (a 32.5 year-old right-handed, Caucasian male). Then, we registered the brains of other subjects in this study to this preliminary reference brain. We determined the point correspondences across their surfaces according to the methods described below and calculated the distances of those points from the corresponding points on the preliminary reference. Finally, we selected the brain for which all points across its surface were closest (in the least squares sense) to the average of the distances across those points for the entire sample as the final reference.
4) Morphological Descriptions of the Surface of the Hippocampus Surface
A four-step procedure described below was developed to obtain the morphological descriptions of the hippocampus surface. First, we registered the brains of all subjects to the cerebrum of the selected reference subject by using a rigid-body similarity transformation. The method of mutual information [58] was employed to calculate seven parameters (three translations, three rotations, and a global scale). Second, we rigidly coregistered to one another the hippocampus within the coregistered brains using a rigid-body transformation. Third, we identified correspondences between the points on the surfaces of the hippocampus by deforming these structures into the hippocampus of the reference brain using an algorithm based on fluid dynamics [59], [60]. Fourth, we calculated signed Euclidean distances of each point in the hippocampus of each subject from the corresponding point in the reference hippocampus. Distances of the points on the undeformed surface of the hippocampus of each subject that were positioned inside the boundary of the reference structure were labeled as negative, whereas distances for points positioned outside of the reference structure were labeled as positive.
5) Heteroscedastic Linear Model
To control the effects of covariates (age and gender) on our models of surface morphology, we considered a heteroscedastic linear model in each point on the reference surface
| (24) |
where xt and gt denote the log(age) and gender of the tth subject, respectively, and yt(d) is the signed Euclidean distance for the tth subject in the dth point. In model (24), we do not include an adjustment term for overall intracranial volume, because the effects of brain size already have been taken into account by first coregistering the cerebrums of different subjects to the cerebrum of a reference subject (see Section III-C-4).
We are primarily interested in testing the morphological changes of the hippocampus over time across gender groups, i.e., we are testing the null hypotheses H0 : β4 = β5 = 0 at all points on the surface of the hippocampus. Thus, we have
6) Smoothing the Surface of Hippocampus
We smoothed the signed Euclidean distance measures of all 123 subjects using the heat kernel smoothing with parameters σ = 1 and 16 iterations, which gave an effective smoothness of about 4 mm [53].
IV. Results
A. Simulation Studies: Set I
1) Type I Error Rates
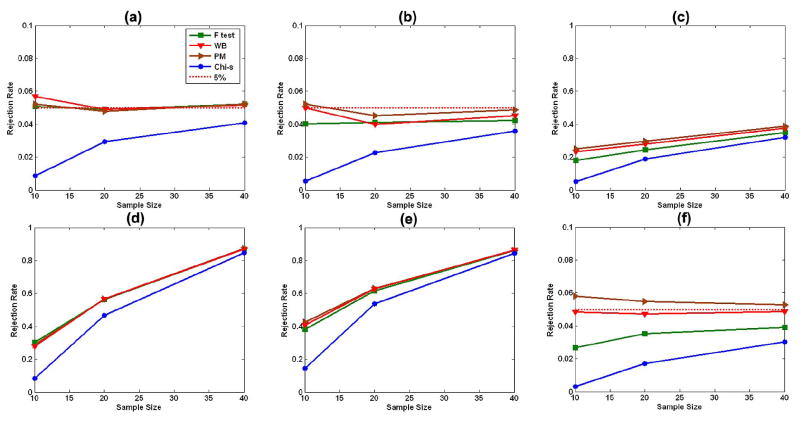
Overall, the rejection rates for the permutation test and wild bootstrap method were accurate for all sample sizes (n = 10, 20, or 40) and for the three differing distributions of error terms [Fig. 2(a)–(c)]. In particular, the wild bootstrap performed well even when the data were Gaussian distributed with heterogeneous variances, because Wn in the wild bootstrap accounted for inhomogeneity of variance across subjects. Although the F test was accurate in the presence of Gaussian N(0, 1) errors Fig. 2(a), Type I error rates associated with application of the F test declined for error terms that followed either the skewed distribution χ2(2) − 2 Fig. 2(b) or the Gaussian distribution with heterogeneous variances Fig. 2(c). This decline in Type I error was caused by applying the upper percentile of the F distribution to the F test, whereas when not assuming that the data were Gaussian distributed with homogeneous variance, the distribution of the F test was not in fact F distributed. Moreover, in all cases, the asymptotic χ2 test for Wn was highly conservative because it was applied in the context of a small sample size.
Fig. 2.
Simulation study: Type I and Type II error rates. Rejection rates of the wild bootstrap method (WB), the permutation method (PM), the F test, and the χ2 test for Wn are calculated for sample sizes of 10, 20, 40 subjects and for differing error distributions at the 5% significance level. (a)–(c) The estimated Type I error rates under the null hypothesis. (d)–(f) The estimated Type II error rates under the alternative hypothesis. Three distributions of error terms are Gaussian N(0, 1) [(a) and (d)], χ2(2) – 2 [(b) and (e)], and Gaussian with heterogeneous variances [(c) and (f)].
2) Type II Error Rates
We observed that Type II error rates for the F test, the permutation test, and the wild bootstrap method were similar under N(0, 1) errors and for all sample sizes [Fig. 2(d)–(f)]. Compared with the rates of Type II error during application of the permutation test and the wild bootstrap method, however, the power of the F test to reject the null hypothesis declined modestly when the distributions of errors either were skewed Fig. 2(e) or were Gaussian with heterogeneous variance Fig. 2(f); this increase in Type II error when noise was not Gaussian distributed reflected the consequence of applying the F test when the F test was not F distributed. Under all sample sizes and distributions of errors, the asymptotic test for Wn produced the highest rates of Type II error, because the upper 95th percentile of the χ2-distribution was much higher than the upper 95th percentile of the sample distribution of Wn when the sample size was small. Consistent with our expectations, the statistical power for rejecting the null hypothesis increased with the sample size n.
B. Simulation Studies: Set II
1) Family-Wise Error Rates
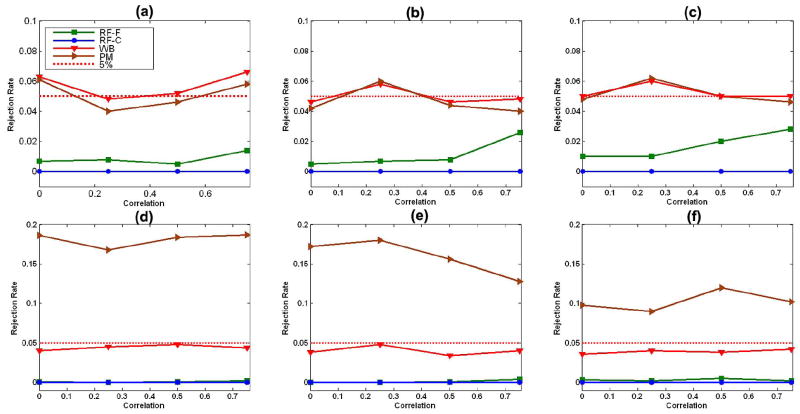
In the presence of random errors with homogeneous variance, the permutation test based on the t statistic performed very well for all sample sizes [Fig. 3(a)–(c)]. In the presence of random errors with heterogeneous variance, in contrast, the permutation test was excessively liberal under all sample sizes [Fig. 3(d)–(f)], though less so as n increased [Fig. 3(d)-(f)]. In the presence of random errors with heterogeneous variance, the distributions of data in the two groups differed substantially from one another, invalidating the assumption of complete exchangeability, and causing the inflation of family-wise error rates during application of the permutation test.
Fig. 3.
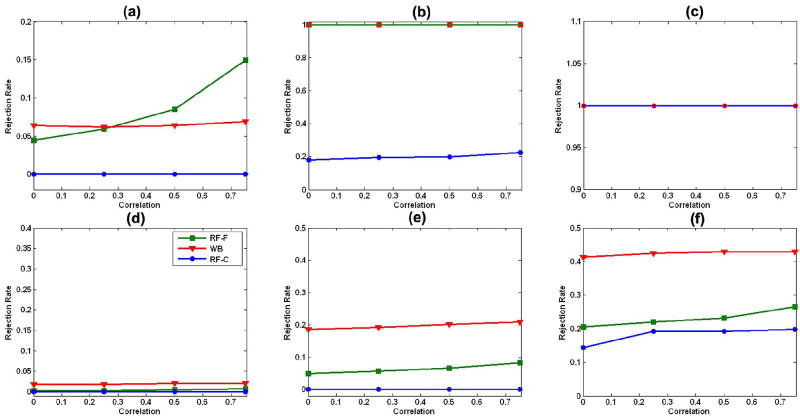
Family-wise error rates with two covariates: family-wise error rates of the robust test procedure (WB), the permutation method (PM), random field F tests (RF-F), and the χ2 field based on Wn(d) (RF-C) under the linear model (19) with two covariates (Covs) (20). We consider sample sizes of 10, 20, and 40 subjects, four differing correlations, ρ = 0, 0.25, 0.5, and 0.75, and two differing distributions, including homogeneous variance (HMV) and heterogeneous variance (HTV), at the 5% significance level. (a) n = 10, 2 Covs, and HMV; (b) n = 20, 2 Covs, and HMV; (c) n = 40, 2 Covs, and HMV; (d) n = 10, 2 Covs, and HTV; (e) n = 20, 2 Covs, and HTV; (f) n = 40, 2 Covs, and HTV.
For model (19) with two covariates, our robust test procedure worked well for relatively small sample sizes (n = 10, 20, and 40) and in the presence of random errors with either homogeneous or heterogeneous variance [Fig. 3(a)–(f)]. Under model (19) with three covariates, however, the family-wise error rates for our robust test procedure were not particularly accurate in the presence of random errors with either homogeneous or heterogeneous variance for the smallest sample size, n = 10 [Fig. 4(a) and (d)]; in contrast, they approximated the 5% significance level at the larger sample sizes of n = 20 and 40. Thus, sample size and the number of covariates can influence somewhat the finite performance of our robust test procedure.
Fig. 4.
Family-wise error rates with three covariates: family-wise error rates of the robust test procedure (WB), random field F test (RF-F), and the χ2 field for the Wald-type test statistics (RF-C) under the linear model (19) with three covariates (Covs) in (21). We consider sample sizes of 10, 20, and 40 subjects, four differing correlations ρ = 0, 0.25, 0.5, and 0.75, and two differing distributions, including homogeneous variance (HMV) and heterogeneous variance (HTV), at the 5% significance level. (a) n = 10, 3 Covs, and HMV; (b) n = 20, 3 Covs, and HMV; (c) n = 40, 3 Covs, and HMV; (d) n = 10, 3 Covs, and HTV; (e) n = 20, 3 Covs, and HTV; (f) n = 40, 3 Covs, and HTV.
The F field for the F statistic and the χ2 field for Wn were highly conservative for relatively small sample sizes (n = 10, 20, and 40), when including two or three covariates, and in the presence of random errors with either homogeneous or heterogeneous variance (Figs. 3 and 4). Differing distributions of random errors significantly influenced the family-wise error rates of the F field for the F statistic and the χ2 field for Wn. Larger correlations (or heavier smoothing) improved the performance of the F field for the F statistic when we compared its family-wise error rates with the 5% significance level. Overall, the F field for the F statistic yielded a highly conservative test, even with sample sizes as high as 40 and when the correlation of errors across two neighboring voxels on the reference sphere was as high as 0.75.
2) Average Power
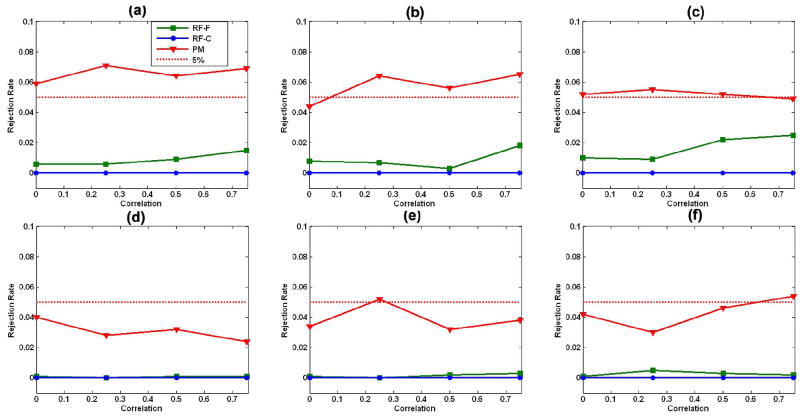
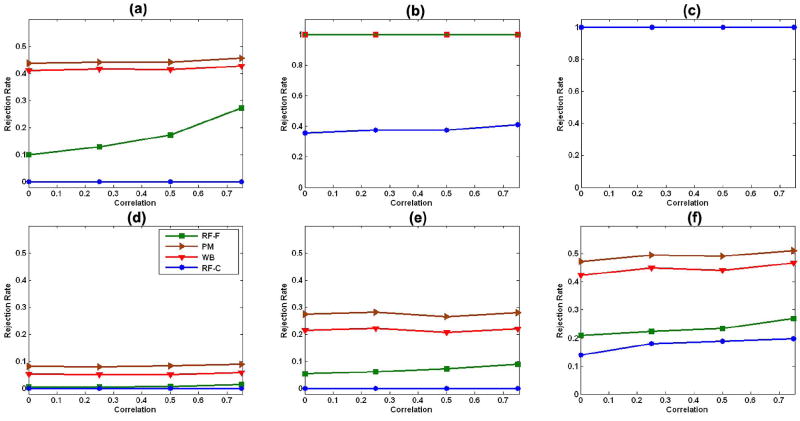
For model (19) with two covariates, compared with our robust test procedure, the permutation test based on the t statistic had slightly larger average power in detecting statistically significant vertices in an ROI [Fig. 5(a) and (d)–(f)], and both the permutation test and our test procedure had much larger average power than did the F field for the F statistic and the χ2 field for Wn [Fig. 5(a), (b), and (d)–(f)].
Fig. 5.
Statistical power with two covariates: average powers of the robust test procedure (WB), the permutation method (PM), the F field F test (RF-F), and the χ2 field for Wn(d) (RF-C) under the linear model (19) with two covariates (Covs) (20). We consider sample sizes of 10, 20, and 40 subjects, four differing correlations ρ = 0, 0.25, 0.5, and 0.75, and two differing distributions, including homogeneous variance (HMV) and heterogeneous variance (HTV), at the 5% significance level. In (b), the lines for PM, WB, and RF-F overlay one other, while in (c), all four lines overlay one other. (a) n = 10, 2 Covs, and HMV; (b) n = 20, 2 Covs, and HMV; (c) n = 40, 2 Covs, and HMV; (d) n = 10, 2 Covs, and HTV; (e) n = 20, 2 Covs, and HTV; (f) n = 40, 2 Covs, and HTV.
For model (19) with three covariates, the robust test procedure had larger average power than did the F field for the F statistic and the χ2 field for Wn under heterogeneous variances [Fig. 6(d)–(f)]. However, under homogeneous variance, large correlations (e.g., ρ ≥ 0.5), and n = 10, the F field for the F statistics was more sensitive than was the robust test procedure Fig. 6(a).
Fig. 6.
Statistical power with three covariates: average powers of the robust test procedure, the F field F test (RF-F), and the χ2 field for Wn(d) (RF-C) under the linear model (19) with three covariates (Covs) (21). We consider sample sizes of 10, 20, and 40 subjects, four different correlations ρ = 0, 0.25, 0.5, and 0.75, and two differing distributions, including homogeneous variance (HMV) and heterogeneous variance (HTV), at the 5% significance level. In (b), the lines for RF-F and WB overlay one other, while in (c), all lines overlay one other. (a) n = 10, 3 Covs, and HMV; (b) n = 20, 3 Covs, and HMV; (c) n = 40, 3 Covs, and HMV; (d) n = 10, 3 Covs, and HTV; (e) n = 20, 3 Covs, and HTV; (f) n = 40, 3 Covs, and HTV.
C. Real-World Example
1) Assessing Assumptions of the Model
We investigated whether the general linear model was appropriate for this study. We calculated test statistics for assessing the validity of the two assumptions of the general linear model: normality and homogeneous constant variance of the data. Based on the residuals after fitting the general linear model, we calculated the Shapiro–Wilk and Cook–Weisberg statistics to test the assumptions of a Gaussian distribution and the homogeneous variance for the error terms [61], [62]. These statistics rejected the assumptions of normality (Fig. 7) and homogeneous variance (not presented here) at many points on the surfaces of the both left and right hippocampus for both the original distance measures [Fig. 7(a)–(d)] as well as the smoothed distance measures [Fig. 7(e)–(h)]. The application of smoothing techniques, however, improved the normality of the random errors [Fig. 7(e)–(h)].
Fig. 7.
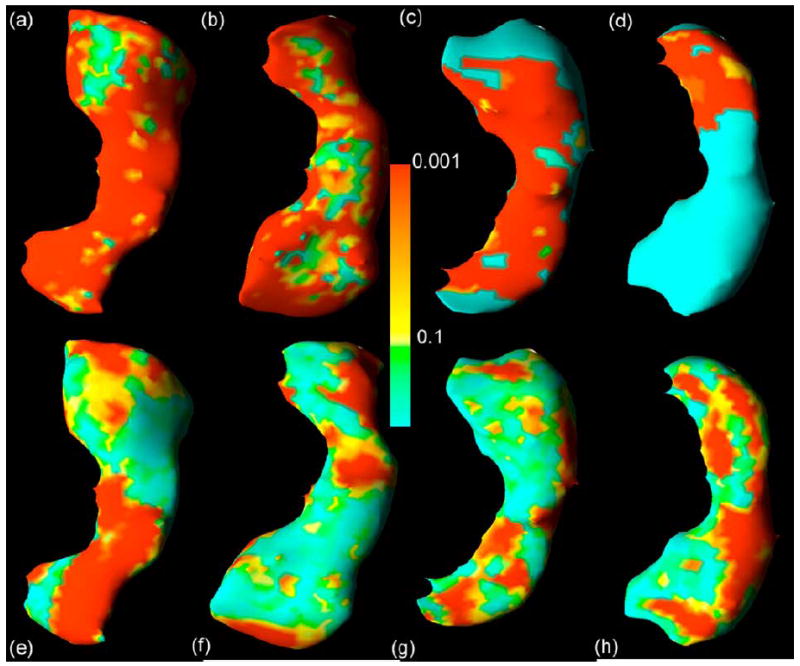
Assessing normality at the surface of the hippocampus. Color-coded maps display the uncorrected p values for the Shapiro–Wilk test of normality at the surface of the hippocampus in data from 123 healthy children and adults registered to a template surface. Top row shows the unsmoothed images. Bottom row shows the images after smoothing with a heat kernel. Panels (a and e) right hippocampus dorsal view, with the anterior portion of the hippocampus located at the top of the figure; (b and f) right hippocampus ventral view, with the anterior portion of the hippocampus located at the bottom of the figure; (c and g) left hippocampus dorsal view, with the anterior hippocampus located at the top; (d and h) left hippocampus ventral view, with the posterior hippocampus located at the bottom. Smoothing reduces substantially the number of voxels at the surface of the hippocampus that violate assumptions of the normality of distribution of signed Euclidean distances of points on the surface of the hippocampus of each subject in the dataset from corresponding points on the surface of the reference hippocampus.
Because the assumptions of the general linear model are invalid, the use of random field theory to analyze these imaging data is inappropriate, at least without prior spatial smoothing of the data [2], [6], [23]. Moreover, the permutation method based on the statistic cannot be applied directly to the model (24), which contains multiple covariates.
2) Analysis of Hippocampal Surface
We used the signed Euclidean distances to detect and localize statistically significant differences in the morphology of the hippocampus over time across gender groups. We tested these differences using gender-by-log(age) and gender-by-[log(age)]2 interactions in model (24) at each point of the surface of the hippocampus. The p-values based on the asymptotic χ2 test were color-coded in each point of the reference hippocampus [Fig. 8(a), (b), (f) and (g)]. To correct for multiple comparisons, we applied our robust test procedure to calculate the adjusted p value at each point on the surface of the reference hippocampus [Fig. 8(c), (d), (h), and (i)]. Color-coded maps of p value maps using either the uncorrected χ2 test alone or the corrected resampling method indicated large-scale differences in surface morphology across gender groups. The resampling method, however, captured far fewer points of differences in morphology of the hippocampus mainly in the head portion of the hippocampus (Fig. 8) [63].
Fig. 8.
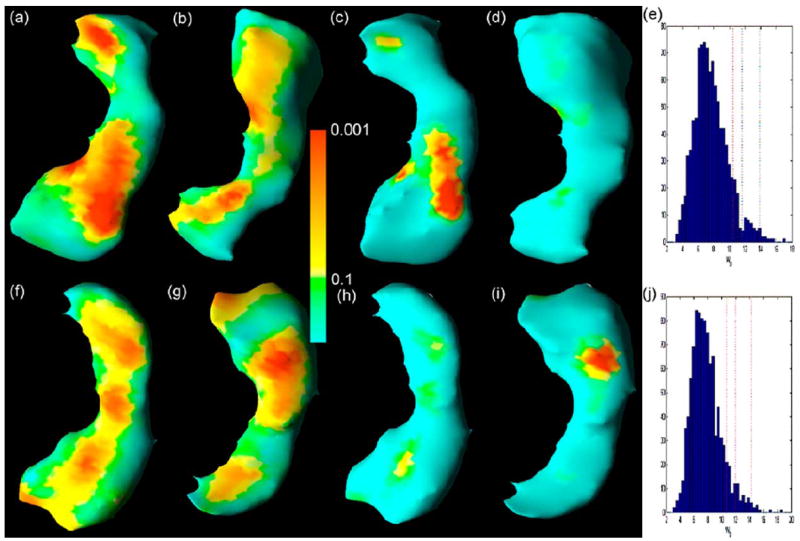
Significance testing at the surface of the hippocampus: color-coded maps of p values and adjusted p values for the Wald-type test statistics. Row 1: right hippocampus. Row 2: left hippocampus. Columns 1 and 2: raw p values of the Wald-type test statistics based on a χ2 distribution. Columns 3 and 4: adjusted p values of the Wald-type test statistics based on our robust test procedure for the correction of multiple comparisons. Panels (e and j): histograms of based on the bootstrap samples. Spatial orientations of the hippocampus are the same as the corresponding views in Fig. 7. After correction for multiple comparisons, statistically significant interactions of gender-by-log(age) and gender-by-[log(age)]2 remain in the head of both the right (c) and left (i) hippocampus.
We compared findings using the linear model and our heteroscedastic linear model for these data. When testing gender-by-log(age) and gender-by-[log(age)]2 interactions, we calculated the − log10(p) value of the F statistic and the − log10(p) value of Wn based on the wild bootstrap method at each point of the surface of the reference hippocampus. We observed that combining the heteroscedastic linear model with the wild bootstrap method increased the number of statistically significant points (− log10(p) > 1.3) on the surface of the hippocampus in each hemisphere [Fig. 9(a) and (b)].
Fig. 9.
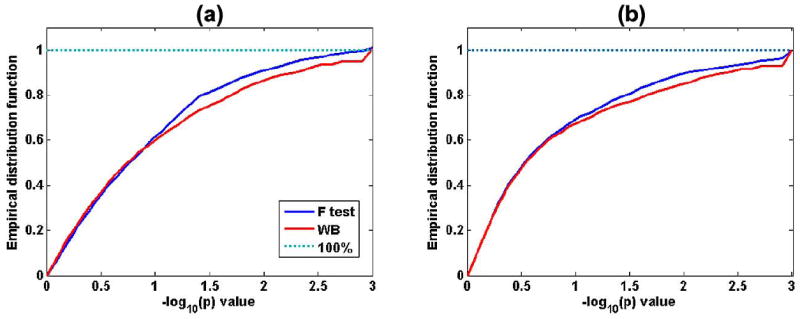
Distribution functions of − log10(p) values of test statistics at the surface of the Hippocampus. Empirical distribution functions of −log10(p) values of the F statistic and − log10(p) values of Wn based on the wild bootstrap method are shown. Combining the heteroscedastic linear model with the wild bootstrap increases the number of significant points (− log10(p) > 1.3) on the surface of the hippocampus in each hemisphere: (a) left hippocampus; (b) right hippocampus.
V. Conclusion and Discussion
We have developed a method for the analysis of anatomical imaging data based on a heteroscedastic linear model and a wild bootstrap method. The use of the heteroscedastic linear model avoids the assumptions of homogeneous variance across subjects and the Gaussian distribution of imaging data, that we have shown to be invalid in one real-world imaging dataset. The robust test procedure not only accounts for multiple comparisons across all voxels of the brain region under investigation, but it also asymptotically preserves the dependence structure among the Wald-type test statistics. We have used simulation studies to show that the robust test procedure provides accurate control of the family-wise error rate for relatively small to moderate sample sizes. Our analysis of a real-world dataset demonstrates the applicability of our test procedure to anatomical imaging data, as well as fMRI and PET data.
Our robust test procedure differs from other multiple comparison procedures for controlling the Type I error, including random field theory methods, permutation methods, and the false discovery rate. Computationally simple methods that employ random field theory depend on the validity of several stringent assumptions, including a Gaussian distribution for the imaging data and the smoothness of the spatial autocorrelation function [21]. Without formally assessing the validity of these assumptions, the application of random field theory can yield a very conservative statistical test (Figs. 3-6) [21]. Permutation methods outperform those of random field theory methods in various settings, even when the small sample size is small, although when not accounting for the presence of heterogeneous variances across subjects, permutation methods can be anticonservative (see the simulation results in Section IV). Moreover, the permutation methods may not be widely applicable to neuroimaging studies that require the statistical control of multiple covariates (e.g., age, gender, diagnoses, or genotype) without invoking stringent assumptions about the data, such as the presence of identical and independently distributed random errors. However, when the assumption of complete exchangeability is valid, the permutation test is almost the best. Methods of statistical analysis based on the false discovery rate can accurately control the false discovery rate, whereas the robust test procedure can accurately control the family-wise error rate. Moreover, the false discovery rate requires an accurate estimation of the p value for each hypothesis at each voxel, and under the heteroscedastic linear model, calculating the p value accurately for each hypothesis requires a large number of bootstrap samples in the wild bootstrap method.
We also note several advantages and limitations of our robust test procedure for controlling Type I error. Type I error rates when using the wild boostrap method are reasonably small in the presence of either heterogeneous variances across subjects or skewed distributions of error terms (Fig. 2). The robust test procedure can accurately control the family-wise error rate under various scenarios examined (Section IV), and it can increase the sensitivity of detecting statistically significant differences in brain structure when the variances across subjects vary significantly across voxels. However, when the homogeneous variance and Gaussian assumptions underlying the general linear model are truly valid, the use of the wild bootstrap method yield slightly reduced statistical power (Section IV) [37]. Moreover, for small significance level, say α = 1%, the number of replications S in the robust test procedure must be increased in order to accurately estimate pD and pD(d). Running the robust test procedure for large S can be computationally intensive [42].
Many aspects of this work merit further research. One is to examine the performance of our robust test procedure in the analysis of data from other imaging modalities, including PET and fMRI. Another is to extend our robust test procedure to the inclusion of cluster size inference in controlling the rate of Type I errors [22], [57], [64]-[66]. Our robust test procedure may lead to a simple test of cluster size in assessing the significance of all numbers of interconnected voxels greater than a given threshold (e.g., ). We will formally study the cluster size test elsewhere. Finally, we may use the generalized least squares estimator of β instead of β̂, when prior information concerning Ω is available.
Acknowledgments
The authors would like to thank the Editor, the Associate Editor, and two anonymous referees for valuable suggestions, which greatly helped to improve our presentation. They would also like to thank Dr. J. Royal for his invaluable editorial assistance and Dr. M. Chung for his helpful comments.
This work was supported in part by the Suzanne Crosby Murphy Endowment at Columbia University Medical Center and in part by the Thomas D. Klingenstein and Nancy D. Perlman Family Fund. The work of H. Zhu was supported by the NSF under Grant SES-0643663. The work of J. G. Ibrahim was supported by the NIH under Grant GM 70335 and Grant CA 74015. The work of N. Tang was supported by in part by NSFC under Grant 10561008 and in part by NSFYN under Grant 2004A0002M. The work of D. B. Rowe was supported by the NIH under Grant EB000215. The work of B. S. Peterson was supported in part by the NIDA under Grant DA017820 and in part by NIMH under Grant MH068318 and Grant K02-74677.
Appendix I
Proof of the Restricted Least Squares Estimate
The restricted least squares estimate of β under H0 : Rβ = b0 can be obtained by minimizing the following objective function:
| (A.1) |
where λ = (λ1, … , λr)T. Taking the first derivative of l(λ, β) with respect to β and λ, respectively, yields
and ∂λl = 2(Rβ−b0).
Then, β̃and λ̃ satisfy
| (A.2) |
| (A.3) |
It follows from (A.2) that
| (A.4) |
Substituting the above β̃ into (A.3) yields
| (A.5) |
Substituting λ̃ into (A.4), we have
Appendix II
Proof of Equation (13)
Following the arguments of Appendix I, the restricted least squares estimate of β in model (11) can be expressed by
Because β̂* = (XT X)−1 XT Y*, we have
where RX = R(XT X)−1XT. From the above, we can easily prove (13).
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Available: http://www.fil.ion.ucl.ac.uk/spm/
References
- 1.Mazziotta JC, Toga AW, Evans AC, Fox P, Lancaster J. A probabilitic atlas of the human brain: Theory and rationale for its development. NeuroImage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- 2.Ashburner J. Ph.D. dissertation. Univ. London; London, U.K.: 2001. Computational neuroanatomy. [Google Scholar]
- 3.Ashburner J, Friston KJ. Voxel-based morphometry: The methods. NeuroImage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- 4.Chung MK. Ph.D. dissertation. McGill Univ.; Montreal, QC, Canada: 2001. Statistical morphometry in neuroanatomy. [Google Scholar]
- 5.Thompson PM, Toga AW. A framework for computational anatomy. Comput Visual. 2002;5:13–34. [Google Scholar]
- 6.Thompson PM, Rapoport JL, Cannon TD, Toga AW. Automated analysis of structural MRI data. In: Lawrie S, Johnstone EC, Weinberger D, editors. Brain Imaging in Schizophrenia. Oxford U.K.: Oxford Univ. Press; 2003. [Google Scholar]
- 7.Mechelli A, Price CJ, Friston KJ, Ashburner J. Voxel-based morphometry of the human brain: Methods and applications. Curr Med Imag Rev. 2005;1:105–113. [Google Scholar]
- 8.Thompson PM, Cannon TD, Narr KL, van Erp T, Poutanen V, Huttunen M, Lonnqvist J, Standertskjold-Nordenstam CG, Kaprio J, Khaledy M, Dail R, Zoumalan CI, Toga A. Genetic influences on brain structure. Nature Neurosci. 2001;4:1253–1358. doi: 10.1038/nn758. [DOI] [PubMed] [Google Scholar]
- 9.Thompson PM, Cannon TD, Toga AW. Mapping genetic influences on human brain structure. Ann Med. 2002;24:523–536. doi: 10.1080/078538902321117733. [DOI] [PubMed] [Google Scholar]
- 10.Csernansky JG, Joshi S, Wang L, Haller JW, Gado M, Miller JP, Grenander U, Miller MI. Hippocampal morphometry in schizophrenia by high dimensional brain maping. Proc Nat Acad Sci USA. 1998;95:11406–11411. doi: 10.1073/pnas.95.19.11406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Plomin R, Kosslyn SM. Genes, brain and cognition. Nature Neurosci. 2001;4:1153–1154. doi: 10.1038/nn1201-1153. [DOI] [PubMed] [Google Scholar]
- 12.Narr KL, Cannon TD, Woods RP, Thompson PM, Kim S, Asunction D, van Erp TG, Poutanen VP, Huttunen M, Lonnqvist J, Standerksjold-Nordenstam CG, Kaprio J, Mazziotta JC, Toga AW. Genetic contribution to altered callosal morphology in schizophrenia. J Neurosci. 2002;22:3720–3729. doi: 10.1523/JNEUROSCI.22-09-03720.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wright IC, Sham P, Murray RM, Weinberger DR, Bullmore ET. Genetic contributions to regional variability in human brain structure: Methods and preliminary results. NeuroImage. 2002;17:256–271. doi: 10.1006/nimg.2002.1163. [DOI] [PubMed] [Google Scholar]
- 14.Styner M, Lieberman JA, McClure RK, Weinberger DR, Jones DW, Gerig G. Morphometric analysis of lateral ventricles in schizophrenia and healthy controls regarding genetic and disease-specific factors. Proc Nat Acad Sci USA. 2005;102:4677–4872. doi: 10.1073/pnas.0501117102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dryden I, Mardia K. Statistical Shape Analysis. New York: Wiley; 1998. [Google Scholar]
- 16.Fletcher P, Joshi S, Lu C, Pizer SM. Gaussian distribution on lie groups and their applications to statistical shape analysis. Inf Process Med Imag. 2003:450–462. doi: 10.1007/978-3-540-45087-0_38. [DOI] [PubMed] [Google Scholar]
- 17.Thompson PM, Woods RP, Mega MS, Toga AW. Mathematical/computational challenges in creating population-based brain atlases. Hum Brain Mapp. 2000;9:81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Evans AC B.D.C. Group. The NIH MRI study of normal brain development. NeuroImage. 2006;30:184–202. doi: 10.1016/j.neuroimage.2005.09.068. [DOI] [PubMed] [Google Scholar]
- 19.Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW. Mapping cortical change across the human life span. Nature Neurosci. 2003 Jan;6:309–315. doi: 10.1038/nn1008. [DOI] [PubMed] [Google Scholar]
- 20.Friston K, Holmes AP, Worsley KJ, Poline JB, Frith CD, Frackowiak RSJ. Statistical parametric maps in functional imaging: A general linear approach. Hum Brain Mapp. 1995;2:189–210. [Google Scholar]
- 21.Nichols T, Hayasaka S. Controlling the family-wise error rate in functional neuroimaging: A comparative review. Statist Meth Med Res. 2003;12:419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- 22.Cao J, Worsley KJ. Applications of random fields in human brain mapping. In: Moore M, editor. Spatial Statistics: Methodological Aspects and Applications. Vol. 159 New York: Springer; 2001. [Google Scholar]
- 23.Salmond CH, Ashburner J, Vargha-Khadem F, Connelly A, Gadian DG, Friston KJ. Distributional assumptions in voxel-based morphometry. NeuroImage. 2002;17:1027–1030. [PubMed] [Google Scholar]
- 24.Cook DR, Weisberg S. Residuals and Influence in Regression. London, U.K.: Chapman Hall; 1982. [Google Scholar]
- 25.Luo W, Nichols T. Diagnosis and exploration of massively univariate fMRI models. NeuroImage. 2003;19:1014–1032. doi: 10.1016/s1053-8119(03)00149-6. [DOI] [PubMed] [Google Scholar]
- 26.Dudoit S, Shaffer JP, Boldrick JC. Multiple hypothesis testing in microarray experiments. Statist Sci. 2003;18:71–103. [Google Scholar]
- 27.Davatzikos C. Why voxel-based morphometric analysis should be used with great caution when characterizing group differences. NeuroImage. 2004;23:17–20. doi: 10.1016/j.neuroimage.2004.05.010. [DOI] [PubMed] [Google Scholar]
- 28.Lin DY. An efficient Monte Carlo approach to assessing statistical significance in genomic studies. Bioinformatics. 2005;6:781–787. doi: 10.1093/bioinformatics/bti053. [DOI] [PubMed] [Google Scholar]
- 29.Woolrich MW, Behrens TEJ, Beckmann CF, Jenkinson M, Smith SM. Multilevel linear modelling for FMRI group analysis using Bayesian inference. NeuroImage. 2004;21:1732–1747. doi: 10.1016/j.neuroimage.2003.12.023. [DOI] [PubMed] [Google Scholar]
- 30.Beckmann CF, Jenkinson M, Smith SM. General multilevel linear modeling for group analysis in FMRI. NeuroImage. 2003;20:1052–1063. doi: 10.1016/S1053-8119(03)00435-X. [DOI] [PubMed] [Google Scholar]
- 31.Friston KJ, Stephan KE, Lund TE, Morcom A, Kiebel S. Mixed-effects and fMRI studies. NeuroImage. 2005;24:244–252. doi: 10.1016/j.neuroimage.2004.08.055. [DOI] [PubMed] [Google Scholar]
- 32.White HL. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica. 1980;48:817–838. [Google Scholar]
- 33.Eicker F. Asymptotic normality and consistency of the least squares estimators for families of linear regressions. Ann Math Statist. 1963;34:447–456. [Google Scholar]
- 34.Flachaire E. Bootstrapping heteroscedastic regression models: Wild bootstrap vs. pairs bootstrap. Computational Statist Data Anal. 2005;49:361–376. [Google Scholar]
- 35.Godfrey LG, Tremayne AR. The wild bootstrap and heteroscedasticity-robust tests for serial correlation in dynamic regression models. Comput Statist Data Anal. 2005;49:377–395. [Google Scholar]
- 36.Searle SR, Casella G, McCulloch CE. Variance Components. New York: Wiley; 1992. [Google Scholar]
- 37.Long JS, Ervin LH. Using heteroscedasticity consistent standard errors in the linear regression model. Am Statist. 2000;54:217–224. [Google Scholar]
- 38.Davidson R, MacKinnon JG. Heteroskedasticity-robust tests in regression directions. Ann de l’INSEE. 1985;59/60:183–218. [Google Scholar]
- 39.MacKinnon JG, White HL. Some heteroskedasticity consistent covariance matrix estimators with improved finite sample properties. J Econometrics. 1985;21:53–70. [Google Scholar]
- 40.Liu RY. Bootstrap procedure under some non-i.i.d. models. Ann Statist. 1988;16:1696–1708. [Google Scholar]
- 41.Mammen E. Bootstrap and wild bootstrap for high dimensional linear models. Ann Statist. 1993;21:255–285. [Google Scholar]
- 42.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. London, U.K.: Chapman Hall; 1993. [Google Scholar]
- 43.Kannurpatti SS, Biswal BB. Bootstrap resampling method to estimate confidence intervals of activation-induced CBF changes using laser Doppler imaging. J Neurosci Meth. 2005;146:61–68. doi: 10.1016/j.jneumeth.2005.01.021. [DOI] [PubMed] [Google Scholar]
- 44.Aronowich A, Adler RJ. The behaviour of chi squared processes at critical points. Adv Appl Probability. 1985;17:280–297. [Google Scholar]
- 45.Worsley KJ. Local maxima and the expected Euler characteristic of excursion sets of chi2, F and t fields. Adv Appl Probability. 1994;26:13–42. [Google Scholar]
- 46.van der Vaart AW, Wellner J. Weak Convergence and Empirical Processes. New York: Springer; 1996. [Google Scholar]
- 47.Nichols T, Holmes AP. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum Brain Mapp. 2002;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hayasaka S, Phan LK, Liberzon I, Worsley KJ, Nichols TE. Nonstationary cluster-size inference with random field and permutation methods. NeuroImage. 2004;22:676–687. doi: 10.1016/j.neuroimage.2004.01.041. [DOI] [PubMed] [Google Scholar]
- 49.Mumford J, Nichols TE. The problem of inflated type I errors with simple group model. NeuroImage. 26:1258. [Google Scholar]
- 50.Kerstin JP, Bansal R, Zhu HT, Whiteman R, Amat J, Quackenbusch G, Martin L, Durkin K, Blair C, Royal J, Hugdahl K, Peterson B. Hippocampus and Amydala morphology in attention-deficit/hyperactivity disorder. Arch Gen Psychiatry. 2006;63:795–807. doi: 10.1001/archpsyc.63.7.795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cressie AC. Statistics for Spatial Data. 2. New York: Wiley; 1993. [Google Scholar]
- 52.Logan BR, Rowe DB. An evalution of thresholding techniques in fMRI analysis. NeuroImage. 2004 May;22:95–108. doi: 10.1016/j.neuroimage.2003.12.047. [DOI] [PubMed] [Google Scholar]
- 53.Chung MK, Robbins S, Dalton KM, Davidson RJ, Alexander AL, Evans AC. Cortical thickness analysis in autism via heat kernel smoothing. NeuroImage. 2005;25:1256–1265. doi: 10.1016/j.neuroimage.2004.12.052. [DOI] [PubMed] [Google Scholar]
- 54.Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Statist Soc, Ser B-Statist Methodol. 1995;57:289–300. [Google Scholar]
- 55.Shaffer JP. Multiple hypothesis testing: A review. Ann Rev Psychol. 1995;46:561–584. [Google Scholar]
- 56.Worsley KJ, Andermann M, Koulis T, MacDonald D, Evans AC. Detecting changes in nonisotropic images. Hum Brain Mapp. 8:98–101. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<98::AID-HBM5>3.0.CO;2-F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hayasaka S, Nichols T. Validating cluster size inference: Random field and permutation methods. NeuroImage. 2003;20:2343–2356. doi: 10.1016/j.neuroimage.2003.08.003. [DOI] [PubMed] [Google Scholar]
- 58.Viola P, Wells WM. Alignment by maximization of mutual information. Int J Comput Vision. 1997;24:137–154. [Google Scholar]
- 59.Christensen G, Rabbitt RD, Miller MI. 3D brain mapping using a deformable neuroanatomy. Phys Med Biol. 1994;39:609–618. doi: 10.1088/0031-9155/39/3/022. [DOI] [PubMed] [Google Scholar]
- 60.Bansal R, Staib L, Wang Y, Peterson B. Roc-based assessments of 3D cortical surface-matching algorithms. NeuroImage. 2005;24:150–162. doi: 10.1016/j.neuroimage.2004.08.054. [DOI] [PubMed] [Google Scholar]
- 61.Cook DR, Weisberg S. Diagnostics for heteroscedasticity in regression. Biometrika. 1983;70:1–10. [Google Scholar]
- 62.Zhu HT, Zhang HP. A diagnostic procedure based on local influence measure. Biometrika. 2004;91:579–589. [Google Scholar]
- 63.Pruessner JC, Collins DL, Pruessner M, Evans AC. Age and gender predict volume decline in the anterior and posterior hippocampus in early adulthood. J Neurosci. 2001;21:194–200. doi: 10.1523/JNEUROSCI.21-01-00194.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Poline JB, Mazoyer B. Cluster analysis in individual functional brain images: Some new techniques to enhance the sensitivity of activation detection methods. Hum Brain Mapp. 1994;2:103–111. [Google Scholar]
- 65.Roland PE, Levin B, Kawashima R, Kerman S. Three-dimensional analysis of clustered voxels in 15O-butanol brain activation images. Hum Brain Mapp. 1993;1:3–19. [Google Scholar]
- 66.Friston KJ, Worsley KJ, Frackowiak RSJ, Mazziotta JC, Evans AC. Assessing the significance of focal activations using their spatial extent. Hum Brain Mapp. 1994;1:214–220. doi: 10.1002/hbm.460010306. [DOI] [PubMed] [Google Scholar]