Abstract
Nickel-responsive protein NikR regulates the nickel uptake in nickel-dependent bacteria by interacting with the operator of nikABCDE and subsequently repressing the transcription of NikABCDE, an ABC-type nickel transporter system. The function of NikR and its affinity for the operator DNA is highly conformation-dependent, which has been confirmed by three independent crystallographic studies on NikR proteins from different bacteria. Depending on the intracellular nickel concentration, NikR is able to adopt either the open form or one of the two closed forms (cis and trans) that differ in the domain-domain arrangement. Only the closed cis form is optimal for DNA binding. We examined the low-resolution vibrational spectrum of NikR in each conformational form using the elastic network model and observed large-scale domain-domain vibrations that are closely related to the conformational transitions required for function, particularly the symmetric bending mode and the asymmetric twisting mode. This analysis on the intrinsic dynamics coded in the three-dimensional molecular construct allows us to examine the proposed mechanisms of NikR regulation from the standpoint of protein collective motions. Our findings further support the three-state equilibrium hypothesis proposed by others, and imply that an isolated closed cis form may be dynamically unstable but can be stabilized by DNA binding. However, we also found that the simple Cα-model used in the current analysis is insufficient to capture the impact of nickel binding on the protein dynamics, for which an all-atom model with detailed atom typing is more appropriate.
INTRODUCTION
Nickel is a biologically important transition metal to the well-being of many microbes (1). Several enzymes have been identified as nickel-dependent since the groundbreaking discovery of Bartha and Ordal in 1965 (2), including glyoxalase I, peptide deformylase, methylcoenzyme M reductase, urease, hydrogenases, superoxide dismutase, carbon monoxide dehydrogenase, and acetyl-coenzyme A synthease (3–5). The proper functioning of these enzymes is required for the survival of many bacteria in a harsh living environment. Nickel enters prokaryotic cells through two different channels, ATP-binding cassette (ABC) type nickel transporter systems and nickel-specific permeases, both of which are tightly regulated so that the intracellular concentration of nickel is maintained at a nontoxic level. In the presence of excess nickel, NikR, the most studied nickel-binding regulatory protein, has been found to modulate the gene transcriptions of several proteins that are involved in nickel uptake, transport, and storage by binding to their operon DNA sequences (6). One such example is the five-component NikABCDE nickel transporter system of Escherichia coli, the biosynthesis of which is suppressed in the presence of excess nickel content (7–9).
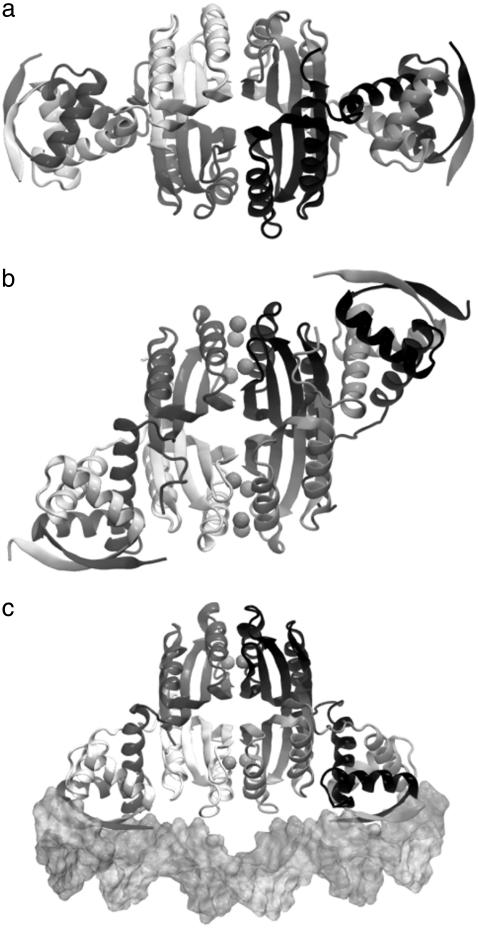
The structural basis of nickel regulation by NikR has recently emerged from three independent x-ray crystallographic studies on different sources, Escherichia coli (10,11), Pyrococcus horikoshii (12), and Helicobacter pylori (13), which uniformly identified distinct conformational states of NikR associated with different nickel-binding conditions (Fig. 1). The apo form of NikR roughly has the shape and symmetry of a carbon dioxide molecule (Fig. 1 a), in which the carbon and two oxygen atoms correspond to the central tetrameric domain and the two dimeric DNA binding (DBD) domains, respectively. The DBD domains belong to the ribbon-helix-helix family (14), which holds the operator DNA-recognizing anti-parallel β-sheets. Nickel is required for optimal DNA binding. Two sets of nickel-binding sites with different binding affinities (Kd = 7 pM and 30 nM) have been identified in the tetrameric domain. The low-affinity binding site is only occupied in the presence of excess nickel, which drastically increases the DNA binding affinity from 30 nM to 15 pM (8,9,15).
FIGURE 1.
Three different conformational states of NikR (ribbon diagrams) have been structurally determined by x-ray crystallography. (a) The open form of NikR-apo from Pyrococcus horikoshii (PDB ID: 2BJ3); (b) the closed trans form of NikR with nickel (spheres) bound to the high-affinity sites from Pyrococcus horikoshii (PDB ID: 2BJ7); and (c) the closed cis form of NikR bound to the minor grooves of a palindromic DNA (surface) from Escherichia coli (PDB ID: 2HZV).
The crystallographic studies on different NikR orthologs and their complexes revealed that nickel or DNA binding have great impact on the molecular shape and thermodynamic fluctuations. In contrast with the linear and open domain-domain arrangement in the apo form, NikR may also conditionally adopt two other more compact and closed conformations with the two DBD domains in trans (Fig. 1 b) or cis (Fig. 1 c) configurations relative to the tetrameric domain. One schematic representation of the relationship between various NikR conformational states under different binding conditions has been proposed based on available structural information by Chivers and Tahirov (12). They suggested that the open and two closed states exist in a preestablished thermodynamic equilibrium and the conformational preference is affected by nickel and DNA binding, while others seems to favor an induced-fit description (16), in which the conformational transitions of transcription factors are the direct consequence of ligand binding (17–20). After all, the closed conformations were only observed in the complexes of NikR with nickel or both nickel and DNA.
Whether the observed distinct conformational states in NikR are a result of preestablished equilibrium or ligand-induced fit can be decided if the exact kinetics of transitions between the ending conformational states is known (21). If the ligand binding event occurs only after the conformational transition, the thermodynamic equilibrium mechanism is more appropriate and vice versa. Capturing conformational transition events of long timescale is a challenging task that requires carefully designed and well-executed experiments. First-principle computer simulation of protein dynamics is ideal for this type of study; however, it is hardly practical to observe such molecular motions of low frequency and large magnitude at atomistic level. Fortunately, these motions are often a limited number of mechanical movements of larger protein building blocks (domains or flexible loops) in simple fashion (22), which can be computationally extracted with relative ease. The availability of multiple structures of the apoprotein and holoproteins of NikR should allow us to analyze and compare the intrinsic motions programmed in different three-dimensional folds so that a picture of the NikR regulation mechanism can be drawn from the standpoint of protein dynamics.
The separation of low-frequency motions from those of high-frequency can be achieved by quasiharmonic analysis of a molecular dynamics (MD) simulation (23,24), or normal node analysis (NMA) using either an all-atom (25) or reduced Cα representation (26–28). The latter is also known as Gaussian network model (GNM) or elastic network model (ENM), which has become a powerful decomposition technique to analyze thermal equilibrium fluctuation associated with the intrinsic dynamics and elasticity of biological macromolecules (29–38). The fundamental assumption behind GNM or ENM is that the long timescale low-frequency motions are relatively insensitive to structure details and are only determined by spatial connectivity (27). Hence, a reduced system representation can be used and lengthy energy minimization can be avoided, which requests a significantly smaller computational cost compared to the traditional NMA method or quasiharmonic analysis, and yet is able to describe the low frequency motions accurately. GNM and ENM have been successfully applied to analyze the function-related concerted motions of proteins. An overview of the theory and recent advances were given by Bahar and Rader (39) and Tama and Brooks (40), and the reasons for its success and its limitations were discussed in great detail in an excellent review by Ma (41).
Of all the NikR crystal structures determined, we chose to perform the ENM analysis on those of Chivers and Tahirov (12) from Pyrococcus horikoshii (PhNikR) because these structures have the least missing residues. The structures solved by Schreiter et al. (11,12) and Dian et al. (13) have long stretches of missing residues due to local disorder in the crystals, and are not suitable for ENM analysis without extensive modeling of the missing residues, except the NikR-operator DNA complex (PDB ID: 2HZV). The ENM analysis program that we used was developed in our lab by combining VMD, a molecular visualization program (42), and Octave, a free linear and nonlinear numerical package (43). In the following sections, we will first present the details of the analysis that were performed in this work and follow it by the Results and Discussion.
METHODS
ENM, also known as the anisotropic GNM analysis, is technically equivalent to normal mode analysis, which decomposes the intrinsic dynamics of a nonlinear molecular construct (N atoms or particles) onto 3N − 6 orthogonal directions under the harmonic approximation. The decomposition is done by diagonalizing the Hessian matrix (H) of the molecular construct,
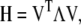 |
(1) |
where Λ and V are the eigenvalue and eigenvector matrices of H. The theory and technical details of ENM can be found elsewhere (44). In the framework of ENM, the molecular construct contains only Cα atoms, which are connected by harmonic springs of uniform strength (k) if they are within certain distance (Rcut) from each other. The potential energy of this elastic network is a simple summation over all possible interacting pairs as indicated here:
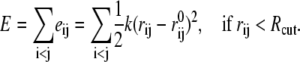 |
(2) |
Once Rcut is decided (usually a value between 12 and 15 Å is chosen), the calculation of the Hessian matrix is straightforward, for which we used Rcut = 13 Å and a VMD script. For diagonalization, we utilized the eig numerical routine in Octave, which solves for the eigenvalues and eigenvectors of a matrix in a multiple-step process beginning with a Hessenberg decomposition followed by a Schur decomposition.
A number of PhNikR crystal structures have been determined by Chivers and Tahirov (12), of which we have focused on the apo-PhNikR (PDB ID: 2BJ3), the open and the closed (trans) conformations of PhNikR with nickel bound to the high-affinity sites (PDB ID: 2BJ1 and 2BJ7). Most of the missing residues are near the C-terminus of the tetrameric domain, except Asp65 and Glu66 of chain D in 2BJ3. These two residues were built from the corresponding residues of chain A by superposition, followed by short local minimization. To examine the impact of nickel binding to the low-frequency motions of PhNikR, we included the bound nickel into the ENM analysis of relevant conformational states. For the cis conformation of the closed NikR, we used the only crystal structure available (PDB ID: 2HZV) that was solved with a palindromic DNA bound by Schreiter et al. (11). The computed eigenvectors were visualized using VMD and are illustrated as solid cones centered on Cα atoms, the lengths of which are proportional to the magnitudes of vibrations given by the eigenvectors.
RESULTS AND DISCUSSION
Numerous studies have demonstrated that the intrinsic motions of proteins, particularly low-frequency motions, are closely associated with their biological function. The dynamic trait of a three-dimensional fold is increasingly recognized as an equally important component that determines the compatibility between the protein fold and functionality. For NikR, the intrinsic dynamics of the three-dimensional scaffold is even more crucial because of the significant conformational difference between the apo form (open) and the functional form (cis closed) associated with nickel and DNA binding. Although the structural determination of distinct NikR states has laid down the foundation for unveiling the regulatory mechanism for which NikR has been optimized, the functional motions of different conformational states are not immediately clear from visual examination of the structures. In principle, the thermodynamic motions can be directly calculated from classical MD simulations; however, the timescales of these functionally coupled motions (often microseconds) are far beyond the limit of most all-atom MD approaches on large systems. In addition, long simulations also suffer from the accumulated error in numerical integration of Newton's equation of motion and any artifacts in the underlying energy function. As progress is being made in addressing these issues in the brute force realization of low-frequency motions, we decided to first study the normal motions of NikR at different conditions using ENM, from which qualitative pictures of the conformational transitions and the function of nickel can be examined.
PhNikR-apo
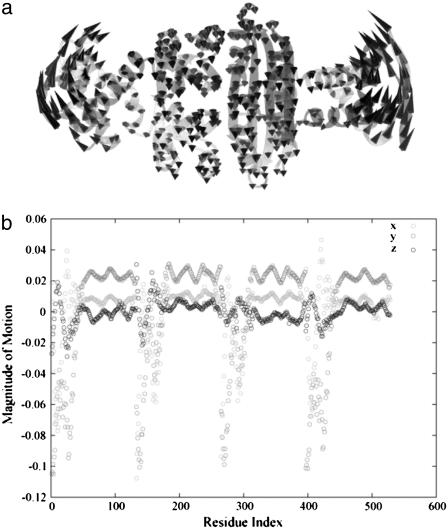
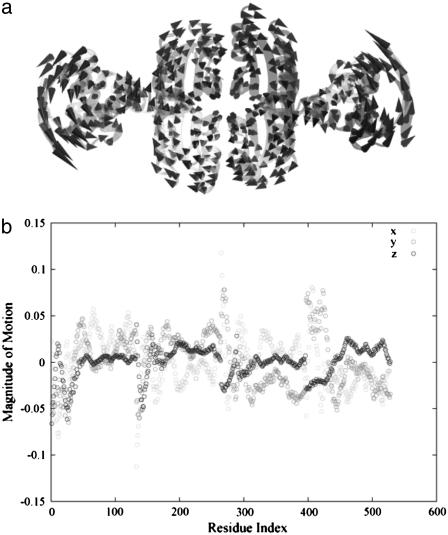
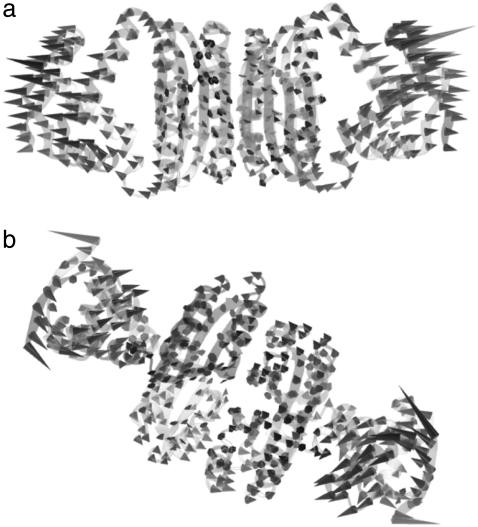
Diagonalization of the Hessian matrix of PhNikR-apo resulted in the motion vectors of harmonic oscillators (eigenvectors) and their corresponding frequencies (eigenvalues), typically arranged in ascending order, the first six of which describe rigid body motions. The next few modes of PhNikR-apo show a range of intriguing domain-domain vibrational modes. In the normal mode analysis of carbon dioxide, the slowest vibration is the bending mode, in which the molecule departs symmetrically from linearity. A similar symmetric bending mode (Fig. 2 a) was found to have the lowest frequency in the open PhNikR-apo, in which the two DBD domains display large-magnitude-correlated motion in the XY plane with respect to each other, and the tetrameric domain displays anticorrelated motion in the same plane with respect to the DBD domains with much smaller magnitude (Fig. 2 b). The second nontrivial vibration mode appears to be an asymmetric twisting motion (Fig. 3 a), in which two DBD domains and the tetrameric domain rotate in the opposite directions about the twofold rotational axis (z axis) that goes through the center of Fig. 3 a and points toward the viewer. The overall magnitudes of motion in the DBD and tetrameric domains are comparable to those seen in the symmetric bending mode, and the DBD domains are again significantly more mobile than the tetrameric domain (Fig. 3 b). Displacements along the symmetric bending and asymmetric twisting mode vectors effectively bring the two DBD domains into positions that resemble those found for the closed cis and trans crystal conformations, respectively. Hence, these correlated motions appear to be the most relevant to the biological function of NikR and represent the conformational transitions of interest.
FIGURE 2.
In the vibrational spectrum of PhNikR-apo computed by ENM, the first mode (the slowest normal motion) is a symmetric bending mode (a), in which the two DBD domains show large-magnitude concerted movements (b), most likely related to the open-to-cis transition, which leads to the functional form of NikR optimal for DNA binding.
FIGURE 3.
Following the symmetric bending mode is an asymmetric twisting mode along the twofold rotational axis (a), in which the DBD and tetrameric domains rotate in opposite directions in different magnitudes (b). Its connection with the closed trans conformation is evident.
The meanings of the other low-frequency modes are more difficult to assign based on visual examination. For example, the third nontrivial vibration mode is another symmetric bending of the DBD domains with respect to the tetrameric domain but in a different plane that is roughly perpendicular to that of the first mode (Fig. 4). The following two vibration modes involve large-magnitude DBD domain rotations around the long axis of NikR, one of which is shown in Fig. 5 where both DBD domains rotate clockwise when viewed from either end of the molecule. It is not surprising due to the symmetric molecular construct of NikR that many of these low-frequency modes correspond to highly organized domain-domain motions. However, we were pleased with the correspondence between the first two vibrational modes and the function of NikR. Moreover, it is impressive that functionally relevant vibrational modes are strongly encoded in such an efficient manner.
FIGURE 4.
The third low-frequency vibration mode of PhNikR-apo is a different symmetric bending mode of the DBD domains with respect to the tetrameric domain. The direction of bending is nearly orthogonal to that in Fig. 2.
FIGURE 5.
The fourth low-frequency vibrational mode of the open PhNikR-apo is a domain-domain rotation mode around the long axis of the protein. PhNikR is placed so that one of the DBD domains is close to the viewer while the other is further away and rendered with less intensity. Both DBD domains show clockwise rotations along the long axis when viewed from either end.
PhNikR with Ni bound at high-affinity sites
NikR is known to have two sets of nickel-binding sites with different binding affinities, which modulate the affinity of NikR for its receptor. Indeed, the DNA binding affinity of PhNikR is increased by ∼500-fold when both nickel-binding sites are occupied. Unlike other NikR proteins in the family, PhNikR has two sets of high-affinity binding sites (primary and auxiliary), each of which accommodates four nickel ions and is located in the nodal plane that separates the tetramer into two equal parts consisting of one DBD domain and one-half of the tetrameric domain. When nickel binds to both the high affinity sites, PhNikR can assume both the open form (PhNikR-Ni-1) and the closed trans form (PhNikR-Ni-2). To qualitatively understand the impact of nickel binding on the intrinsic dynamics of NikR, we included all eight nickel ions in our ENM analysis.
The open form (PhNikR-Ni-1)
The binding of nickel to the high-affinity sites does not induce large conformational changes to the open form of PhNikR. The backbone root mean-square deviations (RMSD) of the tetrameric domain (residues 52–132) and of both domains (residue 2 to 132) are <1.6 Å and 2.0 Å, respectively. The vibration frequencies (λi) and modes (vi) of PhNikR-Ni-1 (residues 2–132) were computed and compared to those of PhNikR-apo. Although changes in the vibrational modes were expected as the structural deviation is large enough to affect the contact matrix calculation (Rcut = 13 Å), the domain-domain motions suggested by the low-frequency modes are in general unchanged from those of PhNikR-apo. Some are more preserved than others, as indicated by the dot products of corresponding eigenvectors (Table 1). This includes two symmetric bending modes mentioned previously (i = 1, 3) and the asymmetric twisting mode (i = 2). Greater differences were observed in the eigenvalues 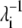 (Table 1), which are related to the mean-square fluctuations of individual residues via
(Table 1), which are related to the mean-square fluctuations of individual residues via
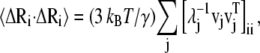 |
(3) |
where ΔR is the n-dimensional fluctuation vector and vj is the eigenvector of order j. The 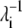 values of the low frequency end of the vibrational spectrum are noticeably increased due to the structural changes as a result of nickel binding, particularly those of the symmetric bending and asymmetric twisting modes. It seems to suggest that the binding of nickel to the high-affinity sites stimulate residue fluctuations and subsequently enable better access to the closed conformations. To appreciate the significance of the increase in λ−1, we created 10 structures with Cα-RMSD at ∼2.2 Å for residues 2–132 by displacing the Cα carbon positions along the 10 low-frequency vibrational modes. The mean λ−1 values of the resulting conformations are 28.5 and 14.0 for the symmetric bending and asymmetric twisting modes with standard deviations of 6.8 and 2.3, respectively. Although the mean values confirm an increase in λ−1 upon nickel binding, the increase may not be statistically significant enough to imply greater residue mean-square fluctuation in PhNikR-Ni-1. We note that PhNikR-Ni-1 has a much higher mean temperature factor than PhNikR-apo (81.1 and 54.1 Å2, respectively).
values of the low frequency end of the vibrational spectrum are noticeably increased due to the structural changes as a result of nickel binding, particularly those of the symmetric bending and asymmetric twisting modes. It seems to suggest that the binding of nickel to the high-affinity sites stimulate residue fluctuations and subsequently enable better access to the closed conformations. To appreciate the significance of the increase in λ−1, we created 10 structures with Cα-RMSD at ∼2.2 Å for residues 2–132 by displacing the Cα carbon positions along the 10 low-frequency vibrational modes. The mean λ−1 values of the resulting conformations are 28.5 and 14.0 for the symmetric bending and asymmetric twisting modes with standard deviations of 6.8 and 2.3, respectively. Although the mean values confirm an increase in λ−1 upon nickel binding, the increase may not be statistically significant enough to imply greater residue mean-square fluctuation in PhNikR-Ni-1. We note that PhNikR-Ni-1 has a much higher mean temperature factor than PhNikR-apo (81.1 and 54.1 Å2, respectively).
TABLE 1.
The dot products of the first 10 eigenvectors (vi, i ∈ [1, 10]) of PhNikR-apo and PhNikR-Ni-1
| Mode index i | vi, PhNikR–Ni–1· vi, PhNikR–apo |
 , PhNikR–Ni–1 , PhNikR–Ni–1
|
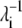 , PhNikR–apo , PhNikR–apo
|
|---|---|---|---|
| 1 | 0.81 | 39.32 | 30.63 |
| 2 | 0.50 | 17.79 | 14.90 |
| 3 | 0.81 | 12.59 | 10.87 |
| 4 | 0.21 | 11.32 | 8.80 |
| 5 | 0.03 | 8.53 | 6.50 |
| 6 | 0.88 | 3.84 | 3.36 |
| 7 | 0.54 | 3.37 | 2.96 |
| 8 | 0.10 | 2.80 | 2.54 |
| 9 | 0.33 | 2.79 | 2.35 |
| 10 | 0.23 | 2.12 | 1.88 |
The closed trans form (PhNikR-Ni-2)
The crystal structure of the closed trans conformation with nickel bound to the high-affinity sites is available for all three NikR orthologs. In general, they display similar asymmetric DBD domain closing onto the tetrameric domain (Fig. 6), possibly as a result of the asymmetric twisting vibration mode described earlier; however, the structure of E. coli NikR (PDB ID: 2HZA) shows the least domain-domain contact, suggesting that the closing action might be half complete. The open-close conformational transition requires different structural adjustments from each individual domain in PhNikR. The tetrameric domain is largely intact with a backbone RMSD of 1.8 Å (residues 52–132), and the structural changes within the DBD domains are more substantial due to the domain closing motion, mainly in the packing of secondary structural elements.
FIGURE 6.
The superposition of the tetrameric domains of the open (solid) and the closed trans (shaded) conformations of PhNikR. While the backbone RMSD (residues 52–132) of the tetrameric domain is 1.8 Å, there is noticeable rearrangement of the secondary structure elements due to the conformational transition.
With the intrinsic vibrational modes of PhNikR-apo, it is possible to decompose the overall conformational displacement observed in PhNikR-Ni-2 (in Cartesian space) and highlight the most significant contributing motions. We understand that the real conformational transition between two well-defined states may not be captured by the harmonic approximation; however, this type of analysis can still be useful in offering a simplified (low dimension) and meaningful picture of an otherwise complicated process. The conformational displacements in the vibrational space (Fig. 7) was computed by projecting the normalized displacement vector in Cartesian space onto the eigenvectors vi after the tetrameric domain of PhNikR-Ni-2 was superimposed with that of PhNikR-apo to eliminate center-of-mass translation and rotation, also known as overlap value analysis (45). The mean and standard deviations of all vibrational displacements are 0.0002 and 0.02, respectively. Major contributions come from the few low-frequency modes (Table 2), most significantly the asymmetric twisting mode (Fig. 3), while the contribution from the symmetric bending mode (Fig. 2) is nearly zero. In addition, major displacements were seen in three other modes (i = 4, 6, and 9), which may also be involved in the conformational transition. Mode 4 has been described earlier (Fig. 5) as a DBD domain clockwise rotation around the long axis. Mode 6 (Fig. 8 a) can be best characterized as symmetric DBD domain stretching, while the complicated motion of mode 9 is shown in Fig. 8 b.
FIGURE 7.
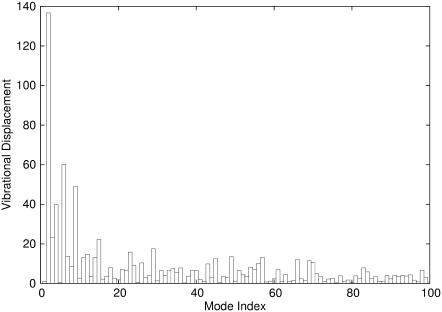
The contributions to the conformational displacements between the open form and the closed trans form from the first 100 low-frequency vibrational modes of PhNikR-apo. The mean and standard deviation of all vibrational displacements are −0.0074 and 4.76, respectively.
TABLE 2.
The overlap values or the vibrational displacements between PhNikR-apo and PhNikR-Ni-2 contributed by the first 10 modes of PhNikR-apo (vi, i ∈ [1, 10])
| vi | Displacement |
|---|---|
| 1 | 0.003 |
| 2 | 0.472 |
| 3 | 0.080 |
| 4 | 0.137 |
| 5 | 0.002 |
| 6 | 0.208 |
| 7 | 0.047 |
| 8 | 0.030 |
| 9 | 0.169 |
| 10 | 0.009 |
FIGURE 8.
In additional to mode 2 (asymmetric twisting) and 4, two other vibrational modes are also important contributors to the open-to-trans transition: (a) mode 6 and (b) mode 9.
Considering the dominant contribution from the asymmetric twisting mode of PhNikR-apo to the formation of the closed trans conformation, one might expect a similar low-frequency mode in the vibrational spectrum of PhNikR-Ni-2 to recover the open conformation. Surprisingly, this restoring mode appears at the fifth position (Fig. 9) and the first four low-frequency modes are the familiar symmetric bending modes (Fig. 10) and the DBD domain rotation modes (Fig. 11). Tama and Sanejouand (46) observed, in a normal mode analysis of 10 proteins with open and closed conformational states picked out of the Database of Macromolecular Movements (http://bioinfo.mbb.yale.edu/MolMovDB/), that the motion vectors computed using the open form seemed to represent the overall conformational displacement better than those from the closed form in terms of the overlap value. Tama and Sanejouand argued that NMA (either elastic potentials or full atomic potentials) ought to perform better on open forms because protein domains are more clearly defined (46). An interesting observation, but we found the claim difficult to justify, as the theory of NMA (regardless of the nature of the potential) applies to all well-defined thermodynamic states. It is premature to arrive at such a conclusion only because we do not yet have a general and effective approach to sample the multidimensional transition paths connecting the two end states, the nature of which can be far more complicated than a simple two-state scenario. The eigenvectors computed at the closed form may be just as informative as those from the open form. The recent published work of Song and Jernigan on domain-swapped proteins (47) illustrated that the normal motions computed from the closed state could be better understood if the conformational displacement was expressed in terms of rigid-body translation and rotation of swapping domains. However, this rigid domain treatment is not applicable in our case. The biologically relevant asymmetric twisting mode of PhNikR-Ni-2 appearing at higher energies brings forth several questions that perhaps can only be answered by further experimental or computational studies:
Is it possible that a direct route from the closed trans form to the functional cis form may have been established as a result of the altered energy landscape and the intrinsic motions? If the low-frequency motions are tightly regulated and tied to the functions that a molecular construct is to support, the changes in the order of vibration modes of PhNikR-Ni-2 may suggest the possibility of a different rearrangement scenario.
If the scenario is not changed and the open form is a necessary connection between the trans and cis forms, does the reordering of low-frequency modes suggest a stepwise transition mechanism where the displacements along the low-frequency modes are sequentially arranged?
As a result of the asymmetric twisting mode appearing at higher energies, the residue fluctuations along this direction are also suppressed, λ−1 dropped from 14.90 to 5.48. Is this the reason why the closed trans form is stable and amenable to crystallization? After all, the isolated open cis form has evaded structure determinations.
Finally, it is certainly possible that we are reading too much into these simplified computations and that we cannot expect the ordering to always follow our expectations regarding biological function.
FIGURE 9.
The asymmetric twisting mode of the closed trans conformation, appearing at the fifth position in the vibrational spectrum of PhNikR-Ni-2.
FIGURE 10.
The symmetric bending modes of PhNikR-Ni-2.
FIGURE 11.
The DBD domain rotation modes of PhNikR-Ni-2.
EcNiR-Ni-DNA
Although the crystal structure of PhNikR-Ni-DNA is not yet available, the intrinsic motion analysis on the closed cis form was carried out using the structure (PDB ID: 2HZV) of an EcNikR-dsDNA complex solved by Schreiter et al. (10,11) with the DNA removed. The isolated cis form, if stable, will presumably adopt a similar conformation. As one might have expected, the first low-frequency mode of the closed cis form is the same symmetric bending mode (Fig. 12) seen in PhNikR-apo, and it is not difficult to picture the restoration of the open form after the vibration vector. We speculate that the isolated cis conformation may be energetically unstable compared to the open and the trans forms due to the large-scale DBD domain vibrations. Once the DBD domains recognize and bind to the major grooves of the operator DNA segment, we propose that the restoring motion of the DBD domains would be greatly reduced. To analyze the intrinsic dynamics of DNA-bound NikR, we included the backbone phosphor atoms (P) and the base-bonding carbon atoms (C1*) of the 2-deoxyribose rings as a minimal representation of the double-stranded DNA, which should be sufficient for our purposes, into the ENM analysis. In the first few low-frequency modes, the DBD domains and the DNA segments that they directly bind appear to be merged into one single dynamic domain, displaying similar concerted motions. The first vibrational mode of the complex is shown in Fig. 13, in which the most mobile region consists of 6–7 basepairs from the central stretch that are beyond 13 Å from the protein and the magnitude of motion in the DBD domain is greatly restrained. The two new DBD-DNA dynamic domains move concertedly away from the viewer, while the rest of the complex moves in the opposite direction. The symmetric bending mode was found as the second (Fig. 14), suggesting that this is still an important vibration for the function of the complex.
FIGURE 12.
The symmetric bending mode of the closed cis form of NikR computed from the conformation found in the crystal structure of the EcNiR and DNA complex structure (PDB ID: 2HZV), very similar to that found in the PhNikR-apo.
FIGURE 13.
The first low-frequency vibrational mode of the EcNiR-dsDNA complex viewed from two different angles that are orthogonal to each other, showing the redistribution of residue fluctuations from the DBD domains to the central segment of the dsDNA upon binding. The formation of the binary complex rigidifies the DBD domains as well as the interacting DNA basepairs. The central segment of the DNA is relatively unrestrained, therefore experiencing larger residue fluctuations.
FIGURE 14.
The second vibrational mode of the EcNikR and DNA complex is the familiar symmetric bending mode seen in PhNikR-apo, involving both the DBD domain and the interacting basepairs.
CONCLUSION
We studied the intrinsic dynamics of three different forms of the nickel regulatory protein NikR using the Gaussian network model. This effort allowed us to examine the regulatory mechanism from the standpoint of essential molecular dynamics. Essential protein dynamics of long timescales is a subject of great interest because of its strong connection to the biological function of many proteins. Moreover, these motions have proven to be difficult to capture through experimental or computational means. In bacterial nickel regulation, the conformational response of NikR proteins to the intracellular nickel concentration is elegantly modulated owing to the intrinsic molecular vibrations programmed in the three-dimensional construct, which has been selected under evolutionary pressure.
On a large scale, the symmetric DBD-tetrameric-DBD domain arrangement in the open apo form determines two of the low-frequency vibrational patterns, symmetric bending and asymmetric twisting, and the corresponding closed conformations, cis and trans. The ability to deform along these two vibrational modes, which are the most significant contributors to the open-close transitions, is inherent to the structure and does not depend on nickel or DNA binding. However, the binding of nickel to the high-affinity sites does seem to facilitate the conformational transition by stimulating residue fluctuations, particularly in vibrations that involve large-scale DBD domain motions. Future molecular dynamics simulations of PhNikR-apo and PhNikR-Ni-1 should be able to provide higher-resolution evidence as to the effects of nickel binding on the magnitude of thermodynamic fluctuations. The striking correspondence between the low-frequency modes and the two closed conformations, and the minimal difference observed in the low-frequency motion vectors of the open PhNikR-apo and PhNikR-Ni-1, further supports the three-state equilibrium hypothesis. In addition, the induced-fit description does not seem to match with the facts that both the open and closed trans forms of PhNikR-nickel complexes have been structurally determined and only the closed cis form binds to the operator DNA efficiently. Although only the closed cis form is optimal for DNA binding, our analysis shows that it is dynamically unstable because of the large magnitude of restoring motion. The binding of the operator DNA at least dynamically stabilizes the cis conformation by redistributing the fluctuations in the DBD domains to the most susceptible region in the DNA. Oppositely, the closed trans form is dynamically more stable, but what functional role it plays during the regulation by NikR remains unclear since it is not an efficient conformation to bind the operator DNA, and yet identified in every NikR that has been structurally studied.
The ENM analysis has proven to be an effective approach that is capable of extracting qualitatively correct low-frequency intrinsic motions that are functionally meaningful, despite the fact that it is technically a low-resolution derivative of normal mode analysis method built on the simple harmonic approximation. However, we remind ourselves that the interpretation of ENM results, no matter how appealing and indicative they seem, is a subjective exercise and should not be interpreted as conclusive without further experimental or higher-resolution computational evidence. The usefulness of vibration modes from ENM is limited by the resolution and the oversimplification of interaction potentials. It is successful in capturing the characteristics of low-frequency motions, but it is difficult to measure the effect of metal or ligand binding to protein dynamics. Direct simulation of the conformational transitions and thermodynamic evaluation of relative stabilities still remain the long-term goal.
Editor: Gregory A. Voth.
References
- 1.Hausinger, R. P. 1994. Nickel enzymes in microbes. Sci. Total Environ. 148:157–166. [DOI] [PubMed] [Google Scholar]
- 2.Bartha, R., and E. J. Ordal. 1965. Nickel-dependent chemolithotrophic growth of two Hydrogenomonas strains. J. Bacteriol. 89:1015–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ermler, U., W. Grabarse, S. Shima, M. Goubeaud, and R. K. Thauer. 1998. Active sites of transition-metal enzymes with a focus on nickel. Curr. Opin. Struct. Biol. 8:749–758. [DOI] [PubMed] [Google Scholar]
- 4.Maroney, M. J. 1999. Structure/function relationships in nickel metallobiochemistry. Curr. Opin. Chem. Biol. 3:188–199. [DOI] [PubMed] [Google Scholar]
- 5.Mulrooney, S. B., and R. P. Hausinger. 2003. Nickel uptake and utilization by microorganisms. FEMS Microbiol. Rev. 27:239–261. [DOI] [PubMed] [Google Scholar]
- 6.Dosanjh, N. S., and S. L. J. Michel. 2006. Microbial nickel metalloregulation: NikRs for nickel ions. Curr. Opin. Chem. Biol. 10:123–130. [DOI] [PubMed] [Google Scholar]
- 7.Pina, K. D., V. Desjardin, M. A. Mandrand-Berthelot, G. Giordano, and L. F. Wu. 1999. Isolation and characterization of the NikR gene encoding a nickel-responsive regulator in Escherichia coli. J. Bacteriol. 181:670–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chivers, P. T., and R. T. Sauer. 2000. Regulation of high affinity nickel uptake in bacteria. Ni2+-dependent interaction of NikR with wild-type and mutant operator sites. J. Biol. Chem. 275:19735–19741. [DOI] [PubMed] [Google Scholar]
- 9.Chivers, P. T., and R. T. Sauer. 2002. NikR repressor: high-affinity nickel binding to the C-terminal domain regulates binding to operator DNA. Chem. Biol. 9:1141–1148. [DOI] [PubMed] [Google Scholar]
- 10.Schreiter, E. R., M. D. Sintchak, Y. Guo, P. T. Chivers, R. T. Sauer, and C. L. Drennan. 2003. Crystal structure of the nickel-responsive transcription factor NikR. Nat. Struct. Biol. 10:794–799. [DOI] [PubMed] [Google Scholar]
- 11.Schreiter, E. R., S. C. Wang, D. B. Zamble, and C. L. Drennan. 2006. NikR-operator complex structure and the mechanism of repressor activation by metal ions. Proc. Natl. Acad. Sci. USA. 103:13676–13681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chivers, P. T., and T. H. Tahirov. 2005. Structure of Pyrococcus horikoshii NikR: nickel sensing and implications for the regulation of DNA recognition. J. Mol. Biol. 348:597–607. [DOI] [PubMed] [Google Scholar]
- 13.Dian, C., K. Schauer, U. Kapp, S. M. McSweeney, A. Labigne, and L. Terradot. 2006. Structural basis of the nickel response in Helicobacter pylori: crystal structures of HpNikR in Apo and nickel-bound states. J. Mol. Biol. 361:715–730. [DOI] [PubMed] [Google Scholar]
- 14.Chivers, P. T., and R. T. Sauer. 1999. NikR is a ribbon-helix-helix DNA-binding protein. Protein Sci. 8:2494–2500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bloom, S. L., and D. B. Zamble. 2004. Metal-selective DNA-binding response of Escherichia coli NikR. Biochemistry. 43:10029–10038. [DOI] [PubMed] [Google Scholar]
- 16.Koshland, D. E. 1958. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA. 44:98–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang, R. G., A. Joachimiak, C. L. Lawson, R. W. Schevitz, Z. Otwinowski, and P. B. Sigler. 1987. The crystal structure of Trp aporepressor at 1.8 Å shows how binding tryptophan enhances DNA affinity. Nature. 327:591–597. [DOI] [PubMed] [Google Scholar]
- 18.Otwinowski, Z., R. W. Schevitz, R. G. Zhang, C. L. Lawson, A. Joachimiak, R. Q. Marmorstein, B. F. Luisi, and P. B. Sigler. 1988. Crystal structure of Trp repressor/operator complex at atomic resolution. Nature. 335:321–329. [DOI] [PubMed] [Google Scholar]
- 19.Orth, P., D. Schnappinger, W. Hillen, W. Saenger, and W. Hinrichs. 2000. Structural basis of gene regulation by the tetracycline inducible Tet repressor-operator system. Nat. Struct. Biol. 7:215–219. [DOI] [PubMed] [Google Scholar]
- 20.van Aalten, D. M., C. C. DiRusso, and J. Knudsen. 2001. The structural basis of acyl coenzyme A-dependent regulation of the transcription factor FadR. EMBO J. 20:2041–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu, E. W., and D. E. Koshland. 2001. Propagating conformational changes over long (and short) distances in proteins. Proc. Natl. Acad. Sci. USA. 98:9517–9520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gerstein, M., A. M. Lesk, and C. Chothia. 1994. Structural mechanisms for domain movements in proteins. Biochemistry. 33:6739–6749. [DOI] [PubMed] [Google Scholar]
- 23.Karplus, M., and J. N. Kushick. 1981. Method for estimating the configurational entropy of macromolecules. Macromolecules. 14:325–332. [Google Scholar]
- 24.Levy, R. M., M. Karplus, J. Kushick, and D. Perahia. 1984. Evaluation of the configurational entropy for proteins: application to molecular dynamics simulations of an α-helix. Macromolecules. 17:1370–1374. [Google Scholar]
- 25.Brooks, B., D. Janezic, and M. Karplus. 1995. Harmonic-analysis of large systems: 1. Methodology. J. Comput. Chem. 16:1522–1542. [Google Scholar]
- 26.ben Avraham, D. 1993. Vibrational normal-mode spectrum of globular proteins. Phys. Rev. B. 47:14559–14560. [DOI] [PubMed] [Google Scholar]
- 27.Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
- 28.Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
- 29.Cui, Q., G. Li, J. Ma, and M. Karplus. 2004. A normal mode analysis of structural plasticity in the biomolecular motor F1-ATPase. J. Mol. Biol. 340:345–372. [DOI] [PubMed] [Google Scholar]
- 30.Li, G., and Q. Cui. 2004. Analysis of functional motions in Brownian molecular machines with an efficient block normal mode approach: Myosin-II and Ca2+-ATPase. Biophys. J. 86:743–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zheng, W., B. Brooks, S. Doniach, and D. Thirumalai. 2005. Network of dynamically important residues in the open/closed transition in polymerases is strongly conserved. Structure. 13:565–577. [DOI] [PubMed] [Google Scholar]
- 32.Tama, F., M. Feig, J. Liu, C. L. Brooks III, and K. A. Taylor. 2005. The requirement for mechanical coupling between head and S2 domains in smooth muscle Myosin ATPase regulation and its implications for dimeric motor function. J. Mol. Biol. 345:837–854. [DOI] [PubMed] [Google Scholar]
- 33.Tama, F., and C. L. Brooks III. 2005. Diversity and identity of mechanical properties of icosahedral viral capsids studied with elastic network normal mode analysis. J. Mol. Biol. 345:299–314. [DOI] [PubMed] [Google Scholar]
- 34.Tobi, D., and I. Bahar. 2005. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA. 102:18908–18913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rader, A., D. H. Vlad, and I. Bahar. 2005. Maturation dynamics of bacteriophage HK97 capsid. Structure. 13:413–421. [DOI] [PubMed] [Google Scholar]
- 36.Lu, M., and J. Ma. 2005. The role of shape in determining molecular motions. Biophys. J. 89:2395–2401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zheng, W., B. R. Brooks, and D. Thirumalai. 2006. Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations. Proc. Natl. Acad. Sci. USA. 103:7664–7669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zheng, W., and B. R. Brooks. 2006. Modeling protein conformational changes by iterative fitting of distance constraints using reoriented normal modes. Biophys. J. 90:4327–4336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bahar, I., and A. Rader. 2005. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Chem. Biol. 15:586–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tama, F., and C. L. Brooks. 2006. Symmetry, form, and shape: guiding principles for robustness in macromolecular machines. Annu. Rev. Biophys. Biomol. Struct. 35:115–133. [DOI] [PubMed] [Google Scholar]
- 41.Ma, J. 2005. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 13:373–380. [DOI] [PubMed] [Google Scholar]
- 42.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 43.Murphy, M. 1997. Octave: a free, high-level language for mathematics. Linux J. 7:39. [Google Scholar]
- 44.Atilgan, A., S. Durell, R. Jernigan, M. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Marques, O., and Y. Sanejouand. 1995. Hinge-bending motion in citrate synthase arising from normal mode calculations. Proteins. 23:557–560. [DOI] [PubMed] [Google Scholar]
- 46.Tama, F., and Y. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
- 47.Song, G., and R. L. Jernigan. 2006. An enhanced elastic network model to represent the motions of domain-swapped proteins. Proteins. 63:197–209. [DOI] [PubMed] [Google Scholar]