Energetics of Hydrophobic Matching in Lipid-Protein Interactions

Abstract

Lipid chain length modulates the activity of transmembrane proteins by mismatch between the hydrophobic span of the protein and that of the lipid membrane. Relative binding affinities of lipids with different chain lengths are used to estimate the excess free energy of lipid-protein interaction that arises from hydrophobic mismatch. For a wide range of integral proteins and peptides, the energy cost is much less than the elastic penalty of fully stretching or compressing the lipid chains to achieve complete hydrophobic matching. The chain length dependences of the free energies of lipid association are described by a model that combines elastic chain extension with a free energy term that depends linearly on the extent of residual mismatch. The excess free energy densities involved lie in the region of 0.5–2.0 k_BT.nm⁻². Values of this size could arise from exposure of hydrophobic groups to polar portions of the lipid or protein, but not directly to water, or alternatively from changes in tilt of the transmembrane helices that are energetically comparable to those activating mechanosensitive channels. The influence of hydrophobic mismatch on dimerization of transmembrane helices and their transfer between lipid vesicles, and on shifts in chain-melting transitions of lipid bilayers by incorporated proteins, is analyzed by using the same thermodynamic model. Segmental order parameters confirm that elastic lipid chain distortions are insufficient to compensate fully for the mismatch, but the dependence on chain length with tryptophan-anchored peptides requires that the free energy density of hydrophobic mismatch should increase with increasing extent of mismatch.

INTRODUCTION

The function of various membrane-bound enzymes and transporters is found to depend upon—and in a real sense to be controlled by—the chain length of the membrane lipids. In many cases, the enzyme or transport activity reaches a maximum at a certain lipid chain length and is strongly reduced in membranes with either much longer or much shorter lipid chains. Examples include cytochrome c oxidase and the F₁,F₀-ATPase (1), Ca-ATPase (2,3) and Na,K-ATPase (4,5), the MscL ion channel (6), and melibiose permease (7). Optimum activity is thought to be attained when the hydrophobic thickness of the lipid membrane matches the transmembrane hydrophobic span of the protein. The interfacial tension associated with the energetic penalty resulting from hydrophobic mismatch couples to functionally sensitive conformational changes and equilibria. For the Ca-ATPase, the kinetics of both phosphorylation and dephosphorylation depend on the chain length of the host lipid (8,9), as also does the stoichiometry of Ca²⁺ binding (10,11).

Direct insight into the energetics of hydrophobic matching can be obtained from the relative affinities of lipids with different chain lengths. Lee, East and co-workers have determined the equilibrium constants for association of a series of unsaturated phosphatidylcholines with a wide variety of integral proteins (12,13). These relative measurements can be translated directly into the free energy penalty of hydrophobic mismatch. The chain length dependence provides information on the various contributions to the energetics of mismatch. As reviewed by Killian (14,15), possible contributions are elastic distortions of the lipids, conformational distortions of the protein, tilting of transmembrane helices, and aggregation or dimer/oligomer formation of the protein. A further possibility that features strongly in the so-called “mattress” model (16,17) is residual exposure of hydrophobic groups to a hydrophilic environment.

In this work, the chain length dependence of the free energy of mismatch, derived from lipid association constants, is analyzed in terms of the most recent, high-resolution x-ray measurements of lipid bilayer thickness from liquid crystallography ((18,19) and see also (20)). The latter allow not only more accurate definition of the hydrophobic spans of the various proteins, but also—combined with the latest measurements of elastic moduli (21)—a far more precise estimate of the elastic cost of chain extension. The resulting thermodynamic model combines reliable estimates of the chain elastic energy with a free energy of mismatch that depends linearly on the extent of mismatch, in the spirit of the “mattress” model. The effective free energy densities of mismatch that are obtained from fitting the model to experimental lipid affinities provide information on their likely origin. Partial exposure of hydrophobic groups to a hydrophilic environment (but not to water) and/or changes in helix tilt are possible candidates.

Dimer formation by transmembrane peptides and their transfer between vesicles in response to hydrophobic mismatch, as well as the shifts in chain-melting transition induced by lipid-protein mismatch, are considered in light of the thermodynamic model for lipid binding. Finally, the model is also related to the extensions of the lipid chain that are derived from the changes in segmental order parameters by using ²H-NMR.

This work is organized as follows: 1), background x-ray (and ²H-NMR) data on bilayer thicknesses are summarized; 2), theoretical thermodynamic considerations of lipid elastic distortion (including quantitative estimates) and surface free energy densities of hydrophobic mismatch are presented, leading to the conditions for equilibrium; 3), free energy densities of mismatch and hydrophobic spans are derived from the chain length dependence of experimental lipid binding constants, according to the thermodynamic model; and finally 4), the model is applied to measurements of peptide dimerization, shifts in lipid transitions, and lipid chain extension.

BACKGROUND DATA

Almost invariably, experiments on hydrophobic matching have been interpreted by using bilayer thicknesses measured at moderate resolution with x-ray scattering, from which thicknesses of the hydrocarbon region were obtained by subtracting a fixed correction from the phosphate-phosphate separations (22). Higher resolution data are now available from a combination of different methods (18,19,23), and it is therefore preferable to use this newer data. A related issue is calibration of chain segmental order parameters from ²H-NMR to obtain absolute thicknesses of the hydrocarbon region (24,25). This necessary background information is given in the present section.

Chain length dependence of bilayer thickness

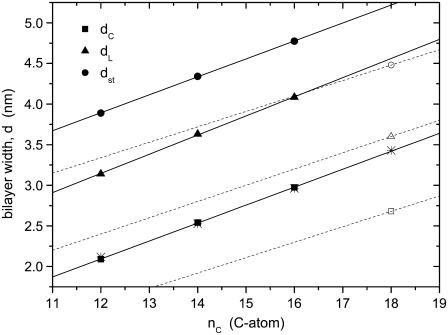
Fig. 1 shows the most recent x-ray refinements of the bilayer thicknesses for saturated phosphatidylcholines, diC(12:0)PtdCho and diC(14:0)PtdCho (18), and diC(16:0)PtdCho (23), in the fluid phase at 30°C. The data for diC(16:0)PtdCho at 50°C are corrected to a notional fluid phase at 30°C by using a thermal expansion coefficient of α_d = −0.0033 K⁻¹ (18). Data are given for the total (anhydrous) bilayer thickness, d_L, for the thickness of the hydrophobic core, d_c, and for the maximum steric thickness calculated from d_c by assuming a constant thickness of 0.9 nm for the headgroup region, i.e., d_st = d_c + 1.8 nm. The bilayer thickness increases linearly with hydrocarbon chain length for bilayers at the same temperature. This is true also if, instead, the data for diC(12:0)PtdCho and diC(14:0)PtdCho are corrected to 50°C by using the same expansion coefficient. An additional experimental rationale for using fixed temperature, rather than reduced temperature, comes from measurements with spin-labeled phospholipid chains (26), which exhibit very similar behavior at the same temperature in the fluid phase, independent of the chain length of the host bilayer.

FIGURE 1.

Chain length dependence, n_C, of the thickness of fluid diacyl phosphatidylcholine bilayers at 30°C. d_L is the anhydrous bilayer thickness (triangles), d_c is the thickness of the hydrocarbon core (squares), and d_st = d_c + 1.8 nm is the steric thickness of the bilayer (circles). Data for diC(12:0)PtdCho and diC(14:0)PtdCho at 30°C are from Kučerka et al. (18) (solid symbols), for diC(18:1)PtdCho and diC(22:1)PtdCho at 30°C are from Kučerka et al. (19) (open symbols), and for diC(16:0)PtdCho at 50°C, corrected to 30°C with an expansion coefficient α_d = (1/d)(∂d/∂T) = −0.0033 K⁻¹ (18) are from Kučerka et al. (23). Solid lines are linear regressions for saturated chains; dashed straight lines connect data for diC(18:1)PtdCho with that for diC(22:1)PtdCho (out of plot range) according to Eqs. 3 and 4. Asterisks are values of d_c derived from ²H-NMR order parameters of per-deuterated diC(n_C:0)PtdCho sn-2 chains (24), corrected to 30°C, with a constant offset adjusted to match best with the solid squares from x-ray diffraction (see text).

For the total bilayer thickness, the chain length dependence from the linear regression shown in Fig. 1 is

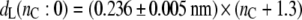(1)

and that for the thickness of the hydrocarbon core is

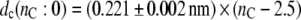(2)

for diC(n_C:0)PtdCho bilayers with saturated chains at 30°C.

Also shown in Fig. 1 is the bilayer thickness for unsaturated diC(18:1)PtdCho bilayers at 30°C (open symbols). The straight dashed lines are calculated from this data and corresponding thicknesses measured for diC(22:1)PtdCho bilayers at 30°C, by the same diffraction methods (19). This yields the following chain length dependences:

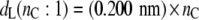(3)

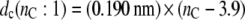(4)

for the thicknesses of diC(n_C:1)PtdCho bilayers with monounsaturated chains at 30°C.

Equations 2 and 4 will be used to interpret experiments on hydrophobic mismatch with saturated and monounsaturated diacyl phosphatidylcholines of different chain lengths. As seen from Fig. 1, it is important that these calibrations be corrected for thermal expansion, so as to correspond to the appropriate measurement temperature.

Chain segmental order parameters

Hydrophobic thicknesses of phosphatidylcholine bilayers can also be obtained from the order parameters of the chain segments, as measured by ²H-NMR (27,28). These have been used to monitor the response of the lipid chains to hydrophobic mismatch with transmembrane peptides (24,25,29), the advantage being that it is possible to deduce values for the extension of the lipid chains immediately adjacent to the protein (24,30). In terms of the mean order parameter, 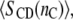of a chain segment CD bond, the thickness of the hydrocarbon core is given by (27)

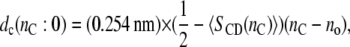(5)

where the length of an all-trans chain segment is 0.127 nm, and n_o allows for end effects. Fitting Eq. 5, with a fixed value of n_o and experimental values of the mean order parameters for the individual per-deuterated sn-2 chains (corrected to 30°C using α_d = −0.0033 K⁻¹) from de Planque et al. (24), to the x-ray diffraction results for n_C = 12, 14 and 16 yields the data given by the asterisks in Fig. 1. Linear regression to these data gives the following chain length dependence for the width of the hydrocarbon core:

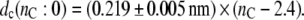(6)

This is the analog of Eq. 2, but incorporates the ²H-NMR data for the gradient of the chain length dependence. It and Eq. 5 will be used later to analyze the extent of elastic deformation of the lipid chains in response to hydrophobic mismatch.

THEORETICAL CONSIDERATIONS

The primary aim is to interpret the chain length dependence of lipid association constants because these are most directly related to the energetics of hydrophobic matching. The free energy associated with hydrophobic mismatch will contain terms from the elastic deformation of the lipids that takes place to reduce the mismatch, from residual uncompensated mismatch, and from any distortion of the protein. Elastic distortion of the lipids has a quadratic dependence on the mismatch (31), whereas the experimental free energies depend linearly on the extent of mismatch (32), as will be seen later. This experimental finding points to a dominant contribution from residual hydrophobic mismatch, and any other interaction that depends linearly on the degree of mismatch. These basic contributions to the free energy of lipid-protein interaction, and the balance of the corresponding forces at equilibrium, are considered in this section.

Energetics of lipid chain deformation: hydrophobic matching

The free energy of elastic chain extension that takes place to alleviate hydrophobic mismatch can be estimated from experimental measurements of the compressibility modulus, K_t, for the thickness of lipid membranes. The thickness elastic modulus (or Young's modulus) is defined for a uniform normal stress (i.e., force per unit area acting normal to the surface). The elastic free energy per lipid molecule that is associated with change in length, l_L, of the lipid is thus given by

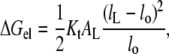(7)

where A_L is the membrane surface area per lipid molecule, and l_o is the length of the undistorted lipid molecule in free bilayers.

The elastic modulus for area extension of fluid diC(18:1)PtdCho bilayers is K_A = 265 ± 18 mN.m⁻¹ at 21°C (21) and the bilayer thickness is d_L = 3.72 nm, corrected to 21°C (33). The corresponding value for the thickness modulus is therefore K_t = K_A/d_L = (0.71 ± 0.05) × 10⁸ N.m⁻², assuming volume incompressibility (34). This value lies within the range of (0.5–0.8) × 10⁸ N.m⁻² reported for diC(18:1)PtdCho from osmotic swelling experiments (35). With a molecular area of A_L = 0.700 nm² for diC(18:1)PtdCho, corrected to 21°C (33), Eq. 7 then becomes

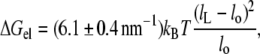(8)

where k_B is Boltzmann's constant, and T is the absolute temperature. Substituting from Eq. 3 for monounsaturated phosphatidylcholines, with l_o = d_L/2, then yields the following expression for the elastic free energy per lipid molecule:

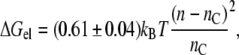(9)

where n is the effective value of the lipid chain length, n_C, that corresponds to d_L = 2l_L in Eq. 3. With the largest mismatch, n − n_C =5 (see below), Eq. 9 predicts an elastic energy cost of ΔG_el ≈ 1.5 k_BT per lipid for complete matching.

In principle, bending distortions of the membrane surface may also contribute to the elastic free energy cost of hydrophobic matching (see, e.g., 36,37,31). However, this is likely to be energetically less significant than the chain extension that is required to achieve matching. The maximum curvature that can be attained will correspond roughly to the outer radius of small, unilamellar, limit-sonicated vesicles, i.e., R ≈ 10–15 nm (38,39), which is also close to the intrinsic curvature of diC(18:1)PtdCho: R_o ≈ 10 nm (40). The maximum energy cost of bending is therefore ΔG_curv = (1/2)k_cA_L/R² ≈ 0.015–0.035 k_BT per lipid, with a bending rigidity of k_c ≈ 10 k_BT for a monolayer (41). Several shells of lipid would be associated with the surface curvature (to make physical sense), but even so the free energy per lipid is almost two orders of magnitude smaller than that for chain stretching.

Recent determinations of lipid binding constants at different lipid/protein ratios show that lipids beyond the first shell do not influence the energetics of association with the protein (42), and correspondingly continuum membrane surface bending cannot contribute significantly. Added to which, there is abundant evidence from lipid spin labels in both reconstituted membranes (43–45) and native membranes (46–49) that the perturbation of the lipid does not extend much beyond the first shell surrounding the protein.

Chain extension is therefore expected to be the energetically dominant contribution to the lipid distortions that take place to achieve hydrophobic matching, and Eq. 7 will be the leading term in the corresponding elastic energy. A harmonic dependence on hydrophobic mismatch, d_P − d_L, as in Eq. 7 for chain stretching, is a feature of several theoretical models for hydrophobic matching (e.g., 50,51), where it is assumed that the lipid distortion compensates for the full extent of mismatch (see left-hand side of Fig. 2). The mean-field calculations of Fattal and Ben-Shaul (52), which make this assumption and have been used as a reference for comparison with experimentally determined lipid binding constants (53,54), yield slightly higher free energies (coefficient ∼7.4 k_BT nm⁻¹) than the experimental estimate in Eq. 8 (55). In part, this may be because lipids beyond the first boundary shell also suffer limited elastic deformation. To first order, this would not be included in the free energy of lipid association that is determined from equilibrium constants by the usual experimental procedures, as was already noted above (see Powl et al. (42)).

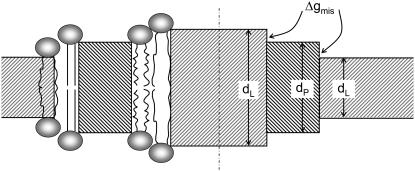
FIGURE 2.

Schematic indication of hydrophobic mismatch. (On the left) The lipid chains extend or compress to compensate for the mismatch in hydrophobic spans of the lipid bilayer (d_L) and the protein (d_P). (On the right) Mismatch imposes an energy penalty from exposure of hydrophobic surfaces of the lipid or protein to a hydrophilic environment of the corresponding partner. The energy cost is equal to the product of the free energy density of exposure, Δg_mis, and the area of exposed interface. In the two outer regions of the lipid bilayer (d_L < d_P), the hydrophobic thickness of the protein exceeds that of the lipid; in the central region of the bilayer (d_L > d_P), the hydrophobic thickness of the lipid exceeds that of the protein.

Continuum elastic treatments of lipid-protein interactions that include surface bending also predict a quadratic dependence of the deformation energy, ΔG_el, on the extent of mismatch, as in Eq. 7, but the effective spring constant is a hybrid between K_A and the bending rigidity, k_c, although weighted in favor of the former (31,56). Recent estimates of deformation energy from continuum elasticity correspond to a coefficient of 8.4 k_BT nm⁻¹ in Eq. 8, if the contact slope at the protein surface is taken to be that which minimizes the deformation free energy, but twice this value if a boundary condition with zero contact slope is assumed (56). Therefore, under conditions where surface bending contributes and continuum elasticity theory may apply, the elastic deformation energy is predicted to be larger—although not necessarily much larger—than that estimated for lipid extension-compression by using Eq. 9. In this case, elastic distortion will be of even lesser significance, relative to residual hydrophobic exposure, than is predicted from Eq. 9.

Equation 9 will be used to account for the energetic cost of lipid chain deformation. It should be adequate for situations, such as lipid binding, in which only the first shell of lipids surrounding the protein is involved (see Williamson et al. (32)). If continuum elasticity plays a role, Eq. 9 will only tend to overestimate the significance of elastic distortion. But, as already stated, the major contribution comes from a free energy term that is linear in the extent of mismatch; this is dealt with in the subsection that immediately follows.

Interfacial free energy density of lipid-protein mismatch

As will be seen later, the elastic energies predicted by Eq. 9 are too large, in most cases, to achieve complete hydrophobic matching (53,54) and, moreover, they cannot account for the approximately linear dependence of lipid binding free energies on hydrocarbon chain length (32). A possible interpretation, which is embedded in the “mattress” model of Mouritsen and Bloom (16), is that hydrophobic regions of the protein or lipid chains are exposed to the polar groups of, respectively, the lipids or protein (see right-hand side of Fig. 2), when this becomes energetically less costly than further elastic distortion of the lipids. Experimental support for this is provided by ²H-NMR measurements of chain extension, which is found to be inadequate to compensate for the hydrophobic mismatch with α-helical transmembrane peptides (24,25).

Assuming energetic equivalence in hydrophobic exposure of lipid and protein, the free energy of residual hydrophobic mismatch, per lipid molecule, is given by

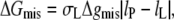(10)

where Δg_mis is the free energy density of hydrophobic-polar interaction (per unit area of lipid-protein interface) in the mismatch region, σ_L is the width of a lipid molecule at the lipid-protein interface, and l_P (= d_P/2) is half the hydrophobic thickness of the protein. The width of a single lipid chain is ∼√(A_L/2) = 0.600 nm in fluid-phase bilayers of diC(18:1)PtdCho (33). Hence, the width of a diacyl lipid molecule can be taken as σ_L = 1.20 nm. Equation 10 is valid for lipid extensions 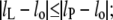otherwise 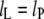and the elastic extension fully compensates for the mismatch.

The free energy density, Δg_mis, in Eq. 10 is equivalent to a surface tension at the lipid-protein interface. As such, it has been used to interpret the effects of lipid-protein interactions on conformational equilibria by using the Laplace equation for the lateral pressure across a cylindrical interface (13,57). It can be shown that this latter approach is identical to the formulation given here in terms of a free energy density (58). Formally, Δg_mis also corresponds to the “solubility parameter” ɛ for hydrophobic-hydrophilic contact in the mattress model (16).

It should be noted that Eq. 10 must not inevitably imply exposure of hydrophobic groups on the lipid or protein. Among other things, this depends on the size of the effective excess free energy density. Phenomenologically, Eq. 10 can describe any process that alleviates hydrophobic exposure and involves a free energy penalty that depends approximately linearly on the extent of mismatch. Possible candidates are conformational changes of the protein, for example, the tilting of transmembrane helices (12,32).

Together with Eq. 7 for elastic distortion, Eq. 10 defines the thermodynamic model for hydrophobic mismatch. Thermodynamic equilibrium is defined by the balance of the corresponding forces that is treated in the next subsection.

Equilibrium extension of interfacial lipids

The net contribution of hydrophobic mismatch to the free energy of lipid-protein interaction, according to the above model, is given by: ΔG_LP = ΔG_el + ΔG_mis. Hence, from Eqs. 7 and 10, the excess free energy per lipid molecule is

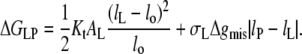(11)

The second term is required in this equation whenever the absolute value of degree of extension is 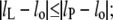otherwise the free energy is given by the first term only (i.e., Eq. 7) with The condition for minimum free energy (∂ΔG_LP/∂l_L = 0), according to Eq. 11, yields an equilibrium length of the protein-associated lipids that is given by

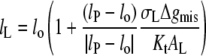(12)

for l_o ≠ l_P. The criterion for inclusion of the second term in Eq. 11 is therefore 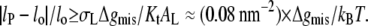For the values of Δg_mis found subsequently, this corresponds to fractional mismatches of 4–8%, i.e., ∼1–2 CH₂ groups, which is met in all except the regions very close to hydrophobic matching. Substituting from Eq. 12 in Eq. 11 then yields

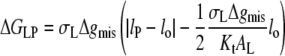(13)

for the excess free energy of lipid-protein interaction at equilibrium. Again substituting from Eq. 3 for monounsaturated phosphatidylcholines (with l_o = d_L/2) and using the value of K_tA_L given above, the dependence of the free energy per lipid molecule on chain length, n_C, is given by

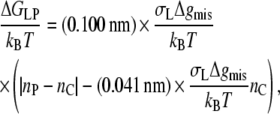(14)

where n_P is the effective value of the lipid chain length, n_C, that corresponds to d_L = 2l_P, i.e., to the hydrophobic thickness of the protein, in Eq. 3. The free energy of lipid-protein interaction therefore depends linearly on lipid chain length, with an asymmetry about the point of hydrophobic matching, n_C = n_P. The extent of the asymmetry depends directly on the ratio of the interfacial free energy density of mismatch to that of elastic extension, i.e., on Δg_mis/K_t (see Eq. 13). The lipid binding energies given below depend bilinearly on chain length as is predicted by Eq. 14, but the asymmetry about the point of matching is small, i.e., the first term in Eq. 14 (which derives directly from Eq. 10) is the dominant one.

EXPERIMENTAL QUANTIFICATION

As already stated in the previous main section, the aim of the thermodynamic model is to interpret the chain length dependence of the lipid binding constants. Fitting the model to the experimental data then yields effective free energy densities of hydrophobic mismatch, Δg_mis, and hydrophobic spans, d_c, for the individual proteins. This is dealt with in the present section, including also an experimental estimate of the possible energy cost for helix tilting.

Lipid binding constants

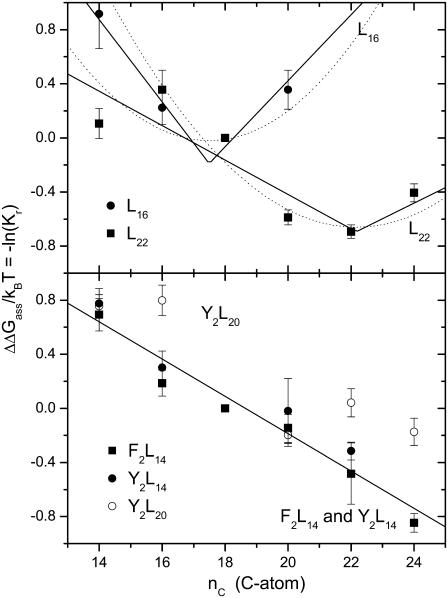
The most direct measure of the energetic cost of hydrophobic mismatch comes from the relative affinities for the protein of lipids with different chain lengths. Fig. 3 shows the relative equilibrium constants, K_r, for association of phosphatidylcholines of different chain lengths with α-helical transmembrane peptides of the type K₂GL_mWL_m+2K₂A (abbreviated L_2m+2) that have different hydrophobic lengths, or contain different aromatic anchoring residues. The relative association constants are determined by tryptophan fluorescence quenching with brominated lipids and are taken from the work of Webb et al. (59) and Mall et al. (60). The upper panel of Fig. 3 shows the effect of hydrophobic mismatch between the lipid membrane and the two peptides L₁₆ and L₂₂. The relative free energy of association, ΔΔG_ass/k_BT = −ln(K_r), reaches a minimum at lipid chain lengths of approximately n_C = 18 and n_C = 22 for peptides L₁₆ and L₂₂, respectively. As seen from the dotted lines in the upper panel of Fig. 3, the predictions of Eq. 9 for the elastic cost of achieving full hydrophobic matching agree fairly well with the experimental lipid association constants for low degrees of mismatch. Only the zero-level for ΔΔG_ass, and the chain length, n (≡ n_P), for hydrophobic matching are adjusted in these calculations. However, Eq. 14 gives a better description of the dependence of ΔΔG_ass on lipid chain length over a wider range of values of n_C. The solid lines in the upper panel of Fig. 3 are least-squares fits of Eq. 14 to the data for L₁₆ and L₂₂; the fitting parameters are n_P and the product σ_LΔg_mis. The values of the free energy density, Δg_mis, that are obtained from such fits are given for these and other peptides and proteins in Table 1.

FIGURE 3.

Chain length dependence of the phosphatidylcholine association constants, K_r, relative to diC(18:1)PtdCho, for association with transmembrane oligoleucine helical peptides with different lengths and different anchoring groups. The different chain length phosphatidylcholines are diC(14:1cΔ⁹)PtdCho, diC(16:1cΔ⁹)PtdCho, diC(18:1cΔ⁹)PtdCho, diC(20:1cΔ¹¹)PtdCho, diC(22:1cΔ¹³)PtdCho, and diC(24:1cΔ¹⁵)PtdCho. The ordinate is plotted to yield the free energy of association ΔΔG_ass/k_BT = −lnK_r, relative to diC(18:1)PtdCho. (Upper panel) Ac-K₂GL₇WL₉K₂A-amide (L₁₆) and Ac-K₂GFL₁₀WL₁₂FK₂A-amide (L₂₂) (data from Web et al. (59)). Error bars are given for a representative ±0.1 uncertainty in K_r. (Solid lines) Least squares fits of Eqn. 14 with the parameters Δg_mis and n_P that are given in Tables 1 and 2, respectively. (Dotted lines) Predictions of Eq. 9 with n = n_P. (Lower panel) Ac-K₂GFL₆WL₈FK₂A-amide (F₂L₁₄), Ac-K₂GYL₆WL₈YK₂A-amide (Y₂L₁₄), and Ac-K₂GYL₉WL₁₁YK₂A-amide (Y₂L₂₀) (data from Mall et al. (60)). (Solid line) Least-squares fit of Eq. 14, with fixed n_P = 25, to the combined data for F₂L₁₄ and Y₂L₁₄.

TABLE 1.

Free energy density of hydrophobic mismatch, Δg_mis, obtained from the chain length dependence of lipid association constants for transmembrane peptides and proteins by fitting with Eq. 14

Peptide/protein	Δgmis/kBT (nm−2)	R	Δl/lo*
L16	2.29 ± 0.45	0.987	0.22 ± 0.06
L22	1.01 ± 0.36	0.882	0.10 ± 0.04
Y2L14 and F2L14	1.09 ± 0.09	0.970	0.11 ± 0.02
KcsA	0.74 ± 0.09	0.967	0.07 ± 0.01
SERCA	0.57 ± 0.35	0.830	0.06 ± 0.04
TbMscL† total	0.49 ± 0.13	0.912	0.05 ± 0.02
Cytoplasmic	0.85 ± 0.25	0.896	0.08 ± 0.03
Periplasmic	0.72 ± 0.16	0.919	0.07 ± 0.02
EcMscL	0.97 ± 0.12	0.973	0.09 ± 0.02
OmpF	1.26 ± 0.12	0.990	0.12 ± 0.02

A value of σ_L = 1.2 nm is used for the width of a lipid molecule. R is the effective regression coefficient.

^*Fractional extension in length of the lipid molecule, predicted from Eq. 12.

^†Values are obtained from quenching of a centrally located tryptophan W⁸⁰ (total), or a tryptophan located either at the cytoplasmic (W⁸⁷) or periplasmic (W⁶⁹) face of MscL.

The lower panel of Fig. 3 shows the effect of adding aromatic anchoring groups, tyrosine (in Y₂L₁₄ or Y₂L₂₀) or phenylalanine (in F₂L₁₄), which replace the outermost leucines in the lysine-anchored L₁₆ or L₂₂ peptides. In these cases, there is no clear minimum in the free energy of association. The values of ΔΔG_ass for Y₂L₁₄ and for F₂L₁₄ decrease monotonically with increasing chain length in an approximately linear fashion. The solid line in the lower panel of Fig. 3 is a least-squares fit of Eq. 14, with fixed n_P ≥ 24 (equivalent to a linear regression), to the combined data from the Y₂L₁₄ and F₂L₁₄ peptides. The slope of the chain length dependence is less for Y₂L₁₄ and F₂L₁₄ than for L₁₆ (see Table 1). This suggests that the additional aromatic residues achieve more efficient (or more adaptable) hydrophobic matching than do the lysine residues alone. The longer peptide Y₂L₂₀ does not display such a pronounced dependence of the lipid association on chain length (for n_C > 16) as do the shorter Y₂L₁₄ and F₂L₁₄ peptides.

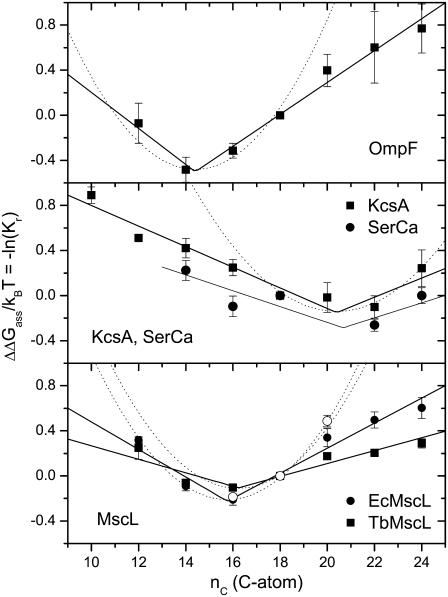
Fig. 4 shows the chain length dependence of the lipid association constants for different transmembrane proteins. These are the β-barrel, trimeric porin OmpF from Escherichia coli (53), the α-helical, homotetrameric potassium channel protein KcsA from Streptomyces lividans (32), the SERCA Ca-ATPase from sarcoplasmic reticulum of skeletal muscle (61), which contains 10 transmembrane helices, and the mechanosensitive channel of large conductance MscL from E. coli (EcMscL) and from Mycobacterium tuberculosis (TbMscL), which is an α-helical homopentamer (54). The values of K_r are obtained by the same fluorescence quenching method as used with the peptides, and the data originate from the same laboratory.

FIGURE 4.

Chain length dependence of the phosphatidylcholine association constants, K_r, relative to diC(18:1)PtdCho, for association with (upper to lower panels): E. coli outer membrane porin, OmpF (data from O'Keeffe et al. (53)); S. lividans K⁺-channel, KcsA (squares) (data from Williamson et al. (32)) and Ca-ATPase, SERCA (circles) (data from East and Lee (61)); and E. coli (solid circles) and M. tuberculosis (squares) mechanosensitive channel of large conductance, EcMscL and TbMscL, respectively (data from Powl et al. (54)). The different chain length phosphatidylcholines are diC(10:0)PtdCho, diC(12:0)PtdCho, diC(14:1cΔ⁹)PtdCho, diC(16:1cΔ⁹)PtdCho, diC(18:1cΔ⁹)PtdCho, diC(20:1cΔ¹¹)PtdCho, diC(22:1cΔ¹³)PtdCho, and diC(24:1cΔ¹⁵)PtdCho. In the case of MscL and KcsA, values are the means of determinations with brominated phosphatidylcholines, relative to unmodified diC(18:1)PtdCho, and those with unmodified phosphatidylcholines, relative to brominated diC(18:1)PtdCho. The ordinate is plotted to yield the relative free energy of association ΔΔG_ass/k_BT = −ln(K_r). Solid lines are least-squares fits of Eq. 14; dotted lines are the predictions of Eq. 9 with n = n_P. Open circles in the bottom panel are the free energies of opening the E. coli MscL channel at zero tension (data from Perozo et al. (6)), expressed per lipid with N_L = 29, and relative to diC(18:1)PtdCho bilayers as reference state.

In most cases, the free energy of association with the transmembrane proteins achieves a minimum at a characteristic lipid chain length, n_C = n_P. Unlike the situation with the L₁₆ and L₂₂ peptides, however, the minimum is much shallower than that predicted by Eq. 9 for an elastic distortion that fully compensates the hydrophobic mismatch (see dotted lines in Fig. 4). As pointed out for KcsA by the original authors (32), the chain length dependence of ΔΔG_ass is essentially linear over an appreciable range of n_C, as predicted by the model embodied in Eq. 14 (see solid lines in Fig. 3). In this respect, the response to hydrophobic mismatch of the transmembrane proteins resembles more closely that of the Y₂L₁₄ and F₂L₁₄ peptides than that of the L₁₆ and L₂₂ peptides, which are anchored solely by lysine residues. The values of the free energy density, Δg_mis, which are obtained from fitting Eq. 14 for the different transmembrane proteins, are listed in Table 1.

A functional comparison with the lipid association constants is afforded by the open circles in the bottom panel of Fig. 4. These are the data of Perozo et al. (6) for the free energy of opening the E. coli MscL channel, which is obtained from values of the tension needed to achieve 50% open channels. To compare with the free energy of lipid association, the values are divided by the number of lipid molecules in the first shell surrounding MscL, N_L = 29 (54), and are referred to ΔΔG_open = 0 for MscL in diC(18:1)PtdCho bilayers. The agreement with the lipid binding data is rather remarkable, indicating that hydrophobic mismatch is responsible for the chain length dependence of both, although nonlinearity is more pronounced for diC(20:1)PtdCho in the case of the channel opening data.

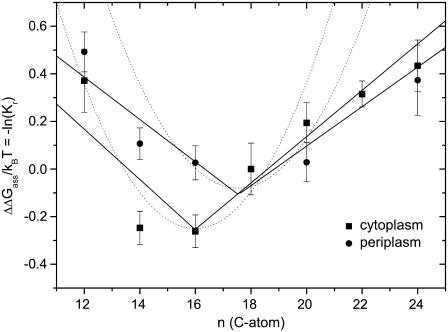
Interestingly, a marked transmembrane asymmetry in hydrophobic matching with the MscL mechanosensitive channel from M. tuberculosis was found recently by Powl et al. (42). Fluorescence quenching of a single tryptophan residue placed either on the periplasmic or on the cytoplasmic side of MscL was induced by brominated lipids. Fig. 5 shows the chain length dependence of the relative lipid association constants at the two faces of MscL. The minimum in the free energy of lipid association, ΔΔG_ass, which corresponds to hydrophobic matching with the protein, is more pronounced (and deeper) on the cytoplasmic side than it is on the periplasmic side of MscL. Also, the free energy of association with the cytoplasmic side of MscL conforms better to the predictions of Eq. 9 with n = n_P than it does with the periplasmic side (see dotted lines in Fig. 5). Nonetheless, ΔΔG_ass increases approximately linearly with phosphatidylcholine chain length in the range above the point of hydrophobic matching, for both the cytoplasmic and periplasmic sides of MscL (solid lines in Fig. 5), in accordance with Eq. 14, just as does the mean value of ΔΔG_ass for the whole protein in Fig. 4. Values of the free energy density, Δg_mis, obtained from the corresponding fits with Eq. 14, are also included in Table 1.

FIGURE 5.

Chain length dependence of the phosphatidylcholine association constants, K_r, relative to diC(18:1)PtdCho, for association with the cytoplasmic (squares) and the periplasmic (circles) faces of the M. tuberculosis MscL channel (data from Powl et al. 42). The different chain length phosphatidylcholines are diC(12:0)PtdCho, diC(14:1cΔ⁹)PtdCho, diC(16:1cΔ⁹)PtdCho, diC(18:1cΔ⁹)PtdCho, diC(20:1cΔ¹¹)PtdCho, diC(22:1cΔ¹³)PtdCho, and diC(24:1cΔ¹⁵)PtdCho. The ordinate is plotted to yield the relative free energy of association ΔΔG_ass/k_BT = −ln(K_r). Solid lines are least-squares fits of Eq. 14; dotted lines are the predictions of Eq. 9 with n = n_P.

The basic thermodynamic model, Eq. 13, therefore describes the chain length dependence of the free energy of lipid-protein interaction quite adequately. Only at low degrees of mismatch (∼2 CH₂) might elastic distortion of the lipid be energetically compatible with full compensation of the hydrophobic mismatch.

Free energy density of lipid-protein association

Table 1 lists the excess free energy densities for interaction of the lipid chains with the protein (per unit area of lipid-protein interface) that are obtained from the lipid association constants. For comparison with Table 1, a value of Δg_mis/k_BT = 0.255 ± 0.015 per CH₂ was obtained with spin-label electron paramagnetic resonance for bovine rhodopsin reconstituted in disaturated phosphatidylcholines (62), and of 0.12 ± 0.01 per CH₂ by fluorescence quenching for SERCA Ca-ATPase reconstituted in trans-monounsaturated phosphatidylcholines (63). From the incremental length per CH₂ group (0.110 ± 0.001 nm in Eq. 2) and the width of a lipid molecule (σ_L = 1.20 nm), this translates to free energy densities of 1.93 ± 0.11 nm⁻² and 0.91 ± 0.08 nm⁻², respectively. For further comparison, a free energy density (or solubility parameter) of 2ɛ/k_BT ≃ 0.54 ± 0.08 nm⁻² was estimated by fitting protein-induced experimental shifts in lipid chain-melting transition temperature with the mattress model (17). These values for Δg_mis are of a magnitude similar to those found here and reported in Table 1. In fitting the mattress model, the value of 2ɛ corresponds to a mismatch with n_C > n_P, whereas a value half this was assumed for a mismatch with n_C < n_P (17). However, the experimental data in Figs. 3 and 4 and the fitted values of Δg_mis given in Table 1 evidence no such pronounced asymmetry.

According to Eq. 12, the size of the effective free energy density, Δg_mis, arising from hydrophobic exposure determines the extent of lipid distortion that takes place in response to hydrophobic mismatch. Values for the relative chain extension, Δl/l_o ≡ (l_L − l_o)/l_o, that are calculated from the corresponding values of Δg_mis by using Eq. 12 are included in Table 1. These can be taken as indicating the fraction of hydrophobic mismatch that is compensated by the elastic distortion of the lipids. The values lie in the range 5–12%, except for the L₁₆ peptide where the value reaches 22%. It should be noted that the asymmetries of the bilinear fits in Figs. 3–5 are correspondingly small, which indicates that the free energies of lipid-protein interaction are dominated by the first term in Eqs. 13 and 14, i.e., by the free energy of uncompensated mismatch that is described by the bilinear dependence given in Eq. 10. This implies that the values obtained for the free energy densities in Table 1 are rather insensitive to the precise value of K_t that is used in the fits, and correspondingly are also insensitive to the exact details of the elastic distortions.

The interfacial free energy densities, Δg_mis, for interaction with the lipid hydrocarbon chains that are given in Table 1, are much less than the interfacial free energy density for the hydrophobic interaction of hydrocarbon chains with bulk water: γ_phob ∼ 8.5 × k_BT nm⁻² (35 mN.m⁻¹; (64–66)). This clearly demonstrates that hydrophobic groups are not exposed to water as a result of the mismatch between lipids and protein. The energetic penalty of mismatch is much lower than that of hydrophobic exposure to water. As reasoned by Sperotto and Mouritsen (17), the excess free energy density corresponds rather to the interaction of hydrophobic groups with a hydrophilic environment: either polar protein side chains or phospholipid headgroups. In this interpretation, the free energy density of hydrophobic-hydrophilic contact can be up to 17 times less than that of hydrophobic contact with bulk water and can vary by up to a factor of 4 (see Table 1).

As mentioned already, the effective values of Δg_mis must not necessarily be interpreted in terms of hydrophobic exposure to a hydrophilic environment. Alternatively, they can quantify any conformational change, or other process alleviating hydrophobic exposure, that involves a free energy penalty, which depends linearly on the extent of mismatch. A reason advanced previously for the relatively weak dependence of lipid binding on chain length is that the protein may distort to alleviate mismatch with the hydrophobic span of the lipid chains (12,32). Indeed it is found that the fluorescence properties (and hence environmental polarity) of the two interfacial bands of tryptophans in KcsA change relatively little with lipid chain length (32). Perhaps significantly also, of the transmembrane proteins in Table 1, the relatively rigid β-barrel protein OmpF has the steepest dependence of lipid association free energy on chain length. The possibility of adaptation by the protein is considered in the next section.

To summarize, viewed as interfacial free energy densities, the values of Δg_mis are far smaller than those involved in the classic hydrophobic exposure of hydrocarbon to water. The relatively low values predict that only a small fraction of the mismatch is compensated by lipid distortion, in agreement with observation (24,25). The small values may correspond to the exposure of hydrophobic groups to a polar environment, but not to bulk water, or may correspond to energetically facile conformational changes.

Energetics of protein deformation

It might be expected that deformation of the protein, like that of the lipid, is accompanied by some elastic penalty. The bulk elastic modulus for protein volume is generally in the region of K_V ∼ (0.4–1) × 10⁹ N.m⁻² (67), which represents deformations that are almost an order of magnitude energetically more costly than those of lipid thickness, which are characterized by an elastic modulus of K_t ∼ 0.7 × 10⁸ N.m⁻². Whereas this bulk modulus might be appropriate to thickness changes in relatively rigid β-barrel proteins, it is unlikely to be applicable for α-helical transmembrane proteins. In the latter case, protein deformations are thought to take place via changes in tilt of the transmembrane helices (12).

A lower estimate for the energetic cost of helix tilt deformations is afforded by the response of the mechanosensitive channel, MscL, to changes in membrane tension. In the latter case, the free energy of channel opening is linear in the membrane tension (68),

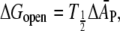(15)

where T_1/2 is the tension for 50% probability of channel opening and 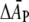is the mean increase in cross-sectional area of the channel on opening. If it is assumed from Eq. 15 that the free energy is effectively linear in the area change, then the value of T_1/2 ≈ 11.8 ± 0.8 mN.m⁻¹ for E. coli MscL (68) sets the energy scale for distortion of the protein thickness. With volume incompressibility (cf. above), the change in protein thickness, d_P, is given by ΔA_P/A_P = −Δd_P/d_P, where the latter can be identified approximately with the fractional change in lipid length. If N_L ∼ 29 (corresponding to a protein outer radius of 2.15 nm; (54)) is the number of first-shell phospholipids surrounding MscL, then the free energy of protein deformation per lipid is estimated as

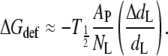(16)

Substituting from Eq. 3 then finally yields

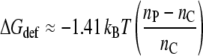(17)

as the contribution of the protein deformation to the free energy of lipid association for dimonounsaturated phosphatidylcholines.

Equation 17 predicts values of (1/k_BT)(∂ΔG_def/∂n_C) ≈ 0.06–0.12 for n_C = 20–14, respectively. This translates to free energy densities Δg_def/k_BT ≈ 0.5–1.0 nm⁻², which are similar in magnitude to the experimental values that are given in Table 1. It should be noted that direct determination of the free energy of channel opening in the absence of tension (see open symbols in the bottom panel of Fig. 4) yields a somewhat steeper dependence on chain length between n_C = 18 and n_C = 20 than does the lipid binding. Thus, helix tilting may not be the sole contribution to the rather shallow chain length dependence of lipid association at higher extents of mismatch. Nonetheless, it appears that protein deformation, via helix tilting, is a quantitatively viable alternative to the exposure of hydrophobic groups to a polar membrane environment.

Hydrophobic thicknesses

The minima in free energy of lipid association in Figs. 3–5 define the chain length, n_P, of the lipid that gives rise to hydrophobic matching. Recent refinements of lipid bilayer thicknesses from x-ray diffraction that are embodied in Eqs. 1–4 afford an improved estimate of the functional hydrophobic span of the proteins for which the chain length dependence of lipid association has been determined. The values of n_P, and the hydrophobic thicknesses, d_c, that are deduced from them by using Eq. 4, are listed in Table 2. For comparison, transmembrane hydrophobic spans that are derived from structures of the proteins (12) are also given in Table 2. More recently, hydrophobic thicknesses have been estimated theoretically from the energetics of inserting the protein crystal structures in a hydrophobic membrane environment (69), using an experimentally based boundary function (70). These values, as listed in the Orientation of Proteins (OPM) database (71), are also given in Table 2. The values for hydrophobic thickness derived from lipid binding experiments, together with consistent measurements of bilayer thickness, lie either between, or close to, the two theoretical estimates. The one exception is OmpF, which nonetheless bears out the expectation that outer-membrane β-barrel proteins have shorter hydrophobic thicknesses than other transmembrane proteins. Mostly, the precision in the estimates obtained here by fitting the chain length dependence is higher than that from either of the single-point estimates on individual protein structures (see Table 2).

TABLE 2.

Hydrophobic thickness (nm) of transmembrane peptides and proteins, and matching to lipid bilayers

	OPM*	Structure†	nP	dc (nm)
L16	–	2.7	17.5 ± 0.3	2.58 ± 0.05
L22	–	3.6	22.2 ± 1.2	3.47 ± 0.30
OmpF	2.42 ± 0.08	2.4	14.4 ± 0.3	2.00 ± 0.05
KcsA	3.31 ± 0.10	3.7	20.4 ± 0.5	3.13 ± 0.10
TbMscL	2.65 ± 0.38	1.8 or 3.4	16.2 ± 0.6	2.34 ± 0.11
EcMscL			15.8 ± 0.3	2.25 ± 0.06
SERCA	3.01 ± 0.18	2.1	20.7 ± 1.3	3.18 ± 0.24

n_P is the chain length of the diC(n_C:1)PtdCho with lowest free energy of association that is obtained by fitting with Eq. 14. d_c is the thickness of the hydrophobic core deduced from n_P by using Eq. 4.

^*Hydrophobic thickness deduced from thermodynamic principles, as listed in the OPM database (http://opm.phar.umich.edu/).

^†Hydrophobic thickness deduced from peptide or protein structure as given by Webb et al. (59) for peptides and by Lee (12) for proteins. Uncertainty for proteins is >±0.1 nm (A. G. Lee, University of Southampton, private communication, 2005).

Criteria other than lipid association have also been used to assess hydrophobic matching. Rotational diffusion measurements of bovine rhodopsin in disaturated phosphatidylcholine membranes suggest that the matching lipid chain length is n_P ≈ 15, which corresponds to a value of d_c = 2.8 nm from Eq. 2 (62). This is significantly less than the hydrophobic span estimated from the structure of rhodopsin: 3.24 ± 0.17 nm for the monomer and 3.05 ± 0.14 nm for the dimer (71). However, the total membrane thickness of d_L = 3.9 ± 0.1 nm from Eq. 1 corresponds rather more closely to that of the whole protein, which is estimated to be 4.1 nm from the crystal structure of bovine rhodopsin (72).

Various studies have indicated an optimum chain length in dimonounsaturated phosphatidylcholines for functional activity of different transmembrane proteins. The transport activities of melibiose permease from E. coli are optimum in diC(16:1)PtdCho (7), for which d_c = 2.30 nm from Eq. 4. On the other hand, the OPM database reports a hydrophobic thickness of 3.19 ± 0.12 nm for the analogous lac permease from E. coli. Activity optima for cytochrome c oxidase and the F₁F_o-ATPase from bovine mitochondria are found in diC(18:1)PtdCho (1) for which d_c = 2.68 nm at 30°C (33). For comparison, the OPM database reports hydrophobic thicknesses of 2.54 ± 0.18 nm for bovine cytochrome oxidase, and 3.59 ± 0.18 nm for the F_o-assembly from E. coli. The structural estimate for bovine cytochrome c oxidase is 2.9 nm (12). Agreement is thus good for bovine cytochrome c oxidase, but not for the F₁F_o-ATPase. An activity maximum in diC(22:1)PtdCho (i.e., d_c = 3.44 nm) is reported for the Na,K-ATPase (5). The three-dimensional structure of this protein is not known at high resolution, although it is closely related to SERCA Ca-ATPase (see Table 2), which is a similar P-type ATPase. For SERCA itself, the activity optimum corresponds approximately to a C(17:1) chain length (11), for which d_c = 2.49 nm, as opposed to the C(21:1) chain length for optimum lipid association (see Table 2).

On the whole, the hydrophobic thicknesses deduced from lipid binding are in reasonable agreement with those deduced from the structures, when using the new values for lipid thicknesses (i.e., Eqs. 2 and 4). Those deduced from activities, however, are less consistent and, in some cases, indicate that functional response to hydrophobic mismatch is more complex than that of simple lipid association.

FURTHER APPLICATIONS

The thermodynamic model was developed to describe the chain length dependence of free energies derived directly from lipid association constants. Here it is now applied to various other experimental measurements that are sensitive to hydrophobic mismatch.

Self-association of transmembrane helices

Formation of a helix-dimer interface involves removal of ΔN_L lipids from contact with each helix. Hence, dimer formation will alleviate hydrophobic mismatch and the mole fraction, X_D, of dimers will depend upon the lipid chain length. The free energy of dimer formation is given by

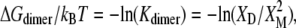(18)

where X_M is the mole fraction of monomers. Mole fraction units are used to distinguish lipid-protein interactions and intradimer interactions from the entropy of mixing (73).

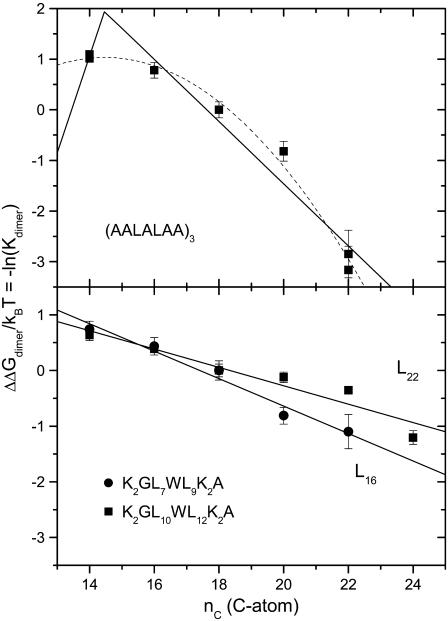
Fig. 6 shows the association constants (K_dimer) for dimer formation of α-helical transmembrane peptides in bilayers of dimonounsaturated phosphatidylcholines with different chain lengths. Formation of antiparallel dimers of Ac-(AALALAA)₃-amide, thought to be driven by alignment of helix dipoles, was monitored by Yano and Matsuzaki (74) from energy transfer between donors and acceptors at the N- and C-termini, respectively. As seen from the upper panel of Fig. 6, the free energy of dimer formation depends nonlinearly on the chain length of the host lipid bilayer. Although a well-defined maximum is not obtained, fitting only Eq. 9, with adjustable amplitude (i.e., ΔG_dimer = −ΔN_LΔG_el), yields a value of n (≡ n_P) = 14.5 ± 0.6 for the optimum matching, which corresponds to a thickness of the bilayer hydrocarbon core of d_c = 2.00 ± 0.12 nm from Eq. 4 and a total bilayer thickness of d_L = 2.89 ± 0.13 nm from Eq. 3. For comparison, the distance between outermost leucine residues is 2.3 nm, allowing for a 15° tilt (74), and the total length of the peptide is 2.9 nm. Additionally, a relatively low value of ΔN_L = 1.7 ± 0.4 is obtained for the number of lipids displaced per dimer, in this model.

FIGURE 6.

Lipid chain length dependence of the association constant for dimer formation, K_dimer, of transmembrane helical peptides. The phosphatidylcholine lipid hosts are diC(14:1cΔ⁹)PtdCho, diC(16:1cΔ⁹)PtdCho, diC(18:1cΔ⁹)PtdCho, diC(20:1cΔ¹¹)PtdCho, diC(22:1cΔ¹³)PtdCho, and diC(24:1cΔ¹⁵)PtdCho. The ordinate is plotted as the free energy of dimerization ΔΔG_dimer/k_BT = −ln(K_dimer), and values are given relative to diC(18:1)PtdCho. (Upper panel) Ac-(AALALAA)₃-amide antiparallel heterodimers with energy-transfer fluorophore couples at either N- or C-terminus (data from Yano and Matsuzaki (74)). Peptide is given a double weighting with respect to lipid in calculating mole fractions because it spans both halves of the bilayer. (Dotted line) Prediction of Eq. 9 with optimization of n_P = 14.5 ± 0.6 and an adjustable multiplicative factor ΔN_L = 1.7 ± 0.4. (Solid line) Least-squares fit of Eq. 14 with fixed n_P = 14.5 and the optimized value of ΔN_LΔg_mis/k_BT given in Table 3. (Lower panel) Ac-K₂GL₇WL₉K₂A-amide (L₁₆) and Ac-K₂GL₁₀WL₁₂K₂A-amide (L₂₂) heterodimers with the corresponding quencher peptides bearing dibromotyrosine instead of tryptophan (data from Mall et al. (76)). Solid lines are least-squares fits of Eq. 14 with fixed n_P = 14 and optimized values of ΔN_LΔg_mis/k_BT given in Table 3.

Fitting the data for (AALALAA)₃ instead with the full Eq. 14, and a fixed value of n_P = 14.5, produces the solid line that is given in the upper panel of Fig. 6. The fitted value for the change in free energy density is ΔN_LΔg_mis/k_BT = 10.5 ± 2.5 nm⁻² (see Table 3), which—with the largest value of Δg_mis/k_BT (≈ 2.3 nm⁻²) in Table 1—yields a minimum value of ΔN_L ≈ 4.6 ± 1.1 lipids displaced per dimer. With the definition of mole fraction used by the authors (see the legend to Fig. 6), this value of ΔN_L refers to one monolayer leaflet of the bilayer, i.e., is numerically equal to the number of lipids per monomer that are displaced from both sides of the bilayer. The number of lipids per helix that contact a linear array of n_α transmembrane helices is 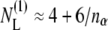(75), which predicts ΔN_L ≈ 3 on dimerization, which lies between the experimental estimates based on Eq. 14 and Eq. 9.

TABLE 3.

Change in effective interfacial free energy density, ΔN_LΔg_mis/k_BT, on forming dimers of transmembrane peptides in bilayers of phosphatidylcholines with different chain lengths

Peptide	ΔNLΔgmis/kBT (nm−2)	R
L16	2.3 ± 0.3	0.986
L22	1.5 ± 0.2	0.959
(A2LALA2)3	10.5 ± 2.5	0.980

Obtained from least-squares fitting of Eq. 14 to the lipid chain length dependences of the free energies of dimerization (σ_L = 1.2 nm). R is the effective regression coefficient. ΔN_L is the number of lipids displaced on dimer formation. Because of the different definition of mole fraction units (see legend to Fig. 6), values for L₁₆ and L₂₂ are per dimer, whereas those for (A₂LALA₂)₃ are per peptide monomer.

Formation of heterodimers of the L₁₆ or L₂₂ peptides with the corresponding peptides that contain bromotyrosine in place of tryptophan was monitored from the quenching of tryptophan fluorescence by Mall et al. (76). As seen from the lower panel in Fig. 6, the free energy of dimer formation becomes increasingly negative with increasing chain length. In contrast to the results with the (AALALAA)₃ peptide, the free energy of dimerization depends linearly on chain length of the host lipid bilayers. Unlike the free energy of lipid association with the L₁₆ and L₂₂ peptides (see Fig. 3), no extremum is found corresponding to hydrophobic matching. Fitting with Eq. 14 and a fixed value of n_P ≤ 14 (equivalent to a linear regression) yields effective values of ΔN_LΔg_mis for the L₁₆ and L₂₂ peptides that are given in Table 3. From the values of Δg_mis/k_BT obtained for lipid binding with the L₁₆ and L₂₂ peptides (see Table 1), it is deduced that respectively ΔN_L ≈ 1.0 ± 0.3 and 1.5 ± 0.8 lipids are displaced per dimer. This is considerably smaller than the lipid displacement associated with formation of dimers, and corresponds to fewer than one lipid displaced per peptide monomer, in either case.

In summary, whereas dimerization of the (AALALAA)₃ peptide can be described by elastic distortion alone but is also reasonably well approximated by Eq. 14, that of the L₁₆ and L₂₂ peptides can only be described by Eq. 14. Therefore, the experiments on dimer formation are reasonably consistent with the thermodynamic model that was used to interpret the lipid binding data.

Intermembrane helix transfer

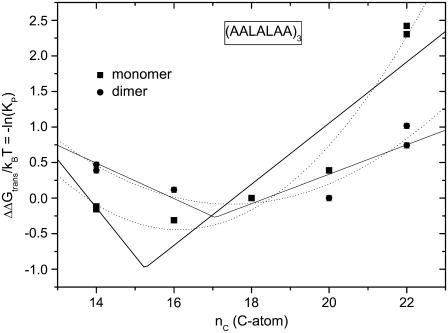
The partitioning of transmembrane peptides between membranes composed of lipids with different chain lengths provides a further means to study the thermodynamics of hydrophobic matching. Fig. 7 shows the dependence on chain length of acceptor membrane lipids for the partitioning of (AALALAA)₃ from C(16:0)C(18:1)PtdCho donor membranes. This data is taken from the work of Yano et al. (77). Values are given separately for the peptide monomer (Fig. 7, squares) and for dimers (circles; values scaled by ×0.5). The free energy of transfer exhibits a rather shallow minimum in the region of n_C =16 for the monomer and n_C =18 for the dimer. Neither of the models used here describes the dependence on chain length of acceptor lipid particularly well. Least-squares optimizations of Eq. 9 (dotted lines in Fig. 7), with an adjustable scaling factor, yield values of N_L = 2.1 ± 0.5 and 1.3 ± 0.3 for the effective number of lipids per helix that are distorted to achieve hydrophobic matching with the monomer and dimer, respectively. Correspondingly, fitting Eq. 14 to the data for the monomer and the dimer (solid lines in Fig. 7) yields effective values of N_LΔg_mis/k_BT = 4.6 ± 1.8 and 1.9 ± 0.6 nm⁻² for monomer and dimer, respectively, that are less than that of ΔN_LΔg_mis deduced for dimer formation of (AALALAA)₃. Thus the effective number of lipids perturbed appears far less than the geometrical estimates of 10 and 7 per helix for monomer and dimer, respectively (75). This argues for an effect of hydrophobic matching that does not scale with the number of lipids. A possible candidate that was proposed by the original authors is the hydrophobic burying of the helix dipole. Interestingly, the free energy of exposure is predominantly entropic for positive mismatch (d_P > d_L) corresponding to a hydrophobic effect, whereas for negative mismatch (d_P < d_L) it is predominantly enthalpic, corresponding to an electrostatic interaction of the helix dipole (77).

FIGURE 7.

Lipid chain length dependence of the partition coefficient, K_P, for transfer of Ac-(AALALAA)₃-amide from C(16:0)C(18:1)PtdCho donor membrane vesicles to acceptor membrane vesicles of diC(n_C:1)PtdCho (data from Yano et al. (77)). The phosphatidylcholine acceptor lipids are diC(14:1cΔ⁹)PtdCho, diC(16:1cΔ⁹)PtdCho, diC(18:1cΔ⁹)PtdCho, diC(20:1cΔ¹¹)PtdCho, diC(22:1cΔ¹³)PtdCho, and diC(24:1cΔ¹⁵)PtdCho. The ordinate is plotted as the free energy of transfer ΔΔG_trans/k_BT = −ln(K_P) for peptide monomers (squares) and is scaled by a factor ×0.5 for dimers (circles); values are given relative to diC(18:1)PtdCho. (Solid lines) Least-squares fits of Eq. 14. (Dotted lines) Predictions of Eq. 9 with optimization of n = n_P and an adjustable multiplicative factor ΔN_L.

Chain-melting transition shifts

The chain-melting transition temperature, T_t, of lipid bilayers is sensitive to the energetics of hydrophobic matching because the bilayer thickness, and hence the extent of hydrophobic mismatch, differs between the gel and fluid phases. The preference of the protein for the fluid phase, relative to the gel phase, is given by the partition coefficient

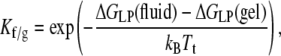(19)

where ΔG_LP(fluid) and ΔG_LP(gel) are the excess free energies of lipid-protein interaction in the fluid (T > T_t) and gel (T < T_t) phases, respectively. From Eq. 13, the difference, ΔΔG_LP(T_t) = ΔG_LP(fluid) − ΔG_LP(gel), in free energy of lipid-protein interaction, per lipid molecule, at the chain-melting transition is given by

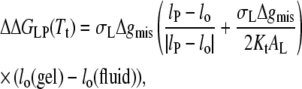(20)

where l_o(gel) and l_o(fluid) are the lengths of the lipid molecules in the gel and fluid phases, respectively. Equation 20 applies in all regions except when the hydrophobic span of the protein lies between that of the gel- and fluid-phase bilayers. For the latter situation, the following relation holds:

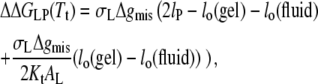(21)

which is valid for l_o(gel) > l_P > l_o(fluid).

The thicknesses of bilayers in the gel phase are complicated by tilting of the phosphatidylcholine molecules, which depends on both chain length and temperature (78). On incorporation of proteins, it is likely that the lipid tilt is diminished or eliminated (17,79). Additionally, the bilayer thicknesses in the fluid phase must be referred to the respective transition temperatures, and therefore are expected to exhibit an effective chain length dependence that is less than that obtained at constant temperature. In view of these uncertainties, the chain length dependence of Δl_t = l_o(gel) − l_o(fluid) will be treated as a parameter to be fitted. For simplicity, it is assumed that the end contributions are approximately equal in fluid and gel phases at T_t, i.e., Δl_t = Δl_inc × n_C, which is not unreasonable and does not strongly influence the results. From Eq. 20, the change in free energy of lipid-protein interaction at the transition is then given by

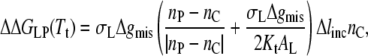(22)

where n_P is the effective value of the lipid chain length, n_C, that corresponds to hydrophobic matching with the protein, in the fluid or gel phase (see later).

Following the treatment of Sperotto and Mouritsen (17) for dilute solutions, the difference in lipid chemical potential between fluid and gel phases is given by

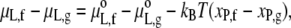(23)

where x_P,f and x_P,g are the mole fractions of protein in the fluid and gel phases, respectively. The standard state for the lipid is the protein-free bilayer and therefore

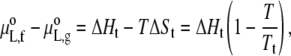(24)

where ΔH_t and ΔS_t are the enthalpy and entropy, respectively, of chain melting in the absence of protein. For binary mixtures with protein, the chemical potentials of gel and fluid lipids are equal along a tie line at constant temperature, i.e., μ_L,f − μ_L,g = 0 in Eq. 23. Combining this condition with Eq. 24 gives the following expressions for the phase boundaries, T_f and T_g, at the fluidus (x_P,f = X_P) and solidus (x_P,g = X_P) ends of the tie line, respectively:

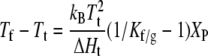(25)

and

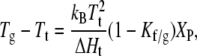(26)

where X_P (= x_P,f + x_Pg ≪1) is the total mole fraction of protein. Substituting for K_f/g from Eq. 19, the dependence on hydrophobic mismatch of the shift in midpoint temperature, 1/2(T_f + T_g), of gel-fluid phase separation is then given by (17)

(27)

which must be used in combination with Eq. 20 or 21.

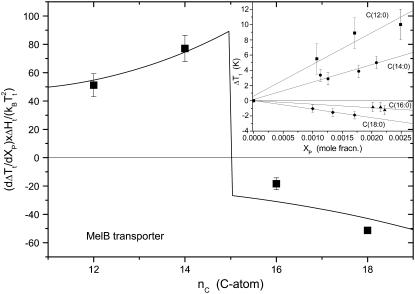
Fig. 8 shows data for the shifts in chain-melting transition of disaturated phosphatidylcholines on incorporation of the melibiose permease from E. coli in diC(n_C:0)PtdCho bilayers. The primary measurements are taken from the work of Dumas et al. (7). As seen from the inset to Fig. 8, the shift in transition temperature, ΔT_t, increases approximately linearly with mole fraction of incorporated protein, over the range up to X_P ∼ 2.10⁻³, in accordance with the predictions of Eq. 27 for dilute solutions. Values of dΔT_t/dX_P obtained from linear regression are given in Fig. 8. These are scaled according to the prefactor on the right of Eq. 27, by using values of ΔH_t and T_t for disaturated phosphatidylcholines from Lewis et al. (80).

FIGURE 8.

Chain length dependence of the shift, ΔT_t, in lipid chain-melting transition temperature with mole fraction, X_P, of the E. coli melibiose permease (MelB) in diC(n_C:0)PtdCho bilayers. The ordinate, dΔT_t/dX_P, is obtained from the linear regressions given in the inset (data from Dumas et al. (7)) and is normalized by the factor 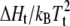obtained from calorimetric data for diC(n_C:0)PtdCho from Lewis et al. (80). (Solid line) Least-squares fit of Eq. 27, incorporating Eqs. 22 and 28, with fixed value of n_P = 15 (see text).

The solid line in Fig. 8 is a nonlinear least-squares fit of Eq. 27 with a chain length dependence that is given by Eq. 22. The chain length dependence of the chain-melting transition temperature of diC(n_C:0)PtdCho bilayers alone (81),

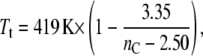(28)

which is obtained from the data for n_C = 12–18 from Lewis et al. (80) is also needed for the fitting. Because it is based on Eq. 22, the fit in Fig. 8 is valid only in the regions outside that of hydrophobic matching, which, from the change in sign of ΔT_t, must occur between n_C = 14 and n_C = 16 for saturated phosphatidylcholines. Activity measurements in the fluid phase of unsaturated diC(n_C:1)PtdCho bilayers display an optimum match for n_C = 16 (7). A fixed value of n_P = 15 is used for the fit shown in Fig. 8; values fixed in the range n_P = 14.1–15.9 do not change the fit at values of n_C outside this range.

The fit shown in Fig. 8, although by no means perfect, reproduces the essential features of the chain length dependence of the transition temperature shift. It produces a value of Δg_mis/k_BT_t = 2.5 ± 0.5 nm⁻² for the free energy density of mismatch. This is comparable to the more direct estimates that are given in Table 1, although on the upper side. The fitted value for the difference in chain length increments between fluid and gel phases is Δl_inc = 0.10 ± 0.02 nm/CH₂. The maximum increment in the gel phase is l_inc(gel) = 0.127 nm/CH₂ for an all-trans chain. This then corresponds to an increment in the fluid phase of l_inc(fluid) = 0.03 ± 0.02 nm/CH₂; correction of the x-ray data for fluid-phase diC(n_C:0)PtdCho in Fig. 1 to the respective transition temperatures produces an effective increment of 0.061 ± 0.002 nm/CH₂. The description of the chain length dependence of the transition temperature shifts by Eqs. 20 and 27 is therefore not unreasonable.

A similar study on the chain-melting transitions of diC(n_C:0)PtdCho bilayers in which bacteriorhodopsin was reconstituted has been conducted by Piknova et al. (82). In this case, however, endogenous purple membrane lipids were still present in the reconstitution. In several cases, the phase behavior was complicated by the appearance of an additional high-melting component, the relative proportion of which increased with increasing protein/lipid ratio, coming to dominate at a ratio of 1:50 mol/mol. From the two phase diagrams at low mole fractions of protein (X_P ≤ 2.10⁻³) that do not have this complication, the shift in chain-melting temperature is dΔT_t/dX_P = +(4.2 ± 0.2) × 10³ K and −(3.8 ± 1.1) × 10³ K for chain lengths of n_C = 12 and 18, respectively. The reversal in sign indicates that hydrophobic matching with bacteriorhodopsin is achieved at a lipid chain length that lies between these two extremes. Using the two data points for n_C = 12 and 18 with Eqs. 22 and 27 yields values of Δg_mis/k_BT = 1.7 ± 0.6 nm⁻² and Δl_inc = 0.17 ± 0.07 nm for bacteriorhodopsin. Within the considerable range of uncertainty, these values are comparable to those deduced from transition temperature shifts for melibiose permease.

Although lipid phase transition temperatures depend on hydrophobic matching in a considerably more complex way than do lipid binding constants, involving both fluid and gel phases, the values deduced for Δg_mis from the same model are nonetheless of a comparable size with both methods.

Adaptation of lipid length

The fractional extension in length, Δl/l_o, of the lipid chains that is predicted from Eq. 12 by using values for the free energy density of hydrophobic mismatch that fit the lipid binding data lies in the approximate range 5–10% (see Table 1). For the lysine-anchored transmembrane leucine-alanine oligopeptide Ac-GK₂(LA)₈LK₂A-amide (KALP23) and arginine or histidine analogs (RALP23 and HALP23), the extension of diC(14:0)PtdCho chains adjacent to the peptide is small (25,83). It can be estimated from the mean ²H-NMR order parameters, as described in the first section, that the fractional extension for KALP23, RALP23, and HALP23 is ∼3% and depends little on the extent of mismatch, increasing to only 5% for KALP31 (84).

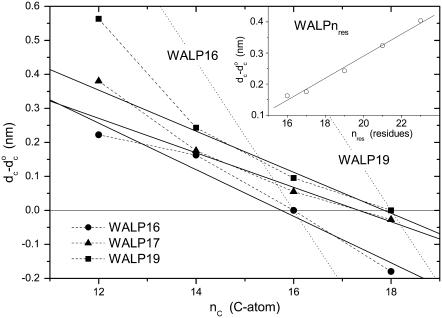
Fig. 9 shows the change in hydrophobic thickness, d_c–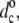 of disaturated phosphatidylcholines that is induced by tryptophan-anchored transmembrane leucine-alanine peptides, Fm-AW₂(LA)₅W₂A-Etn (WALP16) or Fm-AW₂(LA)_mLW₂A-Etn (m = 5, WALP17; m = 6, WALP19). These data are obtained from the increase in mean chain segmental order parameter of the diC(n_C:0)PtdCho lipids in the fluid phase (24), as described for the NMR-derived values of d_c in Fig. 1. To give a consistent description of the chain length dependence (cf. Fig.1), the data are corrected to a common temperature of 30°C, and are scaled up from average values for the whole bilayer to represent the maximal extension of the lipids in immediate contact with the peptides. For the WALP peptides and corresponding YALP and FALP peptides that are anchored by other aromatic residues (83), the fractional diC(14:0)PtdCho lipid chain extension is larger than for the electrostatically anchored peptides (KALP, RALP and HALP) under the same conditions, and lies in the approximate range 5–16%. However, unlike the situation with the KALP peptides and the prediction of Eq. 12, the degree of extension of the lipid chains by the WALP peptides depends clearly on the extent of mismatch. This is seen also from the dependence of the maximal lipid extension on hydrophobic length of the WALP peptides in a phosphatidylcholine of constant chain length, n_C = 14, that is shown in the inset to Fig. 9.

FIGURE 9.

Chain length dependence of the maximal increase in hydrophobic thickness, d_c–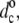 for the diC(n_C:0)PtdCho lipids directly adjacent to Fm-AW₂(LA)_mLW₂A-Etn (WALP2m+7; squares and triangles) or Fm-AW₂(LA)₅W₂A-Etn (WALP16; circles) peptides (²H-NMR order parameters from de Planque et al. (24)). Data from fluid-phase bilayers are corrected to 30°C with α_d = −0.0033 K⁻¹. Solid lines are linear regressions (omitting n_C = 12 for WALP17 and WALP19). Dotted lines are predictions for complete hydrophobic matching according to Eq. 6. (Inset) Dependence on peptide length, n_res, for WALPn_res in di(C14:0)PtdCho (²H-NMR order parameters from de Planque et al. (24,25,83)).

The solid lines in Fig. 9 are linear regressions (omitting n_C = 12 for WALP17 and WALP19) to the chain length dependence of the degree of extension of the lipid chains. Hydrophobic matching is achieved at chain lengths of n_C = 16 and 18 for WALP16 and WALP19, respectively, and the zero-crossing for WALP17 is at n_C ≈ 17.3. From Eq. 6, these values correspond to hydrophobic thicknesses of d_c = 2.77 ± 0.13, 2.94 ± 0.13 and 3.02 ± 0.13 nm for the WALP16, WALP17 and WALP19 peptides, respectively, after correcting back from the reference temperature of 30°C to the actual temperature of measurement. For comparison, the geometrical lengths of WALP16, WALP17 and WALP19 are 2.55, 2.70 and 3.00 nm, respectively, counting the C-terminal ethanolamine as a residue and assuming regular α-helices.

Using the above values of n_C for hydrophobic matching between peptide and lipid, predictions of the total hydrophobic mismatch at other lipid chain lengths according to Eq. 6 are given by the dotted lines in Fig. 9. As concluded from the thermodynamic results analyzed above and in the original NMR work (24), the extent of elastic distortion of the lipid chains that is measured is insufficient to cover the total mismatch fully. Based on the gradients of the linear regressions in Fig. 9, elastic lipid distortion compensates for 31 ± 3, 23 ± 4, and 28 ± 6% of the total mismatch with the WALP16, WALP17, and WALP19 peptides, respectively. This degree of compensation is appreciable but it is by no means complete; nor is the greater-than-linear increase in extension that is induced in diC(12:0)PtdCho by WALP17 and WALP19 (see Fig. 9).

The model that was used successfully to describe the chain length dependence of the lipid binding (Figs. 3–5) predicts a constant elastic distortion of the lipid chains that does not depend on the extent of mismatch (see Eq. 12). This is because a fixed free energy density of mismatch, Δg_phob, corresponds to a constant interfacial tension, which at equilibrium is balanced by an equal tension that is generated at some fixed elastic extension, l_L–l_o, of the lipid chains. A chain extension that depends on the extent of hydrophobic mismatch, such as is found for the WALP peptides in Fig. 9, can be generated only if the excess free energy density of mismatch depends itself on the extent of mismatch. The simplest model is to assume a linear dependence, i.e., of the form Δg_mis(l_P/l_o − 1). The excess free energy of lipid-protein interaction per lipid then becomes (cf. Eq. 11)

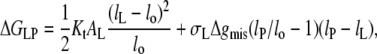(29)

which also ensures that Δg_mis does not contribute when l_o = l_P. From Eq. 29, the equilibrium lipid length becomes (cf. Eq. 12)

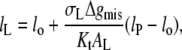(30)

which predicts that the extension, l_L − l_o, increases linearly with the extent of hydrophobic mismatch, l_P − l_o.

Equation 30 is in agreement with the results for WALP peptides in disaturated phosphatidylcholines that are given in Fig. 9, at least for low degrees of mismatch. From the gradients of the linear regressions in Fig. 9 and Eq. 30 together with Eq. 6, it is deduced that Δg_mis/k_BT ≈ 3.2 ± 0.8, 2.4 ± 0.5, and 2.8 ± 0.6 nm⁻² for the WALP16, WALP17, and WALP19 peptides, respectively. A consistent value of Δg_mis/k_BT ≈ 2.4 ± 0.3 nm⁻² is obtained also from the linear regression for WALP16, WALP17, WALP19, WALP21, and WALP23 in diC(14:0)PtdCho (see inset to Fig. 9), assuming an increment in d_P of 0.15 nm per residue for an α-helix. These values for Δg_mis are modulated by the factor ×(l_P/l_o − 1) but, for moderate extents of mismatch, are comparable to the constant values that are given in Table 1 from fitting lipid binding data.

The free energy of lipid-protein interaction per lipid at equilibrium that corresponds to the lipid extension that is given by Eq. 30 is (cf. Eq. 13)

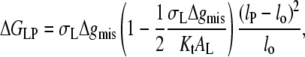(31)

which no longer predicts a linear dependence on lipid chain length. Fitting the data for lipid binding in Fig. 4 with Eq. 31 gives results inferior to those from fitting with Eq. 14, as judged by the values of R² (cf. Table 1). The one exception is EcMscL. Nonetheless, the optimized values of Δg_mis/k_BT are in the range 0.2–1.1 nm⁻², and thus are of a similar magnitude to those deduced from ²H-NMR measurements of the lipid chain extensions induced by mismatch with the WALP peptides.

Measurements of the degree of lipid chain extension by ²H-NMR are therefore in qualitative agreement with predictions from the thermodynamic model, in that elastic deformation is insufficient to compensate for the hydrophobic mismatch. A modified form of the model also yields values of Δg_mis from tryptophan-anchored peptides that are comparable to those obtained directly from lipid binding data.

CONCLUSIONS

The most direct and extensive thermodynamic data on hydrophobic matching are afforded by the relative lipid association constants. Both the lack of dependence on lipid/protein ratio (42) and the agreement between complementary results for the binding of either lipid partner relative to the other (32,54) indicate that the association constants are determined primarily by the energetics of the lipids directly in contact with the protein, and are influenced relatively little by the properties of subsequent lipid shells. The approximately linear dependence of the free energy of association on lipid chain length indicates that the elastic extension or compression of the lipid chains is insufficient to compensate the hydrophobic mismatch fully (at all except small degrees of mismatch). Estimates of the elastic forces involved are in agreement with this conclusion, as are determinations of the degree of extension from segmental order parameters of the lipid chains.

A model incorporating both elastic chain extension and an energy penalty that depends linearly on the residual extent of mismatch is able to describe the dependence of the free energy of association on lipid chain length. The effective free energy density of mismatch could arise from the exposure of hydrophobic groups to a polar environment provided by protein or lipid, but not from exposure directly to water. Alternatively, conformational changes from the tilting of transmembrane helices, as in the mechanosensitive channels, may account for the free energy of mismatch. The thermodynamic model, which is based on the lipid binding data, is closely related to the “mattress” model of Mouritsen and Bloom (16). It differs from the latter in omitting terms that would introduce pronounced asymmetry in the free energy of lipid association for positive and negative mismatch, because this is not observed experimentally.

More limited data from other thermodynamic processes that are sensitive to hydrophobic mismatch are described more or less well by the model used for lipid binding. Dimer formation of transmembrane helices is energetically favored by hydrophobic mismatch. The extent of dimer stabilization is comparable to or less than that corresponding to the number of lipids expected to be displaced from the dimer interface. Transfer of the (AALALAA)₃ peptide between lipid vesicles is disfavored by increased hydrophobic mismatch in the acceptor vesicle, but to an extent that is less than that expected from the dimer stabilization.

The response of the lipid chain-melting transition to hydrophobic mismatch is more complicated than the other cases considered because this involves hydrophobic matching in both the fluid and gel phases of the lipid bilayer, and also possible differences in degree of aggregation in the two phases. Approaches based on ideal mixing, combined with the energetic model used for lipid binding, have some success in describing the chain length dependence of the shifts in transition temperature at low mole fractions of protein. However, lipid binding data provides a more direct and reliable test of the model.

Finally, the degree of lipid chain extension is proportional to the extent of mismatch with different WALP peptides. This is not in accord with the predictions of the basic thermodynamic model and requires that the free energy of mismatch should depend linearly on the extent of mismatch. Possibly this is related to adjustments in orientation of the tryptophan side chains in the WALP peptides. It is not certain whether this applies also to real transmembrane proteins that have tryptophans located at the polar-apolar interface. In general, integral membrane proteins have been found to exert relatively little effect on the segmental order parameters of the lipid chains (85–87).

The model presented here successfully describes and parameterizes the chain length dependence of the energetics of lipid-protein association, and is reasonably consistent with a variety of other processes that are sensitive to hydrophobic mismatch. It therefore should be considered in the interpretation of all future membrane investigations that involve hydrophobic matching.