Ten-Microsecond Molecular Dynamics Simulation of a Fast-Folding WW Domain

Abstract

All-atom molecular dynamics (MD) simulations of protein folding allow analysis of the folding process at an unprecedented level of detail. Unfortunately, such simulations have not yet reached their full potential both due to difficulties in sufficiently sampling the microsecond timescales needed for folding, and because the force field used may yield neither the correct dynamical sequence of events nor the folded structure. The ongoing study of protein folding through computational methods thus requires both improvements in the performance of molecular dynamics programs to make longer timescales accessible, and testing of force fields in the context of folding simulations. We report a ten-microsecond simulation of an incipient downhill-folding WW domain mutant along with measurement of a molecular time and activated folding time of 1.5 microseconds and 13.3 microseconds, respectively. The protein simulated in explicit solvent exhibits several metastable states with incorrect topology and does not assume the native state during the present simulations.

A great deal of attention has been focused on molecular dynamics (MD) simulations of protein folding in an effort to gain insight into the folding process that neither crystal and NMR structures nor computational structure prediction can provide (1). Numerous studies, e.g. (1–6), have shown the successful folding of a disordered polypeptide into native or near-native states using MD. However, achieving a true native conformation, i.e., one with <2.0 Å C_α root mean-square deviation to a crystal structure, has rarely been achieved (6). Most (although certainly not all) ab initio folding simulations to date have been performed using implicit solvent models, both due to the lessened computational cost and because folding kinetics are consistently orders of magnitude faster in implicit solvent (6).

Implicit solvent models have proved capable of ranking the folded state of peptides as the lowest free energy state when tested against sets of decoy conformations (7,8), but in some cases they have been shown to improperly rank the relative free energies of different folding intermediates (9) or improperly rank unfolded states as lower in free energy than the native state after MD runs (8,10). Although there is no guarantee that explicit solvent calculations will fare significantly better, factors such as overemphasis of salt bridging by implicit solvent models (10) should be corrected through the use of explicit solvent. It is thus desirable to attempt simulations of protein folding in explicit solvent both to test their efficacy for the problem and to verify conclusions from implicit solvent studies.

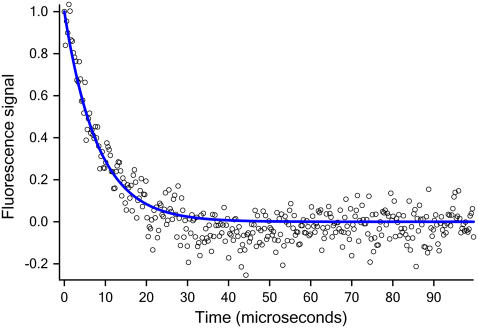
Here we investigate a human Pin1 WW domain, for which mutants have been engineered that fold in 15 μs or less (11–13). To provide a benchmark for the MD simulations, we measured the temperature-dependent folding kinetics of the mutant Fip35. Fip35 was designed as part of a multiprotein survey to have a shortened five-residue (S-RDGS) turn 1, speeding up folding and increasing stability (melting temperature 351 K) (13). Protein preparation and thermodynamic characterization are described in Liu et al. (13). Protein folding kinetics were measured by a laser-induced temperature jump experiment monitoring relaxation of the tryptophan fluorescence lifetime. A two-component analysis of the fluorescence determined the folding rate (see the Supplementary Material). Fig. 1 shows the fast relaxation kinetics. At 352 K, the observed average rate is (8.1 μs)⁻¹. At 337 K, the observed kinetics reveals a 1.5 μs long molecular downhill folding phase (13), and an activated folding rate of (13.3 μs)⁻¹.

FIGURE 1.

Experimental relaxation kinetics of Fip35 with a time resolution of 280 ns at 352 K.

A series of ∼30,000-atom MD simulations, in explicit water, studied the stability of the Fip35 folded state and its folding mechanism. The folded state was modeled from the crystal structure of a WW domain mutant (Protein Data Bank code 2F21 (11)) and placed in a box of TIP3P water with 30 mM NaCl using VMD (14). An unfolded state was generated setting all backbone (φ,ψ) angles to (−135,135). The CHARMM22 force field with CMAP corrections for the protein was used (15). Simulations were carried out using a custom version of NAMD 2.6 (16) that will be described in a separate publication. Details of the simulation parameters and analysis procedure are provided as Supplementary Material.

The native state of Fip35 was subjected to 200 ns of equilibrium MD to verify its stability at the target temperature, with an average and final C_α root mean-square deviation under 1.4 Å. This is consistent with the definition of a true native state and indicates that Fip35 assumes a stable crystal structure conformation on a timescale of hundreds of nanoseconds. These simulations are clearly insufficient to guarantee that this state represents a global free energy minimum; an extensive set of replica exchange simulations or the equivalent may investigate such a claim further.

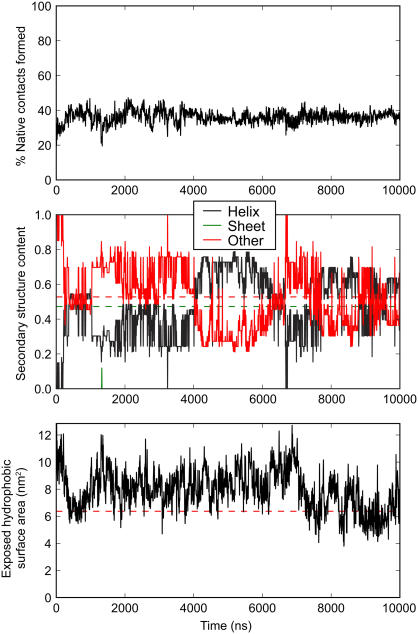
A single trajectory of 10.0 μs was generated to observe the folding process of Fip35 beginning from an extended conformation. A plot of the native contacts, secondary structure, and exposed hydrophobic surface area during the folding trajectory is shown in Fig. 2. Collapse from the initial conformation to a molten globule with a hydrophobic core occurs over the first 500 ns, just slightly shorter than the 1.5 μs molecular phase observed experimentally at the same temperature. Concurrent with hydrophobic collapse, residues 8–20 and 27–34 form a pair of α-helices, encompassing the first β-strand/turn and second turn/third β-strand of the native state.

FIGURE 2.

Percentage of native contacts formed (top), secondary structure content (middle), and exposed surface area of hydrophobic side chains (bottom) through the 10 μs folding trajectory. Values in the native structure are shown as dashed lines.

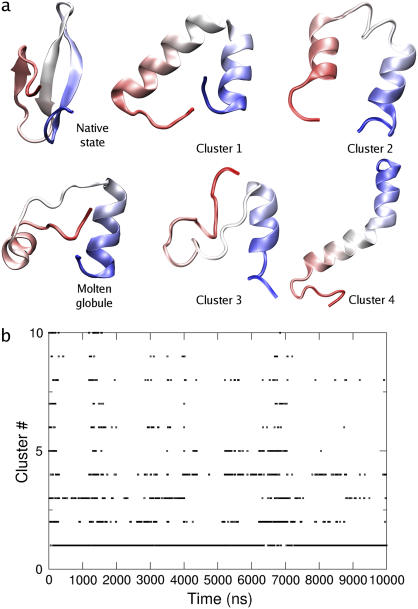
After the initial collapse to a mostly helical state, the trajectory is characterized by a series of interconversions between states containing the two helices present in the initial molten globule, containing one long helix comprising most of the protein, or containing one helix in the vicinity of sheet 1 and disordered coil through the remainder of the protein. Rearrangements between these states are punctuated by portions of trajectory with (intermittently) higher exposed hydrophobic surface area. Representative structures of the four most populated states from clustering analysis of the trajectory are shown in Fig. 3. Of the 27 clusters identified in this analysis, 95% of frames were contained in the four most populated clusters and 99% of frames in the 10 most populated clusters. As seen in the time evolution of the cluster ID, the majority of the trajectory is spent with the system in an equilibrium between the most populated clusters, with little apparent time evolution after the first microsecond of simulation.

FIGURE 3.

(a) Native state, molten globule formed after 500 ns, and most representative structures from clustering analysis. (b) Cluster occupied throughout the trajectory. The first 10 clusters are shown.

The presence of early helical states in the folding trajectory of a β-sheet protein is not surprising, as helical overshoots have been observed in the folding process of small predominantly β-proteins (17). Given that our experimentally observed downhill phase, which could plausibly form a local α-helical structure in 500 ns before going to the correct topology, is only 1.5 μs long, the persistence of α-helical conformations in the 10 μs WW domain trajectory is anomalously long. It may represent either a pathological single trajectory, a bias of the underlying free energy surface in the force field toward helical secondary structure, or kinetic trapping in helical structures, which is more severe in the simulation than in the experimental system. The use of a fully extended starting conformation may also be to blame; the heat denatured state studied in vitro almost certainly contains residual structure, and the fully extended state may be trapped into a nonnative local secondary structure more easily than the heat denatured state. Multicanonical simulations using CHARMM22 without CMAP corrections showed a bias toward α-helical conformations (18), which could be relevant to our results, although it is unclear what effect the backbone cross-terms have on the force field's helical propensity. It should be noted that the only region showing helical structure through the entire simulation corresponded to strand 1 and the first turn of the native structure; characterization of the effects of mutation on WW domain folding have indicated that the rate limiting step for folding is the formation of turn 1 (11), and thus the presence of helical structure in this region would disrupt the normal folding process. The reason for the persistence of this α-helix in the present trajectory will have to be addressed through a combination of experiments to determine whether or not a helical overshoot is present in the folding of this peptide, and replica exchange MD simulations to determine whether the helical states present in this simulation are indeed favored over the native state. Preliminary results starting from a thermally denatured state show a similar helical propensity on the microsecond timescale (data not shown), and thus the presence of a transient helical intermediate in the folding process or difficulties due to the starting conformation are unlikely to explain the MD result, although we cannot rule them out.

This 10 μs trajectory of the WW domain represents one of the longest MD simulations performed to date, and was made possible only through dramatically improved scaling and parallel performance of NAMD (16). Our results suggest a number of follow-up simulations and experiments to further understand why this particular explicit solvent folding trajectory did not achieve a native-like conformation. A sufficiently accurate force field should, in principle, fold a protein to its native state in a single trajectory, on a timescale similar to experiment. With ongoing improvements both in the performance of MD programs and total amounts of computing power available, explicit solvent protein folding trajectories covering the full experimental timescale (and, indeed, MD studies on the submillisecond timescale) will become more common, thus requiring more accuracy and stability from MD force fields. The direct feedback now possible between ultrafast folding experiments and MD simulations will improve the fitness of force fields for simulation of long timescale structural rearrangements of biomolecules. Such data may become as important as the small molecule calibrations used in the past to parameterize force fields.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.