Osmotic Water Transport with Glucose in GLUT2 and SGLT

Abstract

Carrier-mediated water cotransport is currently a favored explanation for water movement against an osmotic gradient. The vestibule within the central pore of Na⁺-dependent cotransporters or GLUT2 provides the necessary precondition for an osmotic mechanism, explaining this phenomenon without carriers. Simulating equilibrative glucose inflow via the narrow external orifice of GLUT2 raises vestibular tonicity relative to the external solution. Vestibular hypertonicity causes osmotic water inflow, which raises vestibular hydrostatic pressure and forces water, salt, and glucose into the outer cytosolic layer via its wide endofacial exit. Glucose uptake via GLUT2 also raises oocyte tonicity. Glucose exit from preloaded cells depletes the vestibule of glucose, making it hypotonic and thereby inducing water efflux. Inhibiting glucose exit with phloretin reestablishes vestibular hypertonicity, as it reequilibrates with the cytosolic glucose and net water inflow recommences. Simulated Na⁺-glucose cotransport demonstrates that active glucose accumulation within the vestibule generates water flows simultaneously with the onset of glucose flow and before any flow external to the transporter caused by hypertonicity in the outer cytosolic layers. The molar ratio of water/glucose flow is seen now to relate to the ratio of hydraulic and glucose permeability rather than to water storage capacity of putative water carriers.

INTRODUCTION

Three models currently attempt to explain sugar-water cotransport. Two of these, carrier-mediated transport and another based on the Curran-MacIntosh three-compartment model (1), which was originally proposed as a model for epithelial water absorption, were proposed by Zeuthen and Stein as alternative explanations for apparent uphill transport of water by the small intestine (2). The third model attributes uphill water flow entirely to an unstirred layer effect at the membrane endofacial surface (3–5). Water transport has also been observed via GLUT2 in oocytes and ascribed to osmotic effects within unstirred layers (6). Zeuthen and co-workers have extended their original carrier-based water cotransport concept to water flow via the low affinity passive glucose transporter, GLUT2 (7). Water flows generated in oocytes expressing either GLUT2 or SGLT have been simulated previously to justify the appropriateness or inappropriateness of the assumption that unstirred layer effects adequately (3–5,8) or inadequately (9) explain water flow.

A major objection to carrier-mediated active water transport is that it contravenes the current orthodoxy requiring transepithelial water movement to be secondary to ion sequestration and accumulation (10,11). A second objection is that transporters belonging to the major facilitator superfamily (MSF) have a central channel through which water can be driven by osmotic pressure (12). A carrier model requiring sequestration of both water and its driving ligands within intramembranous compartments is inconsistent with an unbroken continuously transmitting pathway, as is required for electrical current or osmotic pressure driven water flows. However, the alternative unstirred layer hypothesis is also deficient. This is because the observed rates of solute diffusion within the oocyte cytosol are too rapid to sustain the hypertonicity within the unstirred layer required to generate the observed flow through the oocyte membrane. Additionally, the rates of change of water flow after abrupt change in Na⁺ electrochemical potential or external glucose concentration (3,5,9) occur too rapidly.

Here a version of the Curran-MacIntosh three-compartment model, incorporating an endofacial unstirred layer as a fourth compartment, is used to show that a vestibular compartment within the transporter protein comprehensively explains the phenomena relating to sugar-dependent water flow without recourse to carrier-mediated water flows.

METHODS

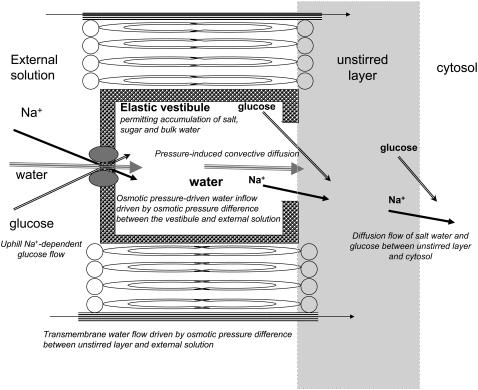
The water transport pathway through MSF protein is outlined in Fig. 1. The external orifice is permeable to glucose and water in GLUT2 and glucose and to sodium and water in SGLT, but is impermeable to all other osmolytes.

FIGURE 1.

Diagram showing routes of water flow across GLUT2 or SGLT and the oocyte membrane. Two routes are shown. One is via the transporter through which water and cotransported solutes pass via the external tight opening, then the vestibule, then via the wide vestibular exit into the external cytosolic layer. The other route permits only water flow determined by the osmotic pressure difference between the outer cytosol and the external solution.

Assuming the transported ligands Na⁺ or glucose have Staverman reflection coefficients (13), σ ≈ 1, at the external opening, osmotic pressure occurs here but not at the wider internal opening where σ ≈ 0 (Fig. 1). The internal radius of the MSF “vestibule” ≈1.5 nm and its volume ≈1.0 × 10⁻²¹ cm³ is sufficient to accommodate ≈500 water molecules or ≈50 glucose molecules. Binding studies (14) and docking studies (15,16) reveal several vestibular sugar docking sites. The available crystal structures of the MFS transporter proteins, e.g., lactose permease (12,16), show that the width of the pore exit at the cytosolic surface is between 1.5 and 2.5 nm. This is three- to fivefold larger than the largest diameter of glucose. Given that oocyte membranes express 3 × 10¹¹ transporters cm⁻² membrane area, the vestibular compartment volume is = 3 × 10⁻¹⁰ cm³ cm⁻². The unstirred layer volume is ≈ 30 nl cm⁻². As transporter turnover numbers ≈50–100 s⁻¹, vestibular glucose will reach a quasi steady state in milliseconds or be rate limited by diffusion within the external solution, whereas oocytic unstirred layer effects develop in 10–100 s. Vestibular hydrostatic pressure will increase with its volume and the elastic modulus of the protein and force fluid and solute by convective diffusion via the wide endofacial opening, toward the cytosolic unstirred layer.

Na⁺, glucose, and water transport through SGLT expressed in Xenopus oocytes as described (3–6,8,9) and glucose and water transport as described via GLUT2 (7) are simulated using the Berkeley Madonna modeling program, version 8.01, developed by R. Macey and G. Oster http://www.berkeleymadonna.com. Modeling facilitated glucose transport and its coupling to water in GLUT2 is simpler and more transparent than models of Na⁺ glucose via SGLT. Since water flows induced by sugar flow via GLUT2 fully illustrate the points currently in contention, these will be described in more detail.

Description of water flow coupled with glucose flow in Xenopus oocytes entails simultaneous equations for glucose and water flow through the transporter GLUT2. As neither the detailed mechanism of glucose transport nor any hypothetical coupling mechanism between glucose and water flow within the transporter are essential to this discussion, glucose transport is treated as a simple symmetrical facilitated transporter which binds glucose with a low K_m (10 mM).

The equations for SGLT are very similar to those for GLUT2, except those extra required for Na⁺-dependent glucose permeation via the external transporter orifice, and they must accommodate Na⁺ permeation within the transport pathway. The equation parameters describing reversible Na⁺-glucose cotransport water are from Kaunitz and Wright (17). As the equations make no specific provision for water transport, any associated water transport comes from other external factors, i.e., the osmotic relations involving water flow between the external solution and unstirred layer adjacent to the inside surface of the membrane (Fig. 1).

Equations for solute and water flows in GLUT2 expressing oocytes

Water and solute flows are described using equations similar to those used by Curran and MacIntosh (1) and adapted from the Kedem and Katchalsky equations (18) describing the relationships between coupled solute and water fluxes across membranes.

Water flows

Net water flow between the external solution _[1] and the vestibule _[2] is assumed to be entirely dependent on the osmotic pressure generated by the osmolar concentration difference between the external solution and the vestibular compartment _[2]. The equations assume that both the nontransported osmoles—mainly KCl, (Os), and glucose, (G)—have reflection coefficients, σ = 1, and hence induce water flow at their full potential. Any hydrostatic pressure buildup within the vestibule opposes water inflow via the external pore.

The L_p coefficient (cm³ cm⁻² s⁻¹ cm⁻¹ H₂O) relating water flow, J_w, to the transmembrane osmotic or hydrostatic pressure gradient is useful as it links flow to pressure, irrespective of whether it is generated hydraulically or osmotically. Hydrostatic pressure can be overlooked with use of the coefficient, P_w (cm s⁻¹), which relates water flow specifically to osmotic pressure. J_i = flux (moles cm⁻² s⁻¹) of solute _i and J_w (cm³ cm⁻² s⁻¹, or here pl cm⁻² s⁻¹) of water,

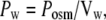where P_osm = J_w/(RTΔOsm), V_w = partial molar volume of water = 18 ml/mole, R is the gas constant, and T = degrees °K, and ΔOsm is the osmolar concentration difference between the adjacent compartments. P_w is introduced to aid model comparability.

Water flow, J_w12, across the external orifice of the transporter between the external solution _[1] and the vestibule _[2] Os = impermeant solute (mOsm kg⁻¹), total osmoles, Tos = G + Os, (mOsm kg⁻¹), L_p13 is the membrane hydraulic permeability (cm³ cm⁻² cm H₂0⁻¹); 26 cm H₂O = osmotic pressure exerted by 1 mOsm at 300°K. Subscripts refer to external solution _[1], vestibule _[2], unstirred layer _[3], and cytosolic layers _[4–10] in the case of transport across GLUT2:

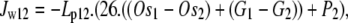(1)

where P₂ is the volume-induced vestibular hydrostatic pressure, cm H₂O with elastic modulus, E = 1–5 dyn cm⁻². It is assumed here that this is similar to any other nonrigid hydrogel (19) and therefore generates only low hydrostatic pressure within the observed range of flow (0.5–2 cm H₂O). There may be situations where this assumption is inappropriate, e.g., when the transporter is incorporated within a rigid membrane structure. Thus vestibular pressure

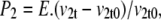where v_2t is the vestibular volume at time t and the elastic modulus, E, of the vestibular wall = 0.2 kPa = 2.0 cm H₂O. The total initial vestibular volume in the oocytes is assigned = 10 pl. Vestibular pressure may become positive or negative according to whether its volume increases or decreases from the initial volume with water flow. Doubling the vestibular volume raises the intravestibular pressure ≈2 cm H₂O. Water flow between the vestibule _[2] and the outer cytosolic unstirred layer _[3] (unstirred layer)

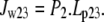(2)

Water flow between the external solution and the unstirred layer depends on the osmotic pressure difference between these compartments but bypasses the transporter route:

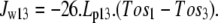(3)

Thus, the total water flow into the cytosol is the result of parallel flows across the transporter and membrane routes = J_w23 + J_w13.

Water flow between the adjacent cytosolic layers occurs by diffusion and relates only to the water activity differences and the water diffusion coefficient, D_W. This, uncoupled water diffusion although fully implemented in the model has no significant effect on either the water or solute flows across the membrane or solute flows within the cytosol but permits a distributed volume change in all layers.

Glucose flows

Glucose flow between the external solution and the vestibule, J_g moles cm⁻² s⁻¹, has a maximal rate, V_m, between two saturable glucose binding sites facing the external and vestibular solutions. The affinity of glucose for these sites, K_m (mM), is the concentration at which the sites are half saturated and is assumed here to be the same for both sites, i.e., K_m = glucose (mM) at 1/2V_m, G = glucose (mM), V_m = maximal velocity of glucose (mole cm⁻² s⁻¹),

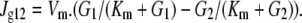(4)

Glucose flow between the vestibule and the unstirred layer _[3] is assumed to be affected both by the mass flow generated by intravestibular pressure and by diffusion generated by the concentration difference between the vestibule _[2] and unstirred layer _[3]. The reflection coefficients of glucose KCl and NaCl at the endofacial pore exit are close to zero. D₂₃ = diffusion coefficient between vestibule and layer (cm² s⁻¹) differs from D₃₄ between layer and cytosol. The diffusion coefficients of glucose and impermeant osmoles are assumed to be uniform within all the cytosolic layers _[3–8], i.e., D₃₄ = D₄₅ = D₅₆ = D₆₇ = D_78. = D₈₉= D₉₁₀. Hence,

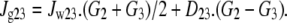(5)

As no significant hydrostatic pressure gradients exist within the cytosol, glucose flow between the unstirred layer _[3] and cytosolic layers _[4–8] is assumed to result only from diffusion. Hence,

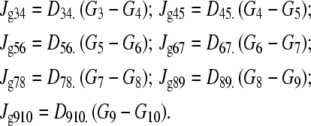(6)

Thus net glucose flow into the vestibule = J_g12 − J_g23 and into the unstirred layer = J_g23 − J_g34.

Impermeant solute flow (KCl)

No significant solute flow other than glucose occurs via GLUT2 between the external solution and vestibule. Thus, osmolar flow between the vestibule and external solution

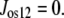(7)

However impermeant solute flow does occur between the vestibule and unstirred layer. It too, like glucose, is subject to pressure-induced convective diffusion flow. The major impermeant solute within the cytosol, KCl, has approximately double the diffusion rate of glucose within cytosol (20). Allowance for the higher relative diffusion rate of impermeant solute is made by the coefficient .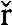

Net impermeant solute flow between the vestibule and cytosol is J_os23 − J_os34, where

(8)

and

(9)

Simulation of diffusive flow within the cytosol

Second-order Fickian solute diffusion within the spherical oocyte cytosol is simulated by a series of first-order diffusion equations between a serial array of concentric spherical shells of uniform width spanning the entire radius of the sphere (5,7). Glucose and solute diffusion are simulated here with an array of eight spherical concentric shells.

The oocyte's spherical geometry places constraints on diffusion not seen in planar lamina. These are simulated by normalizing the radial position of each shell, i, to that of boundary radius, r_e; hence, r_ni = r_i/r_e and each shell volume is proportional to

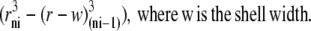The amount of solute required to attain any given concentration within a shell decreases with shell volume toward the center, and the surface area of each shell is proportional to 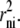Hence, diffusion increases by a factor of 1/r_ni toward the sphere center. The linear first-order diffusion equations for glucose and impermeant solute between adjacent shells (Eqs. 6 and 9 above) are adjusted to take account of the spherical geometry. The average oocyte is assumed to have a radius = 0.05 cm and a water space occupying 40% volume (7). The outer surface area available for transport is assumed = 0.031 cm², and the total sphere water volume = 260 nl.

Simulation of Na⁺-dependent glucose and water flows in SGLT in oocytes

Because low molecular weight solutes diffuse rapidly within the oocyte cytosol, it can be considered a uniform compartment (20,21). Although no substantial difference is observed between simulations using the simpler two-compartment cytosol model or the multishell eight-compartment cytosol model and no advantage is gained from using the larger and slower model, it is adopted here to give comparability with Zeuthen's et al. (7,9,22) and Lapointe's (3,5) models for simulation across GLUT2. The simpler two-compartment cytosol-unstirred layer _[3] and cytosol _[4] is adopted for simulation of the more complex Na⁺, glucose, and water flows in SGLT-expressing oocytes.

The equations describing Na⁺ glucose cotransport water and impermeant solute fluxes are similar to those of glucose and water via GLUT2 (Eq. 4 above) but incorporate the additional requirement of Na⁺-glucose coupled cotransport. This complex phenomenon is modeled here by assuming that Na⁺ and glucose bind symmetrically to saturable sites at either side of the external orifice of the transporter in a similar way to glucose via GLUT2. It is assumed that uncoupled leakage of either Na⁺ or glucose via the transporter is negligible. This is justifiable on the basis that oocyte volume flow does not change in the absence of glucose and the glucose-induced Na⁺ current via the cotransporter is practically abolished by phloridzin (23). Glucose flow via the cotransporter is

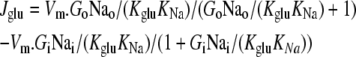(10)

and coupled Na⁺ flux = J_glu.CC. (11).

CC is the coupling coefficient of glucose flux to Na⁺ flux, assumed to be = 1. V_m is maximal glucose flux together with Na⁺ (mole cm² s⁻¹). G = glucose concentration and Na = sodium concentration mM and K_Na= 15 mM K_G = 5 mM are the concentrations of Na⁺ and glucose at half-maximal transporter saturation at either site (17). Na⁺ flow between the vestibule and cytosol is treated separately but similarly to other solutes. Another set of diffusion equations identical in form to Eqs. 8 and 9 above is implemented to generate these flows.

The simulation conditions here in which the external glucose = 1 mM and external Na⁺ = 100 mM generate a steady-state glucose accumulation ratio G_i/G_o in the cytosol sevenfold above the external solution when Na_o/Na_i concentration ratio = 16. Na⁺ is assumed to be accompanied by a single counterion Cl⁻, so that three osmoles are transported per mole Na⁺ during cotransport with glucose (3,6,9). Although glucose accumulation could be increased by model adjustments, these additional complexities are inessential to demonstrate the central hypothesis of this work and have not been implemented.

Simulation of isotonic and hypertonic replacement of external glucose on transport through GLUT2

A key experiment described by Zeuthen et al. (7) uses isotonic addition of the nonmetabolized, but transported, glucose derivative, 3-O-methyl-glucose (3-OMG) (20 mM) to the external solution. When 3-OMG is added, 20 mOsm kg⁻¹ (mOsm) of impermeant solute is simultaneously removed from the external solution; thus the initial condition of 3-OMG addition does not, ipso facto, affect the osmotic relations across the oocyte membrane. Other experiments where solute additions are added hypertonically to the external solution without maintaining the osmolarity of the external solution cause an initial perturbation in oocyte water flow which is difficult to separate from the other water flow components (3,5,9).

All changes in solution, e.g., addition or subtraction of glucose (3-OMG) or addition of phloretin, were simulated by programming a step change with exponential time constants of 1 s⁻¹ or 10 s⁻¹. This simulates the time required to alter the external solutions and avoids spikes in glucose and water flows which generate instability in the numerical integrations.

Numerical integration with variable step lengths in Berkeley Madonna of the cotransport model differential equation

The small size of the vestibule combined with its high throughput of water, Na⁺, and glucose requires that the numerical integration time step be very short. A minimal step of 100 ns and an error tolerance of 1 × 10⁻⁴ give stable integrations over the required range of parameters. Typical simulations requiring 360 virtual seconds of glucose flow using the Berkeley Madonna program required ≈90 s on a personal computer using an Intel Pentium 4 central processor running at a clock speed of 3.2 GHz.

Model testing

Curve fitting

Water flows generated by glucose flow across GLUT2 and SGLT1 have been determined with great precision by Zeuthen and colleagues (22,23). With GLUT2 simulations, three conditions are used to test the validity of the model predictions: the rate and extent of oocyte percentage volume increase after exposure to glucose—(3-OMG) (20 mM); then during the period when 3-OMG is removed isotonically from the external solution and water and 3-OMG exits from the oocyte; and finally, during a period of exposure to the sugar transport inhibitor, phloretin in the external solution, when a portion of the loaded sugar remains within the oocyte. The model parameters are varied to give a least square best fit to all three volume changes. This is done with a program-controlled curve-fitting routine based on the Levenberg-Marquardt algorithm in which the entire parameter set, shown in Table 1 or Table 2 in the case of SGLT simulations, is varied systematically. Using the curve-fitting program with several parameters is relatively slow, requiring 100–200 trial iterations ≈10 h; but the benefit of this approach is that optimal fits are obtained, which are quantified by an estimate of least squares deviation between the predicted and the observed variables. With the GLUT2 model the least square deviation between the observed and model predicted = 0.16, and with the SGLT model the deviation = 0.189.

TABLE 1.

Derived parameters from GLUT2 model fitted to water inflow via GLUT2 expressed in Xenopus oocytes (7) as shown in Fig. 2

	GLUT2 Pw12 cm s−1	GLUT2 Pw12 (phloretin) cm s−1	Membrane Pw13 cm s−1	ks−1	D23 cm2 s−1	D34 cm2 s−1	GLUT Vm nmoles cm−2 s−1	Relative diffusion rate, , KCl/glucose	Vestibule elastic modulus, E, kPa.
Parameter	5.92 × 10−5	3.80 × 10−5	7.86 × 10−6	1000	4.16 × 10−6	2.36 × 10−5	2.27	2.00	0.20
Fluid inflow	0.69	0.00	0.03	−0.01	0.11	0.01	0.04	0.08	0.00
Fluid exit	0.59	0.00	0.00	−0.01	0.11	0.02	0.02	0.06	0.03
Inflow (phloretin)	0.44	0.01	−0.30	0	0.09	0.02	0.02	0.05	0.03
						Sensitivity water/glucose
Early inflow (80)	−0.02	0.00	−0.02	0	−0.00	0.14	−0.48	−0.01	0.00
Late inflow (162)	−0.03	0.00	−0.02	−0.01	−0.02	−0.05	−0.34	−0.01	0.00
Exit (25)	0.03	0.03	−0.05	−0.21	−0.02	0.23	−1.16	−0.01	0.07

The figures in parentheses in the left-hand column are the water/glucose molar flux ratios as simulated during glucose inflow and exit.

TABLE 2.

Sensitivity table for simulation of water flows in oocytes expressing SGLT (23), as shown in Fig. 3

Parameter	D34 cm2 s−1	D23 cm2 s−1	Pw13 cm s−1	SGLT Pw12 cm s−1	SGLT Pw12 (phloridzin) cm s−1	SGLT Vm pmol cm−2 s−1
Condition	2.18 × 10−5	2.03 × 10−6	2.12 × 10−5	2.89 × 10−5	4.75 × 10−7	66.5
Parameter ratio GLUT2/SGLT1	1.08	2.05	0.37	2.05	80	341
Sensitivity 1 mM 3-OMG phase 1	0.215	0.231	0.109	0.080	0.400	0.096
Urea 20 mM phase 2	0.006	0.005	0.089	0.652	0.000	0.393
Inflow 3-OMG phase 3	0.000	−0.048	0.655	0.293	0.000	−0.288
Phloridzin phase 4	0.014	0.211	0.327	0.356	0.000	0.114
Urea 20 mM phase 5	−0.004	−0.139	1.136	0.141	0.024	−0.045

Parameter sensitivities

The sensitivities of the model variables to changes in any individual parameter, k_i, during the three protocol phases were obtained by observing the normalized change in flows or other dependent variables, v_i, with normalized changes in each parameter from the median values of the set of parameters, k_i, obtained from the best fit to the observed data. The normalized sensitivity is

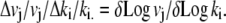The normalized sensitivities are useful only as first-order indicators of the relative weighting of the model parameter effects on the observed variables. As these sensitivities are highly correlated in the case of GLUT2 and SGLT simulations, they are only useful over a narrow range.

RESULTS

Simulation of water flows across GLUT2 in Xenopus oocytes

After isotonic addition of 3-OMG to the external solution, its permeation into the vestibule of GLUT2 renders it hypertonic to the external solution, thereby inducing osmotic water inflow across the external orifice of the transporter (Fig. 1). The osmotic water inflow creates an intravestibular pressure which generates a convective flow of solute to the adjacent unstirred cytosolic layer. The convective-diffusion flow of glucose and water between vestibular and outer cytosolic layers generate a smaller hypertonicity in the outer layers of the cytosol, which causes a secondary osmotic flow across the cell membrane via water-conducting channels outside the glucose transporter.

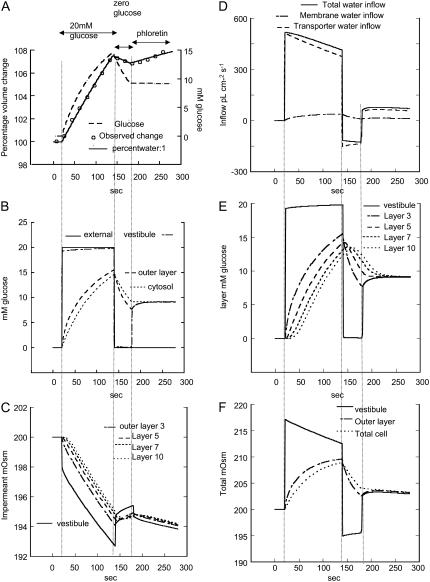
These points are illustrated in Fig. 2, where simulated volume flow across GLUT2 reproduces Zeuthen's experiment (Fig. 7 in Zeuthen et al. (7)). In Fig. 2 A, the solid line shows the percentage change in total oocyte volume, the circles are observed data taken from Zeuthen et al. (7), and the broken line is the simulated 3-OMG uptake monitored as total oocyte glucose concentration. After isotonic 3-OMG (20 mM) addition, oocyte volume increases rapidly (Fig. 2 D). After isotonic glucose removal, the oocyte volume decreases at a slower rate than during uptake (total water outflow has a maximal rate of −150 pl cm⁻² s⁻¹; whereas the maximal inflow rate is 500 pl cm⁻² s⁻¹, Fig. 2 D). After phloretin addition, water inflow increases (7) to 50 pl cm⁻² s⁻¹(Fig. 2, A and D).

FIGURE 2.

Simulation of effects of 3-OMG flows (20 mM) on water flows in oocytes expressing GLUT2. (A) The simulated oocyte percentage volume change (solid line) is superimposed on the observed data (open circles) obtained by Zeuthen et al. (7). The dashed line shows the simulated average cytosolic glucose concentration mM. The leftmost vertical dotted line indicates the time of isotonic addition of 3-OMG (20 mM). The second vertical line is when 3-OMG is removed and the third vertical line is when phloretin is added. (B) The simulated changes in glucose concentration are illustrated as follows in the external solution (solid line), vestibule (dash-dotted), outer cytosolic layer (long dashed), and averaged inner cytosolic layers (short dashed). (C) The simulated changes in osmolarity of the impermeant solute (KCl) are shown in D, and the rates of fluid inflow via the transporter (long dashed) and via the membrane (short dashed) and the total flow (solid line) are shown. (E) The concentrations of glucose mM in the vestibule and from the most external cytosolic layer, 3, to innermost layer, 10, are shown. (F) The total osmolarity (glucose mM + impermeant solute mOsm) in the vestibule (solid line), outer cytosolic layer, (dash-dotted), and average cytosol (dashed) is shown. (C and D) Outputs from some layers are omitted for clarity.

Phase 1: glucose inflow

After 20 mM glucose (3-OMG) addition to the external solution, vestibular glucose rises very rapidly (rise time t_1/2 ≈ 130 ms) and more slowly in the outermost unstirred cytosolic layer and the rest of the cytosol t_1/2 ≈ 30 s (Fig. 2 B). The increase of vestibular glucose concentration is rate controlled by solute diffusion in the external solution. Glucose concentrations in the vestibule, unstirred layer, and total cytosol rise during the loading period to 19.8 mM, 15 mM, and 14 mM, respectively (Fig. 2, B and E). Despite the decrease of impermeant solute in the vestibule and outer layers of cytosol (panel C), net osmolarity increases within the vestibule and then in the cytosol (unstirred layer) due to rises in glucose concentration (Fig. 2 F). The impermeant solute concentration in the vestibule decreases due to convective outflow generated by the rise in vestibular pressure to 0.7 cm H₂O and dilution by water inflow from the external solution. The decrease in impermeant solute concentration within the outer layers of the cytosol is also caused by dilution from water inflow (Fig. 2 C).

In the initial period of exposure to glucose, a significant water flow occurs via the transporter ≈500 pl cm⁻² s⁻¹ before any hypertonicity buildup in the outer cytosolic layers (Fig. 2, D–F). At this time water flow via the membrane is <5% of that via the transporter. Thus, water flow occurs via the transporter, before any significant hypertonicity develops in outer cytosolic layer. This corroborates the view (9) that initial glucose-dependent water inflow is not generated by an unstirred layer effect within the cytosol.

Phase 2: glucose outflow

Glucose (3-OMG) removal from the external solution initiates glucose efflux from the oocyte. During this exit phase, vestibular glucose concentration decreases rapidly from 19.8 mM to 0.1 mM (t_1/2 ≈ 130 ms) and more slowly in the outer cytosolic layers (Fig. 2, B and E). The decrease in vestibular glucose concentration slows glucose exit and accounts for the relatively slow rate of oocyte volume decrease in comparison to the rate of volume increase during phase 1 (panels A and D). Similar effects also may account for asymmetric glucose flows across GLUTs (see Discussion).

Despite a small rise in vestibular impermeant osmolar (KCl) concentration, due to reflux from the cytosol resulting from reversal of the direction of water flow from the unstirred layer (Fig. 2, C and D), there is a net decrease in total vestibular osmolarity because of the larger drop in vestibular glucose concentration (Fig. 2, E and F). The rapid fall in total vestibular osmolarity to 195 mOsm is succeeded by a slower decrease in the total osmolarity in the outer cytosol layer from 209 immediately before glucose removal to 202 mOsm (Fig. 2, E and F).

The decrease in total vestibular osmolarity below that of the external solution _[1] together with the smaller change in the total osmolarity of the outer cytosolic layers reverse the direction of net water flow across the oocyte membrane (Fig. 2 D). A slow decrease in oocyte volume is observed during the glucose efflux period, as found by Zeuthen et al. (7) (Fig. 2 A). The simulations indicate that all fluid outflow generated by glucose loss is via the transporter. However, as a result of the residual cytosolic hypertonicity, during the entire net outflow phase, a small fluid inflow component remains via the membrane (Fig. 2 D).

Phase 3: phloretin effect

Blocking glucose efflux with phloretin (Fig. 2, third vertical dotted line) after 40 s of net glucose efflux when a substantial amount of glucose remains within the oocyte (Fig. 2, A, B, and E) reverses the decrease in vestibular glucose (Fig. 2 B) and prevents further glucose loss from the oocyte (Fig. 2, A–C). Vestibular glucose equilibrates with the higher glucose concentration remaining in the inner layers of the cytosol (Fig. 2, B and E). The resultant rise of the total osmolarity in the vestibule and outer cytosolic layer, above that of the external solution (Fig. 2 F), switches the direction of net water flow, resulting in return of net inward water flow (Fig. 2, A and D). The model simulation shows that this changed direction of water flow is entirely ascribable to a change in direction of water movement via the transporter. Flow via the membrane is only secondarily affected by isotonic removal of external glucose.

Simulation of water transport across SGLT

The experiment simulated here, demonstrating the effects of Na-glucose cotransport via SGLT on water transport in oocytes, is that carried out by Zeuthen et al. (23). Their protocol was designed to illustrate the main features of Na⁺ and glucose-coupled water flows in oocytes expressing SGLT1. The oocytes were isotonically exposed to 1 mM 3-OMG in Na⁺ buffer for 3.5 min (phase 1). At 90 s (phase 2) hypertonic urea (20 mM), which is impermeable to these oocytes, was added to the external solution for 30 s to monitor the effect of an osmotic pressure gradient on oocyte water flow. After removal of urea, the oocytes swelled (phase 3) for another 90 s before the 3-OMG was isotonically removed from the external solution and replaced with phloridzin (200 μM) (phase 4). This caused the 3-OMG-induced Na⁺ current to fall by ≈90%. After a further 3 min, the oocytes were exposed for a second time to hypertonic urea (phase 5) to monitor the osmotic water flow in the phloridzin-inhibited state. Urea had no effect on the 3-OMG-induced current at either stage.

The volume changes are simulated as described in Methods and are displayed together with the experimentally derived observed percentage flows obtained from Zeuthen et al. (23) in Fig. 3 A. The curve-fitting routine using the parameters shown in Table 2 fits the observed data in all phases (1–5) with a least squares difference of 0.162 (Fig. 3 A).

FIGURE 3.

Simulation of effects of 1 mM 3-O methyl D-glucose (3-OMG) and 20 mM urea and phloridzin on water flows into oocytes expressing SGLT1. (A) The simulated oocyte percentage volume change (solid line) superimposed on the observed experimental data obtained from Zeuthen et al. (23) (open circles). The first period starts upon exposure to isotonic 1 mM 3-OMG, the second upon addition of 20 mM hypertonic urea + 1 mM 3-OMG, the third upon removal of urea, the fourth upon isotonic removal of 3-OMG and addition of phloridzin (negligible tonicity), and the fifth period upon addition of 20 mM hypertonic urea + phloridzin. (B) The changes in compartmental 3-OMG during the five experimental periods shown in A. (C) The compartmental and extracellular changes in total osmolarity. (D) The separate water flow rates via the transporter, the membrane, and the total transmembrane flows. (E) The changes in vestibular and unstirred layer total osmolarity mOsm, superimposed on the water flow rates via the transporter and membrane using a 100× faster time base than in A and D.

Phase 1

Rapid accumulation of 3-OMG and NaCl (t_1/2 = 0.7 s) (Fig. 3 B) generates vestibular hypertonicity (10 mOsm) above the external solution (Fig. 3, D and E). This is followed by slower tonicity gains in the cytosolic unstirred layer to 4 mOsm (t_1/2 = 37 s) above the external solution and by an increase in cytosolic tonicity to 3.8 mOsm above that of the external solution (t_1/2 = 39 s). The rate of vestibular osmolar and fluid increase is determined here by the rate of solute mixing and equilibration, k = 1 s⁻¹, between the external solution and the external membrane surface. Vestibular hypertonicity generates fluid inflow via the transporter (150 pl cm⁻² s⁻¹). A small increasing inflow via the cell membrane starting at zero and rising to 7.5 pl cm⁻² s⁻¹ at the end of phase 1 results from the slow rise in cytosolic tonicity (Fig. 3, B and E). Vestibular 3-OMG and Na⁺ concentrations both plateau at ≈6 mM during this phase (Fig. 3 B).

Phase 2

Addition of 20 mM hypertonic urea to the external solution reverses fluid inflows via the transporter and cell membrane, resulting in net reversal of fluid inflow (Fig. 3 D). Simulation shows that during this phase, twice as much water flows via the membrane (150 pl cm⁻² s⁻¹) as the transporter. The consequent loss of oocyte volume increases cytosolic tonicity to 208 mOsm and vestibular tonicity to 216 mOsm. Solute concentration polarization in the vestibule retards the urea-induced fluid outflow via the transporter by 75%, thereby masking its real hydraulic conductivity.

Phase 3

After removal of the hypertonic urea fluid, inflows via the transporter and membrane resume immediately. During this phase fluid inflow is caused mainly by the cytosolic hypertonicity gained in phases 1 and 2.

Phase 4

Phloridzin reduces Na-glucose cotransport by at least 90%, as is evident from 3-OMG-Na⁺-dependent Na⁺-current reduction (23). The transporter water permeability is also reduced by at least 95% (Table 2) (Fig. 3 D).

Phase 5

Because phloridzin both blocks Na-glucose cotransport and reduces the transporter hydraulic conductance, the hypertonic urea-induced fluid outflow is now almost entirely via the membrane water channels (150 pl cm⁻² s⁻¹), as illustrated in Fig. 3 D and Table 2. In phase 5, flow change due to 20 mM urea addition to the external solution = 225 pl cm⁻² s⁻¹, whereas in phase 2 the flow change = 400 pl cm⁻² s⁻¹.

DISCUSSION

The simulations here show that the assumption that water transport is coupled to glucose via an alternating glucose-water carrier is unnecessary. The single feature of the model proposed here, which explains glucose-dependent water “cotransport”, is the presence of a vestibular compartment within the body of the transporter acting as an osmotically active reservoir for transported solutes. A vestibule has been observed in all MSF transporter proteins (12). This discrete compartment where different osmolar concentrations can exist from those in the external solution and outer cytosolic layer permits rapid development of an osmotic gradient and water flow across the narrow external orifice of the transporter. It explains 1), how water flow can occur against an osmotic gradient between the cytosol and external solution, 2), why glucose-coupled water movements are generated before substantial solute accumulation occurring in the outer cytosolic layers, and 3), why even precise estimates of solute concentrations within the outer cytosolic layer underestimate osmotically driven water flows generated by glucose flows across either GLUT2 or SGLT1 (3,5).

The main insight gained from the SGLT simulation is illustrated in Fig. 3 E. Fluid inflow and vestibular tonicity rise in parallel before any significant changes occur in the unstirred layer tonicity or flow across the cell membrane. The rapid fluid inflow, which Zeuthen and colleagues observed and ascribe to carrier-mediated uphill water cotransport (9,23), is seen to be a consequence of the transported solutes. In this case, this is Na⁺ and 3-OMG generating a hypertonic vestibular compartment, which generates a faster osmotic flow via the transporter before any transmembrane osmotic flow resulting from solute accumulation in the outer cytosolic layers has developed.

SGLT and GLUT2

The main difference between sugar transport in SGLT and GLUT2 is that sugar is “actively” coupled to Na⁺ inflow; so 3-OMG concentrations are relatively higher in the vestibular and outer cytosolic layer than those seen with GLUT2 (compare Fig. 3 F with 1 mM external 3-OMG with Fig. 2 B with 20 mM 3-OMG). However, identical principles hold for water coupling in both transporters. Comparison of the parameters between GLUT2 and SGLT reveals that SGLT has a much lower transporter activity, V_m, than GLUT2 and has a lower transporter hydraulic permeability, P_w12, than GLUT2. The model simulations indicate that phloridzin inhibits water transport across SGLT1 more effectively than phloretin inhibits water flow across GLUT2 (Table 2).

Despite the large difference in protocols between the simulations with GLUT2 and SGLT, similar values are obtained for D₃₄ and P_w13 (Tables 1 and 2). These parameters are intrinsic to oocytes and independent of the transporters expressed in the membrane, so their similarity suggests some degree of the consistency in the model simulations.

GLUT2

Reversal of the direction of water flow after phloretin addition during 3-OMG exit across GLUT2 has been cited as evidence indicating that water outflow before phloretin addition must occur against an osmotic gradient via an alternating sugar-water carrier. Zeuthen et al. further adduced this to be evidence of 3-OMG-coupled water cotransport (7,9). They suggest that estimates of water inflow via the transporter during phase 1 can be obtained by subtraction of the water inflow after exposure to phloretin (phase 3) from the water flow during net inflow before removal of external 3-OMG (phase 1) (7).

Instead, the model proposed here shows that water inflow after phloretin addition (phase 3) occurs as a result of the oocyte hypertonicity gained from hypertonic 3-OMG uptake in phase 1. Water outflow, occurring during 3-OMG efflux in phase 2 before application of phloretin, results from “downhill” osmotic flow from the hypotonic vestibule into the external solution. Therefore a carrier supplying energy to generate “uphill” water flow from the hypertonic cytosol to the external solution is no longer required.

The GLUT2 model described here shows that after phloretin blocks glucose exit, reversal of the direction change of water flow is caused by the return of the vestibular osmolarity and outer cytosolic layers to hypertonicity as they reequilibrate with the 3-OMG remaining in the inner cytosolic layers. Hypertonic 3-OMG absorption results from the relatively high ratio of 3-OMG permeability to water permeability during the inflow (Table 1). The model estimates P_glucose/P_w ratio ≈ 3 via GLUT2. Reducing this ratio by coexpression of aquaporins or water-permeable antibiotic channels will reduce the hypertonicity generated.

Does phloretin/phloridzin block water flow completely?

Experimental evidence suggests that phloridzin reduces the hydraulic conductance of SGLT-expressing oocytes (17) and both phloretin and cytochalasin B inhibit water flows in cells expressing GLUTs to levels observed without GLUT overexpression (7,24). However, it is difficult to distinguish between a reduced water flow and zero water flow via GLUT2, when water flows simultaneously via other membrane water channels. The model (Fig. 2 A) indicates that water transport via GLUT 2 is incompletely reduced by phloretin (Fig. 2 D and Table 1). However phloridzin does inhibit water flow via SGLT almost completely (Table 2).

Asymmetry of water and glucose flows

Asymmetric glucose flows across glucose transporters, with higher K_m and V_m for glucose net exit than net entry, have been observed in human erythrocytes (26–28). These effects have been ascribed either to an intrinsic asymmetry in the GLUT1 transporter or to “unstirred layer” effects. As with water cotransport, there has been debate about where the retardation of glucose flow occurs and the extent to which this contributes to asymmetry. The analysis here suggests that the unstirred layer affecting glucose transport resides within the body of the transporter and is largely controlled by the slow rate of glucose diffusion D₂₃ between the vestibule and cytosol. Similarly, ATP interactions at the endofacial surface of avian GLUT1 greatly retard net glucose influx in avian erythrocytes (29) and anti-GLUT1 antibodies binding to the endofacial C-terminal of GLUT1 retards glucose influx in human erythrocytes (30).

Stoichiometry of water/solute flow

A key argument proffered in favor of carrier-mediated water-glucose coupling is the apparent constancy of the water-glucose coupling (7). However, the observed stoichiometry of water-glucose flux apparently differs between glucose inflow and outflow. The stoichiometry of water-glucose exit is estimated by subtraction of the water inflow after phloretin from the outflow during glucose exit and assuming a linear rate of glucose exit. This gives a molar “stoichiometry” of water/glucose flow during glucose exit = 110, whereas during inflow, the estimated stoichiometry = 35 (7). Accurate monitoring of either the initial rates of sugar isotope uptake or exit from oocytes is challenging, as adhering isotope from the loading solution must be removed before influx or efflux determination. If there is a rapid component to glucose uptake or efflux, as has been observed with glucose influx in human erythrocytes (31), then estimates of stoichiometries based on steady-state isotope fluxes are unreliable.

If there were an asymmetric water/glucose stoichiometry across GLUT2 such as that reported (7)—where the unidirectional inflow and outflow processes maintained strict coupling ratios between water and glucose—then at equilibrium—when internal and external glucose concentrations are equal and the cytosol isotonic with the external solution—equilibrium exchange of glucose across GLUT2 should produce a net water exit. The only way to maintain cell volume equilibrium would then be by a secondary osmotic water inflow. The principle of detailed balance requires that “transitions between any two states at equilibrium take place with equal frequency” and expressly forbids maintenance of equilibrium by cyclic processes (32). Water-glucose cotransport via GLUT2 is very unlikely to be an exception to this rule.

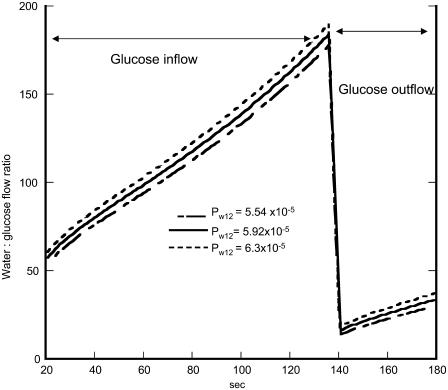
In the simulations shown here, GLUT2 vestibular hypertonicity generated by 3-OMG inflow increases the water/3-OMG flow ratios, and hypotonicity during 3-OMG exit decreases the ratio (Table 1 and Figs. 2 F and 4). The estimated molar ratio of water/3-OMG climbs from 20 to 180 during 3-OMG inflow and abruptly decreases during exit to 20 and returns to 35. These findings differ from those of Zeuthen et al. for GLUT2 (7,9). Most of these differences can be ascribed to uncertainties regarding initial rates of 3-OMG exit and uptake as monitored by isotope flow. This is illustrated by the relatively high sensitivity of the apparent stoichiometry of water/glucose flow during net exit (Table 1) to alteration in the rate of mixing, k, in external solution.

FIGURE 4.

Simulation of the changes in the molar ratio of water/3-OMG inflow via Glut2. The lines shown indicate the effects of changing the parameter values of the transporter P_w12 on inflow phase 1 and outflow phase 2 with varying values of the hydraulic permeability.

Although neither the GLUT2 nor the SGLT models require a fixed relationship between water flow and solute flow via the transporter and none is found, they still simulate the observed data very closely, thus implying that the previous estimates of water/glucose stoichiometry are ambivalent. The best evidence for a tight stoichiometry between water flow and solute flow comes from simultaneous monitoring of water flow and Na current in oocytes expressing SGLT (6,22,23). During steady-state inflows of water and glucose, a reasonably constant ratio between water and solute flow is maintained; however this does not constitute a stoichiometric relationship.

Sensitivity analysis applied to the “stoichiometry” of water/glucose flows

Sensitivity analysis of water/3-OMG “stoichiometry” (Table 1) shows that the molar ratio of water/glucose flow is affected by nearly all of the parameters. The dominant parameters affecting the ratio are V_m and D₃₄. Both these parameters affect the rate of solute uptake, but neither directly alters water flow.

Analysis of model parameter sensitivity in GLUT2

The main observable variables with glucose flow via GLUT2 are the extent and rates of oocyte volume change and the rates of glucose inflow and exit. The multicompartment model presented here has nine parameters affecting water flow. These are the following:

GLUT2 P_w12

The hydraulic conductance obtained by the best fit of the model to the data for GLUT2 = 5.92 × 10⁵ cm s⁻¹ is similar to that observed directly by Zeuthen et al. (20). As expected, this is the most important parameter controlling glucose-dependent fluid inflow in all three phases (Table 1). Fluid inflow during phase 3 is dependent on the hypertonicity developed during the prior loading phase 1 and unloading phase 2 periods. The more hypertonic the cell becomes during phase 1, the higher the water inflow rate will be in phase 3 after application of phloretin.

Membrane P_w23

The hydraulic conductance of oocyte membrane is intrinsically variable between batches of oocytes and can be altered either by aquaporin expression or by exogenous water channel producing antibiotics (3,6,7,9). The membrane fluid conductance P_w13 = 7.86 × 10⁻⁵ cm s⁻¹ giving the best fit to the GLUT2 data is only 13% of the transporter conductance, P_w12 (Table 1). The model prediction is similar to the low value for oocytes hydraulic conductance obtained by Zeuthen et al. (9). Because of its low hydraulic conductance, the flow sensitivities to variation of P_w13 are less than those for P_w12. However, P_w13 has a more dominant effect on fluid inflow in phase 3 with phloretin present because fluid inflow through the transporter is reduced.

Mixing constant k

The mixing constant, k (s⁻¹), which determines the rate of external solution change and equilibration of the replacement solution at the external membrane surface, has no significant effects on net fluid inflow or fluid exit after addition or subtraction of 3-OMG (Table 1). However it does have a significant effect on the apparent stoichiometry of water/glucose exit because of the high initial rate of glucose exit that results from removal of external glucose.

Solute diffusion coefficient between vestibule and cytosol D₂₃

Solute diffusion coefficients between the vestibule and cytosol are unknown. Since glucose may bind to the transporter protein (14–16), or the cytoplasmic projections of the transporter may partially occlude solute flow between the transporter and the cytosol, it is likely that glucose diffusion between the vestibule and cytosol is slower than within the cytosol. The model shows that glucose diffusion between the vestibule and cytosol is only 17% of that in the cytosol, i.e., 4.16 × 10⁻⁶ cm² s⁻¹. This ensures that the vestibular glucose concentration equilibrates almost completely with the external solution concentration during influx and is almost completely void of glucose during exit (Fig. 2, B and E).

Solute diffusion coefficient within the cytosol D₃₄

The solute diffusion coefficient within the cytosol as determined by the model is similar to that observed directly by Zeuthen et al. (7,20). This is too fast to sustain a substantial “unstirred layer” effect in the cytosol. Therefore fluid inflows and outflow are relatively insensitive to changes in D₃₄.

The relative diffusion rate of KCl/glucose

KCl has a higher diffusion coefficient in free solution and cytosol than glucose (3,20). Increased KCl diffusion rates reduce the impermeant solute gradient between the vestibule and cytosol generated by convective diffusion. Raised KCl diffusion rates reduce vestibular depletion of impermeant solute during fluid inflow and reduce concentration polarization of impermeant solute in the vestibule during fluid outflow. As this buffers the effects of vestibular glucose accumulation or depletion on water flows, the sensitivity of increased KCl/glucose diffusion rate ratio, 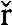, is positive in all three phases.

The maximal velocity, V_m, of glucose transport via GLUT2

Although GLUT2 has a low affinity for glucose and 3-OMG (25), 3-OMG transport via GLUT2 remains a saturable transport process. The observed linearity of the fluid response to a wide range of glucose concentrations is anomalous (7). This nonsaturable increase in water inflow with external 3-OMG is also simulated by the model (not shown) and is consistent with the finding that large alterations in 3-OMG K_m = 25 mM transport via GLUT2 are without any significant effect on water flows, i.e., the sensitivity = zero (not shown in Table 1). Although increasing the V_m of GLUT2 has a positive effect on water inflows and outflow, its sensitivity is reduced by 3-OMG accumulation in the vestibule as a consequence of the low D₂₃, which slows glucose transit through the vestibule and masks the high V_m.

The vestibule elastic modulus, E

The vestibular elastic modulus was assigned to give low intravestibular hydrostatic pressure at the observed flow rates (1–2 cm H₂O) (20). This pressure is sufficient to generate a steady-state flow across the transporters' endofacial openings. Its wide aperture is assumed to have a very high fluid conductance P_w34 = 1.2 × 10⁻³ cm s⁻¹. Alteration of the elastic modulus has a small positive effect on initial outflow after switching from inflow when vestibular pressure = 1–2 cm to outflow when vestibular pressure = −1–2 cm H₂O.

GLUT2 P_w12 phloretin

This parameter is zero during the first and second phases of fluid inflow and outflow, so during these phases its sensitivity is also zero (Table 1). It has a small positive effect on inflow during the phloretin phase 3. The best fit suggests that P_w12 is only reduced by 35% by phloretin.

SGLT parameter sensitivity

The sensitivity Table 2 shows that all the parameters exert some control on fluid inflow across SGLT during the net inflow phase 1. Some parameter sensitivities to water flow are specious, e.g., the large sensitivity of the transporter hydraulic permeability P_w12 obtained in the presence of phloridzin is the result of fitting procedures, which require that a good parameter fit obtained in phases 4 and 5 affects sensitivities in phase 1.

However, the relatively high sensitivity of fluid outflow to urea addition during phase 2 to V_m (0.652) compared with its sensitivity in phase 5 (0.393) is due to increased vestibular solute accumulation during phase 2, which is controlled by V_m This solute accumulation prevents water outflow. In phase 5, V_m is zero, so its sensitivity arises from its effects in phases 1–3.

CONCLUSION

The simulations of water and glucose flows across GLUT2 and SGLT1 expressed in Xenopus oocytes show that both models simulate the experimental observations and conditions and can readily reproduce “uphill” water flow or glucose-induced water inflow before buildup of any substantial unstirred layer. Both these features of “carrier”-mediated water flow are explicable in terms of tonicity changes in the transporters' vestibular compartment. As the vestibular volume is very small, the tonicity changes within them occur rapidly and do not contribute significantly to total solute accumulation within the oocyte cytosol.