A statistical framework for the classification of tensor morphologies in diffusion tensor images

Abstract

Tractography algorithms for diffusion tensor (DT) images consecutively connect directions of maximal diffusion across neighboring DTs in order to reconstruct the 3-dimensional trajectories of white matter tracts in vivo in the human brain. The performance of these algorithms, however, is strongly influenced by the amount of noise in the images and by the presence of degenerate tensors — i.e., tensors in which the direction of maximal diffusion is poorly defined. We propose a simple procedure for the classification of tensor morphologies that uses test statistics based on invariant measures of DTs, such as fractional anisotropy, while accounting for the effects of noise on tensor estimates. Examining DT images from seven human subjects, we demonstrate that this procedure validly classifies DTs at each voxel into standard types (nondegenerate DTs, as well as degenerate oblate, prolate or isotropic DTs), and we provide preliminary estimates for the prevalence and spatial distribution of degenerate tensors in these brains. We also show that the P values for test statistics are more sensitive tools for classifying tensor morphologies than are invariant measures of anisotropy alone.

1. Introduction

Water molecules in the human brain are known to diffuse preferentially along the dominant orientation of white matter (WM) fiber tracts [1–3]. Thus, diffusion tensor imaging (DTI), which tracks the diffusion of water, can be used to map accurately in vivo the structure and orientation of fiber tracts in the WM of the brain. The directional dependence of diffusion in each voxel can be characterized by a 3 × 3 matrix, called a diffusion tensor (DT). In a spectral value decomposition of a DT D, eigenvectors denote the three directions of diffusion, and the corresponding eigenvalues represent the diffusivity of water in each of these three directions [1–3]. Many tractography algorithms attempt to reconstruct major fiber tracts within the human brain by connecting neighboring tensors consecutively along their principal directions (PD) of diffusion [4–11], i.e., the primary direction in which the water molecules in a given voxel diffuse. The reliability and validity of these tractography algorithms therefore depend critically on whether they can successfully determine the correct PD of diffusion in the presence of the noise that is inherent to DT images.

The noise in DT images derives ultimately from the noise present in the set of diffusion-weighted (DW) images from which the DT images are constructed. This noise introduces variability into the estimation of eigenvalues and eigenvectors of both degenerate and nondegenerate tensors [12,13]. A DT is degenerate if at least two of its eigenvalues are equal. The three types of degenerate tensors are isotropic (λ₁ = λ₂ = λ₃ > 0), oblate (λ₁ = λ₂ > λ₃ > 0), or prolate (λ₁ > λ₂ = λ₃ > 0), where λ_i(i = 1,2,3) are the three eigenvalues of the tensor. A DT is thus nondegenerate when all three of its eigenvalues are distinct (i.e., λ₁ > λ₂ > λ₃). While some DTs are, in truth, degenerate, estimated tensors are always nondegenerate because of the influence of noise (e.g., bias introduced by sorting estimated eigenvalues by magnitude); thus, DTs, whose eigenvalues cannot in reality be discriminated, can be misclassified as nondegenerate [12], yielding erroneous estimates of PDs of diffusion. Fiber tracking based on these erroneous estimates of PDs will, in turn, produce fiber pathways that are incorrectly reconstructed, e.g., pathways that do not exist in the brain. Therefore, accounting for the influence of noise and reducing the likelihood of incorrectly estimating the PDs of diffusion is of utmost importance in improving the reliability and validity of fiber tracking using DT images [13–18].

Because invariant measures of anisotropy are relatively robust in the presence of noise, these measures have been used extensively to classify tensor morphologies in DT images [15,16,19–21]. For instance, invariant measures of fractional anisotropy (FA) [19], linear shape (CL) and planar shape (CP) [22] have been used to determine the degree to which a tensor's shape is classified as isotropic, oblate or prolate, respectively. In practice, invariant measures of a tensor are often compared against a fixed value, or threshold, to determine whether the tensor is degenerate [10,23]. However, identifying an appropriate threshold is crucially important for enhancing the likelihood that a tensor morphology will be correctly classified. A threshold that is too low will increase the probability of misclassifying as “nondegenerate” a DT that is actually “degenerate” (Type I error); a threshold that is too high will increase the probability of misclassifying as degenerate a DT that is actually nondegenerate (Type II error). The thresholds that are applied to these invariant measures, however, are usually selected arbitrarily [16].

To classify tensor morphologies, we test sequentially at each voxel of the image three hypotheses that together determine whether tensors are isotropic, oblate or prolate. We use invariant measures as test statistics for each of these three hypotheses. Moreover, we select appropriate thresholds of invariant measures by analytically deriving the limiting distribution of the invariant measure under the null hypothesis, which, in turn, allows us to estimate the probability of making a Type I error in the testing of each hypothesis. Finally, we use P values of the test statistics to improve our classification of tensor morphologies in voxels where the presence of noise obscures discrimination of differences among eigenvalues. Computer simulations confirm that our classification scheme appropriately controls the rates of Type I errors in classifying the morphologies of DTs. Human studies show that P values of the test statistics increase the sensitivity and accuracy of tensor classification.

2. Theory

2.1. A statistical model for tensor estimation

A DT data set consists of n DW images acquired for each subject. A conventional DTI pulse sequence provides m baseline images (i.e., images having zero diffusion weighting) and n−m DW images at each b value. Each image contains N voxels, and thus n DW measurements are made at each of these N voxels. We use the expression {(S_i,r_i,b_i): i = 1,…,n} to denote the entire set of observations at each voxel, where S_i represents the nuclear magnetic resonance (NMR) signal at a voxel, r_i = (r_i,1,r_i,2,r_i,3)^T represents the direction of the applied diffusion gradient, the superscript T denotes the transpose and b_i is the b factor for each DW image [24,25].

Thermal noise in the magnitude of an NMR signal conforms to a Rician distribution [26,27]. In the presence of minimal thermal noise, this Rician distribution is well approximated by a Gaussian distribution [24]. Henceforth, we will focus on a statistical model for nDW measurements at a given voxel that assumes the Gaussian distribution of noise:

$$\text{log}{S}_i=\text{log}{S}_0-b_i{\text{r}}_i^{T}D{r}_i+{\epsilon }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}i=1,\dots ,n,$$ (1)

where ε_i is a random noise component that has a mean of zero and a standard deviation of σ_i, S₀ is signal intensity in the absence of any DW gradient and the DT D = (D_k,j) is a 3 × 3 positive definite matrix such that D_j,k = D_k,j holds for all j,k = 1,2,3. In the field of statistics, Eq. (1) is termed a linear heteroskedastic model [28,29]. Let $\widehat{\theta }={(\text{log}{\widehat{S}}_0,{\beta }^T)}^T$ be an estimate of θ = (logS₀,β^T)^T, where we define β = (D₁₁,D₁₂,D₁₃,D₂₂,D₂₃,D₃₃)^T.

2.2. Invariant measures of degenerate tensors

Numerous invariant scalar indices of DTs have been proposed as summary measures of the intrinsic structural features of fiber tracts at each voxel of the human brain. All of them are functions of the three eigenvalues of a DT. Three principal invariants, {I₁(β), I₂(β) and I₃(β)}, are related to the following characteristic equation [19,20]:

$$\begin{array}{ll}\left|D-\lambda I_{3\times 3}\right|\hfill & =\left(\lambda -{\lambda }_1\right)\left(\lambda -{\lambda }_2\right)\left(\lambda -{\lambda }_3\right)\hfill \\ & ={\lambda }^3-I_1\left(\beta \right){\lambda }^2+\lambda I_2\left(\beta \right)-I_3\left(\beta \right)=0,\hfill \end{array}$$ (2)

where |D−λI_{3 × 3}| denotes the determinant of D−λI_{3 × 3} and I_{3 × 3} is a 3 × 3 identity matrix. The three principal invariants [19,30] are defined as follows:

$$\begin{array}{l}{I}_1\left(\beta \right)=D_{11}+D_{22}+D_{33}={\lambda }_1+{\lambda }_2+{\lambda }_3,\hfill \\ I_2\left(\beta \right)=D_{11}{D}_{22}+D_{11}{D}_{33}+D_{22}{D}_{33}-\left(D_{12}^2+D_{13}^2+D_{23}^2\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\lambda }_1{\lambda }_2+{\lambda }_1{\lambda }_3+{\lambda }_3{\lambda }_2,\hfill \\ I_3\left(\beta \right)=D_{11}{D}_{22}{D}_{33}+2D_{12}{D}_{13}{D}_{23}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}-\hspace{0.17em}\left(D_{33}{D}_{12}^2+D_{22}{D}_{13}^2+D_{11}{D}_{23}^2\right)={\lambda }_1{\lambda }_2{\lambda }_3.\hfill \end{array}$$ (3)

Another commonly used invariant of D is $I_4\left(\beta \right)=I_1^2\left(\beta \right)-2I_2\left(\beta \right)$ [20].

FA and relative anisotropy (RA) normalized in (0, 1) are two of the most commonly used invariant measures [31]. FA and RA are, respectively, defined as

$$\begin{array}{l}\text{FA}\left(\beta \right)=\sqrt{1-I_2\left(\beta \right)I_4{\left(\beta \right)}^{-1}}\hspace{0.17em},\hspace{0.17em}\text{and}\hfill \\ \text{RA}\left(\beta \right)=\sqrt{1-3I_2\left(\beta \right)I_1{\left(\beta \right)}^{-2}}.\hfill \end{array}$$ (4)

Isotropic tensor at each voxel is represented by FA(β) = RA(β) = 0, and maximum anisotropy, by FA(β) = RA(β) = 1. Other invariant measures of DTs include measures of CL and CP [8,20,22,32]. The measures for CL and CP are defined as

$$\begin{array}{l}\text{CL}\left(\beta \right)=\left({\lambda }_1-{\lambda }_2\right)/I_1\left(\beta \right)=2\text{RA}\left(\beta \right)\frac{\text{sin}\left(\pi /3-\varphi \right)}{\text{sin}\left(\pi /3\right)},\hspace{0.17em}\text{and}\hfill \\ \text{CP}\left(\beta \right)=2\left({\lambda }_2-{\lambda }_3\right)/I_1\left(\beta \right)=2\text{RA}\left(\beta \right)\frac{\text{sin}\left(\varphi \right)}{\text{sin}\left(\pi /3\right)},\hfill \end{array}$$ (5)

where ϕ∈[0,π/3] is defined in Eq. (15) in the Appendix. A CL(β) value approaching 1 indicates that a tensor is nonoblate (i.e., the difference between λ₁ and λ₂ is large, indicating that the DT is highly elongated, or “linear”), whereas a CL(β) value near zero, together with a large value of CP(β), indicates that the DT is nearly oblate. A DT with a small CP(β) value (i.e., the difference between λ₂ and λ₃ is small) and a large CL(β) is prolate.

2.3. Test procedure for classifying tensor morphology

We propose a three-step procedure that tests sequentially each of three hypotheses for the presence of a degenerate tensor at a given significance level (i.e., the significance level of a test is the probability of rejecting the null hypothesis when the null hypothesis is true) in each voxel of the imaging volume:

• Hypothesis 1 (to classify isotropic DTs). At the significance level α₁, we use a statistic to test the following hypotheses:

  $$H_0^{\left(1\right)}:{\lambda }_1={\lambda }_3\hspace{0.17em}\text{vs}.H_1^{\left(1\right)}\hspace{0.17em}:{\lambda }_1\ne {\lambda }_3.$$ (6)
• Hypothesis 2 (to classify oblate DTs). At the significance level α₂, we use a second statistic to test the following hypotheses:

  $$H_0^{\left(2\right)}:{\lambda }_1={\lambda }_2\hspace{0.17em}\text{vs}.H_1^{\left(2\right)}:{\lambda }_1\ne {\lambda }_2.$$ (7)
• Hypothesis 3 (to classify prolate DTs). At the significance level α₃, we use a third statistic to test the following hypotheses:

  $$H_0^{\left(3\right)}:{\lambda }_2={\lambda }_3\hspace{0.17em}\text{vs}.H_1^{\left(3\right)}:{\lambda }_2\ne {\lambda }_3.$$ (8)

To classify DT morphologies, we need to combine information from all three hypotheses (a flow chart for sequential testing of the three hypotheses is found in Fig. 1). If unable to reject $H_0^{\left(1\right)}$, we conclude that evidence for the presence of anisotropy in this DT is lacking and classify this DT as isotropic. If, on the other hand, the null hypothesis $H_0^{\left(1\right)}$ is rejected (i.e., the presence of anisotropy is supported), we then test the second and third hypotheses. In that instance, if the null hypothesis $H_0^{\left(2\right)}$ is not rejected and the null hypotheses $H_0^{\left(1\right)}$ and $H_0^{\left(3\right)}$ are rejected, then we have insufficient evidence that this DT is not oblate, and thus, we classify it as oblate. If, in contrast, the null hypotheses $H_0^{\left(1\right)}$ and $H_0^{\left(2\right)}$ are rejected but the null hypothesis $H_0^{\left(3\right)}$ is not rejected, the DT is classified as prolate in shape. If all $H_0^{\left(\text{i}\right)}$ (i = 1,2,3) are rejected, then the DT is classified as nondegenerate (i.e., a PD for the DT can be assigned).

Fig. 1.

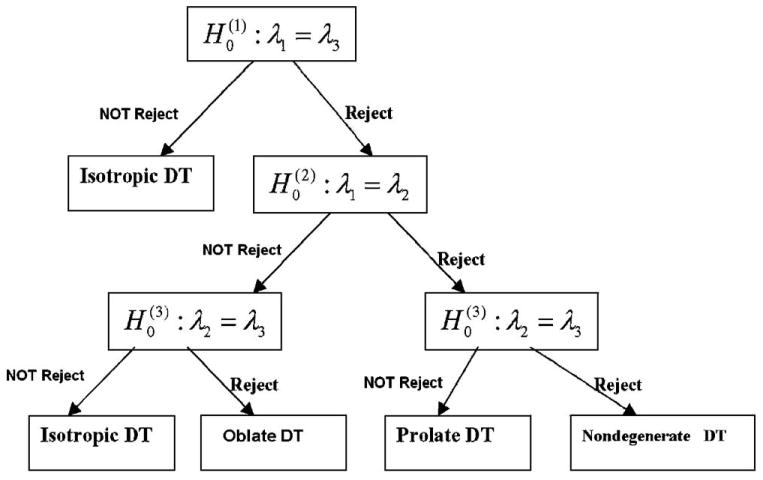
Path diagram for the classification of tensor morphologies.

We propose the use of certain invariant measures as test statistics for each of these three hypotheses. Note that in isotropic tensor, it follows from Eq. (4) that FA(β) = 0 is equivalent to claiming that I₂(β) = I₄(β). To test statistically for the presence of isotropy in a voxel, we can formulate the null hypothesis and its alternative as

$$H_0^{\left(1\right)}:I_2\left(\beta \right)=I_4\left(\beta \right)\hspace{0.17em}\text{vs}.H_1^{\left(1\right)}:I_2\left(\beta \right)\ne I_4\left(\beta \right).$$ (9)

Because $\text{FA}{\left(\beta \right)}^2=\left[I_4\left(\beta \right)-I_2\left(\beta \right)\right]/{{\rm I}}_4\left(\beta \right),\hspace{0.17em}{T}_a\left(\widehat{\beta }\right)=\text{FA}{\left(\widehat{\beta }\right)}^2$ is used as the test statistic for the isotropy hypotheses.

When testing the hypotheses pertaining to oblate and prolate DTs, we consider two additional invariant measures [20]:

$$\begin{array}{l}V\left(\beta \right)={\left[I_1\left(\beta \right)/3\right]}^2-I_2\left(\beta \right)/3\hspace{0.17em}\text{and}\hfill \\ S\left(\beta \right)={\left[I_1\left(\beta \right)/3\right]}^3\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-I_1\left(\beta \right)I_2\left(\beta \right)/6+I_3\left(\beta \right)/2.\hfill \end{array}$$ (10)

These two invariant measures are related to the explicit expression of three eigenvalue–eigenvector pairs [20]. In the Appendix, we show that $S\left(\beta \right)+V\left(\beta \right)\sqrt{V\left(\beta \right)}=0$ is mathematically equivalent to λ₁ = λ₂. Similarly, $S\left(\beta \right)-V\left(\beta \right)\sqrt{V\left(\beta \right)}=0$ is equivalent to λ₂ = λ₃. Thus, we can rewrite Eqs. (7) and (8) that test for the presence of oblate and prolate tensors (i.e., using Hypotheses 2 and 3) as:

$$\begin{array}{l}{H}_0^{\left(2\right)}:S\left(\beta \right)+V\left(\beta \right)\sqrt{V\left(\beta \right)}=0\hspace{0.17em}\text{vs}.H_1^{\left(2\right)}:S\left(\beta \right)+V\left(\beta \right)\sqrt{V\left(\beta \right)}\ne 0;\hfill \\ H_0^{\left(3\right)}:S\left(\beta \right)-V\left(\beta \right)\sqrt{V\left(\beta \right)}=0\hspace{0.17em}\text{vs}.H_1^{\left(3\right)}:S\left(\beta \right)-V\left(\beta \right)\sqrt{V\left(\beta \right)}\ne 0.\hfill \end{array}$$ (11)

For the statistic that tests $H_0^{\left(2\right)}$ against $H_1^{\left(2\right)}$, we propose

$$T_b\left(\widehat{\beta }\right)=S\left(\widehat{\beta }\right)+V\left(\widehat{\beta }\right)\sqrt{V\left(\widehat{\beta }\right)}.$$ (12)

Similarly, we propose $T_c\left(\widehat{\beta }\right)=\hspace{0.17em}V\left(\widehat{\beta }\right)\sqrt{V\left(\widehat{\beta }\right)}-S\left(\widehat{\beta }\right)$ as the statistic for testing $H_0^{\left(3\right)}$ against $H_1^{\left(3\right)}$.

Also, in the Appendix, we derive the asymptotic distributions of $T_a\left(\widehat{\beta }\right)$, $T_b\left(\widehat{\beta }\right)$, and $T_c\left(\widehat{\beta }\right)$ under the null hypotheses as the total number of acquisitions (n) goes to infinity. We then propose a scaled χ² approximation for calculating the P value for each hypothesis (i.e., the probability of having a test statistic more extreme than the one obtained under the assumption of the null hypothesis) for moderate and large n (e.g., n ≥ 25). Computational demands for calculating the three proposed test statistics and their corresponding P values are minimal because reconstruction of tensor fields always includes computation of FA² and other invariant measures, as well as the three eigenvalue–eigenvector pairs, that are used to calculate the test statistics.

3. Materials and methods

3.1. Simulations

3.1.1. Type I and II error rates of the test statistics

We assessed the performance of $T_a\left(\widehat{\beta }\right)$, $T_b\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$ as test statistics for the three hypotheses pertaining to the isotropic, oblate and prolate classifications of tensor morphology, respectively [Eqs. (6), (7), (8)], and we evaluated rates of Type I and Type II errors associated with each of these test statistics. We set λ₁ = ρλ₂ and λ₂ = λ₃ to evaluate $T_a\left(\widehat{\beta }\right)$. We used λ₁ = ρλ₂ = 2ρλ₃ to evaluate $T_b\left(\widehat{\beta }\right)$, and we set λ₁ = 1.5λ₂ and λ₂ = ρλ₃ to evaluate $T_c\left(\widehat{\beta }\right)$. Because the three hypotheses were constructed to test for DTs having differing shapes, DTs of differing shape were used as the basis for evaluating the performance of each of the proposed test statistics. We only considered a diagonal DT D and simulated the DW images for each such tensor. Three differing degrees of anisotropy, having ratios ρ = 1, ρ = 1.5 and ρ = 3 were studied. The mean diffusivity $\overline{\lambda }=\left({\lambda }_1+{\lambda }_2+{\lambda }_3\right)/3$ was set equal to 0.7 × 10⁻³ mm²/s, a value typical for normal cerebral tissue [12]. NMR signals were generated using $S_0\hspace{0.17em}\hspace{0.17em}\text{exp}(-b_i{\text{r}}_i^{T}D{r}_i)$. Complex Gaussian noise with a standard deviation σ₀ was then added to the real channel signal, and the resulting DW magnitude images were calculated. The distribution of noise in these DW images was Rician. We fixed S₀ at 1500 but varied σ₀ to provide a range of differing signal-to-noise ratios (SNR = S₀/σ₀) of 10, 15, 20 and 25 in these DW images, respectively. The DTI acquisition consisted of m = 5 baseline images with b = 0 s/mm² and n−m = 25 directions of diffusion gradients arranged uniformly in 3-dimensional space at b = 1000 s/mm² [33]. For each simulation, two significance levels (αs of 5% and 1%) were considered, and 10,000 replications were used to estimate significance levels. A procedure described in the Appendix was used to estimate the DTs and to calculate the P value for testing each of the three hypotheses. We also computed FA, $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ for each simulated data set.

We further evaluated $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ under the null hypotheses. We investigated the empirical behavior of $\text{CL}\left(\widehat{\beta }\right)$ as a function of SNR when λ₁ = λ₂ = 0.84 and λ₃ = 0.42, when the true value of CL(β) was zero. Similarly we considered $\text{CP}\left(\widehat{\beta }\right)$ as a function of SNR when λ₁ = 0.9 and λ₂ = λ₃ = 0.6, when the true value of CP(β) was 0. We generated 10,000 simulated data sets to estimate the mean and standard deviation of $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ at 20 different values of SNR varying from 5 to 40.

3.1.2. Evaluating the test statistics assuming the presence of fiber crossings

We further examined the performance of the three test statistics when modeling the presence of multiple fibers in a single voxel (as will occur when multiple fibers cross within the brain) [34–37], a situation in which the single DT model for Eq. (1) can fail. For our simulated data, we generated NMR signals for a voxel having two different fibers components:

$$S_0\lfloor f\text{exp}\hspace{0.17em}\left(-b_i{\text{r}}_i^T{D}_1{r}_i\right)+\left(1-f\right)\text{exp}\hspace{0.17em}\left(-b_i{\text{r}}_i^T{D}_2{r}_i\right)\rfloor ,$$ (13)

where f∈[0,1] and 1−f are the signal fractions of the DTs D₁ and D₂. We added complex Gaussian noise of standard deviation σ₀ to the real channel signal. We set S₀ = 1500 and varied σ₀ to obtain the NMR magnitude images with differing SNRs of 10, 15, 20 and 25, respectively. We placed, within a single voxel, a DT, D₁, representing WM in which [λ₁,λ₂,λ₃] = [1.4,0.35,0.35] and a second tensor, D₂, representing the presence of either WM [1.4,0.35,0.35] or gray matter (GM) [0.7,0.7,0.7] (units: 10⁻³ mm²/s). Thus, two combinations of D₁ and D₂ were studied: (1) WM+WM or (2) WM+GM. For the case of WM+WM, the angle between the PDs of D₁ and D₂ was set to 90°. Two differing values for f, f = 0.5 and f = 0.25 were studied. Ten thousand replications were used to estimate the rejection rates of the three test statistics for each tissue combination at the significance level of 5%.

We further demonstrated that multiple fibers present within a single voxel can lead to degenerate tensors when we used a model for a single DT [Eq. (1)]. Note that the estimated tensor D cannot recover the two tensor components within the NMR signal of this voxel. However, for a relatively small b value, the estimated D approximated a pseudo DT, D_pseudo = f D₁+(1−f)D₂, which is the weighted sum of the two DTs, D₁ and D₂ [38]. When f = 0.5, neither D₁ nor D₂ dominated signal within the voxel, whereas a D₁ should have dominated the two-DT model at f = 0.25. In the case of WM+WM, the three eigenvalues of D_pseudo were given by λ_1,p = 1.4(1−f)+0.35f, λ_2,p = 0.35(1−f)+1.4f and λ_3,p = 0.35f+0.35(1−f), respectively. At f = 0.5, λ_1,p = 0.875, λ_2,p = 0.875 and λ_3,p = 0.35; however, the three eigenvalues of D_pseudo were given by 1.1375, 0.6125 and 0.35, respectively, at f = 0.25. Similarly, for the case of WM+GM, the three eigenvalues of D_pseudo were 1.05, 0.525 and 0.525 at f = 0.5 (or 0.875, 0.6125 and 0.6125 at f = 0.25). Based on the above analysis, we expected that the null hypotheses $H_0^{\left(1\right)}$ (λ₁ = λ₃) and $H_0^{\left(3\right)}$ (λ₂ = λ₃) would be rejected for the WM+WM case at f = 0.5 and that all three null hypotheses would be rejected for the WM+WM case at f = 0.25. For the WM+GM case, we expected to classify the DT as prolate in morphology.

3.1.3. In vivo human data

We acquired DT images of the brains of seven healthy adult subjects (four men and three women; right-handed; mean age 28±4.2 years). Informed consent was obtained from all participants according to guidelines set forth by the institutional review boards at Columbia University and New York State Psychiatric Institute. Images were acquired on a GE 3.0-Tesla whole body MRI scanner (Milwaukee, WI, USA). The data matrix of 128 × 128 was zero-padded to 256 × 256. Other imaging parameters were TE/TR = 73.5/6925 ms, FOV = 24 cm, 3.0-mm slice thickness with no gap, 34 contiguous slices parallel to the anterior and posterior commissure (AC–PC) line and NEX = 3. The DTI acquisition scheme was the same as that detailed for the simulation studies above. Phase correction and Array Spatial Sensitivity Encoding Technique (factor = 2) were applied.

For each subject, nonbrain tissue was deleted from the DT images using BET in MRIcro [39]. A linear model for Eq. (1) was used to construct the DTs and three eigenvalue–eigenvector pairs, and the invariant measures, including FA, CL(β) and CP(β), were calculated. For every subject, we used the procedure described in the Appendix to compute at each voxel the test statistic and its associated P value for each of the three hypotheses to classify tensor morphology at each voxel, as well as the prevalence and distribution of degenerate tensors across the imaging volume. Using these test statistics, we (a) assessed the relative performances of tensor classification using the conventionally thresholded maps of invariant measures and maps of −log₁₀(P) for these measures created within our statistical framework; (b) classified isotropic DTs using both maps of FA and −log₁₀(P) maps of T_a(β); (c) classified oblate DTs using maps of CL(β) and −log₁₀(P) maps for T_b(β); (d) noted the general anatomical localizations of the various classes of DT morphology within the human brain; (e) determined the prevalence of the various classes of tensor morphology within the human brain.

4. Results

4.1. Simulations

4.1.1. Type I and II error rates of the test statistics using simulated data

Table 1 presents estimates for the rejection rates of the statistics $T_a\left(\widehat{\beta }\right)$, $T_b\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$ in our simulated DTI data set at two significance levels (αs of 5% or 1%). We observe that in isotropic tissues, the rejection rates of $T_a\left(\widehat{\beta }\right)$ are reasonably close to the respective significance levels for this small sample of 30 DW measurements. Overall, the rejection rates in all cases were accurate, and Type I (false positive) errors were not excessive (Table 1). Consistent with our expectations, statistical power for detecting nondegenerate tensors increased with the eigenvalue ratio ρ (the “power” of a test statistic is the probability that the test will reject a false null hypothesis or that it will not make a Type II error; thus, the higher the power, the greater the chance of obtaining a statistically significant result). Furthermore, an increasing SNR reduced the Type II (false negative) error rate and improved the power of the test statistic $T_a\left(\widehat{\beta }\right)$ to detect differences between λ₁ and λ₃. The rates of Type II errors for the statistic $T_a\left(\widehat{\beta }\right)$ were low for SNRs near 10. Similar results were obtained for simulations using $T_b\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$, except that rejection rates at the 0.01 and 0.05 levels for $T_c\left(\widehat{\beta }\right)$ were slightly higher than the corresponding significance levels when ρ = 1. We conclude, based on the Type I and II errors of the three statistics in these simulations, that the three proposed test statistics can be used to identify tensor morphologies and that they have satisfactory statistical properties under the most commonly used statistical model for estimating DTs [Eq. (1)].

Table 1.

Comparison of the rejection rates for the test statistics $T_a\left(\widehat{\beta }\right),\hspace{0.17em}{T}_b\left(\widehat{\beta }\right),\hspace{0.17em}{T}_c\left(\widehat{\beta }\right)$ and the invariant measures FA, $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ under the single-DT model

SNR	$T_a\left(\widehat{\beta }\right)$ and FA; DT: λ1 = ρλ2 = ρλ3
	DT:ρ = 1			DT:ρ = 1.5			DT:ρ = 3
	α = 1%	α = 5%	FA>0.2	α = 1%	α = 5%	FA>0.2	α = 1%	α = 5%	FA>0.2
10	0.017	0.072	0.677	0.163	0.337	0.913	0.946	0.987	1.000
15	0.016	0.068	0.202	0.408	0.624	0.890	1.000	0.999	1.000
20	0.015	0.060	0.028	0.736	0.893	0.889	1.000	1.000	1.000
25	0.014	0.055	0.002	0.928	0.999	0.916	1.000	1.000	1.000
	$T_b\left(\widehat{\beta }\right)$ and CL; DT: λ1 = ρλ2 = 2ρλ3
	DT:ρ = 1			DT:ρ = 1.5			DT:ρ = 3.09
	α = 1%	α = 5%	CL>0.2	α = 1%	α = 5%	CL>0.2	α = 1%	α = 5%	CL>0.2
10	0.020	0.069	0.189	0.217	0.403	0.671	0.998	0.999	0.999
15	0.015	0.048	0.025	0.509	0.723	0.682	1.000	1.000	1.000
20	0.013	0.046	0.002	0.807	0.927	0.694	1.000	1.000	1.000
25	0.009	0.045	0.000	0.962	0.995	0.714	1.000	1.000	1.000
	$T_c\left(\widehat{\beta }\right)$ and CP; DT: λ1 = 1.5λ2, λ2 = ρλ3
	DT:ρ = 1			DT:ρ = 1.5			DT:ρ = 2.98
	α = 1%	α = 5%	CP>0.2	α = 1%	α = 5%	CP>0.2	α = 1%	α = 5%	CP>0.2
10	0.015	0.050	0.311	0.098	0.224	0.651	0.594	0.810	0.984
15	0.019	0.058	0.092	0.276	0.473	0.601	0.951	0.990	0.999
20	0.018	0.059	0.018	0.524	0.739	0.622	1.000	1.000	1.000
25	0.017	0.061	0.002	0.744	0.890	0.617	1.000	1.000	1.000

Four differing SNRs (10, 15, 20, and 25) and 10,000 simulated data sets were used for each case.

In Table 1, we also presented the rejection rates of comparing the invariant measures FA, $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ against the conventional threshold of 0.20 for these measures in detecting degenerate tensors. We observed that Type I errors for all three invariant measures were exceedingly high when the SNR was 10; when using FA as the classifier for degeneracy, for instance, the Type I error rates were as high as 0.667, even though its Type II error rates were low. Although increasing the threshold for FA decreased the rate of Type I errors, it was at the expense of increasing Type II errors. When using FA as the invariant measure for detecting degenerate tensors, we therefore must derive the distribution of FA in order to control the rate of Type II errors for any given Type I error rate. Moreover, as SNR increased from 10 to 25, the Type II error rate for $\text{CL}\left(\widehat{\beta }\right)$ decreased slowly from 0.329 (= 1−0.671) to 0.286 (= 1−0.714), while the Type II error rate for $T_b\left(\widehat{\beta }\right)$ decreased quickly from 0.597 (= 1−0.403) to 0.005 (= 1−0.995). We attributed this slow decline in Type II error rates for $\text{CL}\left(\widehat{\beta }\right)$ with increasing SNR to the fact that the true CL(β) = 0.1667 happened to be close to the fixed arbitrary threshold of 0.20. In fact, if the true value of CL(β) even more closely approximated the fixed threshold 0.20, then the Type II error rate for $\text{CL}\left(\widehat{\beta }\right)$ was as high as 0.50 even for large SNRs, because CL(β) was a statistically unbiased estimate of CL(β) for nonoblate DTs, and the probability of $\text{CL}\left(\widehat{\beta }\right)$ being greater than CL(β) was 0.50. For $\text{CP}\left(\widehat{\beta }\right)$ at ρ = 1.5, we observed that the Type II error rate for $\text{CP}\left(\widehat{\beta }\right)$ actually increased from 0.349 (= 1−0.651) to 0.383 (= 1−0.617) with increasing SNRs (Table 1). This example demonstrated that using a fixed threshold for invariant measures is inappropriate for the valid classification of tensor morphologies across different SNRs.

We calculated the means and standard deviations of $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ under the null hypotheses for detection of oblate and prolate DTs. Ideally, CL(β) and CP(β) should equal zero and, yet, the mean values of both CL(β); and $\text{CP}\left(\widehat{\beta }\right)$ were greater than zero, and their standard deviations were relatively large (Fig. 2). As expected, the means and standard deviations of $\text{CL}\left(\widehat{\beta }\right)$ [and $\text{CP}\left(\widehat{\beta }\right)$] decreased with increasing SNRs.

Fig. 2.

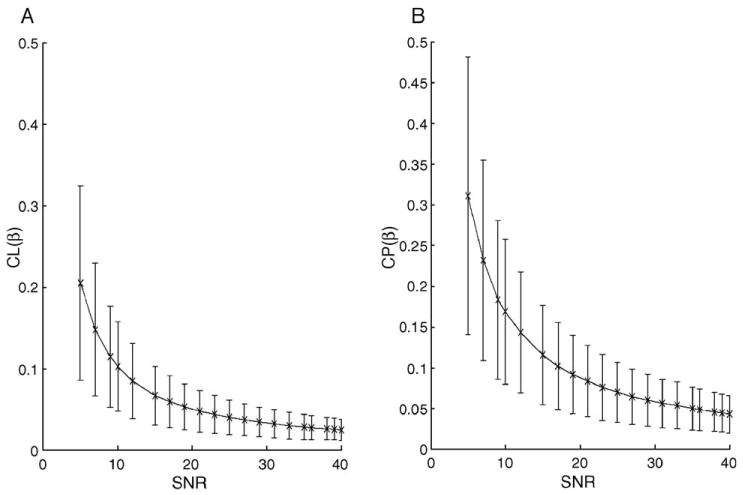
Results from a simulation study of evaluating $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ under the null hypotheses. Panels (A) and (B) show the mean value and the standard deviation of $\text{CL}\left(\widehat{\beta }\right)$ and $\text{CP}\left(\widehat{\beta }\right)$ as a function of SNR based on 10,000 simulated data sets. (A) Twenty differing SNRs, from 5 to 40, were evaluated. The DT was specified as λ₁ = λ₁ = 0.84 and λ₃ = 0.42, and the true value of CL(β) equaled zero. (B) The DT was specified as λ₁ = 0.9 and λ₃ = λ₂ = 0.6, and the true value of CP(β) equaled zero.

4.1.2. Evaluating the test statistics assuming the presence of fiber crossings

Table 2 presents the estimated rejection rates of the statistics $T_a\left(\widehat{\beta }\right)$, $T_b\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$ at the significance level .05 under the two-DT model. We conclude that the pseudo DT had an oblate shape for voxels containing two DTs representing WM+WM at an f = 0.5 because the rejection rates of $T_a\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$ were high, while those of $T_b\left(\widehat{\beta }\right)$ were close to the significance level of 5%. However, for the voxels containing two DTs representing WM+WM at f = .25, the pseudo DT was nondegenerate. In voxels containing two DTs representing WM+GM, the rejection rates of the three statistics suggest that the pseudo DT was prolate in shape for both f = 0.25 and f = 0.5. Thus, these results indicated that multiple fibers present within a single voxel can lead to misclassification of tensor morphologies.

Table 2.

Comparison of the rejection rates for the test statistics $T_a\left(\widehat{\beta }\right),\hspace{0.17em}{T}_b\left(\widehat{\beta }\right)$ and T_c(β) under the two-DT model at the significance level .05

SNR	f = 0.5			f = 0.25
	$T_a\left(\widehat{\beta }\right)$	$T_b\left(\widehat{\beta }\right)$	$T_c\left(\widehat{\beta }\right)$	$T_a\left(\widehat{\beta }\right)$	$T_b\left(\widehat{\beta }\right)$	$T_c\left(\widehat{\beta }\right)$
D2:[λ1,λ2,λ3] = [1.4,0.35,0.35]
10	0.659	0.063	0.587	0.926	0.738	0.1667
15	0.962	0.043	0.953	0.999	0.972	0.365
20	0.999	0.035	0.999	1.000	0.999	0.619
25	1.000	0.027	1.000	1.000	1.000	0.832
D2:[λ1,λ2,λ3] = [0.7,0.7,0.7]
10	0.729	0.682	0.047	0.227	0.203	0.045
15	0.977	0.969	0.046	0.466	0.410	0.057
20	0.999	0.999	0.055	0.728	0.674	0.068
25	1.000	1.000	0.050	0.911	0.869	0.069

The first DT component is D₁:[λ₁,λ₂,λ₃] = [1.4,0.35,0.35] and the second component is presented in the table. Four differing SNRs {10, 15, 20, 25} and 10,000 simulated data sets were used.

4.1.3. In vivo human data

4.1.3.1. Assessing performance of tensor classification using maps of invariant measures and maps of −log₁₀(P) values of statistics for testing three hypotheses

Using a single representative subject, we presented maps of invariant measures (Fig. 3A–C) and −log₁₀(P) maps (Fig. 3D–F) for testing hypotheses in axial images positioned through the dorsum of the body of the caudate nucleus. The map of FA values (Fig. 3A) showed that significantly anisotropic voxels (those with relatively large FA values) were located almost exclusively within the WM. We observed a similar scenario in maps of $\text{CL}\left(\widehat{\beta }\right)$ (Fig. 3B) and maps of $\text{CP}\left(\widehat{\beta }\right)$ (Fig. 3C). All −log₁₀(P) maps represented images of the −log₁₀(P) value for $T_i\left(\widehat{\beta }\right)$ (i = a,b,c). By convention, a voxel having a P value <.05, corresponding to a −log₁₀(P) value >1.31 was regarded as significant. All −log₁₀(P) values <5 were set equal to 5 in order to improve the distribution of plotted P values. A DT having a value of −log₁₀(P) for T_a(β) of 5 (i.e., P = 10⁻⁵) was highly anisotropic. The brightest voxels in the invariant measure maps (Fig. 3A–C) typically corresponded to the brightest voxels in the −log₁₀(P) maps (Fig. 3D–F). The maps of $T_i\left(\widehat{\beta }\right)$ (i = a,b,c), however, identified more voxels as anisotropic, nonoblate and nonprolate than did the maps of invariant measures.

Fig. 3.

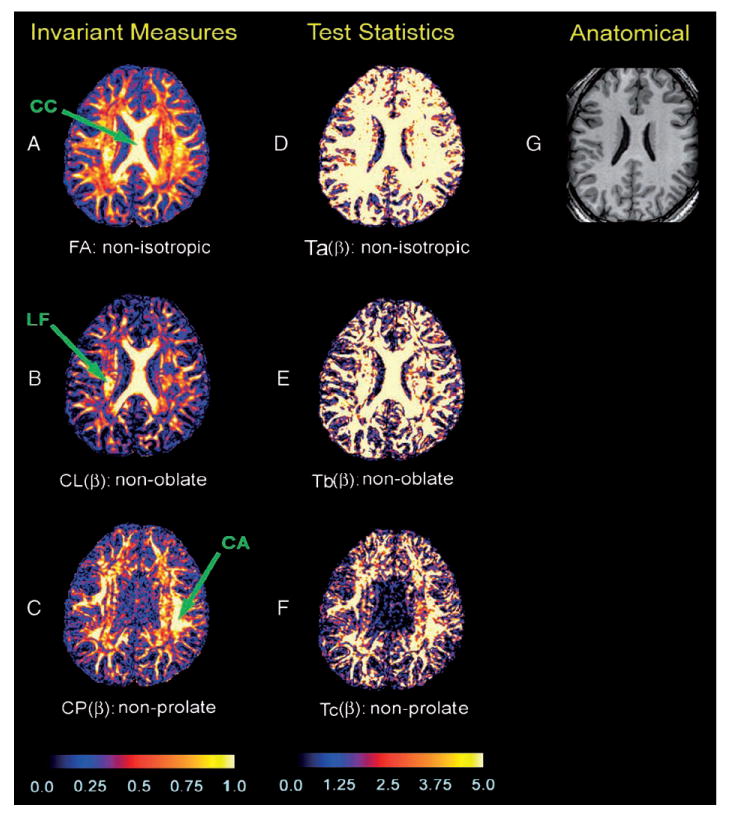
Maps of the invariant measures and −log₁₀(P) values associated with test statistics in a single subject. Shown here is an axial slice through the dorsal aspect of the body of the caudate nucleus and the body of the corpus callosum. (A) FA values depicting the degree anisotropy in each voxel. (B) $\text{CL}\left(\widehat{\beta }\right)$ values depicting the degree of nonoblate morphology in each voxel. (C) $\text{CP}\left(\widehat{\beta }\right)$ values representing the degree of nonprolate shape in each voxel; the color bar denotes differences between brain regions in the value of invariant measures. The scale of the color coding ranges from 0 to 1, with black representing the lowest value (0) and white representing the highest value (1). (D) The −log₁₀(P) values of test statistic: $T_a\left(\widehat{\beta }\right)$. (E) The −log₁₀(P) values of test statistic: T_b(β). (F) The −log₁₀(P) values of test statistic: $T_c\left(\widehat{\beta }\right)$. The color scale reflects the size of the values of −log₁₀(P), with black to blue representing smaller values (0–1), and red to white representing higher values (1.88–5). (G) The corresponding slice of the T1-weighted anatomical image. CC = corpus callosum; LF = longitudinal fasciculi; CA = cortical association fibers.

4.1.3.2. Classifying isotropic DTs using maps of FA and maps of −log₁₀(P) values for T_a(β)

The −log₁₀(P) value for $T_a\left(\widehat{\beta }\right)$ seemed to be more sensitive and specific in classifying the morphologies of DTs as anisotropic or isotropic than were FA values alone. The −log₁₀(P) map for $T_a\left(\widehat{\beta }\right)$ (Fig. 4C), for example, identified fibers within the narrow “bridge” of tissue within the septum pellucidum that the simple FA map did not identify (Fig. 4D). In addition, our procedure for the detection of degenerate tensors classified as isotropic the voxels containing cerebrospinal fluid (CSF) that surround the septum (Fig. 4B and C), whereas the conventional mapping of FA at those voxels indicated that their average FA value was 0.120 (S.D. = 0.06), close to the FA value in the septum pellucidum. Thus, the FA map was unable to discriminate CSF from cerebral tissue in this region. Furthermore, values of −log₁₀(P) for the $T_a\left(\widehat{\beta }\right)$ test statistic in voxels within the caudate nuclei were relatively large (mean = 1.93, S.D. = 1.32), indicating the presence of considerable anisotropy, whereas FA values here were relatively small (mean = 0.15, S.D. = 0.04), incorrectly indicating isotropy when invoking conventional FA thresholds (Fig. 4C and D). Thus, based on these preliminary in vivo data, we conclude that the −log₁₀(P) map for $T_a\left(\widehat{\beta }\right)$ identified some voxels that had small FA values as being isotropic, and it correctly identified some voxels that had similarly small FA values as being anisotropic.

Fig. 4.

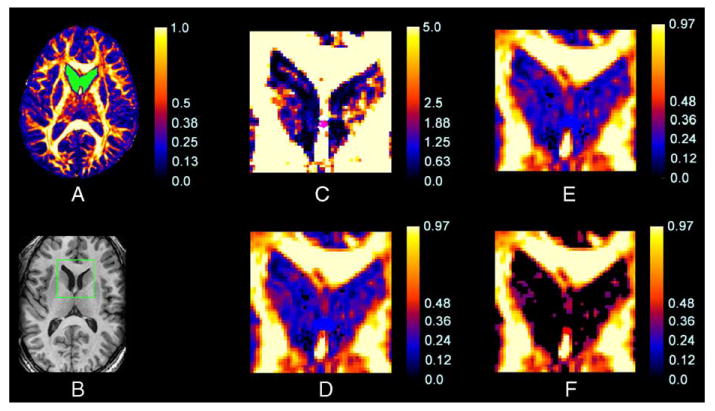
A comparison of the information provided by the map of FA values and the corresponding map of −log₁₀(P) values for $T_a\left(\widehat{\beta }\right)$. Shown here are maps from a single subject in an axial slice at the level of the fornix, genu of the internal capsule, and head of the caudate nucleus. (A) An FA map with the ROI highlighted in green. (B) The corresponding anatomical T1-weighted image of this slice, with a rectangular box indicating the portion of the image magnified in panels (C) through (F). (C) The map of −log₁₀(P) values for $T_a\left(\widehat{\beta }\right)$ in the ROI. The color scale reflects the magnitudes of values of −log₁₀(P), with black to blue representing smaller values (0–1) and red to white representing larger values (1.88–5). (D) The FA map within the ROI. The green circle identifies a voxel on a narrow bridge of tissue in the septum pellucidum that appears as anisotropic in the −log₁₀(P) map (C) but does not appear anisotropic in this FA map. (E and F) The FA maps within the ROI masked by FA thresholds of 0.10 and 0.20, respectively. The color bar denotes the values of FA, with black to blue representing smaller values (0–0.20) and red to white representing larger values (0.4–1). Voxels in the head of the caudate nucleus are incorrectly classified as having degrees of anisotropy similar to CSF using each FA threshold, whereas the −log₁₀(P) map discriminates these two types of tissue successfully in (C).

Table 3 presents the number of voxels in a region of interest (ROI) from a representative subject in which the morphologies of DTs were classified using either the conventionally thresholded FA value (0.20) or the P value for $T_a\left(\widehat{\beta }\right)$ (either .05 or .01). We observed that comparing FA values with a universal threshold would yield a high rate of false-negative errors in classification. At the threshold of P <.01, for example, 133 of all voxels that had FA values <.20 were still labeled as anisotropic. In contrast, if the 621 voxels with FA <0.20 were truly isotropic, then about seven voxels would have been labeled as isotropic using a threshold for the P value for $T_a\left(\widehat{\beta }\right)$ of <.01. We therefore expected a false-negative rate of approximately 20.42% (= 133/621−0.01 = ≈ 21.42%−1%) in the ROI.

Table 3.

Comparison of invariant measures and test statistics: the number of voxels in the ROI of a representative subject classified into different tensor morphologies

	P <.01	P >.01	Total	P <.05	P <.05	Total
$T_a(\widehat{\beta })$
FA > 0.20	47	16	63	54	9	63
FA < 0.20	133	488	621	214	407	621
Total	180	504	684	268	416	684
$T_b(\widehat{\beta })$
CL > 0.05	101	229	330	157	173	330
CL < 0.05	4	350	354	13	341	354
Total	105	579	684	170	514	684

4.1.3.3. Classifying oblate DTs using maps of $\text{CL}(\widehat{\beta })$ and maps of −log₁₀(P) values for $T_b(\widehat{\beta })$

The map of −log₁₀(P) values for $T_b\left(\widehat{\beta }\right)$ revealed that some tensors having a small $\text{CL}\left(\widehat{\beta }\right)$ value actually did have small differences between λ₁ and λ₂, whereas other tensors with a small $\text{CL}\left(\widehat{\beta }\right)$ value had statistically large differences between λ₁ and λ₂ and, thus, were misclassified as oblate when using conventional measures of morphology outside of proper statistical framework. Whereas the mean $\text{CL}\left(\widehat{\beta }\right)$ value in the portion of an ROI containing primarily CSF was 0.05 (S.D. = 0.03), values of −log₁₀(P) for $T_b\left(\widehat{\beta }\right)$ were small in those same voxels (Fig. 5B). Furthermore, values of −log₁₀(P) for $T_b\left(\widehat{\beta }\right)$ were relatively large in voxels within the caudate nuclei, indicating the presence of DTs having nonoblate shapes; the $\text{CL}\left(\widehat{\beta }\right)$ values for DTs in these voxels, however, were relatively small (mean = 0.056, S.D. = 0.028) and incorrectly suggested the presence of DTs having oblate shapes (Fig. 5C–E). Indeed, at a rejection rate of 0.05, 122 voxels within the caudate nuclei were misclassified using $\text{CL}\left(\widehat{\beta }\right)$ as being nonoblate (Fig. 5B).

Fig. 5.

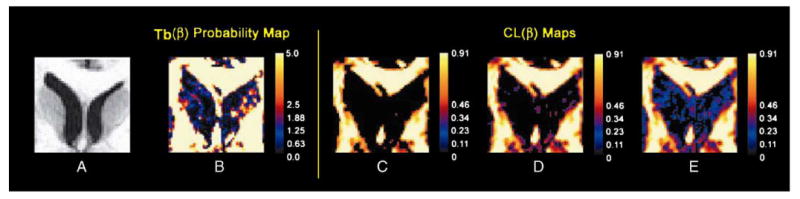
Maps of $\text{CL}\left(\widehat{\beta }\right)$ and the −log₁₀(P) values for $T_b\left(\widehat{\beta }\right)$ in a single slice from a single subject. (A) The rectangular ROI of the T1-weighted anatomical image. (B) The same rectangular ROI in the map plotting the value of −log₁₀(P) for $T_b\left(\widehat{\beta }\right)$. (C–E) $\text{CL}\left(\widehat{\beta }\right)$ maps within the ROI masked with thresholds of 0.15, 0.10 and 0.05, respectively. Nearly all voxels in the head of the caudate nucleus and in the CSF are incorrectly classified.

Using a universal threshold for $\text{CL}\left(\widehat{\beta }\right)$ values can also generate many false-positive errors in the classification of DTs as having a CL. We assessed the use of invoking three arbitrary thresholds for $\text{CL}\left(\widehat{\beta }\right)$: 0.05, 0.10 and 0.15 (Fig. 5C–E). These thresholds classified tensors as oblate, respectively, within 96.2%, 91.5% and 51.75% of voxels in the ROI (Fig. 5C–E). In contrast, at P values of .05 or .01 for the $T_b\left(\widehat{\beta }\right)$ statistic testing for the presence of oblate DTs, 75.15% and 84.65% of the total number of voxels in the ROI, respectively, were categorized as oblate (Table 3).

4.1.3.4. Anatomical localizations of the various classes of DT morphology within the human brain

We determined the anatomical location of the various classes of degenerate DTs across the imaging volumes for our seven adult subjects using P values for the sequential statistical testing of our three hypotheses for DT morphologies (Fig. 6D–F). Specifying significance levels of (α₁,α₂,α₃) = (0.05,0.05,0.05) when testing the three hypotheses, DTs classified as isotropic were located primarily in CSF or GM. DTs classified as oblate were positioned primarily along the boundaries of regions containing isotropic tissue, such as CSF or GM, or else as small islands within intensely anisotropic tissues, such as WM. In each of these general locations, both the directions and magnitudes of the DTs change abruptly across voxels. The oblate DTs, therefore, were most likely the products of partial volume averaging of the morphologies of DTs in voxels that contained two or more tissue types that differed in structural organization. This interpretation is supported by maps superimposing the location of oblate DTs on a conventional, 3-color map of the PDs of DTs (Fig. 6G–I); oblate DTs were positioned primarily at locations of fiber crossing and along the boundaries of differing tissue types. DTs classified as prolate were located primarily within the intensely anisotropic WM of the corpus callosum, longitudinal fasciculus and association fibers directly beneath cortical GM, as well as in certain GM structures, such as the thalamus and body of the caudate nucleus. DTs classified as either anisotropic or nondegenerate were positioned mainly within cortical and subcortical WM.

Fig. 6.

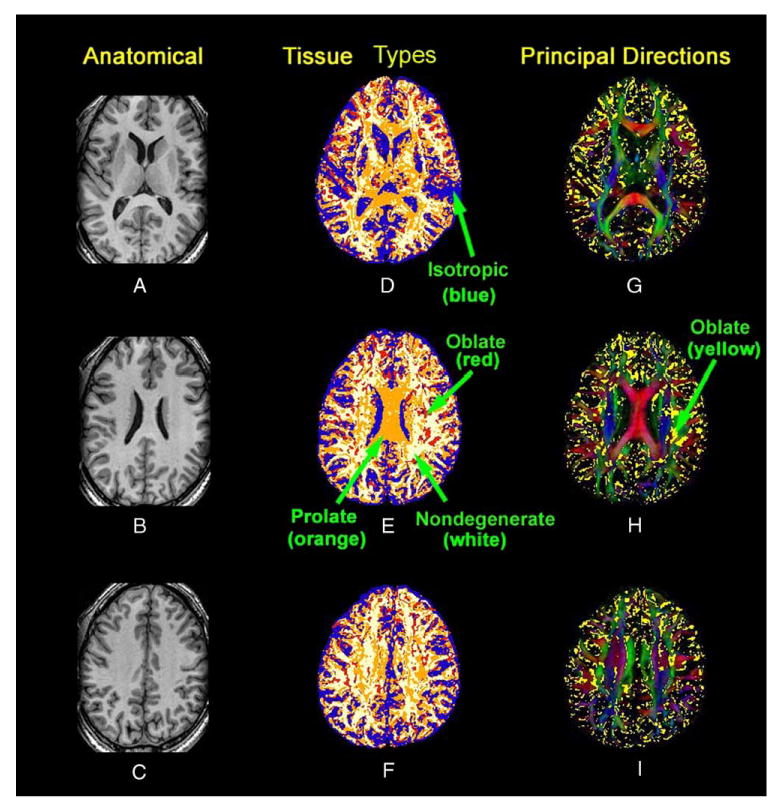
Maps of tissue types and the weighted PD in three slices from a single subject. Rows from top to bottom show slices from progressively more dorsal axial slices. (A–C) The T₁ weighted anatomical images. (D–F) Maps of tissue types: white = nondegenerate DTs; red = oblate DTs; yellow = prolate DTs; blue = isotropic DTs. (G–I) Principal direction maps: yellow = overlay indicating DTs having an oblate shape.

4.1.3.5. The prevalences of various classes of tensor morphology within the human brain

We assessed the prevalence of the four morphological classes of DTs (nondegenerate, oblate, prolate and isotropic) within the brains of our seven adult subjects (Table 4). We found that 34.29% were isotropic, 12.1% were oblate, 28.1% were prolate and 25.5% were nondegenerate. Most tractography algorithms can track fibers across voxels containing either anisotropic or prolate DTs; these classes of tensors, which together accounted for 53.6% of the total number of voxels in the brain (with more than half of these being prolate), were located primarily within white and GM, as expected. Attempting to track fibers through other (degenerate) tensor types will necessarily lead to errors [23]. We identified a prevalence of degenerate tensors that was 60-fold greater than those detected using a previous method [18].

Table 4.

The number and proportion of DTs classified into various morphologies in seven adult subjects

	Isotropic	Oblate	Prolate	Nondegenerate	Total
Number of Voxels
Mean	178630	62490	146020	131700	518830
S.D.	27253	9269	11934	11201	35838
Percentage
Mean (%)	34.29	12.04	28.13	25.54	100
S.D. (%)	3.50	1.55	0.86	3.11

5. Discussion

Our procedure for detecting degenerate tensors differs substantially from a previously proposed method [18] in that our approach tests for the presence of specific morphological features of DTs within a statistical framework that accounts for the noise that is inherent in all DTI data. Unlike the prior method, ours is applicable to the classification of DTs within individual voxels, without relying on information from DTs at neighboring voxels. It allows determination of the prevalence and spatial locations of nondegenerate, isotropic, oblate and prolate DTs throughout the brain. Moreover, using the P values associated with the proposed test statistics maximizes the probability of correctly classifying the shapes of DTs because these P values account for the amount of noise within a given voxel, the number of DW images, the acquisition scheme and the model for noise in the data. Indeed, both our simulated and in vivo human data support this claim.

The previously proposed method for detection of degenerate tensors assumes that the tensor field is smooth when it uses information from surrounding voxels to search for degeneracy [18]. Although assuming the smoothness of fiber tracts in general may be reasonable, our findings show clearly that it is unjustified at the boundaries of tissues that differ substantially in their degree of anisotropy or in the orientation of their DTs (Fig. 6). Searching for degenerate tensors in the entire imaging volume under the assumption of smoothness of the tensor field may therefore lead to misclassification of tensor morphologies, particularly near the boundary between differing tissue types. That our method identified a vastly larger number of degenerate tensors than did the prior method and in, precisely, these anatomical regions of discontinuity in DT orientation and degree of anisotropy, further suggests that an assumption of smoothness will lead to erroneous classification.

In order to use invariant measures of anisotropy as test statistics, we needed to characterize their distributions. A bootstrapping method [40,41] was recently used to approximate the distributions of invariant measures in DT images [16,42]. Bootstrapping [16,42], however, cannot be used to calculate P value for testing hypothesis in DT images because it cannot approximate the distribution of a test statistic under the null hypothesis [43]. Moreover, bootstrapping at each of the large number of voxels in the human brain would likely prove computationally intensive and, therefore, prohibitive. Instead, we derived analytically the asymptotic null distributions of the test statistics (see Appendix) and used these null distributions to test sequentially three hypotheses that together classified the morphologies of tensors at each voxel. This analytic approach is also computationally satisfactory because calculating a P value using a scaled χ² approximation is much faster than is use of numerical simulations such as bootstrapping. Our simulations demonstrated empirically that the scaled χ² distribution provides good statistical power for the detection of degenerate tensors, while simultaneously limiting Type I (false positive) errors.

The P value for testing each of three sequential hypotheses quantifies the degree of tensor degeneracy at each voxel. For example, for the isotropic hypothesis, a small P value in a voxel denotes a low probability of obtaining a particular FA value in that voxel under the null hypothesis (λ₁ = λ₃). In practice, we can choose a fixed significance level (such as .05 or .10) as a universal threshold, with P values higher than that threshold being classified as isotropic (or as oblate or prolate).

In practice, any procedure that directly compares FA values (or $\text{CL}\left(\widehat{\beta }\right)$ or $\text{CP}\left(\widehat{\beta }\right)$ values) to a fixed, arbitrary threshold without considering their stochastic behavior can yield high false-positive and false-negative error rates for the detection of degenerate tensors. The stochastic properties of FA values [or $\text{CL}\left(\widehat{\beta }\right)$ or $\text{CP}\left(\widehat{\beta }\right)$ values] are mainly influenced by the DT at a particular voxel, the number of DW images used in estimating the DT, and the SNR characteristics of the DW images. Similar observations have been reported previously for RA² and other anisotropy indices [12,15,44]. Based on our findings, we conclude that the stochastic behavior of these invariant measures must be adequately characterized before the invariant measures themselves can be used reliably to classify tensor morphology.

Further research should determine whether combining information from invariant measures of anisotropy, such as CP(β), with the P values for the classification of tensor morphologies, can improve the analyses of DT images, including the performance of fiber tracking algorithms. For example, our human studies have shown that oblate tensors account for 12.1% of voxels located in regions containing both GM and WM or crossing fibers (Fig. 6). Moreover, our simulations have shown that a combination of two WM tensors in a voxel can lead to classification of the pseudo tensor in that voxel as oblate. Once our procedure has identified a tensor as oblate, we can then further investigate whether the tensor's oblate shape is caused by a combination of WM and GM or by crossing fibers. If the tensor contains multiple fibers, we can estimate the component DTs and apply our classification procedure to each component. The resulting information on the shape of each tensor can then be used for fiber tracking itself or for further development of fiber tracking algorithms that can function better in areas where fibers cross.

Many related topics warrant further research. First, because we used the asymptotic distributions of the invariant measures to classify tensors, our results are limited to data sets containing DW images that are moderate or large in number (e.g., n ≥ 25). For a small number of DW images (e.g., n ≤ 12), we can resort to parametric bootstraping methods [43] for accurately approximating the distributions of invariant measures, such as T_a(β), under our null hypotheses. Bootstrapping at each voxel in the human brain will nevertheless remain computationally intensive, even with a smaller number of images. Second, we used the least squares estimate for the statistical model in Eq. (1) to reconstruct DTs. Tensor estimates may therefore be subject to substantial biases under a low SNR, because Eq. (1) is not a good approximation of NMR signals. Using a weighted linear fit may improve slightly the accuracy of estimated DTs for moderate and high SNRs. Moreover, because our method is limited to a single-tensor model for Eq. (1), other possible causes of degenerate tensors, such as the presence of multiple tensors within a voxel, should be investigated further [36–38]. Also, because structural artifacts in DW images, including brain pulsation and involuntary movement of the subject, can generate unusual behavior of the data that diverge substantially from that in a normal or Rician model, post-processing techniques such as correction of eddy current distortions must be used before applying the test procedures proposed here. Moreover, the findings based on the ROI located between ventricles could be affected by the effects of cardiac-related pulsations. Finally, although we focused here on use of invariant measures as test statistics for the classification of tensor morphology, other statistics, such as those based on eigenvalues, may prove helpful in further characterizing tensor morphologies and in identifying the presence of degenerate tensors.

Appendix

We derive the asymptotic null distributions of T_a(β), T_b(β) and T_c(β) in the Appendix. We first review several standard results for the model (1) [28,29,45]. We then present the key ideas of deriving the asymptotic null distributions of T_a(β), T_b(β) and T_c(β). We also propose a simple method of approximating P values of the three test statistics. Finally, we include a detailed procedure for computing the P values of the three test statistics.

For the statistical model shown in Eq. (1), we can calculate a least square estimate of θ, denoted by $\widehat{\theta }={\left(\text{log}{\widehat{S}}_0,{\widehat{\beta }}^T\right)}^T={\left(\text{∑}_{i=1}^n{z}_i{\text{z}}_i^T\right)}^{-1}\hspace{0.17em}\text{∑}_{i=1}^n{\text{z}}_{\text{i}}\text{log}{S}_i$, where ${\text{z}}_i={(1,-b_i{r}_{i,1}^2,-2b_i{r}_{i,1}{r}_{i,2},-2b_i{r}_{i,1}{r}_{i,3},-b_i{r}_{i,2}^2,-2b_i{r}_{i,2}{r}_{bi}{r}_{i,2}{r}_{i,3},-b_i{r}_{i,3}^3)}^T$. Let ${\theta }_{\ast }={(\text{log}\hspace{0.17em}{S}_{0\ast },{\beta }_{\ast }^T)}^T$ be the true value of θ and n, the number of DW images for each subject. Under certain conditions [28,45], we can show that as n → ∞, $\sqrt{n}\left(\widehat{\theta }-{\theta }_{\ast }\right)$ converges to Z in distribution, where Z is a normal random vector with mean zero and covariance matrix Σ_θ, denoted by N{0,Σ_θ}. The covariance matrix Σ_θ is estimated as follows:

$$\begin{array}{l}{\sum }_{\theta }={\left(n^{-1}\sum _{i=1}^n{\text{z}}_i{\text{z}}_i^T\right)}^{-1}\hspace{0.17em}\left[n^{-1}\sum _{i=1}^n{\text{z}}_i{\text{z}}_i^T{e}_i^2{(1-h_i)}^2\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\times \hspace{0.17em}{\left(n^{-1}\sum _{i=1}^n{\text{z}}_i{\text{z}}_i^T\right)}^{-1},\hfill \end{array}$$ (14)

where ${\text{e}}_i=\text{log}\hspace{0.17em}{S}_i-{\text{z}}_i^T\widehat{\beta }$ is a residual and $h_i={\text{z}}_i^T{(\text{∑}_{j-1}^n{\text{z}}_j{\text{z}}_j^T)}^{-1}{\text{z}}_i$ [32]. Because β is a subvector of θ, $\sqrt{n}\left(\widehat{\beta }-{\beta }_{\ast }\right)$ converges to N{0,Σ_β}, where Σ_β is the corresponding matrix of Σ_θ.

We define φ in the CL and CP measures for Eq. (5) as follows:

$$\varphi =\text{acos}\hspace{0.17em}\left(S\left(\beta \right)/\left[V\left(\beta \right)\sqrt{V\left(\beta \right)}\right]\hspace{0.17em}\right)/3$$ (15)

and S(β)² ≤ V(β)³ [20]. If RA(β) > 0, we have the following equivalent relationships:

$$\begin{array}{l}\varphi =\frac{\pi }{3}\iff S\left(\beta \right)+V\left(\beta \right)\sqrt{V\left(\beta \right)}=0\iff {\lambda }_1={\lambda }_2;\hfill \\ \varphi =0\iff S\left(\beta \right)-V\left(\beta \right)\sqrt{V\left(\beta \right)}=0\iff {\lambda }_2={\lambda }_3.\hfill \end{array}$$

Notation

We introduce some notation as follows. Let f(β) be a function of β. The first derivative of f(β) with respect to β is a 6 × 1 vector given by ∂ _βf(β). The second derivative of f(β) with respect to β is a 6 × 6 matrix given by ${\partial \hspace{0.17em}}_{\beta }^2\hspace{0.17em}f\left(\beta \right)$. For instance, the (1,2)th element of the matrix ${\partial \hspace{0.17em}}_{\beta }^2\hspace{0.17em}f\left(\beta \right)$ is $\frac{{\partial }^{2}f\left(\beta \right)}{\partial {\beta }_1\partial {\beta }_2}=\frac{{\partial }^{2}f\left(\beta \right)}{\partial D_{11}\partial D_{12}}$. A Taylor expansion of f(β) at β_* is given by

$$\begin{array}{l}f\left(\beta \right)=f\left({\beta }_{\ast }\right)+{\left(\beta -{\beta }_{\ast }\right)}^T\hspace{0.17em}\left[{\partial }_{\beta }\hspace{0.17em}f\left({\beta }_{\ast }\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}+\hspace{0.17em}0.5{\left(\beta -{\beta }_{\ast }\right)}^T\hspace{0.17em}\left[{\partial }_{\beta }^2\hspace{0.17em}f\left(\beta \prime \right)\right]\hspace{0.17em}\left(\beta -{\beta }_{\ast }\right),\hfill \end{array}$$ (16)

where β_*i is the ith element of β_* and β′ is a point in a neighborhood of β_*.

Asymptomatic null distribution of $T_a\left(\widehat{\beta }\right)$

We first study the asymptotic null distribution of ${\text{FA}}^2\left(\widehat{\beta }\right)=\left[I_4\left(\widehat{\beta }\right)-I_2\left(\widehat{\beta }\right)\right]/I_4\left(\widehat{\beta }\right)$ below. If the diffusion ellipsoid is isotropic, then we have T_a(β_*) = 0 and ∂ _βT_a(β_*) = 0. Using Eq. (16), we can employ the delta method [46] to show that

$$\begin{array}{l}n{T}_a\left(\widehat{\beta }\right)=0.5I_4^{-1}\left({\beta }_{\ast }\right)\sqrt{n}{\left(\widehat{\beta }-{\beta }_{\ast }\right)}^T{\sum }_1\sqrt{n}\left(\widehat{\beta }-{\beta }_{\ast }\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\times \hspace{0.17em}\left(1+o_p\left(1\right)\right),\hfill \end{array}$$ (17)

where o_p(1) denotes that a sequence of random vectors converges to zero in probability, and ${\sum }_1={\partial \hspace{0.17em}}_{\beta }^2{T}_a\left(\beta \right)$. It follows from Eq. (4) that Σ₁ is a constant matrix. Let γ_i(i = 1,…,6) be six eigenvalues of Σ_βΣ₁. As n → ∞, $n{\text{FA}}^2\left(\widehat{\beta }\right)$ converges to a weighted χ² distribution Z with representation $I_4^{-1}\left(\beta \ast \right){\sum }_{i=1}^6{\gamma }_i{z}_i$ in distribution, where z_i(i = 1,…,6) represents six independent ${\chi }_1^2$ random variables and ${\chi }_1^2$ denotes a χ² distribution with one degree of freedom.

Asymptomatic null distribution of T_b(β)

For T_b(β), we can similarly establish its asymptotic distributions under $H_0^{\left(2\right)}$. If the diffusion ellipsoid is oblate in shape, then we have T_b(β_*) = 0 and ∂ _βT_b(β_*) = 0. Using Eq. (16), we can again employ the delta method [46] to show that

$$\begin{array}{l}n{T}_b\left(\widehat{\beta }\right)\hspace{0.17em}=\hspace{0.17em}0.5\sqrt{n}{\left(\widehat{\beta }-{\beta }_{\ast }\right)}^T\hspace{0.17em}{\sum }_2\left({\beta }_{\ast }\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \hspace{0.17em}\sqrt{n}\left(\widehat{\beta }-{\beta }_{\ast }\right)\hspace{0.17em}\left(1+o_p\left(1\right)\right),\hfill \end{array}$$

where ${\sum }_2\left(\beta \right)={\partial \hspace{0.17em}}_{\beta }^2{T}_b\left(\beta \right)$. Let ${\gamma }_i^{\prime }(i=1,\dots ,6)$ be six eigenvalues of Σ_βΣ₂(β_*). As n → ∞, $T_b\left(\widehat{\beta }\right)$ converges to a weighted χ² distribution Z with representation ${\sum }_{\text{i}=1}^6{\gamma }_i^{\prime }{z}_i$ in distribution. The last step is to estimate Σ₂(β_*). We suggest calculating Σ₂(β_*) under the null hypothesis $H_0^{\left(2\right)}$. If λ₁ = λ₂, then $D={\lambda }_1{I}_{3\times 3}-({\lambda }_1-{\lambda }_3)e_3^T{e}_3$. We can obtain estimates of (log S₀,λ₁,λ₂,e₃)^T by minimizing the residual sum of squares as follows:

$$\begin{array}{ll}\left(\text{log}{\stackrel{\sim }{S}}_0,{\stackrel{\sim }{\lambda }}_1,{\stackrel{\sim }{\lambda }}_2,e_3\right)\hspace{0.17em}=\hfill & \text{argmin}\sum _{i=1}^n\{\text{log}{S}_i-\text{log}{S}_0+b_i{\text{r}}_i^T\hfill \\ & \times \hspace{0.17em}\left[{\lambda }_1{I}_{3\times 3}-({\lambda }_1-{\lambda }_3)e_3^T{e}_3\right]r_i{\}}^2.\hfill \end{array}$$ (18)

Finally, we can obtain $D={\stackrel{\sim }{\lambda }}_1{I}_{3\times 3}-{(\stackrel{\sim }{\lambda }}_1-{\stackrel{\sim }{\lambda }}_3{)\stackrel{\sim }{\text{e}}}_3^T{\stackrel{\sim }{\text{e}}}_3$ and then evaluate ${\sum }_2\left(\stackrel{\sim }{\beta }\right)$. Based on the preceding steps, we obtain the estimated ${\gamma }_1^{\prime }$ for i = 1,…,6. In our experience, this algorithm has proven effective.

Asymptomatic null distribution of $T_c\left(\widehat{\beta }\right)$

For $T_c\left(\widehat{\beta }\right)$, we can similarly establish its asymptotic distributions under $H_0^{\left(3\right)}$. In particular, it follows from Eq. (16) that $n{T}_c\left(\widehat{\beta }\right)=0.5\sqrt{n}{\left(\widehat{\beta }-{\beta }_{\ast }\right)}^T{\sum }_3\left({\beta }_{\ast }\right)\sqrt{n}\left(\widehat{\beta }-{\beta }_{\ast }\right)\hspace{0.17em}\left(1+o_p\left(1\right)\right),$ where ${\sum }_3\left(\beta \right)={\partial \hspace{0.17em}}_{\beta }^2{T}_c\left(\beta \right)$. Let ${\gamma }_1^{″}\left(i=1,\dots ,6\right)$ be six eigenvalues of Σ_βΣ₃(β_*). As n → ∞, $T_c\left(\widehat{\beta }\right)$ converges to a weighted χ² distribution Z with representation ${\sum }_{i=1}^6{\gamma }_i^{″}{z}_i$ in distribution. We easily estimate Σ_β as discussed before. The next step is to estimate Σ₃(β_*) under the null hypothesis $H_0^{\left(3\right)}$. When λ₁ = λ₂, we know that $D={\lambda }_2{I}_{3\times 3}+({\lambda }_1-{\lambda }_2)e_1^T{e}_1$. We obtain estimates of (log S₀,λ₁,λ₂,e₁)^T by minimizing the residual sum of squares as follows:

$$\begin{array}{cc}\left(\text{log}{\stackrel{\sim }{S}}_0,{\stackrel{\sim }{\lambda }}_1,{\stackrel{\sim }{\lambda }}_2,e_1\right)\hspace{0.17em}=\hfill & \text{argmin}\hspace{0.17em}\sum _{i=1}^n\hspace{0.17em}\{\text{log}{S}_i-\text{log}{S}_0+b_i{\text{r}}_i^T\hfill \\ & \times \hspace{0.17em}\left[{\lambda }_2{I}_{3\times 3}+({\lambda }_1-{\lambda }_2)e_1^T{e}_1\right]r_i{\}}^2.\hfill \end{array}$$ (19)

Finally, we obtain $D={\stackrel{\sim }{\lambda }}_2{I}_{3\times 3}+{(\stackrel{\sim }{\lambda }}_1-{\stackrel{\sim }{\lambda }}_2{)\stackrel{\sim }{\text{e}}}_1^T{\stackrel{\sim }{\text{e}}}_1$ and then evaluate ${\sum }_3\left(\stackrel{\sim }{\beta }\right)$.

Approximation of P values

In each voxel, the P value of testing the isotropic hypothesis can be calculated as:

$$p=\text{Pr}\hspace{0.17em}\left(Z\ge T_a\left(\widehat{\beta }\right)\right).$$ (20)

The weighted χ² distribution Z can be approximated by substituting the estimated ${\widehat{\gamma }}_i(i=1,\dots ,6)$. Instead of relying on the precise mixture distribution, we use the moment matching technique to match the mean and variance of c₀χ²(v) with those of Z, that is, $c_{0}v={\sum }_{i=1}^6{\gamma }_i$ and $c_0^{2}v={\sum }_{i=1}^6{\gamma }_i^2$, which gives $c_0={\sum }_{i=1}^6{\gamma }_i^2/{\sum }_{i=1}^6{\gamma }_i$ and $v={({\sum }_{i=1}^6{\gamma }_i)}^2/{\sum }_{i-1}^6{\gamma }_i^2$. The scaled χ² approximation works well in the test hypothesis for isotropy [47]. Similarly, we can construct a scaled χ² approximation for $T_b\left(\widehat{\beta }\right)$ and $T_c\left(\widehat{\beta }\right)$.

Our procedures for computing the P values of the three test statistics are:

• Step 1. Compute $\widehat{\theta }$, Σ_θ and Σ_β based on Eq. (14).

• Step 2. Compute $T_a\left(\widehat{\beta }\right)={\text{FA}}^2$, Σ₁ and the six eigenvalues of Σ₁Σ_β, γ_i(i = 1,…,6).

• Step 3. Compute $T_b\left(\widehat{\beta }\right)=\sqrt{V\left(\widehat{\beta }\right)}V\left(\widehat{\beta }\right)+S\left(\widehat{\beta }\right)$ and estimate ${(\stackrel{\sim }{\lambda }}_1{,\stackrel{\sim }{\lambda }}_2,e_3)$ in Eq. (18). Compute $D={\stackrel{\sim }{\lambda }}_1{I}_{3\times 3}-{(\stackrel{\sim }{\lambda }}_1-{\stackrel{\sim }{\lambda }}_3{)\stackrel{\sim }{\text{e}}}_3^T{\stackrel{\sim }{\text{e}}}_3$, ${\sum }_2\left(\stackrel{\sim }{\beta }\right)$, and the six eigenvalues of ${\sum }_2\left(\stackrel{\sim }{\beta }\right){\sum }_{\beta }$, ${\gamma }_i^{\prime }(i=1,\dots ,6)$.

• Step 4. Compute $T_c\hspace{0.17em}\left(\widehat{\beta }\right)=\sqrt{V\left(\widehat{\beta }\right)}V\left(\widehat{\beta }\right)-S\left(\widehat{\beta }\right)$ and estimate ${(\stackrel{\sim }{\lambda }}_1{,\stackrel{\sim }{\lambda }}_2,e_1)$ in Eq. (19). Compute $D={\stackrel{\sim }{\lambda }}_2{I}_{3\times 3}+\left({\stackrel{\sim }{\lambda }}_1-{\stackrel{\sim }{\lambda }}_2\right){\stackrel{\sim }{\text{e}}}_1^T{\stackrel{\sim }{\text{e}}}_1$, ${\sum }_3\left(\stackrel{\sim }{\beta }\right)$, and the six eigenvalues of ${\sum }_3\left(\stackrel{\sim }{\beta }\right){\sum }_{\beta }$, ${\gamma }_i^{″}\left(i=1,\dots ,6\right)$.

• Step 5. Compute c₀ and v based on γ_i (i = 1,· · ·,6). Approximate the P value by using

• $p=\text{Pr}\hspace{0.17em}\left(c_0\hspace{0.17em}{\chi }^2\left(v\right)>T_a\hspace{0.17em}\left(\widehat{\beta }\right)\right)$.

Similarly, we can calculate the P value of for $T_b\left(\widehat{\beta }\right)$ (or $T_c\left(\widehat{\beta }\right)$) by using $\{{\gamma }_i^{\prime }:i=1,\dots ,6\}$ (or $\{{\gamma }_i^{″}:i=1,\dots ,6\}$).