Assessment of different genetic distances in constructing cotton core subset by genotypic values

Abstract

One hundred and sixty-eight genotypes of cotton from the same growing region were used as a germplasm group to study the validity of different genetic distances in constructing cotton core subset. Mixed linear model approach was employed to unbiasedly predict genotypic values of 20 traits for eliminating the environmental effect. Six commonly used genetic distances (Euclidean, standardized Euclidean, Mahalanobis, city block, cosine and correlation distances) combining four commonly used hierarchical cluster methods (single distance, complete distance, unweighted pair-group average and Ward’s methods) were used in the least distance stepwise sampling (LDSS) method for constructing different core subsets. The analyses of variance (ANOVA) of different evaluating parameters showed that the validities of cosine and correlation distances were inferior to those of Euclidean, standardized Euclidean, Mahalanobis and city block distances. Standardized Euclidean distance was slightly more effective than Euclidean, Mahalanobis and city block distances. The principal analysis validated standardized Euclidean distance in the course of constructing practical core subsets. The covariance matrix of accessions might be ill-conditioned when Mahalanobis distance was used to calculate genetic distance at low sampling percentages, which led to bias in small-sized core subset construction. The standardized Euclidean distance is recommended in core subset construction with LDSS method.

INTRODUCTION

The concept of core collection was proposed by Frankel (1984) and developed by Brown (1989). A core collection is defined as a representative sample of the entire collection with minimum repetitiveness and maximum genetic diversity of a plant species and its relatives, and the other part of the initial collection is defined as reserve collection (Frankel, 1984). The core collection serves as a working collection that can be evaluated and utilized preferentially, which provides a convenient way to study and utilize germplasm resources and has received extensive attention all over the world.

One common approach for constructing a core collection is stratifying the whole collection by growing regions or ecotype and then selecting representative core accessions from each of the classified groups to form core subsets, and the whole core collection is constructed by combining all core subsets (Brown, 1995; Qiu et al., 2003). For a core collection, representativeness is the most important property. The main way to improve the representativeness of a core collection is to select more representative core subsets from the whole collection (Wang et al., 2007a). Cluster analysis has been widely used as an important tool to reduce redundancy and select core accessions within groups in germplasm research (van Hintum, 1995; Zewdie et al., 2004; Upadhyaya et al., 2006; Mosjidis and Klingler, 2006). Genetic distance and cluster method are main impact factors in core subset construction. Different genetic distance or cluster method leads to different core subset. In core subset construction, the least distance stepwise sampling (LDSS) has been proved to be a valid method for eliminating the influence of different cluster methods (Wang et al., 2007b). However, genetic distance calculation is premise for cluster analysis. The validities of different genetic distances in constructing core subsets by LDSS method have not been deeply investigated. The objective of present research was to use different common genetic distances and different common cluster methods to construct core subsets to evaluate the validities of different genetic distances.

MATERIALS AND METHODS

Materials

One hundred and sixty-eight cotton genotypes came from the same growing region and were used as a germplasm group to construct core subsets. All the 168 genotypes were planted for 2 years with 2 replications per year. The observed data of 20 quantitative traits on those plants were recorded. There were 11 agronomy traits (height of plant, height of fruiting branch, length of fruiting node, length of boll stalk, number of fruiting branch per plant, number of bolls per plant, incidence of infected plant, index of wilt disease, growth period, boll weight, and lint percentage), 5 fiber traits (length, uniformity, strength, elongation and micronaire) and 4 seed traits (seed length, seed width, ratio of length to width and kernel weight) in this initial germplasm group.

Core subset construction

Core subsets were constructed by LDSS method (Wang et al., 2007b). First, a precise sampling percentage of the core subset was determined based on other researches. Next, the genetic distances between accessions were calculated and accessions were grouped by hierarchical cluster analysis based on the genetic distance. One accession from a subgroup with the least distance, which was unique in the whole dendrogram, was randomly removed, and another accession of the subgroup was sampled. Then, the genetic distances among the remained accessions were calculated again, and the sampling was performed by the same way. The stepwise samplings were performed until the percentage of the remained accessions reached the given sampling percentage.

The sampling performed in this method was based on the subgroup with the least genetic distance, which could efficiently eliminate redundant accessions. Moreover, the constructing result of this method was not affected by cluster methods because subgroup with least distance was unique in each procedure of cluster (Wang et al., 2007b). Coincidence rate of range (CR) and variable rate of coefficient of variation (VR) (Hu et al., 2000; Upadhyaya and Ortiz, 2001; Kang et al., 2006) were adopted to evaluate the representativeness of core subsets.

Genetic distances and cluster methods

Six commonly used genetic distances (Euclidean distance, Euclid; standardized Euclidean distance, Seuclid; Mahalanobis distance, Mahal; city block distance, Cityblock; cosine distance, Cosine; correlation distance, Correlation) (Chen et al., 2002) were used to assess genetic distances among accessions. Four hierarchical cluster methods (nearest distance method, Single; furthest distance method, Complete; unweighted pair-group average method, Average; Ward’s method, Ward) (Chen et al., 2002) were used to perform clustering to construct different core subsets by combining six genetic distances.

In each combination (a genetic distance plus a cluster method), 84 core subsets were constructed based on 21 sampling percentages ranging from 10% to 30% with 4 replications per sampling percentage. Further, 2016 core subsets were achieved from the 24 combinations (6 genetic distances combining 4 cluster methods) for 84 core subsets. Core subsets constructed by Complete random method were treated as controls.

Validation of core subsets

The initial germplasm group was treated by the principal components analysis to validate the core subsets. Distribution of the core accessions and the reserved accessions was plotted by the first two principal components at the sampling percentages of 20%, 25% and 30%. Core subsets constructed by Complete random method were treated as control (Xu et al., 2006).

Data management

Mixed linear model approach (Zhu and Weir, 1996) was used to predict genotypic values of all cotton genotypes in each quantitative trait to eliminate environmental and GE (genotypical×environmental) effects. The model is:

Y_hk(ij)=μ+E_h+R_i(h)+C_j(h)+G_k(ij)+GE_hk(ij)+ε_hk(ij),

where Y_{hk (ij)} is the observed value of the kth genotype in the hth environment within the ith row and the jth column; μ is the population mean; E_h is the fixed effect of the hth environment; R_{i (h)} is the fixed effect of the ith row within the hth environment; C_{j (h)} is the fixed effect of the jth column within the hth environment; G_{k (ij)} is the random effect of the kth genotype within the ith row and the jth column, G_{k (ij)}~(0,σ_G ²); GE_{hk (ij)} is the random effect of the interaction between the hth environment and the kth genotype, GE_{hk (ij)}~(0,σ_GE ²); ε_{hk (ij)} is the residual effect, ε_{hk (ij)}~(0,σ_ε ²). All genotypic values of each trait were standardized (μ=0, σ=1) and used to construct core subsets. All analyses were conducted in MATLAB software, version 6.5.

RESULTS

Evaluation of different genetic distances

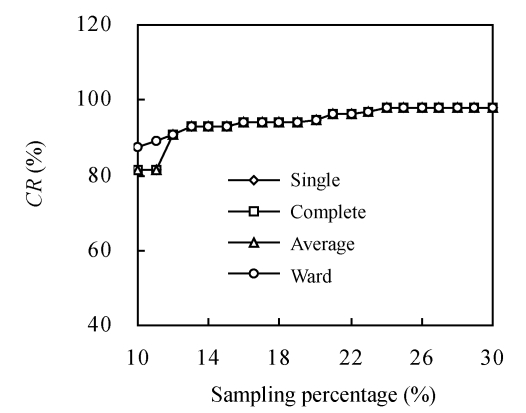
CR had been proved to be more robust than VR (Wang et al., 2007a), and we, therefore, chose CR to investigate the representation of different cluster methods combining different genetic distances in constructing core subsets. With the sampling percentage increasing, CR increased in all combinations (Fig.1). In all the five genetic distances (Euclid, Seuclid, Cityblock, Cosine and Correlation), core subsets constructed by the four cluster methods (Single, Complete, Average and Ward) showed completely the same changing curve in CR. By comparing the accessions in each core subset, all these four core subsets with the same sampling percentage and genetic distance were composed of the same accessions. However, Ward combining Mahal showed different CR changing curve compared to the other three cluster methods when the sampling percentage was less than 12%, while the four cluster methods combining Mahal showed exactly the same CR changing curve when the sampling percentage was over 12% (Fig.1).

Fig. 1.

The changing trend of coincidence rate of range (CR) of core subsets constructed by different hierarchical cluster methods combining Mahal distance

In order to find out why Mahal showed larruping to the other genetic distances in CR, we checked the courses of calculation in all the 6 genetic distances. The sample covariance matrix of Mahal was found to be ill-conditioned when the sampling percentage was less than 12% (more than 400 elements in initial data sample matrix).

Representativeness of core subsets constructed by different genetic distances

Since all cluster methods constructed the same core subsets in one genetic distance (except Ward in Mahal), core subsets constructed by the cluster method of Single were used to determine the representativeness of core subsets constructed by different genetic distances. At all the five sampling percentages (10%, 15%, 20%, 25% and 30%), core subsets constructed by Euclid, Seuclid, Mahal and Cityblock had significantly larger (α=0.05) CR than those constructed by Cosine and Correlation, and there was no significant difference for CR in core subsets constructed by Euclid, Seuclid, Mahal and Cityblock (Table 1). Core subsets constructed by Cosine had significantly larger CR than those constructed by Correlation at 25% sampling percentage, and there was no significant difference for CR in core subsets constructed by Cosine and Correlation at other four sampling percentages (Table 1).

Table 1.

Coincidence rate of range (CR) and variable rate of coefficient of variation (VR) of core subsets constructed by different sampling percentages and genetic distances combining Single cluster method

Genetic distance	CR (%)					VR (%)
	10%*	15%	20%	25%	30%	10%	15%	20%	25%	30%
Euclid	90.30a	92.60a	94.60a	96.06a	96.79a	151.31a	137.80a	132.15a	127.43a	123.49a
Seuclid	89.61a	93.29a	95.92a	96.78a	98.03a	150.06a	139.66a	132.33a	127.46a	123.41a
Mahal	81.12a	91.69a	93.83a	96.10a	97.56a	132.39b	134.82a	130.44a	125.64a	122.37a
Cityblock	88.74a	92.39a	94.39a	95.41a	96.01a	148.73a	138.55a	130.12a	126.03a	122.39a
Cosine	58.03b	63.33b	69.65b	72.92b	74.10b	93.16c	93.34b	94.37b	92.87b	93.78b
Correlation	58.24b	68.52b	64.61b	66.88c	71.04b	94.68c	99.46b	90.75b	89.25b	91.45b

Values with different letters in the same sampling percentage are significantly different (α=0.05) by Tukey test;

^* Sampling percentage

There was no significant difference for VR in core subsets constructed by Euclid, Seuclid, Mahal and Cityblock at the sampling percentages of 15%, 20%, 25% and 30% (Table 1). At sampling percentage of 10%, core subsets constructed by Euclid, Seuclid and Cityblock had significantly larger VR than those constructed by Mahal, while there was no significant difference for VR in core subsets constructed by Euclid, Seuclid and Cityblock (Table 1). At all the five sampling percentages, there was no significant difference for VR in core subsets constructed by Cosine and Correlation (Table 1).

Changing trend of the representativeness of core subsets constructed by different genetic distances

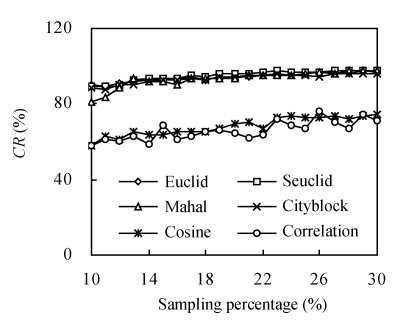
Fig.2 shows the pattern of the representativeness of core subsets constructed by different genetic distances. With the increase of the sampling percentage, CR increased in all the six genetic distances (Euclid, Seuclid, Mahal, Cityblock, Cosine and Correlation). However, CR of core subsets constructed by Cosine and Correlation increased unstably. Core subsets constructed by Cosine and Correlation had significantly lower CR than those constructed by the other four genetic distances at all sampling percentages. Compared to Euclid, Seuclid and Cityblock, Mahal constructed relatively lower CR when the sampling percentage was less than 12%. However, when the sampling percentage was over 12%, Euclid, Seuclid, Mahal and Cityblock showed similar CR. Synthesizing all sampling percentages, core subsets constructed by Seuclid had slightly larger CR than those constructed by Euclid, Mahal and Cityblock.

Fig. 2.

The changing trend of coincidence rate of range (CR) of core subsets constructed by different genetic distances combining Single cluster method

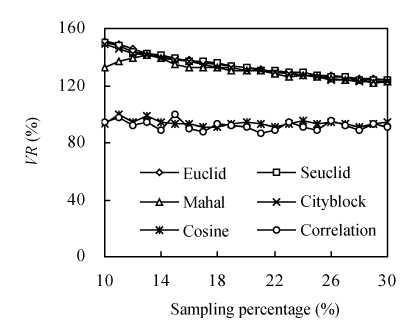
With the increase of the sampling percentage, except for core subsets constructed by Mahal at low sampling percentages (less than 12%), all VR declined (closing to 100%) in all six genetic distances. However, VR of core subsets constructed by Cosine and Correlation decreased unstably (Fig.3). Core subsets constructed by Cosine and Correlation had significantly lower VR than those constructed by the other four genetic distances at all sampling percentages (Fig.3). Compared to Euclid, Seuclid and Cityblock, core subsets constructed by Mahal had larger VR when the sampling percentage was less than 12% (Fig.3). When the sampling percentage was over 12%, Euclid, Seuclid, Mahal and Cityblock led to similar VR (Fig.3).

Fig. 3.

The changing trend of variable rate of coefficient of variation (VR) of core subsets constructed by different genetic distances combining Single cluster method

Validation of core subsets by the principal component analysis

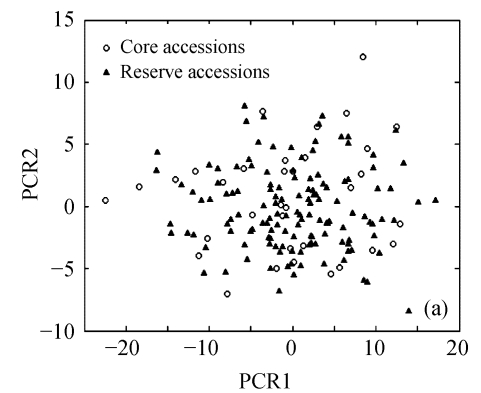
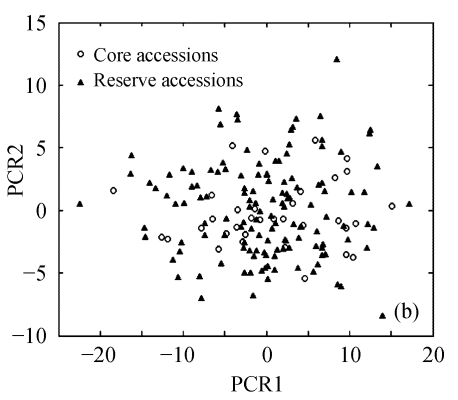
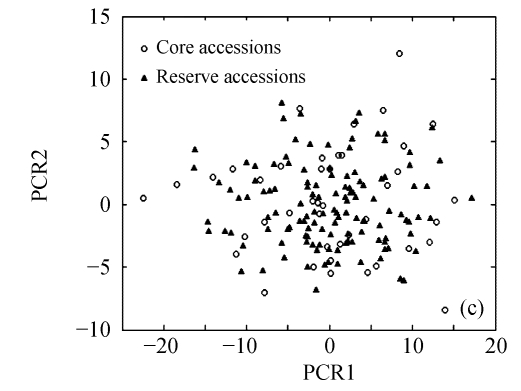
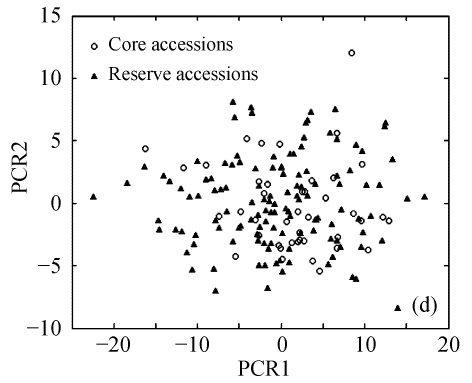
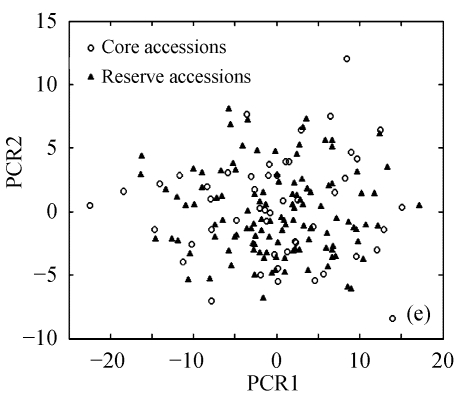
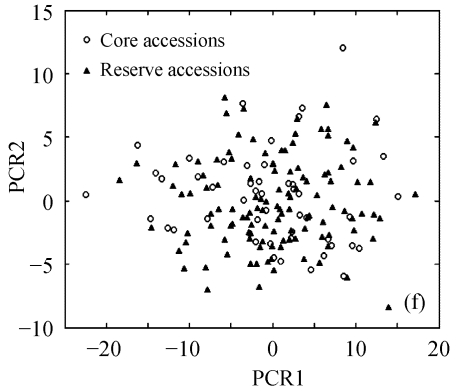
The above results suggest that Seuclid distance might be more suitable for core subset construction than the other five genetic distances. The principal component analysis was conducted to further validate core subsets constructed by Seuclid. The principal component analysis showed that the distribution of core and reserve accessions could be approximately presented by the first two principal components, which could account for 76.43% of the total genetic variation in initial germplasm group (Fig.4). Most extreme accessions were selected in core subsets by Seuclid distance and Single cluster method, while there were many extreme accessions not selected in core subsets by Complete random method (Fig.4). This phenomenon was more significant in low sampling percentages (Fig.4).

Fig. 4.

Principal component plots of core and reserve accessions in the sampling percentages for core subsets constructed by the least distance stepwise sampling (LDSS) method based on Seuclid distance combining Single cluster method or by the Complete random method. (a) LDSS method in 20% sampling percentage (Seuclid+Single); (b) Complete random method in 20% sampling percentage; (c) LDSS method in 25% sampling percentage (Seuclid+Single); (d) Complete random method in 25% sampling percentage; (e) LDSS method in 30% sampling percentage (Seuclid+Single); (f) Complete random method in 30% sampling percentage

DISCUSSION

Phenotypic values are mainly used in the research of constructing core subsets (Rodiño et al., 2003; Okpul et al., 2004; Volk et al., 2005; Yan et al., 2007). The phenotypic values of germplasm materials are easily affected by field conditions and experimental errors. Moreover, the effects of interaction between genotype and environment (GE effects) exist in phenotypic values (Hu et al., 2000). Therefore, a core subset based on phenotypic values may not accurately represent genetic diversity of the initial germplasm group (Tanksley and McCouch, 1997). Mixed linear model approach is an effective method to predict genotypic values from phenotypic values, and eliminate effects of experimental errors, environmental effects and GE effects (Hu et al., 2000; Li et al., 2004). In present research, core subsets were constructed based on genotypic values, which enabled more accurate evaluation of the methods for core subset construction.

The calculation of Mahal involves calculating sample covariance matrix, which may better reflect the genetic relationship among initial accessions. Some researches suggested that core subsets constructed by Mahal were not affected by scalar differences between traits, and more representative than those constructed by Euclid (Hu et al., 2000). However, the results of the present study show that the validity of Mahal may not be better than those of Euclid, Seuclid and Cityblock after genotypic values of each trait were standardized. The present research shows that the covariance matrix of accessions might be ill-conditioned when Mahal was used to calculate genetic distance at low sampling percentages, which led to bias in calculating the genetic distance. It suggests that Mahal might not be suitable for constructing small core subset. The calculations of Euclid, Seuclid and Cityblock do not need to calculate sample covariance matrix, which means that they are available in small core subset construction.

Our results also suggest that Seuclid is slightly more available for core subset construction than Euclid, Mahal and Cityblock. The principal component analysis validated LDSS method and Seuclid distance combining Single cluster method in core subset construction. The Seuclid distance was also validated in maize core subset construction (Crossa et al., 1995; Malosetti and Abadie, 2001). Core subsets constructed by Cosine and Correlation showed bad representativeness compared to those constructed by Euclid, Seuclid, Mahal and Cityblock. The genotypic values used in the present study were quantitative, so Cosine and Correlation may be more suitable for qualitative data in genotypic distance calculation (Yang et al., 1989). Most observed data of germplasm accessions were quantitative, and Seuclid leads to more representative core subsets and is available in any size of germplasm group. Therefore, Seuclid is recommended in core subset construction with LDSS method.