Quantifying biochemical variables of corn by hyperspectral reflectance at leaf scale

Abstract

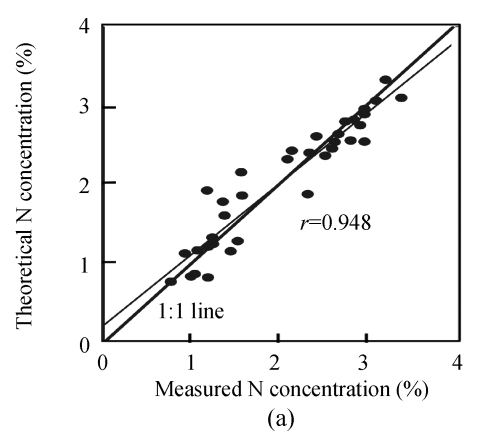
To further develop the methods to remotely sense the biochemical content of plant canopies, we report the results of an experiment to estimate the concentrations of three biochemical variables of corn, i.e., nitrogen (N), crude fat (EE) and crude fiber (CF) concentrations, by spectral reflectance and the first derivative reflectance at fresh leaf scale. The correlations between spectral reflectance and the first derivative transformation and three biochemical variables were analyzed, and a set of estimation models were established using curve-fitting analyses. Coefficient of determination (R ²), root mean square error (RMSE) and relative error of prediction (REP) of estimation models were calculated for the model quality evaluations, and the possible optimum estimation models of three biochemical variables were proposed, with R ² being 0.891, 0.698 and 0.480 for the estimation models of N, EE and CF concentrations, respectively. The results also indicate that using the first derivative reflectance was better than using raw spectral reflectance for all three biochemical variables estimation, and that the first derivative reflectances at 759 nm, 1954 nm and 2370 nm were most suitable to develop the estimation models of N, EE and CF concentrations, respectively. In addition, the high correlation coefficients of the theoretical and the measured biochemical parameters were obtained, especially for nitrogen (r=0.948).

INTRODUCTION

Nitrogen (N) is an essential element for plant growth. N fertilizer in excess of a crop’s nutritional needs may cause environment pollution (Wood et al., 1993). Crude fat (EE) and crude fiber (CF) contents are important qualitative indices for cereal crops to meet variety of needs of commodity (Zhao et al., 2005). Advanced knowledge of those biochemical variables may provide opportunities to manipulate inputs and optimize outputs.

Traditionally, soil testing, plant tissue analysis, and long-term field trials have been used to assess those biochemical characteristics, but these methods are time-consuming and destructive. Therefore, tools that can rapidly quantify the biochemical parameters are needed for proper rate and timing of fertilizer application for crop.

Remote sensing technique has been recognized as a reliable method to estimate various variables related to physiology and biochemistry (Hinzman et al., 1986; McMurtrey et al., 1994; Casanova et al., 1998; Diker and Bausch, 2003; Chen et al., 2007). Measurement of spectral reflectance is non-destructive, rapid and relatively cheap, and can be applied across spatial scales (Gamon and Qiu, 1999), so remote sensing has attracted a great deal of attention in terms of application for crop monitoring so far (Casanova et al., 1998). The remote sensing of foliar biochemical concentration has developed rapidly during the 1980s and 1990s (Curran and Kupiec, 1995; Peterson and Hubbard, 1991; Treitz and Howarth, 1999; Wessman, 1994; Wulder, 1998). Researches in the past decades have shown that remote sensing technology offers a practical alternative to the complicated, slow and expensive chemical methods to estimate foliar chemical concentrations over large geographic areas (Curran, 1989). The use of effective remote sensing techniques can eliminate the need for extensive field sampling (Graeff and Claupein, 2003).

Hyperspectral sensors measure the reflectance in a large number of narrow wavebands, generally with bandwidths of less than 10 nm. With these narrow bands, reflectance and absorption features related to physical and chemical characteristics of specific crop can be detected (Strachan et al., 2002).

An expending body of literature over recent years has focused on developing an understanding of the relationship between reflectance properties and leaf nitrogen concentration (Yoder and Pettigrew-Crosby, 1995; Kokaly, 2001; Graeff and Claupein, 2003; Zhang et al., 2006), but few discussed the estimation of EE and CF concentrations using hyperspectral reflectance. This research aims to exploit the relationship between hyperspectral reflectance at fresh leaf level and biochemical characteristics of corn. The specific objectives of present study are: (1) to identify optimal wavelengths that were significantly related to N, EE and CF concentrations by correlation analysis; (2) to select suitable estimation models for N, EE and CF concentrations by model quality evaluation.

MATERIALS AND METHODS

Experimental design

The field experiment was conducted in 2002 at Zhejiang University Experiment Farm, Hangzhou, Zhejiang Province, China, located at 30°14′ N, 120°10′ E. The experiment area is characterized by monsoon climate with a hot summer and a cool winter, and marked seasonal variations in precipitation. The average annual rainfall is 1374.7 mm. The sandy loam paddy soil had the following properties: pH 5.7, organic matter with 16.5 mg/g and total N with 1.02 mg/g. Six corn cultivars (Zea mays L.), i.e., yedan13 (Laizhou Academy of Agricultural Sciences, Shandong Province), danyu13 (Dandong Academy of Agricultural Sciences, Liaoning Province), sunuo1 and sunuo2 (Academy of Agricultural Sciences, Jiangsu Province), tetian1 and chaotian2018 (Seed Group Company, Zhejiang Province), were grown in 48 plots with nitrogen fertilization treatments of 0, 140 and 240 kg N/ha, respectively. Three replications were set for each treatment.

Measurements of biochemical variables

Three biochemical variables were analysed in this study, i.e., total N, EE and CF concentrations. All biochemical variables were determined by traditional wet chemical analysis according to the following procedures: N concentration was determined by Kjeldahl method; EE and CF concentrations were obtained by international standard methods of GB/T 6433-94 and GB/T 6434-94, respectively (Wang and Yu, 2001). The results were all expressed in percent.

Measurements of spectral reflectance

Hyperspectral reflectance was acquired with an Analytical Spectral Device, FieldSpec Full Range (ASD FieldSpec FR, Analytical Spectral Devices, Inc., Boulder Co., USA) that obtains continuous spectra from 350 nm to 2500 nm with 1.4 nm sampling intervals and 3 nm spectral resolution at spectral range of 350~1000 nm and 2 nm sampling intervals and 10 nm spectral resolution at spectral range of 1000~2500 nm. At ripe stage, three representative plants for each cultivar were cut off at ground level to conduct spectral measurements and biochemical analysis of leaves, stems, ears and sheath separated. The number of samples for analysis was 35. The samples were backed with a black rubber background for spectral measurement, the reflectance of which was nearly zero, and a 50 W halogenate lamp was used as illumination source and set at 0.45 m above the target with the angle of 70°. Fiber tip of spectrometer-operator consistently held approximately 0.1 m above the target with 8° field of view. Immediately after spectra measurement, samples were oven-dried at 105 °C for half an hour and then at 70 °C till the constant weight was acquired. The dry tissue was ground with a mortar and pestle for further biochemical analysis.

Every spectrum used in this analysis was an average of ten individual measurements automatically acquired by the FieldSpec. All measurements were made with a timely white reference calibration and the target reflectance is a relative value corresponding to the white reference reflectance as 1. Noise at the beginning of the spectrum limited the useful data range between 450 and 2500 nm in the analysis.

Calculation of the first derivative spectral reflectance

It has been reported that spectral derivatives have further merits, such as their ability to reduce variability due to changes in illumination or background reflectance properties (Demetriades-Shah et al., 1990; Zhang et al., 1997), which may make them robust spectral estimates of agronomic parameters of plant.

Due to the discrete characteristic of the spectral sampling interval, the derivative spectra were often calculated with the differential method expressed as:

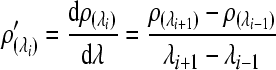, (1)

where λ_i is the wavelength of the band i; ρ_(λi) and ρ′_(λi) are raw reflectance and its first derivative reflectance at the band i, respectively.

Calculations of root mean square error (RMSE) and relative error of prediction (REP)

The performance of models was evaluated by coefficient of determination (R ²) and RMSE. RMSE is an indicator of the average error in the analysis expressed in original measurement unit (Kvalheim, 1987) and calculated by:

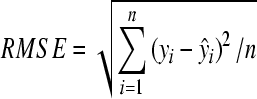, (2)

where y_i and ŷ_i are measured and theoretical values of crop variables, respectively; n is the number of samples.

Another useful parameter is the REP of the model calculated by:

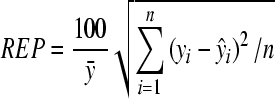, (3)

where ȳ is the mean of measured values.

RESULTS AND DISCUSSION

Correlation between biochemical variables and raw spectral reflectance

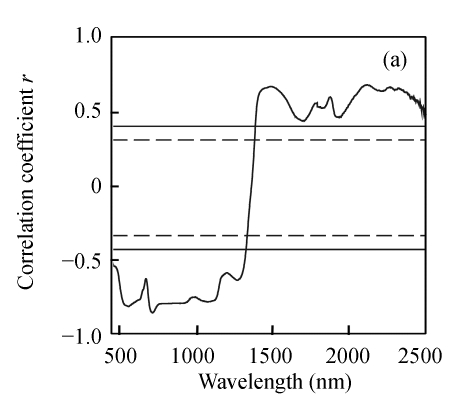
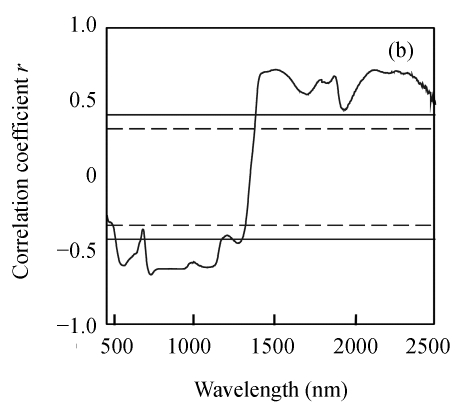
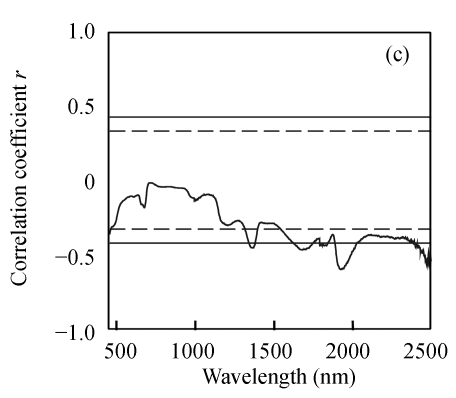
Correlation analysis was done to determine if the reflectance at each wavelength was positively or negatively correlated with three biochemical variables. Fig.1 shows that three biochemical variables were generally positively correlated with reflectance at near-infrared bands and negatively correlated with reflectance within the visible region. The correlation variations of N and EE were very similar, which was probably due to significant correlation between N and EE. However, the correlation coefficients of N were generally higher than those of EE in the visible region but lower in the near-infrared region. The correlation between CF concentration and reflectance was not very strong, and a relative good relationship appeared in limited wavelengths from 1884 nm to 2028 nm. The maximum correlation coefficient for N was located at 716 nm (r=−0.847), for EE at 1507 nm (r=0.772) and for CF at 1924 nm (r=−0.593). Furthermore, the maximum correlation coefficients at the above mentioned wavelengths were all beyond significant level (r=0.418), which indicated the feasibility of using the reflectance at those wavebands to develop the estimation model.

Fig. 1.

Correlogram between three biochemical variables and raw spectra reflectance. (a) N; (b) EE; (c) CF

The solid and the short dash lines represent the significant differences at P=0.01 and P=0.05, respectively

Correlation between biochemical variables and the first derivative reflectance

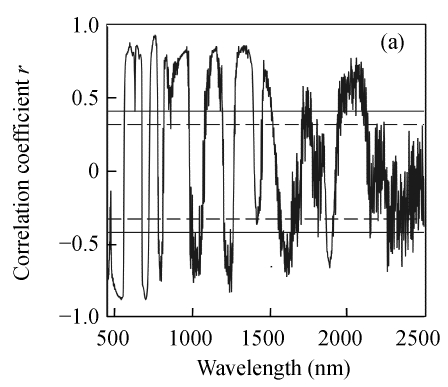
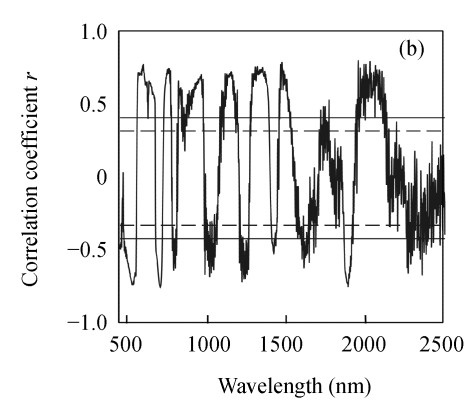
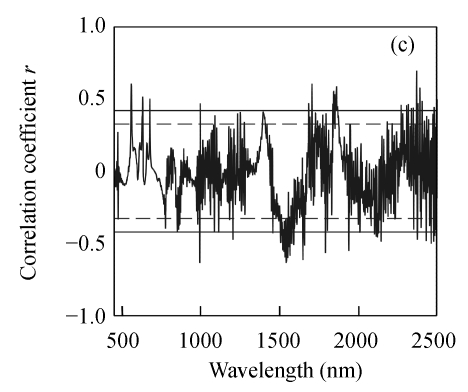
As shown in Fig.2, the correlation coefficients between three biochemical variables and the first derivative reflectance changed dramatically over the wavebands, and N and EE followed a similar pattern. Same to raw hyperspectral reflectance, the correlations between N and EE concentrations and the first derivative reflectance were generally much greater than that between CF concentration and the first derivative reflectance. For N, the highest correlation coefficient located at 759 nm (r=0.944); for EE and CF, the maximum correlation coefficients appeared at 1954 nm (r=0.814) and 2370 nm (r=0.693), respectively.

Fig. 2.

Correlogram between three biochemical variables and the first derivative reflectance. (a) N; (b) EE; (c) CF

The solid and the short dash lines represent the significant differences at P=0.01 and P=0.05, respectively

The first derivative transformation showed higher overall r values than the corresponding raw hyperspectral reflectance. The r values for correlations of three biochemical variables and the first derivative reflectance were found in the following order: N>EE>CF. The correlation of N concentration and reflectance around the above mentioned regions has been reported in previous studies (Blackmer and Schepers, 1994; Blackmer et al., 1996; Stone et al., 1996).

Model development and evaluation

In the present study, linear and nonlinear curve-fitting analyses were used to develop estimation model. Two nonlinear models were adopted, i.e., logarithmic and exponential models. The expressions of linear and nonlinear models are as follows:

Linear model: y=a+bx,

Logarithm model: y=a+b·ln(x),

Exponential model: y=a·exp(bx),

where y is the intended biochemical variable, i.e., N, EE or CF concentration (C _N, C _EE or C _CF); x is the spectral variable, i.e., raw spectra reflectance or the first derivative spectral reflectance at the most sensitive band; a and b are constants.

Two different strategies were used for the development of estimation model. In the first strategy, the reflectance at the selected wavelength was directly used as independent variable to conduct linear and nonlinear regressions; in the second strategy, the first derivative reflectance at the corresponding wavelength was used as independent variable. N, EE and CF concentrations were used as dependent variables in both strategies. The expressions of the developed models are summarized in Table 1.

Table 1.

Expressions of the developed models and results of model evaluation

Independent variable x	Model expressions	R2	RMSE	REP
ρ(716 nm)	CN=−1.38ln(x)+0.351	0.770**	0.272	13.31
ρ′(759 nm)	CN=1.37exp(1457.1x)	0.891**	0.181	8.85
ρ(1507 nm)	CEE=0.879exp(9.983x)	0.587**	0.644	18.69
ρ′(1954 nm)	CEE=1.497exp(3758.8x)	0.698**	0.589	17.11
ρ(1924 nm)	CCF=−395.04x+43.115	0.352*	3.951	14.27
ρ′(2370 nm)	CCF=21099x+34.299	0.480**	3.538	12.78

n=35;

^** Significant at P=0.01 (R ²=0.174);

^* Significant at P=0.05 (R ²=0.106)

The results of model evaluation (Table 1) show that using hyperspectral reflectance and its first derivative transformation could produce an acceptable accuracy. Three biochemical variables were all perfectly related to raw reflectance and its first derivative reflectance at the selected wavelength. The coefficients of determination (R ²) of R (reflectance)-based model and the first derivative R-based model ranged from 0.352 to 0.770 and from 0.480 to 0.891, respectively, with R ² of the first derivative R-based model being generally greater than those of R-based model. Meantime, the highest R ² (0.892) and the lowest RMSE (0.181) were both obtained with the first derivative R-based model, which indicated the superior performance of the first derivative reflectance. Furthermore, the results also showed that among three biochemical variables, N concentration estimation model had the highest R ² value, followed by EE and CF, which indicated that N concentration could be better estimated than EE and CF concentrations. Besides, as the results show, the maximal R ² and the minimal RMSE of developed estimation model were obtained from different models. In most cases, R ² of nonlinear estimation models were greater than those of linear models for both R-based and the first derivative R-based models.

The perfect model should have great R ², small RMSE and REP. Based on above criteria, the following estimation models were selected:

C_N=1.37exp(1457.1ρ′_{(759 nm)}), (4)

C_EE=1.497exp(3758.8ρ′_{(1954 nm)}), (5)

C_CF=21099ρ′_{(2370 nm)}+34.299. (6)

The RMSE and REP of above three estimation models were 0.181 and 9.13, 0.589 and 17.11, and 3.538 and 12.78 for N, EE and CF, respectively.

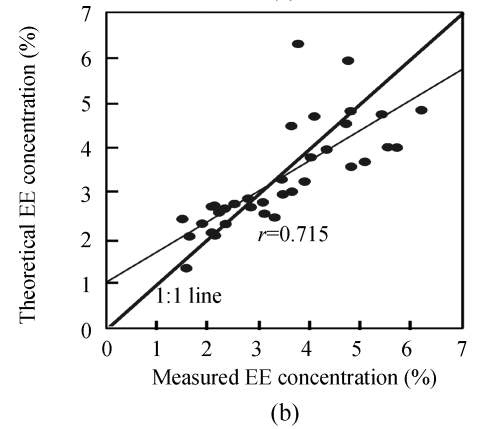
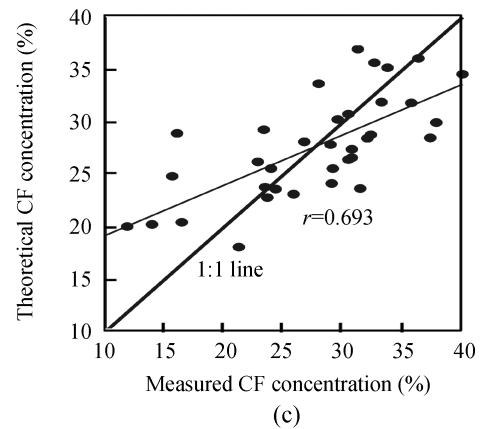
Finally, in order to make the results more convincing and visual, the observed values against the theoretical values obtained by estimation models were plotted in Fig.3. Ideally, an overlap of the regression line with the 1:1 line would indicate a perfect match. Fig.3 shows that the efficiency of the N estimation model was evident, and the regression line between the observed and the theoretical N concentrations nearly overlapped the 1:1 line.

Fig. 3.

Correlation between measured and theoretical values using the optimum estimation models of N (a), EE (b) and CF (c)

Additionally, comparison the performance of CF and EE concentration estimation models showed that the EE model performed better than the CF model. The relationship between theoretical and measured values made the results of this study most encouraging, especially for N concentration estimation (r=0.948). Besides, the results also indicated the great feasibility of hyperspectral reflectance and its first derivative transformation for estimation models of N, EE and CF concentrations.

CONCLUSION

In the present work, the results provide information for the development of the vegetation index using spectral reflectance or the first derivative spectral reflectance at sensitive spectral bands. Band rationing and normalization provide a simple and straightforward means to enhance the biochemical absorption signal while minimizing background effects (Jackson and Huete, 1991).

Furthermore, the encouraging results of model evaluation also showed the promising potential of N, CF and EE concentration estimation models using leaf-level hyperspectral reflectance and its first derivative transformation. Besides, encouraging performance of N estimation model was also proven. The analyses of correlations between spectral reflectance and biochemical variables show that the first derivative transformation provided the most sensitive method and promising predictive potential for biochemical variables.

Although many different N treatments were set, more researches are needed before any concrete conclusions are drawn.