From discrete protein kinetics to continuous Brownian dynamics: A new perspective

Abstract

This article presents a comparative analysis of two sets of data from recent experiments on kinetics of (i) protein unfolding by mechanical force and (ii) channel gating with membrane electric potential. Both situations necessitate a continuous Brownian-dynamic view of protein conformational kinetics. We show that the discrete approach traditional to biochemical kinetics is insufficient for understanding dynamics of protein molecules in an aqueous solution or lipid membrane with varying conditions under which the major activation barrier can disappear. A semiquantitative analysis based on Brownian dynamics in a continuous energy landscape offers a more comprehensive description for motions of biological macromolecules.

Fluctuating conformation is a fundamental characteristic of a protein in an aqueous solution, which differentiates the macromolecule from small organic compounds. Although a protein structure derived from crystallography often provides a static picture, it is essential to remember that conformational flexibility, along with the structure, gives rise to the ultimate functionalities of proteins and enzymes (Karplus and McCammon 1983). Ever since the conception of the allosteric enzyme (Koshland et al. 1966; Monod et al. 1965), the notion of multiple states of proteins has been widely appreciated. Two particularly notable examples are the models for folding kinetics of soluble globular proteins and the gating kinetics of membrane channel proteins. Both these models introduce discrete conformational states which are macroscopic and operationally defined by kinetic experiments (Tsong et al. 1972; Ehrenstein et al., 1974). These models are usually expressed as

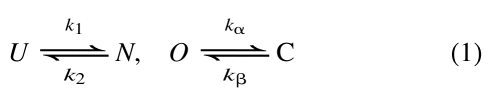(1)

where U and N are unfolded and native states of a soluble protein, with k₁ and k₂ as folding and unfolding rate constants. Similarly, O and C are open and closed states of a membrane channel protein, with k_α and k_β as closing and opening rate constants. When such simple models cannot explain specific experiments, usually more intermediate states are added (Bezanilla et al. 1994; Baldwin 1995). Such is the traditional (old, chemical) approach to kinetic modeling of proteins.

The discrete-state description of proteins, however, neglects conformational motions (i.e., fluctuations) within each state. Energy landscape theory, treating a polypeptide as a polymer, is more realistic view of protein dynamics (Frauenfelder et al. 1991; Wolynes et al. 1995; Zwanzig 1995; Doyle et al. 1997). In this alternative (new, physical) view of protein dynamics, a protein molecule moves from one conformation to another through a continuous change in its molecular bond lengths and angles. Some of the movements are energetically downhill; others are energetically uphill, with heat energy being dissipated to or absorbed from the solvent, respectively. The motion is highly erratic, even on nano- or picosecond timescales, due to the constant thermal agitation from the solvent molecules. Therefore, the protein movement from one conformation to another is very much like Brownian motion in a force field. The relation of this picture to the reactions in equation 1 is that the states U and N (or O and C) are each associated with an energy well. Hence a molecule spends more time in these states than in moving from one state to another (Fig. 1 ▶). Kramers (1940) was the first to provide chemical reactions with such a clear, but stochastic, physical picture. Today such a picture is usually appreciated in molecular dynamic simulations.

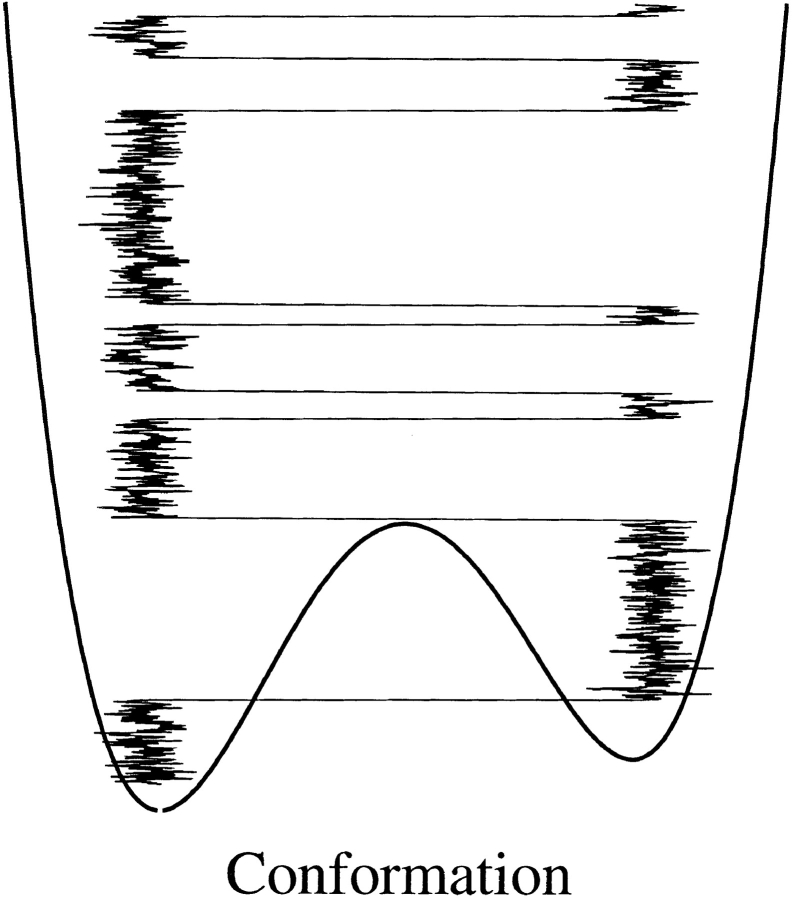
Fig. 1.

Schematic figure showing a continuous energy function with an energy barrier separating two energy wells. Superimposed on the energy function is a Brownian trajectory (i.e., conformational dynamics as a function of time [going upward]). As seen the molecule spends most time fluctuating in either of the two states and moving from one state to another by a seemingly discontinuous transition. This is the nature of chemical transition of a single molecule, A ⇌ B.

Brownian dynamics is not simply a more realistic picture for protein conformational transition. Recent experimental studies on several proteins indicate, more importantly, that it is necessary to invoke a continuous energy landscape to provide comprehensive interpretations for experiments (Qian and Chan 1999; Sigg et al. 1999). There are now a host of laboratory observations that call attention to interpretations based on continuous energy and motion. Most notably are (i) rapid early conformational changes in relaxation kinetics and (ii) nonactivated transitions induced by strong external forces. From a conceptual standpoint, as I shall show, these two types of observations are intimately related to the hysteresis and bond-rupturing phenomena recently observed in the receptor–ligand dissociation under atomic force microscopy (Florin et al. 1994; Moy et al. 1994; Evans and Ritchie 1997; Shapiro and Qian 1997, 1998; Merkel et al. 1999; Qian and Shapiro 1999).

The mathematical model of the Brownian dynamics has been extensively studied by Smoluchowski, Kramers, and others and is summarized in an article reviewing the 50 years following Kramers' theory (Hänggi et al. 1990). It is interesting to note that the merging of discrete with continuous kinetic models has taken four decades in chemistry. It is now time to turn to protein dynamics. The following quotation from Hänggi et al. (1990) provides a historical perspective:

“For unimolecular gas phase reactions, a description of the rate in terms of discrete energy exchange was more suitable than the continuous energy-exchange mechanism underlying energy diffusion in Kramers' model (1940). Work on chemical reactions in condensed phase, for which the Kramers theory is most appropriate, had to await the experimental progress achieved in the late seventies and eighties.”

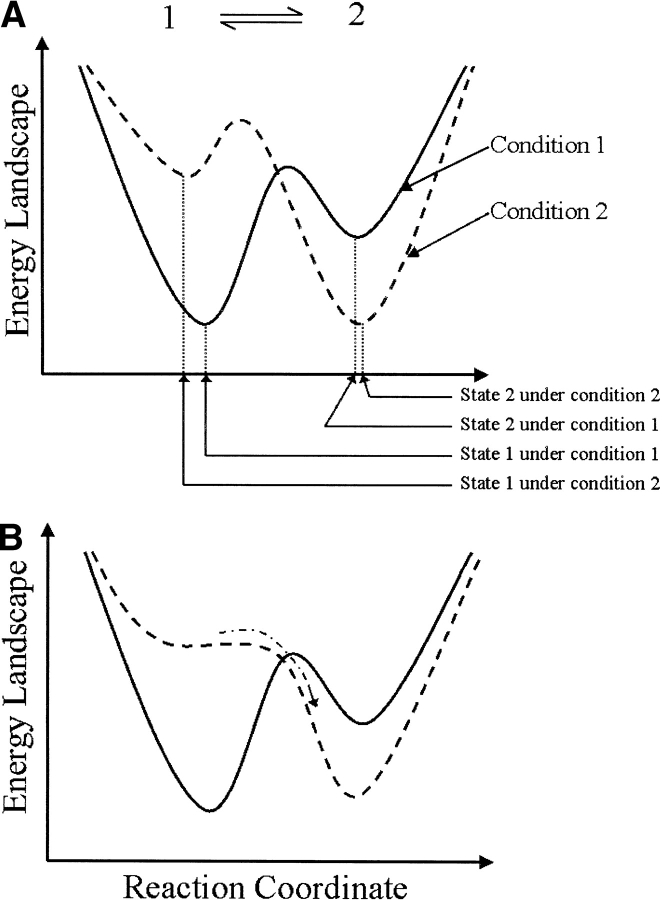
We now discuss the recent experiments and show why the continuous Brownain motion model is essential in understanding the data. It is important, at the onset, to point out that every kinetic relaxation experiment must involve 2 environmental conditions, one before and one after the perturbation, for the protein under study. In protein folding, for example, there are usually different denaturant concentrations or temperatures. For ion-channel gating they are different membrane electric potentials. Recent experiments also apply external mechanical forces to proteins. At time zero, the protein under condition 1 is subjected to condition 2, which initiates the relaxation kinetics of the molecule. In terms of the energy function (potential of mean force), there are two different energy functions corresponding to the two conditions (Karplus and Shakhnovich 1992; Qian and Chan 1999). For the two-state kinetics in equation 1, the corresponding energy landscapes are shown in Figure 2A ▶. Each discrete state is associated with an energy well. The continuous model, however, also includes information on the shape of energy wells, as well as their relative heights; both change with the solvent condition. Immediately after initiation, not only is the thermal equilibrium between the two wells perturbed, but also perturbed is the equilibrium within each of the wells. The response of a protein to the perturbation, therefore, is to readjust its equilibrium distributions within each energy well, as well as to redistribute between the two wells. Because the latter process is thermally driven, whereas the former process is energetically driven, the readjustment involves a rapid early conformational change followed by a slower first-order kinetics. One unique feature of the fast process, however, is that because it is not thermally activated, the kinetic is not exponetial. Experimentally, from such nonexponential Browian process one expects to observe faster relaxation times with faster temporal resolution, reminiscent of fractal behavior.

Fig. 2.

Schematic diagram showing continuous energy functions for a two-state protein kinetics (eq. 1) under two different conditions. (A) The shape of each energy well, as well as the relative heights of the two wells, changes with the condition. (B) Under extreme conditions, the activation-energy barrier can completely disappear. In this case, the relaxation process is an energetically downhill diffusion.

Because the downhill, energetically driven readjustment within each energy well is usually much faster than crossing the barrier between the two states, and because the magnitude of the readjustment is usually small relative to that of the two-state transition, such early kinetic events are difficult to observe experimentally. However, recent experiments on gating of voltage-dependent membrane ion channel proteins have observed a fast kinetic phase (Stefani and Bezanilla 1996), and a Brownian dynamic mechanism has been proposed for the early fast (∼rμs) components in the movement of gating-charge of the channel responding to a sudden change in membrane voltage (Sigg et al. 1999). In the kinetics of protein folding, such a fast energetically downhill event is also observed (Hagen et al. 1996; Sosnick et al. 1996; Qi et al. 1998). In addition, a large amount of experimental observation of various intermediate states in the early time of protein-folding kinetics (known as molten globular states) can be interpreted as a readjustment step responding to a sudden change in denaturant concentration in solvent (Karplus and Shakhnovich 1992; Qian and Chan 1999).

A second situation for which discrete kinetics fail to provide a cogent interpretation is when the perturbation is so large that it completely eliminates the activation barrier, as shown in Figure 2B ▶. Under such conditions, the traditional rate process with thermal activation loses its meaning altogether and the relaxation is a very fast energetically downhill Brownian diffusion. This phenomenon has not been observed in monomeric protein-folding (-unfolding) kinetics. However, such a mechanism lies behind streptavidin–biotin bond rupturing with atomic force microscopy (Shapiro and Qian 1997, 1998), as well as successive unfolding of the giant muscle protein titin by force (Kellermayer et al. 1997; Rief et al. 1997; Tskhovrebova et al. 1997; Qian and Shapiro 1999). Similar behavior also has been observed in the gating kinetics of K⁺ channel with an extreme holding potential (Sigg et al. 1999).

Another important reason for introducing the continuous energy function to augment the discrete-state kinetics is the inability to relate energy to force in the latter framework. Force is the change of energy in response to a change in distance. As we can see, the concept of distance is completely missing in the discrete-kinetics. In the continuous energy landscape, no matter how ill-defined the reaction coordinates are, they provide a conceptual framework. Therefore, the continuous energy landscape provides a bridge between the experimental studies on the kinetics of proteins and more direct measurements of force and displacement on single protein molecules (Kellermayer et al. 1997; Rief et al. 1997; Tskhovrebova et al. 1997; Qian and Shapiro 1999; Fisher et al. 2000; Yang et al. 2000).

The conceptual thrust of the continuous-energy-landscape approach to proteins is that it provides a theoretical language for discussing a wide range of dynamical behaviors of proteins. It has laid a foundation for developing a macromolecular mechanics at a mesoscopic level between the discrete models and the atomic-level molecular dynamics (Qian and Shapiro 1999). It allows important concepts such as force and movement to be discussed on an equal footing as energy and thermodynamic states. With the recent significant progress in biophysical measurements of forces and movements in single protein molecules, models based on continuous Brownian dynamics will become an indispensable part of protein science. In a similar spirit, Eisenberg and his colleagues have developed a diffusion theory for ion movement (not to be confused with protein movement in the gating kinetics) in open channels to augment the traditional discrete-state ion transport models. (For reviews, see Cooper et al. 1988 and Eisenberg 1996.)

The introduction of continuous energy landscapes does not invalidate the discrete transition between two energy wells; rather, it generalizes the discrete model with increasing molecular details. It is well known that with a sufficiently large activation barrier separating two energy wells, there is a rapid equilibrium within each well (Szabo et al. 1980). Furthermore, the transition from one well to another is essentially exponential (i.e., Arrhenius, also known as discrete-state Markovian). This is the theoretical basis for the practice of discrete-state kinetics (e.g., eq. 1). One should recognize, however, that the molecular structures of the discrete states, which usually are defined experimentally through spectroscopy, change with the environmental conditions of the protein. These changes are also reflected in the baselines when fitting discrete multistate models to equilibrium measurements (Qian 1997; Qian and Chan 1999).

Hysteresis is another example that shows how the continuous energy function serves as a unifying theoretical edifice in protein dynamics. This interesting phenomenon has been observed in protein–ligand interaction under external force: The association process under force and the dissociation process under force are significantly different. This is interpreted in Figure 3 ▶. Comparing this model with the well-known protein-folding/unfolding kinetics scheme below, one sees that the main feature of the two molecular processes are indeed identical.

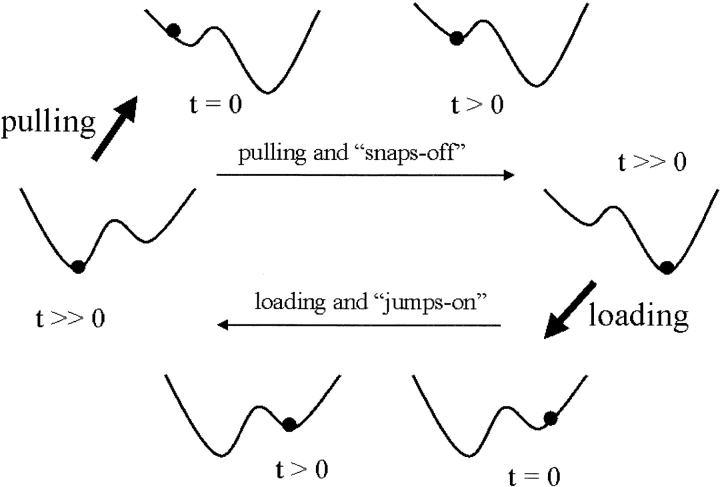
Fig. 3.

When applying a force to a protein–ligand pair, one can either pull the ligand apart from the protein or load the protein with the ligand. The events in these two kinetics processes are schematically shown here. The particle in the diagram represents the ligand that experiences both intermolecular force from the protein (modeled as a 6–12 potential) and the force probe (modeled as a Hookean spring). The energy minimum on the left is the equilibrium position for the intermolecular energy; the energy minimum on the right is the equilibrium position of the spring. For review, see Qian and Shapiro (1999).

In the above scheme, I introduce the term wet molten globule, referring to the collapsed intermediate state commonly observed in the protein refolding kinetics (Baldwin 1993). The wet molten globule has been interpreted as the unfolded state under a native condition (Dill and Shortle 1991; Qian and Chan 1999). The dry molten globule (Kiefhaber et al. 1995), on the other hand, has been interpreted as the folded state under a denaturing condition (Qian and Chan 1999). Both these two states are kinetic intermediates that appear in the transient folding and unfolding processes, respectively. The wet molten globule is a kinetically metastable state before the major activation barrier in the folding process, whereas the dry molten globule is again a kinetically metastable state before the major activation barrier but in the unfolding process. This difference is the same as the hysteresis.

In summary, one important consequence of the energy landscape concept is that within each discrete kinetic state, there could be significant conformational re-adjustment due a changing condition (perturbation) for the protein, such as changes in temperature, solvent, or membrane potential. Therefore, following a sudden change in one of these conditions, a protein undergoes two characteristic kinetic steps: An energetically downhill readjustment into the new equilibrium position within the same discrete state and a thermally activated rate process in which the molecule jumps from one discrete state into another with lower energy. When the perturbation is sufficiently larger, it is also possible that the activation barrier is completely eliminated. Then the kinetics becomes a downhill Brownian diffusion and the relaxation kinetics is no longer exponential. The continuous energy and Brownian dynamics perspective on protein kinetics provides a comprehensive theoretical framework for a host of experimental observations, ranging from protein folding to membrane channel gating to protein–ligand dissociation and protein unfolding under external force.