Abstract
Central to swarm formation in migratory locusts is a crowding-induced change from a “solitarious” to a “gregarious” phenotype. This change can occur within the lifetime of a single locust and accrues across generations. It represents an extreme example of phenotypic plasticity. We present computer simulations and a laboratory experiment that show how differences in resource distributions, conspicuous only at small spatial scales, can have significant effects on phase change at the population level; local spatial concentration of resource induces gregarization. Simulations also show that populations inhabiting a locally concentrated resource tend to change phase rapidly and synchronously in response to altered population densities. Our results show why information about the structure of resource at small spatial scales should become key components in monitoring and control strategies.
The desert locust, Schistocerca gregaria, is one of the world’s most notorious insect pests. Most of the time, it exists at low densities across sub-Saharan Africa and into India. At unpredictable intervals, plagues occur; swarms leave this recession zone and invade neighboring areas of Africa, Asia, and Europe. The crowding-induced phase transition between the “solitarious” and “gregarious” forms involves a suite of changes in behavior, morphometry, color, development, fecundity, and endocrine physiology (1–3). Gregarious individuals become more active and are attracted, instead of repelled, by other locusts. Most phase characters change between instars or accrue across generations through maternal inheritance (4–7), but a solitarious individual’s behavior becomes gregarious after only 4 h of crowding and reverts to solitariousness after only 4 h of reisolation (4, 5, 8). The detailed time course of behavioral-phase change has been quantified only recently and has important implications for selecting the appropriate temporal and spatial scales required to understand locust swarming.
An experimental study has shown that locusts confined in an experimental arena for 8 h are more gregarious if the arena contains a lower density of resource (e.g. food, perches, or favorable microclimatic sites; ref. 8). In the present study, we examine the effects of resource distribution and locust density on gregarization, while keeping the overall density of resource constant.
MATERIALS AND METHODS
Fractal Dimension of Resource.
Fractal surfaces used in the experiment and simulation were created on a 64 by 64 grid by using an algorithm with midpoint displacement (9). Food patches were located on the highest 20 points. The fractal dimension of the resulting distribution is then described by using a box-counting algorithm. The arena is divided into boxes of length r grid squares, and the number of boxes containing food patches is counted. This process is carried out four times with the origin of the boxes successively shifted diagonally across one grid square. By using the mean number of nonempty boxes N(r), the fractal dimension is calculated as −1 times the slope of the linear regression of log N(r) against log r. Because we were interested in the smallest scales, we used only r = 1, 2, and 4. The box-counting method measures the fractal dimension of the resource, not the boundary of the resource. Thus, the more continuous the resource distribution, the closer the fractal dimension is to 2.0. With only 20 points, this box-counting algorithm can result in a maximum dimension of 1.28.
Laboratory Experiment.
Experiments were conducted in a 70-cm by 70-cm Perspex arena with 20 small pots of wheat shoots 1 cm in diameter and 2 cm high. The pots were placed on a 64 by 64 grid within the arena according to the random fractal algorithm. The experiments were performed with isolated-reared (4) mid-second-instar nymphs, whose solitary-reared parents originated from eggs laid by crowd-reared adults. Nymphs were used only once and were deprived of food for 12 h before testing. Tests lasted 8 h, and at the end of each run, the behavioral-phase state of each locust was assayed. For the assay, locusts were isolated and graded according to rates of 13 types of movement and grooming behavior observed over a 10-min period (see ref. 4). We used five resource distributions for experiments with groups of 10 or 20 nymphs. An additional three distributions were used for runs with 10 locusts. Each experiment was performed twice, for a total of 26 runs.
Computer Simulation.
The computer simulation used a continuous two-dimensional arena with edges identified to form a torus. Time was divided into 50,000 iterations; 10,000 iterations were allowed for the population to reach equilibrium, and results were collected over the following 40,000 iterations. As in the experiment, 20 patches of resource were placed by using the random fractal algorithm on a 64 by 64 grid superimposed on the arena. Simulations were run with 10 and 20 initially solitarious locusts, placed at random within the arena.
Model locusts are characterized by (i) a behavioral-phase state, g, which ranges from 0 (solitarious) to 1 (gregarious), and (ii) a Cartesian coordinate. Each locust has periods of movement according to rules with parameters derived from earlier experimental studies (4, 5, 10): the probability of going to a resource patch (P); the probability of leaving a resource patch (Q1); the maximum distance moved in an iteration (R); the rate of increase in movement with gregarization (B); and the phase-dependent probability of leaving an unsuitable patch (Q2). Locusts interact when in the same grid square. A locust experiences a unit of contact whenever another individual starts or finishes movement within its grid square. Locusts that move within an iteration do so synchronously, and contact is calculated at the initiation and end of movement. The rate of behavioral-phase change of an individual at time t is a saturating function of the cumulative amount of contact it experiences (ct) over the preceding 500 iterations. The amount of saturation is adjusted with parameter A (the contact-saturation level; we let A = 40). The gregarization of a locust is updated as gt+1 = gt + 0.01⋅(min(1, ct/A) − 0.5). If gt+1 exceeds the limits 0 or 1, it is given the value of that limit.
An individual’s movement increases with its behavioral gregarization, modelled by bg = 1 + Bg. Endogenous movement, which occurs with probability bgQ1, is proportional to its phase state. Additional contact-induced movement provides an attractive–repulsive response. The probability of moving in the iteration after contact depends on the presence of other locusts; if locusts are present, it decreases with gregarization, bgQ2(1 − g). Otherwise, it increases, bgQ2g. Movement is with equal probability to any point within a distance bgR. If it is contact-induced, then the movement is repeated until the individual is no longer in the same grid square. After the initial movement, an individual may go directly to food with probability P. The patch is chosen at random with probability decreasing with distance from the individual—the probability of moving to patch j is bgP/Σi(dj/di)1.5 where di is the distance (on the torus) between the locust and resource patch i.
RESULTS
Effect of Resource Distribution.
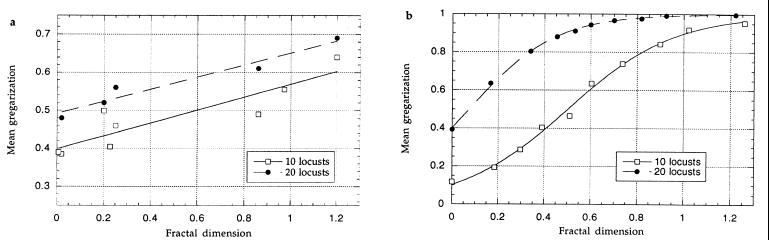
The results of the laboratory experiment show that for a fixed number of locusts and resource patches, the mean gregarization of the population increases with spatial concentration of the resource (Fig. 1a). Least-squares linear regression is y = 0.40 + 0.17x, R2 = 0.80, for 10 locusts, and for 20 locusts y = 0.49 + 0.16x, R2 = 0.95. These lines differ significantly in elevation, with 20 locusts being more gregarized after the 8-h treatment than 10 locusts (analysis of covariance with fractal dimension as covariable, and locust number as treatment gave P < 0.0001 for fractal dimension, F1,10 = 56.3; P < 0.0003 for treatment, F1,10 = 17.8).
Figure 1.
(a) The average behavioral-phase state of the 10 or 20 experimental locusts at the end of 8 h in the arena. Each point represents the mean of two experimental runs with the same resource distribution. There is a significant effect of both fractal dimension and number of locusts (see text). (b) The mean gregarization of the 10 or 20 model locusts over the final 40,000 iterations of a simulation. Parameters were chosen such that a solitarious locust would spend, on average, 10 iterations on a patch followed by 100 iterations away (P = 0.1, Q1 = 0.1, and R = 0.5). Gregarized locusts have a 50% increase in the rate and distance of movement (B = 0.5), and the rate of contact-induced movement is Q2 = 0.5. Results from 124 simulations with 102 different resource distributions were pooled according to fractal dimension, and each point shows the mean of no fewer than 10 simulations.
The results of the simulation show a similar trend to the experimental results; population gregarization increases with locust density and the fractal dimension of the habitat (Fig. 1b). The average population gregarization was not affected by the initial phase state of the model locusts, suggesting that there is a single equilibrium level of gregarization possible for any particular habitat and population density.
Although designed to allow for direct comparison, the laboratory experiment differed from the simulation in two significant ways. First, the experimental arena had edges by which the locusts aggregated. This aggregation increased the basal rate of gregarization so that locusts were partially gregarized after 8 h, even in an arena with widely dispersed food sites. Second, the locusts were observed for only 8 h; thus, the equilibrium level of gregarization might not have been reached.
Disentangling Mechanisms in the Simulation.
How can we explain the effect of resource distribution on gregarization? The resource determines the distribution of locusts. In the experimental arena, locusts tend to stay near food patches. In the simulation, every 1/P movements takes a locust to a resource patch, whereas subsequent movements take it gradually away. Behavioral gregarization of real locusts is triggered principally by contact (11, 12). In the simulation, the rate of behavioral change is a saturating function of the cumulative number of contacts experienced over the preceding 500 iterations. The simulation identifies three mechanisms by which spatial distribution of resource influences the distribution of the cumulative contact ct. The first two act on the mean instantaneous-contact rate, whereas the third acts through the distribution of the cumulative contact.
The Mean Contact Rate.
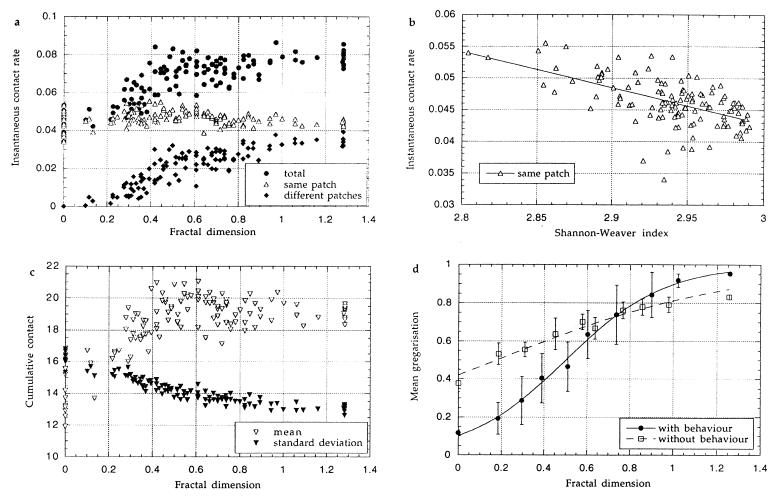
To make explicit the scale at which individual behavior and resource distribution interact, contact can be divided into two (scale-dependent) classes: contact between individuals that have most recently visited the same patch (or are on it) and contact away from a patch between individuals that have recently visited different patches (Fig. 2a). Each of the two mechanisms acting on the mean instantaneous contact rate acts on a different class of contact and over a different spatial scale.
Figure 2.
(a) The effects of resource distribution on the mean amount of instantaneous contact experienced by simulated locusts. Parameter values were chosen such that a locust’s behavior is not affected by its phase state or the presence of other locusts (B = 0.0, Q2 = 0.0, and other parameters as in Fig. 1a). Each point is the mean of a single simulation run. (b) The effect of the uniformity of the resource distribution on the rate of instantaneous contact between locusts that have most recently visited the same patch—from the same simulation runs as in a (i.e., excluding phase-related behavioral changes). (c) The effects of resource distribution on the distribution of cumulative contact. The mean and standard deviations of the distribution of the effective cumulative amount of contact (min(ct, A)) for all individuals of each simulation are shown—from the same simulation runs as in a (i.e., excluding phase-related behavioral changes). (d) The effects of phase-dependent individual behavior on population gregarization. The figure contrasts the effects of using phase-related behavioral changes with the same parameters as in Fig. 1b with the effects of using no behavioral changes with the same parameters as in a. Results are pooled as in Fig. 1b, and the error bars show the standard deviation of the simulation mean.
There is a relationship between the uniformity of the resource distribution and the rate of contact between individuals on or from the same patch (Fig. 2b). The uniformity of the resource distribution is reflected in the distribution of locusts. We measured the latter with the Shannon–Weaver information measure: Σi − pilog pi, where pi is the relative frequency with which patch i is visited. The least-squares linear regression is y = 0.21 − 0.057x, R2 = 0.34. Evenly spaced distributions in either a single clump or evenly scattered have high information measures. Uneven, intermediate distributions which are formed of larger clumps with some scattered patches have lower information measures. In an uneven distribution, there are outlying patches that are visited less frequently. The locusts are therefore effectively concentrated in fewer patches, and the crowding causes greater gregarization.
The second mechanism by which resource distribution affects gregarization acts on the second class of contact. Locusts originating from different patches meet more often the closer together the resource patches (Fig. 2a). This tends to make gregarization increase with fractal dimension.
The rate at which individuals from the same patch meet is high, and the uniformity of distribution affects the rate over a large range of spatial scales. However, the effect is small. For the second mechanism to be significant, individuals must frequently leave the resource patches. This only happens if the patches are the same scale as the range of an individual’s movement over a brief time (minutes). In the simulation, only differences in resource distribution at small spatial scales have a large effect on the total amount of contact.
The Distribution of Contact.
The third mechanism acts through the cumulative contact experienced over a physiologically relevant length of time, rather than simply the mean instantaneous contact rate. Greater movement between patches means a more homogeneous mixing of locusts, leading to a smaller variance in the cumulative amount of contact ct within the population. This is important, because the rate of gregarization is a saturating function of an individual’s cumulative contact. Saturation occurs both because there is a maximal gregarized state (g = 1) and because if ct > A, then the effect on the rate of gregarization is the same as if ct = A. If the mean rate of contact is sufficient for gregarization, then the smaller the variance, the greater the amount of gregarization in a population. With lower mean levels of contact, greater aggregation is necessary for gregarization. In the 500 iterations over which a model locust “remembers” its contact, it will on average have left a resource patch at least five times. In a concentrated resource, a locust is less likely to visit the same patch in succession, and so the cumulative amount of contact is more evenly distributed. Fig. 2c shows the distribution of the effective cumulative amount of contact (min(ct, A)) from individuals most recently on the same patch. The more clumped the resource distribution, the smaller the standard deviation. In contrast to the simple instantaneous contact shown in Fig. 2a, the effective cumulative contact rate is greater in a clumped resource distribution.
Phase-Related Behavior.
The effects of resource distribution on the extent to which locusts interact and hence gregarize are apparent even in the absence of phase-related changes in behavior, as seen in Fig. 2 a–c where such behaviors were excluded. The net result of including phase-related behaviors in simulations is that the contact rate in a population depends on the phase states of the individuals, as well as the distribution of resource. The equilibrium gregarization therefore becomes a more critical function of resource distribution (Fig. 2d) and population density.
When a locust becomes gregarious, it is attracted by other locusts, whereas a solitarious individual is repelled. A gregarious locust, therefore, comes into contact with other locusts more often than does a solitarious locust. The phase-dependent attractive–repulsive behavior of a locust acts to push it towards either gregarious or solitarious extremes. A change in the phase of an individual has a similar effect on the contact experienced by the rest of the population—a gregarious locust has a stronger gregarizing influence than a solitarious one. Attraction among gregarious insects and repulsion among solitarious ones tend to prevent individuals from reversing phase. Because of the behavioral changes, a partial phase change in an individual makes further change in that individual easier. It also increases the probability that the phase of other locusts will change in the same direction. Thus, there is positive feedback from behavioral change acting at both the individual and population level.
The second significant behavioral effect of gregarization is a general increase in movement. Gregarious individuals move further and more often, increasing the amount of contact between individuals. The effect is strongest in clumped habitat, where locusts are closer together, and so a moving individual is more likely to come into contact with others. Increased movement also means that there is greater mixing. When the mean contact rate is low, increased movement works against gregarization by separating individuals, whereupon they begin to resolitarize. At high-contact levels, however, the smaller variance in cumulative contact further increases the rate of gregarization in the population. Phase-dependent rates of movement thus have the effect of homogenizing the phase of the population both when it is solitarious and when it is gregarious.
Population Density.
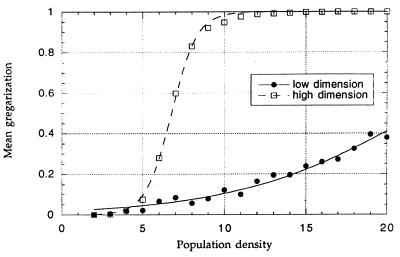
Of key importance in swarm formation is the interaction between the distribution of resources and changes in the size of the locust population in a given area. In the wild, gregarization is usually associated with a local increase in population size through breeding and concentration (13). The experiment shows that gregarization is greater at the higher density of locusts. The model indicates that in a locally scattered habitat (low fractal dimension), gregarization increases only gradually with population size, whereas in locally concentrated habitats (high fractal dimension), gregarization occurs suddenly when the mean amount of contact exceeds the threshold required for gregarization (Fig. 3).
Figure 3.
Mean gregarization as a function of locust density. Simulations were run with 20 patches equally spaced on the grid in a rectangle, maximally (fractal dimension = 0.0) and minimally (fractal dimension = 1.28) spaced. Parameters were the same as in Fig. 1b (i.e., including phase-related behavioral changes). Each point represents the mean of a single simulation run.
DISCUSSION
Earlier field (14, 15) and laboratory (10) reports have indicated that environmental structure influences phase change in locusts. Our experimental results show that for a particular habitat, a larger population will become more gregarized. They also show that a smaller population in a clumped habitat may be more gregarized than a larger population in a scattered habitat. Our model predicts that the increase in population density required for a population to change from solitarious to gregarious is much smaller in a habitat where resource is locally concentrated. The rapid increase in contact rate accompanied by the behavioral positive feedback and the more homogeneous distribution of contact means that population behavior can change rapidly with a small increase in population size. We suggest that swarm formation should be more common and occur more suddenly in habitats where the resource is highly concentrated at smaller spatial scales.
Knowing where gregarization is likely to take place is important for control strategies. Once swarms of adults have formed, their movement and survival depend on wind systems and the availability of food. Control at this point is difficult. Instead, a major aim of desert locust management is to target nascent swarms, before or during the several consecutive generations of crowding necessary for the full phase transition. Existing attempts to predict the emergence of swarms based on time-series analyses of outbreaks have been largely unsuccessful (16–18). Ecologically based forecasting models for S. gregaria and other locust species show more promise (19–26). These models have been based on the properties of populations not individuals. Gregarization is known to depend on the type of vegetation cover (24). Our experiments and simulations show how vegetation architecture and distribution at the smallest spatial scales (i.e., ranges of centimeters to meters, corresponding to locust behavior over minutes and hours), as well as locust densities, can influence gregarization. The differences in distribution we examined are not detectable at the larger scales which provide the focus of many monitoring strategies. To improve control programs, local data, including the fractal dimension of resource or a related measure, should be collected and incorporated into existing models and monitoring programs.
Acknowledgments
This work was supported by grants from the Biotechnology and Biological Sciences Research Council (to M.C. and S.J.S.), Fonds pour la Formation des Chercheurs et l’Aide à la Recherche from the government of Quebec (to E.D.), the United Nations Development Fund (to S.J.S.), and the Wellcome Trust (to D.C.K.).
ABBREVIATIONS
- A
contact-saturation level
- B
rate of increase of movement with gregarization
- c
cumulative contact experienced
- d
distance
- g
behavioral-phase state
- P
probability of going to a resource patch
- Q1
probability of leaving a resource patch
- Q2
phase-dependent probability of leaving a resource patch
- r
length of grid square
- R
maximum distance moved in an iteration
- t
time
References
- 1. Uvarov G B. Grasshoppers and Locusts. Cambridge, U.K.: Cambridge Univ. Press; 1966. [Google Scholar]
- 2.Pener M P. Adv Insect Physiol. 1991;23:1–79. [Google Scholar]
- 3.Pener M P, Yerushalmi Y. J Insect Physiol. 1998;44:365–377. doi: 10.1016/s0022-1910(97)00169-8. [DOI] [PubMed] [Google Scholar]
- 4.Roessingh P, Simpson S J, James S. Proc R Soc London Ser B. 1993;252:43–49. [Google Scholar]
- 5.Roessingh P, Simpson S J. Physiol Entomol. 1994;19:191–197. [Google Scholar]
- 6.Islam M S, Roessingh P, Simpson S J, McCaffery A R. J Insect Physiol. 1994;40:173–181. [Google Scholar]
- 7.Islam M S, Roessingh P, Simpson S J, McCaffery A R. Proc R Soc London Ser B. 1994;257:93–98. [Google Scholar]
- 8.Bouaichi A, Roessingh P, Simpson S J. Physiol Entomol. 1995;20:199–208. [Google Scholar]
- 9.Saupe D. In: The Science of Fractal Images. Peitgen H-O, Saupe D, editors. New York: Springer; 1988. pp. 71–136. [Google Scholar]
- 10.Bouaichi A, Simpson S J, Roessingh P. Phys Entomol. 1996;21:247–256. [Google Scholar]
- 11.Heifetz Y, Voet H, Applebaum S W. J Chem Ecol. 1996;22:1717–1734. doi: 10.1007/BF02272410. [DOI] [PubMed] [Google Scholar]
- 12.Roessingh P, Bouaichi A, Simpson S J. J Insect Physiol. 1998;44:883–893. doi: 10.1016/s0022-1910(98)00070-5. [DOI] [PubMed] [Google Scholar]
- 13.Skaf R, Popov G B, Roffey J. Philos Trans R Soc London B. 1990;328:525–538. [Google Scholar]
- 14.Kennedy J S. Trans R Entomol Soc London. 1939;89:385–542. [Google Scholar]
- 15.Roffey J, Popov G B. Nature (London) 1968;219:446–450. [Google Scholar]
- 16.Cheke R A, Holt J. Ecol Entomol. 1993;18:109–115. [Google Scholar]
- 17.Holt J, Cheke R A. Ecol Modell. 1996;91:131–137. [Google Scholar]
- 18.Sugihara G. Nature (London) 1995;378:559–560. [Google Scholar]
- 19.Blackith R E, Albrecht F O. Acrida. 1979;8:83–94. [Google Scholar]
- 20.Farrow R A, Longstaff B C. Oikos. 1986;46:207–222. [Google Scholar]
- 21.Wright D E. Aust J Ecol. 1987;12:423–437. [Google Scholar]
- 22.Joern A, Gaines S B. In: Biology of Grasshoppers. Chapman R F, Joern A, editors. New York: Wiley; 1990. pp. 415–482. [Google Scholar]
- 23.Roffey J. Desert Locust Population Dynamics: A Preliminary Approach to a Simulation Model. Rome: Food and Agriculture Organization; 1990. [Google Scholar]
- 24.Launois M, Duranton J-F, Launois-Luong M H, Lecoq M, Popov G B, Gaye P-E, Gigault J, Balanca G, Coste C, Foucart A. Présentation Resumée du Biomodèle SGR. Paris: Ministère de la coopération et du développement; 1992. [Google Scholar]
- 25.El-Bashir S, Inayatullah C, Ahmed A O, Abdelrahman H E. Int J Pest Manage. 1993;39:467–470. [Google Scholar]
- 26.Nailand P, Hanrahan S A. S Afr J Sci. 1993;89:420–424. [Google Scholar]