Termites live in a material world: exploration of their ability to differentiate between food sources

Abstract

Drywood termites are able to assess wood size using vibratory signals, although the exact mechanism behind this assessment ability is not known. Important vibratory characteristics such as the modal frequencies of a wooden block depend on its geometry and boundary conditions; however, they are also dependent on the material characteristics of the block, such as mass, density and internal damping. We report here on choice experiments that tested the ability of the drywood termite Cryptotermes secundus to assess wooden block size using a solid wooden block paired with a composite block, the latter made of either wood and aluminium or wood and rubber. Each composite block was constructed to match mass or low-frequency vibratory modes (i.e. fundamental frequency) of the solid wooden block. The termites always chose the blocks with more wood; they moved to the solid wooden blocks usually within a day and then tunnelled further into the solid wooden block by the end of the experiment. Termites offered composite blocks of wood and rubber matched for mass were the slowest to show a preference for the solid wooden block and this preference was the least definitive of any treatment, which indicated that mass and/or damping may play a role in food assessment. This result clearly shows that the termites were not fooled by composite blocks matched for mass or frequency, which implies that they probably employ more than a single simple measure in their food assessment strategy. This implies a degree of sophistication in their ability to assess their environment hitherto unknown. The potential importance of alternative features in the vibrational signals is discussed.

1. Introduction

Small, herbivorous insects are known to use substrate-borne vibration signals in gathering information about their environment and in communication with members of their own species. For example, caterpillars can detect conspecific competitors and predators (Yack et al. 2001; Castellanos & Barbosa 2006; Fletcher et al. 2006), and sap-sucking bugs communicate alarm and attraction with vibratory signals (Cocroft 1996, 2001, 2005; see Čokl & Virant-Doberlet 2003; Virant-Doberlet & Čokl 2004; Cocroft & Rodríguez 2005 for reviews). Substrate-borne vibration signals are well suited for such purposes in small insects owing to biophysical constraints such as the size of the insect and its receptor organs and the environment in which they live (e.g. Michelson & Nocke 1974; Michelson 1978; Bennet-Clark 1998; Stumpner & von Helversen 2001; Cocroft & De Luca 2006).

Termites, being small, herbivorous and social insects, are known to employ vibrational signals. Alarm signals, for example, are well reported (Howse 1964b, 1965; Stuart 1969; Kirchner et al. 1994; Connétable et al. 1999; Röhrig et al. 1999). Recently, it was discovered that drywood termites in the genus Cryptotermes use vibrations to assess wood food volume (Evans et al. 2005) with the suggestion that the frequency response of the wood (i.e. from the elastic by-product of feeding on the block) might be used by the termites as the assessment method. However, this conjecture remains to be explicitly proved. How termites use these signals is not entirely clear and other factors such as wood block mass may also be important.

The vibratory characteristics of any structure are strongly dependent on its material properties (Thomson 1981). Two important material properties that influence structural vibration are the velocity of longitudinal vibrations (speed of sound) and the amount of internal loss (damping) in the material. Wood, the food of drywood termites, displays highly variable material properties (Green et al. 1999) and, for example, may be found as part of a live tree or as a dead log on the ground and is often located in a variety of environments and/or embedded in soil—all these factors might alter the effective vibratory properties and increase the range of material properties the termites encounter. Termites forage in all of these diverse situations so that their ability to assess wood as a food source ought to have evolved to cope with these complexities. The decision to eat a particular piece of wood could be informed by the vibrational signals they receive, which in turn depend on the material properties of the food source.

If Cryptotermes termites do use the frequency response of the wood as the primary assessment method, then perhaps they can be fooled by altering the material properties of a wooden block so as to manipulate the frequency response. It is possible to construct a composite block that presents a wooden surface to termites with a different material behind, thus altering the vibratory response and other characteristics of the composite structure, compared to a block of pure wood. The different materials could include one with low damping and high speed of sound and another with high damping and low speed of sound, relative to wood, and thereby identify which (if any) of these factors are employed by the termites.

Here, we aim to measure the relative importance of the lowest frequency vibratory feature, and mass, by comparing the foraging decision of Cryptotermes secundus when offered paired food choices: one being a block of wood of standard size and the other a composite block with a material composition so that one of these characteristics is altered. As all composite blocks in this study have a discontinuity at the boundary of the wood and the alternate material, we have also compared the effect of a discontinuity in wood (it is plausible that termites have evolved a mechanism to account for discontinuities, which commonly occur in nature in the form of grain irregularities such as knots, cracks or pitch pockets). The source of vibrations is produced by the termites themselves. We aim to elucidate how termites determine wood size and investigate how they use vibrations in information gathering and sensing.

2. Methods

2.1 Materials

Three different materials with differing properties were used. The first material was the wooden food of the termites. The wood used was seasoned Pinus radiata of 20 mm×20 mm cross-section. The wood had an equilibrium moisture content of approximately 12% under the measurement conditions (25°C and 65% RH). The second material was aluminium, and it was chosen because it has a lower damping and higher speed of sound than wood (table 1). The speed of sound was measured in a 2016 mm long sample of the aluminium beam material using resonance techniques (Schlägel 1957). An impact hammer (Brüel & Kjær 8202, S/N:1271062, Nærum, Denmark) was used to excite one end and an accelerometer (Brüel & Kjær 4371, S/N:677677) was used to detect the resulting acceleration at the opposite end. Both the signals from the force transducer in the impact hammer and from the accelerometer were amplified using charge amplifiers (Brüel & Kjær 2635). The frequency response in the frequency range 0–10 kHz was obtained from 16 averages of the power spectrum on a portable FFT analyser (Ono Sokki CF-350, Yokohama, Japan) using a frequency resolution of 25 Hz and a Hanning window with maximum overlap. This method excited the longitudinal modes of the beam, thus the speed of sound was obtained from the frequency of the fundamental mode f₁ by c=2f₁L, for a beam of length L. Here, f₁ was measured, from the frequency response spectrum, as 1237±13 Hz.

Table 1.

Properties of materials. The speed of sound in the longitudinal direction c and the mass density ρ were measured. Nominal values of the damping factor d (equal to tan δ for a loss angle of δ) were obtained from Green et al. (1999), Rosenhain 2003 and Ehsani et al. (2004). All measurements were taken at approximately 25°C. As with most timber species, P. radiata shows great variation in material properties (Green et al. 1999).

material	speed of sound c (m s−1)	density ρ (kg m−3)	damping factor d
aluminium	5040±103	2700±28	10−4
Pinus radiata	4930±100	420±30	10−2
EPDM rubber	45±1	504	10−1

The third material was ethylene propylene diene monomer (EPDM) rubber, and it was chosen because it has a higher damping and lower speed of sound than wood (table 1). This synthetic rubber is used in vibration absorption applications (Ehsani et al. 2004). Both materials were cut to a similar cross-section as the wood (aluminium: 20 mm×20 mm square bar, Capral Aluminium; EPDM rubber: 22.5 mm×22.5 mm square extrusion, Clarke Rubber). The beam resonance method is not appropriate for the rubber because it is too heavily damped. However, it is extremely compliant, enabling measurement of the Young modulus by direct application of a load and measuring the resulting extension. Upon measurement of the density, the speed of sound may be calculated from the relation $c=\sqrt{E/\rho }$.

The speed of sound in wood, and possibly the rubber, may be considered to be orthotropic (i.e. dependent on direction with respect to three perpendicular axes). All speed of sound values considered here are in the longitudinal direction (i.e. along the axis of the blocks) only because the beam dimensions orthogonal to the axis are relatively small compared with the length. Nominal estimates of the damping for each material are given in table 1 (Green et al. 1999; Rosenhain 2003; Ehsani et al. 2004).

2.2 Treatments

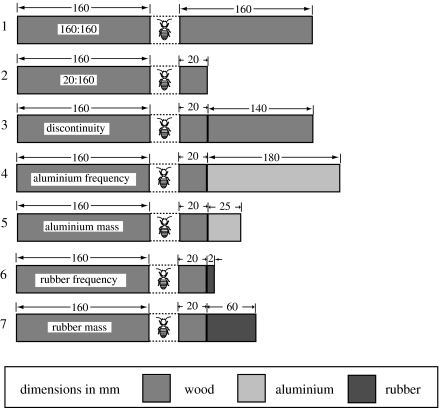
All treatments were designed and made to relate to the standard wooden block of P. radiata, measuring 160 mm×20 mm×20 mm. Treatments 1–3 were controls and treatments 4–7 were composite blocks. Composite block treatments were designed to match the standard wooden blocks of P. radiata in the hypothesized assessment quantities, although each had a 20 mm×20 mm×20 mm block of P. radiata (‘stub’) attached to one end, to present a matched surface. There were 12 replicates in each treatment.

Treatment 1 consisted of pairs of standard 160 mm blocks of wood. This was a control for direction if some external factors have influenced the direction in which the termites chose to tunnel. Treatment 2 was a 20 mm long block of wood, which was a preference control, to confirm that C. secundus did prefer larger food. Treatment 3 was a 160 mm block of wood cut into two blocks (20+140 mm long), which served as a discontinuity control, as all composite blocks in treatments 4–7 had a discontinuity between the wood and the alternative material where the two materials were joined. This treatment tested the effect of a discontinuity in wood and was otherwise identical to the joins in other treatments. Joins comprised two flat faces glued with a hard-setting aliphatic resin (Titebond-II Premium, Franklin International). A small amount of glue was applied to the surface (in the plane perpendicular to the grain) of the stub and the other material, which were then pressed together and clamped for 24 h.

Treatments 4 and 5 were composite blocks of a 20 mm wooden block with aluminium cut to match the standard 160 mm wooden block in frequency (treatment 4) and mass (treatment 5). Treatments 6 and 7 were composite blocks of a 20 mm wooden block and rubber cut to match the standard 160 mm wooden block in frequency (treatment 6) and mass (treatment 7). Details of the size of each component of the composite blocks are listed in figure 1 and calculated in appendix A.

Figure 1.

Schematic setup for bioassays testing the choice of termites between a standard 160 mm×20 mm×20 mm block of wood and another test block. Treatments 4–7 were designed to match the fundamental frequency and the mass of the paired 160 mm×20 mm×20 mm block as indicated. Each central cell contained 15 worker termites. There were 12 replicates for each treatment.

2.3 Vibratory response of treatments

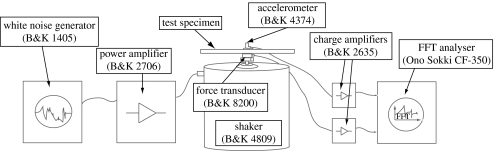
Measurements of the driving point accelerance functions (i.e. ratio of measured acceleration to applied force) of all test blocks were conducted. A white-noise generator (Brüel & Kjær 1405, frequency range 0–20 kHz) was used to drive a shaker (Brüel & Kjær 4809) via a power amplifier (Brüel & Kjær 2706) and a force transducer (Brüel & Kjær 8200, S/N:1321629) was axially mounted to the shaker by a grub screw, which was connected to the block at a point directly below its centre of mass. An accelerometer (Brüel & Kjær 4374, S/N:12939) was mounted above the centre of mass with beeswax. The force and acceleration signals were each amplified with Brüel & Kjær 2635 charge amplifiers and captured to obtain the accelerance power spectrum using a portable FFT analyser (Ono Sokki CF-350), from 128 averages with a Hanning window and maximum overlap, and a frequency resolution of 12.5 Hz (figure 2).

Figure 2.

Experimental setup to determine accelerance transfer functions of composite and wooden beams.

2.4 Bioassays

A preliminary bioassay was performed to evaluate whether the adhesive used in the composite blocks affected the behaviour of C. secundus. This used paired 20 mm×20 mm×20 mm P. radiata wooden blocks. The adhesive was applied, as for the composite blocks, on the face of one block not exposed to the termites. Ten replicates were run, with 15 termite workers per replicate.

The test bioassays were choice experiments in which the termites were offered a choice of a standard 160 mm P. radiata wooden block and one of the other treatments. The wood in each pair was cut consecutively along the grain so that the surfaces of the wood were as identical as possible. The standard block and the test blocks were separated by 15 mm with the near-identical wooden surfaces facing each other, and then joined using aluminium foil and cellulose tape, on three sides so as to create a central space that could house the termites. A clear square of plastic was used on the top side, providing a window to observe the termites (figure 1).

Fifteen C. secundus workers, from the same colony, were used in each replicate. A minimum of five different colonies were used for each treatment. The experiments were conducted in a controlled temperature of approximately 28°C and relative humidity of 80%. The experiments were conducted in the dark (except for a brief period every day for the first 5 days where the position of the 15 workers in each replicate was observed) for 14 days (the minimum length of time required by 15 individuals of C. secundus to tunnel 20 mm), after which the termites were removed and the number and lengths of tunnels were recorded. Data were compared using a one-way ANOVA (between colonies) and paired t-tests (preferences for blocks in paired treatments).

3. Results

3.1 Frequency response functions of test blocks

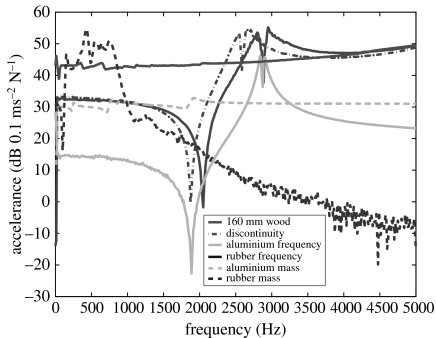
The fundamental frequency of the transverse (i.e. bending) mode under free–free conditions (i.e. no imposed mechanical constraints) for treatment 1 (the standard 160 mm P. radiata wooden blocks) was (mean±s.e.) 3350±108 Hz (n=9) and that for treatment 3 (the 20+140 mm discontinuity control block) was very similar to that of the standard 160 mm block, i.e. 3325±100 Hz (n=3). The fundamental frequencies of treatments 4 and 5, composite blocks with aluminium, were: for treatment 4 (aluminium matched for frequency) 3179±40 Hz (n=3) and for treatment 5 (aluminium matched for mass) 3325±50 Hz (n=3), while the fundamental frequencies of treatment 7 (composite blocks with rubber matched for mass) were 142±4 Hz (n=3). Since the damping is so great for this treatment, the spectral features are very broad and the magnitude of the response decreases with increasing frequency.

In contrast, since the speed of sound in the rubber is so much lower than that for wood, the layer of rubber added to the 20 mm wooden stub in treatment 6 (rubber matched for frequency) was approximately 2 mm, the thinnest layer able to be reliably cut from the rubber material. Consequently, the rubber frequency blocks did not behave as the longer blocks did, being almost cubic in shape, and there were no corresponding simple bending modes. This was also the case for the 20 mm blocks in treatment 2 (size preference control) and for treatment 5 (aluminium matched for mass). Examples of typical driving point accelerance functions for all wooden and test blocks are given in figure 3.

Figure 3.

Accelerance (acceleration/force) response function of test blocks used in bioassay treatments 1 and 3–7.

3.2 Bioassays

There was no effect of the adhesive on the preference of C. secundus, as no significant difference in tunnelling was observed on the paired 20 mm×20 mm×20 mm P. radiata wooden blocks in the number of tunnels (with adhesive 1.2±0.13, without adhesive 1.4±0.16; t₄=−1.630, p=0.178) as well as in the length of tunnels (with adhesive 5.15±1.20, without adhesive 5.35±0.92; t₄=−1.472, p=0.215). Therefore, any observed effects in the test blocks are unlikely to be due to the adhesive.

The amount of tunnelling in blocks by termites from different colonies was highly variable; some replicates had no measurable tunnels at the end of the experiment (which were excluded from the analysis), whereas others had tunnels up to 20 mm in length. The total tunnelling of both blocks in each pair was compared between colonies and a significant difference between colonies was found for the total number of tunnels (F_12,94=4.423, p<0.001) and for the total length of tunnels (F_12,94=9.902, p<0.001). Consequently, tunnelling data were transformed into proportion of tunnelling in the 160 mm standard wooden block for each pair. The raw tunnelling data are presented in appendix B.

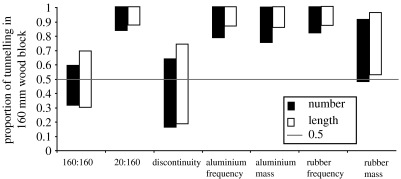
There was no significant difference observed in the tunnelling between paired blocks in treatment 1 (paired 160 mm standard wooden blocks), according to the limits of the 95% confidence intervals of the proportion from each treatment (figure 4). The proportional number of tunnels in the 160 mm standard block in treatment 1 was (mean±s.e. (n)) 0.455±0.071 (11) and the proportional length of tunnels was 0.497±0.100 (11). This is also the case for the discontinuity control (standard 160 mm wooden blocks compared with 20+140 mm wooden blocks with a discontinuity, treatment 3; number of tunnels: t₁₂=1.12, p=0.286; length of tunnels: t₁₂=0.451, p=0.661). This result is important because each composite block had a similar discontinuity in mechanical impedance. If there were a significant preference for either block, interpretation of results of bioassays involving the composite blocks would be ambiguous.

Figure 4.

Proportion of tunnelling in standard 160 mm long wooden block compared to that of the test blocks, in terms of number of tunnels and total length of tunnels made. The columns represent the 95% confidence intervals.

There was a significant preference for the standard 160 mm wooden block over the 20 mm block; proportional number was 0.931±0.048 (12) and proportional length was 0.956±0.039 (12) (figure 4), respectively.

For aluminium frequency (treatment 4), the mean proportion of number of tunnels in the standard 160 mm block was 0.909±0.061 (11) and the proportional tunnel length was 0.946±0.037 (11), while for aluminium mass (treatment 5), the mean proportion of tunnel numbers was 0.879±0.064 (11) and the proportional tunnel length was 0.942±0.041 (11).

For rubber frequency (treatment 6), the mean proportion of tunnel numbers in the standard 160 mm block was 0.924±0.052 (11) and the proportional tunnel length was 0.955±0.041 (11), while for rubber mass (treatment 7), the proportional tunnel number and tunnel length in the standard 160 mm block were 0.613±0.106 (12) and 0.610±0.118 (12), respectively.

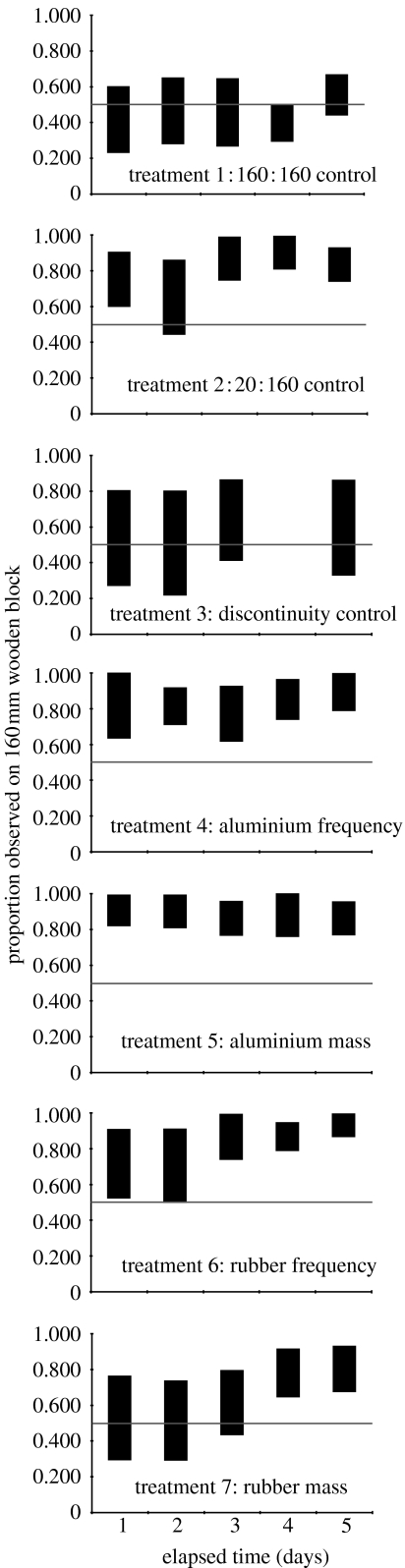
In terms of significance, the proportion of termites observed on either block within each pair agrees with the tunnelling data (figure 5).

Figure 5.

Recorded positions of termites, as a ratio of termites on the standard 160 mm long wooden block compared to its pair in each treatment, during the first 5 days of the experiment. After 5 days, it becomes difficult to observe all the termites because many are inside the wood. The limits of the bars represent the 95% confidence interval.

4. Discussion

The results of the bioassays show clearly that C. secundus prefers larger wooden blocks as food. Although this appears to contradict the results of Evans et al. (2005), the test species in that paper, Cryptotermes domesticus, being a highly invasive pest species, are under different biological constraints compared to the non-invasive C. secundus. Here, the termites showed no preference for solid wooden blocks over those of equal size with a discontinuity, which suggests that they were capable of incorporating the discontinuity into their detection method. The termites preferred standard 160 mm wooden blocks over composite blocks made from wood/aluminium matched for frequency and mass and from wood/rubber matched for frequency and mass. From the observations of their positions (figure 5), it is clear that the termites made their foraging decision fairly rapidly, without having made significant tunnels in the blocks.

It is not clear which material property metrics the termites use to determine their foraging preferences (table 2). The evidence is equivocal for the fundamental frequency. The composite wood/aluminium blocks provided data that were difficult to interpret. The composite wood/aluminium block matched for frequency (treatment 4) was a close match to the 20+140 mm wooden discontinuity block (treatment 3) (figure 3) and thus we might expect the bioassay results for this composite block to match the discontinuity block. However, the termites preferred the 160 mm standard block (figure 4), which suggests that termites use more information than the fundamental frequency for detecting food volume. The termites preferred the standard 160 mm wooden block over the composite wood/aluminium block matched for mass (treatment 5), perhaps because the accelerance response function of the latter was relatively flat and featureless, compared with that of the former, at frequencies that termites are most receptive, viz. low- to mid-kilohertz frequencies (Howse 1964a).

Table 2.

Comparison of material properties relative to the 160 mm standard wooden block and termite tunnelling preferences.

treatment		material property (relative to 160 mm standard wooden block)		preference
nos.	description	frequency	mass
1	160 mm wood (direction control)	same	same	none
2	20 mm wood (preference control)	higher	lower	160
3	20+140 mm wood (discontinuity control)	same	same	none
4	aluminium (match for frequency)	same	higher	160
5	aluminium (match for mass)	flat	same	160
6	rubber (match for frequency)	flat	lower	160
7	rubber (match for mass)	lower	same	160

The composite wood/rubber blocks provided data that were even more difficult to interpret. The composite wood/rubber block matched for frequency (treatment 6) had few features, as seen for treatment 5, and similar preference for the 160 mm standard wooden block (figure 4), which supports the suggestion that the termites may not have been able to distinguish useful measures for this treatment. The termites preferred the standard 160 mm wooden block over the composite wood/rubber block matched for mass (treatment 7), even though the fundamental frequency of the composite block was low. Perhaps because the fundamental frequency was so low (200 Hz), it was either of no interest or could not be detected by the termites.

The mechanism by which termites would perceive mass could be due to the elastic response of the beam in response to feeding (Matsuoka et al. 1996) via detection of the magnitude of the resulting acceleration or displacement through vibroreceptors on the body of the insect (Howse 1964a).

Clearly, the mechanism used by termites to assess wood size is still unknown and requires further investigation. It is difficult to reproduce the small vibratory signals produced by termites. The accelerance response functions (figure 3) were driven and detected over a larger area, and excited with a large amount of energy, relative to that of a termite. There are a range of alternative assessment mechanisms. For example, termites may be sensitive to the attenuation or other changes in the vibratory signals due to the difference in internal losses in both of the materials compared to that of wood. In the case of composite blocks, it is possible that the termites are sensitive to the difference in mechanical impedance at the boundary between the materials. Based on the bulk characteristic impedance of the materials, Z_i=ρ_ic_i, the reflection coefficient can be estimated as

$$R=\frac{Z_2-Z_1}{Z_2+Z_1},$$ (4.1)

where Z₁ is the characteristic impedance of the wood and Z₂ is the characteristic impedance of the other material. Hence, for the boundary at a wood–wood junction, Z₂=Z₁, thus R=0 and there is very little reflection. Based on the values in table 1, R=0.735 for the boundary between aluminium and wood and R=−0.978 for the boundary between rubber and wood; the negative value indicates that there is a phase difference upon reflection of almost 180°. These R values indicate that vibratory signals would not be reflected from wood–wood boundaries, but would be readily reflected from wood–aluminium and wood–rubber boundaries, with a phase shift for the latter.

Although these experiments were conducted on C. secundus only, the vibration sense of other termites is well established (Howse 1964a), and, under similar biological constraints, similar behaviour might also be expected for many other termite species.

The ability of insects or other animals to use substrate signals has been investigated mostly in terms that could loosely be called communication, in the sense that it involved animal-to-animal signalling, such as in caterpillars detecting competitors and predators (Yack et al. 2001; Castellanos & Barbosa 2006; Fletcher et al. 2006), or group-living bugs communicating alarm and attraction to their group members (Cocroft 1996, 2001, 2005), or leaf-cutting ants in attracting their nestmates (Roces et al. 1993). Very little research has been carried out on how insects gain information about their plant food using vibrational signals (see Čokl & Virant-Doberlet 2003; Virant-Doberlet & Čokl 2004; Cocroft & Rodríguez 2005 for reviews). The results of this study suggest that the mechanism used by termites is sophisticated, in the sense that they may use more than simple cues such as the fundamental frequency, or mass, of a food structure, although these may be part of the mechanism. Future studies on termites, and indeed other arthropods, should focus on determining such mechanisms to better elucidate sensory systems and their evolutionary pathways.

Appendix A. Calculation of beam properties

The composite beams in this paper were designed to emulate two vibratory properties of the standard 160 mm×20 mm×20 mm Pinus radiata wooden block: frequency and mass, using two different materials, aluminium and ethylene propylene diene monomer rubber.

A.1 Same frequency

For most materials, the most readily excited type of vibration in a slender (i.e. (L/t)>18 for length L and height t; S˘tubun˘a & Marek 2001), isotropic beam of constant cross-section are transverse waves (Strutt 1869). The frequency f_i of the ith transverse mode in a slender beam with radius of gyration κ and speed of sound in the material c is

$$f_i=s_{i}c\frac{\kappa }{L^2}=\frac{s_{i}ct}{\sqrt{12}{L}^2},$$ (A1)

where s_i are pure numbers dependent on the boundary conditions of the beam, which are essentially free in this study. For a beam of square cross-section, $\kappa =t/\sqrt{12}$. The blocks used in this study were not strictly slender beams, as L/t ranges from 1.1 to 10.0. Therefore, a small correction was required to calculate the expected frequency (S˘tubun˘a & Marek 2001). A correction for shear effects (Hearmon 1958) was also required owing to the low shear modulus of wood (roughly 100 MPa for G_RT and 1 GPa for G_LT and G_LR; estimated from values in other species of pine given by Green et al. (1999)).

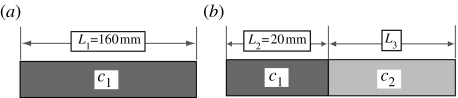
Thus, for low-frequency transverse modes, the frequency may be calculated from the time-of-flight for a longitudinal vibration propagating along the axis of the beam, obtaining an effective speed of sound. The aim was to equal the time-of-flight in a 160 mm long block of wood. If the longitudinal speed of sound in P. radiata and the other material is c₁ and c_2, respectively, and the length of the 160 mm wooden block and 20 mm wooden block is L₁ and L₂, respectively (figure 6), then the length of the other material should be

$$L_3=\frac{c_2(L_1-L_2)}{c_1}.$$ (A2)

Figure 6.

Simple low-frequency calculation of time-of-flight of longitudinal vibrations for (a) standard wooden block and (b) composite block.

Note that this treatment also equalizes the lower-frequency longitudinal modes.

A.2 Same mass

The mass densities of the aluminium and rubber were higher than that for P. radiata wood; furthermore, the cross-sectional area of the beams of these materials was slightly different from that of the wooden beams. Hence, for a composite beam to have the same mass as the standard 160 mm×20 mm×20 mm wooden block, the length of the other material (in millimetre) must be

$$L_3=\frac{{\rho }_1(140\times 20\times 20)}{{\rho }_2{t}^2},$$ (A3)

where ρ₁ and ρ₂ are the mass densities of wood and the other material, respectively, and t is the thickness of the other material.

Appendix B. Raw data from bioassays

The preference measures used in this study were based on the relative amount of tunnelling in each of paired blocks in a bioassay, one of the block being a standard 160 mm×20 mm×20 mm wooden (P. radiata) block. The measured numbers of tunnels and total lengths of tunnels are given in table 3.

Table 3.

Raw tunnel number data from bioassays involving termites feeding on test blocks paired with standard 160 mm long wooden blocks. Replicates were omitted if there were no measurable tunnels in either block.

	160 : 160 control				20 : 160 control
	number		length (mm)		number		length (mm)
block	160 mm	test	160 mm	test	161 mm	test	161 mm	test
1	0	1	0.0	8.0	1	0	6.0	0.0
2	1	1	1.5	5.0	1	0	3.0	0.0
3	1	1	1.5	2.5	1	0	10.0	0.0
4	—	—	—	—	1	0	10.0	0.0
5	1	2	3.0	7.0	2	1	15.5	1.0
6	1	2	0.5	8.5	2	0	10.0	0.0
7	1	1	10.0	3.0	2	0	14.5	0.0
8	1	2	1.5	1.0	2	0	5.0	0.0
9	2	0	2.5	0.0	1	0	10.5	0.0
10	1	1	4.5	3.0	2	2	7.5	6.5
11	1	1	5.5	0.5	1	0	4.0	0.0
12	1	1	4.0	2.5	1	0	0.5	0.0
mean	1.000	1.182	3.136	3.727	1.417	0.250	8.042	0.625
s.e.	0.135	0.182	0.856	0.900	0.149	0.179	1.312	0.540

	discontinuity control				aluminium frequency
	number		length (mm)		number		length (mm)
block	160 mm	test	160 mm	test	160 mm	test	160 mm	test
1	0	1	7.0	0.0	2	0	3.5	0.0
2	0	1	7.0	0.0	—	—	—	—
3	2	2	21.5	1.0	1	0	5.0	0.0
4	2	1	16.5	7.5	1	0	0.5	0.0
5	2	1	0.5	20.5	1	0	11.5	0.0
6	1	2	22.0	1.5	1	1	5.0	1.5
7	2	0	0.0	17.0	2	0	6.0	0.0
8	1	0	0.0	9.0	1	1	7.0	4.0
9	6	0	0.0	9.0	2	0	2.0	0.0
10	1	0	0.0	8.0	1	0	13.0	0.0
11	1	0	0.0	2.0	2	0	7.0	0.0
12	0	2	24.5	0.0	1	0	17.0	0.0
mean	1.500	0.833	8.250	6.292	1.364	0.182	7.045	0.500
s.e.	0.469	0.241	2.887	1.992	0.152	0.122	1.492	0.375

	aluminium mass				rubber frequency
	number		length (mm)		number		length (mm)
block	160 mm	test	160 mm	test	160 mm	test	160 mm	test
1	2	0	2.5	0.0	—	—	—	—
2	2	0	1.5	0.0	1	0	2.0	0.0
3	1	0	6.5	0.0	2	0	2.5	0.0
4	—	—	—	—	1	0	6.0	0.0
5	1	0	8.0	0.0	1	1	6.5	5.5
6	2	0	11.5	0.0	1	0	8.5	0.0
7	1	0	3.0	0.0	1	0	5.0	0.0
8	2	0	12.5	0.0	1	0	5.0	0.0
9	3	0	18.0	0.0	4	0	5.0	0.0
10	1	1	2.0	1.5	1	0	11.5	0.0
11	1	1	17.0	0.2	2	0	13.5	0.0
12	2	1	14.5	3.5	2	1	15.0	0.5
mean	1.636	0.273	8.818	0.473	1.545	0.182	7.318	0.545
s.e.	0.203	0.141	1.869	0.331	0.282	0.122	1.301	0.498

block	rubber mass
	number		length (mm)
	160 mm	test	160 mm	test
1	—	—	—	—
2	1	1	3.5	1.0
3	—	—	—	—
4	1	0	2.0	0.0
5	1	0	17.5	0.0
6	1	1	6.0	10.0
7	0	1	0.0	16.5
8	1	0	12.5	0.0
9	2	0	11.5	0.0
10	1	0	3.0	0.0
11	1	1	16.5	2.5
12	1	1	8.0	10.0
mean	1.000	0.500	8.050	4.000
s.e.	0.149	0.167	1.956	1.884