Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2007 Apr 3;4(15):755–762. doi: 10.1098/rsif.2007.0228

Transmissibility of swine flu at Fort Dix, 1976

Justin Lessler 1,*, Derek AT Cummings 2,3, Steven Fishman 4, Amit Vora 5, Donald S Burke 4,†
PMCID: PMC2373398  PMID: 17412677

Abstarct

The 1976 outbreak of A/New Jersey/76 influenza in Fort Dix is a rare example of an influenza virus with documented human to human transmission that failed to spread widely. Despite extensive epidemiological investigation, no attempt has been made to quantify the transmissibility of this virus. The World Health Organization and the United States Government view containment of emerging influenza strains as central to combating pandemic influenza. Computational models predict that it may be possible to contain an emergent pandemic influenza if virus transmissibility is low. The A/New Jersey/76 outbreak at the United States Army Training Center at Fort Dix, New Jersey in January 1976 caused 13 hospitalizations, 1 death and an estimated 230 cases. To characterize viral transmission in this epidemic, we estimated the basic reproductive number and serial interval using deterministic epidemic models and stochastic simulations. We estimated the basic reproductive number for this outbreak to be 1.2 (supported interval 1.1–1.4), the serial interval to be 1.9 days (supported interval 1.6–3.8 days), and that the virus had at least six serial human to human transmissions. This places the transmissibility of A/New Jersey/76 virus at the lower end of circulating flu strains, well below the threshold for control.

Keywords: influenza; infectious diseases, emerging; basic reproductive number; disease transmission; stochastic processes

1. Introduction

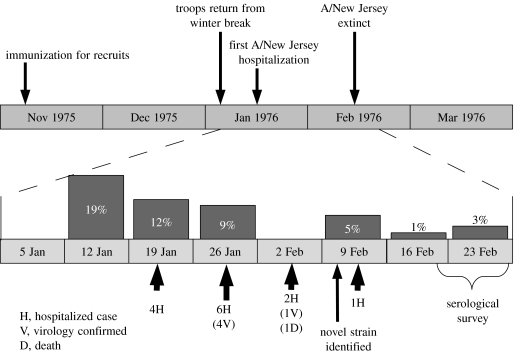
On 4 February 1976, a soldier died at Fort Dix army base from acute respiratory disease (Gaydos et al. 1977a,b, 2006). Analysis of tracheal swabs from this soldier showed that he was infected with a novel H1N1 influenza similar to those circulating in swine. The new virus, dubbed A/New Jersey/76, was of concern since H1N1 strains of influenza had not circulated in the human population since the 1957–1958 pandemic. Since Fort Dix was an infantry training facility, the population was younger and nearly all inhabitants were immunologically naive to any H1N1 influenza strain (Hodder et al. 1977). Subsequent investigations revealed that A/New Jersey/76 had circulated widely in the trainees at Fort Dix between 5 January and 14 February, by which time the virus had apparently gone extinct. Over the course of the epidemic, A/New Jersey/76 caused 1 death, 13 hospitalizations and 230 total cases. The timeline of these investigations and the epidemic they discovered are shown in figure 1. Tables 1 and 2 show hospitalized cases and unit attack rates. Full details of the Fort Dix outbreak and the subsequent investigation are available in the reports of the original investigators and recent summaries (Hodder et al. 1977; Top & Russell 1977; Gaydos et al. 1977a,b; Gaydos et al. 2006).

Figure 1.

Figure 1

Open in a new tab

Key events during the outbreak and investigation of A/New Jersey/76 at Fort Dix. Dark bars indicate the percentage of recruits entering on that week who later had titres to A/Mayo Clinic/103/74 greater than or equal to 1 : 20, when tested during the serologic survey, indicating potential infection with A/New Jersey/76.

Table 1.

Characteristics and outbreak sizes for platoons with at least one A/New Jersey/76 hospitalization and contemporary platoons in the same company. (Adapted from Gaydos et al. (1977a).)

company platoon with hospitalized case other platoons in same company
studied/total in group attack rate per 100 (titres≥1 : 20) studied/total in group attack rate per 100 (titres≥1 : 20)
C4 42/49 26 6/133 17
C2 46/47 24 15/134 40
E1 46/50 26 21/151 19
E6 39/43 56 5/144 20
D6 46/57 17 17/141 18
A5 28/35 7 10/155 0b
A6 7/48a 28 9/144a 0b
Open in a new tab
a

Total number of trainees estimated.

b

Platoons with no infections are not considered in determinations of R0.

Table 2.

Characteristics of soldiers hospitalized with acute respiratory disease showing evidence of infection with A/New Jersey/76. (Patients V1–V5 had virologically confirmed infection, while patients S1–S8 had serologically detected infection. Adapted from Gaydos et al. (1977a).)

patient unit age (years) date of onset (1976) date hospitalized (1976) viral isolate?
S1 E6 17 1/12 1/19 No
S2 D6 19 1/18 1/20 No
S3 E6 18 1/19 1/20 No
S4 E6 18 1/19 1/20 No
S5 A5 20 1/12 1/26 No
S6 A5 21 1/25 1/26 No
V1 HQ 18 1/28 1/29 Yes
V2 D5 19 1/26 1/29 Yes
V3 C4 18 1/28 1/29 Yes
V4 C2 18 1/28 1/30 Yes
V5a E1 19 ? 2/4 Yes
S7 B7 21 2/8 2/8 No
S8 A6 18 1/26 2/9 No
Open in a new tab
a

Patient V5 died at hospitalization on 2/4.

The serious threat of pandemic influenza has been highlighted by the recent infection of humans with avian H5N1 strains. While there has been extensive analysis of historic pandemics (Blumenfeld et al. 1959; Mills et al. 2004; Tumpey et al. 2004; Hollenbeck 2005; Oxford 2005; Viboud et al. 2005), we know little about nature's false starts. Understanding why potentially pandemic viruses fail may help us to contain emerging viral threats. The 1976 outbreak of ‘swine flu’ (A/New Jersey/76) in Fort Dix, New Jersey represents a unique opportunity in this regard. Since this outbreak occurred on an army base with an active Acute Respiratory Disease Surveillance Program, there is a wealth of epidemiological data available with which to analyse its properties.

The dynamics of disease transmission can be characterized by two properties: the basic reproductive number (R0), which is the number of infections caused by a single infectious individual introduced into a completely susceptible population; and the serial interval, which is the average time between someone becoming infected and that person infecting another. Recent work has shown that influenza's dramatic speed of spread through communities is not the result of a high R0, but the result of a modest R0 and a short serial interval (Mills et al. 2004). These characteristics are critically important in determining the success of any containment programme. Recent work also shows that emerging flu strains with an R0 of less than 1.5 could potentially be contained with antiviral drugs and quarantine before becoming pandemic, while control of more transmissible strains is unlikely (Ferguson et al. 2005; Longini et al. 2005).

To gain insight as to whether it is reasonable to expect an emerging influenza strain to have a substantially lower R0 than currently circulating strains, we analysed the dynamic properties of the Fort Dix outbreak using the data presented by the original investigators (Gaydos et al. 1977a,b; Goldfield et al. 1977; Hodder et al. 1977; Kendal et al. 1977; Top & Russell 1977). R0 can be contrasted with the effective reproductive number, R, which is a measure of how transmissible the pathogen is in a population that is not immunologically naive. Owing to the youth of the basic trainees (the average age range of recruits is 19–22 years; Knapik et al. 2006), they tend to be immunologically naive to H1N1 influenza, which had not circulated since 1957 (Hodder et al. 1977; Gaydos et al. 2006). This supposition is supported by the low rates of positives to A/Mayo Clinic/103/74 among soldiers in this age range not exposed to A/New Jersey/76 (Gaydos et al. 1977a; Hodder et al. 1977). For this reason, we believe that estimates of transmissibility in the Fort Dix platoons approximate R0.

2. Methods

We used the case definition adopted by Top & Russell (1977) in our analysis, defining all of those soldiers with antibody titres to A/Mayo Clinic/103/74 greater than or equal to 1 : 20 as cases (table 1). Fort Dix was a training facility, and new recruits were grouped into companies consisting of four platoons of approximately 50 individuals, where they remained throughout their training. Based on their social isolation during basic combat training, we considered each platoon to have an independent outbreak starting from a single A/New Jersey/76 infected individual (Hodder et al. 1977). While we lack onset dates for most cases, we can place an upper bound on the length of this epidemic as 47 days based on troops returning from winter break on 5 January and serological evidence that transmission ended by 21 February (Hodder et al. 1977). A less conservative estimate is 33 days, based on the lack of evidence of transmission after the first week of February (Hodder et al. 1977). We use the second estimate of epidemic length in our analysis.

We estimated the transmissibility of the circulating virus using analytic methods based on deterministic epidemic models (Diekmann & Heesterbeek 2000). The analytic determination for R0 was made by considering the proportion infected in each platoon containing an index case (table 1; Ma & Earn 2006). Individual platoon estimates were combined and confidence intervals created using standard statistical techniques (i.e. inverse variance weighting and the delta method; Rice 1995; Rothman & Greenland 1998; Hethcote 2000).

In addition to the analytic determination of R0, we used a computational model to refine our estimate for R0 and estimate the serial interval. Our model classifies individuals as susceptible, exposed with latent infection, infectious or recovered (an SEIR model). Discrete individuals move through these compartments stochastically. Figure 2 shows the path of the individuals through the model compartments. The distribution of latent and infection periods was based upon published estimates for circulating influenza A viruses (Longini et al. 2004; Ferguson et al. 2005). We ran 10 000 iterations of this model at each parameterization, varying R0 between 0.5 and 3.0 by 0.1 and varying the serial interval between 1.6 and 10.0 by 0.1 day. We used a likelihood-based approach to determine the supported intervals for R0 and the serial interval based on our simulations (Goodman & Royall 1988; Clayton & Mills 1993; Goodman 1993).

Figure 2.

Figure 2

Open in a new tab

Stochastic model of the Fort Dix outbreak. Initially, model runs start with a single infectious individual and 49 susceptible individuals. Individuals then move through compartments stochastically based on the current R0 and the serial interval being simulated. The simulation runs until there are no infectious individuals remaining.

3. Results

The deterministic analysis of final outbreak sizes in platoons yielded an estimate for R0 of 1.09 (95% CI 1.04–1.13; Hethcote 2000). Analytic estimates of R0 based on deterministic models provide a good first approximation of disease transmissibility; but in small populations, such as the affected 50-man platoons, these estimates should be viewed with suspicion. The assumption of continuity made by these models can produce misleading results when applied to small numbers of discrete individuals; such models fail to capture the stochastic effects important in determining the course of an epidemic when small numbers are infected (Diekmann & Heesterbeek 2000). Additionally, our stochastic model uses distributions of the serial interval more consistent with empirical observations (Ferguson et al. 2005). While the point estimate for R0 should be similar using both deterministic and stochastic models, the confidence interval placed on this estimate in deterministic models may underestimate the uncertainty.

To better estimate the plausible range for R0 and the serial interval of A/New Jersey/76, we developed a stochastic model of the Fort Dix outbreak. Results of these simulations are summarized in figure 2. We obtained an estimate for R0 of 1.2 (supported range 1.1–1.4) and an estimate for the serial interval of 1.9 days (supported range 1.6–3.8 days). In comparison, estimates for the 1918 ‘Spanish Flu’ include an R0 of 1.8 with a serial interval of 2.6 days (Ferguson et al. 2005), and an R0 of 2–3 with a serial interval of 4 days (Mills et al. 2004).

The assumption that transmission between trainees occurred predominately within the platoons has ample epidemiologic support. Platoons were kept intact and semi-isolated throughout basic training, having limited interaction with other platoons of the same company and nearly zero interaction with other companies (Gaydos et al. 1977a; Hodder et al. 1977). In companies A5 and A6, circulation of A/New Jersey was confined to index platoons (i.e. those platoons containing hospitalized cases). In those companies where there was transmission in other platoons, attack rates are heterogeneous, indicating independent epidemics in platoons (table 1). Overall, the relative risk of infection with A/New Jersey/76 was 1.5 (95% CI 0.9–2.4), comparing soldiers in index platoons to others in the same company. Companies not containing an index platoon had a further reduced risk of infection, with a relative risk of 0.2 (95% CI 0.1–0.6) when compared with index companies. The percentage of soldiers with antibody titres to A/Mayo Clinic/103/74 of 1 : 20 or higher in these contemporary companies was 4.3% (95% CI 1.6–9.2%), consistent with the background prevalence of antigen in this age group (Gaydos et al. 1977a; Hodder et al. 1977). Based on this evidence, we conclude that transmission of A/New Jersey/76 was predominately within platoons, but there was a low rate of cross platoon transmission within companies, and transmission across companies was a rare event.

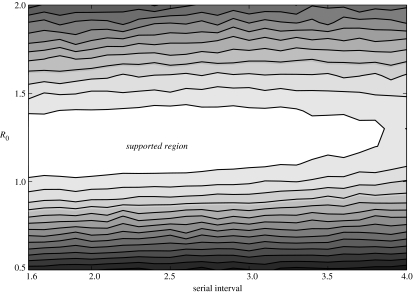
Any relaxation of our assumption of platoon-confined transmission leads to a reduction in our estimate of R0. For instance, if we assume equal mixing at the company level (approx. 200 individuals), the estimate for R0 using the stochastic model becomes 0.9 (supported range 0.8–1.0). This lower estimate of R0 makes the high attack rates seen in some platoons (e.g. the index platoon in company E6) unlikely. This lends further support to our contention that cross platoon transmission was a rare event and gives us confidence that the true value for R0 in this outbreak lies within the range predicted by our simulations (figure 3).

Figure 3.

Figure 3

Open in a new tab

Plot showing the level of support of different values for R0 and the serial interval based on the results of our simulations. Lighter shading represents values with greater support from simulation results, as indicated by the likelihood of observing the given epidemics, given the values for R0 and serial interval. The central white region is the supported region representing the most probable values for R0 and the serial interval (the supported region is a concept from likelihood-based statistics and is roughly equivalent to the 95% confidence interval (Clayton & Mills 1993)).

Based on our estimates of R0, we estimated a lower bound on the length of the longest chain of transmission. If we consider the platoon with most cases (E6) and assume an R0 of 1.2, we estimate the longest chain of transmission to be approximately eight individuals (approx. 12 for an R0 of 1.1). The E6 platoon had a significantly larger epidemic than other platoons, so it may be the case that it had multiple introductions or contained a particularly contagious individual. Examining the platoon with the next highest number of cases (E1), we estimate that there were approximately six serial transmissions in this platoon (approx. 8 for an R0 of 1.1). Based on these calculations and the high number of platoons infected, it is safe to assume that there were at least six, and more probably eight, serial passages of A/New Jersey/76 in humans during the Fort Dix outbreak.

4. Discussion

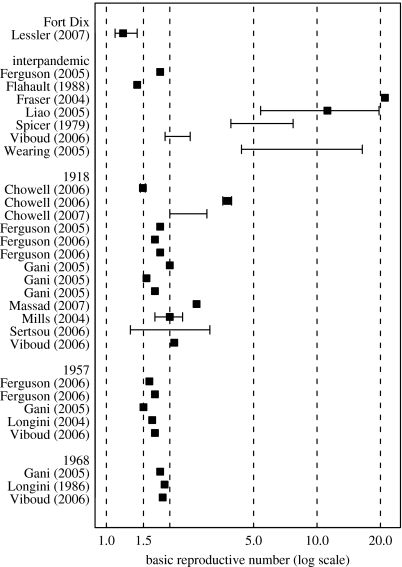
The Fort Dix outbreak presents a unique opportunity to characterize an emerging influenza strain that, while successfully transmitted between humans, never achieved worldwide spread. Our analysis shows that A/New Jersey/76 was not highly infectious, consistent with our expectations for an emerging influenza virus. To put the Fort Dix epidemic in context, we reviewed estimates of the transmissibility of influenza from the literature for interpandemic years 1918, 1957 and 1968. We conducted a search of PubMed and Google Scholar using the terms influenza, transmissibility, basic reproductive number and basic reproductive rate. Estimates of the basic reproductive number using empirical data reported as a point estimate, confidence interval, supported interval or range were gathered and are shown in figure 4. Some estimates are effective rather than basic reproductive, as they are estimates from the increase in incidence in the presence of immunity. The point estimate of the basic reproductive number for the Fort Dix outbreak is lower than all other reported point estimates of the reproductive number. The supported interval we estimated for Fort Dix includes only one estimate from the 1918 outbreak (Sertsou et al. 2006) and one estimate from an interpandemic period (Flahault et al. 1988).

Figure 4.

Figure 4

Open in a new tab

Estimates of the basic reproductive number for influenza appearing in the literature along with our estimate of the basic reproductive number from the Fort Dix outbreak. Estimates are shown for interpandemic influenza, 1918, 1957 and 1968. To fit all the estimates in a graph and still show detail of most estimates (between 1.5 and 2.0), a log scale has been used on the x-axis. Squares, point estimates; lines surrounding point estimates, confidence or supported intervals; lines alone, ranges (or ranges of estimates created using several different techniques). Sources of estimates are listed on the left (Spicer 1979; Rvachev & Longini 1985; Longini et al. 1986; Flahault et al. 1988; Fraser et al. 2004; Longini et al. 2004; Mills et al. 2004; Ferguson et al. 2005; Gani et al. 2005; Liao et al. 2005; Longini et al. 2005; Wearing et al. 2005; Chowell et al. 2006; Ferguson et al. 2006; Sertsou et al. 2006; Viboud et al. 2006; Chowell et al. 2007; Massad et al. 2007).

A curious aspect of the Fort Dix outbreak is that it failed to cause an epidemic outside the military population, despite a clear ability for human to human transmission. This failure to spread was clearly not due to containment measures beyond those intrinsic to the structure of a basic training facility (e.g. social distancing), as the epidemic had ended by the time it was detected (Gaydos et al. 1977a,b). We hypothesize that the epidemic of A/New Jersey/76 ran its natural course, reaching extinction due to the depletion of susceptibles in the infected platoons and an inability to maintain transmission outside of this favourable environment. It was hypothesized at the time that the A/New Jersey/76 virus was competitively displaced by the A/Victoria strain, the predominant influenza A virus of that year (Top & Russell 1977). We find no reason to invoke competition or any other extrinsic factor to explain the disappearance of A/New Jersey/76.

The low R0 of this virus observed in military platoons, an ideal situation for disease transmission, suggests that A/New Jersey/76 may not have been fit enough to be transmitted outside of this environment (i.e. it has an R0 of less than 1 in a population not living in the confined quarters of a military installation). Once there was no longer adequate supply of susceptibles within the platoons to maintain transmission the virus died out. The soldiers in basic training were socially isolated within platoons, so opportunities for extra-platoon transmission were few and far between further decreasing the chances for the continued survival of the virus. A/New Jersey/76 had yet another challenge for spread outside of the military platoons: the threshold for herd immunity to a virus with an R0 of 1.2 is 17% of the population being immune (9% for an R0 of 1.1; Hethcote 2000). Military vaccines administered before 1969 contained Hsw antigen and H1N1 circulated until 1957, so older personnel may have been protected against the A/New Jersey/76 strain (Hodder et al. 1977; Gaydos et al. 2006), and immunity in even a small fraction of the population would have been adequate to halt the spread of the virus.

That a virus with the odds heavily stacked against it could undergo six or more serial passages through humans is the cause for concern. That this virus did not mutate to be more transmissible in humans or reassort with the circulating A/Victoria strain may be indicative of its lack of fitness, or it may be luck. The greater the number of serial transmissions in humans, the greater the probability of reassortment and adaptation to humans (Antia et al. 2003). As we confront the prospect of the emergence of H5N1 or another avian flu strain, the infection of military recruits and other groups living in close quarters pose some of the greatest risks. Surveillance programmes should take this risk into account, focusing efforts on such high-risk environments.

The fallout from the swine flu outbreak at Fort Dix was a national immunization effort with unfortunate consequences (Dowdle 1997). While the perceived safety of influenza vaccination, the Legionnaires outbreak later that year and the general climate of fear may have led to the implementation of a mass vaccination programme anyway, an analysis of the transmissibility of A/New Jersey/76 may have provided policy makers with more options. If a similar situation were to occur today, when antiviral drugs are available as a first line of defence against pandemic spread, policy makers may have been inclined to take a wait and see approach, knowing that a second emergence would spread slowly and could probably be contained (Longini et al. 2005; Ferguson et al. 2006). For disease dynamics to be considered as part of a public health response, it is necessary that the real-time estimation of these parameters becomes a part of outbreak investigations; fortunately, techniques are being developed to make such estimates (e.g. Wallinga & Teunis 2004; Ferrari et al. 2005).

The Fort Dix experience illustrates that the particular circumstances of emergence of a virus can profoundly affect its subsequent course. The circulation of A/New Jersey/76 within the population of military recruits, despite its apparent low fitness, raises concerns that similarly compact populations may serve as bridges for emerging viruses, providing viruses not yet capable of spreading efficiently in the general population time to adapt. The detection of A/New Jersey/76 and its failure to spread beyond the confines of Fort Dix provides hope that with improvements in surveillance and control techniques, future outbreaks of novel influenzas can be contained before they cause a pandemic.

Acknowledgments

The authors would like to acknowledge the valuable contribution of the original investigators of the Fort Dix outbreak without whom this work would not have been possible. The authors especially thank Dr Frank Top for providing some first person insights into the investigation of this outbreak and Dr Joel Gaydos for his valuable suggestions on the final manuscript. The authors also thank Elizabeth Johnson for statistical guidance and Dr Stephen Cole for his suggestions.

Supplementary Material

Transmissibility of Swine Flu at Fort Dix, 1976: Supporting Materials

This document contains details of the algorithms used to estimate the transmissibility of the 1976 swine flu, including details of the deterministic approach and a full description of the stochastic simulations. The supporting materials also include a sensitivity analysis of the results to important model assumptions

rsif20070228s06.pdf (136.7KB, pdf)

References

  1. Antia R, Regoes R.R, Koella J.C, Bergstrom C.T. The role of evolution in the emergence of infectious diseases. Nature. 2003;426:658–661. doi: 10.1038/nature02104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blumenfeld H.L, Kilbourne E.D, Louria D.B, Rogers D.E. Studies on influenza in the pandemic of 1957–1958. 1. Epidemiologic, clinical and serologic investigation of an intrahospital epidemic, with a note on vaccination efficacy. J. Clin. Invest. 1959;38:199–212. doi: 10.1172/JCI103789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chowell G, Ammon C.E, Hengartner N.W, Hyman J.M. Estimation of the reproductive number of the Spanish flu epidemic in Geneva, Switzerland. Vaccine. 2006;24:6747–6750. doi: 10.1016/j.vaccine.2006.05.055. [DOI] [PubMed] [Google Scholar]
  4. Chowell G, Nishiura H, Bettencourt L.M.A. Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. J. R. Soc. Interface. 2007;4:155–166. doi: 10.1098/rsif.2006.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Clayton D, Mills M. statistical models in epidemiology. Oxford University Press; Oxford, UK: 1993. Likelihood. [Google Scholar]
  6. Diekmann O, Heesterbeek J.A.P. Wiley; Chichester: 2000. Mathematical epidemiology of infectious diseases model building, analysis and interpretation. [Google Scholar]
  7. Dowdle W.R. Pandemic influenza: confronting a re-emergent threat. The 1976 experience. J. Infect. Dis. 1997;176(Suppl. 1):S69–S72. doi: 10.1086/514180. [DOI] [PubMed] [Google Scholar]
  8. Ferguson N.M, Cummings D.A, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, Burke D.S. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
  9. Ferguson N.M, Cummings D.A, Fraser C, Cajka J.C, Cooley P.C, Burke D.S. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ferrari M.J, Bjornstad O.N, Dobson A.P. Estimation and inference of R-0 of an infectious pathogen by a removal method. Math. Biosci. 2005;198:14–26. doi: 10.1016/j.mbs.2005.08.002. [DOI] [PubMed] [Google Scholar]
  11. Flahault A, Letrait S, Blin P, Hazout S, Menares J, Valleron A.J. Modeling the 1985 influenza epidemic in France. Stat. Med. 1988;7:1147–1155. doi: 10.1002/sim.4780071107. [DOI] [PubMed] [Google Scholar]
  12. Fraser C, Riley S, Anderson R.M, Ferguson N.M. Factors that make an infectious disease outbreak controllable. Proc. Natl Acad. Sci. USA. 2004;101:6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gani R, Hughes H, Fleming D, Griffin T, Medlock J, Leach S. Potential impact of antiviral drug use during influenza pandemic. Emerg. Infect. Dis. 2005;11:1355–1362. doi: 10.3201/eid1109.041344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gaydos J.C, Hodder R.A, Top F.H, Allen R.G, Soden V.J, Nowosiwsky T, Russell P.K. Swine influenza-A at Fort-Dix, New-Jersey (January–February 1976). 2. Transmission and morbidity in units with cases. J. Infect. Dis. 1977a;136:S363–S368. doi: 10.1093/infdis/136.supplement_3.s363. [DOI] [PubMed] [Google Scholar]
  15. Gaydos J.C, Hodder R.A, Top F.H, Soden V.J, Allen R.G, Bartley J.D, Zabkar J.H, Nowosiwsky T, Russell P.K. Swine influenza-A at Fort-Dix, New-Jersey (January–February 1976). 1. Case finding and clinical-study of cases. J. Infect. Dis. 1977b;136:S356–S362. doi: 10.1093/infdis/136.supplement_3.s356. [DOI] [PubMed] [Google Scholar]
  16. Gaydos J.C, Top F.H, Hodder R.A, Russell P.K. Swine influenza A outbreak, Fort Dix, New Jersey, 1976. Emerg. Infect. Dis. 2006;12:23–28. doi: 10.3201/eid1201.050965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Goldfield M, Bartley J.D, Pizzuti W, Black H.C, Altman R, Halperin W.E. Influenza in New-Jersey in 1976—isolations of influenza A-New-Jersey-76 virus at Fort-Dix. J. Infect. Dis. 1977;136:S347–S355. doi: 10.1093/infdis/136.supplement_3.s347. [DOI] [PubMed] [Google Scholar]
  18. Goodman S.N. P-values, hypothesis tests, and likelihood—implications for epidemiology of a neglected historical debate. Am. J. Epidemiol. 1993;137:485–496. doi: 10.1093/oxfordjournals.aje.a116700. [DOI] [PubMed] [Google Scholar]
  19. Goodman S.N, Royall R. Evidence and scientific research. Am. J. Public Health. 1988;78:1568–1574. doi: 10.2105/ajph.78.12.1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hethcote H.W. The mathematics of infectious diseases. Siam Rev. 2000;42:599–653. doi: 10.1137/S0036144500371907. [DOI] [Google Scholar]
  21. Hodder R.A, Gaydos J.C, Allen R.G, Top F.H, Nowosiwsky T, Russell P.K. Swine influenza-A at Fort-Dix, New-Jersey (January–February 1976). 3. Extent of spread and duration of outbreak. J. Infect. Dis. 1977;136:S369–S375. doi: 10.1093/infdis/136.supplement_3.s369. [DOI] [PubMed] [Google Scholar]
  22. Hollenbeck J.E. An avian connection as a catalyst to the 1918–1919 influenza pandemic. Int. J. Med. Sci. 2005;2:87–90. doi: 10.7150/ijms.2.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kendal A.P, Goldfield M, Noble G.R, Dowdle W.R. Identification and preliminary antigenic analysis of swine influenza-like viruses isolated during an influenza outbreak at Fort-Dix, New-Jersey. J. Infect. Dis. 1977;136:S381–S385. doi: 10.1093/infdis/136.supplement_3.s381. [DOI] [PubMed] [Google Scholar]
  24. Knapik J.J, Sharp M.A, Darakjy S, Jones S.B, Hauret K.G, Jones B.H. Temporal changes in the physical fitness of US Army recruits. Sports Med. 2006;36:613–634. doi: 10.2165/00007256-200636070-00005. [DOI] [PubMed] [Google Scholar]
  25. Liao C.M, Chang C.F, Liang H.M. A probabilistic transmission dynamic model to assess indoor airborne infection risks. Risk Anal. 2005;25:1097–1107. doi: 10.1111/j.1539-6924.2005.00663.x. [DOI] [PubMed] [Google Scholar]
  26. Longini I.M, Fine P.E.M, Thacker S.B. Predicting the global spread of new infectious agents. Am. J. Epidemiol. 1986;123:383–391. doi: 10.1093/oxfordjournals.aje.a114253. [DOI] [PubMed] [Google Scholar]
  27. Longini I.M, Jr, Halloran M.E, Nizam A, Yang Y. Containing pandemic influenza with antiviral agents. Am. J. Epidemiol. 2004;159:623–633. doi: 10.1093/aje/kwh092. [DOI] [PubMed] [Google Scholar]
  28. Longini I.M, Jr, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings D.A, Halloran M.E. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
  29. Ma J.L, Earn D.J.D. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006;68:679–702. doi: 10.1007/s11538-005-9047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Massad E, Burattini M.N, Coutinho F.A, Lopez L.F. The 1918 influenza A epidemic in the city of Sao Paulo, Brazil. Med. Hypotheses. 2007;68:442–445. doi: 10.1016/j.mehy.2006.07.041. [DOI] [PubMed] [Google Scholar]
  31. Mills C.E, Robins J.M, Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature. 2004;432:904–906. doi: 10.1038/nature03063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Oxford J.S. Preparing for the first influenza pandemic of the 21st century. Lancet Infect. Dis. 2005;5:129–131. doi: 10.1016/S1473-3099(05)01288-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rice J.A. 2nd edn. Duxbury Press; North Scituate, MA: 1995. Mathematical statistics and data analysis. [Google Scholar]
  34. Rothman K.J, Greenland S. 2nd edn. Lippincott Williams and Wilkins; Philadelphia, PA: 1998. Modern epidemiology. [Google Scholar]
  35. Rvachev L.A, Longini I.M. A mathematical-model for the global spread of influenza. Math. Biosci. 1985;75:3–22. doi: 10.1016/0025-5564(85)90064-1. [DOI] [Google Scholar]
  36. Sertsou G, Wilson N, Baker M, Nelson P, Roberts M.G. Key transmission parameters of an institutional outbreak during the 1918 influenza pandemic estimated by mathematical modelling. Theor. Biol. Med. Model. 2006;3:38. doi: 10.1186/1742-4682-3-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Spicer C.C. The mathematical modelling of influenza epidemics. Br. Med. Bull. 1979;35:23–28. doi: 10.1093/oxfordjournals.bmb.a071536. [DOI] [PubMed] [Google Scholar]
  38. Top F.H, Russell P.K. Swine influenza-A at Fort-Dix, New-Jersey (January–February 1976). 4. Summary and speculation. J. Infect. Dis. 1977;136:S376–S380. doi: 10.1093/infdis/136.supplement_3.s376. [DOI] [PubMed] [Google Scholar]
  39. Tumpey T.M, Garcia-Sastre A, Taubenberger J.K, Palese P, Swayne D.E, Basler C.F. Pathogenicity and immunogenicity of influenza viruses with genes from the 1918 pandemic virus. Proc. Natl Acad. Sci. USA. 2004;101:3166–3171. doi: 10.1073/pnas.0308391100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Viboud C, Grais R.F, Lafont B.A, Miller M.A, Simonsen L. Multinational impact of the 1968 Hong Kong influenza pandemic: evidence for a smoldering pandemic. J. Infect. Dis. 2005;192:233–248. doi: 10.1086/431150. [DOI] [PubMed] [Google Scholar]
  41. Viboud C, Tam T, Fleming D, Handel A, Miller M.A, Simonsen L. Transmissibility and mortality impact of epidemic and pandemic influenza, with emphasis on the unusually deadly 1951 epidemic. Vaccine. 2006;24:6701–6707. doi: 10.1016/j.vaccine.2006.05.067. [DOI] [PubMed] [Google Scholar]
  42. Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 2004;160:509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wearing H.J, Rohani P, Keeling M.J. Appropriate models for the management of infectious diseases (vol 2, pg e320, 2005) Plos Med. 2005;2:813. doi: 10.1371/journal.pmed.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Transmissibility of Swine Flu at Fort Dix, 1976: Supporting Materials

This document contains details of the algorithms used to estimate the transmissibility of the 1976 swine flu, including details of the deterministic approach and a full description of the stochastic simulations. The supporting materials also include a sensitivity analysis of the results to important model assumptions

rsif20070228s06.pdf (136.7KB, pdf)

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES