Abstract
Population fragmentation is a major problem for the conservation of mammalian species. Since the spread of an infectious disease is related to the intensity of contacts between individuals, fragmentation destabilizes the way the parasites circulate in their host population. Recently, Zinkernagel has proposed that a reduction in the frequency of infections by a parasite could lead to the emergence of severe forms of the disease, previously avoided because the disease was contracted early in life and attenuated by maternal antibodies. However, it is still unclear whether this change in disease expression increases the global mortality it induces because the disease becomes more severe and also less frequent. Here, we use a mathematical model to link population fragmentation with the hypothesis of Zinkernagel. Firstly, we show that there is a change in the severity of the disease during the fragmentation process, especially at a local scale, suggesting that host population fragmentation could be a widespread mechanism of disease emergence. Secondly, we show that the emergence of the severe form of the disease can lead to a significant increase in its induced mortality. Finally, we determine the types of interactions for which the fragmentation of the host population could be the most dangerous.
Keywords: maternal antibodies, attenuated disease, emerging disease, population fragmentation, stochastic model
1. Introduction
The threat of emerging diseases, such as AIDS or SARS has motivated the study of the mechanisms leading to the emergence of novel syndromes (Cohen 2000; Morens et al. 2004). The mechanisms classically evoked to explain disease emergence are a combination of (i) an increased level of exposure to a pathogen agent (e.g. due to a novel proximity between species), (ii) the mutation of a microparasite, and (iii) an increased level of susceptibility of the host population (e.g. through exposure to drugs or pollution). Moreover, most attention is paid to the emergence of the pathogen agent and emergence of the disease by a simple change in the expression of the agent is often overlooked. As an exception, Zinkernagel (2001, 2003) proposed an alternative mechanism for the emergence of poliomyelitis in the 1950s.
The mechanism is based on the fact that maternal antibodies can change expression of a pathogen, especially its severity. At low transmission rates, a large proportion of the hosts become infected after maternal antibodies have waned and thus can develop a severe form of the disease. In contrast, at high transmission rates most hosts are infected when carrying maternal antibodies (Fouchet et al. 2006). The disease is then less severe and, according to Zinkernagel, induces an immune response, which protects the host from potential re-infections. A reduction in the transmission rate thus changes the interaction from a situation where most diseases are attenuated by maternal antibodies to a situation with rare but severe diseases since the severe form of the disease emerges from a reduction in the transmission rate of its associated parasite. Zinkernagel (2001, 2003) argued that improvement of hygiene could have been a cause of severe disease emergence, such as poliomyelitis in the 1950s, because it reduces the frequency of contacts we have with parasites.
The fact that an intense circulation of a parasite helps to reduce its severity is a phenomenon known as endemic stability (Norval et al. 1992). In a modelling framework, Coleman et al. (2001) have shown that endemic stability is dependent on two conditions: (i) the average severity of the infection increases with age and (ii) secondary infections are of reduced severity. Clearly, the emergence scenario of Zinkernagel can extend to all host–parasite interactions that fulfil these two conditions. The second condition is achieved in many interactions since it is fulfilled by immune memory. Maternal antibodies have been shown to achieve the first condition, e.g. in measles (Bennett et al. 1999) or in respiratory syncitial virus in mice (Crowe et al. 2001), cotton rats (Sigmodon hispidus; Prince et al. 1985, 1987; Walsh et al. 1994) and calves (Bos taurus; Kimman et al. 1988). However, maternal antibodies are not the only way to fulfil the first condition of increasing infection severity with age. For example, rubella is benign, except during pregnancy when it may cause malformations to the foetus (congenital rubella syndrome, CRS) and so an early infection in girls facilitates avoidance of the dangerous effects of the disease. An interesting case in point is that of rabbit haemorrhagic disease virus and probably European brown hare syndrome, respectively, infecting rabbits (Oryctolagus cuniculus) and brown hares (Lepus europaeus). Newborns are resistant to these diseases because they lack the receptors on which the virus binds to infect the cells (Ruvoën-Clouet et al. 2000). As a result, the severity of the infection increases progressively with age and asymptomatic infections does not prevent active immunization of the host (Robinson et al. 2002 for rabbit and Zanni et al. 1993 for brown hare). Lastly, resistance below the given age is observed, but not yet fully understood, for several diseases, such as under 18 months for malaria (Snow et al. 1998; Wagner et al. 1998) and under 12-year old for SARS (Hon et al. 2003; Leung et al. 2004).
Habitat loss with subsequent population fragmentation is a widespread phenomenon accentuated by anthropogenic activities, which threatens many species, especially mammals. Similar to the improvement of hygiene in humans, the fragmentation of a large population into a number of poorly connected subpopulations also alters the circulation of the pathogen and can be responsible for disease emergence in wildlife populations. Indeed, continuous populations favour the spread of the pathogen agent, conferring early infection on the young rarely leading to severe diseases. In contrast, in small isolated populations, the pathogen agent frequently disappears and the isolation of the host population prevents its rapid reintroduction. During the disease-free period, young animals lose their maternally derived protections without encountering infection. When the pathogenic agent is re-introduced, most individuals are fully susceptible and most infections are severe. Although in the past, it was accepted that population fragmentation reduced the level of infection of the population and thus reduced the impact of the pathogen (Hess 1994, 1996), more recent studies have shown that fragmentation also destabilizes the whole host–pathogen interaction. For example, Carlsson-Graner & Thrall (2002) have shown that increasing fragmentation leads to fewer populations being diseased, but the few diseased populations are more severely affected. This was because resistance genes spread more readily in increasingly connected systems.
Here, we use a stochastic metapopulation model to investigate the effect of population fragmentation on the dynamic of emergence of new pathologies. We demonstrate that even though the severe form of the disease has disappeared from the population before the fragmentation process, it can re-emerge after the circulation of the microparasite is disrupted during the fragmentation process. Population fragmentation could, therefore, be an important cause of disease emergence in wildlife populations. However, one could argue that such emergence of severe disease is not important because it does not necessarily lead to an increase in the impact of the disease. Indeed, with fragmentation, epidemics becomes not only more severe but also more rare. Moreover, protection by maternal antibodies is not perfect and the mild form of a disease can also be a source of additional mortality. We therefore focus on the change of impact during the course of fragmentation and show that in most situations the impact of the parasite is increased by fragmentation. The model allows us to define situations where fragmentation could be most harmful for the host.
2. Material and methods: the mathematical model
Previous models have raised the question of the impact of a disease whose severity increases with host age (Anderson & May 1991; Bunimovich-Mendrazitsky & Stone 2005; Fouchet et al. 2006). Even if these models consider different interactions with different underlying assumptions, all were deterministic and converged towards the same conclusion: the transmission of the disease is the key factor to determining its impact. At some stage in disease transmission, the impact of the pathogen becomes negligible. However, in a previous study (Fouchet et al. 2006), we also suspected an important effect of disease extinctions and re-introductions on disease severity, which could not be assessed using a deterministic approach. The model we present here integrates these two important effects.
2.1 Evolution within a subpopulation (local scale)
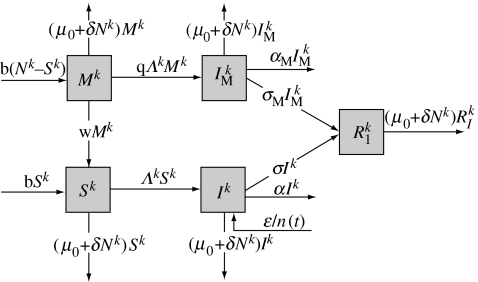
In each subpopulation, we extend the basic susceptible–infected–recover (SIR) model (figure 1) to incorporate the attenuation of the disease by maternal antibodies by adding two categories that represent susceptible individuals partly protected by maternal antibodies (M) and infected individuals whose disease is attenuated by maternal antibodies (‘mildly infected’, IM). The term severe disease represents the disease of individuals in the infected compartment (I).
Figure 1.
Flow diagram between the five categories of the model for the kth subpopulation: susceptible (S), partly protected by maternal antibodies (M), infected (I), mildly infected (IM) and recovered (R).
In order to take localized extinction of the parasite into account, the model is stochastic based on continuous Markov chains with transition rates given in table 1. b is the host birth rate, and μ0+δNk is the density-dependent mortality rate, where Nk is the number of hosts living in the kth subpopulation. As a result, whatever the subpopulation, the number of hosts per subpopulation in the disease-free metapopulation varies around the same carrying capacity K=(b−μ0)/δ, but we will see later that this carrying capacity evolves during the course of the population fragmentation. w is the rate at which young animals lose their maternal protection, α and αM are the additional mortality rates induced by the severe and the mild diseases, respectively, and σ and σM are the recovery rates of individuals affected by the severe and the mild diseases, respectively. Individuals protected by maternal antibodies get infected at a rate that is q times that of susceptible individuals and always develop the mild form of the disease. We assume that the immunity acquired after recovery (from any form of the disease) is lifelong and fully protects against further re-infection. A version of the code is available from the first author upon request.
Table 1.
Transition rates of the Markovian model.
| initial state | final state | transition rate |
|---|---|---|
| (Si,Mi,Ii,IM,i,Ri) | (Si+1,Mi,Ii,IM,i,Ri) | τ1,i=bSi |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi+1,Ii,IM,i,Ri) | τ2,i=b[Mi+Ii+IM,i+Ri] |
| (Si,Mi,Ii,IM,i,Ri) | (Si−1,Mi,Ii,IM,i,Ri) | τ3,i=(μ0+δNi)Si |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi−1,Ii,IM,i,Ri) | τ4,i=(μ0+δNi)Mi |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii−1,IM,i,Ri) | τ5,i=(μ0+δNi+α)Ii |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii,IM,i−1,Ri) | τ6,i=(μ0+δNi+αM)IM,i |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii,IM,i,Ri−1) | τ7,i=(μ0+δNi)Ri |
| (Si,Mi,Ii,IM,i,Ri) | (Si−1,Mi,Ii+1,IM,i,Ri) | τ8,i=Λi(t)Si |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi−1,Ii,IM,i+1,Ri) | τ9,i=qΛi(t)Mi |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii−1,IM,i,Ri+1) | τ10,i=σIi |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii,IM,i−1,Ri+1) | τ11,i=σMIM,i |
| (Si,Mi,Ii,IM,i,Ri) | (Si+1,Mi−1,Ii,IM,i,Ri) | τ12,i=wMi |
| (Si,Mi,Ii,IM,i,Ri) | (Si,Mi,Ii+1,IM,i,Ri) | τ13,i=ϵ/n(t) |
2.2 Connectivity between subpopulations
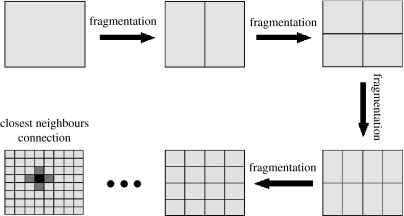
Subpopulations are arranged into a unity square with n(t) subpopulations at time t. The number of subpopulations varies with time because the host population is fragmented every 10 years (figure 2). Initially, the population is not fragmented, i.e. there is only one subpopulation. After 10 years, the subpopulation is divided vertically into two. Each individual is then randomly moved with equal probabilities into one of the two resulting subpopulations. To represent the fact that the resulting subpopulations are twice as small as the original one, δ is multiplied by 2, so that the carrying capacity (K) is finally divided by 2. After 10 years, each subpopulation is again divided into two but this time horizontally. As before, each individual of a given subpopulation is randomly moved with equal probabilities into one of the two resulting subpopulations and δ is multiplied by 2. The process continues, with subpopulations divided into two every 10 years, alternately vertically and horizontally. As a result, at any time the population can be represented by a square comprising several small rectangles (figure 2). We assume that the transmission of the pathogen only occurs between neighbouring subpopulations. As a result, movement of the pathogen between two given subpopulations tends to become more difficult during the course of the fragmentation. For simplicity, we do not consider the migration of individuals between subpopulations.
Figure 2.
Fragmentation of the host population: every 10 years, each subpopulation is divided into two subpopulations of equal size. Each individual is randomly moved into one of the two resulting subpopulations. Subpopulations are divided alternately vertically and horizontally. At any time, each subpopulation has a set of direct neighbours (grey) with whom parasite exchanges are possible.
We use the proportionate mixing law for the transmission of the disease. The force of infection in subpopulation k, Λk(t) is the per capita rate of acquisition of infection of susceptible individuals and comprises transmission within and between subpopulations,
where β0 is the local transmission rate, i.e. between individuals of the same subpopulation, λβ0 is the transmission rate between individuals of neighbouring subpopulations and η(k,t) is the set of adjacent neighbours (figure 2) of the kth subpopulation at the time t. We assume that mildly infected individuals contaminate other individuals at a rate which is always ρ times that of the infected individuals. Definitive extinction of the pathogen does not happen due to regular re-introduction of a severely infected individual at a rate ϵ, each subpopulation having the same probability of receiving the re-introduced infected individual.
2.3 Parameters
Simulations of the model are performed with diverse parameter values. However, to assess the impact of each parameter, we chose one value for each parameter that we define as the standard value. We assess the impact of a given parameter by varying it (and only it) from its standard value (table 2). We describe the host population as having a 1-year life expectancy and young animals lose their maternal antibodies at the age of one month. The case mortality of the severe infection is 0.5, i.e. severely infected hosts have a 50% probability of dying from the disease; whereas it is 0.05 for the mild form of the disease. Both forms of the disease last for one month. Maternally protected individuals are equally susceptible to the infection than the susceptible ones and mildly infected individuals are as infectious as severely infected ones. The local transmission rate of the disease (β0) has been chosen from simulation of the deterministic homogeneous mixing equivalent of the model (see electronic supplementary material). The value β0=100 corresponds to a situation where the intense circulation of the pathogen strongly limits the number of severe diseases. Finally, we chose ϵ=1/12, which corresponds to a re-introduction of the parasite into the entire metapopulation from an external source every year.
Table 2.
Standard values of the parameters (time unit for the parameters is the month) with alternative values that have been tested.
| parameter | symbol | standard value | values tested (if any) |
|---|---|---|---|
| birth rate | b | 0.08 | 0.01, 0.02, 0.04, 0.16 |
| initial mortality rate | μ0 | 0.008 | |
| density-dependent mortality rate (before fragmentation) | δ | 5.625×10−5 | |
| rate of waning of maternal antibodies | w | 1 | |
| mortality rate from severe disease | σ | 0.5 | |
| recovery rate from severe disease | α | 0.5 | |
| mortality rate from mild disease | σM | 0.95 | |
| recovery rate from mild disease | αM | 0.05 | 0, 0.1, 0.15, 0.2 |
| local transmission rate | β0 | 100 | 50, 200, 400 |
| between neighbours transmission rate | λ | 0.01 | 10−1, 10−3 |
| relative susceptibility of maternally protected individuals | q | 1 | 0.5 |
| relative infectiousness of mildly infected individuals | ρ | 1 | 0.5 |
| external re-introduction rate | ϵ | 0.083 | 0.0083, 0.83 |
The simulation starts with only one severely infected individual released into the fully susceptible population. The population is then made up of only one subpopulation composed of 1280 individuals (K=5×28), corresponding to δ=5.625×10−5. The simulation ends after 90 years, following eight fragmentation events. The population is then made up of 256 subpopulations, each having a carrying capacity of five individuals.
We use the standard Monte-Carlo approach to simulate the process (Cow & Miller 1965). We thus obtain plausible outcomes of the model that we consider replicates. However, a simple replicate does not teach us anything about the variability in the outcomes of the model. To evaluate this variability, we generate several replicates of the same process and estimate confidence intervals for the mean behaviour of the model. Here, we consider only 10 replicates. Even if this number seems a priori small, we show below that it is sufficient to obtain accurate confidence intervals for the variables we estimate using the model. All means and confidence intervals are calculated using the same method. The variable of interest is calculated for each of the 10 replicates, giving us 10 values of the random variable for which we assume a normal distribution. This allows a simple calculation of the mean and 95% confidence interval of the random variable. All runs are considered for the estimation of means and confidence intervals.
3. Results
3.1 Emergence of the severe form of the disease
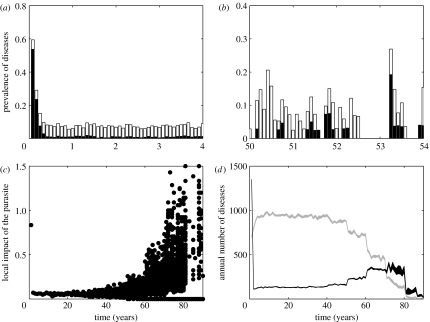
After the introduction of one severely infected individual, the microparasite spreads rapidly, resulting in a high number of severe disease cases (figure 3a). After this first epidemic, most individuals are immune and the parasite only spreads through newborns. Owing to the high transmission rate of the disease, most individuals are immune and transmit maternal antibodies to their offspring. In addition, young animals get infected rapidly and then develop attenuated disease (figure 3a). As a result, only a small number of individuals die from the severe form of the disease.
Figure 3.
Emergence of the severe form of the disease with fragmentation: (a) an example of prevalence of each form of the disease (white, mild and black, severe) during the first 4 years of the simulation in a subpopulation; (b) as for (a) but after 50 years of the simulation; (c) index of the local impact of the disease defined as the total number of individuals that died from the disease during a given year in a given subpopulation divided by the mean size of the subpopulation during that year. Each point represents one subpopulation for one replicate. Thus for each year, we have N(t)×10 points. In fact, as the time progresses, more points are at 0 and cannot be distinguished from each other; (d) estimation of the mean number of individuals in the entire metapopulation that develop each form of the disease (grey, mild and black, severe) during a given year with 95% confidence intervals.
At an advanced stage of the fragmentation process (figure 3b), the circulation of the microparasite is drastically changed. The population is now made up of small (here K=40) and poorly connected subpopulations, in which the parasite barely persists. Long disease-free periods alternate with epidemics in subpopulations. Most individuals born with maternal antibodies during the inter-epidemic period have lost their maternal protection before becoming infected, so they are susceptible to the severe form of the disease. As a result, when the parasite reappears in the subpopulation, individuals are poorly protected and a large proportion of them develop the severe form of the disease. The parasite can persist over a short period of time but eventually goes locally extinct due to the small size of the host subpopulation.
During the course of fragmentation, the time lapse between the localized extinction of the parasite and its re-introduction increases. As a consequence, the proportion of young animals that do not carry maternal protection increases locally and so the re-introduction of the parasite results in an increasing proportion of deaths from the severe disease (figure 3c). In summary, at the beginning of the fragmentation process, deaths from the disease are rare. The parasite is present in every subpopulation and so most young are in contact with the parasite. Non-exposure during early life is more a matter of bad luck than a question of spatial localization. Deaths from the severe form of the disease are rare and diffuse in the entire population without spatial aggregation. The severe form of the disease can remain undetected over very long periods, especially if the host species is not intensively monitored. In contrast, at an advanced stage of the fragmentation process, deaths from the severe disease are mainly due to local epidemics. Therefore, frequently a large proportion of the individuals from a subpopulation die over a short period. The local density of dead individuals can be very high, increasing the probability of discovering the severe disease.
Interestingly, rapidly after the introduction of the pathogen (t=0), the annual number of infections stabilizes to values (between 910 and 990 mild diseases and between 120 and 140 severe diseases) that are close to the deterministic predictions (957.65 mild diseases and 129.76 severe diseases). The behaviour of the stochastic model during the first 10-year period provides a good estimation of the deterministic one. This is not surprising since initially the host population is large and homogeneous; a situation where deterministic and stochastic models show close outcomes. Later, we will not recall the predictions of the deterministic model.
Beyond local aggregation of the severe forms of the disease, the model also shows that there is a significant increase in the number of severe disease cases (that may or may not result in death) in the entire population (figure 3d). However, this increase in the number of severe disease cases is followed by a decrease in the frequency of mild disease cases.
3.2 Evolution of global parasite-induced mortality
Since mild diseases may also induce additional mortality, we investigate whether or not the impact of the disease will increase or decrease during the course of fragmentation. This question is assessed by estimating the trend in the total number of deaths induced by both forms of the disease, relative to the mean size of the population (figure 4a). We focus on the standard value of the parameters. Clearly, during the course of fragmentation populations are less likely to retain the pathogen (figure 4b). After the fourth fragmentation event, the persistence time of the pathogen within subpopulations shows an important decrease, leading to a higher proportion of disease-free subpopulations (figure 4c). This decrease in the proportion of infected subpopulations leads to a decrease in the frequency of pathogen exchange between subpopulations. This results in an increase in the length of disease-free periods (figure 4b) that explains the increased impact of the pathogen. However, with increased fragmentation fewer subpopulations are infected, even resulting in the global loss of the disease (figure 4c). Subsequent epidemics are not only more severe, but also very rare, leading initially to an increase (until the seventh fragmentation event) and then to a decrease in the global impact of the disease (figure 4a).
Figure 4.
Evolution of the impact of the parasite with the number of fragmentation events (F) experienced by the population. Variables are estimated over 8-year period starting 2 years after the last fragmentation event (t=10F+2) and ending at the beginning of the next one (t=10F+10). The initial 2 years of the period are omitted to discount fluctuations arising from fragmentation of the population; (a) evolution of the impact of the pathogen in relation to the number of fragmentation events (x-axis). For each replicate, the impact of the pathogen is calculated by the total number of dead individuals (from mild or severe disease) during the 8-year period, divided by the mean size of the entire population over that same period; (b) mean time before extinction (solid line) and re-introduction (dashed line) of the pathogen after F fragmentation events (x-axis). Extinction times above 1200 months (100 years) are described as more than 1200. For such values, local extinction within 10 years becomes very unlikely (as in (c)). Extinction and re-introduction times are calculated using specific methods detailed in the electronic supplementary material; and (c) proportion of disease-free subpopulations (solid lines), of unoccupied subpopulations (i.e. where the host species has become extinct, dotted lines) and of disease-free metapopulations (dashed lines) during the 8-year period following the Fth fragmentation event (x-axis). The probability of extinction of the entire metapopulation is calculated for each replicate as the number of times during the 10-year period when the entire metapopulation is extinct, divided by the number of months (n=96) within the period. The same formula applies to the cases of subpopulations where the empty/full state of the metapopulation is replaced by the proportion of subpopulations where at least one individual is infected (mildly or otherwise).
At the end of the simulation, global extinction of the parasite is frequent (figure 4c), so the external re-introduction of the pathogen plays an important role in its impact that will be assessed in more details below. Local extinction of the host is also observed, but after seven fragmentation processes more than 95% of the subpopulations are still occupied by hosts. As a consequence, local extinctions of the host are not an important factor in the model.
3.3 Impact of the parameters
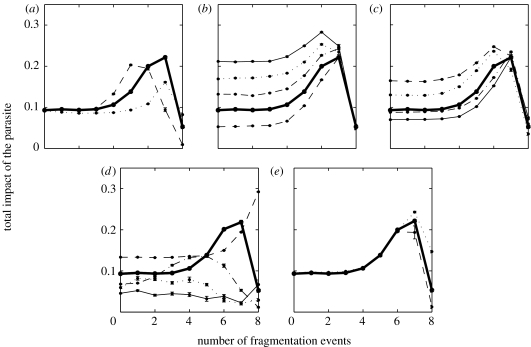
Clearly, the consequence of fragmentation of the host population on the impact of the parasite will depend on the characteristics of the host–parasite interaction through several parameters. The level of connectivity between subpopulations influences the level of fragmentation needed to observe an increased impact of the disease (figure 5a). For higher levels of connectivity between neighbours, the impact of fragmentation occurs later. Indeed, the increased impact of the pathogen is due to the loss of maternal immunity that follows the extinction of the pathogen. But if the level of connectivity between neighbours is high, few individuals will lose their maternal protection before disease re-introduction, i.e. connectivity between neighbours balances regular pathogen extinctions. However, the impact of the disease is greater for intermediate levels of connectivity. For high levels, the former argument holds (re-introductions balance extinctions). For low levels, the impact of the disease remains low as long as individual subpopulations are able to retain the parasite. When the sizes of the subpopulations become too small to keep the parasite over long periods, the frequency of re-introduction of the parasite is low and epidemics are not only more severe but also much rarer, resulting in a lower impact of the disease (compared with situations where the connectivity is higher, figure 5a).
Figure 5.
Effect of the parameters on the evolution of the impact of the pathogen in relation to the number of fragmentation events. The impact of the pathogen is calculated as in figure 4. Results obtained from the basic values of the parameters are represented in each graph by the bold solid line. Each time, the impact of the variation of a small number of parameters (most of the time one) from their basic value was tested. Other parameters are set to their basic value; (a) impact of the level of connectivity between neighbours. λ=0.1 (dotted line), λ=0.01 (standard, bold line), λ=0.001 (dashed line); (b) impact of the additional death rate induced by mild disease, keeping the duration of the disease (αM+σM)−1 constant. αM=0 (dashed line), αM=0.05 (standard, bold line), αM=0.1 (dashed-dotted line), αM=0.15 (dotted line), αM=0.2 (solid thin line); (c) impact of the transmission coefficients of the disease. ρ=q=0.5 and β0=100 (dashed line), ρ=q=0.5 and β0=400 (dashed-dotted line), ρ=q=1 and β0=50 (dotted line), ρ=q=1 and β0=200 (solid thin line); (d) impact of the birth rate. b=0.16 (dashed line), b=0.08 (standard, bold line), b=0.04 (dashed-dotted line); b=0.02 (dotted line) and b=0.01 (solid thin line); (e) impact of the external re-introduction rate. ϵ=0.0083 (dashed line), ϵ=0.083 (standard, bold line) and ϵ=0.83 (dotted line).
Surprisingly, we find that the increasing impact of the disease with fragmentation remains true for relatively high mortality cases induced by the mild form of the disease (figure 5b). Of course, higher mortality results in a reduced relative increase in the impact in relation to fragmentation (figure 5b). Interestingly, after a given number of fragmentation processes (here 7), the impact of the disease is not really dependent on mortality due to mild disease. This is because at this point most infections are severe.
We also analyse the impact of the transmission coefficients of the disease (figure 5c). Unsurprisingly, lower relative transmission rates of mildly infected individuals and lower susceptibility of maternally protected individuals give rise to a smaller relative impact of the disease with fragmentation. This is because at the beginning of the fragmentation process, the transmission of the disease is mainly sustained by mild infections of young animals, i.e. lower transmission coefficients for young animals have the same effect as lower global transmission rates, with a concomitant increase in the impact of the disease. In contrast, as seen above, at an advanced stage of the fragmentation process most diseases are contracted after maternal antibodies have waned. This decrease in the relative impact of the fragmentation can be balanced by assuming a higher transmission rate (figure 5c). Finally, the increase in the transmission rate of the disease is found to have an effect mainly at the beginning of the fragmentation process where it decreases the impact of the disease. At an advanced stage of the fragmentation process, the disease is epidemic and a change in the transmission rate induces only a small change in the duration of the epidemic, which has minimal consequences for the impact of the disease.
Then, we analyse the impact of the birth rate, a correlate of life expectancy in the model host species (at disease-free equilibrium, the death rate is equal to the birth rate). Results show that a species with greater life expectancy will be affected by fragmentation sooner, but with a smaller relative impact (figure 5d). These results can be explained by the fact that a lower birth rate reduces the supply of susceptible individuals, increasing the probability of local extinction for the parasite. A lower persistence time then implies that the population requires an intense connectivity to maintain an endemic circulation of the parasite within each subpopulation through frequent re-introductions. The level of fragmentation required for an increase in the impact of the parasite will then decrease with the persistence of the parasite. The other consequence of low persistence of the disease induced by low birth rates is that the parasite is unlikely to persist in the entire population. When global persistence of the parasite is not attained, the spatial structure of the population is not really important, as long as epidemics induced by external re-introductions can reach every part of the population. So the impact of the disease is then, in our model, mainly driven by external re-introductions that occur randomly, which explains the greater variability of the system for lower birth rates (figure 5d).
Finally, we analyse the impact of the external re-introduction rate of the pathogen (ϵ). Consistently with the fact that no global extinction of the pathogen was observed before the seventh fragmentation event, the rate of external re-introduction has no impact until then (figure 5e). For the two last 10-year periods, a greater external re-introduction rate leads to a greater impact of the pathogen (figure 5e). This is because more frequent re-introductions lead to more epidemics. More frequent re-introductions could have led to a decreased impact of the disease. It is not the case here because values we have tested here (up to one re-introduction every 1.2 months) are not sufficient to provide an early infection of the young in most subpopulations.
4. Discussion
4.1 Emergence of the severe form of the disease and evolution of disease-induced mortality
The spatial organization of a host population can play a major role in determining the impact of a microparasite that is potentially attenuated in early life, e.g. when mothers transfer protective antibodies to their offspring. The introduction of the pathogen in a disease-free population always leads to an epidemic when most infections are severe. But if the population is not much fragmented, the impact of the pathogen rapidly decreases. This is because the pathogen circulates so that young animals are infected while they are still partly protected, develop an attenuated disease and activate their immune system. Only sporadic deaths from the severe disease are observed. In contrast, in highly fragmented populations, the pathogen rapidly fades out locally. Once re-introduced into the subpopulation, individuals are not protected and several cases of the disease can be observed in the same locality. The aggregation of severe disease cases occurs with a simultaneous increase in their frequency so that the severe disease (re-)emerges in the population.
One important question is whether the increase in severe disease frequency of the pathogen is followed by an important increase in its impact in the long term? Our model indicates that it is and allows us to define important factors that could modulate the increased impact of disease in relation to fragmentation. The most important factor is certainly the level of mortality induced by the mild form of the disease, because the prevalence of the mild form of the disease largely decreases during the course of the fragmentation process. Another important factor is the capacity of the parasite to circulate intensively (i.e. to provide regular intense exposure to the young animals) in a situation where the pathogen is locally more persistent. For this reason, the transmission rates of severe and mild diseases and the susceptibility of young individuals are critical factors. Finally, the parasite needs to persist at a scale where the rate of parasite exchange between individuals is high. This requires a high persistence of the parasite that may be achieved in several ways. For example, the distribution of the infectious period (Keeling & Grenfell 1997; Anderson & Britton 2000; Lloyd 2001a,b), the host spatial structure (Bolker & Grenfell 1995; Park et al. 2002), the birth rate (Swinton et al. 1998) and the transmission rate of the parasite (Swinton et al. 1998; Anderson & Britton 2000) are all the well-known factors that can greatly influence the persistence of a parasite in its host population.
Recent studies (Keeling 2000; Keeling et al. 2000a,b) have shown that the capacity of a pathogen to persist over long period had more significant implications than simply describing the epidemic or endemic behaviour of a pathogen within its host population. Keeling (2000) has shown that the capacity of the pathogen to persist within its host population was a key factor in its evolution. In poorly connected metapopulations, endemic strains of the pathogen tend to be selected for, even when less persistent variants are assumed to be fitter. The localized emergence of bubonic plague in humans is interesting in terms of the endemic versus epidemic behaviour of the pathogen. Indeed, Keeling et al. (2000a,b) have proposed that bubonic plague emerges in humans when Yersinia pestis, the bacterium responsible for the disease, is re-introduced in rat populations after long absences, through a mechanism that is described in more detail below. Long-term persistence of the bacteria in rat populations may prevent this emergence. Similarly, our study highlights the local persistence time of the pathogen as a key epidemiological factor that can change the entire relationship between the host and its pathogenic agent.
For the sake of simplicity, we have not considered some features of the host–parasite interaction. One is the possibility of recovered individuals becoming re-infected, a feature that is receiving increasing attention (Codeco & Luz 2001; Glass & Grenfell 2003, 2004; Mossong & Muller 2003; Gomes et al. 2004). In our context, waning of acquired immunity could be a very important factor. Waning immunity significantly increases the circulation of a parasite. For example, in a theoretical framework, Aguas et al. (2006) obtained a very high prevalence of pertussis for relatively low transmission rates in cases of waning immunity. Therefore, waning immunity could greatly reduce the level of parasite transmission required to induce an early infection in young individuals. Significantly, waning immunity increases the duration of persistence of the parasite by providing new susceptible individuals.
4.2 Defining at risk interactions
The conclusions drawn from our model facilitate the identification of the types of interactions that are most likely to lead to significant increases in the impact of the pathogen in relation to fragmentation of populations of its host species. Short-lived species structured into high-density groups are able to maintain parasites locally, thereby favouring high levels of exposure and juvenile infection while young are protected by maternal antibodies. Potentially highly lethal parasites can circulate in these populations without inducing significant mortality rates. These species are most at risk because fragmentation of their populations can then reveal the potential lethality of the parasite. For the same reason, the negative impact of fragmentation would be highest when the pathogen is highly infectious and possesses mechanisms for persistence, such as long-lasting infectious periods, reservoirs (e.g. vectors, infected ground) or reactivation after latency. However, one should remember that we focused here on a particular mechanism of population fragmentation. Other features, like the decrease in connectivity between neighbours, have not been modelled. Incorporating such features into our model could help to more accurately define the host–parasite interactions that are the most susceptible to the effects of fragmentation.
A good example that fits quite well with the criteria discussed above is the rabbit-RHDV system. Rabbits live in social groups that can locally reach very high densities (Palomares et al. 2001). The rabbits have rapid populations turnovers, with half of the population being replaced by newborn each year (Parer 1977; Rogers et al. 1994). But the size of populations dramatically decreased in different areas in the 1980s following the emergence of the rabbit haemorrhagic disease (RHD) caused by the rabbit haemorrhagic disease virus (RHDV; Liu et al. 1984). Circulation of the virus has been reported to have occurred prior to the emergence of the disease (e.g. Rodak et al. 1990b; Moss et al. 2002). These results suggest that rabbits had been exposed to a pre-existing non-pathogenic strain (Rodak et al. 1990a, 1991; Chasey et al. 1995; Nowotny et al. 1997; Trout et al. 1997). However, evidence of such non-pathogenic strains is still lacking especially from the field (but see Capucci et al. 1996). An alternative, but non-exclusive hypothesis is based on the mechanism discussed here. Firstly, rabbit populations have been increasingly fragmented in recent decades (Papillon & Godron 1997; Palomares et al. 2001; Virgos et al. 2003). Secondly, young rabbits are protected against the disease, but can develop an immune response if they are in contact with the virus (Robinson et al. 2002). Lastly, the impact of RHD appears to be highly variable among populations, being high in some populations whereas in others most individuals are carrying protective antibodies against the virus without reported mass mortality from the disease (Rodak et al. 1990a, 1991; Chasey et al. 1995; Capucci et al. 1997; Nowotny et al. 1997). Increased impact of RHD in Europe in relation to rabbit population fragmentation thus represents an interesting alternative to the classical view according to which RHD has emerged through a mutation in the pathogenic agent.
Re-emergence of severe forms of an animal disease with subsequent mass mortality may have consequences for the transmission of pathogens to humans. A good example may be the case of diseases transmitted by fleas, such as the bubonic plague. Keeling & Gilligan (2000a,b) have shown that cases of human plague were strongly correlated to mass mortality in the disease reservoir, rats. Mass mortality of rats causes fleas to search for an alternative host, such as humans, hence transmitting the bacteria. These authors have shown that increased isolation of rat populations led to increased emergence in humans. Indeed in large rat populations, the disease never disappears, causing regular exposure of all individuals. Deaths spread out over time and the rat population is only minimally reduced. In contrast, in poorly connected rat populations, susceptible rats accumulate, resulting in a large epidemic when the pathogen is re-introduced and a significant reduction in the rat population. Consequently, there is a greater likelihood of transmission to humans. Since this mechanism is based on the different impact of the pathogen between epidemic and endemic periods in rats, attenuation of early infections could play an important role by increasing the differential mortality between endemic and epidemic periods, thereby increasing the severity of epidemics.
5. Conclusion
In conclusion, some pathogens may circulate in a population without being detected because they cause little damage to the host population. This low impact may in fact hide a great potential lethality. A change in environmental conditions, e.g. fragmentation of the host population, may upset the balance by preventing early infection of young. Thus, a disease that appears benign could become severe.
Acknowledgments
We thank the ANR ‘Santé-Environnement et Santé-travail’, programme ‘Pathocénoses et émergence des maladies transmissibles: un concept unificateur mis à l'épreuve sur des pathologies exemplaires’ for financial support, M. Guiserix, J.S. Guitton, R. Regoes, L. Crooks, J. O'Brien, O. Matthews and F. Sauvage for their helpful comments.
Supplementary Material
A description of the deterministic homogeneous-mixing version of the model with, as a basic result, the annual number of individuals developing each form of the disease at the equilibrium, according to the pathogen transmission rate. A description of the method used to estimate the persistence and reintroduction times of the pathogen for each stage of the fragmentation process. A description of the impact of the pathogen within each subpopulation and a figure showing how the impact of the pathogen in a subpopulation depends on its number of neighbours
References
- Aguas R, Goncalves G, Gomes M.G. Pertussis: increasing disease as a consequence of reducing transmission. Lancet Infect. Dis. 2006;6:112–117. doi: 10.1016/S1473-3099(06)70384-X. [DOI] [PubMed] [Google Scholar]
- Anderson H, Britton T. Stochastic epidemics in dynamic populations: quasi-stationarity and extinction. J. Math. Biol. 2000;41:559–580. doi: 10.1007/s002850000060. [DOI] [PubMed] [Google Scholar]
- Anderson R.M, May R.M. Oxford University Press; Oxford, UK: 1991. Infectious diseases of humans: dynamics and control. pp. 99–121. [Google Scholar]
- Bennett J, Whittle H, Samb B, Cisse B, Simondon F, Aaby P. Seroconversion in unvaccinated infants: further evidence for subclinical measles from vaccine trials in Niakhar, Senegal. Int. J. Epidemiol. 1999;28:147–151. doi: 10.1093/ije/28.1.147. [DOI] [PubMed] [Google Scholar]
- Bolker B, Grenfell B. Space, persistence and dynamics of measles epidemics. Phil. Trans. R. Soc. B. 1995;348:309–320. doi: 10.1098/rstb.1995.0070. [DOI] [PubMed] [Google Scholar]
- Bunimovich-Mendrazitsky S, Stone L. Modeling polio as a disease of development. J. Theor. Biol. 2005;237:302–315. doi: 10.1016/j.jtbi.2005.04.017. [DOI] [PubMed] [Google Scholar]
- Capucci L, Fusi P, Lavazza A, Pacciarini M.L, Rossi C. Detection and preliminary characterization of a new rabbit calicivirus related to rabbit hemorrhagic disease virus but nonpathogenic. J. Virol. 1996;70:8614–8623. doi: 10.1128/jvi.70.12.8614-8623.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capucci L, Fusi P, Lavazza A, Nardin A, Pacciarini M.L, Rossi C. Identification and characterisation of a nonpathogenic calicivirus related to rabbit haemorrhagic disease virus (RHDV) In: Chasey D, Gaskell R.M, Clarke I.N, editors. Proc. of the 1st Int. Symp. on Caliciviruses of the European Society of Veterinary Virology. European Society of Veterinary Virology and Central Veterinary Laboratory; Weybridge, UK: 1997. pp. 229–237. [Google Scholar]
- Carlsson-Graner U, Thrall P.H. The spatial distribution of plant populations, disease dynamics and evolution of resistance. Oikos. 2002;97:97–110. doi: 10.1034/j.1600-0706.2002.970110.x. [DOI] [Google Scholar]
- Chasey D, Lucas M.H, Westcott D.G, Sharp G, Kitching A, Hughes S.K. Development of a diagnostic approach to the identification of rabbit haemorrhagic disease. Vet. Rec. 1995;137:158–160. doi: 10.1136/vr.137.7.158. [DOI] [PubMed] [Google Scholar]
- Codeco C.T, Luz P.M. Is pertussis actually reemerging? Insights from an individual-based model. Cad Saude Publica. 2001;17:491–500. doi: 10.1590/s0102-311x2001000300005. [DOI] [PubMed] [Google Scholar]
- Cohen M.L. Changing patterns of infectious disease. Nature. 2000;406:762–767. doi: 10.1038/35021206. [DOI] [PubMed] [Google Scholar]
- Coleman P.G, Perry B.D, Woolhouse M.E.J. Endemic stability—a veterinary idea applied to human public health. Lancet. 2001;357:1284–1286. doi: 10.1016/S0140-6736(00)04410-X. [DOI] [PubMed] [Google Scholar]
- Cow D.R, Miller H.D. Chapman and Hall; London, UK: 1965. The theory of stochastic processes. [Google Scholar]
- Crowe J.E, Firestone C, Murphy B.R. Passively acquired antibodies suppress humoral but not cell-mediated immunity in mice immunized with live attenuated respiratory syncytial virus vaccines. J. Immunol. 2001;167:3910–3918. doi: 10.4049/jimmunol.167.7.3910. [DOI] [PubMed] [Google Scholar]
- Fouchet D, Marchandeau S, Langlais M, Pontier D. Waning of maternal immunity and the impact of diseases: the example of myxomatosis in natural rabbit populations. J. Theor. Biol. 2006;242:81–89. doi: 10.1016/j.jtbi.2006.02.003. [DOI] [PubMed] [Google Scholar]
- Glass K, Grenfell B.T. Antibody dynamics in childhood diseases: waning and boosting of immunity and the impact of vaccination. J. Theor. Biol. 2003;221:121–131. doi: 10.1006/jtbi.2003.3181. [DOI] [PubMed] [Google Scholar]
- Glass K, Grenfell B.T. Waning immunity and subclinical measles infections in England. Vaccine. 2004;22:4110–4116. doi: 10.1016/j.vaccine.2004.02.047. [DOI] [PubMed] [Google Scholar]
- Gomes M.G, White L.J, Medley G.F. Infection, re-infection, and vaccination under suboptimal immune protection: epidemiological perspectives. J. Theor. Biol. 2004;228:539–549. doi: 10.1016/j.jtbi.2004.02.015. [DOI] [PubMed] [Google Scholar]
- Hess G. Conservation corridors and contagious disease: a cautionary note. Conserv. Biol. 1994;8:256–262. doi: 10.1046/j.1523-1739.1994.08010256.x. [DOI] [Google Scholar]
- Hess G. Disease in metapopulations: implications for conservation. Ecology. 1996;77:1617–1632. doi: 10.2307/2265556. [DOI] [Google Scholar]
- Hon K.L.E, et al. Clinical presentations and outcome of severe acute respiratory syndrome in children. Lancet. 2003;361:1701–1703. doi: 10.1016/S0140-6736(03)13364-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J. Evolutionary trade-offs at two time-scales: competition versus persistence. Proc. R. Soc. B. 2000;267:385–391. doi: 10.1098/rspb.2000.1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J, Gilligan C.A. Bubonic plague: a metapopulation model of a zoonosis. Proc. R. Soc. B. 2000a;267:2219–2230. doi: 10.1098/rspb.2000.1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J, Gilligan C.A. Metapopulation dynamics of bubonic plague. Nature. 2000b;407:903–906. doi: 10.1038/35038073. [DOI] [PubMed] [Google Scholar]
- Keeling M.J, Grenfell B.T. Disease extinction and community size: modelling the persistence of measle. Science. 1997;275:335–343. doi: 10.1126/science.275.5296.65. [DOI] [PubMed] [Google Scholar]
- Kimman T.G, Zimmer G.M, Westenbrink F, Mars J, van Leeuwen E. Epidemiological study of bovine respiratory syncytial virus infections in calves: influence of maternal antibodies on the outcome of disease. Vet. Rec. 1988;123:104–109. doi: 10.1136/vr.123.4.104. [DOI] [PubMed] [Google Scholar]
- Leung C.W, et al. Severe acute respiratory syndrome among children. Pediatrics. 2004;113:535–543. doi: 10.1542/peds.113.6.e535. [DOI] [PubMed] [Google Scholar]
- Liu S.J, Xue H.P, Pu B.Q, Qian N.H. A new viral disease of rabbits. Anim. Husband. Vet. Med. 1984;16:253–255. [Google Scholar]
- Lloyd A.L. Destabilization of epidemic models with the inclusion of realistic distributions of infectious periods. Proc. R. Soc. B. 2001a;268:985–993. doi: 10.1098/rspb.2001.1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd A.L. Realistic distribution of infectious periods in epidemic models: changing patterns of persistence and dynamics. Theor. Popul. Biol. 2001b;60:59–71. doi: 10.1006/tpbi.2001.1525. [DOI] [PubMed] [Google Scholar]
- Morens D.M, Folkers G.K, Fauci A.S. The challenge of emerging and re-emerging diseases. Nature. 2004;430:242–249. doi: 10.1038/nature02759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moss S.R, Turner S.L, Trout R.C, White P.J, Hudson P.J, Desai A, Armesto M, Forrester N.L, Gould E.A. Molecular epidemiology of rabbit haemorrhagic disease virus. J. Gen. Virol. 2002;83:2461–2467. doi: 10.1099/0022-1317-83-10-2461. [DOI] [PubMed] [Google Scholar]
- Mossong J, Muller C.P. Modelling measles re-emergence as a result of waning of immunity in vaccinated populations. Vaccine. 2003;21:4597–4603. doi: 10.1016/S0264-410X(03)00449-3. [DOI] [PubMed] [Google Scholar]
- Norval R.A.I, Perry B.D, Young A.S. Academic Press; London, UK: 1992. The epidemiology of theleriosis in Africa. [Google Scholar]
- Nowotny N, Bascunana C.R, Ballagi-Pordany A, Gavier- Widen D, Uhlen M, Belak S. Phylogenetic analysis of rabbit haemorrhagic disease and European brown hare syndrome viruses by comparison of sequences from the capsid protein gene. Arch. Virol. 1997;142:657–673. doi: 10.1007/s007050050109. [DOI] [PubMed] [Google Scholar]
- Palomares F, Delibes M, Revilla E, Calzada J, Fedriani J.M. Spatial ecology of Iberian lynx and abundance of European rabbits in southwestern Spain. Wildl. Monogr. 2001;148:1–36. [Google Scholar]
- Papillon Y, Godron M. Distribution spatiale du lapin de garenne (Oryctolagus cuniculus) dans le Puy-de-Dôme: l'apport des analyses de paysages. Gibier Faune Sauvage/Game and Wildlife. 1997;14:303–324. [Google Scholar]
- Parer I. The population ecology of the wild rabbit, Oryctolagus cuniculus (L.), in a Mediterranean-type climate in New South Wales. Aust. Wildl. Res. 1977;4:171–205. doi: 10.1071/WR9770171. [DOI] [Google Scholar]
- Park A.W, Gubbins S, Gilligan C.A. Extinction times for closed epidemics: the effects of host spatial structure. Ecol. Lett. 2002;5:747–755. doi: 10.1046/j.1461-0248.2002.00378.x. [DOI] [Google Scholar]
- Prince G.A, Hemming V.G, Horswood R.L, Chanock R.M. Immunoprophylaxis and immunotherapy of respiratory syncytial virus infection in the cotton rat. Virus Res. 1985;3:193–206. doi: 10.1016/0168-1702(85)90045-0. [DOI] [PubMed] [Google Scholar]
- Prince G.A, Hemming V.G, Horswood R.L, Baron P.A, Chanock R.M. Effectiveness of topically administered neutralizing antibodies in experimental immunotherapy of respiratory syncytial virus infection in cotton rats. J. Virol. 1987;61:1851–1854. doi: 10.1128/jvi.61.6.1851-1854.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson A.J, So P.T.M, Muller W.J, Cooke B, Capucci L. Statistical models for the effect of age and maternal antibodies on the development of rabbit haemorrhagic disease in Australian wild rabbits. Wildl. Res. 2002;29:663–371. doi: 10.1071/WR00119. [DOI] [Google Scholar]
- Rodak L, Granatova M, Valicek L, Smid B, Vesely T, Nevorankova Z. Monoclonal antibodies to rabbit haemorrhagic disease virus and their use in the diagnosis of infection. J. Gen.Virol. 1990a;71:2593–2598. doi: 10.1099/0022-1317-71-11-2593. [DOI] [PubMed] [Google Scholar]
- Rodak L, Smid B, Valicek L, Vesely T, Stepanek J, Hampl J, Jurak E. Enzyme-linked immunosorbent assay of antibodies to rabbit haemorrhagic disease virus and determination of its major structural proteins. J. Gen. Virol. 1990b;71:1075–1080. doi: 10.1099/0022-1317-71-5-1075. [DOI] [PubMed] [Google Scholar]
- Rodak L, Smid B, Valicek L. Application of control measures against viral haemorrhagic disease of rabbits in the Czech and Slovak Federal Republics. Rev. Sci. Tech. OIE. 1991;10:513–524. [PubMed] [Google Scholar]
- Rogers P.M, Arthur C.P, Soriguer R.C. The rabbit in continental Europe. In: Thompson H.V, King C.M, editors. The European rabbit. The history of a successful colonizer. Oxford University Press; Oxford, UK: 1994. pp. 22–63. [Google Scholar]
- Ruvoën-Clouet N, Ganiére J.P, André-Fontaine G, Blanchard D, Le Pendu J. Binding of rabbit hemorrhagic disease virus to antigens of the ABH histo-blood group family. J. Virol. 2000;74:11 950–11 954. doi: 10.1128/JVI.74.24.11950-11954.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snow R.W, Nahlen B, Palmer A, Donnelly C.A, Gupta S, Marsh K. Risk of severe malaria among African infants: direct evidence of clinical protection during early infancy. J. Infect. Dis. 1998;177:819–822. doi: 10.1086/517818. [DOI] [PubMed] [Google Scholar]
- Swinton J, Harwood J, Grenfell B.T, Gilligan C.A. Persistence thresholds for phocine distemper virus infection in harbour seal Phoca vitulina metapopulations. J. Anim. Ecol. 1998;67:54–68. doi: 10.1046/j.1365-2656.1998.00176.x. [DOI] [Google Scholar]
- Trout R.C, Chasey D, Sharp G. Seroepidemiology of rabbit haemorrhagic disease (RHD) in wild rabbits (Oryctolagus cuniculus) in the United Kingdom. J. Zool. Lond. 1997;243:846–853. [PubMed] [Google Scholar]
- Virgos E, Cabezas-Diaz S, Malo A, Lozano G, Lopez-Huertas D. Factors shaping European rabbit abundance in continuous and fragmented populations of central Spain. Acta Theriologica. 2003;48:13–122. [Google Scholar]
- Wagner G, Koram K, McGuinness D, Bennett S, Nkrumah F, Riley E. High incidence of asymptomatic malaria infections in a birth cohort of children less than one year of age in Ghana, detected by multicopy gene polymerase chain reaction. Am. J. Trop. Med. Hyg. 1998;59:115–123. doi: 10.4269/ajtmh.1998.59.115. [DOI] [PubMed] [Google Scholar]
- Walsh E.E, Schlesinger J.J, Brandriss M.W. Protection from respiratory syncytial virus infection in cotton rats by passive transfer of monoclonal antibodies. Infect. Immun. 1994;43:756–758. doi: 10.1128/iai.43.2.756-758.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanni M.L, Benassi M.C, Scicluna M.T, Lavazza A, Capucci L. Clinical evolution and diagnosis of an outbreak of European brown hare syndrome in hares reared in captivity. Rev. Sci. Tech. Off. Int. Epiz. 1993;12:931–940. doi: 10.20506/rst.12.3.727. [DOI] [PubMed] [Google Scholar]
- Zinkernagel R.M. Maternal antibodies, childhood infections, and autoimmune diseases. N. Engl. J. Med. 2001;345:1331–1335. doi: 10.1056/NEJMra012493. [DOI] [PubMed] [Google Scholar]
- Zinkernagel R.M. On natural and artificial vaccinations. Annu. Rev. Immunol. 2003;21:515–546. doi: 10.1146/annurev.immunol.21.120601.141045. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
A description of the deterministic homogeneous-mixing version of the model with, as a basic result, the annual number of individuals developing each form of the disease at the equilibrium, according to the pathogen transmission rate. A description of the method used to estimate the persistence and reintroduction times of the pathogen for each stage of the fragmentation process. A description of the impact of the pathogen within each subpopulation and a figure showing how the impact of the pathogen in a subpopulation depends on its number of neighbours