Soft protein–protein docking in internal coordinates

Abstract

The association of two biological macromolecules is a fundamental biological phenomenon and an unsolved theoretical problem. Docking methods for ab initio prediction of association of two independently determined protein structures usually fail when they are applied to a large set of complexes, mostly because of inaccuracies in the scoring function and/or difficulties on simulating the rearrangement of the interface residues on binding. In this work we present an efficient pseudo-Brownian rigid-body docking procedure followed by Biased Probability Monte Carlo Minimization of the ligand interacting side-chains. The use of a soft interaction energy function precalculated on a grid, instead of the explicit energy, drastically increased the speed of the procedure. The method was tested on a benchmark of 24 protein–protein complexes in which the three-dimensional structures of their subunits (bound and free) were available. The rank of the near-native conformation in a list of candidate docking solutions was <20 in 85% of complexes with no major backbone motion on binding. Among them, as many as 7 out of 11 (64%) protease-inhibitor complexes can be successfully predicted as the highest rank conformations. The presented method can be further refined to include the binding site predictions and applied to the structures generated by the structural proteomics projects. All scripts are available on the Web.

Molecular recognition is involved in all biological processes. Detailed energetic and structural knowledge of interactions between biomolecules is fundamental to understand the complex regulatory and metabolic pathways that occur in living organisms and also to design drugs for blocking or modifying these interactions. A large number of protein structures have been experimentally determined and deposited in the Protein Data Bank (PDB; Bernstein et al. 1977), and this number will grow rapidly with the development of new high-throughput technologies in structural genomics (Sanchez and Sali 1998). However, only a small fraction of numerous protein–protein complexes has been experimentally characterized so far. In this context, theoretical prediction of protein–protein complexes is becoming critically important in structural biology.

In recent years, several groups have developed a variety of tools in an attempt to solve the so-called protein–protein docking problem, that is, the prediction of the geometry of a complex from the atom coordinates of its uncomplexed constituents (for review, see Sternberg et al. 1998). Early protein–protein docking algorithms used exclusively a geometric criterion (Connolly 1986; Yue 1990) based on the shape complementarity. Purely geometry-based rigid-body docking methods perform well in an artificial task of rebuilding a complex after separation of its bound subunits (Katchalski-Katzir et al. 1992; Helmer-Citterich and Tramontano 1994; Vakser and Aflalo 1994; Fischer et al. 1995; Norel et al. 1999). However, the results of docking uncomplexed subunits were unsatisfactory because of both induced conformational changes and inaccuracies of the energy function that can only be poorly represented by a geometrical fitness term (Vakser and Aflalo 1994; Fischer et al. 1995; Norel et al. 1999).

There are two general strategies to improve the efficiency of these simplistic rigid-body methods. One is the inclusion of binding determinants other than pure surface complementarity, such as hydrogen bonding (Meyer et al. 1996), electrostatic energy (Bacon and Moult 1992; Hart and Read 1992), solvation (Cummings et al. 1995), or hydrophobicity (Wallqvist and Covell 1996). A second strategy is to simulate, or at least mimic, the induced conformational fit on binding. The simplest methods to include molecular flexibility were limited to the softening of the geometric criteria, allowing some overlap of the interacting surfaces (Jiang and Kim 1991; Vakser 1995). This soft approach has been complemented with the inclusion of additional energetic terms (Walls and Sternberg 1992; Ausiello et al. 1997; Gabb et al. 1997; Palma et al. 2000). Energy optimization with explicit treatment of flexibility can be more accurate, but a full conformational search is still not practical. However, because molecular association involves only small conformational changes in most of the known protein–protein complexes (Betts and Sternberg 1999; Conte et al. 1999; Norel et al. 1999), computational requirements can be dramatically lowered by limiting conformational flexibility to interface side-chains, as has been performed for protein-ligand docking (Schnecke and Kuhn 2000) and for protein–protein docking (Cherfils et al. 1991; Shoichet and Kuntz 1991; Weng et al. 1996; Jackson et al. 1998; Camacho et al. 2000). A similar strategy, based on the Internal Coordinate Mechanics (ICM; Li and Scheraga 1987^; Abagyan and Mazur 1989^; Mazur and Abagyan 1989^; Abagyan and Argos 1992), was successfully applied to the prediction of an antibody-lysozyme complex (Totrov and Abagyan 1994) and was later tested in a blind prediction contest (Strynadka et al. 1996a). The ICM pseudo-Brownian method (Abagyan et al. 1994) with subsequent global optimization (Abagyan and Totrov 1994) of the interface side-chain rotations proved to be highly accurate but, at the same time, computationally too expensive to be tested on large databases of complexes.

In this paper, we propose a two-step docking procedure (rigid-body docking followed by ICM side-chain optimization) that uses a fast soft-interaction energy function precalculated on a grid (Goodford 1985). The use of grid potentials, instead of the explicit energy, drastically increased the speed of the procedure. The method has been applied to a set of 24 protein–protein complexes in which the three-dimensional (3D) structures of their subunits (bound and free) are known. To our knowledge, it constitutes the largest application of a fully automated docking method to a diverse set of protein–protein complexes predicted from the 3D structures of uncomplexed subunits. The optimized docking and refinement procedure correctly predicted seven out of 11 protease-inhibitor complexes with no major backbone rearrangement on binding, which is a clear improvement over previously reported results.

Results

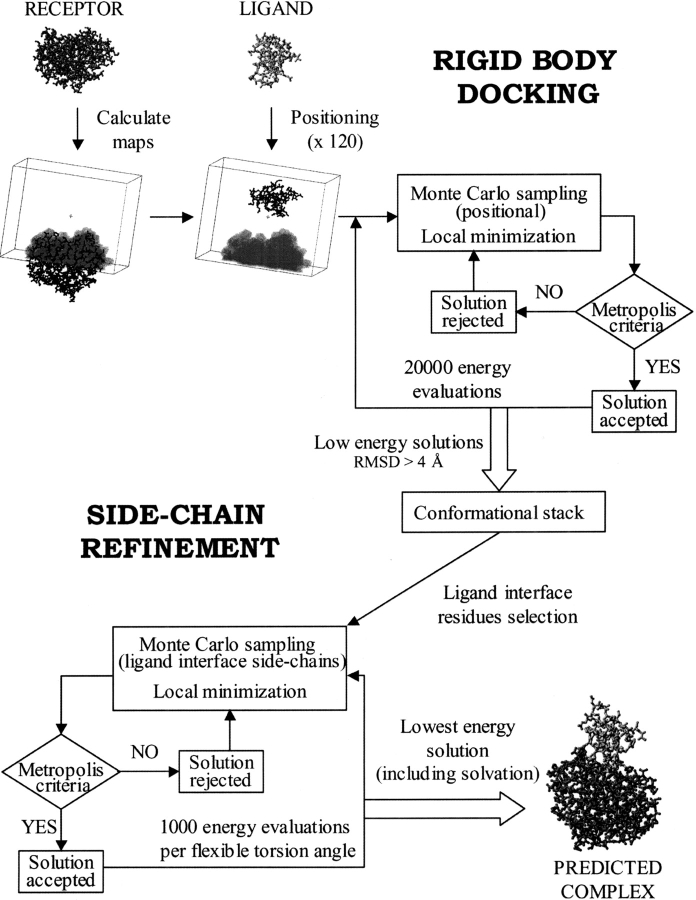
A two-step docking procedure (Fig. 1 ▶) using soft grid potentials (see details in Materials and Methods) is presented here. The algorithm was tested on a nonredundant data set of protein–protein complexes with available 3D coordinates for their subunits in both bound and unbound conformation (see Materials and Methods). We initially applied the fast rigid-body step to the rebuilding of the 24 test case complexes, starting from the coordinates of the complexed subunits. Next, we tested the same procedure on the unbound subunits of these complexes. The parameters of the simulations were subsequently improved, and the grid potentials were optimized. Finally, the solutions generated during the rigid-body step were further refined by flexible minimization of the ligand interface side-chains (Fig. 1 ▶).

Fig. 1.

Flowchart of the docking procedure used in this work.

Redocking complexed molecules

The initial docking procedure (first rigid-body step; Fig. 1 ▶) was applied to the rebuilding of the structures of the 24 complexes using the coordinates of their complexed subunits. Although these initial conformations are unrealistic, the redocking experiment is an important first test of the conformational sampling procedure and the energy function used. The results are shown in Table 1. The procedure always found a solution with root mean square deviation (RMSD) <1.3 Å from the experimental structure (calculated for the ligand interface C^α atoms when only the receptor C^α atoms were superimposed onto the crystallographic structure) within the 30 lowest energy conformations. The RMSD for the near-native solution ranged from 0.3 (complex 1cho) to 1.3 Å (complex TEM1). In Figure 2 ▶ are shown the near-native solutions obtained for these two extreme cases. According to the scoring function used (see Materials and Methods), the near-native solution ranked first in all complexes except for one (cytochrome c peroxidase/cytochrome c complex; see Discussion).

Table 1.

Redocking complexed subunits

					Other docking methods
Complex PDB	Res (Å)	Receptor name	Ligand name	ICM dockinga	Nussinovb	FTDOCKc	BiGGERd
Protease-inhibitor
1ca0	2.10	Chymotrypsin	APPI	1 of 30 (0.4)	—	—	—
1cbw	2.60	Chymotrypsin	BPTI	1 of 30 (0.4)	—	—	—
1acb	2.00	Chymotrypsin	Eglin C	1 of 30 (0.5)	1 of 1121 (0.9)	—	18 of 1000 (0.6)
1cho	1.80	Chymotrypsin	Ovomucoid	1 of 30 (0.3)	1 of 471 (0.5)	40 of 218 (0.8)	—
1cgi	2.30	Chymotrypsinogen	HPTI	1 of 30 (0.4)	—	3 of 161 (1.0)	—
2kai	2.50	Kallikrein A	BPTI	1 of 30 (0.8)	11 of 1227 (1.2)	38 of 502 (0.4)	—
2sni	2.10	Subtilisin BPN	CI-2	1 of 30 (0.3)	1 of 1367 (1.1)	8 of 54 (0.6)	—
2sic	1.80	Subtilisin BPN	SSI	1 of 30 (0.4)	1 of 1229 (1.1)	22 of 30 (0.8)	2 of 1000 (3.8)
1cse	1.20	Subtilisin Carlsberg	Eglin C	1 of 30 (0.3)	2 of 1024 (1.3)	—	—
2tec	1.98	Thermitase	Eglin C	1 of 30 (0.3)	1 of 1042 (1.2)	—	77 of 1000 (3.6)
1taw	1.80	Trypsin (bovine)	APPI	1 of 30 (0.7)	—	—	—
2ptc	1.90	Trypsin (bovine)	BPTI	1 of 30 (0.4)	1 of 1027 (0.6)	91 of 513 (0.7)	—
3tgi	1.80	Trypsin (rat)	BPTI	1 of 30 (0.3)	—	—	—
1brc	2.50	Trypsin (rat)	APPI	1 of 30 (0.7)	—	—	—
Enzyme-inhibitor
1fss	3.00	Acetylcholinesterase	Fasciculin II	1 of 30 (0.4)	—	—	—
1bvn	2.50	α-amylase	Tendamistat	1 of 30 (0.4)	—	—	—
1bgs	2.60	Barnase	Barstar	1 of 30 (0.6)	—	—	—
1ay7	1.70	Ribonuclease sa	Barstar	1 of 30 (0.7)	—	—	—
TEM1e	1.70	TEM-1 β-lactamase	BLIP	1 of 30 (1.3)	—	—	—
1ugh	1.90	UDG	UGI	1 of 30 (0.4)	—	—	—
Electron transport
2pcb	2.80	Cyt c Peroxidase	Cytochrome c	4 of 30 (1.2)	—	—	—
2pcf	NMR	Cytochrome f	Plastocyanin	1 of 30 (1.1)	—	—	—
Antibody-antigen
1mlc	2.10	Fab D44.1	Lysozyme	1 of 30 (0.4)	—	2 of 507 (0.8)	—
1vfb	1.80	Fv D1.3	Lysozyme	1 of 30 (0.5)	20 of 2181 (1.5)	240 of 631 (0.7)	—

^a Rank of best solution and total number of conformations obtained in this work; in parentheses: r.m.s.d. (Å) calculated for the ligand interface C^α atoms of the best solution when only the receptor C^α atoms are superimposed onto the equivalent atoms of the real structure.

^b Global docking followed by hydrophobicity and connectivity filters (Norel et al. 1999); r.m.s.d. (Å) calculated for the ligand heavy atoms when only receptor is superimposed onto the real structure.

^c Global docking and filtering with distance restraints (Gabb et al. 1997); r.m.s.d. (Å) calculated for all C^α atoms when both receptor and ligand C^α atoms are superimposed onto the real complex.

^d Global docking (Palma et al. 2000); r.m.s.d. (Å) calculated for the ligand C^α atoms when only the receptor C^α atoms are superimposed onto the real structure.

^e No coordinates deposited in PDB: the structures were kindly provided by the authors (Strynadka et al. 1996b).

Fig. 2.

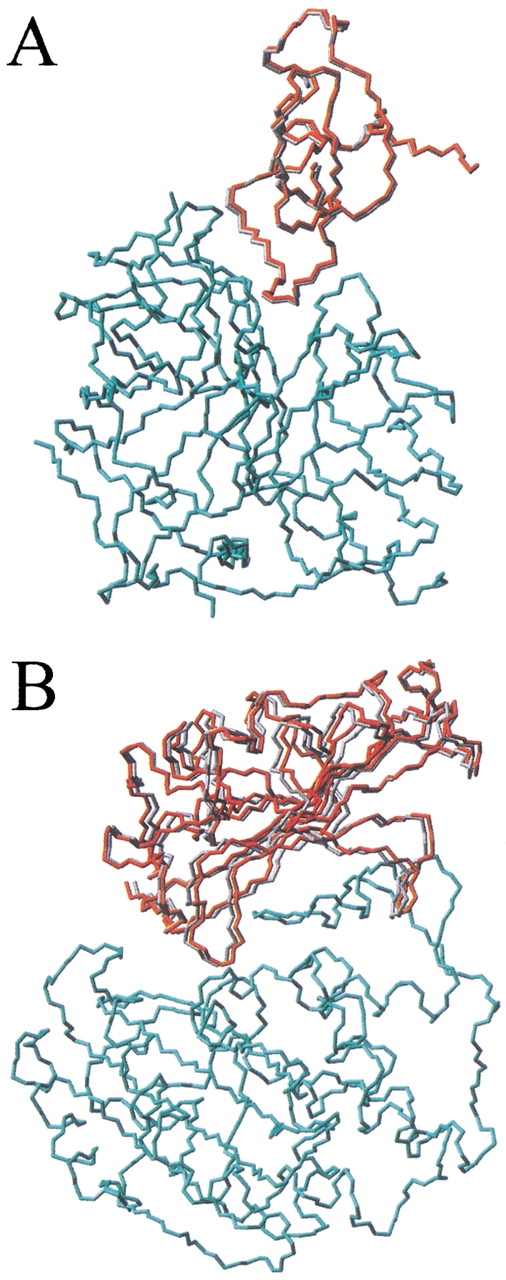
Representation of the near-native solutions obtained after redocking complexed subunits: (A) 1cho; root mean square deviation (RMSD), 0.3 Å; and (B) TEM1; RMSD, 1.3 Å. In red is represented the predicted ligand molecule, compared with the real structure (in gray). Only the receptor C^α atoms (in cyan) are optimally superimposed onto the corresponding atoms of the real complex. For clarity, only backbone atoms (nitrogen, C^α, and carbonyl carbon) are shown.

This preliminary test indicates that the evaluation function is able to score properly the native solution and permits a fast conformational sampling starting from a random position. These results encouraged us to apply this algorithm to the more realistic problem, that is, the prediction of the complex structure starting from the unbound subunits.

Docking unbound molecules

The rigid-body docking procedure (see Materials and Methods) was also applied to the unbound subunits of the 24 complexes. The results are shown in Table 2 (original maps column). The number of total conformations obtained for each complex ranged from 4078 to 7378. It was possible to find a solution close to the real structure (RMSD <4.0 Å) in all test cases but one (2pcf; RMSD, 5.3 Å). After sorting solutions according to their energy values, the near-native conformations ranked from 1 (complex TEM1) to 3981 (complex 1acb). This wide scope of rank values clearly reflected the limitations of the rigid-body approach in the realistic situation (starting from unbound subunits), in which a softer energy function is needed to overcome the energy penalties arising from the rigidity of the interacting side-chains. Furthermore, although the rigid simulation could tolerate relatively large errors in most energy terms as long as the shape was complementary (when using complexed subunits), the real simulation imposed much stricter requirements to the accuracy of all energy terms.

Table 2.

Docking unbound subunits

	Receptor		Ligand		ICM dockinga			Other docking methodsb
Complex PDB	PDB	Res (Å)	PDB	Res (Å)	Original maps	Optimized maps	Refinement	Nussinovc	FTDOCKd	FTDOCKe	BiGGERf
Protease-inhibitor
1ca0	5cha	1.67	1aap	1.50	24 of 4153 (1.7)	6 of 228 (1.4)	1 of 228 (1.2)	—	—	—	—
1cbw	5cha	1.67	1bpi	1.10	167 of 5492 (1.2)	5 of 231 (0.9)	1 of 231 (0.7)	—	—	—	—
1acb	5cha	1.67	1egl	NMR	3981 of 4511 (B.D.)g	135 of 239 (B.D.)g	102 of 239 (Backbone Def.)g	—	—	—	—
1cho	5cha	1.67	1omu	NMR	10 of 5063 (1.2)	7 of 242 (2.6)	1 of 242 (1.0)	2 of 2289 (1.6)	11 of 86 (1.2)	1 of 86 (1.3)	6 of 1000 (2.9)
1cgi	1chg	2.50	1hpt	2.30	18 of 5261 (3.6)	8 of 256 (3.4)	12 of 256 (3.1)	—	3 of 94 (1.8)	3 of 94 (2.2)	9 of 1000 (3.7)
2kai	2pka	2.05	1bpi	1.10	823 of 4078 (3.8)	36 of 241 (4.1)	2 of 241 (5.5)	9 of 4222 (1.2)	130 of 364 (1.5)	2 of 364 (1.3)	Not found
2sni	2st1	1.80	2ci2	2.00	243 of 4286 (2.9)	66 of 220 (2.5)	1 of 220 (2.9)	92 of 3582 (2.6)	8 of 26 (1.8)	4 of 26 (2.6)	16 of 1000 (1.3)
2sic	2st1	1.80	3ssi	2.30	67 of 4109 (2.4)	37 of 223 (2.4)	7 of 223 (1.9)	—	Not found	—	15 of 1000 (3.3)
1cse	1sbc	2.50	1egl	NMR	70 of 7378 (B.D.)g	167 of 246 (B.D.)g	40 of 246 (Backbone Def.)g	—	—	—	—
2tec	1thm	1.37	1egl	NMR	172 of 5613 (B.D.)g	175 of 247 (B.D.)g	146 of 247 (Backbone Def.)g	—	—	—	—
1taw	5ptp	1.34	1aap	1.50	288 of 4086 (2.2)	1 of 228 (3.5)	1 of 228 (2.9)	—	—	—	—
2ptc	5ptp	1.34	1bpi	1.10	569 of 4632 (1.8)	41 of 229 (1.0)	3 of 229 (2.0)	1 of 3453 (1.2)	16 of 229 (1.5)	11 of 229 (1.6)	52 of 1000 (2.7)
3tgi	1ane	2.20	1bpi	1.10	1756 of 5718 (1.1)	23 of 243 (0.6)	1 of 243 (0.8)	—	—	—	—
1brc	1bra	2.20	1aap	1.50	87 of 4651 (2.3)	1 of 237 (3.7)	1 of 237 (1.8)	—	—	—	—
Enzyme-inhibitor
1fss	2ace	2.50	1fsc	2.00	66 of 6649 (1.7)	51 of 264 (1.5)	7 of 264 (1.7)	—	—	—	11 of 1000 (3.2)
1bvn	1pif	2.30	2ait	NMR	2689 of 5858 (1.8)	2 of 265 (5.0)	7 of 265 (5.0)	—	—	—	—
1bgs	1a2p	1.50	1a19	2.76	139 of 6279 (3.9)	55 of 290 (3.4)	212 of 290 (4.2)	—	—	—	35 of 1000 (1.9)
1ay7	1rge	1.15	1a19	2.76	484 of 4765 (3.9)	208 of 284 (5.2)	156 of 284 (6.2)	—	—	—	—
TEM1h	retmh	1.90	bliph	2.10	1 of 4512 (2.4)	2 of 240 (2.8)	12 of 240 (3.1)	—	—	—	—
1ugh	1akz	1.57	2ugi	2.20	72 of 6560 (2.4)	9 of 300 (2.8)	9 of 300 (4.8)	—	—	—	—
Electron transport
2pcb	1ccp	2.20	1hrc	1.90	3307 of 5193 (2.3)	80 of 252 (4.1)	46 of 252 (3.2)	—	—	—	18 of 1000 (2.4)
2pcf	1ctm	2.30	1ag6	1.70	19 of 6037 (5.3)	58 of 283 (4.9)	9 of 283 (5.2)	—	—	—	—
Antibody-antigen
1mlc	1mlb	2.10	1lza	1.60	2435 of 5099 (3.3)	21 of 259 (5.3)	16 of 259 (5.1)	—	41 of 590 (1.2)	—	Not found
1vfb	1vfa	1.80	11za	1.60	51 of 4253 (B.D.)g	30 of 291 (B.D.)g	75 of 291 (Backbone Def.)g	—	176 of 707 (2.1)	—	Not found

^a Rank of best solution and total number of conformations obtained in this work; in parentheses: r.m.s.d. (Å) calculated for the ligand interface C^α atoms of the best solution when only the receptor C^α atoms are superimposed onto the equivalent atoms of the real structure.

^b This is not a comparison between different docking methods, but rather a compilation of the results. The receptor coverage/restraints differ between the algorithms, so a direct comparison between the results could be misleading.

^c Global docking followed by hydrophobicity and connectivity filters (Norel et al. 1999); r.m.s.d. (Å) calculated for ligand heavy atoms when only receptor is superimposed onto the real structure.

^d Global docking and filtering with distance restraints (Gabb et al. 1997); r.m.s.d. (Å) calculated for all C^α atoms when both receptor and ligand C^α atoms are superimposed onto the real complex.

^e Global docking, filtering with distance restraints and refinement with solvation (Jackson et al. 1998); r.m.s.d. (Å) calculated for all C^α atoms when both receptor and ligand C^α atoms are superimposed onto the real complex.

^f Global docking (Palma et al. 2000); r.m.s.d. (Å) calculated for the ligand C^α atoms when only the receptor C^α atoms are superimposed onto the real structure.

^g Ligand backbone deformation upon binding (r.m.s.d. of the unbound ligand backbone atoms in the interface >1.8 Å from the complexed ligand structure).

^h No coordinates deposited in PDB: the structures were kindly provided by the authors (Strynadka et al. 1992, 1994, 1996b).

The sampling procedure, however, worked efficiently. Because our method uses local gradient minimization, the best possible solution is the local minimum of the potential energy nearest to the crystallographic structure. The distance between local minima provides a measure of the fineness of our configurational sampling, which in preliminary studies was found to be only 1 to 2 Å on average. The efficient sampling procedure always found this best possible solution (near-native local minimum), even though it was not correctly ranked for all complexes. This indicated that to improve the rank of the best solution for the different complexes, we needed to focus on the optimization of the evaluation function.

We considered two general ways of improving the scoring function: (1) It should be softer to overcome geometric inaccuracies derived from the rigidity of the interacting side-chains of the unbound subunits; and (2) it should reflect more accurately the contribution of the different energy terms to the interaction energy for the near-native solution. A softer scoring function should decrease the penalties derived from the wrong conformation of the interacting unbound side-chains and thus should lower the energy of the near-native solution. However, making a function softer may also increase the number of false positives. This tradeoff can be optimized.

The need to calculate correct energies for approximate geometries leads to contradictory requirements of energy functions and prompted us to adjust the forcefield parameters and the balance of the energy terms to reflect their different responsiveness to small geometrical errors. Substantial variations of reported estimates for several terms (e.g., hydrogen bonding, hydrophobic effect) also indicate that the balance of the energy terms can be improved even for ideal geometries.

Optimizing potential maps

Softer van der Waals potentials were generated by decreasing the overlap penalty from 1.5 to 1.0 kcal/mole (see Materials and Methods). This substantially improved the rank of the near-native solution in half of the complexes (not shown). Further reduction of this truncation value did not help, because extremely soft potentials resulted in the generation of many new false positives during simulations.

The scoring function was also improved by modifying the relative weight of the different energy terms (the initial relative weight for each map was 1.0; see Materials and Methods, equation 5). New weighting values (used to reevaluate the accumulated low-energy docking solutions) were generated through a simplex minimization method (Nelder and Mead 1965), using the logarithm of the sum of the ranking values for all best solutions as an objective function (the logarithm function was used here to avoid an excessive influence of the poorly ranked complexes). With this methodology, we derived the optimal evaluation function represented in equation 1:

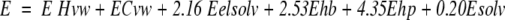1

New docking simulations were performed with these optimized maps (see Materials and Methods for an explanation of the different energy terms). Because the near-native solution was now expected to be better ranked, we selected only the 400 lowest energy solutions, which were further compressed to remove geometrically similar conformations. The results are shown in Table 2 (optimized maps column). In general, there was a significant improvement in the rank values of the near-native solutions. In two complexes (1taw and 1brc) the near-native conformation ranked first (according to their energy values), and in two other cases (TEM1 and 1bvn), it ranked second. Furthermore, almost all complexes (20 out of 24) contained a near-native solution within the first 100 lowest energy solutions. In three of the four remaining complexes (1acb, 1cse, and 2tec), the ligand molecule (eglin C) shows major backbone movement on binding, which justifies the poor rank of the near-native solution.

Final step: Refinement of interface side-chain conformations

Although the rank values of the near-native solution significantly improved for almost all complexes when using the maps optimized for the unbound molecules, there were only two cases in which the near-native solution ranked first. To improve the docking results starting from the unbound subunits, the interface side-chain conformations of the rigid-body docking solutions needed to be minimized by a second refinement step (Fig. 1 ▶). An explicit refinement of all interface side-chains (both receptor and ligand) using a complete energetic description of the system is computationally extremely expensive. Besides, a comparison of the side-chains in the unbound and bound subunits for the 24 complexes shows larger differences for ligand interface side-chains (average RMSD, 1.97 Å) than for receptor interface side-chains (average RMSD, 1.16 Å). For that reason, we attempted a partial refinement procedure, using the receptor grid potential maps for the intermolecular energy and an explicit full atom calculation for the internal energy of the ligand flexible side-chains (see Materials and Methods). The inclusion of flexibility in the ligand interface side-chains helped to partially overcome the steric penalty derived from the rigidity of the receptor side-chains, and therefore, the steric overlap tolerance could be reduced (i.e., the overlap penalty increased). The cutoff limit of the van der Waals map potential was thus increased to 1.5 kcal/mole to make the potentials more realistic. The results are shown in Table 2 (refinement column). Refinement of the interacting side-chains seemed to be insufficient to properly score the near-native solutions in those complexes that undergo major backbone rearrangement on binding (1acb, 1cse, 2tec, 1vfb). However, for the remaining 20 complexes, the near-native solution was, in general, significantly better ranked after refinement (it was found within the 20 lowest energy solutions in 17 of them). Moreover, in 35% of these complexes (seven out of 20), the near-native solution was correctly ranked as the lowest energy conformation. Figure 3 ▶ represents the structures of the near-native and lowest energy solutions obtained for each complex. Interestingly, all the complexes in which the near-native solution ranked first were of a protease-inhibitor type.

Fig. 3.

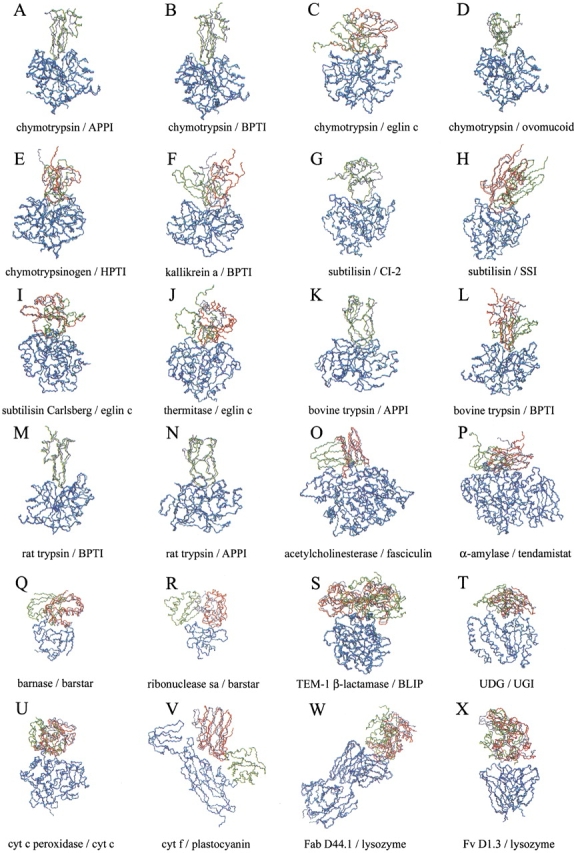
Representation of the near-native (in red) and lowest energy (in green) solutions after docking unbound subunits and further refinement of the ligand interface side-chains. For those complexes in which the near-native conformation was the lowest energy solution, only the latter is represented (in green). The real ligand structure is represented (in gray) for comparison. Only the receptor C^α atoms (in blue) are optimally superimposed onto the corresponding atoms of the real complex (in cyan). For clarity, only backbone atoms (nitrogen, C^α, and carbonyl carbon) are shown. The root mean square deviation (RMSD) of the near-native predicted structure respect to the real complex (calculated for the ligand interface C^α atoms when the receptor is optimally superimposed onto the real one) is indicated. (A) 1ca0, RMSD 1.2 Å; RANK 1; (B) 1cbw, RMSD 0.7 Å; RANK 1; (C) 1acb, RMSD 4.3 Å; RANK 102; (D) 1cho, RMSD 1.0 Å; RANK 1; (E) 1cgi, RMSD 3.1 Å; RANK 12; (F) 2kai, RMSD 5.5 Å; RANK 2; (G) 2sni, RMSD 2.9 Å; RANK 1; (H) 2sic, RMSD 1.9 Å; RANK 7; (I) 1cse, RMSD 2.5 Å; RANK 40; (J) 2tec, RMSD 8.1 Å; RANK 146; (K) 1taw, RMSD 2.9 Å; RANK 1; (L) 2ptc, RMSD 2.0 Å; RANK 3; (M) 3tgi, RMSD 0.8 Å; RANK 1; (N) 1brc, RMSD 1.8 Å; RANK 1; (O) 1fss, RMSD 1.7 Å; RANK 7; (P) 1bvn, RMSD 5.0 Å; RANK 7; (Q) 1bgs, RMSD 4.2 Å; RANK 212; (R) 1ay7, RMSD 6.2 Å; RANK 156; (S) TEM1, RMSD 3.1 Å; RANK 12; (T) 1ugh, RMSD 4.8 Å; RANK 9; (U) 2pcb, RMSD 3.2 Å; RANK 46; (V) 2pcf, RMSD 5.2 Å; RANK 9; (W) 1mlc, RMSD 5.1 Å; RANK 16; and (X) 1vfb, RMSD 3.1 Å; RANK 75. Complexes 1acb, 1cse, 2tec, and 1vfb present ligand backbone deformation on binding (RMSD of the unbound ligand backbone atoms in the interface >1.8 Å with respect to the complexed structure, after optimal superimposition of all ligand Cα atoms), so the indicated RMSD values for them may not reflect the accuracy of the predicted near-native conformations.

Discussion

In this work, we analyzed a soft protein–protein docking method consisting of a fast pseudo-Brownian Monte Carlo minimization (Abagyan et al. 1994) in a grid potential representation and a further ICM side-chain optimization (Abagyan and Totrov 1994). Because an ideal docking procedure should aim to predict the structure of any protein–protein complex, without focusing on specific features of a particular case, we attempted to test and optimize a docking method on the largest data set of protein–protein complex structures with available structural information for their individual unbound subunits. When rebuilding a protein–protein complex from their bound subunits (preliminary test), the near-native solution was the lowest energy conformation in 23 out of 24 complexes. In Table 1, our method is compared with other published docking procedures that have been already used to dock unbound subunits (and systematically tested in more than three complexes). Norel et al. (1999) predicted the near-native solution as the lowest energy conformation in six out of 10 complexes analyzed. The docking programs FTDOCK (Gabb et al. 1997) and BiGGER (Palma et al. 2000) were unable to predict the correct solution as the lowest energy conformation for any of the complexes analyzed here, which shows that docking prediction, even starting from complexed subunits, is still a very difficult task. The results obtained by the ICM docking procedure in rebuilding a complex from their bound subunits indicate that both the energy function and conformational sampling are reasonable.

Regarding the realistic problem of docking the free molecules to predict a complex structure, we performed a two-step procedure (rigid-body docking and refinement of ligand side-chains of resulting conformations) that found a near-native solution as the lowest energy conformation in seven out of 24 complexes. The results are compared with other published docking methods in Table 2. The FTDOCK rigid-body docking program followed by a refinement step (Jackson et al. 1998) found only one complex (out of five) in which the near-native solution ranked first. This program uses distance restraints to filter solutions, and presents much worse results when no experimental information is included in the procedure (in the best case, the near-native solution is ranked the 87th). Similarly, Norel et al. (1999) found a first ranked near-native solution in only one complex (out of four). They applied a global search docking and a connectivity filter, with no experimental restraints. The BiGGER docking method (Palma et al. 2000) also performed a global search without any experimental information and was tested on one of the largest data sets of protein–protein complexes, but it did not find the near-native solution within the five lowest energy conformations in any of the 11 complexes analyzed.

All groups reported different criteria to evaluate the best solutions. We calculated the RMSD for the ligand interface C^α atoms (when only the receptor is superimposed onto the crystallographic structure), which reflects more accurately the proximity to the real complex structure in terms of number of correct contacts. If more ligand atoms out of the interface are included in the calculation of the RMSD, as in Norel et al. (1999) and BiGGER (Palma et al. 2000), the possibility exists that the overall ligand position can be close to the real complex structure, whereas the interacting residues have incorrect contacts. More inaccuracy (in evaluating the good contacts) can be introduced when both receptor and ligand atoms are included in the calculation of RMSD and both molecules are used in the superimposition onto the complex structure, as in FTDOCK reported values (Gabb et al. 1997; Jackson et al. 1998).

The performance of our method, in terms of computational time, is comparable to the other published docking procedures. For most of the complexes, the ICM rigid-body docking step took from 2 to 7 h, and the final side-chain refinement ∼7 to 20 min per structure on a 667-MHz Alpha processor (4 to 10 h for the rigid-body docking step and 10 to 30 min per structure for the refinement on a 700-MHz Pentium III workstation running Linux). The FTDOCK rigid-body step typically took ∼6 h using eight SGI R10000 processors simultaneously (48 h/CPU; Gabb et al. 1997) and the refinement step took 10 to 40 min per structure in a SGI R10000 (Jackson et al. 1998). Norel et al. (1999) reported CPU times of 2 to 6 h on a 133-MHz personal computer. The total CPU times for the BiGGER method ranged from 2 to 8 h on a 450-MHz Pentium II personal computer (Palma et al. 2000).

Our method uses a semi-global search approach, in which a 3D box is automatically generated around a previously selected receptor binding site. The size of the box, covering approximately half of the receptor surface, is limited by computer memory (a big box that would completely cover a receptor molecule of 200 to 300 residues is currently beyond the capacity of standard computational equipment but can be performed on high-end computers). The selection of the receptor binding area is the only manual intervention in our procedure, and only a vague idea of the location of the receptor binding site is required, because approximately half of the receptor surface is covered during sampling. In a typical docking problem, it is not uncommon to have some information available about the receptor binding site, either from experimental data and comparative modeling, or by using computational methods for predicting putative protein–protein interaction sites from sequences (Pazos et al. 1997; Gallet et al. 2000), or from the individual protein surfaces (Jones and Thornton 1997a, b; Conte et al. 1999). However, because we were concerned about the impact of the box location on the docking results, we attempted a fully unrestricted sampling of the receptor surface by selecting several overlapping receptor binding sites (20 vertices of a dodecahedron around the receptor are typically sufficient to completely cover its surface). The solutions obtained in the different simulations were combined and stored in one conformational set, the 400 lowest energy conformations compressed, and the interacting side-chains further refined as usual. We tested this global approach on three representative protease-inhibitor complexes: 1ca0, 2sni, and 1taw. For all of them, the near-native solution was correctly predicted as the lowest energy solution after refinement of the solutions generated through a systematic global search around the receptor. These are essentially the same results we obtained with the local docking procedure (a box defined around the binding site), which indicates that the increased number of possible conformations caused by large surface sampling still does not lead to false positives.

There are several major factors that contributed to the improvement of the conformational sampling and the evaluation function for rigid-body docking of unbound subunits, with respect to the previously described ICM-based methods (Totrov and Abagyan 1994, 1997; Strynadka et al. 1996a). Inclusion of solvation in electrostatic potential eliminated false positives generated by an overestimation of electrostatic interactions between solvated residues. Van der Waals potentials, although appropriate for redocking complexed subunits, were made softer to overcome the rigidity of side-chains when docking unbound subunits. Decreasing the relative weight values for van der Waals potentials also improved substantially the scoring and accuracy of the best solution for most of the complexes.

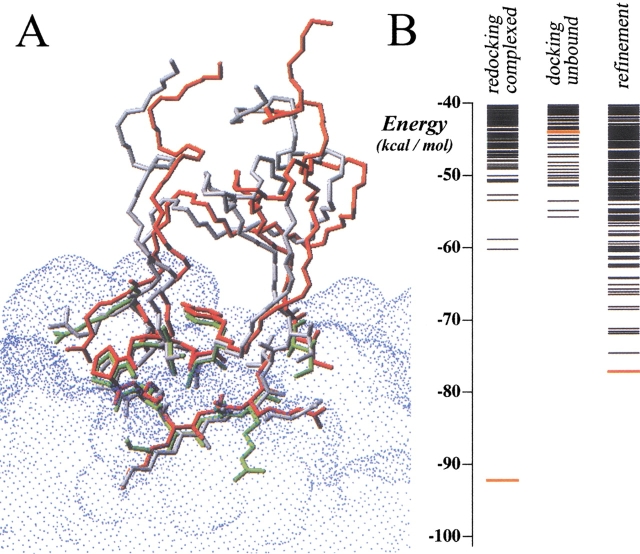
Refinement of ligand side-chains proved to be very efficient for most of the cases, especially for protease-inhibitor complexes, in which the scoring of the best solution can be greatly affected by a reduced number of bad contacts (typically generated by one or two ligand side-chains), which can be overcome after refinement. Thus, provided that there is no major backbone rearrangement on binding, our procedure has a high probability (64%) of predicting the correct structure of a protease-inhibitor complex from the individual subunits. In these correctly predicted complexes, an average of 4.9 ligand interface residues had a wrong side-chain conformation before refinement (defined as residues with RMSD of side-chain heavy atoms with respect to the real structure >2.5 Å), of which 1.7 residues per complex improved their RMSD by >1 Å after refinement. An average of 7.3 residues per complex had a correct side-chain conformation before refinement (RMSD <2.5 Å), of which only 0.1 residues per complex became worse (>1 Å) after refinement. This indicates that refinement is mainly improving the interface side-chains that had a wrong conformation, and it is not moving out of the way side-chains that were already close to the real complex structure. A typical case is 3tgi, with a near-native solution that scored very poorly after rigid-body docking in the nonoptimized maps (rank, 1756), then improved extraordinarily with the optimized maps (rank, 23), and finally became the lowest energy solution after refinement (the predicted structure is practically identical to the real one, as can be seen in Fig. 4 ▶).

Fig. 4.

(A) Three-dimensional model of the best solution achieved for complex 3tgi after docking unbound subunits (in green) and after the refinement step (in red), compared with the crystallographic structure (in white). Only the C^α atoms of the receptor molecules have been optimally superimposed. The conformation of the interface side-chains of the best solution after rigid-body docking (in green) was very different from the crystallographic structure (in white), which contributed to its poor scoring. After refinement, the interface side-chains (in red) had the same conformation as in the crystallographic structure (in white). (B) Distribution of solutions for complex 3tgi obtained after redocking complexed molecules, after docking unbound subunits, and after interface side-chain refinement. Red line represents the best solution.

For non–protease-inhibitor complexes, the near-native solution was found within the top 20 solutions in more than half of the complexes (six out of 10), although in none of the cases was ranked first. For the complexes 1bgs, 1ay7, 2pcb, and 1vfb, the best solution ranked >40. The bad results obtained for the complex 1vfb can be justified, because the ligand presents major backbone movement on binding (RMSD >1.8 Å). However, the electrostatic complex 2pcb is more intriguing, because it was the only case in which the near-native structure was not ranked first after redocking complexed subunits. In fact, the possible impact of crystal forces in determining the structure of the complex (Pelletier and Kraut 1992) causes some concern about whether the structure of the complex in the crystal is the same as the structure in solution (Zhou et al. 1995; Erman et al. 1997; Moore et al. 1998; Mei et al. 1999; Wang and Pielak 1999). Regarding 1bgs and 1ay7, it is more difficult to rationalize the high rank of their near-native solutions. An average of 12.5 ligand interface residues in nonprotease complexes had a wrong side-chain conformation before refinement (defined as residues with RMSD of side-chain heavy atoms >2.5 Å), of which 2.1 residues per complex improved (>1 Å) after refinement. An average of 4.0 residues per complex had a correct side-chain conformation before refinement (RMSD <2.5 Å), of which only 0.4 moved away (>1 Å) after refinement.

The accuracy of the ligand side-chains after rigid-body docking may explain why side-chain refinement improved the ranking of the docked conformations preferentially for protease-inhibitor systems, although further analysis will be needed to understand why some complexes are more amenable to prediction than others. In general, complexes of the protease-inhibitor type (all of which have small convex ligand interfaces) present a smaller number of clashes after docking the unbound subunits. Those clashes can be resolved with side-chain optimization, as we have shown here. However, complexes with big planar interfaces can present a greater number of wrong ligand side-chains and may also need refinement of the receptor (which is beyond our current computational capabilities). Despite these greater difficulties, the refinement still helps the ranking of the correct solutions for these complexes.

The docking procedure described in this work can be applied systematically to the large databases of domain structures generated by emerging structural genomics programs. Increasingly available structural data, improvement in computational capabilities, and introduction of experimental distance restraints (from nuclear magnetic resonance or mutational data) could lead to the unequivocal prediction of the native solution for the majority of the protein–protein complexes in a living organism.

Materials and methods

Rigid-body docking

The rigid-body docking step (see scheme in Fig. 1 ▶) was performed by sampling different positions and orientations of the ligand molecule with respect to the receptor molecule (the position of which is fixed) using a pseudo-Brownian Monte Carlo procedure (Abagyan et al. 1994) implemented in the MolSoft ICM 2.8 program (MolSoft 2000). For practical reasons, in a protein–protein complex, the receptor was defined as the bigger protein and the ligand as the smaller one (if both molecules had the same size, the choice were made arbitrarily). Five types of grid potentials (Goodford 1985; Totrov and Abagyan 1997) were precalculated as follows (Totrov and Abagyan 2001). The van der Waals interactions are described by the 6–12 potential (equation 2):

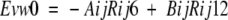2

where R_ij is the distance between the two atoms i and j, and parameters A_ij and B_ij are calculated from the ECEPP/3 molecular mechanics forcefield (Nemethy et al. 1992). The extreme sensitivity of the van der Waals potential to small conformational changes may introduce a large noise in the intermolecular energy function. For that reason, we used a smoother form of the potential, with most of the repulsive part truncated by a cutoff value E_max (equation 3).

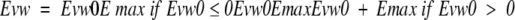3

Two different van der Waals potentials are calculated for a hydrogen atom probe (E_Hvw) and for a heavy atom probe (E_Cvw; a generic carbon of 1.7-Å radius was used). The electrostatic potential (E_el^solv) was calculated using a modified Coulomb's law with a distance-dependant dielectric constant ɛ = 4r, corrected by the atomic solvent-accessible surface to account for the solvation effect on the intermolecular pairwise electrostatic interactions. The hydrogen-bonding potential (E_hb) was calculated as spherical Gaussians centered at the ideal putative donor and/or acceptor sites, according to equation 4.

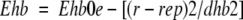4

where E⁰_hb =2.5 kcal/mole (an average of various estimates), d_hb = 1.4 Å (radius of the interaction sphere), and r_ep was the radius vector of the interaction center, which was placed 1.7 Å from the atom. The hydrophobicity potential (E_hp) was calculated as roughly proportional to the buried hydrophobic surface area, with a free-energy density of 30 cal/mole per Ų. The energy estimate used during simulations is described by equation 5:

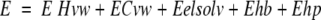5

The solvation energy (E_solv), based on atomic solvent-accessible surfaces (Wesson and Eisenberg 1992), was added to the total energy to reevaluate the docking solutions obtained from unbound subunits. Van der Waals potentials were initially truncated to a maximum energy value (E_max; see equation 3) of 1.5 kcal/mole to avoid intermolecule repulsive clashes arising from the rigidity of their side-chains.

The grid potential maps generated from the receptor molecule were defined in a box around the known or hypothetical receptor binding site, covering approximately half of the total receptor surface. The ligand molecule was positioned in random orientation inside the grid potential box and was systematically rotated to generate 120 different starting conformations, using the following procedure (Totrov and Abagyan 1994): (1) an imaginary dodecahedron is created around the ligand and firmly attached to it; (2) the 20 vertices of this dodecahedron are sequentially oriented toward the receptor; and (3) six 60° rotations are made around the axis defined by the centers of mass of receptor and ligand, thus generating a total of 120 starting orientations. For each starting conformation, a pseudo-Brownian Monte-Carlo (Abagyan et al. 1994) optimization was performed, sampling only the six positional variables of the ligand. Each iteration of the procedure consisted of a random move in the position of the ligand, with a translation amplitude of 12 Å and a rotational angle of 12 Å divided by the molecule radius (in Å), followed by local energy minimization (up to 200 steps of conjugate gradient minimization). New conformations generated after each iteration were selected according to the Metropolis criterion (Metropolis et al. 1953) with a temperature of 300K and 5000K for the docking of the bound and unbound conformations, respectively. Higher temperature when using the unbound subunits helped to improve sampling. Each simulation was terminated after 20,000 energy evaluations (10,000 energy evaluations for docking bound conformations). All the conformations accumulated after the 120 different simulations were merged in a single conformational set. This conformational set was compressed by comparing the atomic coordinates of all conformations and removing geometrically similar conformations, so that only the lowest energy conformations with pairwise RMSD for the ligand interface C^α atoms >4 Å were retained (Abagyan and Argos 1992).

Refinement of ligand side-chain conformation

The resulting conformations after the first rigid-body step were further optimized by an ICM (MolSoft 2000) global optimization algorithm, with flexible interface ligand side-chains and a grid map representation of the receptor energy. Side-chain torsion angles of the ligand surface residues in the vicinity of 4.0 Å of the receptor were changed in each random step using a Biased Probability Monte Carlo procedure (Abagyan and Totrov 1994). Loose restraints (Abagyan et al. 1994) were imposed on the positional variables of the ligand molecule to keep it close to the starting conformation. The simulation temperature was set to 300 K. The number of total energy evaluations (N_Eval) for each simulation was proportional to the number of flexible interface torsion angles (N_FreeVar) of the ligand, as described by equation 6:

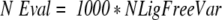6

The energy function used during simulations, equation 7, consisted of the internal energy for the ligand (E_int) and the intermolecular energy based on the same optimized potential maps used in the docking step (see Results):

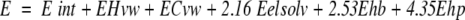7

The internal energy (E_int) included internal van der Waals interactions (not truncated), hydrogen bonding and torsion energy calculated with ECEPP/3 parameters (Nemethy et al. 1992), and the Coulomb electrostatic energy with a distance-dependent dielectric constant (ɛ = 4r). The configurational entropy of side-chains (Abagyan and Totrov 1994) and the surface-based solvation energy (Wesson and Eisenberg 1992) were included in the final energy to select the best refined solutions.

Selection of the protein–protein complexes database

We have tested the docking procedure on a nonredundant data set of protein–protein complexes in which the 3D structures of their subunits (bound and free) are known. Because the goal here is the prediction of a protein–protein complex from its individual subunits, we have not included any permanent macromolecular assembly (e.g., oligomeric proteins, virus capsids), the components of which do not fold separately to perform independent functions before association. When more than one complex was found in the asymmetric unit, only one copy was retained. Table 1 details the PDB (Bernstein et al. 1977) files of the 24 complexes used in this work. Most of them are enzyme-inhibitor complexes, and more than half are protease-inhibitor complexes. There are two electron transfer protein–protein complexes and two antibody-antigen complexes. The corresponding unbound structures are listed in Table 2. The atomic coordinates for the complex TEM-1 β-lactamase/BLIP (Strynadka et al. 1996b) and their free subunits (Strynadka et al. 1992, 1994) were kindly provided by their authors.

A Web server with the script files of the protein–protein docking algorithm is available at http://www.scripps.edu/~jfrecio/ICMprotdock/.

Abbreviations

• PDB, Protein Data Bank

• ICM, Internal Coordinate Mechanics

• RMSD, root-mean-square deviation