Recursive domains in proteins

Abstract

The domain is a fundamental unit of protein structure. Numerous studies have analyzed folding patterns in protein domains of known structure to gain insight into the underlying protein folding process. Are such patterns a haphazard assortment or are they similar to sentences in a language, which can be generated by an underlying grammar? Specifically, can a small number of intuitively sensible rules generate a large class of folds, including feasible new folds? In this paper, we explore the extent to which four simple rules can generate the known all-β folds, using tools from graph theory. As a control, an exhaustive set of β-sandwiches was tested and found to be largely incompatible with such a grammar. The existence of a protein grammar has potential implications for both the mechanism of folding and the evolution of domains.

Studies of the topological properties of known folds have provided fundamental insights into the folding process (Doolittle 1995). By analyzing the database of known structures, one can compute statistical properties of folds and deduce hypothetical folding rules. Such rules may reflect global organizational constraints, such as chirality (Woolfson et al. 1993), the noncrossing property (Richardson 1977), and the tendency of β-sheet to preserve hydrogen bond patterns (Baker and Hubbard 1984; Stickle et al. 1992). Alternatively, the rules may take the form of local structure generators, from which structure evolves via iterative application of elementary steps (Richardson 1977; Efimov 1993a, b ,Efimov 1996, Efimov 1997; Lesk 1995). This latter approach has the potential to generate novel folds, which can, in turn, be screened for global constraints from the former approach.

The application of elementary rules to generate structure from basic building blocks is an intrinsically hierarchical process (Crippen 1978; Rose 1979). Richardson's composition rules for β-sheet are an example of this approach (Richardson 1977). Quoting from her concise formulation:

Assuming that the α helices and β strands are already present at least statistically, let us say that each succeeding step in any possible folding pathway for a β sheet must consist of either (1) forming a ±1 or ±1× connection between two β strands adjacent in sequence, or (2) taking either a β strand or a prefolded unit and laying it down next to a prefolded part of the sheet with which it is also contiguous in sequence.

Using her rules, consecutive β-strands grow into larger hydrogen-bonded structures in successive steps, and blocks of strands obtained in this way coalesce, providing they are consecutive in the chain. Of course, it is tempting to hypothesize that such procedures are related to actual protein folding pathways (Richardson 1977; Stirk et al. 1992; Hutchinson and Thornton 1993; Zhang and Kim 2000).

How does one uncover the grammar of a language? Assuming that protein folds can be generated from a set of simple rules, how might such rules be discovered? Effective rules should have the potential to generate a diverse range of physically feasible folds, including previously unobserved structures. The ubiquitous occurrence of super-secondary structures (Levitt and Chothia 1976) across unrelated families indicates that there is a physical basis for their independent formation and motivates our choice of simple rules.

Formally, the rules are operators. Their operands are structures, and an operation results in a new operand. This is a familiar definition, similar to binary addition.

Motivated in large part by Richardson's early work (Richardson 1977), we propose four simple folding rules for all-β proteins, corresponding to the four prevalent super-secondary structure β-motifs: β-hairpin, β-β-β unit, jelly roll, and Greek key. As such, the rules embody physically based topological and hydrogen-bonding relationships between neighboring strands. Two strands are classified as neighbors when they either (1) are consecutive in sequence or (2) become juxtaposed in space from a previously applied folding rule. This later relationship is identified via closure. When a folding rule juxtaposes two strands, they are classified as neighbors under closure, after which they become a valid object for subsequent applications of the folding rules. In general, closure results in new neighborhood relationships that incorporate the topology from previous folding steps, in a process that is intrinsically hierarchic.

A recursive domain is defined as a compact fold, or part of a fold, that can be generated by repeated application of the four folding rules, with closure. Whenever a protein fold can be generated entirely from the folding rules, it is composed of one recursive domain. Otherwise, it can be partitioned into multiple recursive domains, each of which is generated entirely by the rules. If the rules successfully capture the underlying folding process, then we might expect single-domain proteins to be comprised of a single recursive domain, with larger proteins comprised of only a small number of recursive domains. To test this expectation, the number of recursive domains was computed for each protein in two large all-β test sets. One set consists of representatives of SCOP (structural classification of proteins) families, and the other consists of representatives of SCOP folds (Murzin et al. 1995). The second set is a subset of the first one, of course, but it was included as a control to ensure that folds which span many SCOP families do not bias the results.

The test is performed in a fully automatic way, using graph-theoretic tools. A recursive domain translates conveniently into the language of graph theory, as described in the Appendix.

We find that the majority of families (∼80%) of small β-proteins correspond to a single recursive domain, whereas larger proteins are typically comprised of a small number of recursive domains. Specifically, >90% of all proteins, both families and folds, can be decomposed into at most three recursive components.

Is the ability to represent a protein by a small number of recursive domains a characteristic behavior for protein folds, or will the composition rules decompose any compact assembly of β-strands into just a few recursive domains? To address this question, we tested all possible up-down 2 × 4 beta-sheet topologies. Only 14% of these topologies can be generated as a single recursive domain.

The folding rules

We propose four folding rules for all-β proteins (Fig. 1 ▶). These rules were used to parse representatives from a set of 224 all-β protein families and a set of 80 all-β folds, both sets taken from the SCOP database (Murzin et al. 1995) and selected by ASTRAL (Brenner et al. 2000). A small number of proteins (10 families and three folds) that are either essentially all loops or noncompact were removed from the ASTRAL compendium. The folding rules were then applied to every protein in both sets. A contact area threshold between interacting strands was introduced to ensure compactness. In particular, two strands are said to interact only when the surface buried between them exceeds 20% of the total area of the smaller fragment.

Fig. 1.

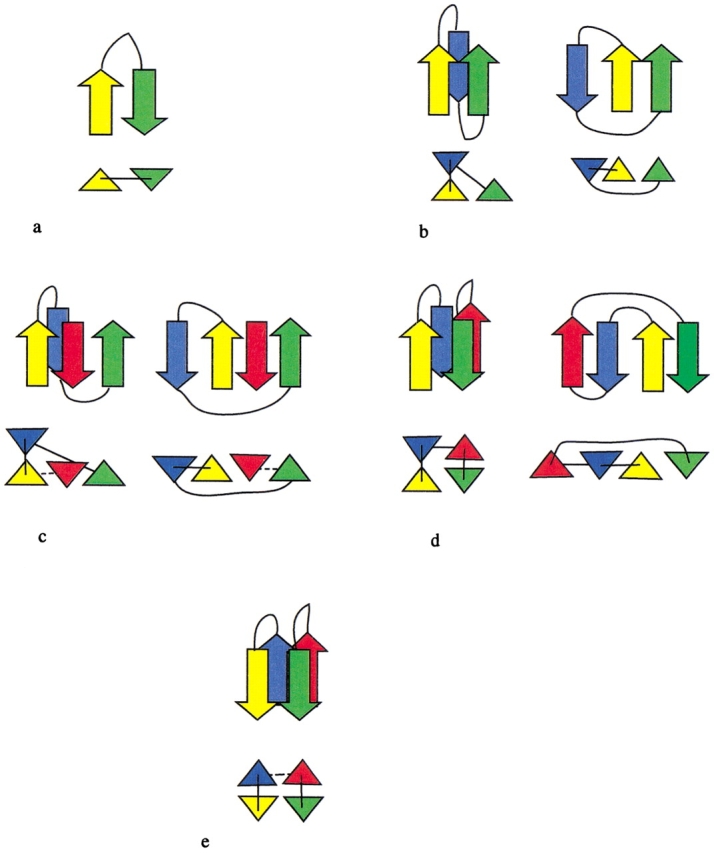
The four folding rules. Each rule is illustrated by two diagrams: (Top) β-Strands are represented by arrows (pointed along the N-to-C direction), and chain connectivity is given by thin lines; (bottom) strands are represented by triangles (pointed in the N-to-C direction), chain connectivity is indicated by thin lines, and hydrogen bonding established by previous folding rules is indicated by a dashed line. (a) Hairpin rule. (b) β-Wind rule, shown for two typical configurations. (c) Indirect β-wind rule, shown for two typical configurations. (d) Antiparallel bridge, shown for two typical configurations. (e) Parallel bridge rule.

The structural motifs seen in proteins have become familiar through repetition, thanks to the work of numerous structural biologists (Berman et al. 2000). The four rules presented in this paper are intended as a formal statement of such motifs, and their definition was accomplished through a process of trial and error. We started with the simplest rule, the stipulation that two successive strands can interact to form a hairpin. Additional rules were then devised and tested against the SCOP family database, and those that proved effective in the recursive parsing of domains were retained. In all cases, the choice and acceptance of these rules was guided by intuition, with emphasis on local and super-secondary structure motifs. Although this approach does not guarantee that our rules are either optimal or complete, it does show that a few simple rules are sufficient to generate essentially the entire set of all-β folds.

Specifically, the four folding rules were motivated by prevalent super-secondary structure motifs found in proteins. Each rule represents an observed topological relationship between/among neighboring strands.

1. Hairpin rule (Fig. 1a ▶): Based on the β-hairpin, this rule simply groups two neighboring strands into a hairpin.

2. β-wind rule (Fig. 1b ▶): Based on the β-β-β motif (Efimov 1993b), this rule groups three consecutive β-strands, but the middle strand can be replaced by a helix or loop. The rule results in parallel hydrogen bonding between strands one and three. To ensure compactness, the middle strand is required to have substantial contact area with the first (see Technical Details). There are two variants of the rule, depending on whether the first and middle strands are hydrogen bonded.

3. Indirect β-wind rule (Fig. 1c ▶): This rule is similar to the β-wind rule, but lacks hydrogen bonding between the first and third strands. Instead, both strands are hydrogen bonded to a third, interposed strand. The interposed strand is constrained to be hydrogen bonded with one of its neighbors as a consequence of a previously applied rule. This restriction precludes incorporation of an unrelated strand from another part of the chain.

4. 1. Antiparallel bridge rule (Fig. 1d ▶): Based on the 2-2 Greek key motif (Hutchinson and Thornton 1993), this rule groups four consecutive strands that are related by antiparallel hydrogen bonding between the two middle strands and the two external strands. The bridge rule collapses this ribbon into a double arch. To ensure compactness, significant contact area is required between the two pairs of hydrogen-bonded strands. The figure shows two typical conformations allowed by this rule.
   2. Parallel bridge rule (Fig. 1e ▶): This rule is similar to the antiparallel bridge rule, but in this case, the two pairs of hydrogen-bonded strands are parallel. When one pair resides in a recursive domain, then the second pair is also included in that domain. Additionally, if there is significant contact area between the two pairs, all four strands collapse to a common recursive domain. The parallel bridge rule was motivated by parallel runs of a β-helix.

With the exception of the interposed strand in the indirect β-wind rule, these rules apply only to neighboring strands. By definition, neighboring stands are either sequentially consecutive or become so on recursion. This condition, together with restrictions on the interposed strand in the indirect β-wind rule, ensures that sequentially nonadjacent strands are not subject to a folding operation unless they have been brought together via rule-based iteration.

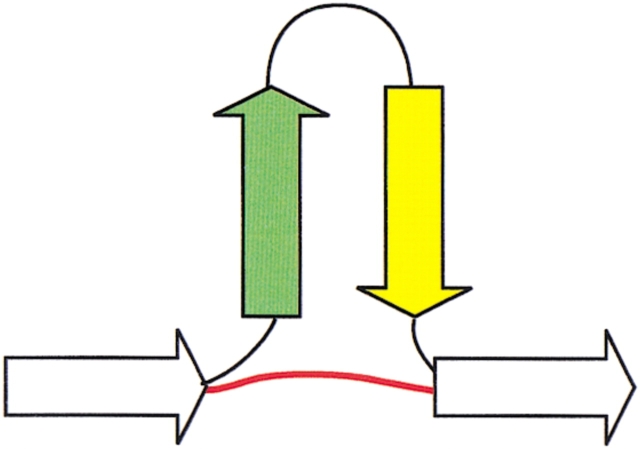
Along with the four folding rules, there is an explicit closure operation (Fig. 2 ▶). Without closure, decomposition would be arrested at the level of super-secondary structure and isolated β-strands. This follows from the fact that super-secondary structure is local, in that it is comprised of consecutive elements of secondary structure. However, once identified, the presence of a unit of super-secondary imposes spatial restrictions on remaining components of the fold. In particular, strands that are distant in sequence can be restricted to be close in space. In effect, the closure operation introduces a new virtual connection, like a shortcut through the sequence. As such, two secondary structures are classified as neighbors if they are consecutive in sequence or if they are linked by a virtual connection that is realized on application of closure. Correspondingly, the folding rules are applicable to both consecutive strands and nonconsecutive strands that become neighbors via these virtual connections.

Fig. 2.

The closure operation extends the concept of locality to residues that are close in space though not necessarily in sequence. For example, on hairpin formation the first and the last residues in the hairpin become three-dimensional neighbors, as illustrated here. A conceptual shortcut through the sequence is introduced when this occurs, illustrated by the red line. In general, two secondary structures are considered to be neighbors when they are consecutive in the sequence or when they become neighbors via a shortcut established by the closure operation.

No specific precedence is imposed on the folding rules; they can be applied in any order. As such, there can be many folding pathways corresponding to a given fold.

Multistep hierarchic decomposition is illustrated for the jelly roll motif (Stirk et al. 1992) in Figure 3 ▶. A jelly roll is a ribbon of antiparallel strands, and it can be parsed by reiterating the hairpin rule. Initially, the hairpin rule is applied to strands s3–s4 (Fig. 3a ▶), the only two strands that are sequential neighbors. On closure, s2–s5 become neighbors, and the hairpin rule is applied again (Fig. 3b ▶), after which s1–s6 become neighbors, followed by a final application of the hairpin rule (Fig. 3c ▶). At this point, the motif has been reduced to three consecutive hairpins (Fig. 3d ▶). Ultimately, the jelly roll in Figure 3 ▶ can be reduced to a single recursive domain. Initially, each secondary structure is classified as a recursive domain, containing itself as a singleton. Strands that can be grouped by any folding rule become members of the same recursive domain. Accordingly, each application of a folding rule has the potential to merge two or more recursive domains into one, as illustrated for the jelly roll example in Figure 3 ▶. The hairpin folding rules identify three recursive domains, each annotated by a different color in Figure 3d ▶. Clearly, the hairpin rule alone has a limited capacity to generate interesting recursive domains. However, the indirect β-wind rule can be applied to strands s1–s2–s3–s4, merging all three hairpins into one recursive domain. Alternatively, the antiparallel bridge rule could be applied twice: first to strands s2–s3–s4–s5 and then to strands s1–s2–s5–s6, again merging all three hairpins into one recursive domain. In general, the folding pathway obtained by successive applications of the folding rules is not unique. Figure 4 ▶ follows the step-wise decomposition of desulfoferrodoxin (1dfx, residues 37–125) into a single recursive domain. Alternate panels document successive partitions into recursive components; these are interleaved with panels illustrating the pertinent folding rules.

Fig. 3.

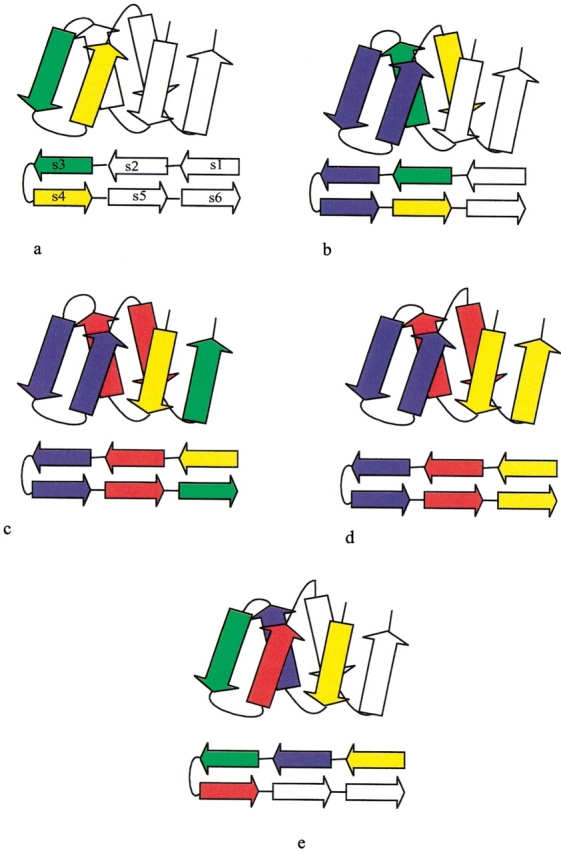
Generation of a jelly roll fold using folding rules. (a) The hairpin rule is applied to strands s3–s4, the only two strands that are consecutive in sequence. On closure, strands s2 and s5 now become neighbors. (b) The hairpin rule is applied to strands s2–s5. On closure, strand s1 and s6 now become neighbors. (c) The hairpin rule is applied to s1–s6. (d) At this point, the motif has been reduced to three consecutive hairpins. (e) Application of the indirect β-wind rule incorporates all strands into a single recursive domain.

Fig. 4.

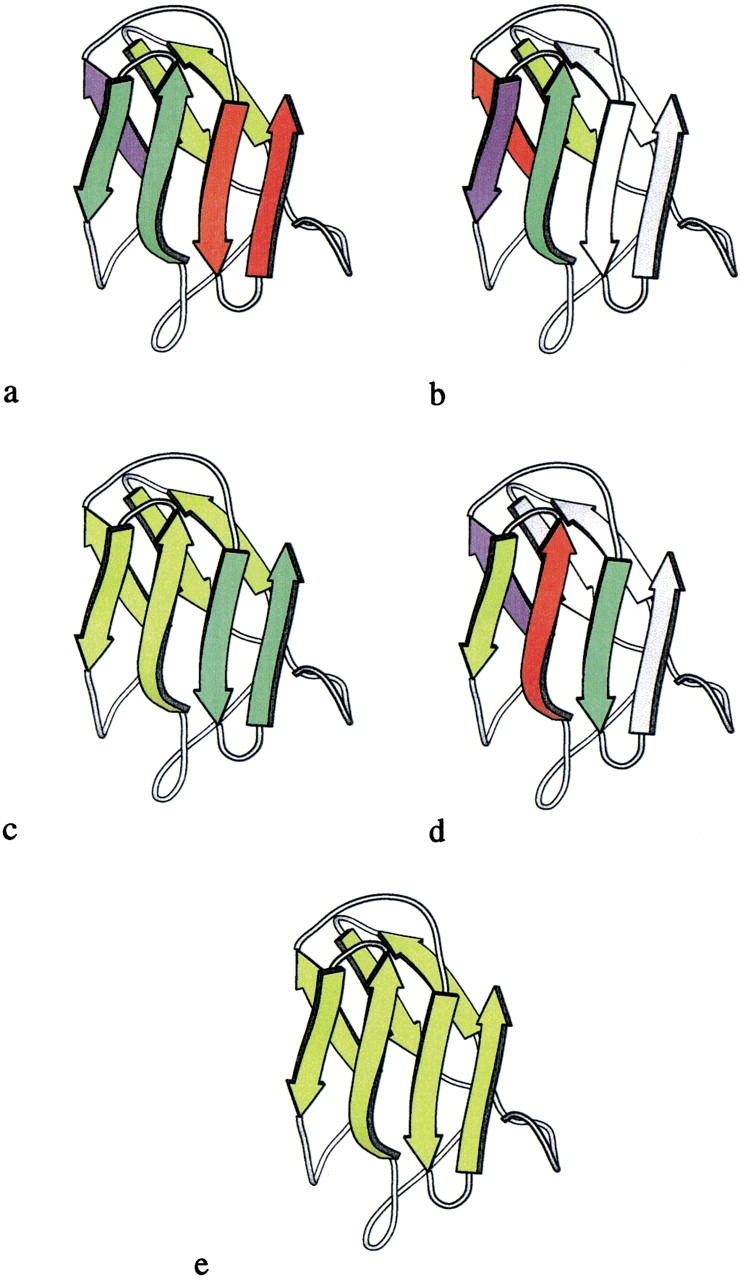
Evolution of the recursive domain of desulfoferrodoxin (1dfx, residues 37–125). In each panel, strands that are operands for a folding rule are shown in arbitrarily chosen colors, and remaining parts of the structure are in white. The colors are reassigned in each successive panel. Initially, three hairpins are identified and colored red, green, and chartreuse in a. On application of the antiparallel bridge rule, the blue, chartreuse, red, and green strands in b resolve into a single recursive domain, shown in chartreuse in c. Then, on application of the indirect β-wind rule to the chartreuse, blue, red, and green strands in d, the entire fold reduces to a single recursive domain, shown in chartreuse (e).

In each particular case, the application of a particular folding rule involves threshold decisions about technical details, such as strand continuity or contact area. These issues are described in Technical Details.

Technical details

Application of the rules requires identification of secondary and super-secondary structure from atomic coordinates. Often, there is some degree of structural ambiguity, and objective definition requires that thresholds be adopted. In the present study, which is limited to recursive domains in all-β proteins, no distinction need be made between helices and loops.

The DSSP (database of secondary structure in proteins) algorithm (Kabsch and Sander 1983), with minor modifications, was used to identify β-strands in proteins of known structure. The three modifications are as follows: (1) A β-strand must be at least two residues in length, but optionally, a strand of three or fewer residues can be treated as a loop; (2) if two consecutive β-strands are hydrogen bonded to a β-third strand, and directionality is preserved (i.e., both strands are parallel to the third strand or both are antiparallel to the third strand), they are classified as one distorted β-strand; and (3) two β-strands interrupted by a single residue are treated as one distorted β-strand, providing they are approximately colinear.

The β-wind, indirect β-wind, and bridge rules are applied only if the relevant fragments interact. Fragments are defined to interact when the contact area buried between them is at least 20% of the total area of the smaller fragment.

Finally, two strands are considered to be hydrogen bonded if their direction is similar (either parallel or antiparallel) and the contact area between their backbones is at least 25% of the total area of the shorter strand. In rare instances, this definition can classify two proximate strands as hydrogen bonded even if they lack explicit donor/acceptor interactions.

Results

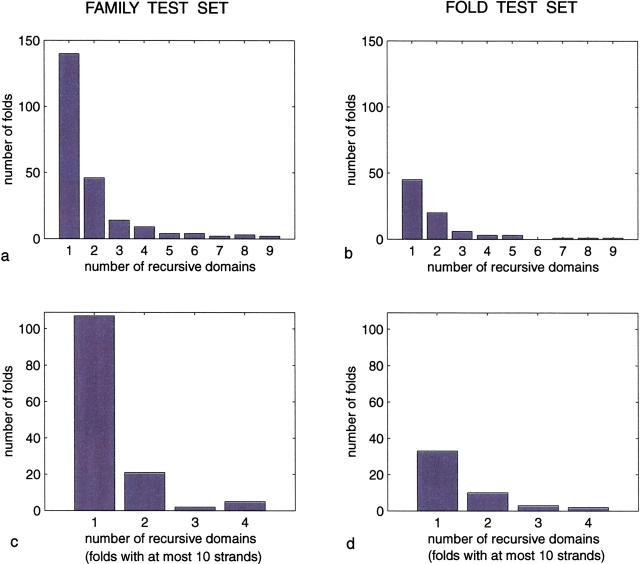
Our folding rules are sufficient to partition most small proteins into a single recursive domain, with larger proteins giving rise to only a small number of such domains. These results, shown in Figure 5 ▶, were derived from two test sets, one corresponding to the SCOP family level and the other to the SCOP fold level.

Fig. 5.

Number of recursive domains for proteins in both test sets, one corresponding to SCOP families. (a, b) The distribution of recursive domains for proteins in the two test sets. (c, d) This same distribution is shown when the test sets are restricted to the subset of proteins with at most 10 strands.

In greater detail, these results are broken into SCOP family–SCOP fold pairs. The first pair of diagrams is a histogram showing the distribution of recursive domains for proteins in each test set, and the second pair is a similar histogram in which the test sets are restricted to proteins with at most 10 strands.

Summarizing these results for SCOP families, 62% of the folds can be fully generated by our folding rules as a single recursive domain, 83% by two such domains, and 89% by three such domains. For the subset of proteins restricted to at most 10 strands, 80% reduce to one recursive domain and 95% to two such domains. Similar results are seen for SCOP folds: the corresponding percentages are 56%, 81%, and 89%, respectively, for the full set, and 68% and 90%, respectively, for the restricted set.

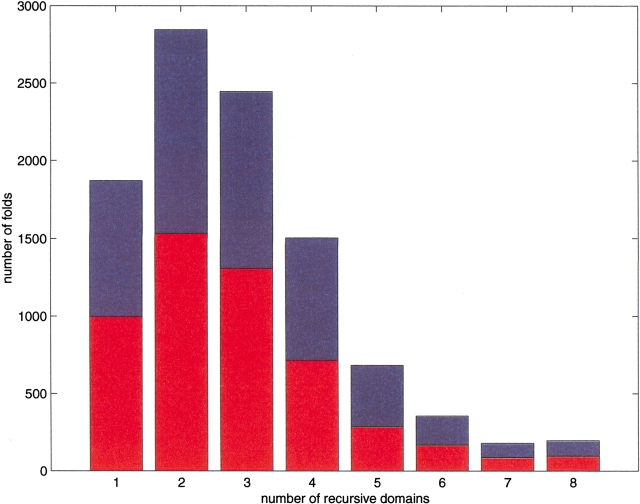
As a control, we tested whether random assembly of strands can also be reduced to a small number of recursive domains, or whether instead this is a characteristic property of proteins. To this end, all combinatorially possible eight-strand sandwiches with up-down topology were generated, and the folding rules were applied to this control set. The distribution of recursive domains is shown in Figure 6 ▶ (upper bars). Only 18% of these topologies can be generated by a single recursive domain. Clearly, the distribution for a random assembly of β-strands differs from that of authentic proteins, even when restricted to a β-sandwich.

Fig. 6.

Histogram showing the number of recursive domains for the set of all combinatorially possible up-down eight-strand sandwiches (upper bars), and the corresponding histogram when limited to noncrossing topologies (lower bars).

Protein folds having more than three recursive domains were examined individually. Do proteins in this set of exceptions represent counter-examples to our basic premise that beta-folds can be generated from simple rules? This is a crucial question.

The set of exceptions is dominated by β-propellers, in which the number of recursive domains equals the number of blades. None of our rules collapse the blades in a single domain, although it would be simple to devise such a rule; for example, two neighboring recursive domains can collapse along a common hydrophobic core. However, such a rule would be different in kind than the ones proposed here, and we did not consider such an extension at this stage. Of the remaining eight proteins, four are explained by an incorrect secondary structure assignment caused by a minor threshold violation.

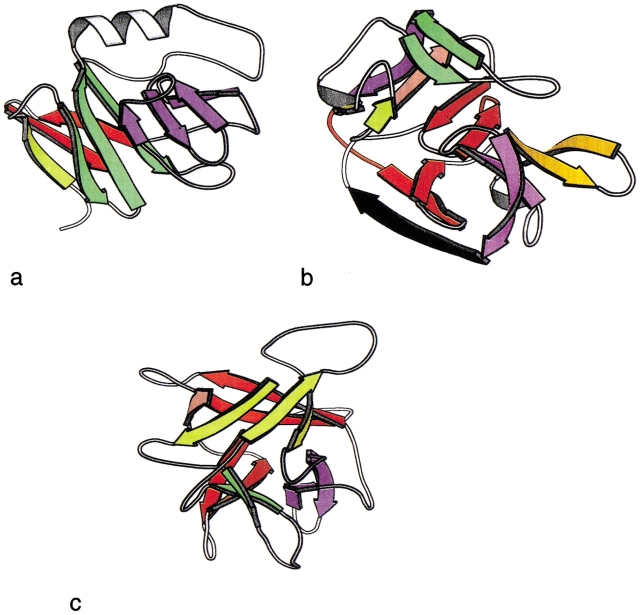
The remaining two proteins from the fold test set are shown in Figure 7 ▶. One is an ISP domain, described in SCOP as a two-domain protein, in which one of the domains is a six-stranded sandwich or barrel. The representative of this fold chosen by ASTRAL is the ISP subunit of the mitochondrial cytochrome bc1-complex (1rie). Our rules partition this subunit into four recursive domains. Interestingly, another structurally similar member of this family (the ISP subunit from chloroplast cytochrome bf complex, 1rfs) can be generated as a single recursive domain using the rules.

Fig. 7.

Representative folds with more than three recursive domains. Each recursive domain is shown in a different color. (a) ISP domain (1rie). (b) Hedgehog/inteindomain (1at0). (c) β-Trefoil (1wba).

The second exception is the Hedgehog C-terminal (Hall et al. 1995) autoprocessing domain. This protein is a member of the Hedgehog/inteindomain SCOP family, a complex fold of five beta-hairpin units and a β-ribbon arc. The rules identify the hairpins but failed to find any other reducible fragments. This protein has an inteindomain, and the resultant fold may depend on the excised segment.

Examining proteins in the family test set revealed one additional exception, a β-trefoil (1wba). However, this fold is not an exception in the fold test set. Closer examination shows that the antiparallel bridge rule obtains for most of the other representatives of this fold, but this particular case is an exception.

Are there conceivable β-folds that nature avoids? Our approach formalizes the intuition that observed folds are dominated by conformations in which chain connectivity avoids random hops between disparate points in space. Others have addressed such questions as well.

Richardson (1977) documented two such fold properties, one based on structural chirality and the other on the topology of the backbone. The first property is completely independent of ours. When applied after the fact to structures generated using our rules, about half can be rejected because they lack the correct orientation. Her second property is a noncrossing criterion, and it is related to ours. In the context of a two-layer β-sandwich, the noncrossing property can be stated as follows: let the two β-sheets be embedded on opposite sides of a cube, with interstrand connections that traverse the surface of the cube. Retain only those sheets for which no two loops cross. Eliminating structures that fail to satisfy the noncrossing property would further decrease the list of acceptable folds.

We tested the degree to which the set of folds generated by our rules can be captured by Richardson's noncrossing criterion (Fig. 6 ▶, lower bars), and we find that this criterion eliminates <37% of all combinatorially possible up-down eight-strand sandwiches. Furthermore, although the number of recursive components that satisfy the noncrossing restriction is reduced in comparison to a random assembly of β-strands, their distribution is similar.

Naturally-occurring β-sheet topologies were also analyzed by Zhang and Kim (2000), who observed that among the 96 possible topologies for four-stranded sheet, only 42 are observed. The investigators identified two characteristic properties of the underrepresented topologies. One group, G1, includes sheets in which two parallel strands are situated in opposition to two antiparallel strands. The second group, G2, includes sheets in which two sequentially consecutive strands occupy nonadjacent positions in the sheet, for example, the first and fourth positions. There is only one pair of strands in G2 that is consecutive in both sequence and structure.

The first of these two criteria is independent from ours and has the potential to be an additional screen for valid fold candidates. The second criterion involves the degree to which main-chain connectivity is free to hop at random in a four-stranded β-sheet topology, and it is a special case of the property that we address in this paper.

Accordingly, we tested whether our recursive domain formalism can rationalize the absence of G2 topologies among observed folds. Given that four-stranded sheets do not occur in isolation, we adopted a broader test set consisting of all theoretically possible 2 × 4 up-down sandwiches. A count was made of the number of times each four-strand sheet topology in G2 is represented (1) in this test set and (2) in a reduced test subset that was restricted to include only sandwiches having one recursive domain. One expects that G2 topologies will occur rarely in the reduced test subset. Indeed, there are 5040 occurrences of folds from G2 in the unrestricted test set, but only 4.9% remain in the reduced subset. Moreover, when the test subset is further reduced by removing topologies that fail to satisfy the noncrossing property, only 1.9% remain. It follows that G2 topologies are selectively depleted in recursive domains.

In essence, our folding rules quantify the impression gleaned from visual inspection: β-folds show a simple, underlying organization, with orderly patterns of chain connectivity.

Discussion

A grammar is a compact description of a language. The set of rules that comprise the grammar is finite, but the language may contain an infinite number of sentences, as is the case for natural languages.

In the preceding, we introduced a grammar for all-β protein domains, based on four simple composition rules. With this definition, a domain corresponds to a collection of β-strands that can be lumped into a single structural unit on application of the rules, with closure. The rules were motivated by four types of commonly observed super-secondary structure. Using them, we showed that almost every all-β fold can be iteratively decomposed into a small number of recursive domains, usually just one. Here, our goal has been to explore the rules, not to tinker with them, and we expect that an improved rule set could be devised with modification and/or extension. Also, the existence of similar rules that span α- and α/β-proteins is anticipated.

The four simple rules provide a compact description of folding for all-β proteins, and they give rise to the observed hierarchic organization of proteins (Crippen 1978; Rose 1979) quite naturally. Often, there are multiple ways to generate a given fold using the rules, and the absence of a unique parse tree is consistent with the existence of multiple folding paths. Richardson (1977) made a similar observation years ago.

Do these abstract rules have physical correlates in the actual mechanism of protein folding? We suspect so. The fact that unrelated proteins can be generated from the same set of simple rules is strongly suggestive, with the following as a plausible connection. At the cartoon level of resolution (∼5 Å), a protein structure can be described as a series of isodirectional segments (i.e., α-helices and β-strands) interconnected by tight turns and larger loops (Rose and Seltzer 1977). This partitioning is already anticipated in the unfolded molecule by sterically imposed, conformational bias (Srinivasan and Rose 1999; Pappu et al. 2000). Segmental bias is then fortified on folding as water—a poor solvent for polypeptide chains—squeezes the protein from its midst, pushing it toward compactness. It seems likely that our rules, which were abstracted from observed structural motifs, are a reflection of this underlying process.

Evolution is the history of contingent experiments of nature (Gould 1989), recorded in life's molecules. Do the structures of these molecules evolve at random? Or, are there hidden constraints on their patterns (Banavar et al. 2002), scope, and complexity? The very existence of a grammar argues for the latter view. Some structures, albeit conceivable, are simply not valid sentences in the language of proteins. Further, if a grammar for proteins is anchored in the chemistry of polypeptide chains, then the set of valid folds is predetermined, and evolution can only fill in the blanks. It is our conjecture that the discovered grammar is an expression of nature, not just a coincidental post hoc invention that happens to be consistent with the facts of life.

Appendix

Translation to graph theory

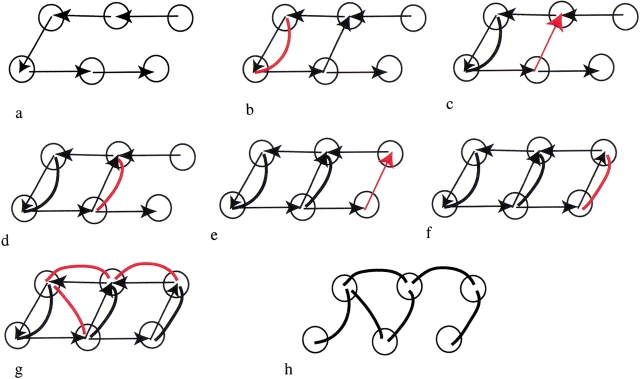
A practical, step-wise procedure for partitioning a fold into its recursive domains was implemented, using graph theory (Fig. 8 ▶). In particular, our definition of a recursive domain was chosen deliberately to correspond to the graph-theoretic concept of a connected component. In graph theory, two vertices belong to the same connected component of a graph if there is a connecting path between them. This is precisely the definition a recursive domain, as described below. Accordingly, a protein can be partitioned into recursive domains by an algorithm that identifies connected components in a graph (Cormen et al. 1990).

Fig. 8.

Consecutive steps in the construction of the graph for a jelly roll, from Fig. 3 ▶. Vertices correspond to individual strands, and they are connected by neighbor edges, represented by directed arrows. Domain edges are shown as bold lines. Initially, all neighbor edges are between sequentially consecutive strands, and there are no domain edges. In each successive panel, new domain edges introduced on application of either a folding rule or closure operation are shown in red. (a) Initial graph. (b) Hairpin rule. (c) Closure. (d) Hairpin rule. (e) Closure. (f) Hairpin rule. (g) Indirect β-beta wind. (h) Final graph after removing neighbor edges.

In our graph of an all-β fold, each vertex corresponds to a β-strand. The graph will have two types of edges: domain edges and neighbor edges, which are introduced as a result of folding rules or closure operations, respectively.

Domain edges connect strands within the same recursive domain. At the start of the procedure, before a folding rule is applied, there are no domain edges in the graph. On application of a folding rule, any strands grouped by the rule become members of the same recursive domain and are connected by a domain edge. In general, two strands belong to the same recursive domain if there is a path along domain edges connecting the vertex corresponding to one strand to the vertex corresponding to the second strand. The relation of belonging-to-the-same-recursive-domain is transitive.

Neighbor edges reflect information about neighboring strands. At the start of the procedure, the only neighbor edges are between pairs of strands that are consecutive in sequence. New neighbor edges can be introduced on closure. At each new iteration, the closure operation simply searches the graph for the existence of pairs of vertices corresponding to strands that are distant in sequence but close in space. Such pairs arise as a consequence of spatial restrictions that are imposed by the folding rules during the previous iteration. If such a pair is found, then a neighbor edge is introduced. In effect, the neighbor edge is a short-cut between the two vertices. Unlike domain edges, neighbor edges have a direction: the vertex corresponding to the strand that is closer to the N terminus is the beginning of the edge, and the vertex corresponding to the strand that is closer to the C terminus is the end of the edge.

To partition a protein into recursive domains, the folding rules are applied repeatedly until no further application is possible. At this point, the graph will have a number of domain edges. Next, recursive domains are determined. Only domain edges are pertinent for this step; neighbor edges are disregarded.