Side-chain modeling with an optimized scoring function

Abstract

Modeling side-chain conformations on a fixed protein backbone has a wide application in structure prediction and molecular design. Each effort in this field requires decisions about a rotamer set, scoring function, and search strategy. We have developed a new and simple scoring function, which operates on side-chain rotamers and consists of the following energy terms: contact surface, volume overlap, backbone dependency, electrostatic interactions, and desolvation energy. The weights of these energy terms were optimized to achieve the minimal average root mean square (rms) deviation between the lowest energy rotamer and real side-chain conformation on a training set of high-resolution protein structures. In the course of optimization, for every residue, its side chain was replaced by varying rotamers, whereas conformations for all other residues were kept as they appeared in the crystal structure. We obtained prediction accuracy of 90.4% for χ₁, 78.3% for χ_{1 + 2}, and 1.18 Å overall rms deviation. Furthermore, the derived scoring function combined with a Monte Carlo search algorithm was used to place all side chains onto a protein backbone simultaneously. The average prediction accuracy was 87.9% for χ₁, 73.2% for χ_{1 + 2}, and 1.34 Å rms deviation for 30 protein structures. Our approach was compared with available side-chain construction methods and showed improvement over the best among them: 4.4% for χ₁, 4.7% for χ_{1 + 2}, and 0.21 Å for rms deviation. We hypothesize that the scoring function instead of the search strategy is the main obstacle in side-chain modeling. Additionally, we show that a more detailed rotamer library is expected to increase χ_{1 + 2} prediction accuracy but may have little effect on χ₁ prediction accuracy.

Side-chain modeling plays an important role in molecular docking and protein structure prediction. Protein side chains make a dominant contribution to molecular recognition (Vasquez 1996). Homology modeling of a protein from its sequence using the structure of its homolog is widely used in structure-based drug design (Lybrand 1995). Detailed information about the binding site of the target protein is essential to generate new lead compounds. The ab initio protein folding problem can be divided into two sequential tasks of approximately equal computational complexity: the generation of nativelike backbone folds and the positioning of side chains on these backbones (Huang et al. 1998). The combinatorial complexity of the entire problem is merely additive for the two steps, rather than multiplicative, which makes this task computationally feasible.

Protein side chains tend to exist in a limited number of low energy conformations called rotamers (Ponder and Richards 1987). Instead of considering the full geometrically possible conformational space, only a small number of rotamers can be used to describe most naturally occurring conformers of a side chain. Growth of the Protein Data Bank (PDB, Berman et al. 2000) provides more high-quality protein structures for statistical analysis, which increases the reliability and completeness of rotamer libraries. Two types of rotamer libraries have been developed, namely, a backbone-independent library (Ponder and Richards 1987; Tuffery et al. 1991; De Maeyer et al. 1997; Lovell et al. 2000) and a backbone-dependent library (Dunbrack and Karplus 1993). Both of them have been widely used for predicting side-chain conformations. As a consequence, the speed and efficiency of finding an optimal protein conformation is dramatically enhanced compared with the continuous space methods.

Even when rotamer libraries are used, the combinatorial nature of side-chain placement on a given protein backbone has been often cited as the main obstacle to the correct prediction of side-chain conformation (Lee and Subbiah 1991; Eisenmenger et al. 1993; Petrella et al. 1998). Many strategies have been proposed to solve this problem: Monte Carlo searches (Holm and Sander 1992; Vasquez 1995), genetic algorithms (Tuffery et al. 1991), neural networks (Hwang and Liao 1995), mean-field optimization (Koehl and Delarue 1994; Mendes et al. 1999), dead-end elimination (DEE) method (Desmet et al. 1992; De Maeyer et al. 1997), and actual combinatorial searches (Dunbrack and Karplus 1993; Wilson et al. 1993^; Bower et al. 1997). Although DEE is considered to be the most powerful algorithm, designed to identify global minimum energy conformations, its predictions are far from being 100% accurate even for the core residues (De Maeyer et al. 1997; Looger and Hellinga 2001). Recently, Xiang and Honig (2001) obtained the greatest accuracy for core residues with an extensive library of 7560 rotamers. However, their methods did not show advantages for all residues. Thus, a scoring function might be the real obstacle for side-chain prediction.

Unlike search strategies, relatively less attention has been paid to the scoring function. The simplest energy functions, which are limited to estimating Van der Waals interactions by a Lennard-Jones potential, appear to give excellent results for buried nonpolar amino acids (Vasquez 1996). However, these approaches do not give accurate results for exposed, partially exposed, or buried polar residues. The use of electrostatic or hydrogen-bonding terms, which are typical of commonly used force fields, have not shown a significant improvement over the simple Van der Waals potential (Vasquez 1996; Bower et al. 1997^; De Maeyer et al. 1997). Wilson et al. (1991) added a desolvation energy term to the AMBER force field. The weight of the desolvation energy was derived from protein–ligand interaction. However, the combined scoring function did not prove to be successful in side-chain modeling (Wilson et al. 1993). The failure of force field applications indicates that special energy functions should be used for side-chain modeling. Samudrala and Moult (1998) used a discriminatory function based on a statistical analysis of atomic contacts in protein structures for selecting side-chain rotamers, given a protein backbone. Their program, however, does not perform better than others.

The PDB contains many high-quality protein structures for derivation or testing of scoring functions. Wilson et al. (1993) tested their scoring function by searching for an optimal conformation for a single residue. Different rotamers were checked at the position of the search while other residues were fixed in their conformations observed in the experimental structure. However, the test was done only on one protein. Petrella et al. (1998) did a similar test of CHARMM energy functions for side-chain prediction on 10 proteins.

Instead of testing existing potential functions, we developed a scoring function by minimizing the average root mean square (rms) deviation between the lowest energy rotamer and real conformation in the search for a single residue rotamer. During this minimization, the weights of different energy terms were optimized. The derived scoring function exhibited better performance than the CHARMM or AMBER force field in predicting the conformation of a single residue side chain in the tested proteins. Then we used the derived scoring function combined with a Monte Carlo algorithm to predict the side-chain conformations of an entire protein. The results are discussed and compared with other side-chain modeling programs.

Results and Discussion

The scoring function

The optimized scoring function was found to be

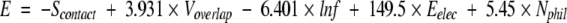1

where S_contact, V_overlap, and E_elec are contact surface, overlapped volume, and electrostatic interaction energy between the rotamer and other parts of the protein, respectively; f is the observed frequency of the rotamer given a backbone conformation; and N_phil is the number of totally buried nonhydrogen-bonded hydrophilic atoms at the interface. The values in the equation are the optimized weights of the energy terms (the weight for S_contact was set to –1, see Materials and Methods).

The weights for the energy terms were optimized in the following way. Starting from random parameters, the average rms deviation of the predicted side chains from the true structure was calculated for each training protein. The mean rms deviation value of the 15 training proteins was minimized. The Monte Carlo searches converged very fast. For the 20 repetitions of parameter optimization procedure, the minimized rms deviation values were in the narrow range of 0.714–0.717 Å. However, the optimized values of parameters displayed larger variance. The average values and standard errors of the weights for volume overlap, backbone dependency, electrostatic interaction, and desolvation energy were 3.912 ± 0.072, –6.427 ± 0.145, 152.1 ± 13.5, and 5.316 ± 0.385, respectively. We accepted the parameter values when the objective function value was minimized to the lowest value (0.714 Å). The derived scoring function took the form of equation (1). Table 1 lists the prediction results for the 15 training proteins.

Table 1.

Prediction results for the 15 training proteins

			%χ1 correctc		%χ1+2 correctd		No. of predicted residues
PDB	Average rms deviationa (Å)	Overall rms deviationb (Å)	All	Core	All	Core	All	Core
1a8q	0.588	1.060	94.2	98.1	82.9	91.6	225	104
1amm	0.726	1.171	93.5	100	81.5	94.9	154	55
1bd8	0.839	1.409	81.8	92.7	73.6	92.3	121	41
1cem	0.648	1.098	91.8	97.3	82.7	91.7	292	150
1chd	0.784	1.397	87.7	92.3	66.1	75.6	154	65
1edg	0.730	1.258	88.8	94.4	76.4	86.9	329	161
1ifc	0.795	1.077	90.3	100	79.6	96.2	113	32
1mla	0.618	1.006	90.3	95.2	80.3	88.1	227	105
1nar	0.795	1.185	88.9	95.7	72.7	86.0	262	117
1npk	0.728	1.321	90.2	97.6	78.9	100	122	41
1thv	0.741	1.255	89.2	95.8	74.8	82.1	167	71
1vjs	0.736	1.133	90.5	94.7	78.3	90.6	391	190
2baa	0.731	1.149	88.8	90.2	80.0	83.3	178	82
2end	0.680	1.048	95.8	100	79.6	83.8	113	45
2pth	0.578	1.057	93.6	96.6	86.7	92.9	140	58
Mean	0.714	1.175	90.4	96.0	78.3	89.1	199	88

^a Averaging the root-mean-square (rms) deviation calculated for each residue.

^b Global root-mean-square deviation of nonalanine side-chain atoms.

^c Percentage of side chains with χ₁ correctly predicted.

^d Percentage of side chains with both χ₁ and χ₂ correctly predicted.

(PDB) Protein Data Bank.

Furthermore, we probed the contribution of individual energy terms to the prediction of the side-chain conformation (Table 2). For example, we compared the traditionally used Van der Waals interactions (attractive/repulsive terms) with the corresponding terms from Equation 1: contact surface/overlapped volume. It appears that contact surface/overlapped volume performs better than Van der Waals potential (Table 2). This may be because the contact surface/overlapped volume describes the complementary packing of the rotamers more accurately. As other workers have mentioned (Vasquez 1996; Bower et al. 1997^; De Maeyer et al. 1997), steric interactions play the most important role in determining side-chain conformations. It is also well known that rotamers are strongly backbone dependent (Dunbrack and Cohen 1997). Thus, it is not surprising that a combination of contact surface, volume overlap, and backbone dependency results in 89.2% accuracy for χ₁ and 74.6% for χ_{1 + 2}. The prediction results show only moderate improvement when electrostatic interactions are added. Since electrostatic interactions mainly affect conformations of polar residues, the improvements for some polar residues are significant. For example, χ_{1 + 2} prediction accuracy of Asn is improved from 41.6% to 53.0%. Addition of the desolvation energy term (the buried surface of nonhydrogen-bonded polar atoms) results in only a small improvement of the predictions (Table 2), but the predicted structures contain fewer clearly incorrect conformations with totally buried nonhydrogen-bonded polar atoms. We have probed other forms of desolvation energy potential, such as atomic contact energy (Zhang et al. 1997) or buried surfaces of hydrophobic and hydrophilic atoms at the interface, but the prediction results showed no apparent improvement (Table 2).

Table 2.

The roles of different energy items in the scoring function

									%χ1 correct		%χ1+2 correct
Van der waalsa	Surface and volume	Backbone dependency	Electrostatic energy	Desolvation energyb	ACEc	Sphi and Sphod	Average rms deviation	Overall rms deviation	All	Core	All	Core
+	−	−	−	−	−	−	1.094	1.723	79.0	91.0	60.0	79.6
−	+	−	−	−	−	−	1.003	1.619	82.5	94.0	64.3	82.5
−	−	+	−	−	−	−	1.290	2.065	72.1	74.0	52.3	58.5
−	+	+	−	−	−	−	0.778	1.254	89.2	95.2	74.6	86.9
−	+	+	+	−	−	−	0.741	1.211	89.9	95.2	77.1	87.9
−	+	+	+	+	−	−	0.714	1.175	90.4	96.0	78.3	89.1
−	+	+	+	−	+	−	0.729	1.162	90.1	95.4	77.5	88.1
−	+	+	+	+	−	+	0.730	1.173	90.0	95.6	77.1	88.6

^a CHARMM Van der Waals potential functions were used. All atom radii were scaled by 0.9 to relieve the errors caused by discrete rotamers.

^b The number of completely buried nonhydrogen-bonded polar atoms

^c Atomic contact energy (Zhang et al. 1997

^d Buried surfaces of hydrophobic and hydrophilic atoms.

Testing of the derived scoring function

The derived scoring function was tested with the 15 proteins selected as described in Materials and Methods. Single residue conformations were predicted. The prediction results of the testing proteins are slightly different from those of the training proteins (Table 3). We believe these differences are due to the properties of the set of testing proteins. Specifically, the training proteins are on average larger than the testing proteins and have a higher percentage of core residues, which are easier to correctly predict than are surface residues. Thus the prediction accuracy of the training proteins is slightly better than that of testing proteins (Tables 1 and 3). When the testing proteins are predicted by a scoring function derived from themselves, the results are very similar to those predicted by the scoring function derived from the training proteins (Tables 3 and 4). This indicates that the scoring function derived from the training proteins performs well on other proteins.

Table 3.

Testing of the derived scoring function on 15 proteins

			%χ1 correct		%χ1+2 correct		No. of predicted residues
PDB	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core	All	Core
153l	0.663	1.056	92.0	96.8	77.5	89.1	149	63
1ako	0.851	1.528	89.7	98.0	76.4	88.5	234	101
1arb	0.515	0.818	95.5	94.9	87.4	88.7	202	97
1bj7	0.710	1.129	91.0	97.9	75.7	91.7	133	48
1cex	0.648	1.289	90.4	98.3	78.6	97.7	136	59
1dhn	0.856	1.365	89.5	100	65.1	86.4	105	33
1hcl	0.971	1.538	85.6	95.0	62.9	77.5	257	100
1koe	0.726	1.325	89.6	94.8	83.2	91.9	144	58
1mml	0.845	1.283	88.7	94.9	70.4	85.3	221	79
1noa	0.551	1.087	91.3	100	85.0	91.7	80	23
1thx	0.648	0.971	88.4	100	73.5	95.2	95	33
1whi	0.771	1.437	88.1	100	78.9	100	101	30
2cpl	0.680	1.247	90.9	100	79.0	97.2	132	59
2hvm	0.627	0.950	92.3	98.0	78.2	90.4	221	99
2rn2	0.956	1.632	92.1	100	74.3	96.7	127	43
Mean	0.735	1.244	90.4	97.9	76.4	91.2	156	62

Table 4.

Comparison of the prediction results for the 15 testing proteins calculated by scoring functions derived from different data sets

			%χ1 correct		%χ1+2 correct
	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core
Scoring function Ia	0.735	1.244	90.4	97.9	76.4	91.2
Scoring function IIb	0.722	1.218	90.6	97.8	77.0	90.6

^a Derived from the training proteins.

^b Derived from the testing proteins themselves.

The strategy of searching for a single residue conformation has been used by Wilson et al. (1993) to test the AMBER nonbonded energy plus a weighted solvation term. Petrella et al. (1998) used the same strategy to test the CHARMM22 energy function. Instead of using a rotamer library, Petrella et al. rotated χ₁ and χ₂ of side chains at the intervals of 5° or 10°, which made the prediction results less feasible computationally to model side chains simultaneously for an entire protein. Here, the protein used by Wilson et al. (PDB code 2alp) and the 10 proteins of Petrella et al. (PDB code 5pti, 1crn, 2cro, 1ctf, 4fxn, 1hiv, 1lz1, 3app, 3rn3, 3tln) were also used to test our scoring function (2fox and 4tln were used here instead of 4fxn and 3tln, which have been updated in the March 2001 release of PDB). The results calculated by our scoring function were compared with those listed by Wilson et al. and Petrella et al. (Table 5). Our scoring function achieves better results than that of the CHARMM22 or AMBER force field. These results may indicate that force fields that are widely used in molecular mechanics calculations may not necessarily be the best for side-chain modeling.

Table 5.

Comparison of potential energy functions in searching a single residue

			%χ1		%χ1×χ2 correct
	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core
AMBER	0.68	1.21	82	—	—	—
This work	0.58	1.00	94	—	—	—
CHARMM	—	—	86.8	94.9	77.4	89.5
This work	—	—	88.8	96.2	80.3	91.1

χ_1×χ₂, the number of residues with both dihedral angles correct or, in the cases of valine, threonine, serine, and cysteine, only the single angle correct over the total number of rotatable residues. The prediction results of AMBER force field and the calculated protein were given in Wilson et al. (1993); those of CHARMM and calculated proteins were listed in Petrella et al. (1998).

The predicted results of 18 residue types were analyzed for the 30 training and testing proteins (Table 6). In general, the percentages of correctly predicted hydrophobic residues were much larger than those of hydrophilic residues. This is expected because more hydrophobic residues are buried compared with hydrophilic residues. Surprisingly, the conformations of most buried hydrophilic residues, except χ₁ of Ser and χ_{1 + 2} of Asp, Asn, and His, are predicted, as well as those for buried hydrophobic residues. Serine may be too small to be affected by steric conflicts. Similarly, carboxylate group of aspartic acid is not sensitive to χ₂ rotation concerning steric or electrostatic interactions. The poor χ_{1 + 2} prediction of Asn and His may be partly due to the fact that the observed frequency of a rotamer, given backbone conformation, is not correctly evaluated (see Materials and Methods). The two aromatic residues, Phe and Tyr, were predicted accurately (χ₁ correct >97%; χ_{1 + 2} correct >93%). Pro was poorly predicted (χ₁ correct = 85%; χ_{1 + 2} correct = 78%). The two rotamers of Pro are rather similar in shape and do not depend on the backbone conformation significantly. Cys side chain was 100% accurately predicted for both core and surface residues, which indicated that our simple strategy to manipulate disulfide bridges (see Materials and Methods) was successful. The average percentage of crystal structure side chains within 40° of any rotamer in the library is 99.1% for χ₁ and 97.2% for χ_{1 + 2} (Table 6). However, the average prediction accuracy is only 91.1% for χ₁, and 77.6% for χ_{1 + 2}. For core residues, the corresponding values are 99.5%, 98.2%, 97.0%, and 87.5%, respectively. Thus, it should be possible to further increase prediction accuracy by adopting better scoring functions.

Table 6.

Prediction results of 30 high-quality proteins arranged by residue types

	%χ1 correct		%χ1+2 correct		%χ1a consistent with rotamer model		%χ1+2 consistent with rotamer model		Number of residues
Residue type	All	Core	All	Core	All	Core	All	Core	All	Core
Arg	89.0	98.2	74.4	91.2	98.5	100	96.7	100	336	57
Asn	92.5	100	61.9	79.2	99.7	100	93.1	97.4	318	77
Asp	92.4	100	66.3	71.9	100	100	92.9	93.3	395	89
Cys	100	100			100	100			106	85
Gln	84.5	98.1	68.2	94.2	97.9	100	96.7	100	239	52
Glu	81.6	94.9	68.7	92.3	98.8	97.4	97.5	97.4	326	39
Ile	96.6	98.1	88.8	93.9	99.4	99.6	98.6	98.9	349	263
Leu	93.6	96.3	82.8	85.8	97.4	98.0	95.4	96.0	500	352
Lys	86.2	100	70.2	84.2	98.0	100	97.4	100	439	19
Met	89.5	96.0	81.6	90.7	97.4	100	97.4	100	114	75
Phe	99.6	100	96.3	97.5	100	100	98.5	98.5	271	204
Pro	85.4	90.8	78.4	82.8	100	100	100	100	301	87
Trp	96.6	100	84.0	86.7	100	100	98.3	97.3	119	75
Val	92.1	92.7			97.7	97.5			441	314
Ser	74.7	82.6			99.2	100			383	132
Thr	91.9	97.6			99.2	99.2			372	123
Tyr	97.6	100	93.7	96.5	99.6	100	98.8	99.3	254	143
His	96.2	100	70.7	78.6					157	56
Mean	91.1	97.0	77.6	87.5	99.1	99.5	97.2	98.2	296	125

^a The percentage of crystal structure side chains within 40° of any rotamer in the library.

Modeling the side chains for a whole protein

DEE, which detects and eliminates rotamers that cannot be the members of global minimum energy conformation, is the most powerful algorithm in side-chain modeling (Desmet et al. 1992; Voigt et al. 2000); however, it cannot be used together with our scoring function. DEE assumes that the total rotamer–rotamer interaction energy is the sum of the interaction energy between any two rotamers. This is not true for contact surface, volume overlap, or the number of totally buried nonhydrogen-bonded polar atoms, which can only be calculated when conformations of all side chains are known. Thus, we used the Monte Carlo-simulated annealing method to model the side-chain conformations of a whole protein. Because the derived scoring function performed equally well on the training and testing proteins, both sets were combined and used to test the program. For the 30 resulting proteins, we obtained average predictions of 87.9% for χ₁, 73.2% for χ_{1 + 2}, and 1.34 Å for rms deviation (Table 7). These results are clearly inferior to the differences between the experimental structure and the model built from the most similar rotamers, which indicates that we are still far from the maximal prediction accuracy possible with the current rotamer set (Table 8).

Table 7.

Side-chain construction on the 30 high-quality proteins

			%χ1 correct		%χ1+2 correct
PDB	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core
1a8q	0.663	1.170	92.0	97.1	76.6	80.3
1amm	0.887	1.384	90.3	100	73.4	89.7
1bd8	0.879	1.537	81.0	90.2	70.3	88.5
1cem	0.725	1.250	90.4	95.3	76.7	86.1
1chd	0.826	1.474	87.0	93.9	65.2	73.2
1edg	0.741	1.281	89.4	94.4	73.2	83.6
1ifc	0.964	1.358	83.2	96.9	69.3	92.3
1mla	0.733	1.294	89.0	95.2	75.3	89.6
1nar	0.843	1.213	84.7	91.5	68.3	80.7
1npk	0.783	1.347	87.7	95.1	75.6	92.9
1thv	0.828	1.374	85.6	87.3	74.8	92.3
1vjs	0.930	1.522	84.7	90.0	66.9	78.3
2baa	0.793	1.311	86.5	90.2	76.9	85.0
2end	0.700	1.067	94.9	100	79.6	86.5
2pth	0.730	1.310	90.0	93.1	80.5	90.5
1531	0.738	1.248	92.0	95.2	73.9	87.0
1ako	1.042	1.705	81.2	89.1	64.1	80.8
1arb	0.594	1.125	93.6	92.8	81.1	82.3
1bj7	0.705	1.111	90.2	97.9	74.8	86.1
1cex	0.652	1.297	90.4	98.3	78.6	97.7
1dhn	1.006	1.591	85.7	100	65.1	86.4
1hcl	1.026	1.592	81.7	89.0	61.4	71.3
1koe	0.849	1.492	84.7	87.9	75.3	86.5
1mml	0.849	1.289	86.4	94.9	71.0	88.5
1noa	0.534	1.024	91.3	100	82.5	91.7
1thx	0.629	0.918	87.4	97.0	75.0	95.2
1whi	0.899	1.758	85.2	100	70.4	92.9
2cpl	0.733	1.288	89.4	100	78.0	91.7
2hvm	0.687	1.089	91.0	98.0	73.9	89.0
2rn2	1.017	1.677	90.6	100	67.3	93.3
Mean	0.800	1.337	87.9	95.0	73.2	87.0

Side-chain conformations were modeled simultaneously, given protein backbone and sequence.

Table 8.

Comparison of the native and predicted structures with the structure built from rotamers most similar to real conformation

			%χ1 correct		%χ1+2 correct
	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core
Native/Built	0.412	0.570	98.5	99.3	94.3	96.7
Predicted/Built	0.596	1.314	88.1	95.2	73.7	87.1
Predicted/Native	0.800	1.337	87.9	95.0	73.2	87.0

Thirty high-quality proteins were calculated and averaged. The rotamer with the lowest rms deviation from the crystal structure side chain was defined as the most similar rotamer.

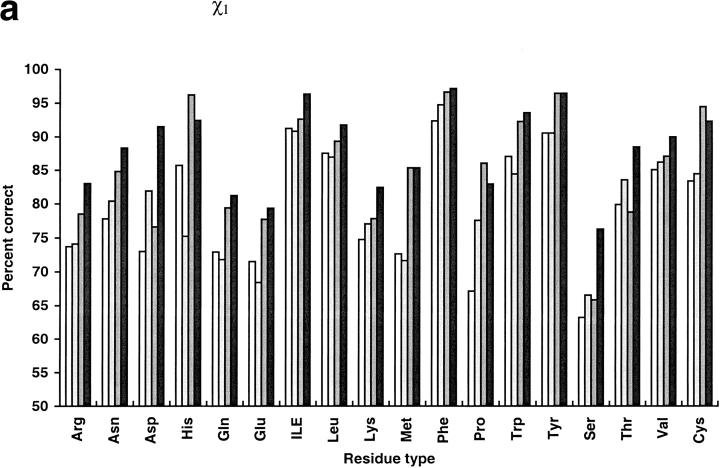
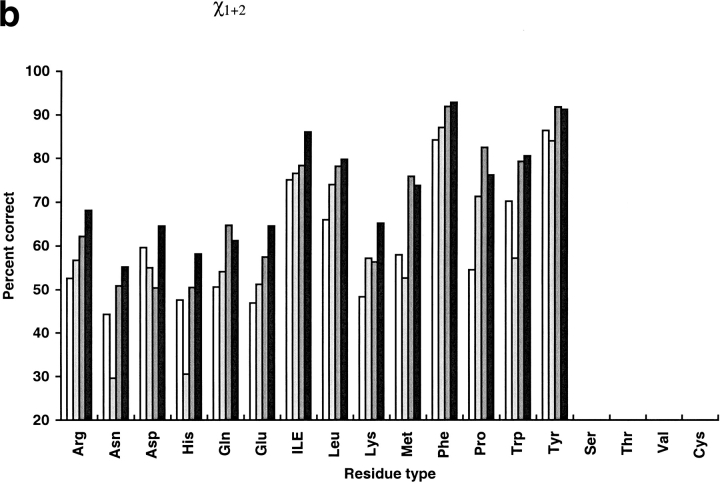
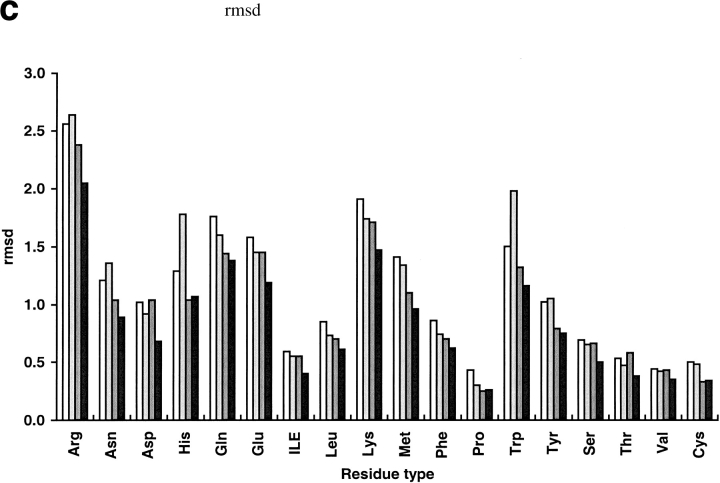
We compared our program with the torso program from the MAXSPROUT package (Holm and Sander 1991), SCWRL2.2 (Bower et al. 1997), and that of Mendes et al. (1999). Like our method, torso was based on the Monte Carlo algorithm. The other two programs are the best available side-chain modeling programs developed in the last several years (Mendes et al. 1999). Mendes et al. used self-consistent mean field theory and a flexible rotamer model that handled a continuous ensemble of conformations around the classic rigid rotamer. SCWRL initializes a structure with residues in their most favorable backbone-dependent rotamers and systematically resolves steric clashes. Among the 30 selected proteins, the terminal carbonyl oxygen named "OXT" was not found in the PDB files of five proteins (1cem, 1nar, 1vjs, 1arb, and 1mml) and they could not be operated by the Mendes program. Twenty-five other proteins were used in comparison (Table 9 and Figure 1 ▶). The prediction accuracy of SCWRL is similar to torso but lower than the Mendes algorithm. Compared with the program of Mendes et al., our program has an improvement of 4.4% in average χ₁ prediction, 4.7% in average χ_{1 + 2} prediction, and 0.21 Å in average global rms deviation. For core residues, the differences are small: 1.8% improvement in χ₁ prediction and 3.3% improvement in χ_{1 + 2} prediction. Our method has a more significant advantage for surface residues. SCWRL and torso run much faster than our program and the Mendes algorithm. However, our program is two times faster than the Mendes algorithm. Both SCWRL and our program use the rotamer library of Dunbrack (Dunbrack and Karplus 1993). Our program shows an advantage over SCWRL in average χ₁ prediction, χ_{1 + 2} prediction, and rms deviation for all residue types. SCWRL predicted χ_{1 + 2} of Asn and His poorly because it does not contain a mechanism to distinguish θ and 180° + θ of χ₂ angles of the two residues. The Mendes algorithm, using the Tuffery rotamer library (Tuffery et al. 1991) shows obvious disadvantages for small polar residues such as Ser, Thr, and Asp. It predicted χ₁ more accurately for Pro, Cys, and His, and χ_{1 + 2} for Gln, Met, Tyr, and Pro. The Mendes algorithm also predicted χ₁ of Tyr and Met with the same accuracy as our methods. Cysteines were predicted with a high correct percentage by the Mendes algorithm partly because the program takes the disulfide bridge pairings as input.

Table 9.

Comparison of our side-chain modeling program with other methods

			%χ1 correct		%χ1+2 correct		Computing time (hours)
	Average rms deviation (Å)	Overall rms deviations (Å)	All	Core	All	Core
Holm and Sander	1.074	1.707	79.4	89.5	60.7	75.6	0.05
Scwrl	1.040	1.696	80.7	88.0	62.3	74.5	0.5
Mendes et al.	0.968	1.560	83.5	93.6	68.6	84.4	120
This work	0.802	1.348	87.9	95.4	73.3	87.7	40

Twenty-five of the 30 carefully selected proteins, which could be operated by all programs, were calculated and averaged. The computational results of Holm and Sander (1991), SCWRL (Bower et al. 1997), Mendes et al. (1999), and this work were equally evaluated as described earlier. The computing time was counted on a Silicon graphic 400MHZ IP30 processor.

Fig. 1.

Comparison of prediction results over different residue types. Results of Holm and Sander (1991) are shown in white, the results of SCWRL (Bower et al. 1997) are in light gray, the results of Mendes et al. (1999) are in dark gray, and the results of this work are in black. Percent correct within 40° for χ₁ (a), percent correct within 40° for χ_{1 + 2} (b), and rmsd (c) were plotted for each residue type.

We also compared our program with the Mendes algorithm on the Mendes et al. testing proteins. Five of the 20 high-quality protein structures used by Mendes et al. were also included in our training and testing proteins. Thus the comparison was done on the other 15 proteins: 2erl, 1cbn, 5rxn, 1bpi, 1igd, 1ptx, 1ctj, 1plc, 9rnt, 1aac, 256b, 1isu, 2ihl, 2hbg, and 1xnb. Among them, 12 proteins contain ligands. We removed all ligands in the calculation, which affected the performance of the Mendes algorithm. Because Mendes et al. included ligands in their calculation, the calculated results here are not as accurate as those presented by Mendes et al. (1999). Our method shows a significant advantage over the Mendes algorithm: 3.7% in average χ₁ prediction, 6.1% in average χ_{1 + 2} prediction, and 0.12 Å in average global rms deviation (Table 10). We then investigated the effect of protein resolution on prediction accuracy. Because the Mendes algorithm is only effective on very high quality proteins and very time consuming, we compared our methods with SCWRL. The prediction ability of the two programs deteriorates as the resolution of a crystal structure decreases (Table 11). Bower et al. (1997) noted that the lower resolution structures might be poorly predicted because they contained errors in side-chain assignments. Our methods show an advantage over SCWRL for both high and low resolution structures.

Table 10.

Comparison of our program with that of Mendes et al. on their testing proteins

			%χ1		%χ1+2
	Average rms deviation (Å)	Overall rms deviation (Å)	All	Core	All	Core
Mendes et al.	0.922	1.477	83.9	94.9	65.4	87.6
This work	0.775	1.362	87.6	97.4	71.5	90.5

Fifteen very high quality proteins were calculated and averaged, which were used by Mendes et al. (1999) and not selected to train or test the scoring function in this work. All ligands were not included in calculation.

Table 11.

Effect of resolution on prediction accuracy

Resolution	0.0 to 1.6 (Å)		1.6 to 2.0 (Å)		2.0 to 2.5 (Å)		2.5 to 3.0 (Å)		Total
No. of structures in average	15		49		48		11		123
	Scwrl	This work	Scwrl	This work	Scwrl	This work	Scwrl	This work	Scwrl	This work
Average rms deviation (Å)	1.009	0.778	1.050	0.866	1.195	1.034	1.311	1.184	1.125	0.949
Overall rms deviation (Å)	1.652	1.348	1.652	1.392	1.781	1.580	1.861	1.745	1.721	1.492
%χ1 correct of all residues	82.8	89.2	79.3	84.5	73.7	78.3	70.7	75.7	76.8	81.9
%χ1 correct of core residues	88.7	95.8	87.3	92.7	83.0	89.1	80.0	88.2	85.1	91.3
%χ1+2 correct of all residues	64.8	75.1	59.4	68.9	53.6	61.5	47.8	55.0	56.8	65.5
%χ1+2 corrct of core residues	75.8	88.5	72.5	83.9	68.6	79.0	60.2	71.3	70.3	81.4

PDB codes were downloaded from ftp://fccc.edu/dunbrack/pub/culledpdb updated on March 8, 2001. All the selected proteins were single-chain proteins, which contained no ligands and had fewer than 50% sequence identities.

The prediction results for modeling of the whole protein simultaneously are inferior to those of searching for a single residue conformation (Tables 1, 3, and 7). For the 30 tested proteins, the prediction accuracy decreases 2.5% for χ₁ and 4.1% for χ_{1 + 2}. The decreased accuracy of the prediction results for the whole protein modeling may be due to the errors caused by rotamer approximation. Compared with searches for a single residue conformation, the positional errors double when both interacted residues are represented by rotamers. To eliminate the rotamer approximation effect, we included the real conformation to the rotamer library to substitute for the rotamer with the lowest rms deviation. The scoring function was reoptimized. For the 30 selected proteins, the average accuracy was 92.2% for χ₁ and 84.2% for χ_{1 + 2} when a single residue conformation was predicted. The prediction accuracy in this case depends on the scoring function only. Thus our scoring function can potentially be significantly improved. Then we modeled all side chains simultaneously. The average accuracy was 91.1% for χ₁ and 82.6% for χ_{1 + 2}. These values represent improvements of 3.2% for χ₁ and 9.4% for χ_{1 + 2} compared with predictions that used standard rotamer library. The improvements in χ_{1 + 2} prediction are larger than the improvements in χ₁ prediction. Thus a more detailed rotamer library is expected to increase χ_{1 + 2} prediction accuracy; however, it should have little effect on χ₁ accuracy. The prediction accuracy decreases by 1.1% for χ₁ and 1.6% for χ_{1 + 2} compared with the single residue predictions. These small decreases might be caused by the search strategy or occur for other reasons.

Conclusions

We have developed a new and simple scoring function for side-chain modeling. Compared with the CHARMM and AMBER force fields, our scoring function shows clear advantages in predicting the conformation of a single residue. Our scoring function was combined with a Monte Carlo algorithm to place all the side chains onto a protein backbone. The prediction results compared favorably with existing methods. It appears that the search strategy is not the main obstacle in side-chain modeling, but better scoring function and more detailed rotamer library are needed to achieve higher accuracy. A detailed rotamer library is expected to increase χ_{1 + 2} prediction accuracy; however, it will have little effect on χ₁ accuracy.

Materials and methods

Scoring function

Five energy terms are considered in the scoring function: backbone dependency, contact surface, overlapped volume, electrostatic interactions, and desolvation energy.

The backbone-dependent rotamer library and rotamer energies

The backbone-dependent rotamer library of Dunbrack is used in this study (Dunbrack and Cohen 1997). The intrinsic energies of rotamers are represented by their expected frequencies (f), given a backbone conformation, which are derived by Bayesian statistical analysis of protein side-chain rotamer preferences (Dunbrack and Cohen 1997). Here, lnf is considered an energy term and is called backbone dependency. The Dunbrack library is modified as follows. (1) Polar hydrogen atoms, which are absent in the Dunbrack library, are added for the convenience of calculating electrostatic interactions. Each χ₂ for Ser and Thr and χ₃ for Tyr are assigned three possible values: –60°, 60°, and 180°. The frequency of the new rotamers is set to one-third of the observed frequency of their parent rotamer. (2) Three protonation states of His with the same expected frequencies are considered, N_δ1 protonated, N_ɛ2 protonated, and both. (3) We supplemented additional rotamers to correct for the lack of defined rotameric states for the amide planes of Asn and Gln and for the aromatic plane of His in the Dunbrack library. χ₂ of Asn and His and χ₃ of Gln are flipped 180° to make new rotamers. Thus the rotamer numbers of these residues are doubled and the expected frequencies are correspondingly reduced by one-half. Bond lengths and angles from Engh and Huber (1991) are used to build the rotamer library. The rotamers with standard geometries are placed on the protein backbone by superimposing N, C, and C_α atoms.

Contact surface and volume overlap

The contact surface and overlapped volume between the selected rotamer and other parts of the protein (termed protein environment, which consists of all atoms in a protein that do not belong to the selected rotamer) are calculated by the grid-based method. CHARMM22 atom radii are used (Brooks et al. 1983; Mackerell et al. 1998). The grid step is set to 0.6 Å. The selected rotamer and the protein environment are mapped using the same strategy. The grid points within the Van der Waals radius (r) of an atom are labeled as interior points. The first layer of grid points on the atom surface (between r and r+0.6 Å) are labeled as surface points. In case of a conflict, for example, if a grid point is an interior point of one atom but is a surface point of another atom, the interior points override surface points. The overlapped volume (ų) is counted according to the number of grid points that belong to the interior points of the rotamer and protein environment simultaneously. Each co-occupied grid point corresponds to 0.216 ų volume overlap. The contact surface (ų) is counted as the number of grid points that belong to the surface points of the rotamer and interior points of the protein environment, the interior points of the rotamer and surface points of the protein environment, or the surface points of both sides. Interactions between the rotamer and local backbone, which starts from the C_α of the last residue to the C_α of the next residue at the searched position, are not considered. They are assumed to be included in the backbone-dependent rotamer energy. Special attention is paid to the joint between the local backbone and other parts of the protein. A plane cuts the joining bond perpendicularly at the middle point to separate the surface and interior grid points of the two joined atoms. The grid points on the side of the local backbone are not considered. For two cysteine residues (residue 1 and residue 2) that form a disulfide bridge, the overlapped volume of S_γ1– S_γ2, S_γ1–C_β2, or C_β1–S_γ2, is not counted. We consider that two cysteine residues form a disulfide bridge when the distance between the two sulfur atoms is within 2.09 ± 1 Å and both angles of C_β–S–S are within 104.2° ± 30°. Here, 2.09 Å and 104.2° are CHARMM22 parameters for a disulfide bridge.

Electrostatic interactions

The electrostatic interactions between the modeled rotamer and the protein environment are calculated as follows:

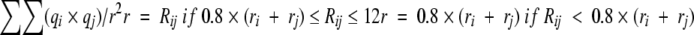where indices i and j refer to the atoms of the rotamer and the environment, respectively, q_i and q_j are partial charges, and r_i and r_j are atom radii from CHARMM22. R_ij is the distance between the two atoms. The summation is over all atoms i and j for which R_ij ≤ 12. Similar to the calculation of contact surface and volume overlap, the electrostatic interactions between the selected rotamer and the local backbone are not considered.

Desolvation energy

Desolvation energy is evaluated as the number of totally buried (<5% solvent accessible surface) nonhydrogen-bonded hydrophilic atoms. Polar H and O and nonprotonated N of His that can be an acceptor of a hydrogen bond are considered as hydrophilic atoms. Solvent-accessible surface area is calculated as described by Zou et al. (1999). The probe radius is set to 1.2 Å. The radii of polar hydrogen atoms are set to 1.0Å. The radii of other atoms are taken from CHARMM and are scaled by 0.8. The definition of hydrogen bonds is similar to that of Dahiyat et al. (1997):

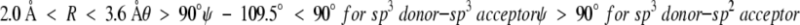where R is the distance between donor and acceptor of a hydrogen bond, θ is the donor-hydrogen acceptor angle, and ξ is the hydrogen-acceptor base angle (the base is the atom attached to the acceptor).

Minimization methods

Continuous minimization methods by simulated annealing are used (Press et al. 1992). The basic ideas follow the Metropolis Monte Carlo simulation except that a modified downhill simplex method is used to generate random changes (Metropolis et al. 1953; Nelder and Mead 1965). The "moves" include reflections, expansions, and contractions of the simplex. −T × lnɛ [T is the temperature; ɛ is a small random number in the range of (0,1 )] is added to the stored function value associated with every vertex of the simplex, and a similar random variable is subtracted from the function value of every new point that is tried as a replacement point. The modified function values of the new and old points are compared. This procedure takes a downhill step while sometimes takes an uphill step and converges to a local minimum in the limit T → 0. In this study, the weight of the contact surface is set to –1 (because favorable interactions are defined as having negative energy) and those of the other four energy terms are subject to optimization. For the training protein, a single residue is checked for different rotamers at each trial, and other residues are unchanged from the experimental structure. The rms difference between the lowest-energy rotamer and the real conformation is calculated and averaged for all the residues of the protein. The mean value of the averaged rms deviations for the training proteins is the objective function value to be minimized. Initial values of the parameters to be optimized are set to ±lnɛ (ɛ is a random number as was the case earlier). The simulated annealing temperature starts from 0.01 and is gradually reduced to 0 with the step of 0.001. Two thousand moves are made at each temperature.

Training and testing protein sets

The proteins for training and testing sets were chosen according to the following criteria. Sequence identity cutoff was set to 50%, the resolution cutoff was set to 1.8 Å, and the R-factor cutoff was set to 0.2. A total of 761 chains that met the criteria were downloaded from ftp://fccc.edu/dunbrack/pub/culledpdb on March 8, 2001. Only single-chain proteins with 100–500 monomers and containing no incomplete side chains or ligands were kept. A total of 30 proteins meeting all the requirements were selected: 1a8q, 1amm, 1bd8, 1cem, 1chd, 1edg, 1ifc, 1mla, 1nar, 1npk, 1thv, 1vjs, 2baa, 2end, 2pth, 153l, 1ako, 1arb, 1bj7, 1cex, 1dhn, 1hcl, 1koe, 1mml, 1noa, 1thx, 1whi, 2cpl, 2hvm, 2rn2. The first 15 proteins were used to derive the scoring function and the remaining proteins were used for testing. The program REDUCE (Word et al. 1999) was used to add hydrogen atoms to all proteins. Nonpolar hydrogen atoms were deleted. The amide plane of Asn or Gln and the aromatic ring of His were flipped if needed to form more hydrogen bonds. When a residue had multiple conformations, only the one with the highest occupancy was used.

Modeling the side chains for an entire protein

Metropolis Monte Carlo-simulated annealing methods (Metropolis et al. 1953) with the rotamer library of Dunbrack (Dunbrack and Cohen 1997) are used to predict side-chain conformations, given a protein backbone conformation and sequence. Initially, the rotamers for the sequence are selected at random. Then, a rotamer substitution is made at a selected position. The frequency to select a position is proportional to the number of rotamers for the residue in the position. One rotamer is selected at random and the interaction energy with the other parts of the protein E_new is calculated using the derived scoring function. If the energy value is lower than the previous energy E_old, the move is accepted, or the move is accepted with the probability exp[(E_old–E_new)/T]. The initial temperature T is set to 50 and is scaled by 0.8 after each cycle. A total of 25 cycles are repeated. We hold the temperature constant at each cycle for 10,000 substitutions or 1,000 successful substitutions, whichever comes first.

Evaluation methods

Several evaluation methods for side-chain modeling programs have been proposed (De Maeyer et al. 1997). We make sure that the evaluation methods obey the same standards when the results obtained by different programs are compared. Unless specifically indicated, all computational results in this work are evaluated as the following. C_β is included in rms deviation calculation and hydrogen atoms are excluded. Incomplete residues, Ala, or residues with alternative conformation are not evaluated. Residues with <20% solvent accessibility are considered as core residues. If the χ₁ angle of a predicted residue is within 40° of the experimental value, the residue is considered correctly predicted until χ₁. χ_{1 + 2} only refers to residues that have more than one side-chain dihedral angle (not including Ser, Thr, Val, and Cys). χ_{1 + 2} is considered correctly predicted when both χ₁ and χ₂ are within 40° of their experimental values. For residues with a rotational symmetry axis (Asp, Glu, Phe, and Tyr), we consider the torsion angle corresponding to this axis correct if either of the symmetric conformations obeys the above criteria, and the rms deviation is calculated from the closest symmetric conformation. Asn, Gln, and His especially are compared with the structures resulting from running REDUCE.