Statistical potentials for fold assessment

Abstract

A protein structure model generally needs to be evaluated to assess whether or not it has the correct fold. To improve fold assessment, four types of a residue-level statistical potential were optimized, including distance-dependent, contact, φ/Ψ dihedral angle, and accessible surface statistical potentials. Approximately 10,000 test models with the correct and incorrect folds were built by automated comparative modeling of protein sequences of known structure. The criterion used to discriminate between the correct and incorrect models was the Z-score of the model energy. The performance of a Z-score was determined as a function of many variables in the derivation and use of the corresponding statistical potential. The performance was measured by the fractions of the correctly and incorrectly assessed test models. The most discriminating combination of any one of the four tested potentials is the sum of the normalized distance-dependent and accessible surface potentials. The distance-dependent potential that is optimal for assessing models of all sizes uses both C_α and C_β atoms as interaction centers, distinguishes between all 20 standard residue types, has the distance range of 30 Å, and is derived and used by taking into account the sequence separation of the interacting atom pairs. The terms for the sequentially local interactions are significantly less informative than those for the sequentially nonlocal interactions. The accessible surface potential that is optimal for assessing models of all sizes uses C_β atoms as interaction centers and distinguishes between all 20 standard residue types. The performance of the tested statistical potentials is not likely to improve significantly with an increase in the number of known protein structures used in their derivation. The parameters of fold assessment whose optimal values vary significantly with model size include the size of the known protein structures used to derive the potential and the distance range of the accessible surface potential. Fold assessment by statistical potentials is most difficult for the very small models. This difficulty presents a challenge to fold assessment in large-scale comparative modeling, which produces many small and incomplete models. The results described in this study provide a basis for an optimal use of statistical potentials in fold assessment.

Usefulness of a protein structure model depends on its accuracy (Baker and Sali 2001). Thus, it is necessary to estimate accuracy of a three-dimensional (3D) model before it is used. The assessment must generally begin with predicting whether or not the model has at least the correct fold. Such coarse assessment may then be followed by an evaluation of model's detailed features, such as loops and sidechains. The fold has to be assessed almost invariably for all of the models predicted by ab initio methods (Jones 1997; Ortiz et al. 1999; Xia et al. 2000; Bonneau and Baker 2001; Pillardy et al. 2001) and threading of sequences into structures (Bowie et al. 1991; Godzik et al. 1992; Jones et al. 1992; Sippl and Weitckus 1992; Torda 1997). In addition, fold assessment is frequently also needed for models calculated by comparative modeling (Browne et al. 1969; Blundell et al. 1987; Martí-Renom et al. 2000). Comparative or homology modeling builds a model for a protein sequence (target) on the basis of its alignment to known related protein structures (templates). It consists of fold assignment, target-template alignment, model building, and model assessment. Comparative modeling based on <30% sequence identity between the target and the template is common; more than half of all known protein sequences that are detectably related to known protein structures currently share <30% sequence identity with the closest template structure (Pieper et al. 2002). In this low range of sequence similarity, comparative models frequently have an incorrect fold because they are built on an incorrect template structure or a substantially incorrect alignment with the correct template structure. Objective fold assessment is especially important in large-scale, automated comparative modeling of whole genomes in which no user intervention is possible (Martí-Renom et al. 2000). In automated modeling, accurate fold assessment increases the number of the validated models because it identifies the models with the correct fold that are based on statistically insignificant sequence similarity to known protein structures. Fold assessment also increases the average accuracy of the validated models because it weeds out the models with an incorrect fold that are based on statistically significant sequence similarity to unrelated structures or to incorrectly aligned related structures.

A large variety of criteria have been used by the methods for assessing protein structure models. These criteria include deviation from standard bond lengths, bond angles, and dihedral angles (Vriend 1990; Engh and Huber 1991; Morris et al. 1992; Laskowski et al. 1993,1998) residue or atom packing density (Gregoret and Cohen 1991), molecular mechanics energy functions (Novotny et al. 1984, 1988; Petrey and Honig 2000), distribution of residues between the solvent accessible and buried positions (Bryant and Amzel 1987; Huang et al. 1995), atomic and residue solvation energy (Eisenberg and McLachlan 1986; Baumann et al. 1989; Chiche et al. 1990; Still et al. 1990; Vila et al. 1991; Holm and Sander 1992: Koehl and Delarue 1994^; Schaefer et al. 1998^; Vorobjev et al. 1998^; Cramer and Truhlar 1999; Dominy and Brooks, III 1999; Lazaridis and Karplus 1999^; Rapp and Friesner 1999^; Gatchell et al. 2000^; Kollman et al. 2000^; Lee et al. 2000^; Petrey and Honig 2000^; Wang and Kollman 2000^; Zhang et al. 2001), spatial distribution of charged groups (Bryant and Lawrence 1991), distribution of atom–atom distances (Colovos and Yeates 1993), main-chain hydrogen bonding (Laskowski et al. 1993), residue environments (Lüthy et al. 1992; Topham et al. 1994), sequence similarity to related known structures (Sánchez and Sali 1998; Jones 1999), similarity between the secondary structure assignment from the model and secondary structure prediction from the sequence (Jones 1999), atomic volume deviation (Pontius et al. 1996), residue–residue contact area difference (Abagyan and Totrov 1997), occluded surface of residues (Pattabiraman et al. 1995), and a large variety of knowledge-based potentials of mean force or statistical potentials (Hendlich et al. 1990; Casari and Sippl 1992; Colovos and Yeates 1993; Bauer and Beyer 1994; Kocher et al. 1994; Rooman and Wodak 1995; Jernigan and Bahar 1996; Jones and Thornton 1996; Park and Levitt 1996; Moult 1997; Park et al. 1997; Vajda et al. 1997; Furuichi and Koehl 1998; Melo and Feytmans 1998; Rooman and Gilis 1998; Betancourt and Thirumalai 1999; Rojnuckarin and Subramaniam 1999; Lazaridis and Karplus 2000; Tobi and Elber 2000; Tobi et al. 2000; Vendruscolo et al. 2000a). The statistical potentials are generally the single most informative criterion for distinguishing between the models with the correct and incorrect folds, although model assessment may be augmented by simultaneous use of several model features (Jones 1999a,Sánchez and Sali 1999). Statistical potentials are derived from known protein structures and quantify the observed preference of the different residue or atom types to be exposed to the solvent, or to interact with each other in a pairwise or higher order fashion. In addition to assessing of experimentally determined and theoretically predicted protein structures, the statistical potentials have been used in a variety of other applications, including the ab initio protein structure prediction (Sun 1993; Bowie and Eisenberg 1994; O'Donoghue and Nilges 1997; Chiu and Goldstein 2000; Tobi and Elber 2000), fold recognition or threading (Jones et al. 1992; Maiorov and Crippen 1992; Sippl and Weitckus 1992; Bryant and Lawrence 1993;Ouzounis et al. 1993; Huang et al 1995; DeBolt and Skolnick 1996^; Miyazawa and Jernigan 1996^, Miyazawa and Jernigan 2000^;Reva et al 1997^;Jones 1999b^; Kolinski et al. 1999^; Panchenko et al. 2000^; Skolnick et al. 2000), detection of native-like protein conformations (Hendlich et al. 1990; Casari and Sippl 1992; Bauer and Beyer 1994; Samudrala and Moult 1998; Simons et al. 1999; Gatchell et al 2000; Vendruscolo et al. 2000b), and prediction of protein stability (Gilis and Rooman 1996, Gilis and Rooman 1997).

In this study, we analyze the effect of the many variables that define the derivation and the use of statistical potentials for discriminating between comparative models with correct and incorrect folds. The tested statistical potentials include distance-dependent, contact, accessible surface and main-chain dihedral angle potentials. The test models with the correct and incorrect folds for proteins of known structure were constructed to be representative of the models obtained from genome-wide comparative modeling calculations, which produce many small, incomplete, and inaccurate models. The criterion used to discriminate between the correct and incorrect models was the Z-score of the model energy. The performance of a given potential was quantified by two tests, the fraction of the correctly assessed test models and the receiver operating characteristic curve.

We begin the Results and Discussion section by characterizing the models used to test various statistical potentials. We continue by describing the performance of the individual and combined potential types. We conclude by summarizing the main lessons learned from the study. In the Materials and Methods section, we describe the derivation of the test models and define all of the tested statistical potentials, as well as the criteria used to assess their performance.

Results and Discussion

Test models

A large set of models is necessary to assess the performance of the statistical potentials in discriminating between the good and bad comparative models. Large sets of good and bad comparative models for proteins of known structure were generated by ModPipe (Materials and Methods). A good model has the correct fold and is based on a substantially correct alignment; it has >30% of its C_α atoms modeled with an error of less than 3.5 Å. On the other hand, a bad model has an incorrect fold or is built on the correct fold using a poor alignment; it has <15% of its C_α atoms modeled correctly.

Distributions of several features of the good and bad models are compared in Figure 1 ▶. By construction, good models are based on a match with an alignment score higher than 22 nats (Altschul 1998), whereas the bad models are based on matches from 15 to 20 nats. As a result, most of the bad models are based on <30% sequence identity to the template structure, whereas most of the good models are based on <40% sequence identity (Fig. 1A,B ▶). Most of the good and bad models are shorter than 200 residues (Fig. 1C,D ▶). Because a local sequence alignment program was used to generate the alignments needed for modeling, many good and bad models cover only a fraction of the modeled chain. Good models, in general, cover a larger fraction of the modeled chain relative to the bad models (Fig. 1E,F ▶). Most of the good models contain whole domains, whereas most of the bad models correspond to a fraction of a domain only (Fig. 1G,H ▶). Most of the good models have a high percentage of their C_α atoms modeled correctly (Fig. 1I,J ▶).

Fig. 1.

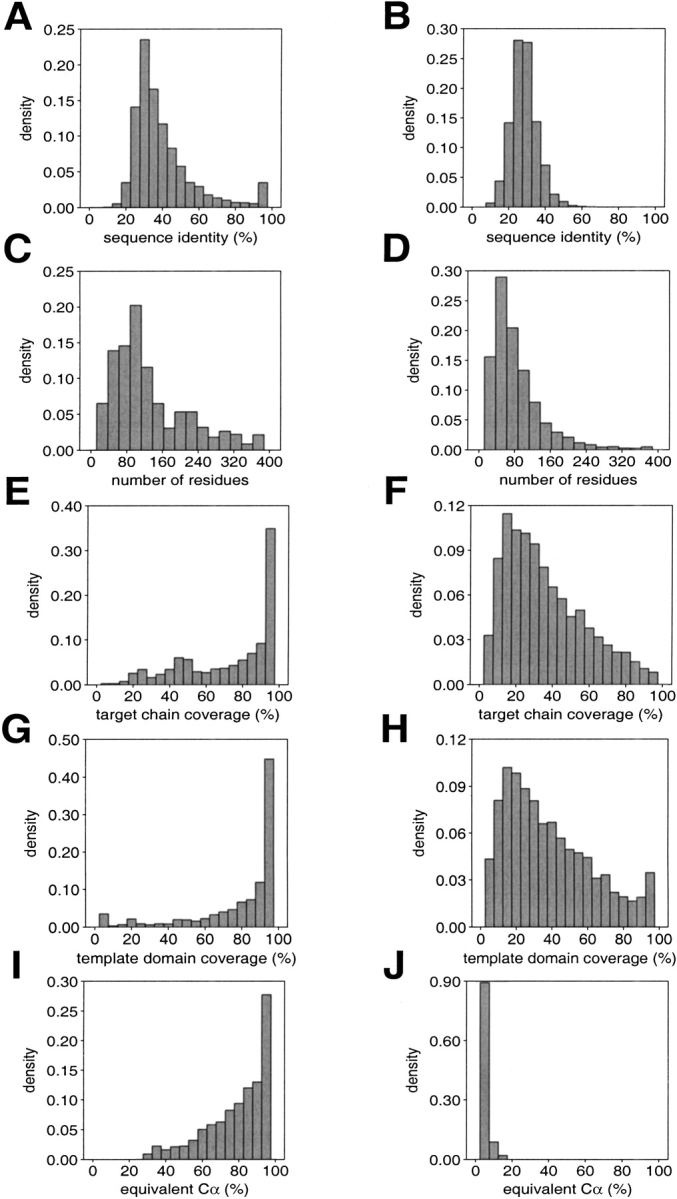
Properties of the good (left) and bad models (right). (A,B) Percentage sequence identity between the target and the template. (C,D) Model length. (E,F) Target chain coverage (the fraction of the target chain residues that were modeled). (G,H) Template domain coverage (the fraction of the template domain residues that were aligned to the target chain). The domain coverage was calculated using the domain definitions in the CATH database (Orengo et al. 1997). (I,J) Structural overlap between the target model and the actual target structure expressed as percentage of the equivalent C_α atoms (Materials and Methods).

When ModPipe is applied to whole genomes, distributions of model length and percentage sequence identity are similar to those in Figures 1A ▶–D (Sánchez and Sali 1998). Thus, the current test set of models is probably a good benchmark for the performance of statistical potentials in the assessment of models from genome-wide comparative modeling.

The jack-knife procedure to derive and test the potentials was not used. In other words, the potentials were assessed by using test models, some of which had actual structures of their sequences and of their homologs in the set of known structures from which the potentials were derived. There are four reasons for this apparent lack of statistical rigor.

First, 210 different statistical potentials were calculated and ∼10,000 models were assessed with each potential. Thus, it was impractical in terms of the CPU time to recalculate each potential for each model assessment. The price for assessing many potentials under many conditions was paid by omitting the jack-knife aspect of the evaluation.

Second, the bias in the evaluation is expected to be small or insignificant, because models with significant errors, not the actual structures, were used for testing.

Third, the main aim was to find an optimal potential for model assessment, not to determine the absolute performance of the tested potentials. This aim requires only that the relative performances of the potentials be assessed reliably. The relative performance is expected to be a more robust feature of the learning and test sets of models than the absolute performance.

And finally, it is not certain, even conceptually, that rigorous testing of a method should not rely on structures similar to those from which the potentials were derived. In practice, the statistical potentials are to be used to assess comparative models that by construction are similar to known protein structures. All of the known protein structures are legitimate sources for the statistical potential used in practical model assessment, including those known structures that happen to be related to the assessed model. Thus, it might be that an evaluation of a fold assessment method for comparative modeling that does not eliminate the homologs between the learning and test sets is more accurate even in the absolute sense than an evaluation that does eliminate the overlap. This argument does not apply to evaluating model assessment for the ab initio protein structure prediction.

Distance-dependent potentials

Distance-dependent potentials are the most used statistical potentials for fold recognition (Jones et al. 1992; Sippl and Weitckus 1992), protein structure assessment (Sippl 1993;Melo and Feytmans 1998;Jones 1999b), and ab initio protein structure prediction (Jones 1997; Xia et al, 2000). In this study, the distance-dependent potentials were derived as described earlier (Sippl 1993;Melo and Feytmans 1998) (Materials and Methods). The critical parameters that define a distance-dependent potential include the range, the resolution (bin size), and the types of the interaction centers. Thus, we explored the effect of varying these parameters on the ability of the distance-dependent potential to discriminate between the good and bad models.

Range

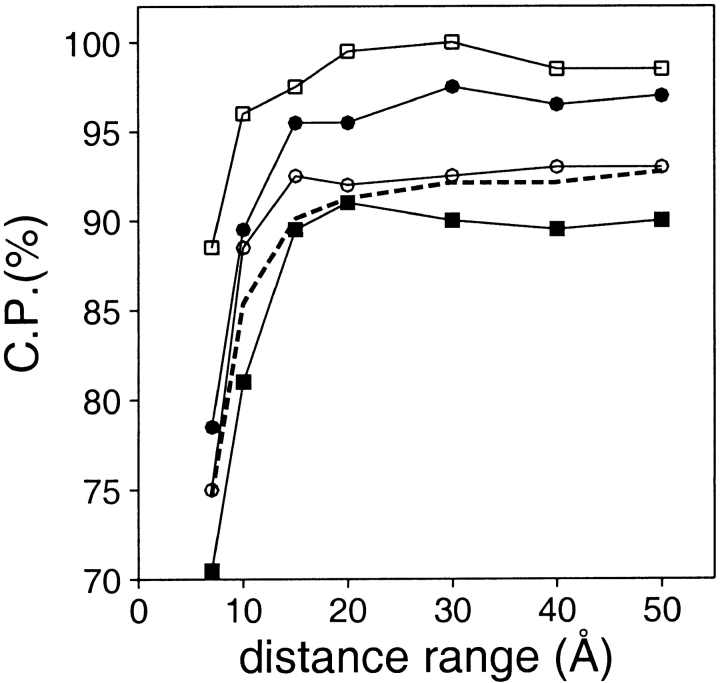
To test the effect of the distance cutoff on the ability of a distance-dependent potential to discriminate between the good and bad models, we derived several potentials by varying only their range from 7 to 50 Å (Fig. 2 ▶). The performance of the potential increases with the distance range, depending on the size of the evaluated model. For models larger than 100 residues, the discrimination plateaus at 30 Å. This result is in agreement with prior observations that optimal fold recognition was achieved by distance-dependent potentials cut at 30 Å (Sippl and Jaritz 1994; Furuichi and Koehl 1998). For smaller models, however, this cutoff is ∼20 Å. It is easier to discriminate between the good and bad models for large models than for short models. Thus, the size of a model should be taken into account when designing a model assessment method.

Fig. 2.

Performance of the distance-dependent potential as a function of its range. The percentage of the correctly predicted cases for the optimal Z-score cutoff (Materials and Methods). The performance is shown separately for the four sets with 100 good and 100 bad test models each (100/100 sets) (Materials and Methods): The very small models (▪), the small models (○), the medium size models (•), and the large models (□). The performance on the 400/400 test model set is indicated by the broken line. The potentials were calculated as specified in Table 1, except for the varying distance range.

Resolution

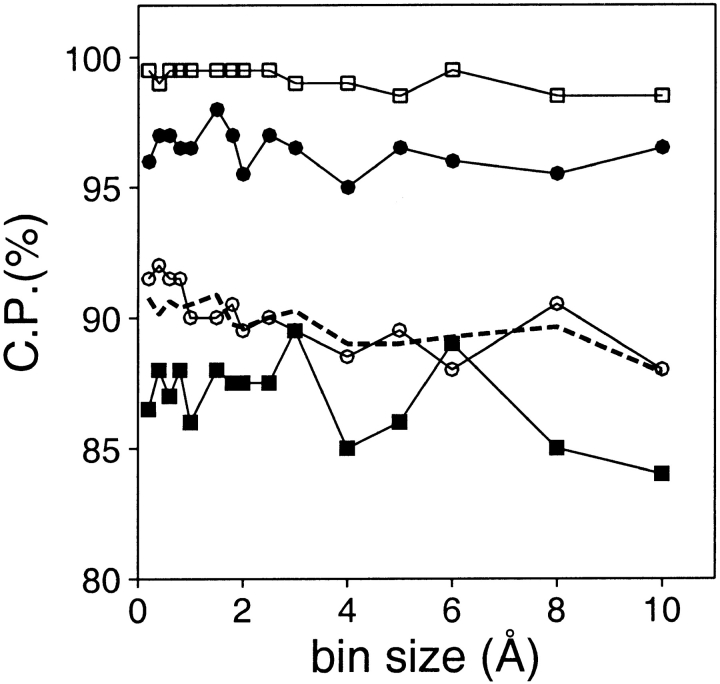
The resolution of an atomic distance-dependent potential has to be sufficiently high to allow for accurate representation of the different atom type pairs (Melo and Feytmans 1997). In contrast, potentials at the residue level that use only C_α atoms, C_β atoms or sidechain centers to describe an interaction should require lower resolution for optimal performance. To explore how the resolution influences the performance of a potential, several statistical potentials were derived with bin sizes ranging from 0.1 to 10 Å (Fig. 3 ▶). There is a slight improvement in the discriminating power of a potential at a higher resolution for the medium size and large models. In contrast, the small models exhibit a larger improvement in the performance upon increase in resolution. These results suggest that a resolution higher than 2 Å should be used with residue-level potentials. Most of the distance-dependent potentials described in the literature are within this range of resolution (Sippl 1990; Jones et al. 1992; Lemer et al. 1995; DeBolt and Skolnick 1996; Park and Levitt 1996; Park et al. 1997).

Fig. 3.

Performance of the distance-dependent potential as a function of its resolution (bin size). The potentials were calculated as specified in Table 1, except for the varying bin size. See the legend to Fig. 2 ▶ for information about the different test model sets represented by the different symbols.

Interaction centers

Traditionally, residue-based statistical potentials are calculated using only C_α atoms, C_β atoms, both C_α and C_β atoms, or centers of the selected mainchain and sidechain atoms (Lemer et al. 1995). In this work, we use only the mainchain and C_β atoms because only a low-resolution representation of protein structure was expected to be sufficient for the main aim, a coarse fold assessment. In addition, the potentials using only the mainchain and C_β atoms have the advantage that the energy Z-score can be calculated rapidly for a large set of sequences with a given structure, because there is no need to rebuild the sidechain atoms. This, in turn, made it possible to explore many potentials under many conditions.

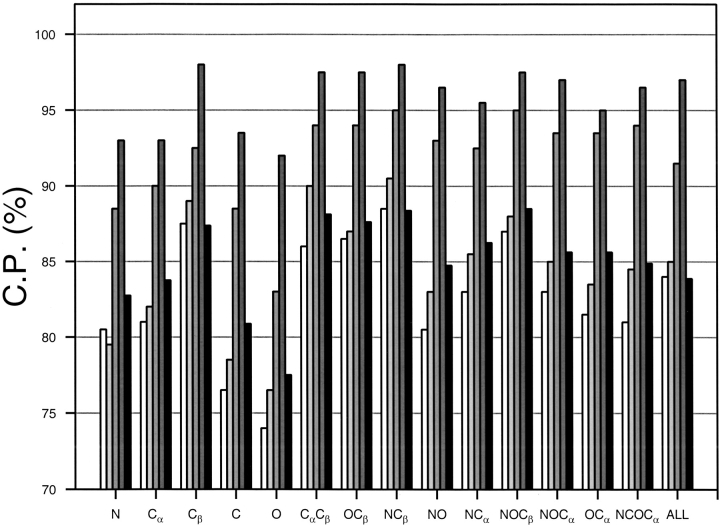
To assess the performance of the distance-dependent potentials with different types of interaction centers, 25 potentials for several combinations of the mainchain (N, C_α, C, O) and C_β atoms were calculated (Fig. 4 ▶). The best single atom interaction centers are the C_β atoms. A probable reason is that the C_β atom contains more information about the orientation of the sidechain than any mainchain atom. In contrast, the carbonyl carbon and oxygen atoms have the lowest performances, suggesting that these atoms carry the least amount of information about the sidechain interactions. Using more than one atom per residue slightly improves the performance of the potential. The statistical potentials involving only (C_α, C_β) (Sippl 1993) and (N, O, C_β) (Jones et al. 1992) perform slightly better than the potentials for all the mainchain atoms. The interaction centers for the potentials in Figure 4 ▶ are the individual atoms. These potentials performed better than the potentials involving the centers of the selected atoms (data not shown). Thus, the use of the mainchain centers is an unnecessary approximation that leads to a loss of information and to reduced discrimination between the good and bad models by a potential. Apparently, this is not the case when the sidechain centers are used in comparison with the C_α and C_β potentials (Kocher et al. 1994). In this work, however, statistical potentials using sidechain centers of any kind were not assessed because a large-scale calculation of the energy Z-scores with such potentials is impractical.

Fig. 4.

Performance of the distance-dependent potential as a function of its interaction centers. The atom types whose coordinates were used as the interaction centers are listed on the x-axes. The potentials were calculated as specified in Table 1 except for the varying interaction centers and the potential range of 15 Å. The results for the four 100/100 test sets with models of increasing size are indicated by bars of increasing darkness; the results for the 400/400 set of test models are indicated by the black bars.

Sequence separation

Residues that are close in sequence are restrained to be close in space due to the covalent connectivity between the adjacent residues. Therefore, sequentially local interactions should not be mixed with the sequentially nonlocal interactions when calculating a potential. This distinction should also help to benefit from the specific patterns of interaction in the regular local structures such as α-helices, β-strands, and β-turns. Generally, a potential is extracted and used with the same specification of sequence separation k (Materials and Methods) (Hendlich et al. 1990; Jones et al. 1992;Sippl 1993; Kocher et al. 1994; Park and Levitt 1996; Park et al. 1997; Reva et al. 1997; Rojnuckarin and Subramaniam 1999). However, it is possible to extract a potential only for the nonlocal non-bonded interactions (Melo and Feytmans 1998) and then use it for all of the nonbonded interactions. This approach turned out to be optimal for the ab initio modeling of loops in protein structures (Fiser et al. 2000). Thus, we derived and tested local (2 < k ≤ 8) and nonlocal (k ≥ 9) nonbonded potentials separately (Fig. 5 ▶).

Fig. 5.

Performance of the distance-dependent potential as a function of its range and sequence separation. (A) Potentials were derived from and used for assessing both the local (2 < k ≤ 8) and nonlocal (k ≥ 9) interactions. (B) Potentials were derived from and used for assessing only the nonlocal interactions. (C) Potentials were derived from and used for assessing only the local interactions. (D) Potentials were derived from the nonlocal interactions, but used to assess both the local and nonlocal interactions, irrespective of their k. See the legend to Fig. 2 ▶ for additional information about the potentials and the different test model sets represented by the different symbols.

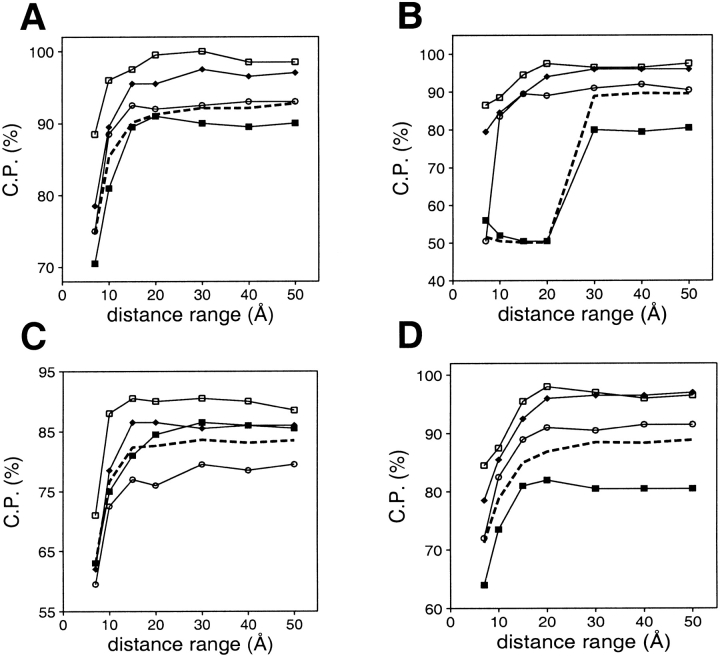
The best discrimination between the good and bad models is achieved when the local and nonlocal interactions are assessed by potentials derived from the local and nonlocal interactions, respectively (Fig. 5A ▶). The potentials derived from and used to assess only the nonlocal interactions generally perform well, except for the very small models (Fig. 5B ▶). This failure was expected because the number of nonlocal interactions in the very small models is low. Except for the very small models, the nonlocal interactions are more informative than local interactions in all of the tested distance ranges (Fig. 5B,C ▶). An assessment of both local and nonlocal interactions by a potential that was derived only from the nonlocal interactions (Fig. 5D ▶) is better than an assessment of the local (Fig. 5C ▶) or nonlocal (Fig. 5B ▶) interactions on their own.

Known structures for calculating potentials

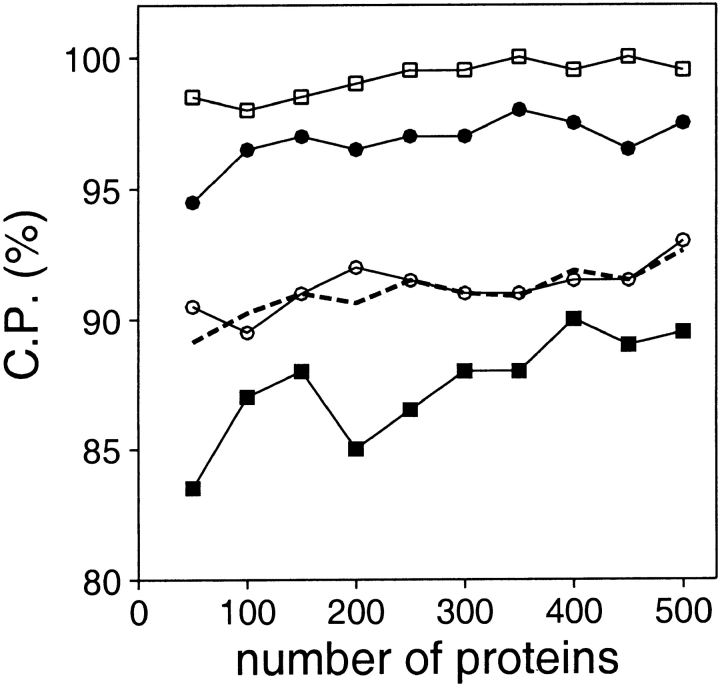
Two main aspects of the known protein structures used to derive distance-dependent statistical potentials were explored, i.e., their number and their size. The number of nonredundant structures in the PDB is limited and some types of interactions may not be sampled densely. Thus, it is important to assess how the performance of a statistical potential depends on the number of protein structures that were used to derive it. To address this question, distance-dependent potentials were derived from 10 sets of known structures containing from 50 to 500 structures (Fig. 6 ▶). Discrimination between the good and bad models generally increases with the number of structures used to derive the potential, which is in agreement with previous observations (Sippl and Jaritz 1994; Furuichi and Koehl 1998). However, the improvement of the performance of the potentials upon a 10-fold increase in the number of known structures is small, especially for the medium size and large models, which is consistent with the lack of impact of the database size on the contact potentials (Miyazawa and Jernigan 1996).

Fig. 6.

Performance of the distance-dependent potential as a function of the number of known protein structures used to extract the potential. The potentials were calculated from the 10 sets containing from 50 to 500 known structures (Materials and Methods), as specified in Table 1, except for the potential range of 15 Å. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

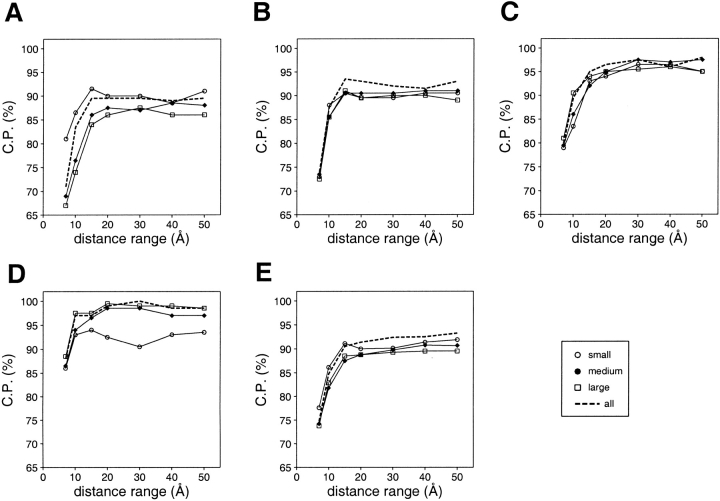
The second aspect considered in this study was dependence of model assessment on the size of the known structures used to extract the potential. This exploration was motivated by the previous observations, (1) that statistical potentials depend on the size of the known structures used in their derivation (Sippl 1993; Thomas and Dill 1996; Furuichi and Koehl 1998), although there is some discussion about the generality of this dependence (Bahar and Jernigan 1997), (2) that model size is informative in model evaluation (Sánchez and Sali 1998;Jones 1999b), and (3) that the energy Z-score of a native structure depends strongly on its size (Sippl 1993). Performance of the distance-dependent statistical potential was explored here as a function of the size of the known structures used to derive the potential, its distance range, and size of the assessed models (Fig. 7 ▶). For the small and medium size models, discrimination between the good and bad models does not depend significantly on the size of the known structures used to extract the potential (Fig. 7B,C ▶). For the very small and large models, it is better to use potentials derived from similarly sized known structures (Fig. 7A,D ▶). For the very small models, this trend becomes weaker when the distance range of the potential increases beyond 15 Å (Fig. 7A ▶). For the large models, the worst discrimination is observed for a potential extracted from the small structures only, especially when the distance range is larger than 15 Å (Fig. 7D ▶), because only a few distant residue–residue contacts occur in small models, thus resulting in highly unfavorable energy values for the distant residue pairs. As such pairs occur frequently in large structures, large models are assessed as unfavorable solely because of their size, not because of their errors. For discriminating between the good and bad models of all sizes, the best performance was achieved by a potential that was derived from known structures of all sizes (Fig. 7E ▶) at all tested distance ranges.

Fig. 7.

Performance of the distance-dependent potential as a function of its range and the size of the known structures used to calculate the potential. Four sets of known protein structures were used to extract the potentials: small (<100 residues; ○), medium (100–200 residues; •), large (>200 residues; ▪), and all (the sma-med-large set; broken line) (Materials and Methods). Model assessment by these potentials was evaluated separately for the four 100/100 very small (A), small (B), medium size (C), and large model test sets (D), as well as for the combined 400/400 test set (E) (Materials and Methods). The potentials were calculated as specified in Table 1.

Residue types

In addition to the standard 20 residue types, two residue type definitions were used to calculate a distance-dependent potential, the Wang and Wang residue type group definition that clusters the 20 standard residue types into five groups (Wang and Wang 1999) and the HP model that clusters the 20 standard residue types into two groups according to their hydrophobicity (Huang et al. 1995). For the 400/400 test model set, the fraction of the correctly predicted cases for the distance-dependent potentials using 20 residue types, the HP model, and the Wang and Wang residue type groups were 92.1%, 88.5%, and 84.8%, respectively. Thus, a decrease in the number of residue type groups reduces the discrimination between the good and bad models by the potential.

Subsets of test models

We also compared the predictive power of the distance-dependent statistical potentials by assessing the different subsets of the good and bad models (Materials and Methods). The predictive power of the potentials does not depend strongly on the number of hetatoms (Materials and Methods), the number of chains, or the percentage sequence identity between the modeled sequences and the templates used to build the assessed models (data not shown). Of the model features tested here, only the size of a model has a major impact on the predictive power of the potentials (see above). Discrimination is more difficult for the small models than it is for the large models. It is tempting to speculate that a model tends to be small when it covers only a fraction of the modeled chain and that the reason for a relatively poor assessment of a small model is its incompleteness; evaluation of a model of an incomplete protein domain is clearly difficult because the environment of the modeled protein fragment is missing. However, the average coverage of the target chain by the correctly assessed models is approximately independent of the model size (data not shown). Thus, the main reason for poor performance in the case of small models is the relatively small number of interactions that are available for discriminating between the good and bad small models. This interpretation is consistent with the previously observed dependence of the Z-score on the size of a model (Sippl 1993). The major challenge in model evaluation remains the assessment of small models.

Contact potentials

The contact potentials are the simplest description of pairwise interactions. They are similar to the distance-dependent potentials, except that they have only two values, the energy of interaction below a contact distance cutoff and zero above it (Miyazawa and Jernigan 1985; DeBolt and Skolnick 1996; Park and Levitt 1996; Park et al. 1997).

Range

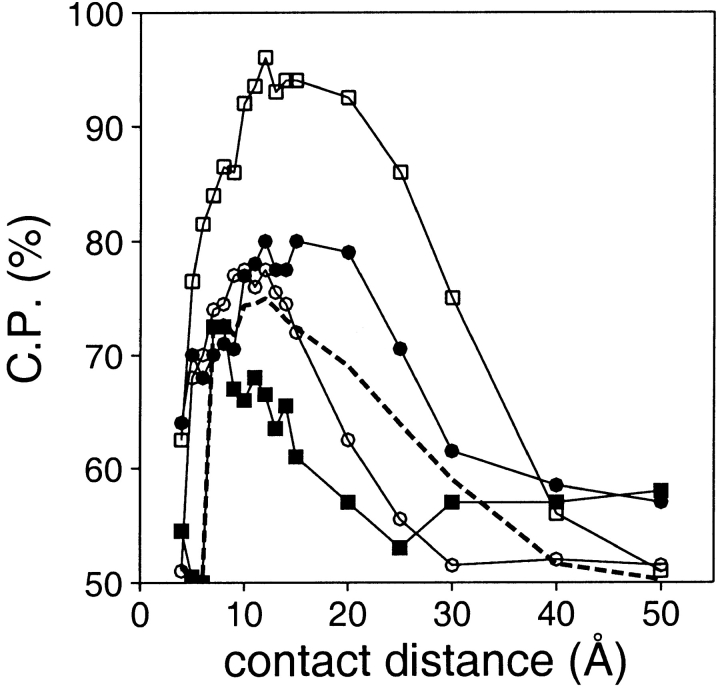
Several contact potentials with different distance ranges were calculated and tested (Fig. 8 ▶). Similarly to the distance-dependent potentials, discrimination is easier for the large models than it is for the small models. In contrast to the distance-dependent potentials, there is a clear optimal distance range for discriminating between the good and bad models. The optimal distance range of the contact potential increases with the size of the assessed model. Optimal distance values are ∼9 Å for the very short models, 11 Å for the small models, 13 Å for the medium size models, and 15 Å for the large models. Thus, contact potentials are less convenient than the distance-dependent potentials for discriminating between the good and bad models, because different contact potentials need to be used to have an optimal discrimination over all model sizes. Performance of the optimal contact potential is comparable with that observed for the distance-dependent potentials only in the case of the large models. For the smaller models (<200 residues), the contact potentials are inferior to the distance-dependent potentials. As a result, no further calculations with the contact potentials were performed in this study.

Fig. 8.

Performance of the contact potential as a function of its contact distance. The interaction centers were the C_β atoms. All the contacts with k ≥ 2 were considered. The reference state used to calculate the potentials was other residues (Materials and Methods). The potentials were extracted from the sma-med-lar set of known protein structures. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Dihedral angle potentials

Statistical backbone dihedral angle potentials were described previously (Kocher et al. 1994;Gilis and Rooman 1997,Gilis and Rooman 2001). In the current study, the φ/Ψ dihedral angle potentials for each of the 20 standard residue types (Materials and Methods) did not separate well between the good and bad models, in comparison with the distance-dependent statistical potentials. For example, the fraction of the correctly predicted cases is 67%, 73%, 74%, 84%, and 70% for the four 100/100 very small, small, medium size, and large model sets, and the 400/400 test set, respectively. One of the reasons may be that the relative content of the residues with the native backbone dihedral angles in the bad models is significantly larger than that of the native nonbonded contacts. In other words, the difference between the bad and good models in terms of the backbone dihedral angles may be significantly smaller than the difference in terms of the residue–residue contacts. Because of the poor performance, no further calculations were carried out with the dihedral angle potentials.

Accessible surface potentials

Accessible surface potentials depend on an approximate measure of the residue burial or exposure to the solvent. Accessible surface potentials complement the distance-dependent potentials (Jones et al. 1992;Sippl 1993; Kocher et al. 1994; O'Donoghue and Nilges 1997;Melo and Feytmans 1998;Jones 1999b). Thus, the accessible surface potentials were assessed here on their own and in combination with other statistical potentials. In this study, the accessible surface potentials were derived as described earlier (Sippl 1993;Melo and Feytmans 1998) (Materials and Methods).

Distance and burial ranges

Two different ranges exist for the accessible surface potentials used in this study, the distance range and the burial range. The distance range is the radius of the sphere surrounding a residue. The burial range is the maximal number of residues observed in the sphere around a residue and corresponds to the minimal solvent exposure. The optimal values for these two ranges were expected to be dependent on each other.

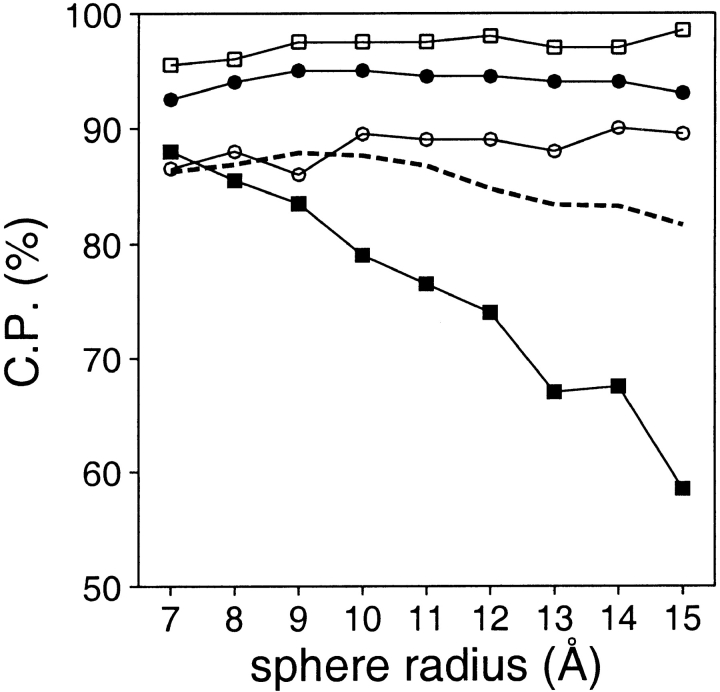
Several accessible surface potentials with varying distance range and a constant burial range were calculated and assessed (Fig. 9 ▶). For models larger than 50 residues, good discrimination is achieved over all of the tested distance ranges. The correct prediction rate is approximately constant for potentials with distance ranges from 7 to 15 Å. On the other hand, for the very small models, the rate of the correctly assessed models steadily decreases with the distance range of the potential. Thus, if a single accessible surface potential with good performance over the whole range of protein sizes is required, the distance range should be small (e.g., <9 Å). Whereas a larger distance range results in a small improvement for models larger than 50 residues, it strongly worsens the performance for the very small models.

Fig. 9.

Performance of the accessible surface potential as a function of its distance range (sphere radius). The potentials were calculated as specified in Table 2, except for the burial range of 200 atoms and the varying sphere radius. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

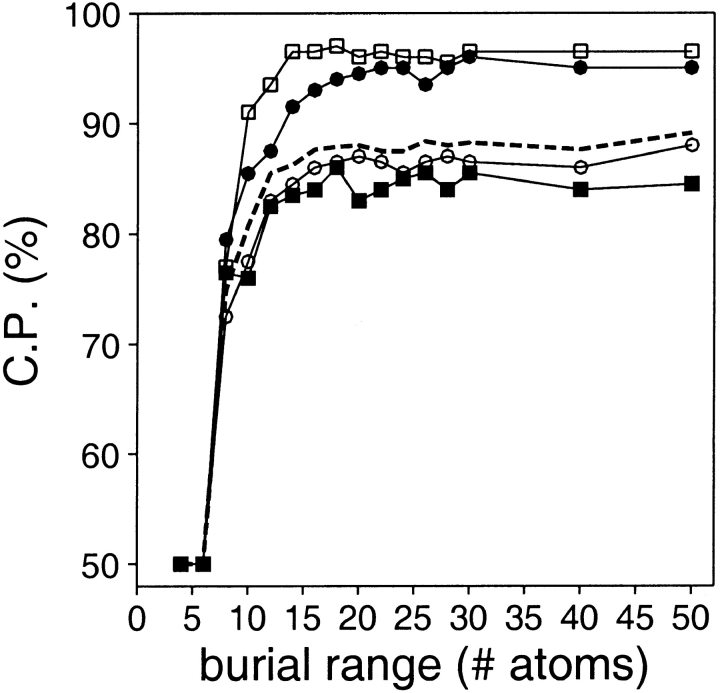
Accessible surface statistical potentials with a variety of burial ranges were also calculated and evaluated (Fig. 10 ▶). The performance of the accessible surface potentials as a function of the burial range is described by an asymptotic curve. These curves reach their maxima at the burial range that depends on the size of the assessed models. For the very small, small, medium size, and large models, the smallest burial range required to reach the maximum discrimination is ∼12, 15, 18, and 18 atoms, respectively. Thus, contrary to the distance range, there is a single optimal burial range for assessing models spanning all sizes (i.e., 18 atoms).

Fig. 10.

Performance of the accessible surface potential as a function of its burial range. The potentials were calculated as specified in Table 2, except for the varying burial range. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

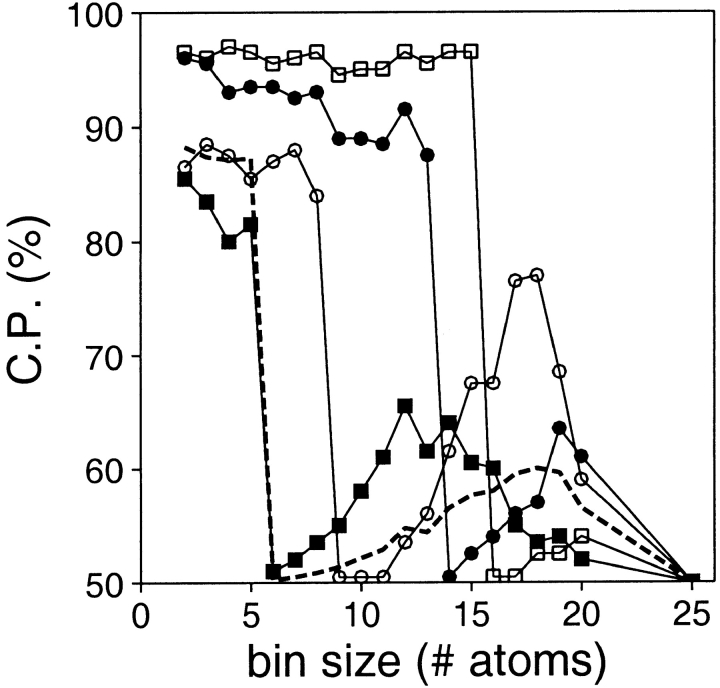
Resolution

Several accessible surface potentials with fixed distance and burial ranges but variable burial resolution were calculated (Fig. 11 ▶). The performance of the accessible surface potential depends strongly on its resolution, in contrast to that for the distance-dependent potentials (Fig. 3 ▶). This dependency varies with the size of the assessed models. For all model sizes, the potential performs best at the high end of the resolution spectrum. The performance falls sharply above a threshold that depends on the model size. The threshold is 5, 8, 13, and 15 atoms for the very small, small, medium size, and large models, respectively.

Fig. 11.

Performance of the accessible surface potential as a function of its resolution (bin size). The potentials were calculated as specified in Table 2, except for the burial range of 30 atoms and the varying bin size. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Interaction centers

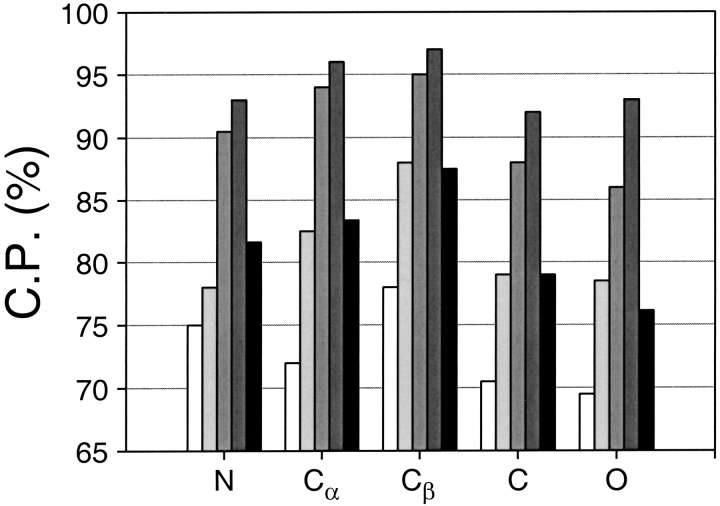
The dependence of the performance of the accessible surface potentials on the different interaction centers (Fig. 12 ▶) is similar to that of the distance-dependent potentials (Fig. 4 ▶). The highest discrimination is obtained for the potential that uses the C_β atoms to define the residue accessibility. As pointed out above, it appears that the C_β atoms retain more information about the direction of the sidechain and thus better describe residue accessibility than any other single atom type.

Fig. 12.

Performance of the accessible surface potential as a function of its interaction centers. The potentials were calculated as specified in Table 2, except for the distance range of 10 Å and the varying interaction centers. See the legend to Fig. 4 ▶ for the different test model sets represented by the different bar shades.

Sizes of assessed model and known structures for calculating potentials

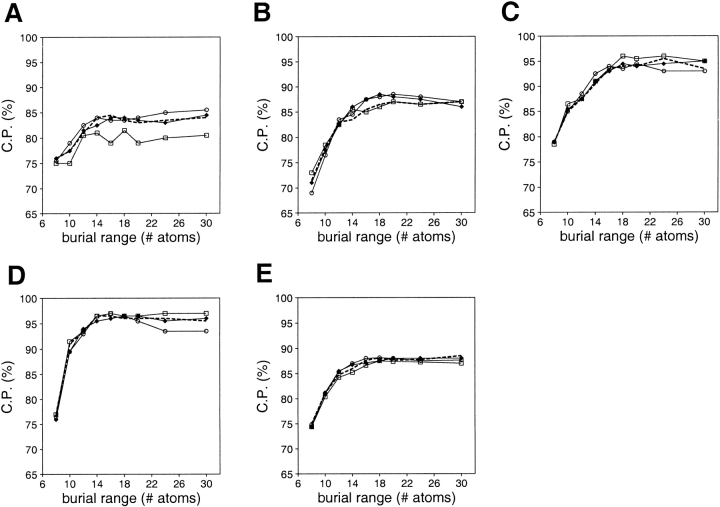
Model assessment by accessible surface potentials was evaluated as a function of the size of the assessed model and the size of the known protein structures used to calculate the potential (Fig. 13 ▶). The discriminative ability of a potential increases with the size of the assessed model, similarly to the distance-dependent statistical potentials. The performance is worst for the very small models, presumably for the same reasons as in the case of the distance-dependent potentials. The size of the known structures used to derive the potential influences its discriminant power slightly. Assessment of a model is best by a potential that was derived from known structures of the same size, especially for the very small models.

Fig. 13.

Performance of the accessible surface potential as a function of its burial range and the size of the known structures used to calculate the potential. Four sets of known protein structures were used to extract the potentials: small (<100 residues; ○), medium (100–200 residues; •), large (>200 residues; □), and all (the sma-med-large set; broken line) (Materials and Methods). Model assessment by these potentials was evaluated separately for the four 100/100 very small (A), small (B), medium size (C), and large model test sets (D), as well as for the combined 400/400 test set (E) (Materials and Methods). The potentials were calculated as specified in Table 2.

Residue types

The ability of an accessible surface potential to assess models was tested as a function of the three residue-type classifications described above. For the 400/400 test model set, the fraction of the correctly predicted cases for the accessible surface potentials using the 20 standard residue types, the Wang and Wang residue type groups (Wang and Wang 1999), and the HP model (Huang et al. 1995) were 87.5%, 83.8%, and 84.1%, respectively. As for the distance-dependent potential, there is a loss of information when the 20 standard residue types are classified into a smaller number of groups, which can be avoided by using the 20 standard residue types.

Combined potential

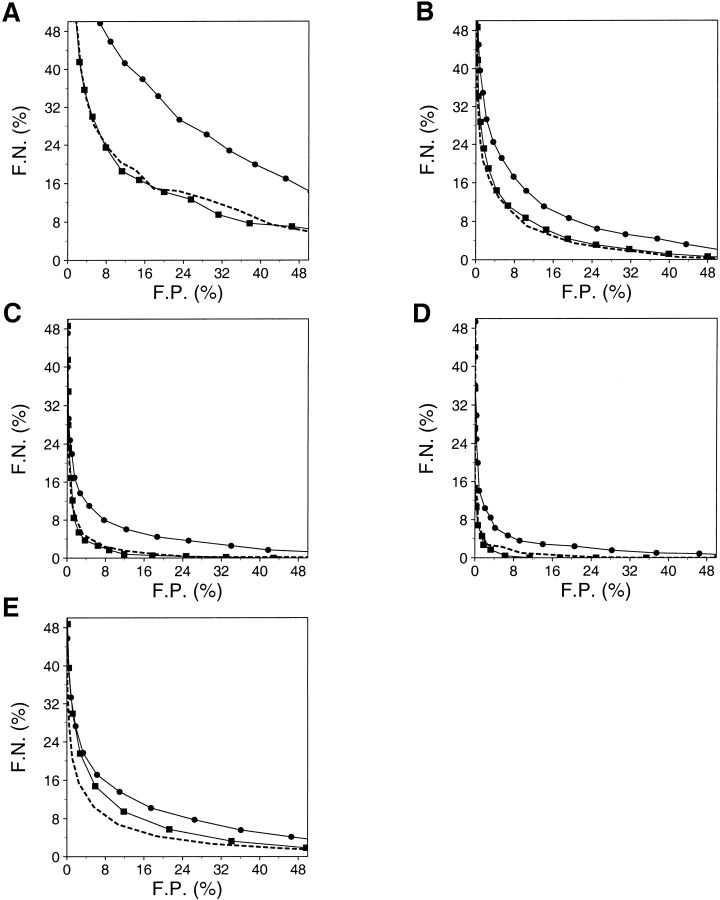
A combination of potentials that evaluate different aspects of a model (e.g., residue solvent accessibility and residue–residue contacts) performs better than the single potentials on their own (Sippl 1993; Kocher et al. 1994). Two specific potentials were combined (Materials and Methods) and tested (Fig. 14 ▶), the optimal distance-dependent potential (Table 1) and the optimal accessible surface potential (Table 2). On the 3375/6270 test set of models, the distance-dependent potential performed better than the accessible surface potential, but worse than the combined potential. The specificity and sensitivity of any of the three potentials for the very small models is poor. The difficulty of assessing the very small models is a major hurdle for an improvement of the overall performance. For the medium size and large models, the potentials have low rates of false positives and false negatives (Fig. 14 ▶). For example, at the maximum rate of the correct prediction, the fractions of the false positives and false negatives for assessment by the combined potential are 8.9% and 8.5%, respectively. If the structure space reference were used for the calculation of the Z-score instead of the sequence space reference, the performance would be better by approximately two percentage points (Fig. 15 ▶). Many different combinations of potentials, including varying weighing of the distance-dependent, contact, φ/Ψ dihedral angle, and accessible surface potentials, were tested, but none of them performed better than the sum of the normalized distance-dependent and accessible surface potentials (data not shown).

Fig. 14.

Performance of the optimal distance-dependent, accessible surface, and combined statistical potentials. The performance is described by the ROC curves, which plot the fraction of false negatives (F.N.) as a function of the fraction of false positives (F.P.) (Materials and Methods). The lower the curve, the better the discrimination between the good and bad models. The ROC curves for the accessible surface potential (•), the distance dependent potential (▪), and the combined potential (broken line) are plotted. (A) The 443/1922 test set of the very small models, (B) the 1103/2600 test set of the small models, (C) the 1126/1412 test set of the medium size models, and (D) the 703/336 test set of the large models. (E) The performance of the potentials is also evaluated by the 3375/6270 set of all good and bad models.

Table 1.

The optimized distance-dependent statistical potential

Parameter	Value
interaction centers	Cα and Cβ
residue type classification	20 standard residue types
range	30 Å
resolution	0.50 Å
sequence separation k, derivation	3, 4, 5, 6, 7, 8, ≥9
reference state	other atoms
sequence separation k, use	3, 4, 5, 6, 7, 8, ≥9

The listed parameters are optimal for all sizes of the tested models. The potential was calculated from the sma-med-lar set of known protein structures, unless specified otherwise. The optimal performance for a given model size is obtained by deriving the potential only from the known structures of similar size.

Table 2.

The optimized accessible surface statistical potential

Parameter	Value
interaction centers	Cβ
residue type classification	20 standard residue types
distance range	9 Å
burial range	40 atoms
resolution	2 atoms
sequence separation k, derivation	k ≥ 1
reference state	other atoms
sequence separation k, use	k ≥ 1

The listed parameters are optimal for all sizes of the tested models, except for the quoted distance range, which corresponds to the optimal average performance over the 400/400 test set of models of all sizes. The potential was calculated from the sma-med-lar set of known protein structures, unless specified otherwise. The optimal performance for a given model size is obtained by deriving the potential only from the known structures of similar size, and by varying the distance range according to Fig. 9 ▶.

Fig. 15.

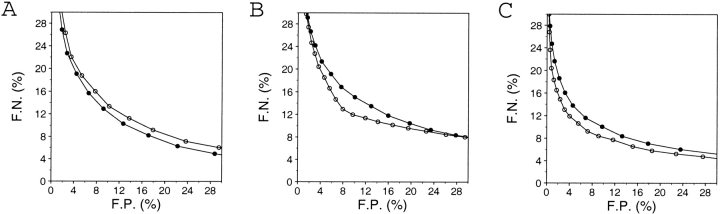
Performance of the sequence space (•) and structure space (○) references for the calculation of the energy Z-scores. The predictive power is assessed for the 3375/6270 test model set. The statistical potentials and the polyprotein implemented in the program ProsaII were used (Sippl 1993). (A) Distance dependent potential. (B) Accessible surface potential. (C) The combined potential.

Conclusions

Four types of a residue-level statistical potential were optimized for fold assessment in large-scale genome-wide comparative modeling. These potentials included distance-dependent, contact, φ/Ψ dihedral angle, and accessible surface statistical potentials. The following main conclusions were reached:

1. For an instructive optimization of fold assessment by statistical potentials, the test set of models must be representative of the models to be assessed by the new method. The test set of models used here is believed to be representative of the models from large-scale comparative modeling (Fig. 1 ▶).

2. The energy Z-score obtained by randomizing the order of residues in the tested sequence, while keeping the structure constant, is almost as good as that obtained by randomizing the structure, while keeping the sequence constant (Fig. 15 ▶).

3. The most discriminating combination of any one of the four tested potentials is that of the distance-dependent and accessible surface potentials (Fig. 14 ▶). The distance-dependent potential is more informative than the contact potential, and the φ/Ψ dihedral angle potential has small discriminative power.

4. The distance-dependent potential that is optimal for assessing models of all sizes uses both C_α and C_β atoms as interaction centers, distinguishes between all 20 standard residue types, has the distance range of 30 Å, resolution of 0.5 Å, and is derived and used by taking into account the sequence separation of the interacting atom pairs (Table 1, Fig. 14 ▶). The terms for the sequentially local interactions (k ≤ 8) are significantly less informative than those for the nonlocal interactions (Fig. 5 ▶).

5. The accessible surface potential that is optimal for assessing models of all sizes used C_β atoms as interaction centers, distinguishes between all 20 standard residue types, and has the burial range of 40 atoms (Table 2, Fig. 14 ▶). The optimal distance range depends on the model size, with 9Å resulting in the best performance averaged over all model sizes.

6. The performance of the tested statistical potentials is not likely to improve significantly with a further increase in the number of known protein structures used in their derivation (Fig. 6 ▶).

7. Model size should be taken into account as explicitly as possible when assessing the fold of a model. The parameters of fold assessment whose optimal values vary significantly with model size include the size of the known protein structures used to derive the potential and the distance range of the accessible surface potential (Figs. 7, 9, 13 ▶ ▶ ▶).

8. Fold assessment by statistical potentials is most difficult for the very small models (Fig. 14 ▶). Small models are difficult to assess because of the relatively small number of pairwise interactions by which they are judged, not because of their incompleteness. This difficulty presents an important challenge to fold assessment in large-scale comparative modeling, which produces many small models.

9. Attributes of a model other than an energy Z-score may have to be used to improve fold assessments. Such attributes may include model size, fraction of a domain modeled, the significance score of the modeling alignment, and the energy Z-score of the closest template structure.

The results described in this study provide a basis for an optimal use of statistical potentials in fold assessment. They also indicate future directions for the development of more sensitive fold assessment for large-scale comparative modeling (e.g., Conclusions 7 and 9).

Materials and Methods

Test models

To evaluate the usefulness of the statistical potentials for fold assessment, large sets of good and bad protein structure models were needed. The two sets of models were calculated by large-scale comparative modeling (Sánchez and Sali 1998) of the protein chains representative of the Protein Data Bank (PDB) of known protein structures (Berman et al. 2000). The models were classified as good or bad depending on their structural similarity to the actual structure of the target protein. All of the models are available at http://guitar.rockefeller.edu.

Models with the correct fold (good models)

The good models were built on the basis of the correct templates and mostly correct alignments between the target sequences and the template structures. The models were obtained by applying ModPipe to 1085 chains representative of the PDB (Sánchez and Sali 1998). These representative sequences corresponded to the protein chains in PDB that shared <30% sequence identity or were >30 residues different in size. The templates for comparative modeling by ModPipe were 1637 PDB chains with <80% identity to each other or more than 30 residue difference in length. Each target sequence was aligned separately with each one of the 1637 known structures by use of the program ALIGN that implements local sequence alignment by dynamic programming (Altschul 1998). Only the target-template alignments with a significance score higher than 22 nats (corresponding approximately to the PSI-BLAST E-value of 10⁻⁴) were used, resulting in 3993 models. Models with <30% structural overlap with the actual experimentally determined structure were eliminated. Structural overlap was defined as the fraction of the equivalent C_α atoms upon least-squares superposition of the two structures with the 3.5 Å cutoff. This procedure also removed models based on correct templates that had a poor alignment and models based on templates that had large domain or rigid body movements with respect to the target structure. The final set contained 3375 good models.

Models with an incorrect fold (bad models)

The bad models were built on the basis of a template with an incorrect fold, a template structure with large rigid body shifts, or an incorrect alignment with the correct template. The models were obtained as described above, except that only the target-template alignments with the significance score between 15 and 20 nats were used; this procedure resulted in 7669 models for the 1085 representative chains. Models with >15% structure overlap with the actual target structure were eliminated. The final set contained 6270 bad models.

Subsets of models

The test set of models containing all of the 3375 good and 6270 bad models is termed the 3375/6270 test set. To analyze the discrimination between the good and bad models by the statistical potentials, the good and bad models were grouped into several subsets on the basis of a variety of criteria. Four 100/100 test sets were created, each one of which contained randomly selected 100 good and 100 bad models of defined size, very-small models (<50 residues), small models (50–100 residues), medium size models (100–200 residues), and large models (> 200 residues). Another test set, the 400/400 set, was created by combining all four 100/100 sets.

All of the good and bad models were also subdivided into the following test sets: very-small models (443/1922), small models (1103/2600), medium size models (1126/1412), and large models (703/336); models based on templates with <40 atoms in nonstandard residue types but water (hetatoms) (2393/5371) and other models (982/899); models based on templates without other chains in the same PDB file (1055/2891) and other models (2320/3379); models based on sequence identity of <30% (890/3722) and other models (2485/2548); models based on sequence identity of <30% and sequence length of >100 residues (614/1578), and models based on sequence identity of >30% and sequence length of more than 100 residues (1188/142).

Known structures for calculating potentials

Protein structures that were solved by X-ray crystallography at a resolution higher than 2.5 Å, with >50 residues, without duplicated or missing atoms and without chain breaks were extracted from the September 1999 version of PDB. Representative structures were selected such that they shared <30% sequence identity with each other or were >30 residues different in length, resulting in the sma-med-lar set with 760 chains. To assess the dependence of the statistical potentials on the size of the structures from which they were extracted, three subsets of the sma-med-lar set that contained only chains of a certain size were created, the small subset containing protein chains with <100 residues (229 chains), the medium subset containing chains with 100–200 residues (232), and the large subset containing chains with >200 residues (299). To assess the dependence of the statistical potentials on the number of structures from which they were extracted, 10 subsets of the sma-med-lar set were generated randomly, containing 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500 chains. To evaluate the effect of the interactions of a chain with other subunits in a complex, two subsets of the sma-med-lar set were generated, the mon subset containing structures from the PDB files with single chains (273 chains) and the mul set containing chains from the PDB files with more than one chain (225); PDB files with single chains but with a crystal symmetry operator to generate additional chains in the crystal unit cell were excluded. All the PDB sets are available at http://guitar.rockefeller.edu.

Statistical potentials

A total of 210 statistical potentials were calculated by varying the following features that define their functional form as follows: (1) type of an interaction center (e.g., individual atoms, gravity centers of several atoms); (2) residue and atom type classification; (3) type of potential (e.g., accessible surface potential, distance-dependent potential); (4) maximum range; (5) bin size for frequency histograms obtained from known structures; (6) for two-residue potentials, sequence separation of residues used to extract the frequency histograms; (7) reference state used to calculate the accessible surface statistical potentials; (8) sequence separation used to calculate the total energy of a model; and (9) set of known protein structures used to extract the frequency histograms. The distinction between features (6) and (8) needs an explanation. A statistical pair potential extracted only from the sequentially nonlocal interactions in the known protein structures (Melo and Feytmans 1998), supplemented by stereochemical restraints, is optimal for describing both the local and nonlocal nonbonded interactions in the modeling of loops (Fiser et al. 2000). Thus, optimizations of the calculation and use of a statistical potential should be done independently from each other. Next, all of the statistical potentials tested in this study are defined in detail.

Distance-dependent statistical potential

The distance-dependent, nonbonded statistical potentials were calculated as described (Sippl 1993; Melo and Feytmans 1997):

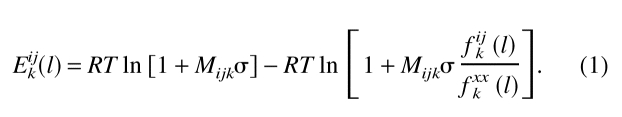M_ijk is the number of occurrences for the interaction center type pair ij separated by k residues in sequence (i.e., k = |I − J|, where I and J are the residue indices of interaction center types i and j, respectively):

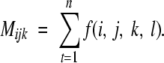2

n is the number of classes of distances. σ is the weight given to each observation. σ = 1/50 was used (Sippl 1990), so that with 50 observations f^ij_k(l) and f^xx_k(l) have equal weights for the calculation of E^ij_k(l). f^ij_k(l) is the relative frequency of occurrence for the interaction center type pair ij at sequence separation k in the class of distance l.

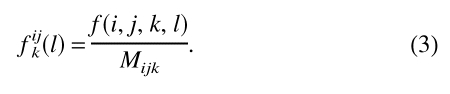f^xx_k(l) is the relative frequency of occurrence for all the interaction center type pairs at sequence separation k in the class of distance l:

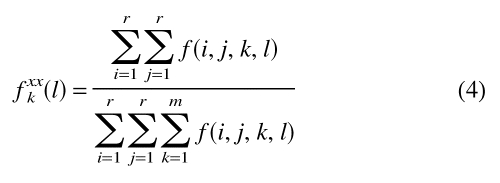in which r is the number of different interaction center types and m is the number of classes for the sequence separation. The temperature T was set to 293 K, corresponding to RT of 0.582 kcal/mole, where R is the gas constant.

Contact statistical potential

Contact potentials were calculated similarly to the distance-dependent potentials, except for using a single bin with a size equivalent to the range of the potential and considering as equivalent all the interactions between interaction centers with the sequence separation k ≥ 2.

Accessible surface statistical potential

The accessible surface potentials were calculated as described (Sippl 1993;Melo and Feytmans 1998). The accessible surface of an interaction center is defined as the number of interaction centers within a sphere around the central interaction center; the radius of the sphere is the distance range of the potential. In the case of a known multimeric structure, the neighbor counts were performed only for the interaction centers belonging to the representative chain, but all of the other chains in the PDB file were included in the calculation. From these distributions, the statistical potential was calculated as follows:

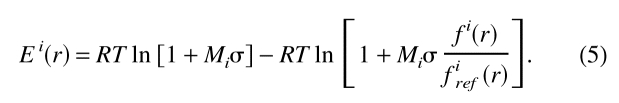M_i is the frequency of the interaction center type i in all the burial classes:

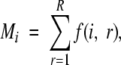6

where R is the number of the burial classes and σ represents the weight given to each observation (usually σ = 1/50). fⁱ(r) is the relative frequency of occurrence of the interaction center type i in the burial class r:

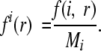7

fⁱ_ref (r) is the reference state. Two different reference states were tested. The first one represents the overall relative frequency of occurrence of the interaction center type i in the burial class r, assuming that the interaction centers are distributed homogeneously over the distance range of the potential. This reference corresponds to an interaction center having no preference for any of the different accessibility states and it can be expressed as:

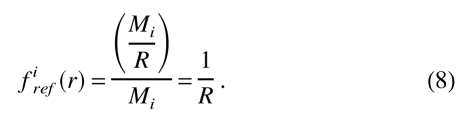Thus, in this case, fⁱ_ref(r) is a constant that depends on the number of burial classes defined for the potential. The second reference state was equivalent to that used for the distance-dependent potentials. Here, fⁱ_ref(r) is the relative frequency of occurrence for all the interaction centers in the burial class r:

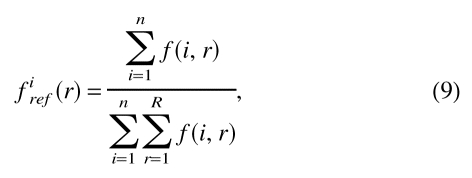in which n is the number of interaction center types.

φ/Ψ dihedral angle statistical potential

The φ/Ψ dihedral angle potentials were obtained for each of the 20 residue types for each of the five areas of the Ramachandran map (Ramachandran et al. 1963). The Ramachandran maps were extracted from a representative set of 1000 protein structures (217,807 residues) that shared <60% sequence identity to each other or had >30-residue length difference, and were determined by X-ray crystallography at a resolution of 2.3 Å or better (Fiser et al. 2000). The Ramachandran plot spanned by the φ and Ψ dihedral angles was divided into 5° × 5° bins. The frequency of residues in each bin was obtained separately for each of the 20 standard residue types. The φ/Ψ dihedral angle statistical potential was defined as:

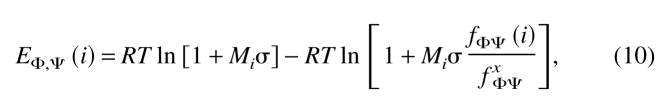in which σ represents the weight given to each observation (usually, σ = 1/100). M_i is the number of observations for residue type i in all of the dihedral angle classes:

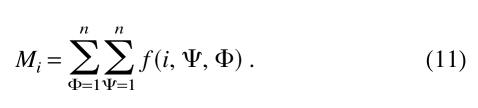n is the number of the dihedral angle bins (i.e., 72). f_φΨ(i) is the relative frequency of occurrence of residue type i with dihedral angles φ and Ψ:

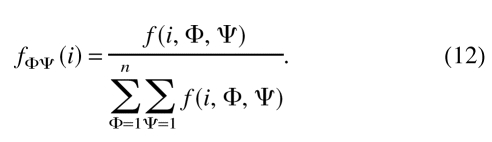f^x_φΨ is the reference distribution that corresponds to the relative frequency of occurrence for all residue types with dihedral angles φ and Ψ:

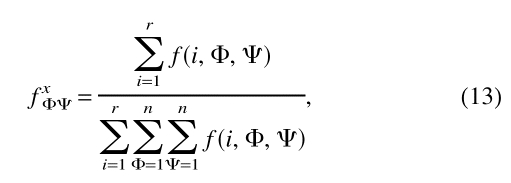in which r is the number of residue types (the 20 standard residue types were used).

Energy

For distance-dependent potentials, the energy of a protein structure model is a sum of the individual terms over all interaction center pairs i and j, sequence separations k, and distance classes l:

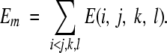14

For contact potentials, the energy was calculated similarly. For accessible surface and φ/Ψ dihedral angle statistical potentials, the energy of the protein is equal to the sum of the terms for all of the residues. In addition, the combined energy was defined as the sum of the normalized energies (e.g., the normalized distance-dependent and accessible surface energies). The normalization was achieved by dividing the energy of a certain type (e.g., distance-dependent energy) by the standard deviation of its individual terms.

Energy Z-score

Before an energy was used to discriminate between the good and bad models, it was transformed into a Z-score of energy (Sippl 1993):

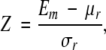15

in which E_m is the energy of the model, μ_r and σ_r are the average and standard deviation of the reference energy distribution, respectively. Two different reference energy distributions were calculated and compared. The first approach involved randomization of the order of amino acid residues in the tested model (sequence space reference). This procedure was repeated 200 times, generating 200 models with the same conformation, but different sequences. By construction, the residue composition of these random sequences was identical to that of the original sequence. The energies of the random-sequence models were then used to obtain the average and standard deviation of the reference energy distribution. The second derivation of the reference energy distribution keeps the original sequence, but changes its conformation (structure space reference). The sequence was threaded thousands of times through a set of nonredundant native protein folds (Sippl 1993). This collection of conformations was then used to obtain the average and standard deviation of the energy for the calculation of the Z-score.

The performances of the Z-scores calculated by the two methods were similar, as measured by the receiver operating characteristic curve (see below; Fig. 15 ▶). The two reference frames were compared only for the ProsaII statistical distance-dependent, accessible surface and combined potentials (Sippl 1993). The performances of the two reference frames are similar. For the distance-dependent potentials, the sequence space reference was slightly better than the structure space reference. For the accessible surface potentials, the opposite was the case. For the combined potential, the structure space reference performed slightly better than the sequence space reference. However, for all subsequent calculations, the sequence space reference was used because it is significantly more efficient in terms of the CPU time than the structure space reference.

The fraction of the correctly predicted cases

The fractions of false positives (FP) and false negatives (FN) are defined as:

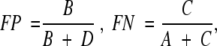16

in which A is the number of true positives (good models predicted as good), B is the number of false positives (good models predicted as bad), C is the number of false negatives (bad models predicted as good), and D is the number of true negatives (bad models predicted as bad). The fraction of the correctly predicted cases or the correct classification rate at the optimal value of the Z-score cutoff was used to assess the performance of a given statistical potential in fold assessment as follows:

17

in which the prime is used to indicate the corresponding values at the Z-score cutoff that results in the maximal correct classification rate.

Receiver operating characteristic curves

Receiver operating characteristic (ROC) curves (Theodoridis and Koutroumbas 1999) were also used to assess the statistical potentials. An ROC plot is obtained by plotting the false negatives fraction (1–sensitivity) against the corresponding false positives fraction (1–specificity) for all cutoffs on the Z-score.

The area under the ROC curve represents the probability of incorrect classification over the whole range of cutoffs. This area is usually taken to be an important index because it provides a single measure of overall accuracy that is not dependent upon a particular feature threshold. The area under the curve ranges from 0.0 to 0.5. If it is 0.5, the scores for the good and bad models do not differ (no discriminating power), whereas a value of 0.0 indicates no overlap between the two sets of models (perfect discrimination).