Improved detection of homologous membrane proteins by inclusion of information from topology predictions

Abstract

A total of 20%–25% of the proteins in a typical genome are helical membrane proteins. The transmembrane regions of these proteins have markedly different properties when compared with globular proteins. This presents a problem when homology search algorithms optimized for globular proteins are applied to membrane proteins. Here we present modifications of the standard Smith-Waterman and profile search algorithms that significantly improve the detection of related membrane proteins. The improvement is based on the inclusion of information about predicted transmembrane segments in the alignment algorithm. This is done by simply increasing the alignment score if two residues predicted to belong to transmembrane segments are aligned with each other. Benchmarking over a test set of G-protein-coupled receptor sequences shows that the number of false positives is significantly reduced in this way, both when closely related and distantly related proteins are searched for.

As a result of the genome sequencing projects, we are faced with an exponentially increasing number of protein sequences, but with only a very limited knowledge of their function. Because the experimental determination of function is a nontrivial task, the quickest way to gain some understanding of these proteins is by relating them to proteins with known properties. Improving the algorithms that examine these relationships is a fundamental challenge in bioinformatics today.

Many algorithms have been developed to increase the sensitivity and specificity of homology searches for globular proteins. These algorithms often use evolutionary and structural information to improve the detection of related proteins. However, they may not be generally applicable to membrane proteins, as membrane proteins have different structural features (von Heijne 1981) and different amino-acids composition and residue exchangeabilities (Tourasse and Li 2000). Helical integral membrane proteins account for 20%–25% of all proteins encoded in a typical genome (Krogh et al. 2001) and their central importance in many cellular processes makes it of great importance to increase the ability to detect related membrane proteins. Here we present modifications of the standard Smith-Waterman, and profile search algorithms increase the specificity and sensitivity of homology searches for membrane proteins.

The detection of globular proteins can be improved by including information from secondary structure predictions (Fischer and Eisenberg 1996; Rice and Eisenberg 1997; Rost et al. 1997; Hargbo and Elofsson 1999). To our knowledge, similar schemes have not been described for integral membrane proteins (for which classical secondary structure prediction methods do not work) (Wallace et al. 1986). Considering that membrane protein topology predictions are much more accurate than secondary structure prediction in globular proteins (Krogh et al. 2001), we have tested whether such predictions can be used to improve homology searches of membrane proteins.

For helical membrane proteins (White and Wimley 1999; Popot and Engelman 2000), topology predictions provide secondary structure information, that is, they pin-point likely transmembrane α-helical segments. We have thus extended the classical Smith-Waterman (Smith and Waterman 1981) and profile (Gribskov et al. 1987) search algorithms by including helix predictions from the topology prediction program TMHMM (Krogh et al. 2001). This resembles the use of secondary structure predictions in threading methods (Fischer and Eisenberg 1996; Rost et al. 1997). However, there are two differences, first, information from one of the best-performing membrane protein topology prediction methods, TMHMM (Krogh et al. 2001), is used and second, no information about the true secondary structure is used; instead, we match a prediction against a prediction. Further, we have tested as similar modification of profile searches (Gribskov et al. 1987) to detect related membrane proteins.

One problem during development and fine-tuning of the methods used in database searches is the need to know the true relationship between the different proteins in a test set. During the last few years, several studies have proposed new ways to evaluate methods for detecting relationships between proteins (Abagyan and Batalov 1997; Brenner et al. 1998; Park et al. 1998; Salamov et al. 1999; Lindahl and Elofsson 2000). These studies differ in detail but have a common theme, they use an existing structural classification to create the benchmark used for evaluating the performance of different search methods. The use of structural protein-family databases such as SCOP (Murzin et al. 1995) and CATH (Orengo et al. 1997) has enabled the creation of test sets in which the true relationship can be quite accurately assumed. However, for membrane proteins, no such high-quality test sets based on 3-D structural databases exist so far. To circumvent this problem, we have chosen to use the GPCRDB database (Horn et al. 2001). GPCRDB purportedly includes all known and predicted 7-TM receptors, and we thus assume that all proteins in GPCRDB are 7-TM receptors and that all other proteins found in SWISS-PROT (Bairoch and Apweiler 1996) but not in GPCRDB are not 7-TM receptors. A similar benchmark was used recently by Rehsmeier (Muller et al. 2001). This study showed that a nonsymmetric score matrix performed better than a standard (symmetric) substitution matrix for helical membrane proteins. However, no comparison with multiple sequence-based methods, such as PSI-BLAST (Altschul et al. 1997), was made.

In contrast, we now report that the inclusion of information about predicted transmembrane segments leads to a significant improvement over standard sequence-alignment methods, including the iterative multiple sequence-alignment method PSI-BLAST.

Results

Inclusion of information about predicted transmembrane segments in standard search algorithms

In the tests reported here, information about transmembrane segments predicted by TMHMM was included in standard Smith-Waterman (SW) and profile-search implementations simply by adding an extra score when two residues that are both predicted to belong to transmembrane segments are aligned (see Materials and Methods). For the profile search methods, the extra score is added only after the sequence profile has been generated by PSI-BLAST, not during the iterative construction of the profile.

Our test sets (see Table 1) were derived from the GPCRDB database as described in the Materials and Methods section. The classification in GPCRDB is based on classes, that is, proteins with broadly similar function and rather close sequence homology. The whole GPCRDB can be considered as the superfamily of G-protein-coupled receptors. We have used both of these levels for the tests described below.

Table 1.

Description of test set

Class	No. of seq. in GPCRDB	No. of seq. in Test set
Rhodopsin like	1207	50
Secretin like	86	19
Metabotropic glutamate/phermone	62	18
Fungal phermone	16	4
cAMP receptors	4	1

The relationships between protein sequences span a broad range, from almost identical sequences to apparently unrelated sequences sharing only a similar overall fold. Finding homologous sequences on the various levels of similarity poses different problems for search algorithms. For globular proteins, we have shown that the inclusion of evolutionary information (multiple sequence alignments) is most important for the detection of proteins at the superfamily level, and that the inclusion of structural information mainly helps at the fold level (Lindahl and Elofsson 2000).

To study the detection of membrane proteins at different homology levels, we performed two different tests. First, we tested the ability to detect sequences within a GPCRDB class. Here, hits to GPCR sequences outside a class are ignored, see Table 2. Second, we tested the ability to detect GPCRs from different classes. Here, hits to GPCR sequences in other classes are considered correct, whereas hits to sequences in the same class are ignored. This is identical to how the performance of fold recognition methods was investigated at different levels of relationship (Lindahl and Elofsson 2000).

Table 2.

Summary of how correct and false matches are stated in the two tests used in this study

	Class test	Superfamily test
ClassA–ClassA	correct	ignored
ClassA–ClassB	ignored	correct
ClassA–nonGPCR	false	false

ClassA–ClassA represents a match between two proteins from the same class, ClassA–ClassB represents a match between two proteins from different classes, and ClassA–nonGPCR represents a match between a GPCR and non-GPCR.

Performances as measured by the Matthews correlation coefficient (Mc) are shown in Table 3. In this Table, we report results for the standard Smith-Waterman sequence alignment (SW) method, for standard PSI-BLAST searches using different E-value cutoffs (PSI⁻³, PSI⁻⁵, and PSI⁻¹⁵), and for these methods augmented with information about predicted transmembrane helices from TMHMM (TMSW, TMPSI⁻³, TMPSI⁻⁵, and TMPSI⁻¹⁵).

Table 3.

Methods used in this study and the best obtained Matthews correlation coefficient at GPCR class and superfamily GPCR levels

Name	Description	Mc–class	Mc–superfamily
SW	Smith-Waterman, BLOSUM-62	0.83	0.01
PSI−3	PSI-BLAST, 5-iterations, E-value 10−3	0.95	0.60
PSI−5	PSI-BLAST, 5-iterations, E-value 10−5	0.96	0.46
PSI−15	PSI-BLAST, 5-iterations, E-value 10−15	0.98	0.16
TMSW	Smith-Waterman with TMHMM predictions	0.93	0.22
TMPSI−3	Profile alignment with TMHMM predictions using the PSI−3 profiles	0.96	0.62
TMPSI−5	Profile alignment with TMHMM predictions using the PSI−5 profiles	0.97	0.50
TMPSI−15	Profile alignment with TMHMM predictions using the PSI−15 profiles	0.98	0.22

Inclusion of transmembrane segment predictions increases the sensitivity when detecting closely related proteins

Performances as measured by the Matthews correlation coefficient (M_c) are shown in Table 3. In this table, we report results for the standard Smith-Waterman sequence alignment (SW) method, for standard PSI-BLAST searches using different E-value cutoffs (PSI⁻³, PSI⁻⁵ and PSI⁻¹⁵), and for these methods augmented with information from TMHMM (TMSW, TMPSI⁻³, TMPSI⁻⁵, and TMPSI⁻¹⁵).

Concerning the detection of proteins that belong to the same GPCR class, Table 3 (column M_c-class) shows that TMSW performs significantly better than standard Smith-Waterman alignments: a M_c of 0.93 versus 0.83. For PSI-BLAST and TMPSI, the highest M_c is obtained if a strict cutoff is used. The highest correlation coefficients, 0.98, are thus seen for PSI⁻¹⁵ and TMPSI⁻¹⁵. The inclusion of information about predicted transmembrane segments results in only limited improvements to the M_c in this case. The table also shows that PSI-BLAST and TMPSI are able to detect almost all proteins within a class of GPCRs.

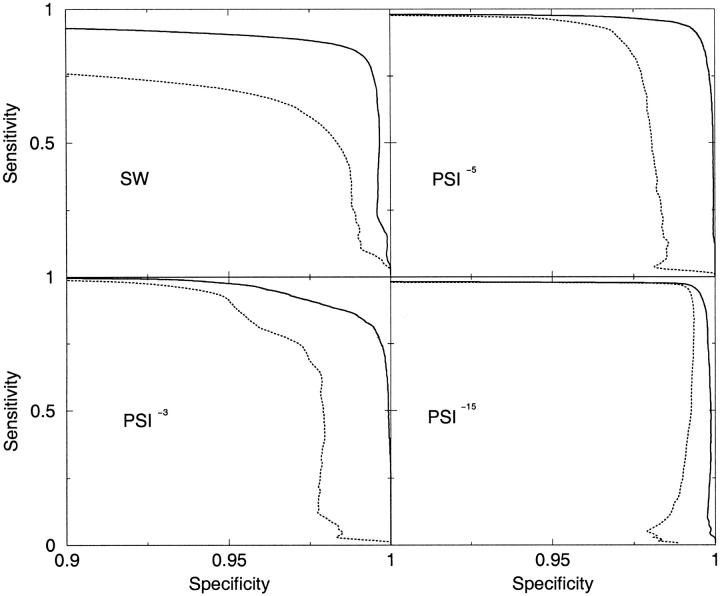
A more detailed understanding of the performance can be obtained from spec-sens plots, see Figure 1 ▶. It is clear that TMPSI has a significantly higher specificity than PSI-BLAST, irrespective of the cutoff E-value. Without the information about transmembrane segments, it is necessary to use an E-value cutoff of 10⁻¹⁵ to increase the specificity beyond 98%. For the single-sequence-based methods, transmembrane segment information significantly increases both the specificity and sensitivity.

Fig. 1.

Comparison of the SW and PSI algorithms (broken lines) and the modified TMSW and TMPSI algorithms (solid lines) for the ability to distinguish GPCRs from the same class. The creation of the profiles were made using PSI-BLAST and three different cutoffs (10⁻³, 10⁻⁵, and 10⁻¹⁵). Note the scale on the x-axis.

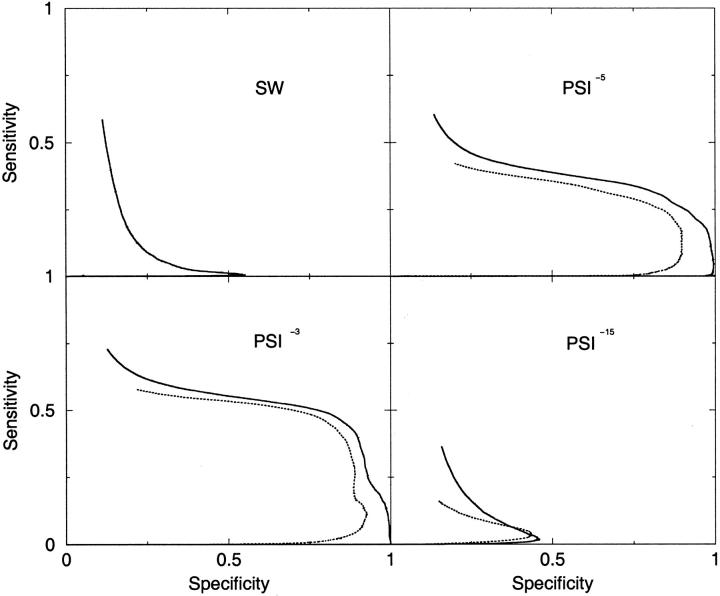
For distantly related GPCRs, it can be seen that PSI-BLAST with a less restrictive E-value cutoff performs significantly better than SW or PSI-BLAST with the 10⁻¹⁵ cutoff, see Figure 2 ▶. Compared with the standard SW method (M_c = 0.01) the increase in performance is remarkable (M_c = 0.60 for PSI⁻³), see Table 3. PSI⁻³ detects almost 50% of the nonclass-related GPCRs at 80% specificity.

Fig. 2.

Comparison of the SW and PSI algorithms (broken lines) and the modified TMSW and TMPSI algorithms (solid lines) for the ability to detect distantly related GPCRs, that is, GPCRs from different classes. The creation of the profiles were made using PSI-BLAST and three different cutoffs, (10⁻³, 10⁻⁵, and 10⁻¹⁵). Note the scale on the x-axis.

In conclusion, the inclusion of predicted transmembrane segments improves the detection rate significantly, mainly by reducing the number of false positives, that is, by increasing the specificity.

Discussion

PSI-BLAST is not ideally tuned to detect membrane proteins

A series of recent studies show that PSI-BLAST is better than SW for the detection of distantly related globular proteins (Park et al. 1998; Lindahl and Elofsson 2000). In fact, PSI-BLAST is one of the most sensitive sequence-based database search methods available and it is also fast enough to be used on large databases. Due to the iterative approach and the position-specific profiles, PSI-BLAST is able to find more distantly related sequences than most other methods. However, the underlying statistics used in BLAST is calculated from globular proteins and not from membrane proteins. Because unrelated transmembrane segments are more similar to each other than unrelated globular regions, the E-values reported by BLAST will be too small for unrelated membrane proteins. The simplest way to avoid this problem is to use a more restrictive E-value cutoff for the inclusion of proteins in the iterative BLAST search. This has been suggested by others (Jones et al. 1994; McGuffin et al. 2000). However, to our knowledge no one has systematically optimized the E-value for membrane protein searches. An alternative possibility is to mask so-called low-complexity regions (transmembrane helices often score in this category) in BLAST. However, when applied to membrane proteins, this throws away much information from the outset in an uncontrollable way, and we have chosen not to use this option. Further, it might be possible that one could make PSI-BLAST better able to calculate E-value by changing the standard amino acid composition used.

In Figures 1 and 2 ▶ ▶ it can be seen that PSI-BLAST performs significantly better than the SW method, both for the detection of closely and distantly related GPCRs. For closely related proteins, the best specificity is obtained for the very restrictive cutoff of 10⁻¹⁵. For distantly related proteins, however, PSI-BLAST performs better when the E-value is less restrictive (see Fig. 2 ▶). The high error rate for PSI-BLAST on our test set stands in contrast to the performance obtained for globular proteins, in which ∼35% of the family related proteins can be detected before any false positives (Lindahl and Elofsson 2000) and even a significant proportion of superfamily related proteins can be detected without any false positives.

High-scoring false hits seem to be a problem when PSI-BLAST is used without manual checking of the sequences incorporated into the profiles. Once a false hit is incorporated, every subsequent iteration might result in more false hits being included, and the final result will be biased by a high number of high-scoring incorrect matches. The top 100 false hits in the PSI⁻¹⁵ search are mainly caused by five GPCR sequences in the test set. Of the 100 highest-scoring false positives from SWISS-PROT, 57 have no predicted TM-helices, 35 have one, and 2 have 8 regions according to TMHMM. This shows that, at most, two of these proteins may in fact be GPCRs (that have not found their way into GPCRDB) and that PSI-BLAST runs an obvious risk of incorporating high-scoring false hits both to transmembrane and globular proteins. The mediocre performance of PSI⁻¹⁵ for detecting distantly related proteins further suggests that using very restrictive cutoffs is not without problems.

However, it is well known that PSI-BLAST performs very well to detect closely and distantly related globular proteins.

The performance increase using predicted secondary structures is quite marginal for globular proteins (Lindahl and Elofsson 2000). This puts forward the question as to when parameters should be optimized for a particular case and when it is appropriate to use general parameters. Here, we use a standard substitution matrix for membrane proteins, whereas in earlier studies it has been shown that the use of a special matrix might improve performance (Muller et al. 2001). In general, it could be possible that the best performance would be obtained by use of a special set of parameters for each class of proteins (such as globular, fibrous, porins, etc.), or even for each type of secondary structures. However, taking into account the difficulties in optimizing these parameters, we think that, in general, it is better to use parameters that are general. This study shows an exception to this assumption, as the transmembrane regions differ significantly from globular regions in proteins. However, due to the limitations with this benchmark, we do not think it is possible to obtain the ideal values for gap penalties and substitution matrices. Therefore, we choose to use default values to as large a degree as possible.

Predicted secondary structures improve detection of membrane proteins

As can be seen in Figures 1 and 2 ▶ ▶, the use of transmembrane predictions significantly helps in the detection of related membrane proteins (at least insofar as the GPCR superfamily is representative of membrane proteins in general). The best results are obtained using TMPSI, that is, by a combination of profiles from PSI-BLAST profiles and TMHMM predictions. Using TMPSI, it is possible to obtain a specificity higher than 99.5% for the detection of GPCRs from the same class. The inclusion of TMHMM predictions in a profile search is seen to increase the specificity compared with PSI-BLAST alone. However, no significant improvements are seen at lower specificity. This indicates that the inclusion of predicted membrane regions into profiles mainly functions as a filter to avoid incorrect matches, whereas it does not significantly increase the detection of distantly related proteins. Comparing Figures 1 and 2 ▶ ▶, it seems as if the best compromise to detect both closely and distantly related GPCRs might be to use TMPSI⁻⁵.

It should be noted that information from TMHMM was only included in the final profiles, that is, it was not used during the creation of the profiles. From the improvements seen for TMSW compared with SW, it seems safe to assume that if this were done, additional improvement would be obtained. We have not tested this possibility, as the inclusion of TMHMM predictions into PSI-BLAST is technically not straight forward. We will explore this possibility in future work.

Conclusions

In this study, we have introduced a novel modification to the Smith-Waterman and profile-based methods that is shown to increase their ability to detect related helical membrane proteins. The improvement is based on the inclusion of information about predicted transmembrane segments in the alignment algorithm. This is done by adding a constant to the alignment score if two residues predicted to belong to transmembrane segments are aligned with each other. Benchmarking shows that the number of false positives is significantly reduced in this way, both when closely related and distantly related proteins are searched for. With these modifications, we find that almost all G-coupled receptors from a class can be detected reliably, and that about half of the G-coupled receptors from different classes can be detected at a specificity of 80%.

Materials and methods

Test set

A test set was created from the sequences in the GPCRDB (December 2000 release) (Horn and Cohen 2001). This set of sequences was reduced by removing sequences with high-sequence identity. The final test set contained 100 sequences from 5 classes, in which no 2 sequences had more than 50% sequence identity according to FASTA, see Table 1. The number of sequences from the Rhodopsin-like class was reduced so as not to bias the tests toward this class. Beside these five classes, there is a set of less well-characterized classes/families in GPCRDB; these were excluded from the test set as the relationships of these proteins are less clear. Each sequence in the test set was then searched against SWISS-PROT (release 39 ). To easily detect hits to related sequences, all sequences with >95% sequence identity to any sequence in the GPCRDB was excluded from SWISS-PROT and replaced by the corresponding sequences in GPCRDB before the comparisons were made. This approach may lead to problems if SWISS-PROT contains GPCRs that are not present in GPCRDB, in which case, hits to related sequences will incorrectly be considered as false. However, we think that it is reasonable to assume that most GPCRs in SWISS-PROT are present in GPCRDB. This assumption is, in any case, necessary, and any incorrect assignments should average out when different methods are compared.

Search algorithms

For the standard Smith-Waterman (SW) algorithm (Smith and Waterman 1981), we used the BLOSUM62 matrix (Henikoff and Henikoff 1992), a gap-opening penalty of −10, and a gap-extension penalty of −4. Computational limitations made it impossible to make a systematic search using different matrices and/or gap-penalties.

The approach used to add information about predicted transmembrane segments is similar to the one used in earlier fold recognition/threading techniques (Fischer and Eisenberg 1996). Thus, the score for an alignment is calculated as:

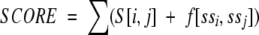where S[i,j] is the standard alignment score for aligning residues i and j, and f(ss_i ss_j) is a score dependent on residues i and j are both predicted to belong to transmembrane segments:

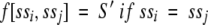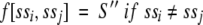In this study we have used S' = 1 and S' = 0.

The difference from the earlier studies is that we use predicted transmembrane segments both for the query and the target sequence, whereas in the threading methods, the predicted secondary structure of the query is matched against the real secondary structure of the target.

The location and orientation of possible transmembrane helices are predicted using TMHMM (Krogh et al. 2001). If the residues in an aligned pair are both predicted to be located in a transmembrane helix, an additional positive score of one is added to the substitution score, as indicated above. The same substitution matrix and gap penalties as used in the standard Smith-Waterman search are used also in this case.

For the PSI-BLAST searches, we have used the default PSI-BLAST parameters, except for the E-value used to include a sequence in the next iteration and for the number of iterations. We have used three E-values (10⁻³, 10⁻⁵, and 10⁻¹⁵) and a maximum of five iterations. Low-complexity regions were not masked in the PSI-BLAST runs.

Finally, the novel TMPSI method includes both the information from TMHMM and the multiple sequence information from PSI-BLAST. In this method, a standard profile search (Gribskov et al. 1987) is performed, using the profile obtained from PSI-BLAST. In addition, we add a score of one for each residue in the query profile and SWISS-PROT protein when both are predicted to be in transmembrane segments. For the query profile, the prediction of transmembrane segments is the same as that obtained for the initial seed sequence in the PSI-BLAST run. A gap opening penalty of −10 and a gap extension penalty of −4 was used. Due to computational limitations, we were not able to examine more parameter values.

Comparison and assessment

We have used spec-sens plots (Rice and Eisenberg 1997; Hargbo and Elofsson 1999) as our primary measure of performance. The main advantage of this is that such plots measure the ability of a method to reliably find all pairwise matches in the database. The fraction of possible correct hits found, sensitivity, is defined as:

in which TP(score) is the number of correct hits having a score above score, and FN(score) being the number of correct hits with a score less than score. The specificity measures the probability that a pair of sequences with a score greater than a certain threshold really is a true hit, defined as:

in which FP(score) is the number of false hits that have a score above score and TP is defined as above. The sensitivity is plotted as a function of specificity, each point corresponding to a certain score. This measure is similar, but not identical, to plots in other studies in which sensitivity, referred to as Fraction of homologous pairs detected, was plotted against Rate of false positives, (Park et al. 1997, 1998; Muller et al. 2001). Fraction of homologous pairs is identical to sensitivity, whereas Rate of false positives is defined as:

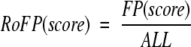where ALL is the total number non-related protein pairs.

In addition we have used the Matthews correlation coefficient (M_c) (Matthews 1975) for measuring the performance.

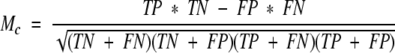where TN is the number of correct hits that have a score less than score and TP, FP and FN are defined as above.

Score normalizations

For all the SW, TMSW and TMPSI algorithms the raw score S was normalized by the length m and n of the compared sequences, following studies of the expected score for unrelated proteins (Altschul et al. 1997):

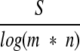For PSI−BLAST, the E−value was used for scoring.

The Pmembr program, used in this study, is available both as a webserver, and as source code from http://www.sbc.su.se/~arne/pmembr/.