Classification of G-protein coupled receptors by alignment-independent extraction of principal chemical properties of primary amino acid sequences

Abstract

We have developed an alignment-independent method for classification of G-protein coupled receptors (GPCRs) according to the principal chemical properties of their amino acid sequences. The method relies on a multivariate approach where the primary amino acid sequences are translated into vectors based on the principal physicochemical properties of the amino acids and transformation of the data into a uniform matrix by applying a modified autocross-covariance transform. The application of principal component analysis to a data set of 929 class A GPCRs showed a clear separation of the major classes of GPCRs. The application of partial least squares projection to latent structures created a highly valid model (cross-validated correlation coefficient, Q² = 0.895) that gave unambiguous classification of the GPCRs in the training set according to their ligand binding class. The model was further validated by external prediction of 535 novel GPCRs not included in the training set. Of the latter, only 14 sequences, confined in rapidly expanding GPCR classes, were mispredicted. Moreover, 90 orphan GPCRs out of 165 were tentatively identified to GPCR ligand binding class. The alignment-independent method could be used to assess the importance of the principal chemical properties of every single amino acid in the protein sequences for their contributions in explaining GPCR family membership. It was then revealed that all amino acids in the unaligned sequences contributed to the classifications, albeit to varying extent; the most important amino acids being those that could also be determined to be conserved by using traditional alignment-based methods.

The functional and structural annotation of proteins is an important task in proteomics (O'Donovan et al. 2001). There is a strong need for efficient and reliable methods for the analysis of protein sequence data. Existing methods rely mainly on alignment- and similarity-based comparisons. Basing the analysis on common patterns and profiles may implicitly take into account that the structure and function of proteins are determined by the physicochemical properties of their sequence constituents. However, a method that uses a direct quantitative measure of the physicochemical properties of the amino acids would seem a more rational approach. For example, proteins created by divergent or convergent evolution may lack obvious sequence similarity, although they share similar structural organization and biological properties. In such a situation, attempts to align protein sequences might produce ambiguous results or fail.

In the past, quantitative descriptions of peptide sequences have been attempted using physicochemical z-scales (Hellberg et al. 1987; Wold et al. 1993; Sandberg et al. 1998). Such scales are based on the principal physicochemical properties of the amino acids of the peptide sequences and have been used to characterize the properties of synthetic peptides in QSAR (quantitative structure-activity relationship) studies (Nyström et al. 2000) and short signal peptide sequences of bacterial proteins (Edman et al. 1999). Moreover, an attempt was made to use z-scales for the characterization of bacterial proteins (Sjöström et al. 1995). The latter study was able to successfully assign the location of the bacterial proteins to different cellular compartments (i.e., cytoplasmic, inner membrane, periplasm, and outer membrane), and it seemed quite promising, prompting the possibility that physicochemical scales of proteins might be useful in their functional characterization.

However, to make any meaningful calculations based on the physicochemical descriptions derived from the amino acids sequences, it is necessary to obtain uniform matrices over the whole dataset. This may be done by prior alignments of peptide sequences. However, due to the unequal length of protein sequences, such alignments are seldom possible, and it is therefore desirable to find methods that can transform the physicochemical descriptions into uniform matrices. Autocross-covariance (ACC) transforms were developed (Wold et al. 1993) and applied in some of the studies mentioned above (Sjöström et al. 1995; Edman et al. 1999). In the present study, we further developed and validated approaches for protein classification and functional analysis based on alignment-independent physicochemical descriptions of protein sequences. We used 929 cloned Class A (rhodopsin-like) G-protein coupled receptors (GPCRs) of the GPCR database and validated our approach on 535 novel sequences taken from a newer release of the same database.

Results

The method was developed in two steps. In a preliminary trial, we made quantitative physicochemical descriptions of the protein sequences in an alignment-dependent way. Based on these descriptions, an improved method was then derived that used descriptions of the physicochemical properties of the protein sequences in an alignment-independent way.

Alignment-based method

We retrieved the 929 sequences for Class A GPCRs from the May 1999 release of the GPCR database (www. gpcr.org/7tm/; Horn et al. 1998). These sequences represented 12 known families of GPCRs and orphan receptors, which besides the orphans were the amine, peptide, glycoprotein hormone, opsin, olfactory, prostanoid, nucleotide-like, cannabinoid, platelet-activating factor, gonadotropin-releasing hormone, thyrotropin-releasing hormone, and melatonin receptors. This dataset is hereinafter referred to as the "original dataset". (See Fig. 1 ▶ legend for further details). Because the sequence lengths of the receptors varied from 290 to 834 amino acids, it was not possible to make full sequence alignments. Therefore, only the seven cell membrane-spanning alpha-helical regions were aligned separately, according to the known conserved amino acid positions (Baldwin et al. 1997). Prostanoid receptors (40 sequences) had to be excluded, as it was impossible in these to reliably identify the amino acids generally conserved in the fourth and fifth transmembrane (TM) helices of GPCRs. After we performed the alignments, we translated a total of 135 amino acid positions (20, 20, 20, 18, 20, 19, and 18 from TM1–TM7, respectively) of the remaining 889 GPCRs into physicochemical descriptions by representing each amino acid with the five z-scales derived by Sandberg (Sandberg et al. 1998).These z-scales are the principal components of 26 physicochemical properties of amino acids, and represent hydrophobicity, steric properties and polarizability, polarity (z₁–z₃), and electronic effects of amino acids (z₄, z₅). (The 26 descriptors of physicochemical properties are: molecular weight, van der Waals volume, heat of formation, energy of highest occupied molecular orbital, energy of lowest unoccupied molecular orbital, log P, α-polarizability, absolute electronegativity, absolute hardness, total molecular surface area, polar molecular surface area, nonpolar molecular surface area, number of hydrogen bond donors, number of hydrogen bond acceptors, indicator of positive charge in the side chain, indicator of negative charge in the side chain, NMR α-proton shifts at pD = 2, 7, and 12.5, and seven descriptors represent thin layer chromatographic mobilities using different stationary and mobile phases.) Principal component analysis (PCA) on the dataset thus obtained resulted in a multicomponent model with more than 100 significant principal components (PCs), indicating that a wide diversity exists in the chemical properties of the receptor sequences. However, as seen in Figure 1A ▶, even the three first PCs provide a lot of information about the trends in the model. Thus, the plot reveals clear separation of amine, olfactory, glycoprotein hormone, and opsin receptor families. Additionally, the opsin receptor subfamilies form completely separated clusters.

Fig. 1.

Three-dimensional plots representing the three first components of PCA models of 889 GPCRs from the original dataset (40 prostanoid GPCRs are excluded). Each receptor is represented by a sphere in the space of the first three principal components of physicochemical descriptors. Spheres are color-coded according to receptor family membership: rose, amine (n = 200); white, peptide (n = 297); violet, glycoprotein hormone (n = 23); salad green, opsins (n = 131); amber/orange, olfactory (n = 63); green, nucleotide-like (n = 45); gray, cannabinoid (n = 9); magenta, platelet-activating factor (n = 4); blue, gonadotropin-releasing hormone (n = 7); yellow, thyrotropin-releasing hormone and secretagogue (n = 13); red, melatonin (n = 13), and cyan, orphan receptors (n = 84). (A) PCA model using alignment-based approach. The amino acids of TM1–TM7 were separately aligned for 884 GPCRs according to known patterns (5,6). For each TM respectively, 20, 20, 20, 18, 20, 19, and 18 (total 135) amino acids were used. The plot reveals clear separation of amine, olfactory, glycoprotein hormone, and opsin receptor families. The subfamilies of opsin receptors form completely separated clusters as well. (B) PCA model for ACC-based approach with normalization and without centering of z-scales. Note that receptor classes merge into each other. (C) PCA model for ACC-based approach using centering of z-scales and applying normalization. Note that receptors form distinct clusters. Orphan receptors fall to a large extent within the cluster of peptide receptors. For B and C, L = 80.

We tested the ability to use the alignment-based physicochemical descriptions to distinguish the 11 families (according to the GPCR database classification; see Fig. 1 ▶ legend) of the rhodopsin-like GPCRs by performing a PLS (partial least squares projection to latent structures) analysis. Although the families differ substantially in both the number of representatives and the degree of branching into sub- and subsub-families, the analysis resulted in a highly significant model, proving validity of the classification scheme. The obtained 18-component model explained R²Y = 93.2% of the total variance of Y (i.e., family membership of receptors) with a predictive ability Q²_cum = 90.3% according to cross-validation. The model was additionally validated by response permutations (Eriksson et al. 1997). The negative value of the Q²_cum intercept obtained indicated that random assignment of class membership data would not produce a predictive model.

Autocross-covariance transformations

Despite its success, the above approach relied on sequence alignments. Moreover, only the transmembrane parts of the GPCRs had been accounted for. Therefore, in a second attempt we applied modified autocross-covariance (ACC) transformations (see Methods, Eqs. 1 and 2) over the whole sequences prior to PCA and PLS analyses. The modified ACC transforms were developed because the ACC transforms originally described (Wold et al. 1993) gave inferior results for the present dataset. As seen from Eqs. 1–3, three parameters will affect the outcome of the modified ACC transforms, namely the maximum lag L, centering of descriptors, and degree of normalization p. The fine-tuning of these parameters was necessary to maximize the resolution of the method.

ACC terms may be calculated with lags up to the length of the shortest sequence in a dataset. The use of ACCs with large lags might account for interactions of amino acids at distant parts in a sequence. However, even for closely related proteins, the lengths of segments connecting functional units often differ substantially. As a result, the probability of assigning an interaction to the same ACC term would be inversely proportional to the distance between the interacting positions. ACC terms with extremely large lag would thus be less helpful in finding similarities in related sequences, but on the other hand one could presume that increasing the maximum lag up until some point would provide better characterization compared to a short maximum lag, as it would result in more ACC variables.

Prior to the PCA and PLS calculations, variables are centered for the given set of observations. Thus, in the alignment-based approach, each descriptor became centered for the amino acid composition of its sequence position. Centering of descriptors prior to PCA or PLS therefore did not influence the analysis. However, when the ACC preprocessing was applied, centering could, during some conditions, give a significant effect. If the amino acids of proteins had been randomly present, the use of z-scales with or without centering prior to ACC would create the essentially same results. However, because the natural amino acids occur with different frequency, which has remained relatively constant during evolution (Benner et al. 1994), precentering would affect the outcome of the ACC terms. We therefore compared the original and the centered z-scales (see Eq. 3). (For centered z-scales, the model will become balanced in inverse proportion to the occurrence of amino acids in the GPCRs). Moreover, if the algebraic sum of products of an ACC was proportional to the number of multiplications, the normalization by (n−l) would account for differences in sequence length (c.f. Eqs. 1 and 2). However, such proportionality is true only in some particular situations, for example, if there were some specific patterns that occurred regularly. Another possibility would be if the sequence consisted predominantly of amino acids with either positive or negative descriptor scores. If this was not the case, or if some patterns are present only a given number of times, the situation would be different.

Accordingly, we created PCA models based on unnormalized (p = 0, Eqs. 1 and 2) and normalized (p = 1) ACC terms. (For some tests, PLS models were elaborated with P = 0.5, as well). The resolution of the resulting models was compared by calculating ρ values (Eq. 6) (Table 1A) and by visually inspecting 3D plots (Fig. 1 ▶). As can be seen from the table, the ρ values decreased when maximum lags increased from 10 to about 40–80, whereas increasing the maximum lags to 120–160 led only to marginal further improvements in the models. Centering of z-scales prior to ACC led also to appreciable improvements of all models. The unnormalized ACC terms also gave somewhat better models compared to the case when full normalization was used. The increase in resolution achieved for the models using centering is also evident when one compares the three first PCs for a model using centering (Fig. 1C ▶) with one that did not use centering (Fig. 1B ▶).

Table 1.

Comparison of ρ values (A) and predictive ability and goodness of fit (B)

A. Comparison of ρ values extracted from different PCA modelsa
			Maximum lag
Sequence processing	z-scales	Normalization of ACC terms (p)	—	10	20	40	80	120	160
1 Alignment based	—	—	0.38	—	—	—	—	—	—
2 ACC transformed	original	1	—	0.73	0.68	0.65	0.65	0.65	0.64
3 ACC transformed	original	0	—	0.64	0.61	0.59	0.59	0.59	0.59
4 ACC transformed	pre-centered	1	—	0.64	0.54	0.49	0.47	0.48	0.46
5 ACC transformed	pre-centered	0	—	0.64	0.56	0.48	0.47	0.45	0.45

B. Predictive ability (Qcum2) and goodness of fit (Rcum2) for normalized and non-normalized ACC pre-processed PLS models of 11 classes of GPCRsb
				Maximum lag
	z-scales	Normalization of ACC terms (p)	Measure	20	40	60	80	100	120	160
a This comparison uses alignment based and ACC transformed descriptors of 884 GPCR sequences. The data set excludes prostanoid, but includes orphan receptors.
bp denotes normalization according to Eq. 1 and 2.
1	pre-centered	1	Qcum2	0.735	0.829	0.859	0.877	0.857	0.855	0.832
		R2Ycum	0.849	0.903	0.924	0.936	0.934	0.940	0.943
2	pre-centered	0	Qcum2	0.747	0.830	0.879	0.882	0.870	0.876	0.858
		R2Ycum	0.838	0.903	0.924	0.936	0.941	0.946	0.934

PLS models (excluding prostanoids and orphans, and extracting 18 components, as had been done for the alignment-based models) were created using precentered ACC terms and maximum lags between 10 and 160. It is well known that the goodness of fit R² for PLS models generally increases with model complexity (i.e., number of terms), while the predictive power Q² _cum reaches a maximum and thereafter heads downwards (Baroni et al. 1993; Eriksson et al. 1997). The highest Q²_cum was recorded with L = 80 both for p = 0 and p = 1 (Table 1B). Further refinements were obtained by elaborating the degree of normalization. Thus the predictive ability of a precentered model was distinctly improved when p = 0.5 (i.e., Q²_cum = 90.5% for model 5a of Table 2A), showing the existence of an optimal choice for the degree of normalization. Thus, the predictive ability of the ACC preprocessed model was at least as good as that for alignment-based model (Q²_cum of 90.3%). Table 2A reveals that precentered z-scales improve model predictability, as well as goodness of fit, over original z-scales. When we took into account only significant PLS-components (see Materials and Methods for details), models with 12–17 components resulted. Interestingly, the models with the fewest PLS components were obtained for the models 4a and 5a (Table 2A) that used precentered z-scales, which also generated the models with the best predictive capacity.

Table 2.

Comparison of the predictive ability (Q_cum²) and goodness of fit (R²Y_cum) of PLS models obtained from GPCR sequences using ACC transformed descriptors with maximum lag 80

A. Models of 11 receptor classes (prostanoid and orphan receptors not included)
			A-component models		18 component models
Centering of z-scales	Normalization (p)	A	R2Ycum	Qcum2	R2Ycum	Qcum2
1a original	1	17	0.912	0.833	0.918	0.844
2a original	0.5	16	0.909	0.866	0.922	0.879
3a original	0	16	0.905	0.841	0.920	0.858
4a centred	1	12	0.890	0.820	0.936	0.877
5a centred	0.5	12	0.894	0.860	0.939	0.905
6a centred	0	16	0.925	0.871	0.936	0.882

B. Models of 12 receptor classes (prostanoid receptors included). p denotes normalization according to Eq. 1 and 2
			A-component models		18 component models
Centering of z-scales	Normalization (p)	A	R2Ycum	Qcum2	R2Ycum	Qcum2
A denotes the number of significant PLS components according to cross validation. A-component model represents the PLS model with A number of components. 18-component models represent PLS models with 18 PLS components.
1b original	1	16	0.886	0.800	0.904	0.826
2b original	0.5	18	0.910	0.864	0.910	0.864
3b original	0	17	0.897	0.836	0.906	0.847
4b centred	1	13	0.885	0.814	0.922	0.860
5b centred	0.5	13	0.888	0.858	0.927	0.895
6b centred	0	17	0.918	0.872	0.925	0.880

Due to the alignment independence of the new approach, it was a simple matter to include prostanoid receptors. In addition, for the dataset including these receptors, the best predictive capacity was achieved for precentered, partially normalized ACCs (Table 2B). The best model, 5b of Table 2B (with 18 extracted components), was further validated by response permutations, giving R² intercepts from 0.22 to 0.33, and Q² intercepts from −0.02 to −0.03. Model 5b was used in all subsequent calculations and is hereinafter referred to as the "final model."

Functional classification of GPCRs

The final model was used to assess the receptors' conformity to the known GPCR families according to the principal chemical properties of their amino acid sequences. Thus, Y values were calculated from the X descriptors and used to predict family membership of the 845 receptors originally included in the model, as well as for the orphan receptors that previously were not possible to include because of their unknown class membership. Moreover, family memberships of the novel receptors from a newer release of the GPCR database (www.gpcr.org/7tm/ release 5.1, March 2001) were predicted and compared to the memberships declared in the database.

Calculated class membership for GPCRs within model

The high Q²_cum value of the final model indicated that calculation of family memberships should delineate members and nonmembers of the different GPCR classes. We assessed this for all of the GPCRs of the original dataset, which showed that the model assigned correct membership, except in one case (see below). Results from the classification are illustrated in Fig. 2A ▶, which show the conformity (i.e., Y values) calculated for all of the 929 GPCRs to the prostanoid receptor family (Fig. 2A ▶). As can be seen, all of the prostanoid receptors separate completely from the other GPCR classes. The results of the same analysis for peptide receptors is shown in Fig. 2B ▶: the peptide receptors separate clearly from other receptor classes, except from the orphan receptors. Thus some of the orphan receptors seem to classify with peptide receptors, whereas others don't. Repeating the analysis for the rest of the receptor classes showed correct assignment, except in one case, namely for GRHR_CLAGA, which is a gonadotropin-releasing hormone receptor (GRHR) that showed higher conformity to the peptide receptor family than to the GRHR family (conformity to respective family being 0.63 and 0.42). In contrast, none of the GRHR nonmembers received a conformity score higher than 0.09 to the GRHR family.

Fig. 2.

Calculated family membership (i.e., predicted Y values, representing conformity to family) of 929 GPCRs. The plots represent data calculated using the PLS model 5b of Table 2B. Panel A shows conformity to prostanoid receptor family, and panel B to peptide receptor family. (a) Amine, (b) peptide, (c) glycoprotein hormone, (d) opsins, (e) olfactory, (f) prostanoid, (g) nucleotide-like, (h) cannabinoid, (i) platelet-activating factor, (j) gonadotropin-releasing hormone, (k) thyrotropin-releasing hormone, (l) melatonin, and (m) orphan receptors.

External prediction of new GPCRs

In addition to cross-validation, the final model was also validated by performing external predictions. This was made by analyzing 535 new rhodopsin-like GPCRs with known family membership retrieved from the March 2001 release of the GPCR database. Thus, the conformity of each new sequence to each of the 12 GPCR families was calculated by applying the final model, and the results were compared to the family membership assigned in the database (Table 3). Table 3 thus gives the predicted conformities of members/nonmembers to each GPCR family; for the majority of the receptors, a correct assignment and a clear separation from other classes could be done. Of the 535 receptors, only 14 were mispredicted (i.e., receiving a higher Y value for a different GPCR family than the one declared in the GPCR database). Thirteen GPCRs (seven GHRH, four olfactory, one nucleotide-like and one TRH receptor) were wrongly classified as peptide receptors, while one olfactory receptor (Q9YHY3) was classified as an amine receptor. Further inspection of Table 3 shows that the mispredictions were made essentially for families with a large number of new entities compared to the numbers in the training set (i.e., the olfactory and gonadotropin-releasing hormone receptors). Nevertheless, regarding the mispredicted GRHRs, they received the second-highest conformity values to the GRHR family, which was higher than for any nonmembers to the GRHR family, with an exception of two orphan receptors (O77152 and Q9VM96) (data not shown).

Table 3.

External prediction of membership to GPCR class using the PLS model

			Predicted Y (members/non-members)
No.	Family	No. of new entries	>0.8	0.6–0.8	0.4–0.6	<0.4	Mispredicted
1	Amine	62	44/0	13/0	3/1	2	0
2	Peptide	164	107/0	36/2	20/9	1	0
3	Glycoprotein hormone	9	2/0	6/0	1/0	0	0
4	Opsin	99	90/0	6/0	3/0	0	0
								Q9YHY3, O93551, Q9WU88,
5	Olfactory	167	59/0	30/0	60/0	18	5	Q9WU94, Q9YHY2
6	Prostanoid	5	4/0	1/0	0/0	0	0
7	Nucleotide like	8	3/0	1/0	3/0	1	1	O00398
8	Cannabinoid	3	2/0	0/0	1/0	0	0
9	Platelet activating factor	2	2/0	0/0	0/0	0	0
								Q9I8V4, Q9I986, Q9IA91, Q9PT72,
10	Gonadotropin-releasing hormone	11	3/0	1/0	0/0	7	7	Q9PW33, Q9YGN8, Q9YGN9
11	Thyrotropin-releasing hormone	3	0/0	0/0	2/0	I	1	O93414
12	Melatonin	2	2/0	0/0	0/0	0	0
	Total	535	318/0	94/2	93/10	30	14

Shown are the number of entities within ranges of conformity values (Y-values) for new entries in the GPCRDB database for members and non-members to the 12 GPCR families calculated from the model. Shown are also the number of mispredicted entries and their identifiers (see text for details).

The class membership of 165 new orphan receptors retrieved from the March 2001 release of the GPCR database was also predicted (Table 4). Most orphan receptors (65) ranged closest to the peptide GPCRs, followed by the amine GPCRs (19). Five were closest to the glycoprotein hormone receptor family, and one was closest to the olfactory receptor family. To identify possible outliers, that is, to identify sequences that were not likely belonging to the rhodopsin-like GPCRs, we calculated the distance-to-model (DmodX, see SIMCA 1998) of the PCA model. For one of the orphan receptors, namely GPCR_LIMST, the DmodX value significantly exceeded the critical value (see SIMCA 1998). Inspection of the GPCR_LIMST indicated that this could be explained by the presence of an extremely long (767 aa) extracellular terminal, containing low-density lipoprotein-binding (LDL) receptor motifs not shared by other GPCRs (Tensen et al. 1994).

Table 4.

Prediction of family membership of 90 (out of 165) orphan receptors calculated from the PLS model

Peptide	33 Q9NFV1	Amine
	34 KI01_RAT
1 Q89609	35 GPRF_HUMAN	1 Q9NJS7
2 GPR7_HUMAN	36 ADMR_RAT	2 YTJ5_CAEEL
3 GPRA_RAT	37 BONZ_HUMAN	3 YDBM_CAEEL
4 GPRA_HUMAN	38 GPRJ_HUMAN	4 Q9XTK1
5 O75194	39 ADMR_HUMAN	5 Q9NJS8
6 GPR8_HUMAN	40 Q9NPB9	6 Q23013
7 RDC1_RAT	41 Q9TV17	7 P90927
8 BONZ_MACNE	42 O75898	8 O18512
9 O42444	43 KI01_HUMAN	9 YQNJ_CAEEL
10 VK02_SPVKA	44 O93281	10 Q19449
11 GPR1_HUMAN	45 GPRF_MACMU	11 O45732
12 P92045	46 HM74_HUMAN	12 O44986
13 Q9JLZ0	47 GPRK_HUMAN	13 YYI3_CAEEL
14 Q9N0Z0	48 Q18228	14 Q22895
15 GUSB_BOVIN	49 GPRF_MACNE	15 Q9XTF5
16 BONZ_CERAE	50 Q9VM96	16 O15969
17 RDC1_HUMAN	51 GPRF_CERAE	17 O75963
18 Q22995	52 O02043	18 Q22490
19 RDC1_MOUSE	53 H963_HUMAN	19 O15970
20 O44148	54 ADMR_MOUSE
21 VC03_SPVKA	55 O44426	Glycoprotein hormone
22 BONZ_MACMU	56 GPRO_RAT
23 Q9NFV0	57 Q18534	1 Q94979
24 RDC1_CANFA	58 DUFF_HUMAN	2 Q9NCB6
25 Q9UE21	59 YKR5_CAEEL	3 Q9VEG4
26 VQ3L_CAPVK	60 YWO1_CAEEL	4 Q18759
27 GPR1_RAT	61 EBI2_HUMAN	5 GLHR_ANTEL
28 GPRH_HUMAN	62 O77152
29 Q9NFV3	63 GPRJ_MOUSE	Olfactory
30 Q9TV16	64 O43495
31 GPR1_MACMU	65 GPRC_MOUSE	1 O88628
32 Q9NFV2

The receptors shown are arranged in order of decreasing conformity (predicted Y) to respective family.

We also applied the model to 600 nonGPCR protein sequences of 400 amino acids length retrieved from the TrEMBL database (Bairoch and Apweiler 2000). By applying conformity scores for membership to GPCR families and DmodX, we found that all sequences separated from the GPCRs (data not shown).

Functional importance of chemical properties of amino acids

The importance of the chemical properties for each amino acid in the protein sequence for the grouping of proteins into functional classes could be assessed by calculating partial derivatives of the PLS regression equation, δY/δd_a, by using Eq. 7. The analysis revealed that each amino acid of the protein sequences contributes, albeit to varying degrees, with each of the 5 z-scores to the classification. The accumulated δY/δd_a (ΔY_a) could be used to assess the overall contribution for each amino acid. The ΔY_as showed a positively skewed distribution and allowed the identification of amino acids with particular importance for classifications. Thus, this analysis showed that while all amino acids over the whole sequences contributed in the alignment-independent classifications, the amino acids that contributed the most were those that could also be determined to be conserved within their receptor class by using traditional alignment-based methods. For example, in the human α_1A-receptor (A1AA_HUMAN), the most important amino acids for the classification were (in decreasing order of importance): C109, C118, V88, W102, T253, C176, Q177, F289, P242, L286, P131, and D106, which all are positions of conserved amino acids, some with known distinct functions. For example, V88 is conserved in other amine receptors as I, V, or L, which are amino acids sharing the same chemical properties. Another example is W102, which is conserved as W or Y in other amine receptors, which are also amino acids sharing similar chemical properties.

Discussion

The present study illustrates a new principle for protein classification where information regarding the physicochemical properties of amino acids in the primary amino acid sequence is extracted in a quantitative and alignment-independent way. The method is made alignment-independent by applying ACC preprocessing, which is a method that has previously been successfully applied for multivariate-based sequence-property analyses of peptide and DNA sequences. The validity of our present models is shown by applying relevant methods in multivariate analysis, namely cross-validation, response permutation, and external prediction. Most notably, our approach could clearly separate all Class A GPCR receptor families and afford classification of sequences with high accuracy, even when these sequences had not been included in the dataset on which the physicochemical descriptor PLS model for the receptors had been based (i.e., external prediction).

A previous attempt to apply alignment-independent z-scale-based physicochemical classification of proteins was directed towards delineating broad groups of proteins, that is, cytoplasmic, inner membrane, periplasmic, and outer membrane bacterial proteins (Sjöström et al. 1995). In this case, the classification might have been based on quite broad differences in the proteins' physicochemical properties. That is, the cytoplasmic proteins are water-soluble, the membrane proteins contain stretches of hydrophobic amino acids, and the periplasmic and outer membrane proteins contain hydrophobic signal sequences in their N-terminal ends. Moreover, the outer membrane proteins are characterized by lack of long stretches of only hydrophobic amino acids (Sjöström et al. 1995).

In contrast, in the present study the GPCRs represent membrane proteins with varying degree of similarity that all share seven quite similar hydrophobic transmembrane domains and more divergent N- and C-terminal sequences and extra- and intracellular loops. Thus, delineating these more similar proteins would present a more difficult task than delineating between proteins that show broadly differing properties. ACC descriptions use changes in physicochemical property or property combinations over stretches of the protein sequence of different lengths. Thus, an ACC transform may capture sets of characteristic physicochemical patterns in a sequence. For example, such patterns may represent a distinct topology or packing of the protein, or its ability to recognize a particular type of interacting entity. Obviously, the success of our modeling shows that ACC transforms extract sufficient information from the wild-type GPCRs to allow their functional classification. Centering of z-scales for a characteristic amino acid composition of GPCRs prior to ACC transformations proved essential to achieve a good resolving power of the model. The fine-tuning of the ACC transforms may be understood as removing nonrelevant information, such as sequence length, while amplifying class-differentiating properties. In a previous attempt, the original ACC transform (Wold et al. 1993) was applied (Sjöström et al. 1995), but it performed less well in our case. Moreover, in the earlier study by Sjöström et al. (1995), another modification of the ACC transform was tried that centered z-scales for each sequence, but it had essentially failed in the classification of the bacterial proteins and was not considered here.

Here, applying PLS in conjunction with PCA resulted in more complete and reliable characterization of receptors than the use of each of these two methods alone. PCA is unbiased regarding any prior assumptions about the functional roles of the proteins, and it revealed major sequence differences. Our results thus show that the largest differences in physicochemical properties are also the most relevant as to which ligand type the GPCRs interact with. This was because the first 3–4 principal components discriminated well between amine, peptide, hormone protein, opsin, and olfactory receptor families. The DModX parameter of a PCA model is also useful to discriminate between members and nonmembers of a studied protein class. PCA, however, is dependent on the number of members of different protein families included in the dataset. Hence it is advantageous to apply PLS to separate small GPCR families that therefore could not have had any major influence on the first PCA components due to a limited number of representatives. PLS also provides a quantitative assessment of receptor conformity to different GPCR families.

A very important result of the present study was the possibility to trace back from the models the importance of the physicochemical properties of every single amino acid of the original protein sequence (e.g., by using Eq. 7). Applying Eq. 7 showed that the most important amino acids used by the alignment-independent model were also the ones that could be identified to be conserved as to chemical property by using alignment-based approaches. Thus, these data indicate that the ACC transforms contain information similar to that contained within aligned sequences. However, because the ACC transforms are performed over the whole unaligned receptor sequence, they also add useful information in cases in which nonalignable regions contain class-differentiating information. For the alignment-based approach of the present study, this information was of course lost, as these portions of the sequences were not taken into account. On the other hand, ACC transforms may instead just add noise in cases where nonalignable regions do not contain class-relevant information. In view of the fact that many GPCRs bind ligands to their extracellular domains and G-proteins to their intracellular domains, the latter case would seem to be highly improbable.

The limits of the present approach are not yet known. In two previous studies we developed a multivariate approach for the analysis of ligand-receptor interactions where the physicochemical properties of sets of receptors having varying sequences, and sets of different ligands, were correlated to ligand binding affinities (Prusis et al. 2001; Lapinsh et al. 2001). The approach, which we have termed proteo-chemometrics, yielded surprisingly good and sturdy models. Thus, according to the proteo-chemometrics approach, the physicochemical information contained in the varied receptor sequences together with the physicochemical information in the ligands that interact with the receptors seems to contain very relevant information for explaining the ligand binding. The method also allowed us to perform a detailed analysis regarding which amino acids and which chemical properties of the amino acids in the receptors that were essential for the receptors' ligand binding (Lapinsh et al. 2001). The success of the present study and of our two previous studies indicates that there is great potential for the use of multivariate methods for characterization of various protein functions.

A very important result of the present work is the ability of the models to predict the properties of unknown proteins. Of 535 new GPCRs, the model mispredicted only 14. The few mispredictions occurred for seven GHRH receptors, five olfactory receptors, and one nucleotide-like receptor. The mispredictions occurred essentially for receptors belonging to families where a large number of new entities had been entered compared to the numbers of receptors in the training set. As the present approach is completely general, essentially automatic and creates soft models, one may easily incorporate new data when they become available, in order to improve the predictive ability of the models. In the present study we were able to tentatively link 90 of 165 orphan receptors to different receptor classes (peptide, amine, glycoprotein hormone, and olfactory). The information might serve as a guide in the further functional characterization of these receptors. In addition to being applicable to GPCRs, the present approach is completely general and might find use in the functional and structural classification of any protein.

Materials and methods

Principal component analysis (PCA)

PCA is a multivariate method for extracting information from a data matrix with N objects (i.e., receptors) described by M variables (i.e., amino acid chemical descriptors). PCA finds a lower dimensionality model, which approximates the structure of the multivariate data (Wold et al. 1987).

Partial least squares analysis

Partial least squares projection to latent structures (PLS) is an extension of PCA where the relations between two variable blocks are investigated (Geladi and Kowalski 1986). Both X and Y blocks are simultaneously approximated by mathematical models of lower dimensionality, which are correlated. In the present study, a Y variable was created for each class of observation (i.e., family of receptors). A unity value was assigned for members of the class, and all of the other observations were assigned a zero value. The goodness of fit was assessed by calculation of R²Y, as described (Eriksson et al. 1999).

Cross-validation of PLS models

Observations were randomly divided into seven groups. Models were then fitted to the dataset reduced by one of the groups, and predictions for the excluded data were calculated. The procedure was repeated with each group kept out of the model once. The squared differences between predicted and observed values (prediction error sum of squares, PRESS) were divided by the residual sum of squares of the previous extracted component (SS). Predictive ability Q² was then calculated as Q² = 1.0 − PRESS/SS. The cumulative Q² for all components was computed as Q²_cum = 1.0 − Π(PRESS/SS)_a, where Π(PRESS/SS)_a was the product of PRESS/SS for each individual component.

Cross-validation was also used to assess the significance of each extracted component. A PLS component was considered significant if Q² for at least one Y variable was higher than the threshold level 0.097 (Eriksson et al. 1999). However, significant components often followed components considered insignificant. Hence, elaboration of PLS models of the same dimensionality was preferred over terminating on a first insignificant component.

Validation by response permutations

The Y data (i.e., class memberships) were randomly reordered 25 times with unperturbed X data, and separate models were fitted to all of the permuted Ys, extracting as many components as was done in the original model. The results of permutation tests may be displayed by plotting the correlation coefficient between the original Y and the permuted Y, versus the cumulative R² and Q², and drawing the regression line (Eriksson et al. 1997). The intercept of the regression line when the correlation coefficient is zero (i.e., R² and Q² for zero correlation) is a measure of the overfit. For the model to be valid, the desirable intercept limits should be R² < 0.3 and Q² < 0.05 (Eriksson et al. 1997).

Autocross-covariance transformations (ACCs)

ACC terms were calculated as follows:

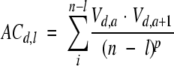(1)

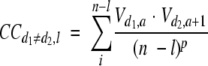(2)

where d = 1, 2,. . ., D (D is the number of descriptors); l = 1, 2, . . ., L (L is the maximum lag); n is the total number of amino acids in the sequence; V is the descriptor value; a is the amino acid position in the sequence; and p is the degree of normalization of the ACC term. The number of terms are LD². The method used here for the calculation of ACCs is a modification of the ACC transforms developed by others (Wold et al. 1993).

Centering of z-scales to the whole dataset

Centering was achieved by applying Eq. (3),

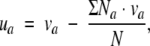(3)

where u_ais the centered descriptor value; v_a is the original descriptor value for amino acid a; N_a is the total number of amino acid a (a = Ala, Arg, Asn, etc. . ..) in the whole dataset; and N is the total number of amino acids in the whole dataset.

Estimation of the resolution of PCA models

The resolution of PCA models was estimated by first calculating the compactness (C) and separation (S) according to Eqs. 4 and 5:

(4)

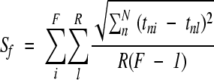(5)

The compactness C_f represents the average distance between the members of the family, and the separation S_f represents the average distance between a member of the family and any receptor in model (whether it belongs to the given family or not). In the formula, F is the number of receptors in the family; R is the number of receptors in the whole dataset; N is the number of principal components; and t_ni, t_nk, and t_nl are the scores of receptors i, k, and l in principal component n. C_f and S_f when taken alone would have no meaning. However, their ratio would be unit-independent and comparable between models. The overall resolution ρ of a PCA model was estimated by calculating the weighted average of the C_f and S_f ratios, according to the formula:

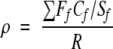(6)

Wherein F_f is the number of receptors in the family and R is the total number of receptors in the dataset. For randomly assigned families, ρ would tend to approach unity, whereas for a set of more clustered objects, ρ would become less than unity. Thus, a lower ρ value indicates that the model gives a better representation of the specific features of the given receptor family. On the other hand, values close to 1 may indicate that the differences between subfamilies or particular receptors are expressed better than the common features of the family.

Functional importance of chemical properties of amino acids

The PLS analysis aims to find characteristic patterns in the protein sequences that are useful for their classification. PLS correlates predictor variables with class variables by creating a PLS regression equation for each class variable. PLS regression coefficients are the projection of predictor variable onto the axis of the class membership variable. Therefore, the regression coefficients characterize the importance of X variables for the Y variable. In the alignment-based models, the X variables were independent from each other and the PLS equation would have been sufficient to assess the variable importance. However, for ACC-based models, each variable expresses interactions throughout all sequence length, and does not characterize any particular sequence position. In order to assess the importance of each initial z-scale variable for this case, we applied the formula:

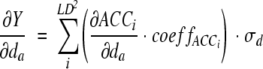(7)

In Eq. (7), d_a is the z scale variable characterizing sequence position a, LD² is the number of ACC terms, ACC is the AC and CC terms according to Eqs. (1) and (2), coeff_ACC is the PLS regression coefficient for the ACC variable, and σ_d is the standard deviation for the z-scale variable in the whole dataset. Thus, the formula estimates the partial derivatives of the ACC functions with respect to the d_a variable. The derivative for Y at d_a is then obtained by the summation of the ACC derivatives multiplied by the PLS regression coefficient. As the ranges of z-scale variables are different, normalization is achieved by multiplying with the standard deviation of respective z-scale. Please observe that as Eqs. (1) and (2) are linear, the derivatives of ACCs are constant. Accordingly, ∂Y/∂d_a is also a constant, which is independent of the value of ∂d_a or any other variable characterizing the same position. In numerical terms, ∂Y/∂d_a corresponds to the change of Y by changing ∂Y/∂d_a by one standard deviation. In the present study, we assessed each sequence position by calculating the sum of the absolute values of ∂Y/∂d_a for all five z-scales, herein termed ΔY_a.

Abbreviations

• ACC, autocross-covariance

• DmodX, distance to model

• GRHR, gonadotropin-releasing hormone receptors

• GPCR, G-protein coupled receptor

• GPCRDB, G-protein coupled receptors database

• PC, principal component

• PCA, principal component analysis

• PLS, partial least squares projection to latent structures

• QSAR, quantitative structure activity relationship

• TRH, thyrotropin release hormone