Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2002 Apr;11(4):957–964. doi: 10.1110/ps.4000102

Dynamical characterization of residual and non-native structures in a partially folded protein by 15N NMR relaxation using a model based on a distribution of correlation times

Françoise Ochsenbein 1,3, Jean-Michel Neumann 2, Eric Guittet 1, Carine Van Heijenoort 1
PMCID: PMC2373535  PMID: 11910038

Abstract

A spectral density model based on a truncated lorentzian distribution of correlation times is used to analyze the nanosecond time-scale dynamics of the partially unfolded domain 2 of annexin I from its 15N NMR relaxation parameters measured at three magnetic field strengths. The use of a distribution of correlation times enables the characterization of the dynamical features of the NH bonds of the protein in terms of heterogeneity of dynamical states in the nanosecond range. The variation along the sequence of the two dynamical parameters introduced, namely the center and the width of the distribution, points out the different types of residual secondary structures present in the D2 domain. Moreover, it allows a physically sensible interpretation of the dynamical behavior of the different residual helices and of the non-native structures. Also, a striking correspondence is found between the parameters obtained using an extended Lipari and Szabo model and the parameters obtained using the distribution of correlation times. This result led us to propose a specific interpretation of the model-free order parameter for internal motions in the nanosecond range in the case of unfolded states.

Keywords: Distribution of correlation times, dynamics, models, proteins, 15N relaxation, unfolded states

In addition to their long-known importance in folding processes, unstructured proteins increasingly appear to play important roles in biological processes (for review, see Dyson and Wright 2001). This reinforces the interest for a detailed characterization of unfolded or partially folded states of proteins. In contrast to fully folded proteins that can generally be described as a well-defined structure with limited fluctuations, unfolded or partially folded proteins are highly dynamical and consist of a wide range of interconverting conformers. This is nicely illustrated by a recent study of an unfolded state comprising residual helices (Korzhnev et al. 1999a, 1999b; Orekhov et al. 1999). The resolution of kinetic equations relative to a helical peptide led to a nearly continuous distribution of transition times from 0.1 to 10 ns. These frequencies are associated with interconversion between various helical states, such as the elongation or shortening of the helix segment by several residues or interconversion between α, π, and 3/10 helical conformations. Within this continuum of frequencies it seems difficult to distinguish separated frequency ranges as in the case of folded proteins. Conversely, the inherent high flexibility of unfolded states makes the knowledge of their dynamical behavior a crucial point for their characterization. NMR spectroscopy remains the most efficient technique to obtain detailed information on the residual structure and on the dynamics of unfolded states (Alexandrescu and Shortle 1994; Frank et al. 1995; Buck et al. 1996; Brutscher et al. 1997; Farrow et al. 1997; Schwalbe et al. 1997; Dyson and Wright 1998; Eliezer et al. 1998, 2000; Meekhof and Freund 1999; Ochsenbein et al. 2001). However, it appears from these studies that, in the case of unfolded proteins, it is difficult to specify and/or interpret the parameters derived from the commonly used model-free approach. The extraction of motion parameters from models based on discrete correlation times, such as the model-free approaches, presents two major difficulties. The first major problem lies in the consideration of a global correlation time, representing the slowest time leading to the complete loss of correlation of motions, which is common to every residue of the protein. This idea of a unique overall correlation time for the whole molecule is questionable in the case of unfolded states. An attempt to alleviate this problem is to use a so-called "local model-free" approach, which consists in fitting one "global" correlation time per residue (Alexandrescu and Shortle 1994). The resulting correlation times are then associated with the reorientation of segments of the protein that have independent dynamical behaviors. Although this approach led to some acceptable results, especially in the case of proteins containing fully folded segments and unfolded tails (Brutscher et al. 1997; van Heijenoort et al. 1998), the independence of the dynamical behavior of each segment and thus the interpretation of the motional parameters obtained remain questionable. The second major problem of the model-free approach is the analysis of internal motions, because they are considered as a whole, without a priori about the type of motions they represent. It is usually accepted for folded proteins that an increase of the order parameter corresponds to a decrease of the amplitude of motions around a given conformation (wobbling in a cone) or between two or more given conformations (jump model) (Lipari and Szabo 1982). However, this physical interpretation may be inappropriate when considering an unfolded protein with no defined structure. Moreover, if motions over a continuous range of frequencies are taking place, the question of the physical meaning of an effective internal correlation time remains open.

A simple way to deal with the notion of motions over a continuum of frequency in the nanosecond range is to introduce a continuous distribution of correlation times in the autocorrelation function. A number of such empirical functions were already proposed in the context of synthetic polymers that share many common features with unfolded states of proteins (for review, see Heatley 1979, 1986). One of these functions, the Cole–Cole distribution was recently applied by Buevich et al. on the unfolded pro-peptide of subtilisin PPS (Buevich and Baum 1999; Buevich et al. 2001). A major limitation of these functions is that they were designed to fit only experimental longitudinal 13C relaxation rate constants and heteronuclear nOes, which are related to spectral densities in the megahertz range. They were not optimized to fit transverse relaxation rate constants, which are related to the spectral density in the kiloHertz range, and which are not relevant to the studies of fast internal dynamics of very large polymers. The derived spectral density function then usually diverges when ω tends toward zero. The direct use of such distribution functions is problematic in the case of small proteins for which transverse relaxation rate constants contain a high contribution of nanosecond time-scale motions and are sensitive to fast internal motions. We propose here the use of a lorentzian distribution of correlation times, characterized by its center τ0 and its width Δ, and extending from zero to an upper value τmax. The physical meaning of τmax, which is introduced to ensure convergence, is discussed.

We applied this approach to the analysis of the 15N relaxation data obtained at three magnetic fields, 500, 600, and 800 MHz, on the partially folded D2 domain of annexin I. This domain is unable to adopt a tertiary fold alone in solution. Conversely, it is fully folded in the entire annexin I, in which it exhibits five helix segments, named A to E, organized in the superhelix motif characteristic of annexin domains (Huber et al. 1992). A structural analysis of this domain was previously performed that showed that the residual structure of the isolated domain 2 of annexin I comprises both native and non-native secondary structure elements (Cordier-Ochsenbein et al. 1996, 1998). The native elements consist of four helix segments corresponding to the B and E native helices as well as a large proportion of the A helix and a small helix population corresponding to the second part of the C helix. On both sides of the residual C helix, the conformation of the polypeptide chain consists in a set of interconverting turn-like structures that prevents the formation of the remaining elements of the native C helix. Finally, the N and C-terminal region and the segment spanning the native D helix remain random coil. These residual structures are illustrated in Figure 1 ▶.

Fig. 1.

Fig. 1.

Open in a new tab

(A) Ribbon representation of the structure of domain 2 of annexin I extracted from the crystal structure of the entire protein (Weng et al. 1993) (top view). (B) Schematic representation of the structural features of isolated domain 2 of annexin I in solution from NMR data (side view). Residual helices are represented as ribbons, regions showing non-native structures are represented in black, unfolded regions are shown in light gray. These figures were drawn using the Molscript program (Kraulis 1991).

We address the question of the dynamical behavior of these different types of residual structures. It should be noted that their coexistence in the same protein makes the isolated domain D2 of annexin I an attractive model for the investigation of the dynamics of partially folded states. A "model-free" analysis of the relaxation data previously performed on this protein led to ambiguous results with a local and extended Lipari and Szabo model being both statistically satisfactory. This emphasized the difficulty to interpret the discrete correlation times and the order parameters obtained from the model-free approach (Ochsenbein et al. 2001). We show here that the use of the lorentzian distribution of correlation times leads to a relevant representation of the dynamical features of the D2 domain. It allows us to discriminate the various types of residual structures of the isolated D2 domain. Values of the center of the distribution of correlation times enable to distinguish the intrinsically stable helices A, B, and C from helix E. In addition, high values of the width of the distribution highlight the heterogeneous dynamical behavior of the interconverting turn-like structures. These results also lead to favor one of the two model-free approaches that fit experimental relaxation data, and bring a physical interpretation, relevant for unfolded states, of the generalized order parameter in term of state heterogeneity.

Results and Discussion

Calculation of the spectral density function for a lorentzian distribution of correlation times

The general expression of the spectral density function derived from the use of a distribution of correlation times is given in the Materials and Methods section (equations 1a–c). When considering a distribution of correlation times, the spectral density is a continuous function of both the frequency ω and the correlation time τ, J(ω,τ) (equation 1c). The general expression of the spectral density function J(ω) is then obtained from the integration along the correlation time dimension of J(ω,τ) weighted by the function of distribution of correlation times (equation 1a) (Heatley 1979). In the special case of symmetrical functions of distribution, such as the lorentzian used here (equation 1b), the resulting spectral density J(ω) becomes a function of two time parameters: the center of the distribution τ0, and the width of the distribution Δ.

One difficulty inherent to the use of continuous distributions of correlation times F(τ) arises from the fact that they extend toward infinity. The integration of F(τ)J(ω,τ) up to infinity then generates large values of the spectral density at low frequency, due to a contribution of the long correlation times that becomes significant. Especially, the integral diverges towards infinity for J(ω=0). These slow motions do not contribute to the NMR experimental relaxation data that contain only the contribution of motions in the ps–ns range, and eventually a contribution due to conformational exchange in the μs–ms range. This last one can be evaluated from the field dependence of J(0) (Phan et al. 1996), cross-correlation rates measurements (Kroenke et al. 1998) or from off-resonance experiments (Mulder et al. 1998; Desvaux and Berthault 1999) and subtracted from the experimental transverse relaxation times. To avoid the divergent behavior of the spectral density function, it is necessary to truncate the distribution function. We thus introduced the parameter τmax, which determines the upper limit of the distribution of correlation times (equation 2b). This parameter corresponds to the slower correlation time leading to the complete loss of correlation of motions. It should be noted that this slower correlation time is not well determined for unfolded states of proteins. It is likely to be much higher than the overall correlation time of a folded protein of the same molecular weight. In the fitting procedure of experimental data, several values of τmax going from 20 to 500 ns were tested. Small values of τmax led to erroneous values of τ0 for some residues (nearly zero with very high uncertainties), whereas too high values of τmax increased the value of χ2exp. Also, changes in the value of τmax did not perturb the relative evolution of the parameters along the sequence of the protein. We thus considered that a value of 100 ns was a reasonable upper limit of the distribution of correlation times. This value would correspond to a maximal gyration radius of 5.2 nm for the protein at 308 K (using a classical Stoke-Einstein relation

graphic file with name M1.gif

T being the temperature in Kelvin, η the viscosity, and k the Boltzman constant), about 2.5 times more than the gyration radius of a folded protein of this size. This maximum gyration radius is comparable to the largest dimension measured for the molten globules of apomyoglobin and alpha-lactalbumin by X-ray scattering scaled by the molecular weight ratio (Kataoka et al. 1995, 1997).

It should be noted that another distribution of correlation times, the Cole–Cole distribution, developed in the context of the analysis of longitudinal 13C relaxation times of polymers, was recently applied to the unfolded protein PSS (Buevich and Baum 1999; Buevich et al. 2001). The same problem of divergence occurs when using this distribution. In this case, the problem lies in the choice of the lower limit of the spectral density function, because RN(Nx,y) values back-calculated during the fitting procedure cannot be obtained from J(0), which is infinite. Ignored in the first report by the authors (Buevich and Baum 1999), this problem was discussed in some details in the second report (Buevich et al. 2001) in which the authors replaced J(0) by the value of the spectral density computed at a frequency equal to one rad•s−1.

Determination of the dynamical parameters

The experimental data, consisting of the nine relaxation parameters, RN(Nz), RN(Nx,y) and heteronuclear (1H-15N) nOes obtained on the partially folded domain 2 of annexin I at three magnetic fields (500, 600, and 800 MHz), were measured as previously described (Ochsenbein et al. 2001). The contribution of slow conformational exchange processes in the μs–ms range was evaluated using the method described by Phan et al. (1996), and was removed from the experimental transversal relaxation rate constants (Ochsenbein et al. 2001).

The simple model considering only a lorentzian distribution of correlation times (equation 3)was not able to reproduce correctly experimental data, that is, the sum of the squared residual errors for the relaxation parameters of each N—H, χ2exp, was more than the critical value χ295% obtained from the Monte Carlo simulations. It was then extended to take into account the possible presence of fast motions in the picosecond time scale (equation 4). A third parameter ALD is thus introduced, which is related to the generalized order parameters S2 or S2f of the model-free approach (Lipari and Szabo 1982; Clore et al. 1990). The need to consider libration motions had been previously reported in dynamical studies of polymers (Dejean de la Batie et al. 1988). The fit of the experimental data against this extended model using JLD2(ω) (equation 4) fulfilled the criteria of goodness of fit for all residues, meaning that the sum of the squared residual errors for the relaxation parameters of each N—H, χ2exp, was lower than the critical value χ295% obtained from the Monte Carlo simulations. The resulting motional parameters are shown in Figure 2 ▶ (left panel).

Fig. 2.

Fig. 2.

Open in a new tab

Dynamical parameters derived from 15N relaxation measurements obtained on the D2 domain at pH 6 and 35°C as a function of the domain sequence. Left panel: lorentzian distribution model (equations 1–2), middle panel: extended model-free approach, right panel: local model-free approach. White boxes on top of the figure delineate the residual helices; gray boxes delineate the non-native turn-like structures. The value of the upper limit of the lorentzian distribution (τmax) is equal to 100 ns•rd−1. Bars represent the standard deviation of simulated parameters. (A) ALD is analogous to the order parameters S2f and S2 associated with fast internal motions in the extended Lipari and Szabo model and in the local model-free approach, respectively. (B) τ0 corresponds to the center of the lorentzian distribution, τs corresponds to the effective internal correlation time for slow internal motions, τclocal is the slowest correlation time adjusted for each residue. (C) Δ corresponds to the width of the lorentzian distribution, S2s corresponds to the generalized order parameter for internal slow motions, τi corresponds to the effective internal correlation time in the local model-free approach. (D) Quality criteria of the fit: the error function χ2exp (filled squares) results from the nonlinear fit of experimental data (see Materials and Methods). The fit was considered as satisfactory if χ2exp is ranged within the 95% confidence limit χ295% (continuous lines) obtained from 500 Monte Carlo simulations, that is, χ2exp < χ295%.

Analysis of the dynamical parameters obtained on the partially folded D2 domain of annexin I

Values of ALD associated with fast internal motions remain uniformly high along the whole backbone of the protein, with a mean value of 0.73 and a standard deviation of 0.03. This indicates that libration motions in the picosecond time-scale participate to around 25% of the total loss of correlation of motions and do not depend on the degree of local structuration.

The center of the distribution τ0 reflects the time scale of the most probable motions, and corresponds to fluctuations involving low-energy barriers. The width of the distribution Δ is related to the dynamical, and thus probably conformational, heterogeneity. From the observation of the evolution of τ0 and Δ along the sequence, three types of behavior can be distinguished (Fig. 2 ▶, Table 1). The first type of behavior is characterized by the highest values of τ0 (1.4 ± 0.2 ns•rd−1) and intermediate values of Δ. The residues following this first dynamical behavior are located in the residual A, B, and C helices. These values of τ0 remain much shorter than those expected for the global reorientation of a domain of the size of the D2 domain. They are more compatible with the independent reorientation of segments of the size of a helix. This suggests that these helices are persistent and behave as independent units. The second type of behavior is characterized by the lowest values of both τ0 and Δ. It involves residues in the unfolded regions and in the residual E helix. Homogeneous (low Δ) and faster (smaller τ0) motions are indeed expected for residues in unstructured regions where local interactions are likely to be limited. The "unfolded type" dynamical behavior of the residues of E helix is more surprising. It indicates that the energy barriers are lower in this helix than in the residual A, B, and C helices. A number of experiments, including structural studies of fragments of the D2 domain, showed that helices A, B, and C have a significant intrinsic helix propensity, contrary to D and E helices (Cordier-Ochsenbein et al. 1998). In particular, according to chemical shift indexes, D and E helices are not formed in isolated short fragments. Because it was also shown that the segment corresponding to the E helix retains a large helical population in the isolated domain 2, it was proposed that this residual E helix is mainly stabilized by transient nonlocal hydrophobic interactions. Our results indicate that the inherent instability of the residual E helix is associated with rapid folding/unfolding rates, leading to correlation times close to those of an unfolded region. The last two regions, located at the extremities of the residual C helix, display a third dynamical behavior. In these two segments, values of τ0 are comparable to those found in unfolded regions and in helix E, but values of the width of the distribution are the highest in the whole sequence (0.7 ± 0.2 ns•rd−1 compared to 0.4 ± 0.2 ns•rd−1). These two regions were shown to adopt non-native structures consisting of interconverting turn-like structures stabilized by local specific interactions such as salt bridges and capping interactions (Cordier-Ochsenbein et al. 1996, 1998). The high values of Δ highlight a higher dynamical heterogeneity in these regions compared to the regions containing residual secondary structures, indicating a wider range of energy barriers for the interconversion between the various non-native turn-like structures. In these regions, the high dynamical heterogeneity appears to be associated with a large structural heterogeneity. In their study, Buevich et al. pointed out a relationship between the widths of the distribution in the nanosecond time scale and the presence of electrostatic interactions (Buevich et al. 2001). Especially, an analysis of the dependence of the width of the distribution on pH led them to propose that formation of ion pairs or hydrogen bonds upon a change of the ionic state of the protein yielded more correlated motions. This results in a larger distribution of states, and consequently, in larger widths of distribution of correlation times. The increase of Δ in the region of non-native structures around helix C in the D2 domain is in full agreement with this hypothesis. However, the authors propose to extend this hypothesis to all kind of inter-residue interactions (electrostatic, dipolar, and hydrophobic), and suggest a correlation between the width of the distribution and an adapted Kyte-Doolitle hydropathy. It should be noted that the correlation found in the case of PPS is rather low (0.43). In our case, no significant correlation is found between the width of the distribution and the absolute values of the Kyte-Doolitle hydropathy (the correlation across the whole sequence is found equal to 0.29; data not shown). Moreover, in the case of the D2 domain, N—H bonds of residues located in stable residual secondary structures, which contain hydrogen bonds and are likely to undergo correlated motions, do not present a significant increase of the width of the distribution, but rather exhibit higher values of the center of the distribution. Our interpretation of the distribution parameters in terms of the presence and nature of residual secondary structures seems more adapted to the case of partially folded proteins.

Table 1.

Mean values of parameters for the various regions of the D2 domain of annexin I, obtained from the model using a lorentzian distribution of correlation times for each residue

A, B and C residual helices Non-native structures Residual E helix Unfolded residues
〈τ0 〉 (ns•rd−1) 1.4 ± 0.2 1.0 ± 0.2 0.9 ± 0.2 0.8 ± 0.3
〈Δ〉 (ns•rd−1) 0.5 ± 0.2 0.7 ± 0.2 0.4 ± 0.2 0.4 ± 0.2
〈ALD〉 0.75 ± 0.03 0.75 ± 0.03 0.76 ± 0.03 0.75 ± 0.04
Open in a new tab

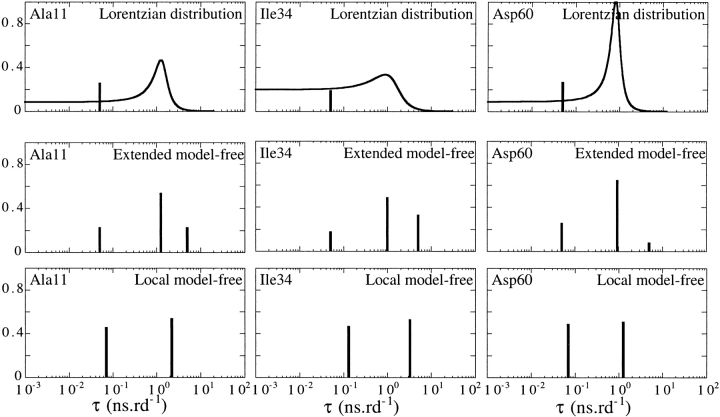
At that point, it is important to compare these results with the more conventional model-free analysis. Figure 2 ▶ shows the motion parameters resulting from a model-free analysis of the D2 domain relaxation data. Two models containing three parameters were able to correctly reproduce the experimental data (Ochsenbein et al. 2001). The first model was an extended Lipari and Szabo model (Clore et al. 1990) with an optimized overall tumbling correlation time equal to 5 ns•rd−1 (Fig. 2 ▶, central panel). The second model was a simple Lipari and Szabo model (Lipari and Szabo 1982) in which the correlation time in the nanosecond range was adjusted on a per-residue basis (Fig. 2 ▶, right panel). Although both models were statistically equally relevant, they led to different motional parameters, emphasizing the difficulty to interpret the discrete correlation times and the order parameters obtained from the model-free approaches. Figure 3 ▶ shows a comparison of the results obtained using the three approaches for three residues: Ala 11, Ile34, and Asp60. Ala 11 is located in the residual A helix and is representative of the residues located in the intrinsically stable helices. Ile 34 is located in one of the segments containing non-native structures. Asp 60 is located at the beginning of the residual E helix and is representative of residues of low helical propensity and of residues in unfolded segments. The figure highlights the localization of the discrete correlation times obtained from the two model-free approaches with respect to the lorentzian distribution of correlation times. The correlation times obtained from a simple model-free approach, consisting of one local correlation time τc per residue and an internal fast correlation time τi, appear to be located on each side of the optimized distribution of correlation times. On the contrary, the slow internal correlation time τs obtained from the extended Lipari and Szabo approach closely matches the center of the distribution of correlation times τ0. The extended Lipari and Szabo approach also contains an overall correlation time, whose optimal value was equal to 5 ns•rd−1 for the D2 domain. The interpretation of such an overall correlation time is difficult in the context of unfolded protein. It is located on the right side of the distribution, and appears necessary to compensate for the contribution of the slowest motions in the nanosecond time scale that are not taken into account by τs and S2s. The generalized order parameter S2f associated with fast internal correlation times is similar to the parameter ALD. In addition to the analogy between τs and τ0, the evolution along the sequence of the D2 domain of the order parameter, S2s matches the evolution of the width Δ of the distribution. Unexpectedly, the correlated evolution of S2s and Δ along the sequence suggests that the order parameter S2s accounts here for the dynamical heterogeneity of motions, rather than for amplitude of motions. This is highlighted by the higher values of S2s (correlated to higher values of Δ) found in the regions containing non-native structures around helix. In this case, this heterogeneity of motions seems related to a heterogeneity of distinct conformational states. Whether this observation can be generalized remains to be evaluated.

Fig. 3.

Fig. 3.

Open in a new tab

Comparison of the distributions of correlation times obtained for three residues of domain 2 of annexin I, Ala11, Ile34, and Asp60 using the three approaches described in the text: lorentzian distribution of correlation times (upper panel), extended model free (middle panel), and local model free (lower panel). A continuous line is used for the lorentzian distribution. Discrete values of correlation times are represented by vertical bars with a height corresponding to their associated order parameter.

Taking into account the inherent flexibility of partially folded states, formalisms based on distributions of correlation times allow a suitable interpretation of relaxation data. The present analysis based on a lorentzian distribution of correlation times yields a clear picture of the dynamical behavior of the partially folded domain 2 of annexin I. It allows us to distinguish between the various types of residual structures found in this domain. It brings a more appropriate description of motions in unfolded states than the model-free approach considering discrete correlation times. Besides, it allows a reinterpretation of the parameters obtained from the extended model-free approach. It highlights the need to take into account the heterogeneity of conformational states in the nanosecond time scale for the interpretation of relaxation data obtained on partially folded states.

Materials and methods

Derivation of the spectral density function corresponding to a lorentzian distribution of correlation times

The general expression for the spectral density function in case of a distribution F(τ) of correlation time is:

graphic file with name M2.gif (1a)
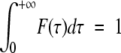graphic file with name M3.gif (1b)
graphic file with name M4.gif (1c)

We used here a lorentzian distribution characterized by:

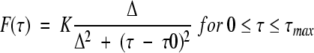graphic file with name M5.gif (2a)
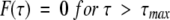graphic file with name M6.gif (2b)

K is a normalization constant such as to satisfy equation 1b, leading to:

graphic file with name M7.gif (2c)

The use of an upper limit τmax is imposed by the divergent behavior of the integral J(0) when τ tends towards infinity. Equation (1a)then becomes:

graphic file with name M8.gif
graphic file with name M9.gif (3)

A contribution of very fast internal motions in the picosecond range was also considered, which was assumed to be independent of the motions in the nanosecond range. The final expression of the spectral density function JLD2(ω) is then:

graphic file with name M10.gif (4)

The second term in the right part of the equation was considered negligible, so that the contribution of fast libration motions was taken into account through the factor ALD. This factor ALD is analogous to the generalized order parameters S2 or S2f used in the model-free approach.

Goodness of fits and uncertainties evaluation

J(ω) in equations 3–4is a function of one to five unknown variables that can thus theoretically be evaluated from the nine independently measured relaxation parameters at the three fields. The additional exchange broadening contribution to transverse relaxation parameters RN(Nx,y) was removed from the experimental values. No exchange contribution has thus to be taken into account in the further described fits.

Motion parameters were optimized for each residue for which the data could be collected from nonlinear least-squares minimization of the error function χ2exp using the Levenburg-Marquardt algorithm (Press et al. 1986) implemented in the MATLAB software.

graphic file with name M11.gif

where δ(X) (X being RN[Nx,y], RN[Nz], or NOE) is the estimated error of the relaxation parameters. The subscripts exp and calc refer to experimental and back-calculated relaxation parameters, respectively. Initial values for parameters were obtained from a grid search minimization. The goodness of the fits and the uncertainties were obtained from statistical analysis (Palmer et al. 1991; Mandel et al. 1995). Five hundred simulated data sets were selected from a Gaussian noise distribution centered on the relaxation rates back calculated from the optimized parameters and corresponding to the previously estimated errors in RN(Nx,y), RN(Nz), and NOEs. A model was considered satisfactory if the optimized χ2exp was within the 95% confidence limit obtained from the 500 Monte Carlo simulations, that is, χ2exp < χ295%. The uncertainties in the values of the model-free parameters are the standard deviation of the simulated parameters.

Acknowledgments

This work was supported by the Centre National de la Recherche Scientifique (CNRS). We thank F. Lauprêtre for enlightening discussions. The 800 MHz spectrometer was purchased with the financial help of the Conseil Régional d'Ile de France and of the Association pour la Recherche contre le Cancer.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.4000102.

References

  1. Alexandrescu, A.T. and Shortle, D. 1994. Backbone dynamics of a highly disordered 131 residue fragment of staphylococcal nuclease. J. Mol. Biol. 242 527–546. [DOI] [PubMed] [Google Scholar]
  2. Brutscher, B., Bruschweiler, R., and Ernst, R.R. 1997. Backbone dynamics and structural characterization of the partially folded A state of ubiquitin by 1H, 13C, and 15N nuclear magnetic resonance spectroscopy. Biochemistry 36 13043–13053. [DOI] [PubMed] [Google Scholar]
  3. Buck, M., Schwalbe, H., and Dobson, C.M. 1996. Main-chain dynamics of a partially folded protein: 15N NMR relaxation measurements of hen egg white lysozyme denatured in trifluoroethanol. J. Mol. Biol. 257 669–683. [DOI] [PubMed] [Google Scholar]
  4. Buevich, A.V. and Baum, J. 1999. Dynamics of unfolded proteins: Incorporation of distributions of correlation times in the model free analysis of NMR relaxation data. J. Am. Chem. Soc. 121 8671–8672. [Google Scholar]
  5. Buevich, A.V., Shinde, U.P., Inouye, M., and Baum, J. 2001. Backbone dynamics of the natively unfolded pro-peptide of subtilisin by heteronuclear NMR relaxation studies. J. Biomol. NMR 20 233–249. [DOI] [PubMed] [Google Scholar]
  6. Clore, G.M., Szao, A., Bax, A., Kay, L.E., Driscoll, P.C., and Gronenborn, A.M. 1990. Deviation from the simple two-parameters model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J. Am. Chem. Soc. 112 4989–4991. [Google Scholar]
  7. Cordier-Ochsenbein, F., Guerois, R., Baleux, F., Huynh-Dinh, T., Chaffotte, A., Neumann, J.M., and Sanson, A. 1996. Folding properties of an annexin I domain: A 1H-15N NMR and CD study. Biochemistry 35 10347–10357. [DOI] [PubMed] [Google Scholar]
  8. Cordier-Ochsenbein, F., Guerois, R., Baleux, F., Huynh-Dinh, T., Lirsac, P.N., Russo-Marie, F., Neumann, J.M., and Sanson, A. 1998. Exploring the folding pathways of annexin I, a multidomain protein. I. Non-native structures stabilize the partially folded state of the isolated domain 2 of annexin I. J. Mol. Biol. 279 1163–1175. [DOI] [PubMed] [Google Scholar]
  9. Dejean de la Batie, R., Lauprêtre, F., and Monnerie, L. 1988. Carbon-13 NMR investigation of local dynamics in bulk polymers at temperatures well above the glass transition temperature. 1. Poly(vinyl methyl ether). Macromolecules 21 2045–2052. [Google Scholar]
  10. Desvaux, H. and Berthault, P. 1999. Study of dynamic processes in liquids using off-resonance rf irradiation processes. Prog. NMR Spectrosc. 35 295–340. [Google Scholar]
  11. Dyson, H.J. and Wright, P.E. 1998. Equilibrium NMR studies of unfolded and partially folded proteins. Nat. Struct. Biol. Suppl. 5 499–503. [DOI] [PubMed] [Google Scholar]
  12. ———. 2001. Nuclear magnetic resonance methods for elucidation of structures and dynamics in disordered states. Methods Enzymol. 339 258–270. [DOI] [PubMed] [Google Scholar]
  13. Eliezer, D., Chung, J., Dyson, H.J., and Wright, P.E. 2000. Native and non-native secondary structure and dynamics in the pH 4 intermediate of apomyoglobin. Biochemistry 39 2894–2901. [DOI] [PubMed] [Google Scholar]
  14. Eliezer, D., Yao, J., Dyson, H.J., and Wright, P.E. 1998. Structural and dynamic characterization of partially folded states of apomyoglobin and implications for protein folding. Nat. Struct. Biol. 5 148–155. [DOI] [PubMed] [Google Scholar]
  15. Farrow, N.A., Zhang, O., Forman-Kay, J.D., and Kay, L.E. 1997. Characterization of the backbone dynamics of folded and denatured states of an SH3 domain. Biochemistry 36 2390–2402. [DOI] [PubMed] [Google Scholar]
  16. Frank, M.K., Clore, G.M., and Gronenborn, A.M. 1995. Structural and dynamic characterization of the urea denatured state of the immunoglobulin binding domain of streptococcal protein G by multidimensional heteronuclear NMR spectroscopy. Protein Sci. 4 2605–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Heatley, F. 1979. Nuclear magnetic relaxation of synthetic polymers in dilute solutions. Prog. NMR Spectrosc. 13 47–85. [Google Scholar]
  18. ———. 1986. Nuclear magnetic relaxation and models for backbone motions of macromolecules in solution. Annu. Rep. NMR Spectrosc. 17 179–230. [Google Scholar]
  19. Huber, R., Berendes, R., Burger, A., Schneider, M., Karshikov, A., Luecke, H., Romisch, J., and Paques, E. 1992. Crystal and molecular structure of human annexin V after refinement. Implications for structure, membrane binding and ion channel formation of the annexin family of proteins. J. Mol. Biol. 223 683–704. [DOI] [PubMed] [Google Scholar]
  20. Kataoka, M., Kuwajima, K., Tokunaga, F., and Goto, Y. 1997. Structural characterization of the molten globule of alpha-lactalbumin by solution X-ray scattering. Protein Sci. 6 422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kataoka, M., Nishii, I., Fujisawa, T., Ueki, T., Tokunaga, F., and Goto, Y. 1995. Structural characterization of the molten globule and native states of apomyoglobin by solution X-ray scattering. J. Mol. Biol. 249 215–228. [DOI] [PubMed] [Google Scholar]
  22. Korzhnev, D.M., Orekhov, V.Y., and Arseniev, A.S. 1999a. The effect of helix-coil transition on backbone 15N NMR relaxation of isolated transmembrane segment (1–36)-bacteriorhodopsin. J. Biomol. NMR 14 357–368. [Google Scholar]
  23. Korzhnev, D.M., Orekhov, V.Y., Arseniev, A.S., Gratias, R., and Kessler, H. 1999b. Mechanism of the unfolding of transmembrane a-helical segment (1–36)-bacteriorhodopsin studied by dynamics simulations. J. Phys. Chem. B 103 7036–7043. [Google Scholar]
  24. Kraulis, P.J. 1991. MOLSCRIPT: A program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallogr. 24 946–950. [Google Scholar]
  25. Kroenke, C., Loria, J., Lee, L., Rance, M., and Palmer, A. 1998. Longitudinal and transverse 1H-15N dipolar/15N chemical shift anisotropy relaxation interference: Unambiguous determination of rotational diffusion tensors and chemical exchange effects in biological macromolecules. J. Am. Chem. Soc. 120 7905–7915. [Google Scholar]
  26. Lipari, G. and Szabo, A. 1982. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecule. 1. Theory and range of validity. J. Am. Chem. Soc. 104 4546–4559. [Google Scholar]
  27. Mandel, A.M., Akke, M., and Palmer, A.G.r. 1995. Backbone dynamics of Escherichia coli ribonuclease HI: Correlations with structure and function in an active enzyme. J. Mol. Biol. 246 144–163. [DOI] [PubMed] [Google Scholar]
  28. Meekhof, A.E. and Freund, S.M. 1999. Probing residual structure and backbone dynamics on the milli- to picosecond timescale in a urea-denatured fibronectin type III domain. J. Mol. Biol. 286 579–592. [DOI] [PubMed] [Google Scholar]
  29. Mulder, F.A.A., de Graaf, R.A., Kaptein, R., and Boelens, R. 1998. An off-resonance rotating frame relaxation experiment for the investigation of macromolecular dynamics using adiabatic rotations. J. Magn. Reson. 131 351–357. [DOI] [PubMed] [Google Scholar]
  30. Ochsenbein, F., Guerois, R., Neumann, J.M., Sanson, A., Guittet, E., and van Heijenoort, C. 2001. 15N NMR relaxation as a probe for helical intrinsic propensity: The case of the unfolded D2 domain of annexin I. J. Biomol. NMR 19 3–18. [DOI] [PubMed] [Google Scholar]
  31. Orekhov, V.Y., Korzhnev, D.M., Pervushin, K.V., Hoffmann, E., and Arseniev, A.S. 1999. Sampling of protein dynamics in nanosecond time scale by 15N NMR relaxation and self-diffusion measurements. J. Biomol. Struct. Dyn. 17 157–174. [DOI] [PubMed] [Google Scholar]
  32. Palmer, A.G.I., Rance, M., and Wright, P.E. 1991. Intramolecular motions of a zinc finger DNA-binding domain from Xfin characterized by proton-detected natural abundance 13C heteronuclear NMR spectroscopy. J. Am. Chem. Soc. 113 4371–4380. [Google Scholar]
  33. Phan, I.Q.H., Boyd, J., and Campbell, I.D. 1996. Dynamic studies of a fibronectin type I module pair at three frequencies: Anisotropic modelling and direct determination of conformational exchange. J. Biomol. NMR 8 369–378. [DOI] [PubMed] [Google Scholar]
  34. Press, W.H., Flannery, B.P., Teutolski, S.A., and Vetterling, W.T. 1986. Numerical recipies, the art of scientific computing. Cambridge University Press, Cambridge.
  35. Schwalbe, H., Fiebig, K.M., Buck, M., Jones, J.A., Grimshaw, S.B., Spencer, A., Glaser, S.J., Smith, L.J., and Dobson, C.M. 1997. Structural and dynamical properties of a denatured protein. Heteronuclear 3D NMR experiments and theoretical simulations of lysozyme in 8 M urea. Biochemistry 36 8977–8991. [DOI] [PubMed] [Google Scholar]
  36. van Heijenoort, C., Penin, F., and Guittet, E. 1998. Dynamics of the DNA binding domain of the fructose repressor from the analysis of linear correlations between the 15N-1H bond spectral densities obtained by nuclear magnetic resonance spectroscopy. Biochemistry 37 5060–5073. [DOI] [PubMed] [Google Scholar]
  37. Weng, X., Luecke, H., Song, I.S., Kang, D.S., Kim, S.H., and Huber, R. 1993. Crystal structure of human annexin I at 2.5 Å resolution. Protein Sci: 2 448–458. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES