Effects of molecular crowding by saccharides on α-chymotrypsin dimerization

Abstract

Given the importance of protein complexes as therapeutic targets, it is necessary to understand the physical chemistry of these interactions under the crowded conditions that exist in cells. We have used sedimentation equilibrium to quantify the enhancement of the reversible homodimerization of α-chymotrypsin by high concentrations of the osmolytes glucose, sucrose, and raffinose. In an attempt to rationalize the osmolyte-mediated stabilization of the α-chymotrypsin homodimer, we have used models based on binding interactions (transfer-free energy analysis) and steric interactions (excluded volume theory) to predict the stabilization. Although transfer-free energy analysis predicts reasonably well the relatively small stabilization observed for complex formation between cytochrome c and cytochrome c peroxidase, as well as that between bobtail quail lysozyme and a monoclonal Fab fragment, it underestimates the sugar-mediated stabilization of the α-chymotrypsin dimer. Although predictions based on excluded volume theory overestimate the stabilization, it would seem that a major determinant in the observed stabilization of the α-chymotrypsin homodimer is the thermodynamic nonideality arising from molecular crowding by the three small sugars.

The effects of thermodynamic nonideality as a result of molecular crowding are likely to influence the extent of macromolecular interactions in biological environments, where solutes can reach intracellular concentrations of 350 g L⁻¹ and occupy 40% of the cell volume (Zimmerman and Trach, 1991). In addition to proteins, nucleic acids, and polysaccharides, these solutes include small molecules termed osmolytes (Yancey et al. 1982; Minton 2001). Osmolytes comprise several classes of small, relatively inert, and highly soluble organic molecules. Sugars from the polyol class are the subject of this study of osmolyte-induced effects on reversible protein dimerization.

High osmolyte concentrations can affect both protein structure and equilibrium stability (Davis-Searles et al. 2001). For example, acid-denatured cytochrome c collapses in a variety of sugar solutions to a form that resembles the native state in size (Morar et al. 2001a) as well as structure (Davis-Searles et al. 1998). For proteins that show two-state equilibrium folding, the stabilizing effect of sugars is monitored as an increase in the apparent equilibrium constant for folding, K_f,app (Saunders et al. 2000). Specifically, osmolyte-induced stabilization is quantified by the slope of the dependence of lnK_f,app on osmolyte concentration, C_osmolyte. For protein stability, this metric, δlnK_f,app/δC_osmolyte, can be as large as 8 M⁻¹ (Davis-Searles et al. 2001).

The effects of osmolytes on the equilibrium constant for protein complex formation, K_2,app, differ from their effects on protein folding in two ways. First, protein-stabilizing osmolytes can destabilize protein complexes (Kornblatt et al. 1993; Xavier et al. 1997). Second, the magnitude of δlnK_2,app/δC_osmolyte tends to be smaller than δlnK_f,app/ δC_osmolyte. For instance, δlnK_2,app/δC_osmolyte for the yeast cytochrome c/cytochrome c peroxidase complex is only 0.5 M⁻¹ (Morar et al. 2001b).

In an effort to understand these differences, we have used α-chymotrypsin dimerization under slightly acidic conditions (Rao and Kegeles 1958; Winzor and Scheraga 1964; Aune et al. 1971) as a model to examine the effects of mono-, di-, and tri-saccharides on protein complex formation. Reversible homodimeric systems such as α-chymotrypsin are ideally suited to study by sedimentation equilibrium in the analytical ultracentrifuge (Milthorpe et al. 1975; Johnson et al. 1981; Wills et al. 1996). Furthermore, homodimerization is easier than protein folding to treat theoretically because the monomer and the dimer are structurally defined entities, whereas the unfolded state of a protein is not. Our approach is to compare measured values of δlnK_2,app/δC_osmolyte for α-chymotrypsin with predictions based on various models of stabilization by osmolytes, including those that focus on chemical (soft or binding) interactions between osmolyte and protein and those that deal with the effects of steric (hard) interactions that arise from the impenetrable nature of atoms.

Results

The characterization of α-chymotrypsin dimerization in acetate-chloride buffer (pH 3.9, ionic strength 0.20 M) is based on analysis of sedimentation equilibrium distributions by means of the Psi function (Wills et al. 1996). The total base-molar concentration, 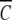(r), of enzyme at radial distance r is related to the molar concentration of monomer, C₁(r_F), at a selected reference radial distance r_F by the expressions

(1a)

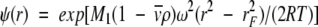(1b)

where K_2,app is the apparent dimerization constant and 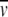, the partial specific volume of α-chymotrypsin, is 0.736 mL g⁻¹ (Schwert and Kaufman 1951). The molecular mass of monomeric α-chymotrypsin, M₁, is 25.2 kD. This value was calculated from the amino acid sequence reported in pdb file 5CHA (Blevins and Tulinsky 1985). ρ is the solvent density of the medium with which the enzyme solution is in dialysis equilibrium, ω is the angular velocity (radians s⁻¹), R is the universal gas constant (J K⁻¹mol⁻¹), and T is the absolute temperature (293 K). 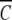(r) was determined from the absorbance at 280 nm, an absorption coefficient (A_{1 cm}^1%) of 20.1 (Egan et al. 1957), and the monomer molecular mass.

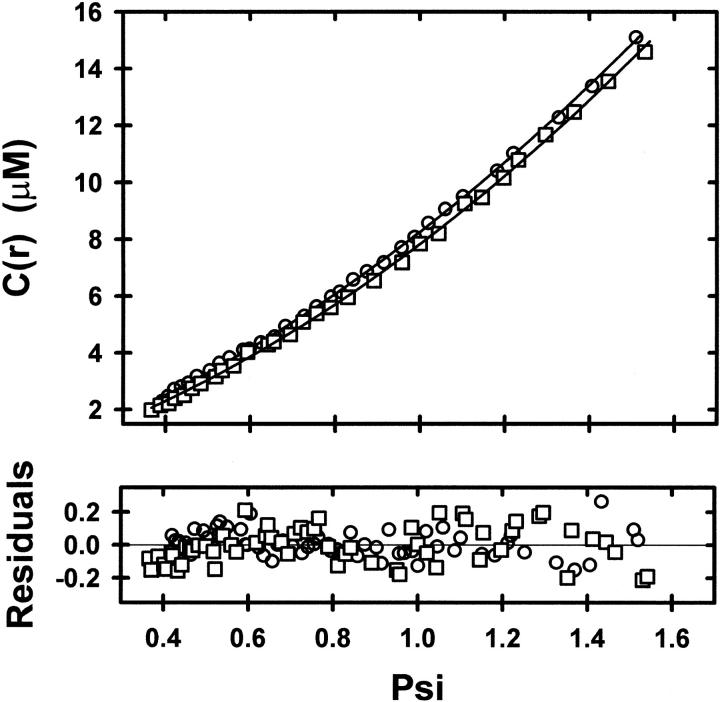
The advantage of direct analysis of sedimentation equilibrium distributions in terms of ψ(r) is that expression of the independent variable (r) in this manner allows ready comparison of results from different experiments by selecting r_F on the basis of a common value for 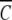(r_F). This feature of the psi analysis is illustrated in Figure 1 ▶, which compares the dependencies of 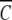(r) on ψ(r) for α-chymotrypsin in acetate-chloride buffer and in the same medium supplemented with 0.2 M raffinose.

Fig. 1.

Psi analysis (equation 1) of sedimentation equilibrium distributions obtained at 20,000 rpm and 293 K for α-chymotrypsin in acetate-chloride buffer, pH 3.9, I 0.20 (○), and in the same buffer supplemented with 0.2 M raffinose (□). The reference radial position, r_F was chosen on the basis of a concentration, 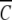(r_F), of 9.9 μM in both distributions. Solid lines denote the best-fit descriptions in terms of equation 1.

Because of the low range of enzyme concentration in these experiments, nonlinear regression analysis of the distribution for the osmolyte-free system (○) in terms of equation 1 to determine K_2,app and C₁(r_F) as curve-fitting parameters effectively yields K₂, the thermodynamic association constant for α-chymotrypsin dimerization. The value of 4.9 (± 0.1) × 10⁴ M⁻¹ for K_2,app obtained from the results shown in Figure 1 ▶ agrees with a previous report of 5.2 (± 0.4) × 10⁴ M⁻¹ under the same conditions (Shearwin and Winzor 1988). On the other hand, the corresponding analysis of the sedimentation equilibrium distribution for α-chymotrypsin in the presence of 0.2 M raffinose (∘) gives a K_2,app of 9.1 (± 0.4) × 10⁴ M⁻¹.

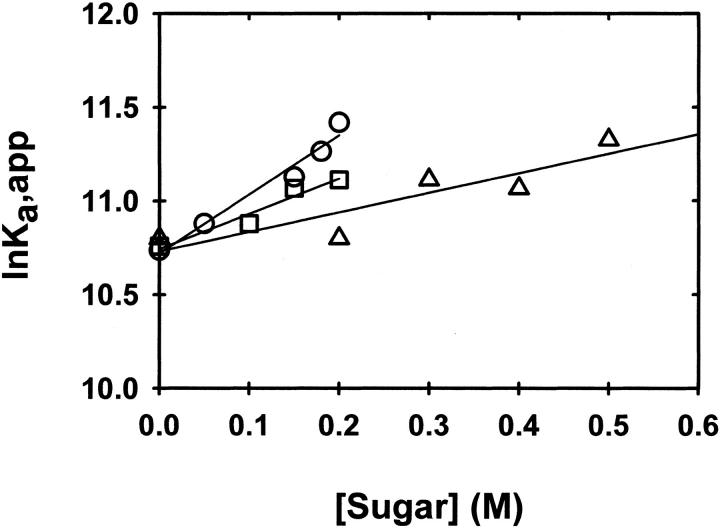
The dependencies of lnK_2,app on the molar concentrations of glucose, sucrose, and raffinose are presented in Figure 2 ▶. The effects of the sugars on α-chymotrypsin dimerization are quantified as the slopes of these linear plots, δlnK_2,app/δC_osmolyte. The slopes and their standard deviations are given in Table 1. The current slope of 1.9 (± 0.3) M⁻¹ for sucrose is smaller than the previously reported value of 8.0 (± 1.3) M⁻¹ (Shearwin and Winzor 1988), which was, however, based on the determination of K_2,app by using omega analysis (Milthorpe et al. 1975). As is evident from Figure 2 ▶ of Shearwin and Winzor (1988), that analysis relies heavily on the accuracy of a curvilinear extrapolation to obtain C₁(r_F)/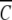(r_F) as the ordinate intercept. Indeed, it was this difficulty that prompted the development of the Psi analysis (Wills et al. 1996).

Fig. 2.

Dependence of the apparent dimerization constant, K_2,app (M⁻¹), upon the concentration of glucose (▵), sucrose (□), and raffinose (○), plotted according to equation 3b.

Table 1.

Observed and predicted effects of sugars on α-chymotrypsin dimerizationa

	δlnK2,app/δCsaccharide (M−1)
Saccharide	Observedb	Transfer-free energy	Excluded volumec
Glucose	1.0 (±0.3)	ndd	4.1
Sucrose	1.9 (±0.3)	0.3	5.9
Raffinose	3.2 (±0.3)	ndd	7.9

^a Conditions: pH 3.9, I 0.20, 293 K.

^b Determined from the slopes of the lines in Figure 2 ▶.

^c Calculated from equations 3b, 4, and 5.

^d nd, not determined because model compound free energies have not been reported.

Discussion

Whereas sugars and related osmolytes such as glycerol and ethylene glycol usually stabilize proteins, they can exert either a stabilizing or a destabilizing effect on protein interactions. For example, the destabilizing effects of glycerol and ethylene glycol on complex formation between bobtail quail lysozyme and a monoclonal antibody are both characterized by a value of −0.3 M⁻¹ for δlnK_2,app/δC_osmolyte (Xavier et al. 1997). Glycerol also destabilizes complex formation between porphyrin cytochrome c and cytochrome b₅ (Kornblatt et al. 1993) but to a lesser extent (δlnK_2,app/δC_osmolyte = −0.07 [± 0.04] M⁻¹). On the other hand, the corresponding value for the cytochrome c/cytochrome c oxidase complex of 0.4 (± 0.1) M⁻¹ signifies glycerol-mediated stabilization (Kornblatt et al. 1993).

We have shown that glucose, sucrose, and raffinose stabilize dimeric α-chymotrypsin to an extent that increases with sugar size (Table 1). Also, the magnitudes of δlnK_2,app/δC_osmolyte (1–3 M⁻¹) are considerably larger than those of 0.3 and 0.5 M⁻¹ reported for the respective stabilizing effects of glucose and sucrose on the interaction between cytochrome c and cytochrome c peroxidase (Morar et al. 2001b).

Our aim is to rationalize the magnitude of δlnK_2,app/ δC_osmolyte for protein complex formation in an attempt to understand the osmolyte-induced stabilization of some interactions but destabilization of others. To that end, we compare our results with the predictions of two analyses: transfer-free energy and excluded volume. Transfer-free energy analysis evaluates the role of chemical interactions between the components, whereas excluded-volume analysis evaluates the consequences of steric interactions between species (Davis-Searles et al. 2001).

Transfer-free energy analysis

Transfer-free energy analysis uses solubility data for model compounds and calculated solvent accessible surface area (SASA) to estimate the difference in the free energies required to transfer the reactants and products from dilute solution to the concentrated osmolyte solution (Liu and Bolen 1995). There are six steps involved in the application of transfer-free energy analysis to protein homodimer formation. (1) The SASA of each atom in the dimer and the monomer is determined. (2) For each state, the SASAs are divided into two groups, backbone and sidechain, and the sidechain atoms are grouped according to amino acid type. (3) The SASAs for monomer are doubled on the grounds that the dimer comprises two monomers. (4) The SASA for each category (the 19 sidechains and the backbone) in the dimer is subtracted from the SASA for each category in the two monomers to give the surface area that is buried on dimerization. (5) These differences are scaled to the standard SASA of each category (Lesser and Rose 1990) to give the apparent number of each category that is buried by dimerization. (6) This number is multiplied by the appropriate model transfer-free energy, after which the transfer-free energies are summed to give the predicted change in dimer stability.

We have performed these calculations, with respect to the effects on sucrose, on three structurally characterized protein complexes: cytochrome c/cytochrome c peroxidase (Morar et al. 2001b; Pelletier and Kraut 1992), bobtail quail lysozyme/monoclonal antibody (Chacko et al. 1996; Xavier et al. 1997), and the α-chymotrypsin dimer (Blevins and Tulinsky 1985). These calculations predict small positive values for δlnK_2,app/δC_sucrose for the three systems: 0.1 M⁻¹ for the lysozyme complex and 0.3 M⁻¹ for the α-chymotrypsin dimer and the cytochrome c complex. Whereas the predicted value for the cytochrome c complex is in reasonable agreement with its experimental counterpart (Morar et al. 2001b), the value calculated for α-chymotrypsin dimerization clearly underestimates the experimental value (Table 1). One source of this discrepancy may be the difference in pH between our experiments and the model studies. We must also consider the fact that the transfer-free energies for highly soluble model compounds come from experiments in which there is more amino acid in solution than there is sucrose (Davis-Searles et al. 2001). Another important factor is discussed below.

It is not strictly correct to compare these calculated transfer-free energies with the observed association constants because the model compound transfer-free energies and the measured differences in protein complex stability contain different information about hard effects. Whereas transfer-free energies contain information about the steric interactions between the amino acid models and the other solution components, the experimental measurement of complex stability includes the contributions of steric interactions between protein species. Although Tang and Bloomfield (2000) question the practicality of estimating a contribution for steric effects, their estimate indicates that the steric part of the transfer-free energy would be about 0.2 kcal mole⁻¹. Even after making this correction, the likely value of δlnK_2,app/δC_sucrose would still only be 0.4 M⁻¹. On the grounds that the stabilization predicted by transfer-free energy analysis underestimates the experimentally measured enhancement for α-chymotrypsin dimerization, we next consider the extent to which the effects can be rationalized on the statistical-mechanical basis of excluded volume.

Consequences of steric effects on protein interactions

In dilute solutions, the assumption is made that all solute molecules have access to the entire volume of the solution, a situation that allows the substitution of concentrations for thermodynamic activities of reactant and product species in the calculation of an equilibrium constant for the interaction. At higher concentrations, however, the inability of two molecules to occupy common space poses a steric constraint on the actual accessible volume. The thermodynamic consequence of this steric effect is encompassed by expressing the thermodynamic activity of a species as the product of its concentration and an activity coefficient, which is greater than unity, because the molar concentration is based on a larger volume than that accessible to the solute.

The advantage of viewing the saccharide-enhanced dimerization of α-chymotrypsin as a consequence of thermodynamic nonideality is that the activity coefficient of species i, γ_i, is amenable to rigorous statistical-mechanical interpretation as

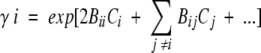(2)

where B_ii and B_ij are the respective second virial coefficients describing steric self-interaction of i and its steric interaction with other species in the solution (McMillan and Mayer 1945; Hill 1959). The use of low enzyme concentrations and high sugar concentrations in the present study means that the activity coefficients of monomer (γ₁) and dimer (γ₂) are dominated by the term containing the saccharide concentration. Furthermore, the absence of charge on sugar cosolutes eliminates any charge–charge contribution to the virial coefficient B_iS (i = 1 or 2), which then equates with the covolume, U_iS. It therefore follows that the apparent dimerization constant obtained in the presence of a high concentration, C_S, of saccharide is related to the thermodynamic equilibrium constant by the relationship

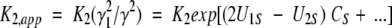(3a)

or, in logarithmic format,

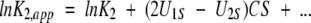(3b)

In this analysis, the stabilization parameter δlnK_2,app/ δC_osmolyte is thus identified with the covolume difference (2U_1S − U_2S). The removal of a molar volume term for saccharide (M_SS) from the original versions of these expressions (Shearwin and Winzor 1988) reflects the subsequent recognition (Wills and Winzor 1992; Wills et al. 1993) that molarity (rather than molality) is the appropriate concentration scale in sedimentation equilibrium.

Assignment of spherical geometry to monomeric enzyme and the saccharide allows the calculation of U_1S as

(4)

where N is Avogadro's number, and where the radius of the monomeric enzyme, r₁, has been taken as 2.44 nm (Shearwin and Winzor 1988; Wills et al. 1996) and r_S as 0.25 nm for glucose, 0.34 nm for sucrose, and 0.43 nm for raffinose. The effective thermodynamic radii for glucose and sucrose emanate from analysis of colligative property data (Winzor and Wills 1995), whereas that for raffinose is an estimate based on bond counting (Edward 1970). Although dimeric α-chymotrypsin was also regarded as a hard, impenetrable sphere in the earlier study (Shearwin and Winzor 1988), it is more appropriate to model the dimer as a prolate ellipsoid of revolution with an axial ratio of 2, in which case (Ogston and Winzor 1975; Nichol et al. 1976)

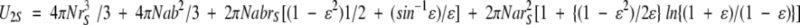(5)

where ɛ² = 1 − (b/a)², b = r₁ = 2.44 nm, and a = 2r₁ = 4.88 nm.

The enhancement of α-chymotrypsin dimerization predicted on the statistical-mechanical basis of excluded volume (Table 1) is certainly larger than that predicted by transfer-free energy analysis but also larger than that observed experimentally. Achievement of better agreement would require a decrease in the estimate of r₁ from its current value of 2.44 nm, which is the Stokes radius deduced from M₁ and the sedimentation coefficient of α-chymotrypsin extrapolated to zero enzyme concentration. Such action would imply penetration by the saccharides of the protein hydration shell.

An obvious problem with predicting the precise extent of excluded volume effects is the absence of information on the exact size and shape of the interacting species, as well as on their surface permeability to osmolyte. That is, the theory only considers interactions between species modeled as hard impenetrable objects (either spheres or ellipsoids). In that regard, the shape assigned to the complex (dimer in the present context) has a large bearing on the magnitude of (2U_1S − U_2S), the slope of the dependence of lnK_2,app on sucrose concentration. For example, consideration of the dimer as a sphere with twice the volume of monomer leads to a magnitude of 8.2 M⁻¹ for the slope parameter (Shearwin and Winzor 1988) in sucrose, whereas its more realistic consideration as a prolate ellipsoid of revolution with an axial ratio of 2 has decreased the value to 5.9 M⁻¹. In other words, the formation of a complex with increased asymmetry is destabilizing from the viewpoint of excluded volume effects. Nevertheless, the effects of molecular crowding on protein self-association will always be in the direction of oligomer stability because of volume conservation. In contrast, the corresponding effects of osmolytes on enzyme isomerization (for which the slope parameter is the difference in covolume for the two isomers) are stabilizing when reaction leads to a decrease in size and/or asymmetry, as observed with ribonuclease (Shearwin and Winzor 1990), and destabilizing when reaction leads to increased size and/or asymmetry (Lonhienne and Winzor 2001).

Uncertainty about the precise sizes and shapes of the interacting species affords considerable latitude for the expression of satisfaction with the extent of agreement between experiment and theoretical prediction on the statistical-mechanical basis of excluded volume—a degree of latitude that would be extended further if osmolyte penetration of the protein hydration shell were to be condoned. In that regard, a decrease in r₁ to 1.95 nm, the radius of unsolvated monomer, (3M₁/[4πN])^1/3, would still not bring about sufficient decreases in the predicted slopes (which then become 2.7, 4.0, and 5.5 M⁻¹) to effect reasonable concordance with their experimental counterparts (Table 1). The observed enhancement of α-chymotrypsin dimerization by osmolytes therefore cannot be rationalized solely on the statistical-mechanical basis of excluded volume.

Because the predicted consequences of thermodynamic nonideality arising from molecular crowding by the three saccharides exceed the experimentally observed extent of dimer stabilization, an unconsidered source of dimer destabilization must be operating. In that regard, the excluded volume treatment of thermodynamic nonideality does entail the assumption/approximation that the space-filling osmolyte is chemically inert. The current disparity between the experimental and predicted extents of enhanced dimerization could, for example, reflect the existence of a preferential chemical interaction between sugar and monomeric α-chymotrypsin, an interaction that would oppose the effects of molecular crowding on the monomer-dimer equilibrium and thus give rise to the seeming destabilization of dimer. Any attempt to establish unequivocally the existence of that putative interaction is rendered difficult by the extremely small binding constant (K < 10 M⁻¹) that is likely to describe an osmolyte-enzyme interaction in a state of flux at the high osmolyte concentrations required to generate the thermodynamic nonideality (Weatherly and Pielak 2001).

This study has drawn attention to the power of the excluded volume treatment for assessing the likely effects of molecular crowding on protein interactions, but it has also illustrated its limitations. The predictions should be regarded as a qualitative rather than an absolute guide because of inherent assumptions about the size and shape of the various species, as well as the chemical inertness of the molecular crowding agent.

Conclusions

Considerations of soft interactions as a potential source of homodimer stabilization do predict enhanced self-association of α-chymotrypsin in the presence of high concentrations of sucrose, but the extent of the predicted stabilization amounts to only 20% of the observed effect. On the other hand, the extent of dimerization enhancement predicted on the statistical-mechanical basis of excluded volume overestimates the experimental values. Nevertheless, the statistical mechanical model predicts reasonably well the change in slope with increasing size of the osmolyte. It therefore seems likely that a significant contribution to the observed enhancement of α-chymotrypsin dimerization emanates from thermodynamic nonideality as the result of molecular crowding by the three saccharides.

Materials and methods

Sample preparation

In accordance with the procedure adopted by Shearwin and Winzor (1988), lyophilized α-chymotrypsin (Worthington Biochemical Corporation) was dissolved in either buffer A (20 mM sodium acetate, pH 3.9, containing 0.18 M NaCl) or buffer A supplemented with varying concentrations of glucose (0 to 0.5 M), sucrose (0 to 0.2 M), or raffinose (0 to 0.2 M). The saccharides were Sigma products. Samples were then subjected to zonal gel chromatography on Sephadex G-50 to remove autolysis fragments and establish dialysis equilibrium with the appropriate buffer. The column (2.4 × 30 cm) was equilibrated with the relevant buffer before use, and the protein eluted at a flow rate of 1 mL per minute. Fractions from the first half of the eluted peak, detected spectrophotometrically at 280 nm, were collected and passed through a 0.2 μm Acrodisc syringe filter (Gelman Laboratory). The concentration was then adjusted with the appropriate buffer to give an absorbance at 280 nm of 0.4 in a 1-cm cuvette.

The activity of α-chymotrypsin decreases at acidic pH, but there will always be some autolysis. Using gel chromatography to pre-equilibrate enzyme with buffer removes small autolysis fragments, but a slightly truncated chymotrypsin molecule would then be included in the chromatographed sample used for sedimentation equilibrium experiments. The self-association behavior of such fragments may differ sufficiently to modify the measured (averaged) dimerization constant for the sample. The discrepancies in K_2,app values between studies may reflect this potential variable. This suggestion has been discussed previously (Voelker and McRorie 1994) and is supported by the reproducibility of K_2,app for a given preparation (Table 1).

Analytical ultracentrifugation

Sedimentation equilibrium experiments were performed on a Beckman XL-A analytical ultracentrifuge at the UNC-CH Macromolecular Interactions Facility. A Ti60 four-hole rotor was used with six-sectored centerpieces, which were filled according to the manufacturer's instructions. The rotor speed was set at 20,000 rpm for 20 h and then increased to 22,000 rpm for an additional 20 h. Absorbance scans at 280 nm were recorded at 2-h intervals throughout each experiment, which was conducted at 293 K. Equilibrium was assumed to have been reached when two consecutive scans gave identical absorption profiles. A meniscus-depletion experiment (45,000 rpm, 6 h) was used to quantify the absorbance baseline offset.

Psi analysis (Wills et al. 1996) was performed with SigmaPlot 2000 (SPSS Inc.). The density of the acetate-chloride buffer was 1.005 g mL⁻¹; those for the sugar-supplemented buffers were calculated as described by Wills et al. (1993) on the basis of partial specific volumes of 0.622 mL g⁻¹ for glucose, 0.616 mL g⁻¹ for sucrose, and 0.608 mL g⁻¹ for raffinose (Lee and Timasheff 1981; Durchschlag 1986).

Solvent-accessible surface areas and transfer-free energy calculation

Solvent-accessible surface areas were calculated by using the program GEPOL (Silla et al. 1991) with the atomic radii given by Lesser and Rose (1990) and a water radius of 0.138 nm. Transfer-free energy calculations were performed with Excel 2000 (Microsoft).