An improved hydrogen bond potential: Impact on medium resolution protein structures

Abstract

A new semi-empirical force field has been developed to describe hydrogen-bonding interactions with a directional component. The hydrogen bond potential supports two alternative target angles, motivated by the observation that carbonyl hydrogen bond acceptor angles have a bimodal distribution. It has been implemented as a module for a macromolecular refinement package to be combined with other force field terms in the stereochemically restrained refinement of macromolecules. The parameters for the hydrogen bond potential were optimized to best fit crystallographic data from a number of protein structures. Refinement of medium-resolution structures with this additional restraint leads to improved structure, reducing both the free R-factor and over-fitting. However, the improvement is seen only when stringent hydrogen bond selection criteria are used. These findings highlight common misconceptions about hydrogen bonding in proteins, and provide explanations for why the explicit hydrogen bonding terms of some popular force field sets are often best switched off.

Force fields are critical to molecular simulation in many aspects of life sciences research. Understanding, analyzing, and predicting three-dimensional structural models of molecular systems—including their conformations, binding affinities, and related properties—all depend on accurate atomic force fields. For this reason, there has been a great deal of effort devoted to the development and improvement of potential energy functions and their parameterization.

The force fields commonly used for determining atom positions within a molecule use a combination of valence (or bonded) and nonbonded energy terms (Weiner and Kollman 1981; Brooks et al. 1983; Karplus 1987; Dinur and Hagler 1991). The overall potential energy of a molecular system may be written as

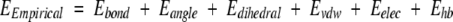where the different energy terms are given by empirical formulae or harmonic functions penalizing deviations from ideal values. These values are determined from small-molecule crystallographic or spectroscopic data or from calibration to quantum mechanics calculations (Lifson and Stern 1982; Brooks et al. 1983; Nemethy et al. 1983; Hermans et al. 1984; Weiner et al. 1984, 1986; Nilsson and Karplus 1986; Dinur and Hagler 1991; Engh and Huber 1991). For macromolecular refinement with data from X-ray crystallography, an additional term is added, E_X-ray, which restrains the model against the diffraction data. The total potential energy is then

where w_a is a weighting factor.

Energy minimizations and dynamics simulations are often limited by inadequate description of the various force field parameters for the systems of interest. For example, if a crystallographically determined structure is energy minimized without structure factor penalty terms (E_X-ray), then deviations from the experimental structure are often much larger (0.5 to 1.5 Å) than the expected error (Roberts et al. 1986), undermining confidence in molecular mechanics analyses. Here we focus on known shortcomings of explicit hydrogen bond force field terms that have led to their common omission from energy minimization (Brooks et al. 1983).

Hydrogen bonds are the key to many phenomena, including the formation and stabilization of secondary structures (Bordo and Argos 1994), protein folding and stability (Dill 1990; Fersht and Serrano 1993), molecular recognition (Fersht 1985), and drug binding and enzymatic reactions that involve transfer of protons (Cleland and Kreevoy 1994; Frey et al. 1994; Hutter and Helms 2000). Therefore, it is important that the geometry of hydrogen bonds be understood as completely as possible and incorporated into accurate potential functions. Appropriate restraining of hydrogen bonding interactions depends greatly on the selection criteria used to identify hydrogen bonds, and on the functional form of the potential describing the interactions.

The resolution of X-ray crystallography data for proteins rarely extends beyond 1.0 Å. For this reason, studies of hydrogen bonds in proteins have been mostly limited to the coordinates of nonhydrogen atoms, that is, donor-acceptor stereochemistry. Thus, the hydrogen bond selection criteria used in some of these studies are based on the distance between the potential donor and acceptor atoms (Ippolito et al. 1990; Mandel-Gutfreund et al. 1995). Other identification procedures use additional criteria for the angle made by donor, acceptor, and acceptor antecedent atoms (Stickle et al. 1992). However, the hydrogen bond geometry can be better understood in terms of the angle and distances involving the positions of hydrogen (Baker and Hubbard 1984), even if the hydrogen positions are modeled only implicitly from their heavy atom neighbors.

Several strategies have been used to account for hydrogen bonding in crystallographic refinement and molecular simulations. The hydrogen bond potential is often implicitly parameterized as a combination of Lennard-Jones (L-J) and electrostatic terms. In force fields that use an explicit hydrogen bonding term, the hydrogen bond potential is typically a distance-dependent function without any directional component. The functional form may be an L-J 6–12 type potential (Hagler et al. 1979; Jorgensen and Rives 1988; Cornell et al. 1995; MacKerell et al. 1998), an L-J 10–12 type (Momany et al. 1975; Brooks et al. 1983; Weiner et al. 1986), an L-J 6–9 type (Hagler et al. 1979; Ewig et al. 1999), or a Morse type potential (Hagler et al. 1974). A cosine directional term has been incorporated into CHARMM (Brooks et al. 1983), Dreiding II (Mayo et al. 1990), and MM3 (Lii and Allinger 1998). In these implementations, the hydrogen bond energy is minimized when the hydrogen bond N-H . . . O is linear, with an angle of 180°. However, these do not reflect the nonlinear directional preferences of hydrogen bonds at the acceptor that are conferred by their covalent component (Baker and Hubbard 1984; Gorbitz 1989; Ippolito et al. 1990; Stickle et al. 1992; Isaacs et al. 1999). Our goal was to develop a direction-dependent hydrogen bond function and appropriate selection criteria that improve crystallographic refinement. The hydrogen bond potential calibrated in this way by the crystallographic protein data would be optimized for protein environments, and could then possibly be used to better describe hydrogen bonds in molecular simulations or the refinement of other proteins.

Macromolecular structures are generally only determinable by combining experimental data with stereochemical restraints. Stereochemistry is especially important at lower resolutions, at which there is less data to define the atomic positions. The relative weighting of experimental data versus stereochemistry is usually determined empirically by cross-validation (Brünger 1997). Cross-validation involves the random selection of a proportion of the data (∼10%) to be omitted from refinement. This data is used to compute a free R-factor (R^free), an unbiased indicator of the quality of the refinement. Brünger (1997) suggested that an appropriate weight could be determined by trial and error, calculating R^free after separate refinements with an array of weights. The value of the weight giving the lowest R^free is thought to provide the best balance of experimental and stereochemical restraints. Here we extend this idea, using R^free to determine the most appropriate of several functional forms for a hydrogen bond restraint and to determine the most appropriate parameters.

Results and Discussion

Improvement of structures using a main-chain hydrogen bond restraint

A drop in R^free after refinement with a 10-protein training set (Table 1) shows the added hydrogen bonding restraint to be beneficial (Table 2). The drop in R^free varies from 0.6% to 1.8%, depending on the protein. This is a small numerical reduction, but large relative to the small increase in the number of stereochemical restraints. For CD2 and β-catenin, 150 and 460 hydrogen bond restraints are added, respectively, compared with the total number of other stereochemical restraints—11,176 and 14,417—for the two structures, respectively. An equivalent number of van der Waals interactions (150 and 460) affect R^free by only 0.07% and 0.03%, compared with 1.6% and 1.4% for the hydrogen bonds.

Table 1.

Protein structures used in the test refinements

PDBa code	Name	Resolution (Å)	Reported Rfree	Reported R	Reference
2CHR	chloromuconate cycloisomerase	3.0	26.4	18.9	Hoier et al. 1994
1A7B	CD2	3.1	30.6	23.9	Murray et al. 1998
2BCT	β-catenin	2.9	28.8	21.1	Huber et al. 1997
1A9B	complex (MHC-I/peptide)	3.2	30.5	25.1	Menssen et al. 1999
1A43	HIV-1 capsid protein	2.6	28.1	22.3	Worthylake et al. 1999
1AVC	bovine annexin VI	2.9	26.8	20.5	Avila-Sakar et al. 1998
6PFK	phosphofructokinase	2.6	25.5	18.8	Schirmer and Evans 1990
1AWU	cyclophilin A	2.34	35.1	31.6	Vajdos et al. 1997
1AS3	GDP-bound G42V mutant G1A1	2.4	27.4	21.2	Raw et al. 1997
1AB4	topoisomerase	2.8	31.0	22.6	Morais Cabral et al. 1997

^a PDB, Protein Data Bank.

Table 2.

Refinement statistics of test protein structures with and without the hydrogen bond restraint

	Refinement without a hydrogen-bond restrainta			Refinement with optimized hydrogen bond restraintsb
PDB code	Rfree (%)	R (%)	Rfree − R (%)	Rfree (%)	R (%)	Rfree − R (%)
2CHR	26.18	17.94	8.24	24.35	19.46	4.89
1A7B	31.64	22.85	8.79	29.06	23.98	5.08
2BCT	28.16	21.13	7.03	26.78	21.58	5.20
1A9B	30.69	25.57	5.12	29.83	25.44	4.39
1A43	27.72	22.07	5.65	26.77	21.93	4.84
1AVC	27.11	19.64	7.47	26.44	19.63	6.81
6PFK	24.02	16.78	7.24	23.54	16.93	6.61
1AWU	35.24	33.58	1.66	34.19	32.62	1.57
1AS3	27.18	21.86	5.32	26.67	21.76	4.91
1AB4	31.16	23.13	8.03	30.65	22.82	7.83

PDB, Protein Data Bank.

^a R-factors are calculated in a consistent manner in this table and differ slightly from those of Table 1, which were calculated in the original structure determinations by the original authors using a variety of scaling procedures and refinement protocols.

^b Hydrogen bond restraint parameters were optimized against each of these training proteins individually.

Another benefit of the hydrogen bonding restraint is that over-fitting is reduced (0.1% to 3.4%), as measured by the difference R^free − R (Kleywegt and Jones 1995; Kleywegt and Brünger 1996) or by the R^free/R ratio (Tickle et al. 1998a,b). As expected, refinement also improves the restrained geometry, both angles and distances, of the hydrogen bonds (Fig. 1 ▶).

Fig. 1.

Main-chain hydrogen bond distances and angles are improved by refinement with the double-well hydrogen bond restraint. A region of chloromucanate cycloisomerase before refinement (a) and after refinement (b) with ɛ = 100. The atoms involved in hydrogen bonding interactions are shown in dark color. N . . . O distances and C = O . . . N angles are indicated.

It is medium-resolution structures that benefit most from the hydrogen bond restraints, because there is insufficient experimental data to determine unique atom positions without adding stereochemical restraints or constraints. High-resolution structures are not improved by the new restraints, but they should not be harmed. Refinement of a high-resolution (1.2 Å) arginine kinase transition state analog complex (M. Yousef, F. Fabiola, J. Gattis, T. Somasundaram, and M. Chapman, in prep.) with the hydrogen bond restraint improves R^free and decreases over-fitting, albeit only marginally (R^free = 17.79 and R = 16.52 with the restraint, compared with R^free = 17.80 and R = 16.45 without). This shows that the hydrogen bonding restraint is not inconsistent with high-resolution crystallographic data. However, it also led us to the counter-intuitive choice of medium-resolution structures over high-resolution structures in the training set, because of the greater sensitivity of their refinements to the correct hydrogen bonding parameters.

Could the beneficial effects of an explicit hydrogen bond restraint be obtained implicitly through an electrostatic term? This was tested using the CNS program, in which introduction of electrostatics also required a change from the default repulsive function to a L-J 6–12 potential. The L-J/electrostatic combination yielded an R^free that was the same as for the repulsive treatment of contacts without a hydrogen bonding restraint. The addition of hydrogen bonding restraints, in both cases, lowered R^free by 0.6% to 1.8%. This shows that implicit electrostatic terms cannot replace explicit hydrogen bonding restraint.

To investigate the impact of the hydrogen bond restraint on poor models, it was included in the initial stages of refinement. With heavy weighting of the hydrogen bond restraint, the quality of refinement was reduced, likely caused by the trapping of the model in a local minimum of the potential energy function. It is recommended that hydrogen bond restraint be used only during the final stages of refinement.

Optimal parameters for the hydrogen bond potential

The parameters for the new restraint include the target donor-acceptor distance (R₀), two target acceptor pseudo-bond angles (θ_low and θ_high), and the strength or weight (ɛ) of a hydrogen bond relative to other stereochemical interactions. They also include cut-off criteria for the selection of hydrogen bonds: θ_cut (the minimal θ) and R_cut (the maximum donor-acceptor distance). All parameters were initially optimized for each of the training proteins independently, and there is some variation (Table 3). There is little variation in the optimal target distance (R₀ = 2.9±0.1 Å). The optimal angles (θ_low and θ_high) lie in a narrow range (5° to 10°) for most of the proteins, with three exceptions. The optimal distance and angle cut values are similar for most proteins, with θ_cut = 90° and R_cut = 3.5 Å in most cases. These values are consistent with earlier protein database (Baker and Hubbard 1984) and quantum mechanical studies (Mitchell and Price 1990). The largest variation is in the optimal weight. The dependence of R^free on ɛ is shown in Figure 2 ▶ for three proteins. Even when a large value is optimal, all nonzero values lead to improvement, and most of the improvement comes with a modest value of ɛ. Higher values might be needed for some proteins if they contain regions of structure that need to be dislodged from an incorrect local energy minimum that does not have good hydrogen bonding configuration.

Table 3.

Optimal hydrogen bond parameters

	Optimal parameters
Protein	ɛ	R0 (Å)	θlow (°)	θhigh (°)	Rcut (Å)	θcut (°)
2CHR	1500	2.9	115	169	3.4	90
1A7B	1600	2.8	115	155	3.5	90
2BCT	100	2.9	112	168	3.4	90
1A9B	300	2.9	115	155	3.5	95
1A43	99	2.9	115	149	3.5	90
1AVC	63	2.9	90	165	3.5	100
6PFK	161	2.9	115	155	3.5	90
1AWU	35	3.0	96	155	3.7	95
1AS3	49	2.9	100	163	3.5	90
1AB4	93	2.9	95	155	3.5	90

Fig. 2.

Free R-factor (R^free) versus weight (ɛ) for the main-chain hydrogen bond restraint. Each refinement was performed with optimized hydrogen bond parameters. Optimal ɛ are indicated by arrows.

It would be desirable to have a single parameter set that can be applied in future refinements without further optimization. The consensus parameter set that was tested was ɛ = 100, θ_low = 115°, θ_high = 155°, R₀ = 2.9 Å, R_cut = 3.5 Å, and θ_cut = 90°. Refinement with this set improved all 10 training structures, although individual optimization of ɛ or all hydrogen bond parameters led to further improvement (Fig. 3 ▶). For future refinements, the consensus angular and distance parameters are likely adequate, but a one-dimensional search for optimal weight might be worthwhile.

Fig. 3.

Results of refinements without the hydrogen bond restraint, or with the restraint and various parameter sets. The consensus parameters were ɛ = 100, θ_low = 115°, θ_high = 155°, R_cut = 3.5 Å, θ_cut = 90°, and R₀ = 2.9 Å.

For our high-resolution test case (arginine kinase), refinement with the consensus parameters slightly reduced R^free (0.01%). In contrast, refinement with a set of nonoptimal parameters (setting, θ_low = 90° and θ_high = 155°) increased R^free by 0.3%. This shows that the optimal parameters obtained based on medium-resolution structures are consistent with those from a high-resolution structure.

Ramachandran plots (Ramakrishnan and Ramachandran 1965) of structures refined with the double-well hydrogen bond restraint show that good φ, ξ stereochemistry is retained. The root mean square difference values are marginally improved with structures refined with the hydrogen-bonding potential.

Hydrogen bond selection criteria

Our selection of hydrogen bonds was based on four criteria: (1) D . . . A distance < R_cut, (2) AA-A . . . D angle > θ_cut, (3) H . . . A distance < 2.7 Å, and (4) D-H . . . A angle > 90°. D indicates donor; A, acceptor; and AA, acceptor antecedent. Many force fields use just the first two criteria for selecting hydrogen bonds (Brooks et al. 1983; Ippolito et al. 1990; Mandel-Gutfreund et al. 1995). This has the advantage that explicit hydrogen positions are not required. The full set of four criteria resembles those of Baker and Hubbard (1984) and requires hydrogen positions to be predicted for those structures at resolutions insufficient to resolve them directly. In refinements reported here, hydrogen positions were predicted automatically by the refinement software.

Figure 4 ▶ shows R^free for refinements using the first two or all four hydrogen bond selection criteria. Refinements with four selection criteria are significantly better than those with two. With large weights, refinements with two criteria are inferior to those with no hydrogen bond restraint at all (ɛ = 0). The two selection criteria are insufficient to eliminate false-positive identifications, and restraining these false interactions distorts the refined structure. This emphasizes the importance of selection criteria that include the H . . . A distance and D-H . . . A angle. Indeed, it is likely that the primary factor in the failure of prior hydrogen bond restraints in some force field sets was insufficiently tight selection criteria.

Fig. 4.

Free R-factor (R^free) versus hydrogen-bond weight for chloromucanate cycloisomerase. Selection of hydrogen bonds is based on two or four criteria. Each refinement was performed with other hydrogen bond parameters fixed at consensus values.

Single- and double-well potentials

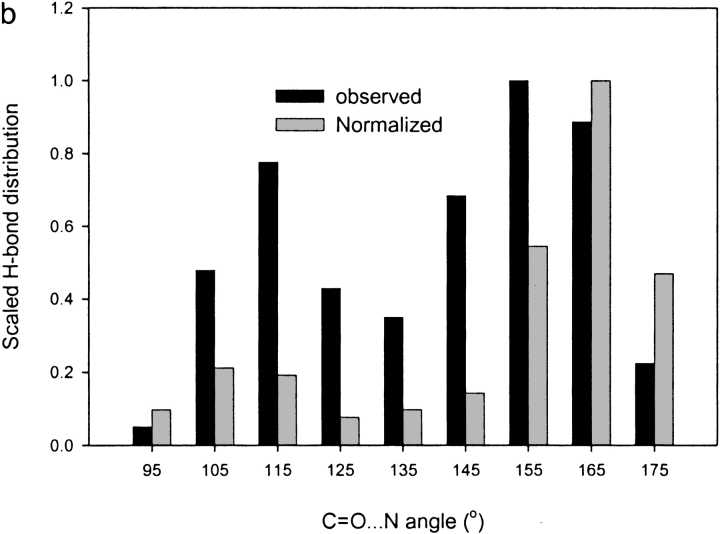
Figure 5 ▶ shows histograms of unrestrained C = O . . . N angles in three structures: β-catenin (2.9 Å), CD2 (3.1 Å) at medium resolution, and arginine kinase at high resolution (1.2 Å). In all cases, the histograms show a bimodal acceptor angle distribution for peptide carbonyl oxygens. It is similar to the distribution seen in analysis of 42 protein structures (Stickle et al. 1992). Stickle et al. (1992) attributed the bimodality directly to different steric constraints for α-helices versus β-sheets. However, our analysis and reexamination of the data presented by Stickle et al. shows that the bimodality extends to carbonyl groups that are neither α nor β. Thus, the bimodality appears to be intrinsic to carbonyl oxygens, owing to both electrostatic and lone-pair covalent contributions to hydrogen bonds. The correlation of the peaks with α and β structure, seen by both Stickle et al. (1992) and ourselves, is a secondary effect in which α and β place different additional steric constraints, choosing differently between two intrinsically allowable carbonyl configurations.

Fig. 5.

Normalized distribution of C=O . . . N acceptor angles before inclusion of hydrogen bond restraints in β-catenin (a; at 2.9Å resolution) and arginine kinase (b; at 1.2 Å resolution) and CD2 (c; at 3.1 Å resolution). The gray bars show the distribution normalized by the nonuniform random distribution (Bowie 1997).

It was shown by Bowie (1997) that a statistical bias exists in the distribution of an angle like the AA-A . . . D angle in three-dimensional space. Briefly, in a random angle distribution, the frequency of occurrence of angles ∼180° is much less than that of angles ∼90°. Following Bowie (1997), we have removed this bias by normalizing the AA-A . . . D angle distribution by the nonuniform random distribution. When normalized in this way, we still observe bimodal distributions, although now the rightmost peak is accentuated (Fig. 5 ▶, gray bars).

Figure 6 ▶ illustrates that refinement of chloromucanate cycloisomerase with a double-well hydrogen bond potential is superior to refinement with a single-well potential or a nondirectional L-J 4–6 potential. This is true for all training set proteins and is consistent with the observed bimodal angular distribution. Refinements with the nondirectional L-J 4–6 potential are superior to those with the single-direction L-J 4–6 potential, showing the importance of angular bimodality in the description of hydrogen bonds.

Fig. 6.

Quality of refinements of chloromucanate cycloisomerase using double-well, single-well, and angle-independent hydrogen bond restraints. Consensus restraint parameters were used.

The improvements in refinement derive from both the new functional form and the stringent selection criteria. Comparison of Figures 4 and 6 ▶ ▶ reveals that the dominant factor is the selection criteria. The incorporation of a double-well angular component to the hydrogen bond potential gives additional improvement in R^free (Fig. 6 ▶), but only if four selection criteria are used.

Not surprisingly, refinement with the double-well hydrogen bond function redistributes C=O . . . N angles, producing larger peaks at the target angles and a reduction in the variance. This is illustrated in Figure 7 ▶ for refinement of chloromucanate cycloisomerase. Those angles initially greater than θ_mid = 135° are moved toward θ_high = 155°, and those initially less than θ_mid are moved toward θ_low = 115°. The number of hydrogen bonds and their distribution at the end of the refinement depends on the weight (ɛ) given to the hydrogen bond potential.

Fig. 7.

Distribution of C = O . . . N angles before and after refinement of chloromucanate cycloisomerase with the double-well hydrogen bond restraint (ɛ = 100)

Side-chain hydrogen bond restraint

The results presented thus far show that refinements of medium-resolution structures are improved with an appropriate main-chain hydrogen bond restraint. We now consider refinements with additional analogous side-chain hydrogen bond restraints. These additional hydrogen bonds could be side-chain to side-chain or side-chain to main-chain. The side-chains of Ser, Thr, and Tyr are involved in hydrogen bonding interactions through hydroxyl groups, Asp and Glu through carboxyl groups, Asn and Gln through carboximide groups, Lys through amino, Arg through guanidium, and His through imidazole groups. Although solvent water figures prominently in hydrogen bonding, the medium-resolution structures most improved by the new restraint had few water molecules explicitly modeled.

Parameters for the side-chain restraints were optimized as they had been for the main-chain. Refinements of the training set proteins with side-chain restraints but no main-chain restraints, reduces R^free. However, refinements with main-chain restraints alone are superior, and the best results are obtained when both main- and side-chain restraints are used. For example, refinements of chloromucanate cycloisomerase and HIV-capsid protein with main-chain restraints alone were improved by up to 0.5% when additional side-chain restraints were added (Fig. 8 ▶). The optimal target angle for the tetrahedral side-chain hydrogen bond acceptor was found to be 109°, consistent with expectations from stereochemistry.

Fig. 8.

Refinement of three proteins as a function of the weight applied to side-chain hydrogen bond restraints. A weight of ɛ_side = 0 implies that no side-chain restraints were applied. Main-chain restraints were included in each case, with the consensus main-chain hydrogen bond parameters.

In summary, this work shows that medium-resolution structures can be improved by an explicit hydrogen bond restraint. Improvement is possible only when stringent selection criteria are used that include explicit hydrogen positions. Angular terms for carbonyl oxygen acceptors help if they have a double-well form but are detrimental if unimodal. This indicates that force fields and energy minimizations that only consider the dipolar term and ignore covalent components are far from optimal.

Materials and methods

Hydrogen bond potential

The functional form of the hydrogen bond potential is as follows:

where ɛ is a weight or strength of the hydrogen bond interaction; σ is related to the distance R₀ at minimal potential, E_min, by σ = R₀√2/3; and θ and θ₀ are the D-A-AA and target D-A-AA angles, respectively. Thus, the hydrogen bond potential has both radial and angular parts. A switching function (Brunger 1992), SW, is applied to smoothly decrease E_hb to zero beyond a cut-off distance (Fig. 9a ▶).

Fig. 9.

Hydrogen bonding restraining potential (E_HB). (a) The radial component of the hydrogen bond potential with (E_HB, solid) and without (dotted) the switching function (SW). (b) The double-well angular component, for which θ_mid is the midpoint between θ_low and θ_high.

The "ideal" C = O . . . N angle at the acceptor oxygen has been a subject of debate (Donohue 1968), and the surveys based on small molecular structures (Mitra and Ramakrishnan 1977) show a wide range of values, between 100° and 160°. Our analysis of individual protein structures confirmed a bimodal acceptor C = O . . . N angle distribution (Fig. 5 ▶), as revealed by Stickle et al. (1992). This is incorporated within our force field term by substituting for θ₀ one of two target angles, θ_low and θ_high, whichever is closer to the current model θ. θ_low and θ_high correspond to hydrogen bonds that are predominantly covalent and electrostatic, respectively. The angle dependence is illustrated in Figure 9b ▶.

The hydrogen bond function was implemented as a module for the crystallographic refinement program CNS (Brünger et al. 1998), in which it adds to the default CNS restraints. The default CNS nonbonded repulsive function is replaced by the hydrogen bond function, when appropriate. Derivatives of the hydrogen bond energy are calculated and added to those calculated by CNS. Thus, all types of optimization performed by CNS, such as conjugate gradient minimization and simulated annealing, are supported with the additional restraint.

Parameterization

Parameters were optimized with medium-resolution structures and their diffraction amplitudes, downloaded from the Protein Data Bank (PDB; Berman et al. 2000). The test reflections that we used to compute R^free were the same as those used in the original structure determinations.

Hydrogen bond geometry can be analyzed directly in terms of angle at the hydrogen, D-H . . . A, and the hydrogen bond distance, H . . . A, as well as indirectly with the angle D . . . A-AA and indirect distance D . . . A, as described in many force field sets (Baker and Hubbard 1984). However, hydrogen positions are required for direct analyses. Because medium-resolution X-ray structures typically do not include hydrogens, they were added at geometrically expected positions using CNS (Brünger et al. 1998). The occupancies of hydrogens were set to zero, so they would not contribute to calculated structure factor amplitudes, and any improvement in the refinement would be entirely owing to the improved stereochemical restraint.

Hydrogen bonding pairs were identified using the selection criteria of the form suggested by Baker and Hubbard (1984): (1) D . . . A distance < R_cut, (2) AA-A . . . D angle > θ_cut, (3) H . . . A distance < 2.7 Å, and (4) D-H . . . A angle > 90°.

Potential donor and acceptor pairs from within the same crystallographic asymmetric unit are identified according to these criteria by the new program module, and are updated on every refinement cycle. (Consideration of crystallographic symmetry and extension to nucleic acids are possible future enhancements.) Generous values of R_cut and θ_cut were used to allow the refinement to improve initially poor hydrogen bond geometry. Control tests were performed with selection criteria 1 and 2 only.

The parameters ɛ, θ_low, θ_high, R_cut, θ_cut, and R₀ were optimized by a grid search for the lowest R^free (Brünger, 1992). At each grid point, R^free calculation followed reciprocal space conjugate gradient refinement. The first parameter to be optimized was ɛ, using crude estimates for the other parameters. ɛ values were obtained first for main-chain hydrogen bonds only. When side-chain hydrogen bonds were added, separate weights were found for main-chain and side-chain interactions. With optimal ɛ, the target angles θ_low and θ_high were optimized, followed by the optimization of R_cut, θ_cut, and R₀. With optimal target angles and optimal R_cut, θ_cut, and R₀ values, the weight ɛ was again optimized.

Side-chain hydrogen bonds were classified into groups based on their geometries. Hydrogen bonds made by sp² and sp³ hybridized acceptors have trigonal and tetrahedral geometries, respectively. The trigonal hydrogen bonds were restrained with a double-well potential, as were the main-chain hydrogen bonds. The tetrahedral hydrogen bonds were restrained with a single-well potential, because it is expected that the covalent component will dominate.