Towards a general model for protein–substrate stereoselectivity

Abstract

Protein–substrate interactions in enzymatic, neurological, and immunological systems are typically characterized by a high degree of stereoselectivity towards complex substrates. We propose a novel stereocenter-recognition (SR) model for stereoselectivity of proteins (or receptors in general) towards substrates that have multiple stereocenters, based on the topology of substrate stereocenters. The model provides the minimum number of substrate locations that need to enter into binding, nonbinding, or repulsive interactions with receptor sites, for stereoselectivity to occur. According to this model, a substrate location may interact with multiple receptor sites, or multiple substrate locations may interact with a single receptor site, but a stereoselective receptor has to offer, in the correct geometry, at least as many interactions as the required minimum number of substrate locations. The SR model predicts that stereoselectivity towards an acyclic substrate with N stereocenters distributed along a single chain requires interactions involving a minimum of N + 2 substrate locations, distributed over all stereocenters in the substrate, such that effectively three locations exist per stereocenter. Thus, enantioselective recognition of molecules with one chiral center requires a protein to interact with a minimum of three substrate locations, while stereoselectivity towards substrates with two or three stereocenters requires interactions with a minimum of four or five substrate locations, respectively, and so on. We demonstrate the general applicability of this model to protein–substrate interactions by interpreting several previous experimental observations.

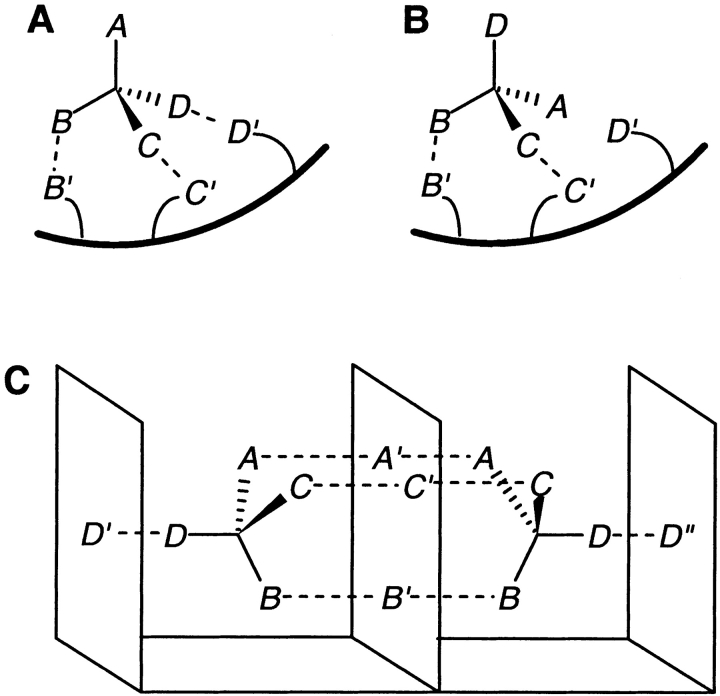
Understanding stereoselectivity in biological molecular recognition processes is extremely important for rational drug design, and for designing proteins and biomimetic receptors. The most widely accepted model for stereoselectivity calls for three-point interactions between receptor and substrate. This derives from the three-point attachment (TPA) model (Easson and Stedman 1933; Ogston 1948), according to which, one enantiomer of a chiral substrate binds to a protein simultaneously at three sites (Fig. 1A ▶), while the opposite enantiomer cannot bind to the same three sites (Fig. 1B ▶). It was later recognized that receptor–substrate binding involves significant conformational changes in both receptor and substrate (Koshland 1958; Koshland et al. 1966). It has also been recognized that in addition to "attachment points" resulting from binding interactions, steric factors and other nonbinding or even repulsive interactions do contribute to the selectivity of receptors towards particular stereoisomers of their substrates. However, the basic idea of a three-point interaction continues to be well accepted (Davankov 1997; Pirkle 1997; Copeland 2000; Ahn et al. 2001), and explanations similar to the TPA model have been proposed for a variety of stereoselective receptors. These include enzymatic systems (Fersht 1999; Copeland 2000), H-2 receptors for histamine (Nederkoorn et al. 1996), ligand binding to chiral porphyrins (Kuroda et al. 1993), taste receptors for sweetness (Shallenberger and Acree 1967; Suami and Hough 1993), and inclusion complexes in cyclodextrins (Ahn et al. 2001). The three-point interaction model is also often cited to explain the mechanisms behind chromatographic enantioresolutions and to design chiral stationary phases and mobile phases for use in chromatography (Dalgliesh 1952; Davankov and Kurganov 1983; Pirkle et al. 1983; Nesterenko et al. 1994; Morris et al. 1996; Vidyasankar et al. 1997).

Fig. 1.

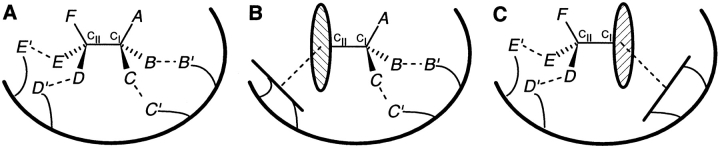
The three-point attachment (TPA) model and the four-location (FL) model. (A) In the TPA model, three groups, B, C, and D on one enantiomer, simultaneously bind to B,′ C′, and D′ on the receptor. (B) Two groups, B and C of the opposite enantiomer, bind to B′ and C′, but the third group D cannot simultaneously bind to D′. (C) In the FL model, binding sites A′, B′, and C′ are positioned on a virtual plane in the receptor such that both enantiomers of a substrate can enter into three simultaneous interactions, but on opposite sides of that plane. This necessitates the presence of a fourth binding site (D′ or D"), to distinguish between substrate enantiomers.

There has been much controversy over the TPA model (Bentley 1983; Booth et al. 1997; Pirkle 1997). It has been pointed out that as both substrates and receptors are chiral entities, the most important factor in chiral discrimination is the formation of diastereomeric adducts, with differing thermodynamic stabilities. A theoretical analysis of interactions between two asymmetric tetrahedra (Topiol and Sabio 1989) points out that in three-dimensional space, four pairs of points are always formally involved in chiral recognition. There is a fourth constraint implicit in all three-point interaction models, arising from the assumption that a substrate can bind only on one side of a receptor surface (Wilcox et al. 1950; Bentley 1983). A directional interaction between the binding plane of an enzyme and the binding plane of a substrate is also a key feature of the polyaffinity model (Bergmann and Fruton 1937). However, more than three sites may be present in proteins, distributed in such a manner that both enantiomers of a substrate can bind, but in two different orientations, resulting in different biological activities. This could happen, for example, if binding sites are distributed between different subunits in a multimeric protein, or buried deep in a cleft, so that a substrate molecule sees binding surfaces all around it. To allow for this possibility, a four-location (FL) model has been proposed recently (Mesecar and Koshland 2000a, 2000b), which rejects the validity of the TPA model, and says that chiral discrimination requires a minimum of four designated locations, either as four attachment sites or as three attachment sites and a direction (Fig. 1C ▶).

The TPA model of Easson and Stedman (1933) was originally proposed to explain the differential recognition of a pair of enantiomers of a substrate with a single chiral center. Similarly, Ogston's TPA model (1948) was meant to explain the enantiospecific conversion of a prochiral substrate. More recently, Sokolov and Zefirov (1991) have proposed a two-point attachment model for enantiospecific conversion of prochiral molecules, but this model is also based on the idea of three interactions, out of which only two are "points of attachment" (Davankov 1997). An important consequence of this is that any model involving three-point interactions can strictly be applied only to substrates that have a single chiral center and to enzymatic action at a prochiral center. However, this has been largely overlooked in most discussions of stereoselectivity, where the picture of three-point interactions has either been invoked or rejected with respect to substrates that have multiple stereocenters. Two rare exceptions may be found in the discussions of the binding of α₂-adrenergic receptors to the drug (1R,2S)-α-methylnoradrenaline (Triggle 1976; Ruffolo 1983), where the two stereocenters in this drug molecule have been explicitly accounted for. Bentley (1983) has listed examples where the TPA model is apparently invalidated because of evidence for interactions at more than three points, but some of these cases are of substrates that have multiple stereocenters (glucopyranoside, l-arabinose). The recently proposed FL model is based on the Mg²⁺-dependent reversal of stereoselectivity in the binding of isocitrate to isocitrate dehydrogenase (IDH), but does not take into account that the isocitrate molecule has two stereocenters.

A substrate molecule with N stereocenters has a maximum of 2^N stereoisomers. In general, protein stereoselectivity for such a substrate can be defined as its ability to preferentially recognize one out of all possible stereoisomers of that substrate. Hence, a stereoselective protein would be both enantioselective and diastereoselective. It may be expected that rather than only three or four points, the number of geometric requirements for such stereoselectivity would be a function of both the number and the topological distribution of stereocenters in the substrate. A large number of biologically important molecules have multiple stereocenters, for example, the anti-inflammatory ephedrines (two stereocenters), the artificial sweetener aspartame (two centers), the carcinogenic epoxides (typically two centers), the antibiotic penicillin (three centers), the insecticide deltamethrin (three centers), the antimalarial drug quinine (four centers), the cytochrome complex inhibitor stigmatellin (four centers), and natural sugars (multiple centers).

A general framework is not available for the stereoselective interactions of proteins (or receptors) with substrates that have multiple stereocenters. Moreover, the binding of a substrate can induce small local or even significantly large global changes in the receptor's three-dimensional structure (Koshland 1958; Koshland et al. 1966), which implies that interactions are not restricted to individual points. It has also long been recognized that substrates can bind to a large part of a receptor surface in a shape-selective manner. These considerations render obsolete the very concept of individual attachment points (Bentley 1983). Stereoselectivity may result from a combination of different kinds of interactions, involving binding, steric hindrance and shape inductive mechanisms. In the following section, we present a general model for protein–substrate stereoselectivity, which accounts for the presence of multiple stereocenters distributed along a single chain in acyclic substrates. The model also accounts for different kinds of interactions between proteins and these substrates. Protein stereoselectivity characteristics would be more complex for branched acyclic substrates (with stereocenters distributed over two or more chains of carbon atoms) and for homocyclic and heterocyclic substrates that have single or multiple stereocenters distributed on their rings; hence, an extension of this model to include these cases will be the topic of a forthcoming publication.

The stereocenter-recognition model

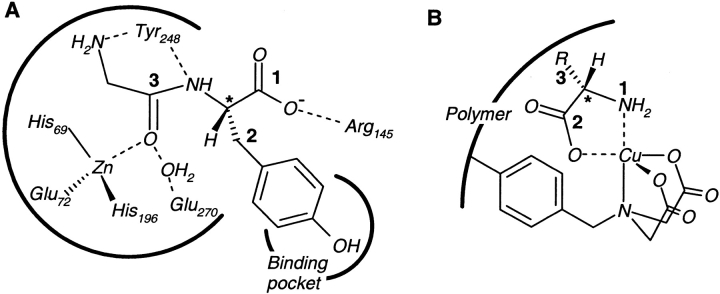
The stereocenter-recognition (SR) model rigorously accounts for the minimum number of locations on each stereocenter in a substrate that need to interact with receptor sites, for a chiral recognition to occur. This model is based on the structural consideration that all substrate stereoisomers would approach the same binding surface(s) of the receptor along the same direction, while allowing for the possibility that different substrate stereoisomers can bind in different conformations (see the discussion about isocitrate binding to IDH enzyme in the section on substrates with two stereocenters). From a thermodynamic perspective, stereoselectivity in receptor–substrate interactions results from either the preferential stabilization of the complex formed by one stereoisomer of a substrate (due to all binding interactions) or the relative destabilization of the complexes formed by other stereoisomers (due to unfavorable interactions like steric hindrance). The number of interactions that determine stereoselectivity can be distinguished from the number of attachment points at which a preferred stereoisomer of a substrate binds to its receptor (Davankov 1997). A substrate location is defined as a functional group or groups attached to a stereocenter in the substrate, which interacts, either favorably or unfavorably with receptor sites. Receptor sites can consist of either specific functional groups in the receptor or the contour of a large part of the receptor surface (Bentley 1983), interacting with one or more substrate locations. These definitions do not apply separately to the receptor or the substrate, but to the receptor–substrate complex. They allow for a broad range of stereochemical and thermodynamic factors in receptor–substrate interactions, and also adequately address the issue of how to count the number of interactions involved. For example, a carboxylate (or an amino or hydroxyl) group attached to a chiral carbon can possibly enter into multiple hydrogen bonds with one or more receptor sites, but would count only as a single substrate location. A substrate location may even consist of many different functional groups capable of interacting with one or more functional groups in a receptor, distributed over the contour of a large part of the receptor surface. This is seen in the binding of glycyl-l-tyrosine to the enzyme carboxypeptidase A (Bentley 1983; Mackenzie et al. 1985). Here, both the free amino group of glycine and the amide group linking l-tyrosine to glycine bind to different receptor sites, but together constitute a single substrate location on the chiral carbon of tyrosine (Fig. 2A ▶). Conversely, one functional group in a receptor may interact with multiple substrate locations, as seen in the chelation of transition metal ions by the amino and carboxylate groups of chiral amino acids (Fig. 2B ▶) (Davankov and Kurganov 1983; Vidyasankar et al. 1997). The receptor may be seen as interacting with the substrate either through a single site (the metal ion) or through two sites (different sites in the coordination sphere of the metal). In either case, the key point is that two substrate locations are constrained through this chelation interaction.

Fig. 2.

Multiple interactions between receptor sites and substrate locations. (A) In the binding of the enzyme carboxypeptidase A to glycyl-l-tyrosine (an asterisk marks the chiral center), the free amino group of glycine and the amide functionality together constitute a single substrate location, interacting with multiple binding groups on a large part of the enzyme's binding surface. (B) In ligand-exchange adsorbents, a transition metal ion (Cu²⁺) is immobilized via a metal chelating ligand. The amino and carboxylate groups form two distinct substrate locations, interacting with the same metal ion.

The SR model therefore accounts only for the minimum number of substrate locations needed for stereoselective interaction with one or more receptor sites. Due to the reciprocal nature of any chiral interaction, it is not necessary to strictly count the number of interacting receptor sites. Although the SR model only addresses binding stereoselectivity, it would, in principle, be valid for transition states, transition state analogs, and inhibitors, with respect to enzymatic activity. The above definition of receptor sites would then include both catalytic sites in an enzyme and sites that only facilitate substrate binding. It must be cautioned that this model solely addresses interactions between a receptor and distinct stereoisomers of its chiral substrate. It does not directly apply to enantioselective enzyme action at a substrate's prochiral carbon, resulting in the introduction of a chiral center in the product.

Results and Discussion

Substrates with a single stereocenter

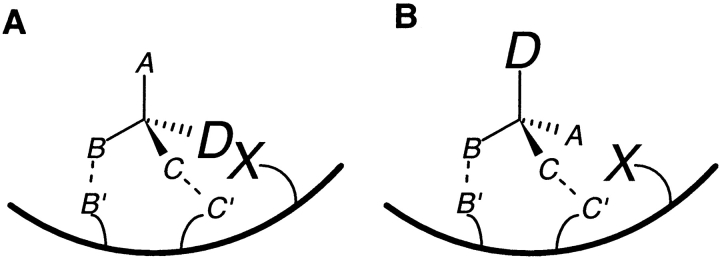
For a substrate with a single chiral center, a receptor needs to distinguish between two enantiomers. As carbon is tetravalent, a maximum of four substrate locations can possibly interact with receptor sites. A receptor that interacts with all four locations in such a substrate will necessarily be enantioselective. Given the constraint of the directionality of approach (Wilcox 1950), a receptor needs to interact with a minimum of three locations in one substrate enantiomer to distinguish between the two enantiomers. All three locations could be involved in binding interactions, as in the TPA model (Fig. 1A, B ▶). Alternatively, the preferred substrate enantiomer could bind to the receptor only at two attachment points, but there might be conditions preventing the opposite enantiomer from binding in an identical fashion. Although the opposite substrate enantiomer would also bind to the same two receptor sites, it might bind in a strained conformation. If this results in sufficient δδG for the total interaction, thermodynamic enantioselectivity would result. One of the most common mechanisms for this would be steric hindrance at one substrate location, while two locations enter into binding interactions with corresponding receptor sites (Fig. 3A, B ▶). Steric factors are known to contribute significantly to the stereospecific proteolytic action of aminopeptidase (Bergmann and Fruton 1937) and chymotrypsin (Fersht 1999). They have also been postulated to play an important role in the binding of amino acids to enantioselective adsorbents used in ligand-exchange chromatography (Davankov and Kurganov 1983; Vidyasankar et al. 1997). From the stereochemical standpoint, steric hindrance should be counted as a third interaction, because it contributes to enantioselectivity. In principle, enantioselectivity could also result from a combination of a single binding and two nonbinding interactions, resulting in only one point of attachment (Davankov 1997). Such cases can be expected to be rare in biological systems, because an increase in the number of unfavorable interactions would decrease the total binding energy. However, irrespective of the number of "points of attachment," if a receptor is to be enantioselective, it needs to interact in some fashion with at least three substrate locations.

Fig. 3.

The contribution of steric interactions to stereoselectivity. (A) In one substrate enantiomer, groups B and C bind to B′ and C′ on the receptor, but the bulky group D faces steric hindrance at the receptor site X. (B) The opposite enantiomer faces no unfavorable steric interaction between X and A, leading to its preferential binding.

Substrates with two stereocenters

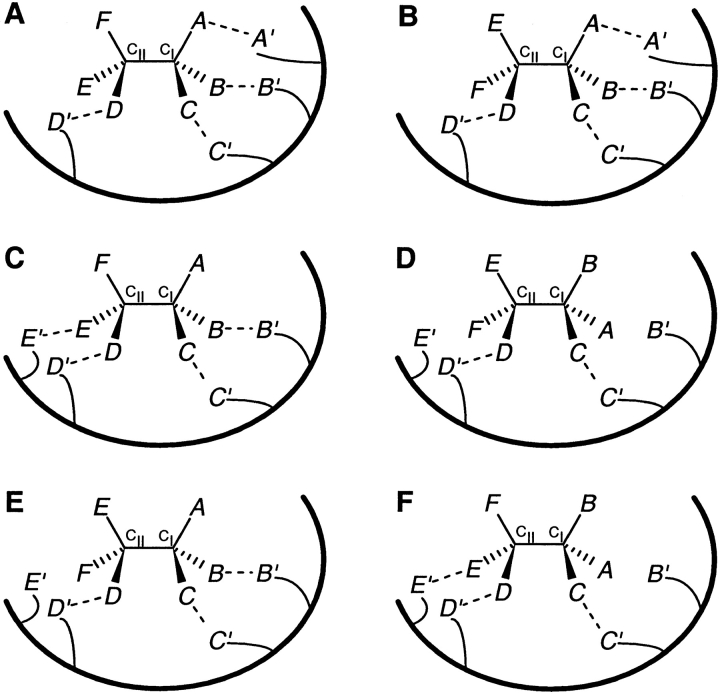
For substrates with two stereocenters (C_I and C_II), stereoselectivity refers to a receptor's preferential recognition of one out of four possible stereoisomers. Figure 4 ▶ shows a receptor's possible interactions with three locations on a substrate with two stereocenters. If these locations are distributed in a (3-0) configuration in one substrate stereoisomer (all three locations directly attached to C_I and none directly attached to C_II; Fig. 4A ▶), its enantiomer can have at most two locations interacting with the receptor (Fig. 4B ▶). If this difference results in sufficient δδG, thermodynamic enantioselectivity will be possible. However, as the receptor does not interact directly with any locations on C_II, it cannot distinguish between the substrate stereoisomer shown in Fig. 4A ▶ and its diastereomer (Fig. 4C ▶) possessing the opposite stereochemistry at C_II. If a receptor interacts with three substrate locations distributed in a (2-1) configuration (two locations directly attached to C_I and one to C_II; Fig. 4D ▶), it may still distinguish it from its enantiomer (Fig. 4E ▶), but not from its diastereomer (Fig. 4F ▶) that has the opposite stereochemistry at C_II. It follows that the (0-3) and (1-2) configurations of substrate locations interacting with the receptor (not shown in Fig. 4 ▶) would likewise fail to distinguish between the two diastereomers that have an opposite stereochemistry at C_I. Thus, the interesting and unexpected conclusion is that a receptor interacting with three locations on a substrate with two stereocenters might succeed in distinguishing a pair of enantiomers, but not diastereomers, resulting only in partial stereoselectivity.

Fig. 4.

Are three interactions with a receptor sufficient for stereoselective recognition of substrates with two stereocenters? (For ease of presentation, the two stereocenters in the substrate are shown adjacent to each other, with each corresponding substrate location binding to a distinct receptor site (also in Figs. 5, 6, and 9 ▶ ▶ ▶). The following arguments would hold true even if: (i) substrate stereocenters are at nonadjacent positions in the chain; (ii) some of the interactions with the receptor are steric in nature; (iii) one substrate location interacts with a receptor site consisting of multiple groups, or a large part of the receptor's surface, in a shape-selective manner; or (iv) multiple substrate locations interact with one receptor site.) (A) A receptor provides three sites (A′, B′, and C′) to interact with three locations of one substrate stereoisomer (referred to as SS²), distributed in a (3-0) configuration (A, B, and C on the C_I stereocenter and none on the C_II stereocenter). (B) The enantiomer of SS² can interact with only two receptor sites (B′ and C′). (C) A diastereomer of SS², with the opposite stereochemistry at C_II, can interact with the same three receptor sites (A′, B′, and C′). (D) A receptor provides three sites (B′, C′, and D′) to interact with three locations of SS², distributed in a (2-1) configuration (B and C on C_I and D on C_II). (E) The enantiomer of SS² can interact with only two receptor sites (B′ and C′). (F) A diastereomer of SS², with the opposite stereochemistry at C_II can interact with the same three receptor sites (B′, C′, and D′).

Figure 5 ▶ takes into consideration four substrate locations interacting with the receptor. If these locations are distributed in a (3-1) configuration, the receptor would still fail to distinguish between the two diastereomers that have an opposite stereochemistry at C_II (Fig. 5A, B ▶). Likewise, the (1-3) distribution of locations (not shown in Fig. 5 ▶) would fail to uniquely recognize the stereochemistry at C_I. However, if the receptor interacts with four locations distributed in a (2-2) configuration on one substrate stereoisomer (two locations directly attached to C_I and two attached to C_II; Fig. 5C ▶), it can distinguish that isomer not only from its enantiomer (Fig. 5D ▶) but also from its two diastereomers (Fig. 5E, F ▶). It must be noted that this requirement of a (2-2) configuration is based solely on a topological argument. The different possibilities involved in the nature of interactions (binding, steric, or repulsive) would lead to various scenarios, two of which are briefly discussed below. If all four substrate locations enter into binding interactions, then the substrate stereoisomer shown in Figure 5C ▶ would be preferentially bound to the receptor. However, if the E—E′ interaction in Figure 5C ▶ represents a steric hindrance and the other three interactions are binding in nature, then the substrate stereoisomer shown in Figure 5E ▶ would be preferentially bound to the receptor. In other real cases, a receptor might need to interact with more than four substrate locations to generate sufficient δδG for thermodynamic stereoselectivity.

Fig. 5.

Four interactions between a receptor and a substrate with two stereocenters. (A) A receptor provides four sites (A′, B′, C′, and D′) to interact with four locations of one substrate stereoisomer (referred to as SS²), distributed in a (3-1) configuration (A, B, and C on C_I, and D on C_II). (B) A diastereomer of SS², with the opposite stereochemistry at C_II, can interact through the same (3-1) configuration with the same four receptor sites. (C) A receptor provides four sites (B′, C′, D′, and E′) to interact with four locations of SS², distributed in a (2-2) configuration (B and C on C_I along with D and E on C_II). (D) The enantiomer of SS² can interact with only two receptor sites (C′ and D′). (E) The diastereomer of SS², with opposite stereochemistry at C_II, can interact with only three receptor sites (B′, C′, and D′). (F) The other diastereomer of SS², with opposite stereochemistry at C_I, can interact with only three receptor sites (C′, D′, and E′). Therefore, a minimum of four interactions, involving substrate locations distributed in a (2-2) configuration, is necessary for unique stereoselectivity (enantioselectivity as well as diastereoselectivity).

We conclude that to selectively recognize one out of four possible stereoisomers of a substrate with two stereocenters, a receptor needs to interact with a minimum of four substrate locations on one stereoisomer, distributed in a (2-2) configuration. This can be explained as a logical extension of the minimum requirement of three locations for a substrate with a single chiral center. For a substrate that has two stereocenters, the (2-2) configuration of substrate locations implies that two locations are directly attached to each of the two stereocenters (Fig. 6A ▶). In addition, all locations on C_II effectively act together as the third location on C_I (Fig. 6B ▶) as they are attached indirectly to C_I via C_II. Similarly all locations on C_I effectively act together as the third location on C_II (Fig. 6C ▶). Thus, a stereoselective receptor has to effectively interact with at least three locations on each stereocenter in the substrate. This is not possible with four substrate locations distributed in the (3-1) or the (1-3) configurations. A higher number of substrate locations, distributed in the (2-3) or (3-2) or (3-3) configurations, will also lead effectively to at least three locations on each stereocenter, and result in stereoselectivity. We demonstrate below how this model explains two previously reported experimental findings.

Fig. 6.

The concept of three effective substrate locations. (A) Four locations distributed in a (2-2) configuration on two stereocenters of a substrate (same as Fig. 5C ▶). (B) The two locations on C_II (shown here as one ellipse) act together as one effective location on C_I, so that the receptor interacts effectively with three locations at C_I, identical to the one stereocenter case (Figs. 1A, 1B, and 3 ▶ ▶). (C) Similarly, the two locations on C_I act together as one effective location on C_II, such that the receptor interacts effectively with three locations at C_II. This leads to three effective locations per stereocenter.

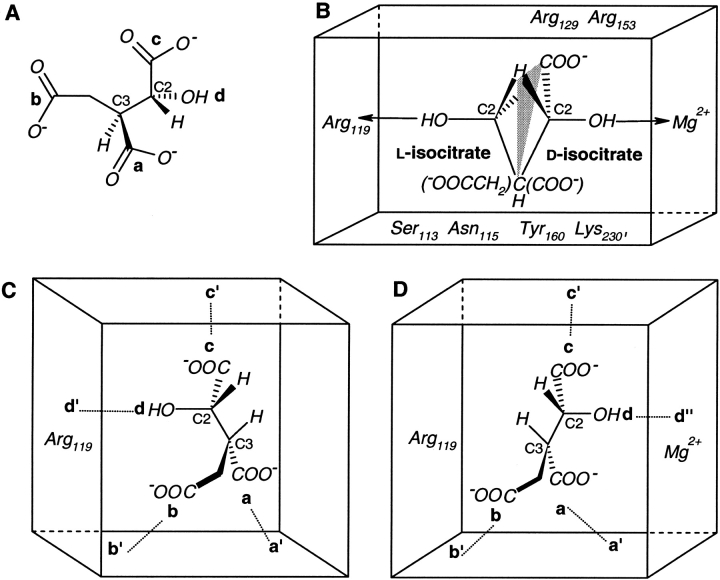
The NADP-dependent enzyme isocitrate dehydrogenase (IDH) from E. coli selectively catalyzes the conversion of (2R,3S)-isocitrate (the d-isomer) to α-ketoglutarate, in the presence of Mg²⁺. Mesecar and Koshland (2000a) report that in the absence of Mg²⁺, only (2S,3R)-isocitrate (the l-isomer) binds to the enzyme active site but catalytic activity is lost. This has led to the proposal of the FL model, based on a conclusion that, ". . . three of the four groups attached to the tetrahedral C2 atom of d- and l-isocitrate bind to the same three locations in the IDH active site. The difference is the fourth group, the hydroxyl of the C2 carbon . . .". The four groups attached to the C2 carbon of isocitrate are —H, the chiral C3 carbon, —COO⁻ and —OH. It should be noted that the —H group makes no direct interactions with enzyme residues or water molecules in the crystal. During catalysis, this group is abstracted by NADP, which is not present in the crystal structure of the metal-free enzyme bound to l-isocitrate. However, a comparison of the enzyme–substrate complexes in the presence and absence of Mg²⁺ shows that the —H group on the C2 carbon occupies the same position with respect to the position of the coenzyme NADP modeled onto the crystal structure (Mesecar and Koshland 2000b).

The metal–ion-dependent stereoselectivity characteristics of IDH are better explained through the SR model for substrates with two stereocenters. Separately accounting for the interactions at the C2 and C3 stereocenters of isocitrate shows that it has four locations distributed in a (2-2) configuration (c and d on C2 and a and b on C3; see Fig. 7A ▶). In both d- and l-isocitrate, the chiral C2 carbon has effectively three locations interacting with the receptor. The —OH and the —COO⁻ groups attached to the chiral C2 carbon form two locations in the substrate. The —CH₂COO⁻ and —COO⁻ groups on the chiral C3 carbon act together as the third location with respect to the chiral C2 carbon. These three locations enter into interactions with specific sites in the enzyme, in such a manner that the —H group on the chiral C2 carbon comes to occupy the same spatial position for both d- and l-isocitrate (Fig. 7B ▶). In both metal-containing and metal-free cases, the same enzyme residues bind to the two locations on the C3 carbon (the —CH₂COO⁻ and —COO⁻ groups) and to one location on the C2 carbon (the —COO⁻ group). The binding of the second location on the chiral C2 carbon (the —OH group) takes place in a metal–ion-dependent manner (Fig. 7C, D ▶). In the presence of Mg²⁺, this —OH group in (2R,3S)-isocitrate binds to the metal ion, whereas in (2S,3R)-isocitrate, it can bind only to the Arg 119 residue of IDH. The latter isomer (2S,3R) is not seen in the IDH binding site in the presence of Mg²⁺ because the former (2R,3S) binds strongly to the metal ion. In the metal-free enzyme, the —OH group of (2S,3R)-isocitrate, still binds to Arg 119, but the absence of the metal ion rules out the binding of the —OH group of the (2R,3S) isomer. Thus, the metal-containing enzyme is stereoselective for (2R,3S)-isocitrate, while the metal-free enzyme is stereoselective for (2S,3R)-isocitrate. In either case, interactions with four substrate locations in the (2-2) configuration determine stereoselectivity.

Fig. 7.

Isocitrate and its interactions with the enzyme isocitrate dehydrogenase (IDH). (A) Four locations in (2R,3S)-isocitrate distributed in a (2-2) configuration, a (—COO⁻) and b (—CH₂COO⁻) on the C3 stereocenter along with c (—COO⁻) and d (—OH) on the C2 stereocenter. (B) Superposition of different interactions of d-isocitrate [(2R,3S)] and l-isocitrate [(2S,3R)] with IDH in the presence and absence of metal (Mg²⁺), respectively. Only the important enzyme residues in the substrate binding site are shown. A hypothetical mirror-plane is shown passing through H, COO⁻, and C3. (C) Schematic representation of (2S,3R)-isocitrate bound to metal-free IDH. a′ (Arg 153, Arg 119, Tyr 160, Lys 230′), b′ (Ser 113, Asn 115), and c′ (Arg 119, Arg 129, Arg 153) are enzyme residues that interact with substrate locations a, b, and c, respectively. d′ (Arg 119 and a water molecule) binds to the —OH group. (D) Substrate locations a, b, and c in (2R,3S)-isocitrate bind to metal-containing IDH at the same three enzyme sites a′, b′, and c′, but the —OH group binds to d" (Mg²⁺ and the enzyme residues bound to it).

As shown in Figure 7 ▶, when an isocitrate stereoisomer binds to IDH, enzyme residues surround the molecule. In both metal-containing and metal-free enzymes, the interactions of four substrate locations (mentioned previously) with corresponding receptor sites ensure that the —H group on the chiral C2 carbon occupies an almost identical spatial position in the IDH–isocitrate complex. When l-isocitrate binds to the metal-free enzyme, the chiral C2 carbon occupies a very different position (compared to that in d-isocitrate with a metal-containing enzyme), so that the bond between this C2 carbon and the —H group is oriented in a different direction (Fig. 7C, D ▶). This might account for the fact that although the metal-free enzyme binds selectively to l-isocitrate, no catalytic activity is observed.

It may be noted that d- and l-isocitrate bind to IDH in two opposite orientations at the C2 carbon, and interact identically at the C3 carbon. It is therefore necessary to study the binding and/or catalytic behavior of IDH towards the (2R,3R) and (2S,3S) stereoisomers of isocitrate, in the presence and absence of metal ions, to obtain better insight into the interactions involved in this system It would also be interesting to study the interactions of all four stereoisomers of isocitrate, in the presence and absence of metal ions, with a bacterial IDH mutant, where Arg 119 has been suitably changed by site directed mutagenesis. It has been shown that mutating homologous arginine residues in rat IDH (Jennings et al. 1997) and porcine IDH (Soundar et al. 2000) result in weaker substrate binding and appreciable loss of catalytic activity. However, in the presence of metal ions, a bacterial mutant might still be stereoselective for (2R,3S)-isocitrate. The metal-free bacterial mutant might interact with the three carboxylate groups in isocitrate, distributed in a (1-2) configuration, but would present no binding sites for the —OH group in any of the isocitrate stereoisomers. If so, the SR model predicts that this would result in loss of stereoselectivity at the C2 carbon of isocitrate.

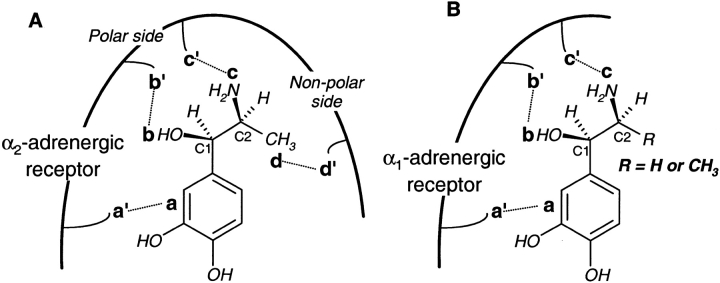
The second example is that of the (1R,2S) stereoisomer of α-methylnoradrenaline, which binds selectively to α₂-adrenergic receptors, and has greater potency as a drug than (1R)-noradrenaline. However, for α₁-adrenergic receptors, (1R,2S)-α-methylnoradrenaline is equipotent to (1R)-noradrenaline. This difference in the drug response of these receptors has been explained in terms of four interactions of (1R,2S)-α-methylnoradrenaline with α₂-adrenergic receptors, as opposed to three interactions with α₁-receptors. Rufollo (1983) postulates that the α-methyl group in the preferred stereoisomer actually binds to some receptor site in the α₂-receptor. Triggle (1976) postulates that the presence of the α-methyl group sterically alters the binding of the three polar groups in the drug molecule (amino, catechol, and the β-hydroxyl) to the α₂-receptor. Under either explanation, the drug action of (1R,2S)-α-methylnoradrenaline at α₂-receptors involves four substrate locations distributed in the (2-2) configuration. These are the catechol and β-hydroxyl groups attached to stereocenter C1 in the molecule, and the amino and α-methyl groups on the second stereocenter C2 (Fig. 8A ▶). However, α₁-receptors do not seem to offer any interaction with the α-methyl group of the substrate, binding only to the other three substrate locations, in a (2-1) configuration (Fig. 8B ▶). Therefore, for α₁-receptors, the potency of (1R,2S)-α-methylnoradrenaline, a drug molecule with two stereocenters, is comparable to that of (1R)-noradrenaline, a molecule with a single stereocenter. The action of other analogous drug molecules at different types of adrenergic receptors may be explained similarly.

Fig. 8.

Interactions of the drug molecules (1R,2S)-α-methylnoradrenaline and (1R)-noradrenaline with α₂-adrenergic and α₁-adrenergic receptors. (A) α₂-Adrenergic receptors interact with four locations in (1R,2S)-α-methylnoradrenaline in a (2-2) configuration, a (catechol) and b (—OH) on the C1 stereocenter along with c (—NH₂) and d (—CH₃) on the C2 stereocenter. (B) α₁-Adrenergic receptors interact only with three locations in both (1R)-noradrenaline (R = H) and (1R,2S)-α-methylnoradrenaline (R = CH₃), so that both drug molecules are equipotent for this receptor.

Substrates with three stereocenters

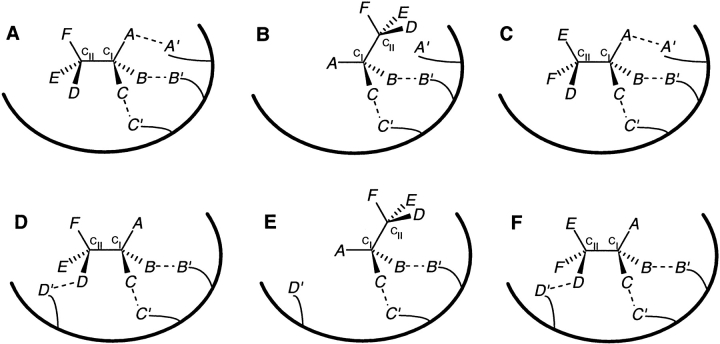
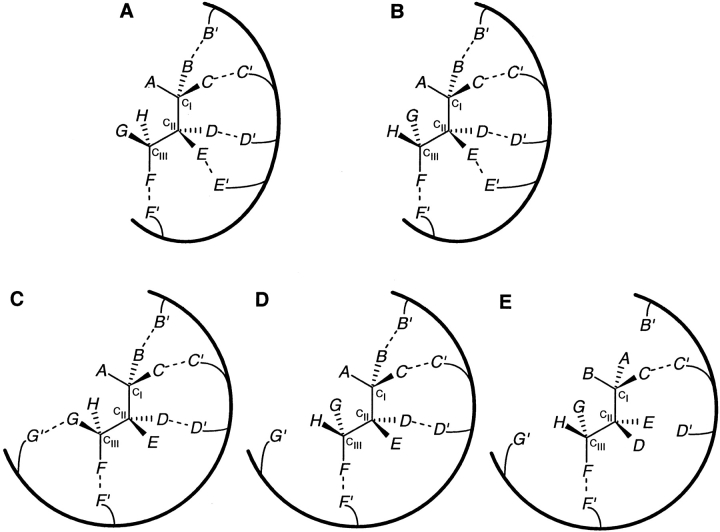
Similar stereochemical considerations would apply to substrates with three stereocenters (C_I, C_II, and C_III), where one out of eight possible stereoisomers needs to be preferentially recognized for stereoselectivity. It is clear that more than four substrate locations would have to interact with a receptor to achieve unique stereoselective (enantioselective as well as diastereoselective) recognition, although a minimum of three locations interacting with the receptor might lead to enantioselectivity. Figure 9 ▶ illustrates two of the many ways in which a receptor can interact with five locations on such a substrate, which are distributed such that there is at least one interacting location directly attached to each stereocenter. The (2-2-1) configuration of substrate locations fails to distinguish between the two diastereomers differing only in the stereochemistry at C_III (Fig. 9A, B ▶). The (1-2-2) configuration (not shown in Fig. 9 ▶) would similarly fail for the two diastereomers differing in stereochemistry at C_I. It follows that the (3-1-1) and the (1-1-3) configurations would also fail, with respect to the stereochemistry at C_III and C_I, respectively. However, distributing five substrate locations in a (2-1-2) configuration can resolve any pair of stereoisomers of the substrate. Figure 9C ▶ shows one stereoisomer interacting through five substrate locations. Its diastereomer differing in stereochemistry only at C_III, can at best interact through four locations (Fig. 9D ▶), and its enantiomer can at best interact through two locations (Fig. 9E ▶). Similar to the two stereocenters case, the degree of freedom in the nature of interactions (binding or steric) would again lead to a large number of possibilities, two of which are presented as follows. If all five substrate locations enter into binding interactions, then the substrate stereoisomer shown in Figure 9C ▶ would be preferentially selected for or bound to the receptor. If the G—G′ interaction in Figure 9C ▶ is steric in nature and the other four are binding in nature, then the substrate stereoisomer shown in Figure 9D ▶ would be preferentially bound to the receptor. The addition of further interactions with other substrate locations on any of these three stereocenters will also result in stereoselectivity. Thus, a minimum of five locations, distributed in the (2-1-2) configuration, is necessary for the unique stereoselective recognition of a substrate with three stereocenters.

Fig. 9.

Receptor interacting with five locations in a substrate with three stereocenters. (A) A receptor interacts with five substrate locations, distributed in a (2-2-1) configuration (B and C on C_I; D and E on C_II; F on C_III), of one substrate stereoisomer (referred to as SS³). (B) The diastereomer of SS³, with opposite stereochemistry at C_III, can also interact through the same five locations. (C) A receptor interacts with the same substrate isomer SS³ via five locations in a (2-1-2) configuration (B and C on C_I; D on C_II; F and G on C_III). (D) A diastereomer of SS³, with the opposite stereochemistry at C_III, can interact with that receptor through only four substrate locations. (E) The enantiomer of SS³ can interact through only two substrate locations.

It may be noted that two locations have to be directly attached to each of the two terminal stereocenters (C_I and C_III), whereas one location is needed on the inner stereocenter (C_II). This can be explained on the basis of the substrate's molecular connectivity. All locations on C_II and C_III, taken together, effectively act as a single location with respect to the stereocenter C_I. Similarly, all locations on C_I and C_II effectively act together as a single location on C_III. However, for the inner stereocenter C_II, all locations on C_I effectively act together as the second location, while all locations on C_III effectively form the third location. Thus, the stereoselectivity requirement of a (2-1-2) configuration for substrates with three stereocenters implies that each stereocenter always has effectively three locations interacting with the receptor. As in the case of substrates with two stereocenters, this is consistent with the SR model's requirement of a minimum of three substrate locations in a molecule with a single stereocenter.

Substrates with multiple stereocenters: Acyclic structures

This argument can now be generalized for acyclic substrates with N stereocenters. If all asymmetric centers were distributed along one chain of carbon atoms, the stereochemical requirements for all the inner stereocenters in this chain would be analogous to those for the C_II stereocenter in substrates with three stereocenters, while the two terminal stereocenters would be analogous to C_I and C_III. A minimum of N + 2 locations, distributed in the (2-1-1-. . . 1-2) configuration, would therefore be necessary for unique stereoselective (enantioselective as well as diastereoselective) recognition. This ensures that each stereocenter has effectively three locations interacting with the receptor. This conclusion would hold true for all linear acyclic substrates and for branched acyclic substrates in which the stereocenters are distributed only along one chain of carbon atoms. For branched acyclic substrates with stereocenters distributed over two or more such chains and for cyclic substrates (homocyclic and heterocyclic), the stereochemical requirements would be more complex. Because a large number of such substrates are biologically important, we plan to extend the SR model to address this issue in a future study.

Conclusions

The stereocenter-recognition (SR) model for protein–substrate stereoselectivity differs from previously proposed models in three significant ways. First, it provides general principles for stereoselective recognition of substrates that have multiple stereocenters, taking into account the minimum number of substrate locations at each stereocenter necessary for recognizing the stereochemistry at that center. The idea of a three-point interaction determining enantioselectivity is derived from discussions of molecules that have a single chiral center. This is a particular case of the SR model discussed here, which shows that in the general case, three interactions may contribute to enantioselectivity, but may not be enough to distinguish between substrate diastereoisomers. For acyclic substrates with multiple stereocenters, the SR model introduces the concept of three effective interactions per stereocenter, taking into account the number of such centers and the topology of the interacting groups attached to those centers. Second, substrate locations are defined in a general manner, to include not only functional groups entering into favorable binding interactions with a receptor, but also groups that can potentially enter into unfavorable interactions due to steric factors. Finally, in the SR model, a receptor site can be either a specific complementary binding functionality or a morphological feature involving a large part of the receptor's surface, interacting with one or more substrate locations. Therefore, in specific cases, the total number of receptor sites interacting with a substrate can be different from the total number of substrate locations that enter into these interactions. However, a receptor has to offer, through one or more sites, at least as many interactions as the minimum number of substrate locations needed for stereoselective recognition. It may be noted that as the number of stereocenters increases in substrates, the number of stereoisomers increases exponentially (maximum 2^N), but the minimum number of interactions needed to distinguish these stereoisomers from one another increases only linearly (N + 2). For homocyclic and heterocyclic substrates one can expect this requirement of a minimum number of locations to be smaller than N + 2 due to ring restrictions, although this remains to be confirmed. In cases where a receptor interacts with less than the minimum number of locations (required for stereoselectivity) on one substrate stereoisomer, the same set of interactions will be achievable with a different stereoisomer of the substrate. Therefore, diastereomers of natural substrate stereoisomers provide an additional degree of freedom whose interactions with proteins (and bioreceptors in general) can be exploited in the search and design of inhibitors, drug molecules, and other synthetic substrates, and also to gain insight into molecular level interactions of proteins with the naturally occurring substrate stereoisomers. From the perspective of stereochemistry or chiral separation technologies, the interaction between a receptor and its substrate would be equivalent to that between a chiral selector and a chiral selectand. Receptor sites would then correspond to interacting functional groups in the chiral selector and substrate locations to those in the chiral selectand. The SR model thus has potential uses in a number of applications, for example, for the rational design of chiral drugs for known pharmacological targets, for identifying specific binding sites in proteins that can be modified to increase or even reverse native stereoselectivities, for appropriately designing chiral selectors for use in chiral separation techniques and for the design of artificial biomimetic receptors.