Abstract
Although much of the motivation for experimental studies of protein folding is to obtain insights for improving protein structure prediction, there has been relatively little connection between experimental protein folding studies and computational structural prediction work in recent years. In the present study, we show that the relationship between protein folding rates and the contact order (CO) of the native structure has implications for ab initio protein structure prediction. Rosetta ab initio folding simulations produce a dearth of high CO structures and an excess of low CO structures, as expected if the computer simulations mimic to some extent the actual folding process. Consistent with this, the majority of failures in ab initio prediction in the CASP4 (critical assessment of structure prediction) experiment involved high CO structures likely to fold much more slowly than the lower CO structures for which reasonable predictions were made. This bias against high CO structures can be partially alleviated by performing large numbers of additional simulations, selecting out the higher CO structures, and eliminating the very low CO structures; this leads to a modest improvement in prediction quality. More significant improvements in predictions for proteins with complex topologies may be possible following significant increases in high–performance computing power, which will be required for thoroughly sampling high CO conformations (high CO proteins can take six orders of magnitude longer to fold than low CO proteins). Importantly for such a strategy, simulations performed for high CO structures converge much less strongly than those for low CO structures, and hence, lack of simulation convergence can indicate the need for improved sampling of high CO conformations. The parallels between Rosetta simulations and folding in vivo may extend to misfolding: The very low CO structures that accumulate in Rosetta simulations consist primarily of local up–down β–sheets that may resemble precursors to amyloid formation.
Keywords: Rosetta, structure prediction, protein folding
One of the central motivations for experimental studies of protein folding is the development of models and ideas that can lead to reliable predictions of native structure. In recent years, experimental studies have focused on characterizing protein folding rates, intermediates, and transition states (Fersht 1998; Jackson 1998; Baldwin and Rose 1999; Plaxco et al. 2000), whereas ab initio structure prediction work has focused on energy functions and search strategies that are in some cases somewhat removed from the actual folding process, such as genetic algorithms (Bowie and Eisenberg 1994; Pedersen and Moult 1997) and exhaustive enumeration (Samudrala et al. 1999). Because of these differences in focus, there has been some question about the current relevance of experimental protein folding studies to protein structure prediction efforts.
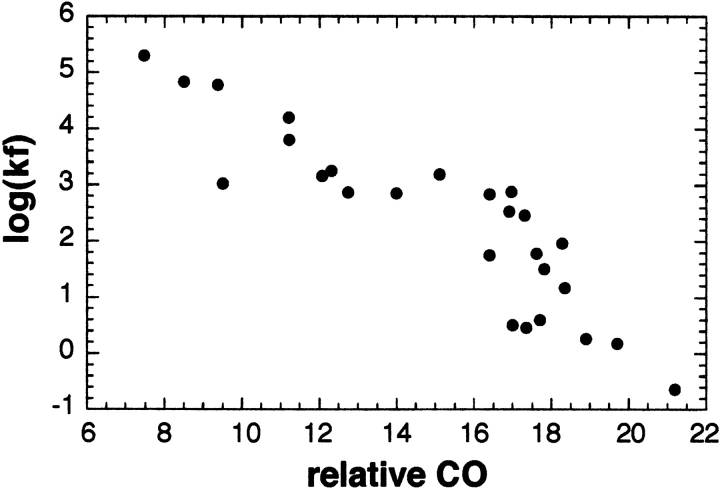
A recent experimental insight into protein folding from experimental work was the finding that protein folding rates are correlated with the relative contact order (CO) of the native structure (Plaxco et al. 1998; Grantcharova et al. 2001). The relative CO is the average sequence separation of residues that form contacts in the three-dimensional structure divided by the length of the protein. As illustrated in Figure 1 ▶, proteins with primarily local (close along the sequence) contacts fold more rapidly than do proteins with primarily nonlocal contacts. The dependence of folding rates on the CO reflects the contribution of chain entropy loss to the folding free energy barrier—low CO proteins can make stabilizing interactions early in folding with less loss in chain entropy than high CO proteins, and hence have lower folding free energy barriers. In the present study, we draw parallels between this experimental insight and current problems in ab initio protein structure prediction.
Fig. 1.
Correlation between relative contact order (CO) and folding rate. The relative CO is plotted against the log folding rate for proteins with structures known to fold via single exponential kinetics (Plaxco et al. 1998; Grantcharova et al. 2001).
We have recently developed a method for ab initio protein structure prediction, Rosetta, which is based on a picture of protein folding in which local sequence segments flicker between different possible local structures, and folding occurs when the conformations and relative orientations of these segments allow burial of the hydrophobic residues and pairing of the β–strands without steric clashes (Simons et al. 1997, 1999a,b; Bonneau et al. 2001). A key assumption underlying the procedure is that the distribution of structures sampled by an isolated chain segment is reasonably well approximated by the distribution of conformations adopted by that sequence segment and related sequence segments in the protein structure database. Nonlocal interactions are optimized by a Monte Carlo search through the set of conformations that can be built from the observed local structures for each sequence segment to produce structures that have low free energy local and nonlocal interactions.
Because the conformational search is a stochastic procedure, different simulations starting from different random seeds will produce different final structures. Our standard procedure is guided by the experimental observation that the folding of most small proteins is a single exponential process; that is, the probability of folding to the native structure is independent of time for an individual polypeptide chain. Thus, if simulations do not become trapped in local minima, the yield of correctly folded structures in many short simulations should be similar to that obtained in a small number of long simulations that involve the same total simulation time. Because of a drastic slowing down of the dynamics in the collapsed state during Rosetta simulations, we have found the many short simulation strategy to be the most effective in practice. Large numbers of independent short simulations are performed, and the resulting structures are clustered to identify the broadest minima in the folding free energy landscape(Shortle et al. 1998). The CASP3 (critical assessment of structure prediction) and CASP4 protein structure prediction experiments have shown that Rosetta is one of the best current methods for structure prediction in the absence of a homolog of known structure (Simons et al. 1999a, Bonneau et al. 2001b).
Results and Discussion
CO and structure prediction
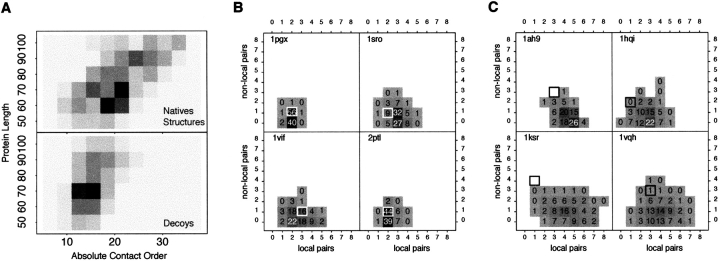
The experimentally observed relationship between CO and protein folding rates prompted us to examine the dependence of Rosetta ab initio folding simulations on the native state CO. Figure 1 ▶ indicates that during the actual folding process, high CO structures are sampled much less frequently than are lower CO structures, and thus, if the simulations parallel the folding process, they might be expected to produce primarily low CO structures. The absolute CO distributions in native and Rosetta–generated structures are compared in Figure 2A ▶. For proteins of >80 residues, high CO conformations are clearly undersampled in the Rosetta–generated structures. For β–sheet proteins, the failure to produce high CO structures results in a critical overabundance of local β–strand pairing arrangements and a deficit of nonlocal strand pairing in the Rosetta–generated conformations relative to native structures (Fig. 2C ▶).
Fig. 2.
Comparison of absolute contact order (CO) distributions of native and simulated structures. (A) The CO distribution of native structures (top) and 152,000 decoys (bottom) generated for 152 proteins using Rosetta for different length ranges (y–axis). Absolute CO was used here rather than relative CO because it more clearly differentiates the native and decoy populations. Because Rosetta decoys do not have explicit side–chains, two residues are considered contacting if their β–carbons are within 8 Å. To avoid biases from the fragment libraries, contacts between residues closer than three sequence positions apart were discounted from the calculation. (B) Two–dimensional histograms of the number of local and nonlocal strand pairings found in Rosetta decoy populations for four relatively local proteins are shown. The numbers superimposed on the boxes correspond to the percentage of decoys in the population of decoys generated for each protein that have that combination of local and nonlocal pairings. The pattern of strand pairing found in the correct native structure for each protein is indicated by a box surrounding the correct bin. Notice that for these four simulations, the native structure falls well within the CO distribution. (C) Same as in B for decoy populations for four proteins with higher CO topologies. The native structures (indicated by black boxes) now fall in sparsely populated or unpopulated regions of the decoy CO distribution, illustrating the need for correcting the systematic CO bias of Rosetta when folding more nonlocal proteins.
The failure to produce substantial numbers of high CO conformations is clearly a problem for ab initio protein structure prediction—many native proteins have COs outside of the range frequently sampled by Rosetta. Initial attempts to remedy the problem by explicitly favoring high CO structures during the simulation were not successful, probably because biases toward nonlocal interactions quench the conformational search process, as do nonlocal constraints(Bowers et al. 2000). A somewhat more successful approach takes advantage of the observation that high CO conformations are generated, albeit at very low frequencies, in standard Rosetta simulations: A very large number of independent simulations are performed, and the resulting conformations are filtered to correct for the drastic overrepresentation of lower CO conformations. This strategy was first tested by attempting the folding of five proteins among the most complex for their size range (four of the five were IgG folds between 80 and 120 residues in length, whereas the fifth was a 126 residue β–propeller [1bfg]). The standard Rosetta protocol produces primarily low CO conformations for these proteins, whereas the correct native states have high COs. After the production of very large numbers of additional independent conformations using approximately two orders of magnitude more computing time, populations were filtered to eliminate the majority of the overly low CO structures (the filtered population is equal in size to the original population but has a higher fraction of high CO conformations; see Materials and Methods). The standard clustering procedure (Bonneau et al. 2001), applied to these CO–normalized populations, resulted in correct first rank clusters for the two smallest proteins in the set (1ten and 1tit; see Fig. 3 ▶), but did not converge on correct models for the three larger proteins (1wiu, 1tul, 1bfg), probably because even this 100–fold increase in sampling was not sufficient to adequately sample higher CO conformations for these larger proteins.
Fig. 3.
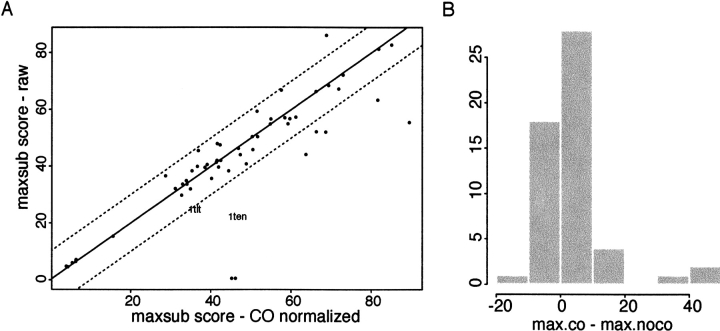
Performance of Rosetta with contact order (CO) filtering. Rosetta simulations were performed for 54 proteins, the conformations with COs lower than that seen in 95% of proteins of similar length and secondary structure class were discarded, and approximately one order of magnitude of more computer time was used to generate additional high CO conformations. The quality of these CO–normalized (filtered and enriched with respect to CO) populations are compared to populations of equal numbers of unfiltered decoy conformations. (A) The similarity to the native structure of the top 10 cluster centers for each protein obtained, both with and without this normalization of the CO distribution, was assessed using MaxSub (Siew et al. 2000). The higher the MaxSub score, the more superimposable a predicted structure is on the native structure. The score is highly correlated with the length of the correctly predicted region for a given prediction and was shown at CASP3 (critical assessment of structure prediction) to reproduce the rankings given to predictions by experts in the field (Siew et al. 2000). The y–axis in the figure is the highest MaxSub score obtained for any of the top 10 cluster centers without CO renormalization; the x–axis is the highest MaxSub score obtained after CO renormalization (2000 conformations were clustered in both cases). The improvements evident for seven of the proteins in the bottom right of the figure are quite large: Before CO normalization, 1kte (far right) was predicted to within 5.5 Å over 75 residues; after CO normalization, 99 residues were predicted to 2.9 Å root mean square deviation (RMSD). For two proteins (1dun and 1c1l; bottom of plot) Rosetta did not converge at all before CO filtering but produced models with 64 of 120 residues predicted with an RMSD of 5.5 Å and 55 of 136 residues predicted at 4.4 Å RMSD. (B) The improvement in MaxSub score obtained for the CO–normalized populations in part A is shown as a histogram.
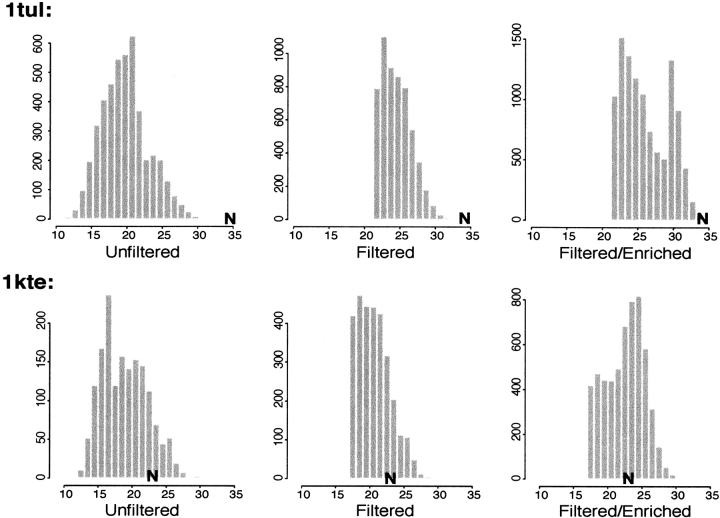
A more comprehensive test of the CO normalization (see Materials and Methods) was performed for the 54 most challenging α/β and β–proteins (between 60 and 150 residues in length) in a previously described test set (Simons et al. 2001) using approximately one order of magnitude more computing time to increase the frequency of higher CO structures, rather than the two orders of magnitude more computing time used in the cases described above. The more extensive normalization performed for the five large β–sheet proteins was not feasible for a large test set, given current computer resources. In a number of cases, significant improvement was seen in the quality of models selected by our automatic clustering procedure (Fig. 3 ▶), despite the only partial readjustment of the CO distributions possible owing to computing time limitations. Comparison of the CO distributions of the unfiltered and CO–normalized decoy populations to the correct native CO values show that for some cases, the filtering and enriching procedure was sufficient to shift the CO distribution into the native range (1kte; Fig. 4 ▶) and lead to correct predictions from populations that, before the filtering, produced incorrect predictions, whereas for other, more topologically complex proteins (1tul; Fig. 4 ▶), the normalization did not sufficiently sample high CO regions of conformational space.
Fig. 4.
Contact order (CO) distributions for filtered and unfiltered decoy populations: For both proteins, the CO of the native protein is indicated on all histograms by a bold "N." Unfiltered indicates standard populations of Rosetta decoys; filtered, populations for which the lower cutoff (shown in Fig. 6 ▶) was applied to remove overly local conformations; and filtered/enriched, populations filtered with the lower CO filter and then enriched with respect to higher CO bins with approximately one order of magnitude more sampling. (Top). The unfiltered CO distribution (left) for 1tul shows that the CO distribution is clearly below what is seen for β–proteins ∼100 residues in length. The minimal filter rids the population of overly local structures but leaves the high CO region near the native state relatively undersampled (middle). The filtered and enriched population still leaves the native–like high CO region of the distribution minimally sampled, and clustering this population produces incorrect fold predictions. (Bottom) The upper tail of the unfiltered CO distribution for 1kte (left) encompasses the native state, but attempts to cluster this protein nevertheless produce overly local, incorrect, cluster centers. The enriched–filtered population (bottom right) is well sampled in the native–like regions of the CO distribution, and clustering this filtered enriched population results in correct top ranked clusters.
Why does the CO enrichment only improve model quality for a relatively small subset of proteins in the test set? First, Rosetta may fail for reasons other than high CO; for example, Rosetta may fail if the secondary structure predictions that contribute to the fragment selection process are in error. Secondary structure prediction methods consider only residues in a window surrounding the residue being predicted and might be expected to be less accurate when a larger percentage of contacts involve residues outside the window. Indeed, secondary structure predictions for high CO structures were somewhat worse than those for low CO structures in CASP4 (data not shown). Second, for a subset of proteins in the test set, the CO distribution was already adequately sampled before the enrichment process, whereas other proteins were so large and complex that the CO filtering was not enough to effect a noticeable improvement. Thus, we see improvement primarily for proteins in the test set on the cusp of what was possible before the CO normalization.
Casp4 results
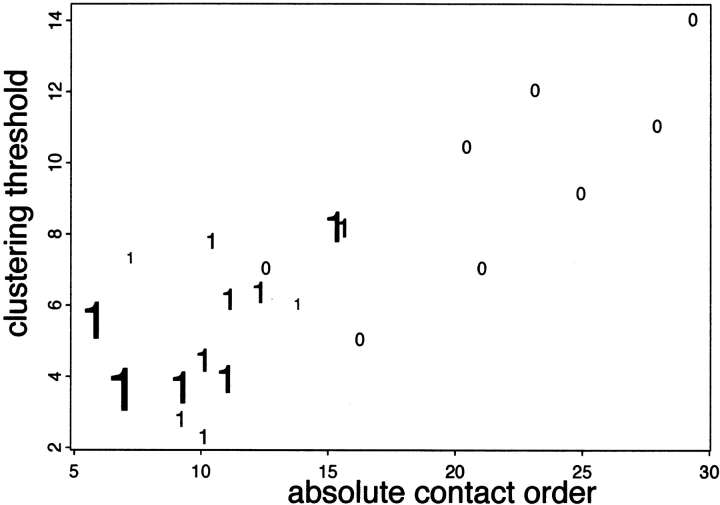
The renormalization of the CO distributions produced by Rosetta was a central part of our ab initio structure prediction protocol during the CASP4 structure prediction experiment. For the larger of the targets, we were unable, even with considerable computer time, to generate CO distributions matching those of native proteins of similar length and secondary structure class. This inability to adequately sample the highest CO structures is consistent with Figure 1 ▶: High CO proteins can take up to six orders of magnitude longer to fold than do low CO proteins, and by analogy, adequately sampling conformational space for high CO proteins may take vastly more computer time. Despite this inability to fully sample higher CO conformations for the larger targets (see Fig. 5 ▶), we produced good blind predictions for 17 of the 21 domains (ranging in size from 70 to 300 residues in length) attempted using our standard ab initio folding protocol (Bonneau et al. 2001b).
Fig. 5.
Contact order (CO) and CASP4 (critical assessment of structure prediction) predictions. The correlation between CO and clustering threshold for CASP4 predictions. The clustering threshold is the root mean square deviation (in Å) of the largest cluster; thus, the smaller the clustering threshold, the more tightly Rosetta converged. Targets for which our best submitted models had significant portions predicted to within 6.5 Å are shown as "1"; targets for which our predictions were incorrect are indicated as zeros. The size of the "1s" are proportional to the Dali Zscore between the best model and the correct native, thus larger "1s" indicate stronger successes. Simulations for most proteins with lower CO native structures converged on correct models, whereas simulations for most high CO proteins were less converged and resulted in incorrect models.
As is evident in Figures 2 and 5 ▶ ▶, there is a strong inverse correlation between the CO of the native state and the probability of the Rosetta method generating a native–like model. Intriguingly, there is also a correlation between the CO of the native structure and the extent to which the simulations for a given target converged. As illustrated in Figure 5 ▶, the simulations for low CO proteins converged more than simulations for high CO proteins. Although the CO of the native structure is not known before the determination of the three–dimensional structure, the results shown in Figure 5 ▶ indicate that CO can be predicted to some degree based on the extent to which the Rosetta simulation of a given protein converged. A somewhat fanciful use of this information would be to predict the folding rate of the protein (Fig. 1 ▶). A more exciting possibility is to use the relationship between simulation convergence and CO to improve the performance of Rosetta on more complex proteins with highly nonlocal structures. After the estimation of the CO of the native structure from the extent of convergence of a set of preliminary simulations, conformations in this CO range could be selected from a very large number of further independent simulations. An obvious feature of this proposed procedure is the likely requirement for very large amounts of computer time (generating suitable numbers of high CO structures could take orders of magnitude of more computer time than used to generate our CASP4 predictions)—this may be an area in which powerful computers such as Blue Gene (http://www.research.ibm.com/bluegene/) could contribute. Given the widely recognized problems with current potential functions (Park and Levitt 1996; Park et al. 1997), computer time has not been a major limitation for most current ab initio prediction strategies (all too many conformations with computed energies lower than the native structure can be generated in relatively small amounts of computer time), and thus, this clear role for substantial computer time is noteworthy.
There is a fairly intuitive explanation of the origin of the CO–simulation convergence relationship. Low CO structures are readily sampled in the short folding times to which our Rosetta simulations correspond. If the native structure is low in CO, there will be a readily accessible low free energy minimum (the native state), and a large fraction of the simulations will end up in the same minimum. Conversely, if the native structure is high in CO, there will not be a readily accessible low free energy minimum, and different simulations will end up dispersed throughout the free energy landscape.
Conclusions
The dependence of both protein folding rates and the success rate of Rosetta on the CO of the native state indicate that the simulation procedure mimics some aspects of the folding of real proteins. The necessity of ordering a large fraction of the chain before large numbers of stabilizing interactions can be formed for high CO proteins is likely to lead to a large entropic barrier to folding both in solution and in silico. The parallels between folding in silico and in vivo may extend further to misfolding. The assembly of misfolded proteins into amyloid fibrils with β–strands perpendicular and β–sheets parallel to the fiber axis is associated with many human diseases (Sunde et al. 1997); recent studies of fibrils derived from an SH3 domain indicate that the strands are packed into quite flat β–sheets (Jiminez et al. EMBO 1999). The most prevalent low CO structures generated in Rosetta simulations consist of flat β–sheets formed by all local β–hairpins (Fig. 2B ▶), and it is tempting to speculate that these structures resemble the precursors to amyloid formation. This conjecture is consistent with the ubiquitous and confounding presence of low CO β–sheet structures in Rosetta simulations, which parallels recent findings that indicate almost all proteins can form fibrils (Bucciantini et al. 2002), and with what is known about the structure of amyloid fibrils. Confirmation, however, must await higher–resolution structural information on fibrils and their precursors. Conversely, the very low CO conformations that accumulate in Rosetta simulations for proteins that form fibrils could perhaps serve as tentative models to guide experimental characterization of the process of amyloid formation.
Although this work deals primarily with the Rosetta ab initio prediction method, the problems we face when predicting larger, more complex topologies also seem to limit other current ab initio procedures; performance on large complex targets was considerably worse for ab initio methods at CASP3 and CASP4. Although the high resolution necessary for drug design is still far out of reach, ab initio structure prediction using Rosetta has now improved to the point at which reasonable models can be produced for large fragments of most domains <150 amino acids in length, and significant progress in predicting the structures of the remaining proteins may be possible with increases in computing power together with use of the CO–simulation convergence correlation.
Materials and methods
Model generation
Fragment libraries for each three– and nine–residue segment of the chain are extracted from the protein structure database using a sequence profile–profile comparison method as described previously (Simons et al. 1997). At no point is knowledge of the native structure used to select fragments or fix segments of the structure. The conformational space defined by these fragments is then searched using a Monte Carlo procedure with an energy function that favors compact structures with paired β–strands and buried hydrophobic residues. Independent simulations are performed (starting from different random number seeds) for each query sequence, and the resulting structures are filtered and then clustered as described below and previously. Before clustering, the majority of structures produced by Rosetta are incorrect (i.e., good structures account for <10% of the conformations produced); for this reason, we refer to conformations generated by Rosetta as decoys.
Determination of CO bins
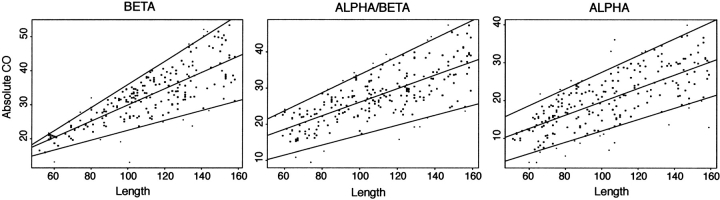
Estimation of the allowable CO range for different length and secondary structure classes was performed using a nonredundant set of proteins from 50 to 160 residues in length provided by Roland Dunbrack (Hobohm et al. 1993). Absolute CO was used as in Figure 1 ▶. Two residues were considered contacting if their β–carbons are within 8 Å. Contacts between residues closer than three positions along the sequence were not included in the calculation. Because CO is length dependent, we chose to make the boundaries of our CO bins length dependent. For each secondary structure class, all possible sets of lines were generated that divided the plot of CO versus length into lower 5%, lower–middle 45%, upper–middle 45%, and upper 5% regions. For each percentile range, the delimiting line that best maintained the specified partitioning of the CO distribution across the entire length interval was then selected. The resultant length-dependent binning of the CO length distribution for native proteins is shown in Figure 6 ▶.
Fig. 6.
Contact order (CO)–length distribution for native proteins. The CO is plotted against length for a nonredundant set of proteins with lengths between 50 and 160 residues in length for three secondary structure classes. Length–dependent CO bins are defined by the three lines present in each plot. The region below the bottom–most line contains 5% of native proteins. The middle line separates the upper 50% CO bin from the lower 50% bin, whereas the top line delimits the upper 5% CO bin. These defining lines were fit to the data as described in Materials and Methods.
Filtering procedure
The protocol for generating decoy populations with improved CO distributions has two main phases. In the first phase of the protocol, decoys are generated using the standard method and discarded only if they have COs lower than that seen for native proteins of comparable length and secondary structure class. This first set of runs thus fills in the lower part of the CO distribution and only discards extremely local (and thus grossly nonnative) conformations. The second phase aims to enrich higher CO regions of the CO distribution seen for native proteins of comparable size and secondary structure. This is performed by generating large numbers of decoys and only accepting conformations that fall within the upper 10% to 20% of the CO distribution seen for the original Rosetta runs for that protein. As roughly one in 10 simulations will produce decoys in the top tenth percentile, setting the cutoff at the tenth percentile will lead to the generation of a roughly equal number of decoys using 10–fold the computing time required to generate the initial population, whereas if the upper limit was set based on the native CO distribution (Fig. 6 ▶), the number of decoys passing the filter in 10× time could be extremely small.
The comprehensive in-house test of the method was performed on 54 proteins from a previously described test set (Simons et al. 2001) by first generating ∼2000 decoys for each protein in the set with only a minimal CO cutoff filter in place (decoys were discarded if their CO was in the lowest 5% bin of the CO distribution for native proteins of comparable length; Fig. 6 ▶; a list of the 54 proteins is available as supplemental information). Approximately 10 times the computer time used to generate the initial runs was then used to generate further decoys with COs >80th percentile in the original runs. The CO–filtered population was then clustered as described below. A population of equal size to the CO-normalized population was also generated and clustered as described below for comparison. A comparison of the results of clustering these two populations (the unfiltered versus the extensively CO–normalized results) is shown in Figure 3 ▶.
For CASP4, an average of 100,000 conformations were generated per target, and those with COs lower than the lower CO cutoff (the lowest delimiting line in Fig. 6 ▶) were discarded (on average ∼70% of the conformations generated were discarded because of low CO or improperly paired beta–strands). Other filters were used as well to ensure proper packing and correct strand arrangement before clustering and model selection (Bonneau 2001; Ruczinski 2002).
Clustering procedure
The procedure for clustering populations of decoys that survive the filtering step has been described previously (Shortle 1998; Bonneau et al. 2001a). Two structures are considered neighbors if they are closer in Cα root mean square deviation than an empirically derived cutoff. The clustering procedure is iterative and begins by calculating a list of neighbors for each structure. The structure with the largest number of neighbors according to this list is then the center of the first, largest cluster. The root mean square deviation cutoff for considering two structures neighbors is started at 8.0 Å and iteratively reduced until the first cluster contains 50 or 100 decoys or until the cutoff has reached a lower threshold of 3.0 Å (a lower resultant clustering threshold is indicative of a more tightly converged population). Once one of these conditions is met, the cutoff is fixed for the remaining iterations. The first cluster center is written out, and its neighbors are removed from the population. The process is repeated on the remaining population until the cluster produced contains fewer than five neighbors. For populations <3000 decoys, the first cluster was set to contain 50 members; for populations >3000, the first cluster was set to contain 100 decoys.
Acknowledgments
R.B. acknowledges the support of an HHMI predoctoral fellowship. We thank Daniel Fischer for suggesting the use of MaxSub to evaluate decoys and for the MaxSub program, and Art Horwich for suggesting the connection to amyloid formation. We thank Formix for effective and innovative administration of the computer resources necessary to complete this study. This work was supported by the Howard Hughes Medical Institute.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.3790102.
References
- Baldwin, R.L. and Rose, G.D. 1999. Is protein folding hierarchic? II: Folding intermediates and transition states. Trends Biochem. Sci. 24 77–83. [DOI] [PubMed] [Google Scholar]
- Bonneau, R., Strauss, C.E.M., and Baker, D. 2001. Improving the performance of ROSETTA using multiple sequence alignment information and global measures of hydrophobic core formation. Proteins 43 1–11. [DOI] [PubMed] [Google Scholar]
- Bonneau, R., Tsai, J., Ruczinski, I., and Baker, D. 2001a. Functional inferences from blind ab initio protein structure predictions. J. Struct. Biol. 134 186–190. [DOI] [PubMed] [Google Scholar]
- Bonneau, R, Tsai, J., Ruczinski, I., Chivian, D., Rohl, C., Strauss, C.E.M., and Baker, D. 2001b. Rosetta in CASP4: Progress in ab initio protein structure prediction. Proteins 45 119–126. [DOI] [PubMed] [Google Scholar]
- Bowers, P.M., Strauss, C.E., and Baker, D. 2000. De novo protein structure determination using sparse NMR data. J. Biomol. NMR 18 311–318. [DOI] [PubMed] [Google Scholar]
- Bowie, J.U. and Eisenberg, D. 1994. An evolutionary approach to folding small α-helical proteins that uses sequence information and an empirical guiding fitness function. Proc. Natl. Acad. Sci. 91 4436–4440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucciantini, M., Giannoni, E., Chiti, F., Baroni, F., Formigli, L., Zurdo, J., Taddei, N., Ramponi, G., Dobson, C.M., and Stefani, M. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature 416 507–511. [DOI] [PubMed] [Google Scholar]
- Fersht, A. 1998. Structure and mechanism in protein science. W.H. Freeman, New York.
- Grantcharova, V., Alm, E., Baker, D., and Horowich, A. 2001. Mechanisms of protein folding. Curr. Opin. Struct. Biol. 11 70–82. [DOI] [PubMed] [Google Scholar]
- Hobohm, U., Scharf, M., and Schneider, R. 1993. Selection of representative protein data sets. Protein Sci. 1 409–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson, S.E. 1998. How do small single-domain proteins fold? Fold Des. 3 R81–R91. [DOI] [PubMed] [Google Scholar]
- Jimenez, J.L., Guijarro, J.I., Orlova, E., Zurdo, J., Dobson, C.M., Sunde, M., Saibil, H.R. 1999. Cryo-electron microscopy structure of an SH3 amyloid fibril and model of the molecular packing. EMBO J. 18 815–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, B. and Levitt, M. 1996. Energy functions that discriminate X-ray and near native folds from well-constructed decoys. J. Mol. Biol. 258 367–392. [DOI] [PubMed] [Google Scholar]
- Park, B.H., Huang, E.S., and Levitt, M. 1997. Factors affecting the ability of energy functions to discriminate correct from incorrect folds. J. Mol. Biol. 266 831–846. [DOI] [PubMed] [Google Scholar]
- Pedersen, J.T. and Moult, J. 1997. Protein folding simulations with genetic algorithms and a detailed molecular description. J. Mol. Biol. 269 240–259. [DOI] [PubMed] [Google Scholar]
- Plaxco, K.W., Simons, K.T., and Baker, D. 1998. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 277 985–994. [DOI] [PubMed] [Google Scholar]
- Plaxco, K.W., Simons, K.T., Ruczinski, I., and Baker, D. 2000. Topology, stability, sequence, and length: Defining the determinants of two-state protein folding kinetics. Biochemistry 39 11177–11183. [DOI] [PubMed] [Google Scholar]
- Ruczinski, I., Kooperberg, C., Bonneau, R., and Baker, D. 2002. Distributions of beta sheets in proteins with application to structure prediction. Proteins 48 85–97. [DOI] [PubMed] [Google Scholar]
- Samudrala, R., Xia, Y., Levitt, M., and Huang, E.S. 1999. A combined approach for ab initio construction of low-resolution protein tertiary structures from sequence. Pac. Symp. Biocomput. 505–516. [DOI] [PubMed]
- Shortle, D., Simons, K.T., and Baker, D. 1998. Clustering of low-energy conformations near the native structures of small proteins. Proc. Natl. Acad. Sci. 95 11158–11162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siew, N., Elofsson, A., Rychlewski, L., and Fischer, D. 2000. MaxSub: An automated measure for the assessment of protein structure prediction quality. Bioinformatics 16 776–785. [DOI] [PubMed] [Google Scholar]
- Simons, K.T., Kooperberg, C., Huang, E., and Baker, D. 1997. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol. 268 209–225. [DOI] [PubMed] [Google Scholar]
- Simons, K.T., Bonneau, R., Ruczinski, I., and Baker, D. 1999a. Ab initio protein structure prediction of CASP III targets using ROSETTA. Proteins 37 171–176. [DOI] [PubMed] [Google Scholar]
- Simons, K.T., Ruczinski, I., Kooperberg, C., Fox, B.A., Bystroff, C. & Baker, D. 1999b. Improved recognition of native-like protein structures using a combination of sequence-dependent and sequence-independent features of proteins. Proteins 34 82–95. [DOI] [PubMed] [Google Scholar]
- Simons, K.T., Strauss, C., and Baker, D. 2001. Prospects for ab initio protein structural genomics. J. Mol. Biol. 306 1191–1199. [DOI] [PubMed] [Google Scholar]
- Sunde, M., Serpell, L.C., Bartlam, M., Fraser, P.E., Pepys, M.B., and Blake, C.C. 1997. Common core structure of amyloid fibrils by synchrotron X-ray diffraction. J. Mol. Biol. 273 729–739. [DOI] [PubMed] [Google Scholar]