Interatomic potentials and solvation parameters from protein engineering data for buried residues

Abstract

Van der Waals (vdW) interaction energies between different atom types, energies of hydrogen bonds (H-bonds), and atomic solvation parameters (ASPs) have been derived from the published thermodynamic stabilities of 106 mutants with available crystal structures by use of an originally designed model for the calculation of free-energy differences. The set of mutants included substitutions of uncharged, inflexible, water-inaccessible residues in α-helices and β-sheets of T4, human, and hen lysozymes and HI ribonuclease. The determined energies of vdW interactions and H-bonds were smaller than in molecular mechanics and followed the "like dissolves like" rule, as expected in condensed media but not in vacuum. The depths of modified Lennard-Jones potentials were −0.34, −0.12, and −0.06 kcal/mole for similar atom types (polar–polar, aromatic–aromatic, and aliphatic–aliphatic interactions, respectively) and −0.10, −0.08, −0.06, −0.02, and nearly 0 kcal/mole for different types (sulfur–polar, sulfur–aromatic, sulfur–aliphatic, aliphatic–aromatic, and carbon–polar, respectively), whereas the depths of H-bond potentials were −1.5 to −1.8 kcal/mole. The obtained solvation parameters, that is, transfer energies from water to the protein interior, were 19, 7, −1, −21, and −66 cal/moleŲ for aliphatic carbon, aromatic carbon, sulfur, nitrogen, and oxygen, respectively, which is close to the cyclohexane scale for aliphatic and aromatic groups but intermediate between octanol and cyclohexane for others. An analysis of additional replacements at the water–protein interface indicates that vdW interactions between protein atoms are reduced when they occur across water.

The computational modeling of protein structure still remains a challenging problem because of insufficiently precise and reliable energy functions. There are many different types of the empirical potentials, including molecular mechanics force fields, various solvation models, statistically derived or knowledge-based score functions, and others (Halgren 1995; Juffer et al. 1995; Sippl 1995; Eldridge et al. 1997; Vajda et al. 1997; Samudrala and Moult 1998; Gordon et al. 1999; Roux and Simonson 1999; Lazaridis and Karplus 2000). Nevertheless, it has been often observed that energies of incorrect protein models, when calculated with the existing potentials, are nearly the same or even better than in the native structure (Yue and Dill 1996; Park et al. 1997; Hao and Scheraga 1999; Lomize et al. 1999a; Simons et al. 2001).

It is accepted that the appropriate energy functions would reproduce the thermodynamic stabilities, that is, free energies of proteins and protein–ligand complexes (Kollman 1993; Fersht 1999). However, the calculation of free energy is a difficult undertaking. For example, molecular mechanics potentials have been designed for calculation of conformational energies (enthalpies) of organic molecules in vacuum (Halgren 1995; Lazaridis et al. 1995). The conformational energy of a protein (several hundreds or thousands of kcal/mole) does not reflect its thermodynamic stability for many reasons. First, all interactions of electrostatic origin, including van der Waals (vdW) dispersion attraction and hydrogen bonds (H-bonds), depend on dielectric properties of the environment (Wood and Thompson 1990; Israelachvili 1992; Leckband and Israelachvili 2001), and therefore their energies are expected to be different in vacuum, within the interior of proteins, and in water. Second, the contributions of ion pairs, H-bonds, or hydrophobic contacts to the protein stability can be significantly reduced when they are formed by flexible side chains (Shortle 1992; Fersht and Serrano 1993; Scholtz et al. 1993; Matthews 1995a), which must be taken into account. Third, the intramolecular energy of the polypeptide chain must be supplemented by conformational entropy (Brady and Sharp 1997) and solvation free energy. The corresponding atomic solvation parameters (ASPs) for different atom types can be derived from experimental transfer energies of model compounds from water to octanol or cyclohexane. However, these organic solvents can serve only as a crude approximation of the protein interior. Moreover, many published solvation parameter sets are poorly consistent with each other (Juffer et al. 1995). Fourth, the quantity of interest is not the energy of the folded structure alone but rather the difference of free energies of folded and unfolded states (Shortle 1992, 1996; Koehl and Levitt 1999).

There are two important questions here: What theory would be appropriate for free-energy calculations, and how to determine parameters of energy functions. Experimental thermodynamics studies provide a basis to resolve these questions. This rapidly evolving field includes measurements and interpretation of free energy, entropy, enthalpy, and heat capacity changes associated with peptide and protein folding, mutations, conformational transitions, ligand binding, or transfer of model compounds (Fersht and Serrano 1993; Matthews 1993, 1995b; Chakrabartty and Baldwin 1995; Makhatadze and Privalov 1995; Robertson and Murphy 1997; Luque and Freire 1998; Gohlke and Klebe 2001; Rees and Robertson 2001). The accumulated data provided energetic estimates of hydrophobic interactions, ion pairs, H-bonds, conformational entropy, and other contributions to the protein stability. However, application of these estimates to the practical modeling of protein structure, such as fold recognition or de novo design, is not straightforward. For example, vdW and solvation energies, which are crucially important for protein modeling, have been estimated using rough approximations. Indeed, all "nonpolar" atoms (sulfur, aliphatic, and aromatic groups) were usually described by a single solvation parameter, even though this was not supported by studies of organic compounds (Makhatadze and Privalov 1994). Also, vdW interactions in proteins were treated as cavity formation or packing density terms (Eriksson et al. 1992; Jackson et al. 1993; Funahashi et al. 2001), that is, not using specific energies for different types of atoms and without explicit distance-dependent potentials.

In the present work, we determined the energies of vdW interactions between specific atom types in the protein interior and ASPs on the basis of published protein-engineering data. To bypass a number of difficulties, we designed a specific model for calculation of the free-energy differences and selected the set of mutants using very restrictive criteria. First, only mutants with high-resolution crystal structures available were used to take into account the conformational relaxation of protein structure after the substitutions. Second, the replaced residues had to be buried from water, because interactions at the protein surface may be different (Shortle 1992; Matthews 1995a). It is important that most of the buried residues had a limited conformational flexibility, judging from the low B-values of their atoms. Third, substitutions of charged residues were not included in the set to omit the explicit Coulomb electrostatics that need to be studied separately. Finally, we used only replacements in α-helices and β-sheets, because the secondary structures can serve as well-defined reference states for calculation of ΔΔG values, whereas the properties of coil are poorly defined and understood (Shortle 1992, 1996; Creamer et al. 1995, 1997; Plaxco and Gross 2001).

Theory

The calculated free-energy changes, ΔΔG^clc, were represented as a combination of contributions of residues that are identical in the wild-type and mutant proteins (ΔΔG_ident) and those that have been replaced (ΔΔG_repl):

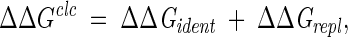(1)

The contribution of identical residues was given by

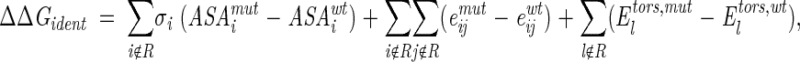(2)

where the summation extends over all atoms i and j that do not belong to the set R of replaced residues; (ASA_i^mut − ASA_i^wt) is the difference of accessible surface areas (ASA) of atom i in the wild-type and mutant proteins, σ_i is the ASP for the corresponding type of atom (Juffer et al. 1995); (e_ij^mut − e_ij^wt) is the difference between interaction energies of atoms i and j (i ≠ j) in the proteins, and (E_l^tors,mut − E_l^tors,wt) is the difference of torsion potentials for angle l.

The contribution of replaced residues ΔΔG_repl was calculated using a model that was designed for substitutions in the regular secondary structures. The model was based on a thermodynamic cycle, in which an α-helix or β-sheet in aqueous solution serves as a reference state (Fig. 1 ▶). For replacement of N α-helical or β-sheet residues (X₁ → Y₁, X₂ → Y₂, . . . X_N → Y_N),

(3)

where ΔG_mut^transition and ΔG_wt^transition are free-energy changes, for the sets of residues (X) and (Y), during conformational transition from the reference to the folded state (Fig. 1 ▶), and ΔΔG^prop,mut and ΔΔG^prop,wt are experimental secondary structure propensities, that is, free-energy changes associated with replacement of the "host" Ala residue by (X) and (Y) residues in the model α-helix or β-sheet (Chakrabartty and Baldwin 1995).

Fig. 1.

Thermodynamic cycle applied for calculation of ΔΔG_repl term from Equations 1 and 3 (a single residue X → Y substitution in α-helix). ΔΔG_Y^prop and ΔΔG_X^prop are experimental secondary structure propensities of residues X and Y, that is, free-energy changes associated with replacement of Ala by X and Y, respectively, in the reference secondary structure. ΔΔG_mut^transition and ΔΔG_wt^transition are energy changes for residues X and Y during the reference to folded state transition. Small arrows indicate vdW interactions of the substituted side chain with backbone of its own α-helix or β-sheet, which remain approximately the same during this transition, and the interactions with the rest of the protein, which arise during this transition. The cycle does not change for multiple replacements X₁ → Y₁, X₂ → Y₂, . . . X_N → Y_N, when (X) and (Y) are sets of residues.

The transition energy for the set of replaced residues R = (X₁, X₂, . . . X_N) in the wild-type protein (ΔG_wt^transition, Fig. 1 ▶) was defined as

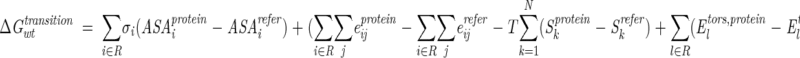(4)

where the first term represents the transfer energy of residues R from the water-exposed reference α-helix or β-sheet to the protein interior; the second term is the difference of interaction energies of side-chain atoms in the protein structure and the reference state; the third term is the conformational entropy contribution that originates from restraining χ angles in the protein structure relative to the model α-helix or β-sheet; and the last term is change of torsion energy during the reference to folded state transition. All substituted side chains of selected mutants had only one allowed conformation in the protein structure, that is, S_k^protein = 0. The transition energy of mutant protein (ΔG_mut^transition, Fig. 1 ▶) was defined as in Equation 4 but with its own set of residues R = (Y₁, Y₂, . . . Y_N).

Thus, theoretical ΔΔG values were calculated as the sum of the following contributions: (1) the enthalpic term describing changes of vdW interaction, H-bond and torsion energies of the protein caused by substitutions of the amino acid residues, (2) conformational entropies of the replaced side chains, (3) transfer energies of protein atoms from water to the protein interior, and (4) the secondary structure propensities (the last two terms include both enthalpic and entropic components). It is important that free energies in Equations 2 and 4 represented a difference between two conformational states of the same chemical structure, because comparisons of dissimilar molecules involve serious problems (Mark and van Gunsteren 1994; Boresch and Karplus 1995; Brady and Sharp 1995).

The described approach is not very different from other models applied for interpretation of protein-engineering data. However, none of these models use explicit vdW interaction and torsion potentials, and they all treat the reference state differently. The most common approximation simply does not consider any reference or unfolded protein states and implies that ΔΔG values arise from the differences of surface areas, cavity volumes, or other structural parameters of the wild-type and mutant folded structures (Shortle 1992, 1996; Matthews 1993). In terms of our model, this means elimination of ΣΣe^refer_ij term from Equation 4 and omitting conformational entropy, torsion potentials, and secondary structure propensities. Apparently, these and other neglected factors do not hinder determination of specific average energies, for example, for buried H-bonds in proteins (Myers and Pace 1996), but they make all the determined energetic parameters highly context dependent. An alternative model uses coil as a reference for calculation of buried surfaces and side-chain conformational entropies (Funahashi et al. 2001); however, it combines the parameters of coil with α-helix and β-sheet propensities, which is a mixture of different reference states.

Our model is also similar to molecular mechanics calculations, with the solvation and conformational entropy terms included (e.g., Morris et al. 1998^; Koehl and Levitt 1999^; de la Paz et al. 2001). However, these studies use potentials that were originally developed for conformational analysis of organic molecules in vacuum and therefore describe a different energy (see Discussion). Moreover, even the functional form of the standard potentials needed to be modified for our purpose. The following deviations from molecular mechanics were found to be important to reproduce the experimental ΔΔG values.

(1) All interatomic repulsions were omitted, because the experimental atomic coordinates were determined with a precision of ∼0.2–0.3 Å, which would produce significant errors in the calculated energies at short interatomic distances. The elimination of repulsions worked well after excluding a few mutants with artificially introduced strong sterical clashes (Liu et al. 2000) and when applied in combination with approximations (5) and (7) below. The 6–12 and 10–12 potentials were modified as follows:

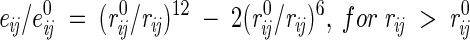(5)

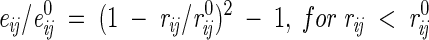for vdW interactions, and

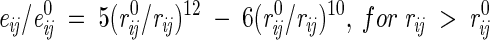for H-bonds, where r_ij is the distance between atoms i and j, e⁰_ij is the adjustable energy at the minimum of the potential, and r⁰_ij are the equilibrium distances, which were taken from ECEPP/2 (Nemethy et al. 1983). For distances shorter than r₀, these functions gradually converge to the point r_ij = 0, e_ij = 0, which practically eliminates the repulsions and allows adjustment of e⁰ values independently of r⁰ distances.

(2) Explicit Coulomb electrostatics were omitted, which is a possible approximation for uncharged groups (Dunitz and Gavezzotti 1999). Therefore, all electrostatic effects were implicitly included in the adjustable vdW and H-bond potentials.

(3) Hydrogen atoms were not included, as usual, in analysis of packing and accessible surfaces in proteins (Tsai et al. 1999). This was required to reduce the number of different atom types and the corresponding adjustable parameters.

(4) H-bonds were identified on the basis of the types of participating atoms and on the angles in A-B . . . C-D systems, where A, B, C, and D are nonhydrogen atoms: At least one of A-B . . . C or B . . . C-D angles had to be >90° in H-bond (otherwise the polar B and C atoms were considered as forming vdW interaction). The spatially closest H-bond partners of polar atoms in each replaced residue were identified automatically, assuming only one acceptor for each NH or OH group and two possible donors for each oxygen, in accordance with statistics of H-bonds in proteins (McDonald and Thornton 1994). This is a departure from molecular mechanics, in which each donor, for example NH group, would form H-bonds with all surrounding acceptor atoms (e.g., all oxygens in a radius of 8 Å), even though it actually could participate in only one H-bond.

(5) All backbone–backbone interactions within α-helices and β-sheets were excluded from Equations 2 and 4, because these interactions were assumed to be the same in wild-type and mutant proteins.

(6) Equation 4 includes energies of interactions between each replaced side chain and backbone of its α-helix or β-sheet in aqueous solution (e_ij^refer). This term is difficult to calculate precisely because it depends on conformational averaging, which is more significant for some residues than others. Moreover, the dynamic averaging can significantly weaken H-bonds, because they are geometrically allowed only in a very narrow range of side-chain torsion angles, whereas vdW contacts are much less specific. It has been empirically found that two approximations, when applied together, provide a good fit of ΔΔG values: (a) All H-bonds between the side chain of the replaced residue (typically Ser or Thr) and the backbone of α-helix or β-sheet containing this residue are absent in the reference secondary structures but appear when the residue is buried in the protein; and (b) the total energy of vdW interactions between the side chain of the replaced residue and the backbone of its own regular secondary structure does not change during the reference to folded state transition (Fig. 1 ▶), so the (e_ij^protein − e_ij^refer) difference in Equation 4 is zero. Therefore, the e_ij^refer sum was omitted, and the corresponding side-chain-backbone vdW interactions (but not H-bonds) were simultaneously excluded from e_ij^protein term.

(7) Summation over a large set of interactions for atoms with imprecise coordinates causes accumulation of errors. Therefore, only interactions of the replaced or strongly shifted residues with each other and with the surrounding atoms, excluding flexible side chains, were taken into account as described in Materials and Methods.

(8) Three buried water molecules that are present in almost all crystal structures of T4 lysozyme and its mutants were included as a part of the protein core, that is, they contributed to the sums of e_ij. The entropic cost of bound solvent (Dunitz 1994) was not included, because these water molecules were present in both the wild-type and mutant structures. Three similar solvent molecules in human lysozyme structure were treated in the same way.

(9) Side-chain torsion potentials were applied using an adjustable energy barrier that was the same for all "aliphatic" C-C and C-S bonds (Momany et al. 1975). The potential was "softened" to account for the imprecisely determined atomic coordinates (see Materials and Methods). Torsion energy in the model α-helix or β-sheet (E_l^tors,refer in Equation 4), originating from dynamic averaging of χ angles in the reference structures, was neglected.

Results

Fixed parameters of the model

Calculations with our model require secondary structure propensities, side-chain conformational entropies, and atomic ASA of residues in the reference α-helix and β-sheet (Table 1). The propensities were taken from published experimental studies (Lyu et al. 1990; O'Neil and DeGrado 1990; Horovitz et al. 1992; Park et al. 1993; Blaber et al. 1994; Minor and Kim 1994a,b); the entropies were estimated from statistical preferences of side-chain conformers in proteins (Blaber et al. 1994; Stapley and Doig 1997), and ASA were calculated in the extended side-chain conformers of the model α-helix and β-sheet, as described in Materials and Methods. The positions in the middle and C-turns of α-helices and in the central and edge β-strands of β-sheets were considered as separate reference states, because secondary structure propensities and ASA in these positions are different (Table 1).

Table 1.

Secondary structure propensities, ΔΔ G (kcal/mole), and side-chain conformational entropies, TS (kcal/mole), for residues in α-helix and β-sheet applied in the present study

	α-helix			β-sheet
	ΔΔGα middlea	ΔΔGα C-turnb	TSc	ΔΔGβ centerd	ΔΔGβ edgee	TSf
ALA	0.0	0.0	0.0	0.0	0.0	0.0
MET	0.20	0.31	1.49	−0.72	0.02	1.46
ARG	0.09	0.14	2.15	−0.45	0.43	2.16
LYS	0.17	0.19	2.15	−0.27	0.40	2.13
GLN	0.28	0.48	1.49	−0.23	−0.04	1.52
GLU	0.33	0.55	1.25	−0.01	−0.31	1.22
LEU	0.14	0.35	0.42	−0.51	0.24	0.70
PHE	0.28	0.69	0.42	−0.86	−0.16	0.62
TYR	0.39	0.82	0.42	−0.96	−0.11	0.60
TRP	0.32	0.84	0.66	−0.54	0.17	0.98
HIS	0.60	0.78	0.78	0.02	0.01	1.07
VAL	0.56	0.88	0.00	−0.82	−0.17	0.45
ILE	0.37	0.81	0.42	−1.00	−0.02	0.69
THR	0.60	0.79	0.28	−1.10	−0.83	0.55
CYS	0.43	0.82	0.42	−0.52	−0.08	0.57
SER	0.47	0.41	0.42	−0.70	−0.63	0.58
ASN	0.64	0.66	0.75	0.08	0.24	1.17
ASP	0.56	0.71	0.53	0.94	0.10	0.97
GLY	0.93	0.91	0.0	1.20	0.85	0.0

^a Average of two scales for the middle helix positions: Park et al. (1993) (ΔΔG_m values at pH 7) and Lomize and Mosberg (1997). The latter scale was derived from data reported by Lyu et al. (1990), O'Neil and DeGrado (1990), and Blaber et al. (1994).

^b Horovitz et al. (1992); this scale was applied for the last three residues in α-helices.

^c Derived from statistical data of Blaber et al. (1994) as described in Materials and Methods.

^d From Minor and Kim 1994a.

^e From Minor and Kim 1994b.

^f Derived from data of Stapley and Doig (1997) as described in Materials and Methods.

The estimated conformational entropies of side chains in α-helix and β-sheet (Table 1) were in agreement with Monte Carlo simulations of entropies in α-helix and coil, respectively (Lee et al. 1994; Creamer 2000; <0.3 kcal/mole differences for individual residues). Thus, the extended polypeptide chain probably puts very similar limitations on the conformational freedom of side chains in β-sheet and coil. The entropies of long linear side chains (Glu, Gln, Met, Lys, and Arg) were nearly identical in α-helix and β-sheet (Table 1), which was unexpected, because conformers with χ¹ = +60 are generally forbidden in α-helices but allowed in β-sheets. This happens because of a compensatory effect: χ² conformers of the long side chains are less restricted in α-helices than in β-sheets.

Adjustable interaction energies and solvation parameters

The adjustable energetic parameters for the protein interior were determined using ΔΔG values and crystal structures of 106 mutants of four proteins (T4, human and chicken lysozymes, and ribonucleases HI) with substitutions of buried, uncharged residues in α-helices and β-sheets, including all appropriate multiple replacements. Several small-to-large substitutions with significant sterical clashes (e.g., T152I, A98V, A98L, A98M, A129F, A129W, and A42V in T4 lysozyme and A32L and A96M in human lysozyme) were excluded from the set, as well as almost all cases in which bound water molecules spatially substitute for the replaced side chains. All the applied ΔΔG values were measured in thermal unfolding experiments. The list of mutants can be found in Materials and Methods and Supplementary materials; it includes 77, 24, 2, and 3 replacements for T4, human and chicken lysozymes, and ribonuclease HI, respectively.

Eighteen adjustable parameters of the model represented five atomic solvation constants, 12 depths of interatomic potentials (nine types of vdW interactions and three types of H-bonds), and a torsion potential barrier for rotation around "aliphatic" C-C and C-S bonds (Table 2). These parameters were determined by a least squares fit as described in Materials and Methods. The relatively small set of adjustable parameters was achieved by excluding hydrogens and considering only five types of atoms: aliphatic carbon, carbon of aromatic and carbonyl groups, oxygen, nitrogen, and sulfur. In addition, all interactions between similar atoms, whose energies could not be reliably distinguished, were combined together. The unification of interactions involving N and O atoms can be justified by their similar polarizabilities: 0.85, 0.78, and 0.74 ų for amine nitrogen, hydroxyl oxygen, and carbonyl oxygen, respectively, whereas polarizabilities of carbon and sulfur are in the 1.12 to 3.06 ų range (Miller 1990). The parameters obtained were determined by two factors: (1) appearance or disappearance of atoms in the mutants (e.g., Ala-Ser replacement yields a number of new O^γ interactions) and (2) conformational relaxation in the mutants that changed distances and accessible surfaces even for atoms that were identical in the wild-type and mutant structures.

Table 2.

Atomic solvation parameters and equilibrium interaction energies obtained by fitting of experimental ΔΔ G values for 106 mutants of T4, human, and hen lysozymes, and HI ribonuclease

Water–protein atomic solvation parameters, σW→P (kcal/moleÅ2)a		vdW interaction energies, e0ij (kcal/mole)b
Cali	0.019 ± 0.004	Cali...Cali	−0.062 ± 0.012
Caro	0.007 ± 0.007	Cali...Caro	−0.021 ± 0.013
S	−0.001 ± 0.010	Caro...Caro	−0.119 ± 0.028
N	−0.021 ± 0.013	S...Cali	−0.064 ± 0.031
O	−0.066 ± 0.011	S...Caro	−0.082 ± 0.031
H-bond energies, e0ij (kcal/mole)		S...S	Undefinedc
C = O...HN	−1.49 ± 0.08	S...N/O	−0.104 ± 0.061
C = O...HO	−1.62 ± 0.14	C...N/O	+0.013 ± 0.019
C − O...HN/HO	−1.84 ± 0.17	N/O...N/O	−0.342 ± 0.088
Torsion energybarrier, E0 (kcal/mole):	3.01 ± 0.24

Cali, carbon of aliphatic groups; Caro, carbon of aromatic and carbonyl groups.

^a Plus sign shows energetically favorable transfer from water to the protein interior.

^b Equilibrium distances r⁰ of 6–12 and 10–12 potentials (Equation 5) were chosen as sums of the corresponding atomic radii, r⁰_i + r⁰_j, taken from ECEPP/2: 2.06 Å − aliphatic C, 1.86 Å − "aromatic" C, 2.07 Å − S, 1.76 Å − N, and 1.58 Å − O (Nemethy et al. 1983), and r⁰ = 2.9 Å for all hydrogen bonds.

^c Energy of S...S interaction was undefined because of insufficient data, as explained in the text. In this fit it was 0.42 kcal/mole.

The determined equilibrium energies of vdW interactions (e⁰ in Table 2) were negative (stabilizing) except carbon–polar energy that was nearly zero or even slightly positive (+0.013 ± 0.019 kcal/mole), which is possible for interactions of dissimilar atoms in a medium (Israelachvili 1992). Thus, the dispersion attraction of carbon and polar atoms to each other is nearly the same as their average attractions to the protein interior, which are included in the solvation (transfer) energy term. The torsion potential barrier was found to be 3.01 ± 0.24 kcal/mole. Torsion energy was important, because many T4 lysozyme mutants had distorted χ angles. The obtained depths of H-bond potentials (1.5–1.8 kcal/mole) were consistent with other experimental estimates (see Discussion).

The determined solvation parameters (σ in Table 2) represent transfer energies per unit area of different atom types from water to the protein interior. In general, they do not correspond closely to any previously published scale describing transfer from water to organic solvents (Eisenberg and McLachlan 1986; Juffer et al. 1995; Vajda et al. 1995; Efremov et al. 1999; Wang et al. 2001). Only the parameter for aliphatics (19 cal/moleŲ) agrees with the value generally suggested for nonpolar groups in proteins, 20–30 cal/moleŲ (Richards 1977).

Different adjustable parameters were unequally represented in the set of mutants. The effective numbers of vdW interactions in the system of linear equations (C_l in Equation 9) varied from 1600 for aliphatic–aromatic to 132 for sulfur–polar pairs, whereas the two least represented categories were polar–polar (53) and sulfur–sulfur (10) interactions. Because of the relatively small number of sulfur–sulfur contacts, which included significant noise, the S . . . S energy was undefined. Unlike other adjustable parameters this energy significantly drifted (−0.3–0.4 kcal/mole) on removal or addition of a few mutants to the set.

Performance of the model

The calculated and observed ΔΔG values were in very good agreement (Fig. 2 ▶): Their overall root mean square deviation (r.m.s.d.) was 0.41 kcal/mole, which is not much higher than the errors in measurement of free-energy changes in the thermal unfolding experiments (∼0.2 kcal/mole). The fit was significantly better than in any other theoretical methods that predict mutational effects in proteins (Miyazawa and Jernigan 1994; Gilis and Rooman 1996, 1997; Topham et al. 1997; Reddy et al. 1998; Carter et al. 2001) For example, the most recent study of Funahashi et al. (2001) yields an r.m.s.d. of 1.8 kcal/mole for 110 mutants of T4 and human lysozymes. The better precision in our case can be explained by two reasons. First, the mutants were selected using very restrictive criteria. Indeed, the deviations for water-accessible residues would be higher as discussed below. Second, we used a more elaborate and accurate model in which all included energy terms and the approximations described in Theory and Materials and Methods were essential.

Fig. 2.

The relation between the experimental and calculated ΔΔG values (kcal/mole) for 106 mutants with substitutions of α-helical (+) and β-sheet (Δ) residues.

The determined parameters and theoretical model worked equally well for mutants from four different proteins: T4 lysozyme, human and chicken lysozymes (the mutations were in two different, all α and α + β, subdomains), and ribonuclease HI (α + β protein). Moreover, we conducted an additional test for 10 barnase mutants that were not included in the main set because their thermodynamic stabilities were measured by chemical denaturaton. The r.m.s.d. of ΔΔG values for 10 barnase mutants was higher (0.57 kcal/mole), possibly because of less precise measurement of the mutant stabilities. (The crystal structures of barnase and its mutants [L14A, I51V, I76A, I76V, I88A, I88V, L89V, S91A, I96A, and I96V] were from 1a2p, 1brh, 1bsa, 1bri, 1bsb, 1brj, 1bsc, 1bse, 1ban, 1brk, and 1bsd Protein Data Bank (PDB) files, respectively, and ΔΔG^50%_urea values were from the work of Serrano et al. 1992.) Thus, all interaction and solvation parameters obtained here probably reflect properties of an average protein interior rather than a specific protein site. The agreement was also nearly identical for replacements in α-helices (91 mutant) and β-sheets (15 mutants) and in different positions within the secondary structures, including N-turn, middle, and C-turn of α-helices, and the central and edge β-strands (Fig. 2 ▶). Thus, the experimental α and β propensities seem to be sufficiently general and precise.

Also, the standard deviations for the individual parameters of our model (e.g., ±0.15 kcal/mole for H-bond energies, Table 2) were significantly lower than could be achieved by a simple averaging of the experimental energies in large sets of mutants (∼±1 kcal/mole for H-bonds, Myers and Pace 1996). The relatively low standard deviations and the high precision of ΔΔG calculations (0.4 kcal/mole) indicate that a majority of "context-dependence" factors were taken into account in the model, and that the determined parameter set (Table 2) may be widely applicable.

Comparison of ASPs for the protein interior, octanol, and cyclohexane

It has been often suggested that protein core can be approximated by nonpolar solvents (Baldwin 1986; Juffer et al. 1995; Vajda et al. 1995). To examine this issue, we compared ASPs for the protein interior, gas phase, wet octanol, and cyclohexane (first four columns in Table 3). The "polarity" of different atom types, that is, the rank order of their transfer energies from water to the different media, was identical for protein and organic solvents: Cali < Caro < S < N < O. However, the absolute values and even the signs of ASP were strongly environment dependent. For example, the ASPs of sulfur, nitrogen, and oxygen for the protein interior, σ_W→P, were intermediate between those for octanol and cyclohexane (σ_W→C, and σ_W→O in Table 3). On the other hand, the ASPs of aliphatic groups were indeed identical for the protein interior and cyclohexane.

Table 3.

Comparison of atomic solvation constants for transfer from water and vacuum to the protein interior, cyclohexane, and octanol (positive σA→B indicates energetically favorable transfer from media A to media B)

Atomic solvation parameters (cal/moleÅ2)
Atom types	Water-protein, σW→Pa	Water-vacuum, σW→Vb	Water-cyclohexane σW→Cb	Water-octanol, σW→Ob	Vacuum-protein, σV→Pc	Vacuum-cyclohexane σV→Cc
Cali	19	9	19	10	10	10
Caro	7	−13	14	15	20	27
S	−1	−34	−10	3	33	24
N	−21	−93	−62	−9	72	31
O	−66	−126	−110	−20	60	16

^a σ_W→P from Table 2.

^b Parameters for vacuum, cyclohexane, and octanol were determined by the least squares fitting of experimental transfer energies of model compounds (see Materials and Methods), which is a standard approach (Eisenberg and McLachlan 1986; Ooi et al. 1987). The standard deviations for solvation parameters varied from ±3 cal/moleŲ (Cali) to ±15 cal/moleŲ (O and N, water-vacuum scale). R.m.s.d. of the calculated and experimental transfer energies for the sets of compounds were 0.7–0.8 kcal/mole after fitting.

^c σ_V→P = σ_W→P − σ_W→V; σ_V→C = σ_W→C − σ_W→V.

The solvation parameters being discussed depend on affinities of atoms to two different media, that is, to water (hydration energy) and to the protein interior, octanol, or cyclohexane. These affinities can be defined as transfer energies of different atom types from the corresponding medium to gas phase (Radzicka and Wolfenden 1988; Makhatadze and Privalov 1995), and they are shown in the second and last two columns in Table 3. The affinities of aromatic and polar groups to the protein interior, σ_V→P, are intermediate between the affinities to water and cyclohexane (−σ_W→V and σ_V→C, respectively; σ_W→V must be considered with a minus sign because it describes transfer in the opposite direction), whereas for sulfur, σ_V→P ≈ − σ_W→V, and for aliphatic groups, σ_V→P ≈ σ_V→C (Table 3). All groups prefer to be in a medium rather than in vacuum, except aliphatic groups, which are energetically unfavorable in aqueous solution because of the hydrophobic effect (Rose and Wolfenden 1993). However, only half of the water–protein transfer energy for aliphatic groups (19 cal/mole Å) comes from the unfavorable hydration (9 cal/mole Å), whereas the remainder comes from the dispersion attractions to the protein interior.

Reduced vdW interactions between protein atoms across water

All parameters in Table 2 describe energetics of the protein core. However, interactions in water could be different. To check this possibility, we calculated the thermodynamic stabilities for an additional set of mutants with replacements of partially water-exposed, inflexible residues using parameters for the protein interior (Table 4). The discrepancies obtained were larger than for buried residues and reflected two different cases.

Table 4.

Energetic effects of replacements at the protein–water interface^a

PDB code	Protein	Mutation	Mutation site	ΔΔGexp. kcal/mole	ΔΔGcalc, kcal/mole	ΔΔGcalc − ΔΔGexp kcal/mole	Referenceb	Commentsc
Case I. Formation of water-accessible cavities:
228L	T4 lysozymed	F104A	Buriede	+3.1	+1.4	−1.7	1
237L	T4 lysozymed	V149A	Buriede	+3.1	+1.5	−1.6	2	Coming H2O
126L	T4 lysozymed	V149T	Buriede	+3.0	+1.0	−2.0	2	Coming H2O
1G06	T4 lysozymed	V149S	Buriede	+4.4	+3.9	−0.5	2	Coming H2O
1G0P	T4 lysozymed	V149G	Buriede	+4.9	+3.0	−1.9	2	Coming H2O
1L99	T4 lysozymed	Q105G	Interface	+1.5	+0.4	−1.1	3	Coming H2O
165L	T4 lysozymed	S117A	Buried	−1.3	−1.3	0.0	4	Coming H2O
1BPT	BPTI	Y23A	Buriede	+5.9	+3.6	−2.3	5
1FAN	BPTI	F45A	Buriede	+6.9	+3.8	−3.1	5
Case IIa. Large-to-small replacements of interfacial residues
1L17	T4 lysozyme	13V	Interface	+0.4	+1.0	+0.6	6
1L00	T4 lysozyme	Q105A	Interface	+0.6	+1.8	+1.2	3	Leaving H2O
1CJ6	Human lysozyme	T11A	Interface	−0.4	+0.6	+1.0	7
1B5V	Human lysozyme	S51A	Interface	+0.2	+3.1	+2.9	8
Case IIb. Small-to-large replacements of interfacial residuesd
1L18	T4 lysozyme	I3Y	Interface	+2.3	+0.6	−1.7	6
Case IIc. Replacements of interfacial residues with similar numbers of atoms
1L98	T4 lysozyme	Q105E	Interface	+0.5f	+0.7	+0.2	3
1G1W	T4 lysozymed	Q105M	Interface	+1.2	−0.3	−1.5	2
1CJ7	Human lysozyme	T11V	Interface	−0.3	−0.5	−0.2	7
1B7N	Human lysozyme	E35L	Interface	+0.5	−1.4	−1.9	9	Leaving H2O

^a ΔΔG_exp = ΔG_mut − ΔG_wt and ΔΔG_calc are experimental and calculated free-energy differences, respectively.

^b References: 1, Xu et al. 1998; 2, Xu et al. 2001; 3, Pjura et al. 1993; 4, Blaber et al. 1995; 5, Kim et al. 1993; 6, Matsumura et al. 1988; 7, Takano et al. 1999b; 8, Takano et al. 1999c; and 9, Takano et al. 1999a.

^c All the newly appearing or disappearing water molecules, which spatially substitute for the replaced side chains, had low B-values. These water molecules were excluded from the protein structure before calculation of ASA and interactions.

^d ΔΔG_clc was calculated relative to pseudo wild-type T4 lysozyme (C54T, C97A).

^e The buried residue became water accessible after replacements.

^f ΔΔG was for the uncharged form of E105 (pH = 2.1).

The first case was formation of water-accessible cavities in the mutants (Case I in Table 4; all ΔΔG_calc − ΔΔG_exp deviations are negative). Some of the newly appearing cavities were wide open to the solvent (F104A and Q105G in T4 lysozyme and Y23A and F45A in BPTI), whereas the others were small and included bound water molecules spatially substituting for the replaced side chain (S117A and V149 mutants). A significant additional destabilization in this case arises from reduced vdW interactions across the water-filled pockets. This destabilizing effect was present even for small cavities containing single water molecules with low B-values, for example, in T4 lysozyme mutants with substituted V149 (Table 4). Such water molecules destabilize protein structure (Matthews 1996), most likely because they are weakly bound and indistinguishable from bulk solvent, especially at the elevated temperature applied for the measurements of mutant stabilities. On the other hand, the penetration of water in the S117A mutant seems to be energetically neutral (ΔΔG_calc = ΔΔG_exp), which probably is a common situation for mutants with artificially incorporated solvent (Xu et al. 2001).

The cavity-forming replacements (Case I) change media in the mutation site, which affects interactions of surrounding atoms. However, the situation is different for the residues situated at the surface in both the wild-type and mutant proteins (Case II in Table 4). In this case, all discrepancies arise from overestimated interactions at the water–protein interface: Their energy was calculated with parameters for the protein core, whereas the actual interactions are weaker. As a result, any large-to-small replacements, in which the mutant loses vdW interactions and H-bonds, were predicted as strongly destabilizing, whereas the actual destabilization was smaller (Case IIa in Table 4, all ΔΔG_calc − ΔΔG_exp deviations are positive). The deviation for a small-to-large replacement (Case IIb) was obviously of opposite sign.

Apparently, vdW attractions of protein atoms became weaker when the atoms were separated by water, which is in agreement with many published theoretical and experimental studies (McLachlan 1963; Wood and Thompson 1990; Leckband and Israelachvili 2001). For example, it was shown that vdW interaction between nonconducting solids and liquids across water are an order of magnitude smaller than that across vacuum (Israelachvili 1992; Leckband and Israelachvili 2001).

Discussion

Energetics of interactions in protein interior

The free-energy differences in our model consist of two main components: (1) liquid–liquid transfer energies, σΔASA and (2) interactions between spatially fixed atoms, e_ij (Equations 2 and 4). The determined solvation and interaction parameters (Table 2) define an optimal decomposition of the experimental free energies into these components, one of which can be better approximated by ASA, and the second that must be described by the pairwise potentials. The significance of both components becomes clear if the ΔΔG values are considered as arising from two corresponding processes: (1) transfer of protein atoms from water to the liquid-like or uniform medium with specific solvation properties, which is similar to formation of a liquid nonpolar droplet in the aqueous solution (Baldwin 1986, 1989), and (2) the liquid to solid transition, when all protein atoms adopt certain spatial positions, which gives rise to the distance-dependent interactions, torsion energies, and the decrease of conformational entropy of the system (e_ij + E^torsion − TΔS in Equations 2 and 4). Hence the (e_ij + E^torsion) term can be interpreted as melting enthalpy of the protein core (Bello 1978; Herzfeld 1991; Graziano et al. 1996). Indeed, the magnitude of vdW interactions obtained here for aliphatic groups was in a good agreement with fusion enthalpies of alkanes (Nicholls et al. 1991), as described below.

Both transfer and freezing processes may actually occur during protein folding and therefore reflected in the experimental unfolding free energies. The transfer process may be related to formation of the molten globule state whose nonpolar residues are buried from water but can move more or less freely, whereas the freezing represents first-order transition from the molten globule to the native structure (Shaknovich and Finkelstein 1989). The cooperative freezing transition must be driven by the increasing packing density of atoms, for example, from 0.44 (the fraction of space occupied by atoms in liquid cyclohexane) to 0.75 in the folded protein (Pace 2001). Indeed, the molten globule states of many proteins have a loosely packed hydrophobic core and gyration radii of 10% to 30% larger than that of the native structure (Arai and Kuwajima 2000).

It is also important to realize that all interatomic interactions occur in a condensed protein medium, not in vacuum, and therefore are expected to follow the "like dissolves like" rule (Israelachvili 1992). Indeed the following trends are obvious. First, the energies of interactions between same atom types increase with "polarities" of the participating atoms (Cali . . . Cali < Caro . . . Caro < N/O . . . N/O), that is, exactly in the same order as transfer energies of aliphatic, aromatic, sulfur, and polar groups from water to the protein interior, vacuum, or cyclohexane (Tables 2 and 3). Second, the interactions of different atom types are usually weaker than interactions of same atoms. For example, aliphatic–aromatic energies are smaller than aromatic–aromatic and aliphatic–aliphatic ones (Table 2). Third, the weakest interactions are observed between atoms with the most dissimilar polarities, whereas sulfur, with an intermediate polarity, interacts equally well with all other atoms. This is consistent with formation of "polarity gradients" in proteins, in which sulfur and aromatic groups often separate polar and aliphatic clusters (Pogozheva et al. 1997; Lomize et al. 1999b).

The determined interaction energies also correlate with atomic polarizabilities, which are directly related to the strength of vdW forces. The polarizabilities of aliphatic carbon, aromatic carbon, and sulfur are 1.12, 1.37, and 3.06 ų, respectively (Miller 1990). Therefore, aromatic–aromatic interactions are stronger than aliphatic–aliphatic ones (a comparison for same atom types), whereas the alphatic–sulfur interactions are stronger than aliphatic–aromatic ones. However, this trend is violated for polar atoms that have the lowest polarizabilities (0.78 and 0.85 ų for hydroxyl oxygen and amine nitrogen, respectively; Miller 1990). Although the polar–carbon interaction is indeed the weakest, as could be expected from the corresponding polarizabilities, the polar–polar energy is the highest (Table 2). This situation can be explained by the hidden electrostatic attractions of NH, OH, and C = O dipoles. The energies of such interactions depend on the mutual orientation of two dipoles. However, after averaging over different rotational orientations, these interactions are attractive and proportional to r⁻⁶ (Israelachvili 1992).

The affinities of atoms to the protein interior (vacuum-protein transfer energies, σ_V→P in Table 3) follow the same general trend as interactions of same atom types, that is, Cali < Caro < S < N ≈ O. The rank order for aliphatics, aromatics, and sulfur correlates with their polarizabilities and therefore can be explained by the increasing dispersion attraction forces. The affinity of polar groups is much higher, possibly because of the electrostatic self-energy of NH, OH, and C = O dipoles in the protein environment, whose effective dielectric constant may be relatively high (4–12; Warshell and Papazyan 1998; Dwyer et al. 2000) as a result of the presence of polar polypeptide backbone, polar side chains, and bound water.

Comparison with independent experimental estimates

The energies obtained for H-bonds (−1.5– −1.8 kcal/mole) were consistent with results of protein-engineering studies, which range from −1 to −2 kcal/mole (Fersht and Serrano 1993; Matthews 1993; Thorson et al. 1995; Myers and Pace 1996; Funahashi et al. 1999; Takano et al. 1999c). They are also in agreement with enthalpy of N-H . . . O = C H-bond in α-helix (−1.3 kcal/mole; Scholtz et al. 1991) and with the contribution of an H-bond to fusion enthalpy of N-acetyl amines of amino acids (−1.3– −1.6 kcal/mole; Graziano et al. 1996). The determined torsion potential barrier (3.0 kcal/mole) was close to 2.7 kcal/mole in ECEPP/2, a value that was derived from spectroscopic studies of organic molecules (Momany et al. 1975).

The determined vdW interaction energies indicate a very strong tendency to formation of aliphatic, aromatic, or polar clusters in proteins, whereas sulfur can serve as an "adhesive" between the polar and nonpolar groups, because it interacts favorably with both. This is in agreement with observations of significant aromatic–aromatic and sulfur–aromatic interactions in peptides and proteins (Fersht and Serrano 1993; Viguera and Serrano 1995). Moreover, the destabilization energy on removal of buried aliphatic side chains correlates with packing densities of surrounding aliphatic groups rather than with densities of any atoms (Serrano et al. 1992; Jackson et al. 1993; Fersht 1999).

The energies of vdW interactions obtained here are easier to compare with the independent estimates for aliphatics, because there are significantly less data for other groups. Moreover, most of the published estimates reflect a combination of vdW and transfer energies. To make a relevant comparison, we excluded all the explicit vdW and H-bond potentials from calculations, exactly as in other studies. Such a simplified approach produces a worse fit with the experimental free energies (r.m.s.d. of ΔΔG increases from 0.41 to 0.83 kcal/mole) and yields a different set of "solvation parameters" that describe transfer from water to the solid protein interior (σ_W→P^solid in Table 5). The obtained σ^solid parameter for aliphatic groups, 41 cal/moleŲ, is in agreement with results of other studies that did not use the explicit vdW potentials (42 cal/moleŲ, Funahashi et al. 1999; >50 cal/moleŲ, Kellis et al. 1989; or 55 cal/moleŲ, Jackson et al. 1993); however, it is two times greater than the actual transfer energy of aliphatic groups from water to the protein interior (σ_W→P = 19 kcal/moleŲ, Table 5), because it includes implicitly the additional vdW interactions in proteins. Thus, ∼50% of the stabilizing energy for aliphatics originates from vdW interactions, whereas the remainder comes from the transfer energy, that is, hydrophobic effect. This share correlates very closely with fusion enthalpy of alkanes, which is ∼0.59 kcal/mole per CH₂ group (Nicholls et al. 1991), that is, also ∼50% of the average contribution of a buried CH₂ group to the protein stability (∼1.27 kcal/mole, Pace 1992). Therefore, the vdW interactions under discussion may indeed represent melting enthalpy of the protein core. This enthalpy for aliphatic groups, (σ_W→P^solid − σ_W→P) = 22 cal/moleŲ, is close to the energy losses induced by formation of water-inaccessible cavities in proteins, which is 20 cal/mole per Ų of the nonpolar (aliphatic) cavity surface created (Eriksson et al. 1992).

Table 5.

Overestimations of water-protein atomic solvation parameters in the model without explicit vdW interactions and H-bonds

Atomic solvation parameters (cal/moleÅ2)
Atom types	Complete model, σW→Pa	No explicit vdW interactions and H-bonds included,b σW→Psolid	Overestimation of solvation parameter, σW→Psolid − σW→P
Cali	19	41 ± 3	22
Caro	7	33 ± 3	26
S	−1	28 ± 5	29
N	−21	23 ± 16	44
O	−66	34 ± 7	100

^a σ_W→P parameters from Table 2.

^b These solvation parameters were determined by least square fit using the same set of mutants but with vdW interactions and hydrogen bonds excluded from Equations 2 and 4. After the fitting, r.m.s.d. of 106 calculated and experimental ΔΔG values was 0.83 kcal/mole and torsion energy barrier was 3.0 ± 0.4 kcal/mole.

The contribution of vdW interactions, (σ_W→P^solid −σ_W→P), is even higher for aromatic groups and sulfur: ∼80% and ∼100% of σ_W→P^solid, respectively (Table 5), whereas the energetics of polar groups is dominated by significantly stronger H-bonds (σ_W→P^solid − σ_W→P 44 and 100 cal/moleŲ). Hence vdW interactions and H-bonds represent a crucial contribution to the protein stability (Eriksson et al. 1992; Serrano et al. 1992; Makhatadze and Privalov 1995; Ratnaparkhi and Varadarajan 2000; Pace 2001), whereas the hydrophobic effect provides 50% of stabilizing energy for aliphatic groups, 20% for aromatics, and nothing for sulfur and polar groups. This situation does not contradict the large positive changes in heat capacity of protein unfolding, which is usually attributed to the hydrophobic effect, because the large heat capacity changes are characteristic for any melting transitions, especially in the presence of hydrogen-bonding networks (Cooper 2000).

The determined σ_W→P^solid "solvation parameters" indicate that burial of polar groups in proteins is energetically favorable (∼30 cal/moleŲ), because their vdW interactions and H-bonds in the protein core outweigh the dynamically averaged hydration by liquid water (Pace 2001). However, this is true only for the native protein structures with saturated H-bonding potential (McDonald and Thornton 1994). The σ_W→P^solid parameters are inappropriate for protein-modeling studies, because all buried polar groups would always be energetically favorable, even when they do not form any H-bonds in incorrect protein models.

Comparison with molecular mechanics potentials

The interatomic energies determined here (Table 2) are generally smaller than in molecular mechanics force fields that describe interactions in vacuum. For example, the H-bond energy is only ∼−1.5 kcal/mole, which is smaller than −4 to −6 kcal/mole values that are generally accepted for H-bonds in vacuum and are applied in many computational studies (Momany et al. 1974; Hermans et al. 1984; Rose and Wolfenden 1993; Gavezzotti and Filippini 1994). The estimated aliphatic–aliphatic energy (e⁰ = −0.06 kcal/mole, Table 2) is also less than the depth of the corresponding CH₂ . . . CH₂ "united atom" potential (−0.14–−0.11 kcal/mole, Lazaridis et al. 1995). Moreover, the depths of all interatomic potentials in Table 2 are smaller than in ECEPP/2, OPLS, and CFF force fields (Momany et al. 1974; Jorgensen et al. 1996; Ewig et al. 1999), except for the polar–polar interactions, which are probably reinforced by the hidden electrostatic attractions in our model. These discrepancies can be explained by two related reasons: (1) The protein interior is a condensed medium in which all forces of electrostatic origin, including the vdW interactions, are expected to be weaker than in vacuum (Israelachvili 1992) and (2) the energies determined here reflect melting enthalpy of the protein core rather than sublimation enthalpy of molecular crystals, which is greater and can be calculated as a sum of the corresponding e_ij potentials in molecular mechanics (Momany et al. 1974; Gavezzotti and Filippini 1997; Ewig et al. 1999).

It is important that the interactions in the protein core follow the "like dissolves like" pattern that has been predicted by the general theory of vdW forces in media (McLachlan, 1963, Israelachvili 1992). For example, the aliphatic–polar energy was determined as nearly zero, which means it does not exceed the average attraction of the participating aliphatic and polar groups to the protein interior, a contribution that is included in the water–protein transfer energies of the aliphatic and polar atoms. However, the situation in vacuum is very different. Here, the molecular mechanics calculations produce a very significant energy of polar–nonpolar interactions that is larger than energies of polar–polar and nonpolar–nonpolar interactions combined (Lazaridis et al. 1995), because the number of polar–nonpolar contacts is greater. The large nonpolar–polar energy originates from the Slater-Kirkwood equation or "combinatorial rules," which state that interaction energy of any pair of dissimilar (e.g., C and O) atoms is an intermediate value between the energies of the corresponding same type (i.e., O . . . O and C . . . C) interactions. However, this approximation was based on the original London theory of dispersion forces that can be applied only in vacuum (Israelachvili 1992).

The application of a universal (in vacuum) vdW parameter set in different media, during the molecular mechanics or dynamics simulations, seems to be a problematic approach, although this is not commonly admitted. The environment-dependence of vdW forces has been justified previously in theoretical and experimental studies of intermolecular interactions in media (McLachlan 1963; Wood and Thompson 1990; Israelachvili 1992; Leckband and Israelachvili 2001). Moreover, it has also been found that vdW energies, when calculated with ECEPP/2 or AMBER potentials, must be reduced several fold to reproduce experimental ligand binding constants (Morris et al. 1998) or stabilities of designed peptides (de la Paz et al. 2001). The reduced interactions across water may be also one of the reasons why surface residues contribute less to protein stability (Shortle 1992; Scholtz et al. 1993; Fersht and Serrano 1993).

Conclusions

In this study, we propose a new approach for development of interatomic potentials that is based entirely on the thermodynamic stabilities of protein mutants instead of using properties of molecular crystals or liquids, such as heats of sublimation or vaporization. The developed energy functions differ from the standard molecular mechanics potentials in two important aspects. First, the intramolecular energy of the protein (vdW interactions, H-bonds, and torsion potentials) in our work describes interactions in the protein interior, not in vacuum, and is related to enthalpy of melting rather than to enthalpy of sublimation. Therefore, vdW interactions and H-bonds are generally weaker than in molecular mechanics and follow the "like dissolves like" rule. Second, the intramolecular energy term is supplemented by side-chain conformational entropy, solvation free energy, and secondary structure propensities to reproduce the experimental ΔΔG values.

The proposed approach works successfully, judging from the low r.m.s.d. of observed and calculated free-energy changes for 106 mutants (0.4 kcal/mole), whereas the number of adjustable energetic parameters of the model was six times smaller than the number of experimental data. The derived interaction and solvation energies seem to be generally applicable for uncharged groups buried in the protein interior on the basis of the following criteria: (1) The model works equally well for a wide variety of microenvironments in four different proteins, (2) the parameters were successfully tested for 10 barnase mutants that were not used for the parameterization, and (3) the results obtained were perfectly consistent with independent experimental estimates of torsion potential barriers, energies of H-bonds, melting enthalpies of alkanes, contributions of aliphatic groups to the protein stability, and energy losses associated with formation of water-free cavities. At the same time, the proposed potentials overestimate vdW interactions across water-filled cavities.

The developed parameters and theoretical model are expected to be helpful for the improvement of modeling methods, including ligand binding, ab initio prediction of protein structure, fold recognition, and computational de novo design, which all should be based on optimization of free energy. However, a number of problems must first be addressed, including quantification of interactions at the water–protein interface and contributions of charged groups, a better treatment of interatomic repulsions, implementation of coil as a reference state, and operating with ΔG rather than ΔΔG values.

Materials and methods

Set of mutants

The set of selected mutants included replacements in β-sheets of T4 lysozyme, I17A, and I27A (Xu et al. 1998); T26S (Matthews 1995b); human lysozyme, I23V, and I59V (Takano et al. 1998, comparison with pseudo wild type); I23V and I59V (Takano et al. 1995, comparison with wild type); I23A, I59A, and I59G (Takano et al. 1997a); Y54F (Yamagata et al. 1998); I59L, I59M, I59S, and I59T (Funahashi et al. 1999); replacements in α-helices of T4 lysozyme, L99I, L99V, L99F, L99M, L99A/F153A, F153L, F153M, F153I, and F153V (Eriksson et al. 1993); I50A and F67A (Xu et al. 1998); M6A, I50M, L66M, I78M, I78A, L84M, L84A, V87A, V87M, L99A, I100A, I100M, M102A, V103A, V103M, F104M, M102A/M106A, M106A, V111A, V111M, L118A, L118M, L121A, L121M, A129M, and F153A (Gassner et al. 1999); L133A (Eriksson et al. 1992); L121A/A129L, L121A/A129M, A129L, and A129M/F153A (Baldwin et al. 1996); M106L and M120L (Lipscomb et al. 1998); L99F/M102L/F153L, L99F/M102L/V111I, L99F/V111I, and M102L (Hurley et al. 1992); L121A/A129M/V149I, L121A/A129M/F153L, L121M/L133V/F153L, L121A/A129V/L133A/F153L, L121A/A129V/L133M/F153L, L121I/A129L/L133M/F153W, and L121M/A129L/L133M/V149I/F153W (Baldwin et al. 1993); A98C (Liu et al. 2000); A42S, V75T, V87T, A98S, and A130S (Blaber et al. 1993); V149C and T152S (Dao-Pin et al. 1991); S117F (Anderson et al. 1993); M6I (Faber and Matthews 1990); N101A, V149I, V149C, T152A, T152S, and T152V (Xu et al. 2001); L99G (Wray et al. 1999); M120A (Blaber et al. 1995); and L46A (Matthews 1995b); human lysozyme, A9S, A92S, V93T, A96S, V99T, and V100T (Takano et al. 2001); V93A, V99A, and V100A (Takano et al. 1997b, comparison with wild type); V93A, V99A, and V100A (Takano et al. 1998, comparison with pseudo wild type); hen lysozyme M12F and M12L (Ohmura et al. 2001); ribonuclease HI, V74L, and V74I (Ishikawa et al. 1993a); and G77A (Ishikawa et al. 1993b). The reference wild-type and pseudo wild-type structures were chosen as 3lzm and 1l63 (T4 lysozyme), 1rex and 2bqa (human lysozyme), 1rfp (hen lysozyme), and 2rn2 (HI ribonuclease) PDB files.

Fitting procedure

The equilibrium interaction energies, solvation constants, and torsion potential barrier were considered as adjustable parameters and determined by solving the overdetermined system of linear equations:

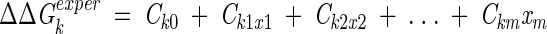(6)

where ΔΔG^exper_k is the observed free-energy difference between mutant k and the corresponding wild or pseudo wild-type protein (k = 1,2, . . . n), the free variables x₁, x_{2, . . . ,} and x_m are the depths of 6–12 and 6–10 potentials (e⁰_ij from Equation 5), ASPs (σ_i), and the height of the torsion potential (E₀). The system was solved using the LSQR program from the LAPACK library (Anderson et al. 1999).

The first, C_k0, term in Equation 6 was defined as follows:

(7)

where ΔΔG^mut,prop ΔΔG^wild,prop, S_p^mut, and S_p^wild are propensities and side-chain conformational entropies of the replaced residue p in mutant and wild-type proteins, and N is the number of replaced residues in mutant k.

Interaction energy

Coefficients of vdW interaction and H-bond energies were defined as

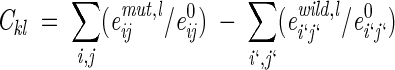(8)

where index l indicates a certain type of interaction (e.g., between aliphatic carbon and sulfur) and (e^mut,l_ij/e⁰_ij) and (e^wild,l_i`j`/e⁰_i`j`) are the corresponding dimensionless energies of interactions in the mutant and wild-type proteins, respectively, described by the modified 6–12 or 10–12 potentials (Equation 5).

To reduce the errors associated with summation over a large set of e_ij energies, only a small set of "active" residues was selected for each pair of mutant and wild-type proteins. This set included all replaced residues and a few additional, also buried, residues that were strongly (typically >0.3 Å) shifted after superposition of the wild-type and mutant structures. The number of additional residues did not exceed seven. Only interactions of atoms within the "active" set and between the "active" and surrounding atoms were included. The "surrounding" atoms (those situated at distances <8 Å from at least one "active" atom) were chosen to be exactly the same in the wild-type and mutant proteins: They represented a union of "surrounding" atoms from both three-dimensional structures. All vdW interactions of the replaced side chains with backbone of their own α-helix or β-sheet, and backbone–backbone interactions were excluded from Equation 8, in accordance with approximations (5) and (6) described in the Theory section. Conformational flexibility of surface side chains also produces significant noise. Therefore, "surrounding" atoms with high B-values (typically >40 for T4 lysozyme mutants), that is, poorly defined spatial positions, were excluded from the calculations of vdW and H-bond energies.

A representation of each variable x_l in system (6) was judged from the sum of the absolute values of corresponding C_kl coefficients:

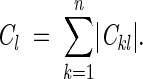(9)

where n is the number of linear equations, that is, wild-type mutant pairs. A small C_l means that parameter x_l is underrepresented in the system and therefore can be poorly determined. For a certain interaction type (e.g., S . . . O), C_l sum can be interpreted as an effective number of the corresponding (S . . . O) interactions in the system, because it is expressed in e_ij/e⁰_ij units: One "complete" interaction in the minimum of potential (e_ij = e⁰_ij) would contribute 1 to the sum. It is important that this is the number of interactions that are different in the wild-type and mutant proteins, because C_kl are the differences of interaction energies e_ij in two protein structures (Equation 8).

Solvation energy

Coefficients of solvation parameters were represented as sums of ASA according to Equations 2 and 4

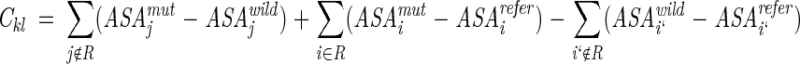(10)

where R is the set of replaced residues. The ASA were included for all "active" and "surrounding" atoms, which were situated at distances closer than 4.5 Å to any "active" atom. ASA of atoms with elevated B-values (i.e., imprecisely determined coordinates) or ASA affected by movements of flexible side chains were assumed to be identical in the wild-type and mutant proteins (ΔASA_j = 0).

Reference ASA of nonhydrogen atoms for all types of residues were calculated in two model structures: (1) An isolated regular α-helix Lys60-Arg80 from T4 lysozyme (the modeled side chain was in position 68, and all other residues were replaced by alanines) and (2) the open, planar β-sheet of protein G (the side chains were modeled in positions 53 and 44 for replacements in the middle and edge β-strands, respectively) and all surrounding residues were replaced by alanines. The two sites in protein G were chosen as in the experimental studies of β-sheet propensities (Minor and Kim 1994a,b) to have a consistent set of parameters. ASA were calculated in "most exposed" conformations of side chains (χ¹ −60° for Thr and Ile, and 180° for all other residues; χ² = χ³ = χ⁴ = 180° for linear side chains; χ² = 90° for Asn, Asp, Phe, Tyr, and His, and χ³ = 90° for Glu and Gln). All ASA were calculated using the program NACCESS (Hubbard and Thornton 1993), radii of Chothia (1975) (oxygen 1.40 Å, trigonal nitrogen 1.65 Å, tetrahedral carbon 1.87 Å, trigonal carbon 1.76 Å, and sulphur 1.85 Å), without hydrogens, and with a 1.4 Å probe radius.

Torsion energy

Torsion potentials were included only for "active" residues and defined as in ECEPP/2, that is, using the same energy barrier for "aliphatic" C-C and C-S (in Met) χ angles and assuming that potentials of all other groups are zero (Momany et al. 1975). The torsion energy coefficient in each equation was determined as

(11)

where E₀ is the torsion energy barrier; χ_i and χ_i` are the corresponding torsion angles in the wild-type and mutant proteins, respectively (e.g., χ¹ of Leu and Met residues after Leu → Met replacement), and the summation was over all side-chain torsion angles of residues from the "active" set.

The torsion potentials were applied in the standard form,

(12)

However, the function was "softened" to account for imprecise atomic coordinates:

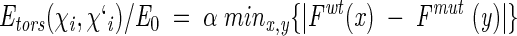where

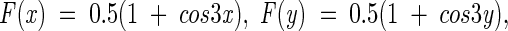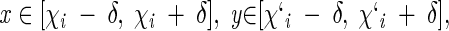(13)

and α = 1 when F(x)^wt < F(y)^mut (accumulation of torsion strain in the mutant) or α = −1 when F(x)^wt > F(y)^mut (relaxation of torsion strain in the mutant).

Here, the allowed deviation Δ was considered as expected error in the calculation of the torsion angle from experimental coordinates. The default value of Δ was chosen as 10°, which corresponds to an uncertainty of 0.3 Å in the atomic coordinates. However, the torsion energy was nullified for flexible angles (typically when at least one of four atoms defining the dihedral angle had B-value >40 in T4 lysozyme mutants), and Δ was chosen as 0° in several cases. The calculations with this equation are straightforward when the mutant and wild-type proteins have the same χ variable. However, when a torsion angle (e.g., χ¹ after Leu → Ala replacement) had no counterpart in the mutant or wild-type protein, the reciprocal χ_i or χ_i` was taken as ±60 or 180°.

Side-chain conformational entropies

Side-chain conformational entropies in α-helix and β-sheet, S (Table 1) were calculated using the usual definition

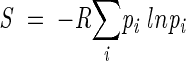(14)

where p_i is the probability of side-chain conformer i, and R, the gas constant (Pickett and Sternberg 1993).

Probabilities p_i were determined from statistical frequencies of side-chain conformers in α-helices and β-sheets (when significant statistics were available in the literature) or simply using the number of allowed side-chain conformers and assuming that all have equal probabilities. In α-helix, statistical data were used for χ¹–χ² conformers of Asp, Asn, Thr, and His residues, whereas the numbers of allowed conformers (1 for Val; 2 for Ile, Leu, Ser, Tyr, Phe, and Cys; 12 for Met and Gln; 8 for Glu, and 36 for Arg and Lys) were applied in all other cases on the basis of the study of Blaber et al. (1994). In β-sheet, statistical frequencies were used for χ¹ and χ² conformers of Leu, Ile, Met, Glu, Gln, Lys, and Arg and χ¹ conformers of other residues (Stapley and Doig 1997), whereas the numbers of allowed conformers for other torsion angles were chosen as follows: three for χ³ and χ⁴ angles of Met, Lys, Gln, and Arg and χ² of Asn; two for χ² conformers for Asp, Trp, and His side chains; and one for χ² of Phe and Tyr. Thus, two symmetric structures of Phe and Tyr residues (χ² ∼−90 and +90°) were considered as representing the same conformer, and the possible contributions of hydroxyl hydrogens to conformational entropy were not taken into account, as in the recent Monte Carlo simulation of side-chain entropies in coil (Creamer 2000).

Atomic solvation parameters

ASPs for transfer from water to cyclohexane, octanol and gas phase (vacuum) for Table 3 were determined by least square fit of the calculated and experimental transfer energies for a series of model compounds. The datasets included analogs of all protein side chains, excluding Gly, Pro, and charged residues (Radzicka and Wolfenden 1988) and several additional compounds for octanol scale (butanol, propanol, o-cresol, 3,4 dimethylphenol, 2,4 dimethylphenol, 2,6 dimethylphenol indole, 1-methylindole, 5methylindole, 7-methylindole, betacarboline, indole-5-methylether, 5-hydroxylindole, cyclohexane, m-cresol, butan-2-ol, n-propylthiol, and diethyl ether) (Abraham et al. 1994; Guardado et al 1997). ASA were calculated using NACCESS in the most extended conformations of the compounds. The conformations were generated by QUANTA and minimized with CHARMM (Molecular Simulations, Inc.).

Abbreviations

• vdW, van der Waals

• ASA, accessible surface areas

• ASP, atomic solvation parameter

• PDB, Protein Data Bank, H-bond, hydrogen bond, BPTI, bovine pancreatic trypsin inhibitor

• r.m.s.d., root mean square deviation