Rapid protein domain assignment from amino acid sequence using predicted secondary structure

Abstract

The elucidation of the domain content of a given protein sequence in the absence of determined structure or significant sequence homology to known domains is an important problem in structural biology. Here we address how successfully the delineation of continuous domains can be accomplished in the absence of sequence homology using simple baseline methods, an existing prediction algorithm (Domain Guess by Size), and a newly developed method (DomSSEA). The study was undertaken with a view to measuring the usefulness of these prediction methods in terms of their application to fully automatic domain assignment. Thus, the sensitivity of each domain assignment method was measured by calculating the number of correctly assigned top scoring predictions. We have implemented a new continuous domain identification method using the alignment of predicted secondary structures of target sequences against observed secondary structures of chains with known domain boundaries as assigned by Class Architecture Topology Homology (CATH). Taking top predictions only, the success rate of the method in correctly assigning domain number to the representative chain set is 73.3%. The top prediction for domain number and location of domain boundaries was correct for 24% of the multidomain set (±20 residues). These results have been put into context in relation to the results obtained from the other prediction methods assessed.

Since the first protein structures were solved, it has been apparent that the polypeptide chain can fold into one or more distinct regions of structure. Such substructures, or domains, are considered as the basic units of folding, function, and evolution and often have similar chain topologies (Holm and Sander 1994).

The identification of domains within a protein sequence is an important precursor for several methods. The structural determination of proteins using X-ray crystallography and especially Nuclear Magnetic Resonance (NMR) is often more successful when solving smaller domain units rather than whole chains. Multiple sequence alignment at the domain level can result in the detection of homologous sequences that are more difficult to detect using a complete chain sequence. It is well known that fold recognition methods perform more reliably if a putative multidomain target is considered in terms of its constituent domains rather than as a whole chain (Jones and Hadley 2000).

The delineation of protein domains within a polypeptide chain can be achieved in several ways. Methods applied by classification databases such as the Dali Domain Dictionary (DDD; Dietmann and Holm 2001), CATH (Orengo et al. 1997), and Structural Classification of Proteins (SCOP); (Murzin et al. 1995) use structural data to locate and assign domains. However, complete automation of domain assignment even from structural data is not a trivial problem (Jones et al. 1998).

Identification of domains at the sequence level most often relies on the detection of global-local sequence alignments between a given target sequence and domain sequences found in databases such as Pfam (Bateman et al. 2000) and SMART (Schultz et al. 2000).

Difficulties in elucidating the domain content of a given sequence at the structural and sequence homology level arise when the target sequence has no experimentally determined structure and searching the target sequence against sequence domain databases results in a lack of significant matches. In such situations, an ab initio approach to domain assignment from sequence is required. Indeed, several attempts have been made, although with limited success, to describe protein domains from sequence alone, including those by Busetta and Barrans (1984)^, Vonderviszt and Simon (1986), and Kikuchi (1988).

Two of the most recently published algorithms that attempt to overcome this difficulty are Domain Guess by Size (DGS; Wheelan et al. 2000) and SnapDRAGON (George and Heringa 2002). DGS aims to predict the likelihood of putative domains within a given sequence based on probability distributions of chain and domain lengths within a representative set. SnapDRAGON is a much more computationally intensive approach that averages several hundred predictions obtained from ab initio simulations of the three-dimensional (3D) structure for a given sequence to assign its domain content. Of the two methods, SnapDRAGON appears to be the most reliable, although the computational requirements (i.e., running hundreds of ab initio simulations for each target sequence) render it impractical for routine use, especially for any kind of genome-scale analysis.

The approach described here is based on the idea that a crude fold recognition algorithm based on the mapping of predicted secondary structures to observed secondary structure patterns in domains of known 3D structure might be reliable enough to parse a long target sequence into putative domains. This is often the way in which a human sequence analyst will attempt to parse a protein into domains when homology-based approaches have been unsuccessful. Automatic analysis of secondary structure is, therefore, a very logical approach. Also, recent improvements in secondary structure prediction accuracy (Jones 1999) where methods now routinely achieve three-state prediction accuracies of 77%, have greatly increased the usefulness of predicted secondary structure in recognizing protein folds.

Although many previous approaches to fold assignment using secondary structure attempted to align strings of secondary structure codes, more successful recent approaches have used scoring scheme based on the alignment of secondary structure elements (Russell et al. 1996). With the recent advances in secondary structure prediction accuracy, secondary structure element alignments methods (SSEA) have been shown to provide a rapid prediction of the fold for given sequences with no detectable homology to any known structure and have also been applied to the related problem of novel fold detection (McGuffin et al. 2001; McGuffin and Jones 2002). In this study we present DomSSEA, a modified form of this method that uses predicted secondary structure to predict continuous domains, aimed at the automated annotation of higher level genome sequence data. We also attempt to evaluate several different methods ranging in their complexity.

Results

Length distributions

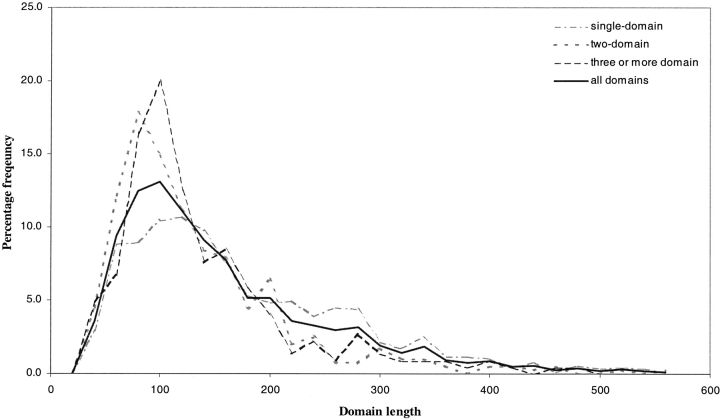
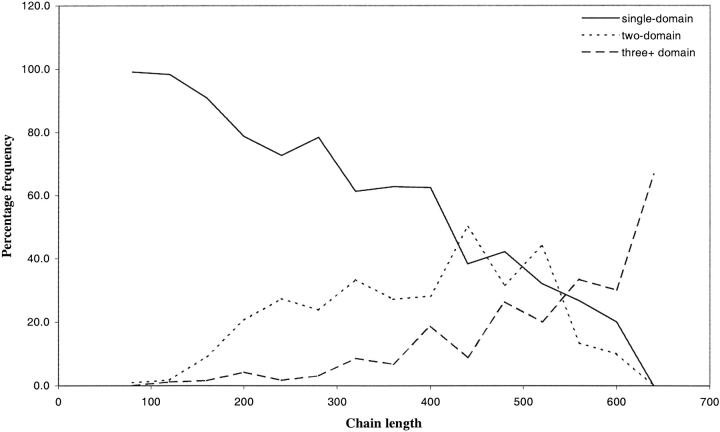
Figures 1 and 2 ▶ ▶ show the length distributions for the chains and domains in the nonredundant set as used in our own implementation of the DGS algorithm. Figure 2 ▶ shows an overlap between the different chain length distributions; the length distributions of single and multidomain chains are not discrete, which has implications in domain prediction. As chain length increases, the likelihood of the chain having a multidomain conformation also increases. Figure 1 ▶ also shows that the mean length for domains found in both single and multidomain chains is similar (150 residues).

Fig. 1.

Domain length distributions as observed in the CATH representative set used in this study. Intervals were calculated with a width of 20 residues. The domain frequencies were used by DGS-M to calculate the probabilities of predicted domain sizes.

Fig. 2.

Frequency of chain lengths of one, two, and three -or more domain chains for a 40-residue length interval. These frequencies were used by DGS-M to calculate the likelihood of the number of domains for a given chain length.

Secondary structure prediction accuracy

PSIPRED secondary structure predictions had a Q₃ accuracy of 76.6% and a Sov score of 72.5%.

Domain number prediction

The success rate of each method in predicting the number of domains for each chain in the nonredundant set can be seen in Table 1. This was measured as the percentage of one, two, and three or more domain chains predicted correctly. Also shown is the success rate for domain number prediction for all the chains in the representative set.

Table 1.

Prediction of one, two, or three or more domain chains

	% Correctly assigned
Prediction of number of domains	All	1 domain	2 domains	3 or more domains
PUU	79.0	81.0	66.0	65.0
DomSSEA observed secondary structure	75.4	83.9	47.5	38.1
DomSSEA predicted secondary structure	73.3	82.3	46.0	36.5
DGS-M	76.7	99.8	1.0	0.0
DGS-W	76.7	100.0	0.0	0.0
Absolute difference in length	66.2	78.4	22.3	38.1
Fasta	60.9	74.9	17.3	7.9
Random (weighted)	61.4	75.8	16.8	6.3
Random (basic)	37.9	45.0	16.8	7.9
Sum of squares	62.0	76.0	17.0	7.0

The percentage of chains given a correctly assigned domain number (top prediction), for single, two, and three or more domain chains, as well as for all chains in the representative set.

The simplest method, random-weighted, sets the lower limit of prediction. A domain number was assigned according to the frequencies found in the representative set. Here the overall success rate was 61.4%, with three-quarters of the single domains correctly assigned, 16.8% of two-domain, and 6.3% of three- or more domains. These values agree with the theoretical values of 76%, 17%, and 7% for single, two, and three or more domain chains, respectively, calculated from the sum of squares of the frequencies of the single and multidomain chains in the nonredundant set.

The comparison of the CATH and DDD assignments set an upper limit for domain prediction. The PUU algorithm used by DDD to assign domains is a fully automated method in contrast to the consensus and manual verification approach used by CATH. Table 1 shows that agreement between the domain databases covers ∼80% of single domain chains, whereas nearly two-thirds of two domain and three -or more domains are given matching assignments.

The results of the all–against–all alignment of sequences in the nonredundant set are close to those values generated by the random method, confirming the lack of discernable sequence identity in the benchmarking procedure.

The top assignments for both DGS-W and DGS-M were most often found to predict the target as a single domain chain. This gives 100% prediction accuracy for single domain chains, but few correct predictions for multidomain chains. Therefore, here the success rate of DGS top hit domain number prediction reflects the percentage of single domain chains in the test set only.

Scoring the all–against–all comparison of the nonredundant set in terms of the absolute difference in length gave an overall success rate of 66.2%. A large percentage of the single domain chains were predicted correctly, with just more than 20% of the two domain chains and more than one-third of the multidomain chains.

Of all the methods, DomSSEA achieves the highest accuracy in predicting domain number, especially for two domain chains. More than 80% of the single domain chains are correctly assigned, with just under one-half of the two domain chains and two-thirds of three or more domain chains predicted correctly. The use of predicted secondary structure over observed does not appear to be overly detrimental to the outcome of the method.

Table 2 shows the percentage of correct and incorrect domain number prediction given by DomSSEA (predicted secondary structure). The majority of false-positive predictions given by DomSSEA tend to be under predictions of domain number (and, in turn, domain boundary frequencies).

Table 2.

Domain number prediction accuracy

	Real (CATH assignment)
Predicted (DomSSEA)	1	2	3 or more
1	82.3	43.1	15.9
2	14.7	46.0	47.6
3 or more	3.0	10.9	36.5

Predicted number of domain boundaries by DomSSEA (predicted secondary structure) vs. real number of domains (assigned by CATH). DomSSEA false positives tend to under-predict domain number.

Boundary prediction for two domain chains

As shown, each method tested predicts domain number with varying levels of success. To provide a more level playing field and facilitate an easier comparison of domain boundary prediction each method was used to predict the domain boundary for the 202 two-domain chains in the nonredundant set (rather than predicting both domain number and boundaries). Therefore, given that the target was known to be two domain by a given method, how often could the cutpoint between the domains be correctly predicted?

Table 3 shows the percentage of top hits giving the correct domain boundary within a window of ±20 residues around the CATH assignment. The methods are ranked in order of success.

Table 3.

Prediction of domain boundaries, given a representative set of two domain protein chains (±20 residues)

Methods	% Correctly assigned boundaries
PUU	81.8
Consensus	52.5
L/(N-1)	49.5
DomSSEA observed secondary structure	49.5
DomSSEA predicted secondary structure	49.0
DGS-M	46.0
Absolute difference in length	44.6
DGS-W	37.1
FASTA	30.0
Random (weighted)	26.8

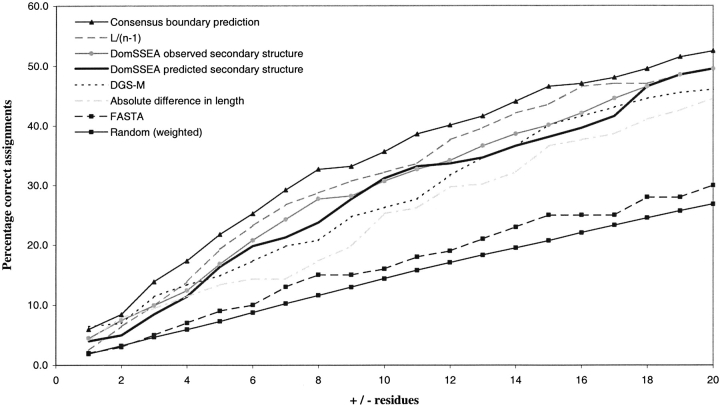
Figure 3 ▶ shows a profile for each method for the percentage of correct assignments for windows of ±1–20 residues.

Fig. 3.

Success rate for the top hit domain boundary assignment for two-domain chains, for window cutoffs between ±1 and 20 residues.

Random boundary assignment provides the baseline in dividing two-domain chains. This random simulation sets the baseline of locating the domain boundary in the two-domain chains, with just under 27% of the linkers correctly located (±20 residues). Again the alignment of sequences resulted in a similar level of prediction accuracy.

The most successful method, and upper benchmark, is the PUU algorithm used by DDD. The common set of chains found in CATH and DDD gave an 81.8% agreement in the domain boundary assignments at ±20 residues.

Interestingly the results from the two implementations of DGS differ somewhat. The results given generated by DGS-W achieved correct assignments in ∼37.1% of the two domain chains, whereas the DGS-M, using probabilities generated from our own dataset, predicted a higher percentage of 46% correct boundary assignments at this cutoff (±20 residues). The success rate of absolute difference in length decreases between DGS-W and DGS-M (±20 residues).

Alignment of predicted secondary structure elements by DomSSEA produced some improvement over the DGS-M, with slightly more than 49% of the predicted two-domain boundaries being correctly assigned (±20 residues).

Clearly, the division of two-domain chains into equal fragments is a useful procedure. Just under one-third of the chains were assigned a correct domain cut. This reflects the degree to which the domain assignment in CATH partitions two-domain chains into equally sized units.

Finally, the method that assigned the most cuts correctly in the absence of 3D structure was the consensus method with ∼52% of the chains assigned a correct cut (±20 residues).

Overall prediction of domain number and domain boundaries

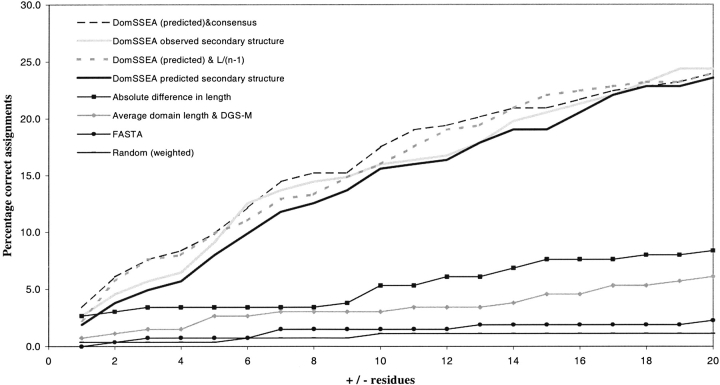
A useful domain identification method must predict domain number and any corresponding domain boundaries with a reasonable degree of reliability. In terms of a fully automated protocol, one must consider the methods as an overall procedure, and the prediction is taken as the top hit assignment. The overall sensitivity of top hit predictions for domain number and boundaries for multidomain chains can be seen in Figure 4 ▶.

Fig. 4.

Overall predictions for multidomain chains, for window cutoffs between ±1 and 20 residues. Correct predictions required both correct domain number and boundary assignments. Success was measured in terms of top hit assignments.

Table 4 demonstrates the effectiveness of each method in giving correct assignments for all chains in the representative set, at ±20 residues as well as for solely multidomain predictions.

Table 4.

Overall prediction of domain number and boundary, for single and multidomain chains (±20 residues)

	% Correctly assigned
Methods	All chains	Multidomain chains
DomSSEA observed secondary structure	70.2	24.7
DomSSEA predicted & consensus	68.6	24.0
DomSSEA predicted & L/(N-1)	68.0	24.0
DomSSEA predicted secondary structure	68.7	23.6
Absolute difference in length	62.0	8.4
Average domain length & DGS-M	66.6	6.1
FASTA alignment	57.9	2.3
Random (weighted)	58.3	1.1
DGS-M	76.6	0.0
DGS-W	76.6	0.0

DGS achieves the highest overall correct assignments (for all chains) as it most often predicts single domain as its top hit. Using the average domain length to predict domain number also achieves a high overall success rate as any chain less than 300 residues in length (two times the domain average) is predicted as single domain.

The use of DomSSEA to both predict domain number and boundaries using predicted secondary structure gives correct assignments for just under 25% of the multidomain chains, at ±20 residues (four times better than the next best method, difference in length). The simple procedure of dividing the chains into equal length, given the domain number was predicted by DomSSEA, results in a similar success rate to boundary assignments by secondary structure element alignment. Using DomSSEA to predict domain number and the consensus method to locate the corresponding domain boundaries proved to assign the greatest number of correct domain boundaries for the multidomain chains over the window cutoffs of ±1–20 residues (Fig. 4 ▶).

In addition to these predictions including a high number of correct assignments for two-domain chains, several correct assignments were made for chains containing three or more domains with just over one-third of domains correctly assigned as three or more domains being given at least one correct domain boundary prediction ±20 residues.

In an attempt to guide the top prediction given by DGS-M, the mean domain length in the representative set (150 residues) was used to predict the number of domains. For example, chain lengths ≤150 residues were predicted as single domain, between 150 and 450 residues as two -domain, and >450 residues (three times the average domain length) as three -or more domains. DGS-M was then used to predict domain boundaries. This achieved a correct domain number and cut prediction for only 3% of the 265 multidomain chains. Another method, the average domain length, was used to predict domain boundaries, for example, a chain length of 320 residues divided at 150 residues from the amino -terminus. However, this resulted in fewer correct predictions than using DGS-M to locate domain boundaries.

The least accurate method is shown to be random prediction, closely followed by sequence alignment.

Discontinuous domain assignment

The analysis and implementation of the methods has so far only focused on the assignment of continuous domains. To gauge the possibility of using DomSSEA to delineate discontinuous domain boundaries, a representative set containing two-domain continuous and discontinuous chains were aligned all–against–all using DomSSEA. Two random baseline measurements were also implemented. Baseline 1 (Table 5) shows the results for predicting discontinuous domain boundaries by equally partitioning the target protein into three equal fragments, thus predicting two linker regions (the most common number of linker regions in two-domain discontinuous chains). Baseline 2 (Table 5) shows the results for randomly predicting the position of two linkers regions.

Table 5.

Prediction of domain boundaries for a representative set of two domain discontinuous chains for boundary windows of ±10 and ±20 residues

	Sensitivity		Selectivity
	±10	±20	±10	±20
DomSSEA	16.4	33.1	24.6	49.7
Baseline 2	13.4	24.4	17.7	32.3
Baseline 1	11.0	24.1	14.6	31.9

Baseline 1 predicts discontinuous linkers by assigning two linkers by equally dividing the chain into three fragments. Baseline 2 also assigns two linkers, but randomly. The sensitivity vs. selectivity measurements show DomSSEA tends to underpredict discontinuous domain linkers.

The percentage of the two-domain discontinuous domains with all linkers correctly predicted was 13% (±20 residues). These chains tended to be those consisting of two or three spanning linkers between domains. The higher complexity of linker arrangement between discontinuous domains makes per protein assignment measurements more restricted. Therefore, linker assignment accuracy was also calculated on a linker basis, that is, the number of linkers in the two-domain discontinuous test set correctly identified. Such prediction accuracy can be measured in two ways: (1) sensitivity, the number of linkers correctly predicted divided by the total number of linkers to predict; and (2) selectivity, the number of correct predictions divided by the total number of predictions made.

Table 5 shows both sensitivity and selectivity values for boundary cutoffs of ±10 and ±20 residues for DomSSEA and two baseline methods. Baseline 1 gives a sensitivity of 11% followed by Baseline 2 with 13.4% at ±10 residues. DomSSEA gives a slightly higher success rate if 16.4% of the discontinuous linkers are assigned correctly at the same cutoff. The selectivity measurements give higher values for the two baseline methods as well as DomSSEA, reflecting its tendency to underpredict discontinuous domain linkers.

Discussion

In this study we have implemented a domain identification method using the alignment of predicted secondary structures of target sequences against observed secondary structures of chains with known domain boundaries. Although mutations at the sequence level can obscure the similarity between homologs, their secondary structure patterns remain more conserved because changes at the structural level are less tolerated. The secondary structure alignment methods used here aim to exploit these conserved features to locate domain regions within secondary structure strings. The increase in accuracy in secondary structure prediction methods in recent years has also made such attempts worthwhile. The overall aim was to evaluate how well domain number and boundaries can be assigned to a given sequence using simple methods, when homology searching to sequences with known domain assignments has been exhausted.

The similarity of the sequence alignment methods to the random methods confirmed that sequence homology was eliminated from the representative set by the PSI-BLAST filter.

In terms of distinguishing between one, two, and three -or more domain chains, DomSSEA is shown to be the most reliable method. Analysis of the two-domain chains as a simple means to measure boundary prediction showed some improvement of DomSSEA over the next best method, DGS, in predicting domain boundaries. However, this is true only when it is used as an overall method that the improvement in accuracy can be seen. It achieves the highest number of correct domain number and boundary assignments for 25% of the multidomain chains (±20 residues; see Fig. 4 ▶).

The comparison of the methods evaluated in this study to DGS was not trivial. Taking only the top assignment from each prediction exposes the limitations of DGS in providing a reliable top guess. We tried to address this issue in two main ways; (1) evaluating the ability of each method to predict the domain boundary for a set of two-domain proteins, thus making a fairer comparison, and (2) using average domain length (calculated from the representative set) to guide the DGS-M domain number prediction and therefore, top predictions. If it is intended that methods are to be used automatically, DGS is less useful than DomSSEA. DGS is more useful as a guide to human experts, as it produces a selection of likely possibilities from which a decision can be made. Fully automatic methods would have to decide on a single answer without human intervention.

A clear observation from this analysis is the frequency with which multidomain chains contain domains of similar length. Figure 3 ▶ shows that at a cutoff of ±10 residues around the CATH cut, 33% of the representative two-domain chains contained a domain boundary at the midpoint of the sequence. To verify that this equal partitioning of chains was not just a feature of the CATH assignment algorithm, the CATH nonredundant set of chains was compared to a common set of chains found in DDD, and another common set of chains was found in SCOP. These common sets were searched for the chains assigned with two equally sized domains by CATH, ±10 residues. Of these chains found in DDD, 88% were also assigned as two domain with a boundary midpoint in sequence, whereas 97% of these chains found in SCOP had similar assignments, ±10 residues. Furthermore, of all the chains assigned as continuous two domain in the DDD common set, and all those assigned as continuous two domain in the SCOP common set, 33% and 34% were given domain cuts midpoint in the sequence, respectively. Therefore, the tendency to partition chains into equal fragments does not appear to be solely a feature of CATH. Although domain number and boundary assignments differ to varying degrees, depending on which two classifications are compared, all three classifications assign >30% of their two-domain proteins with a boundary midway between the carboxyl and amino termini of the sequence.

Indeed, as shown, the equal division of multidomain chains is a successful method in determining domain boundaries given that the correct domain number is known. This is in agreement with the study by Wheelan et al. (2000) showing that domains appear to follow length constraints, and made more salient by observations of protein structural duplication events at the gene level (Heringa and Taylor 1997).

Although DomSSEA (using predicted secondary structure) and the equal partition method predicted domain boundaries with a similar success rate, to what extent do their predictions overlap? If the top two predictions given by DomSSEA are evaluated, 28% of the multidomain chains are given correct domain number and boundary assignments (±10 residues). If the top prediction by DomSSEA is taken, but a second prediction is taken as the number of domains predicted by DomSSEA (second guess) but with the domain boundary predicted by the equal division method, 34% of the multidomain chains are given correctly assigned boundaries (±10 residues). This increase demonstrates fewer overlapping predictions between DomSSEA and the equal division method. (A similar procedure for the partition of two-domain chains gives 41% correct hits for the top two DomSSEA predictions, and 53% if both DomSSEA and the equal division predictions are considered.) Although these boundary prediction methods overlap to some extent, the secondary structure element alignment procedure is able to predict more complex domain arrangements than the simple subdivision method. Such a combination of methods is worthy of consideration.

The assessment of the top 10 assignments given by a prediction method has advantages, allowing correct predictions further down the list to be taken into account. In terms of predicting domain number, however, benchmarking such a top set of assignments could be a rather meaningless measure; in cases where several different domain number predictions are given, it is likely one is going to be correct.

Perhaps more valuable is a top set of predictions for cases where a multidomain chain has been predicted. Here different boundary assignments could be checked and used accordingly. This would most likely be a manual procedure and would be difficult to integrate into an automated annotation method. For example, for a given Critical Assessment of techniques for protein Structure Prediction (CASP) target with no detectable sequence homology to a known structure or domain sequence, one could take the domain number prediction given by DomSSEA. If the target was predicted as two domain, the top three two-domain predictions could be considered. This would give six putative domains to be threaded. For the two-domain chains in the representative set (±20 residues), one of the top three predictions by DomSSEA gave a correct boundary assignment for >60% of the targets. Nevertheless, care would have to be taken benchmarking such a list of hits as the more domain cuts considered, the higher the likelihood of a correct assignment, especially for shorter chains. This, however, would be at the expense of an explosion in the combinatorial number of domains that would need to be tested by threading methods.

Predicting all the domain boundaries correctly within chains of three -or more domains has been found to be a difficult problem for all the methods analyzed. The most successful method was dividing the chains into equal domain lengths. This reflected the observed frequency of those multidomain chains having similar sized domains. However, there are many more multidomain chains having dissimilar sized domain combinations.

A two-domain protein test set containing continuous and discontinuous domains was used to gauge the potential of DomSSEA in predicting discontinuous domain boundaries. Although such an all–against–all alignment of two-domain chains does not give an indication of how introducing discontinuous domains into the DomSSEA library alters domain number prediction and overall assignment accuracy, it does give an insight into boundary prediction given that the correct domain number has been predicted.

With just >13% of the two-domain discontinuous chains given correct assignments for all domain linkers (±20 residues), the boundary prediction accuracy is not high. The calculation of boundary assignment on a per linker basis showed some increase in assignment accuracy of DomSSEA over the baseline random methods.

The selectivity measure of ∼50% of linkers correctly predicted (±20 residues) appears encouraging, but must be tempered by the fact that this value is partially attributable to the observation that DomSSEA tends to underpredict discontinuous domain linkers. This is due in part to the false-positive alignment of chains composed of continuous domains against target chains containing discontinuous domains. How useful a partial knowledge of where discontinuous domain cuts are located within an amino acid sequence is open to question. Only when all the linkers between adjacent domains are located can discontinuous domains be confidently assigned.

Interestingly, although the equal division of continuous chains gave a similar percentage of correct domain assignments to DomSSEA, the same is not so for baseline 1, where the success rate was much lower. This seems to reflect that discontinuous domains are less easily predictable.

Although the addition of discontinuous domains to the DomSSEA library would make discontinuous domain assignment possible to some degree, it would also have a detrimental effect on the reliability of continuous domain assignment, introducing a greater number of false-positive boundary predictions. One would have to weigh up the advantage of assignment of discontinuous domains, with the trade off in reducing continuous assignment accuracy.

If methods such as DomSSEA are to be applied to genomes of higher organisms, as is intended, one must take into account the modularity of higher eukaryotic gene products, especially for larger proteins. A large frequency of multiple domain proteins in higher eukaryotes are made up of continuous domain units, a result of gene duplications and fusion events making proteins containing continuous modular regions of structure the predominant class.

Furthermore, the usefulness of discontinuous domain assignment must also be considered in terms of structure prediction. At present, the ability to predict the structure of such domains using fold recognition, given that fold libraries consist of continuous domains is extremely limited.

Recently, the SnapDRAGON method developed by George and Heringa (2002) has been published, which uses ab initio folding simulations to predict the domain boundaries within a given amino acid sequence. Direct comparison of success rates between SnapDRAGON and DomSSEA is not easy due to the different philosophies used in measuring the accuracy of the methods. However, the success in assignment of domain number appears to be similar, with DomSSEA (using predicted secondary structure) giving correct predictions for 73.3% of protein chains compared to 72.4% by SnapDRAGON. One of the measurements used to assess correct boundary prediction given by SnapDRAGON was by calculating the percentage of all boundary predictions that landed within predicted boundaries, termed the positive prediction value or selectivity. This was shown to be 39.1% for continuous chains in the SnapDRAGON study. A similar calculation for linkers predicted in this analysis by DomSSEA (using predicted secondary structure) reveals a positive prediction value or selectivity of 31.6%. However, the computationally intensive aspect of SnapDRAGON leads to a trade-off between the increase in accuracy of SnapDRAGON versus DomSSEA, and the far greater time required to obtain a SnapDRAGON prediction compared to DomSSEA.

Conclusions

This study has attempted to show what can presently be achieved by using relatively simple methods to predict protein domains from sequence in the absence of homology. Our results have shown that the alignment of secondary structure elements is the most reliable of the methods analyzed for domain number assignment and overall domain number and boundary prediction.

It must be emphasized that although prediction of domain number and domain boundaries can be treated as separate issues, it is the stringent measurement of overall prediction accuracy that is most important, especially when the manual assessment of predictions is difficult. A given method may perform well at predicting domain number or domain boundary, but it is when accuracy in both is combined that the best results are achieved, as DomSSEA has demonstrated.

The methods in this study were tested on a nonredundant set of chains taken from the CATH structural database. Although this is not a full set of genomic sequences, it enables a reliable insight into the effectiveness of these methods in comparison to one another. A future stage will be applying DomSSEA to such genomic data to gauge its usefulness in larger scale genome annotation applications.

Although it must be conceded that methods such as DomSSEA are still somewhat limited in their overall reliability, there is certainly room for such fast procedures to act as a prefiltering stage in automatic genome annotation and threading methods, where domain boundaries cannot be located purely from comparative sequence analysis.

Materials and methods

Dataset

A set of 1314 nonredundant protein chains with X-ray crystallographic resolutions ≤2.5 Å was selected from CATH (version 2.3) (http://www.biochem.ucl.ac.uk/bsm/cath_new/index.html). The set contained no more than 30% pair-wise sequence identity. The representative set used in this study consisted of 1137 chains containing only continuous domains. A further set of 123 discontinuous two-domain chains and 203 continuous two-domain chains, taken from the nonredundant set, were also used to analyze the ability of DomSSEA to locate discontinuous domain boundaries.

All domain predictions for a given chain were compared to assignments given in CATH. Domain number assignments were defined as single, two domain, or three -or more domains. Domain boundary predictions were then made accordingly and compared to boundaries defined by CATH.

Random prediction

Prediction of domain number

As a baseline measure of domain number prediction, the domain number was randomly assigned to each chain in the representative. The random assignments were weighted in terms of the frequencies of single and multidomain proteins in the nonredundant set. The shortest length permissible for a domain was 40 residues, because >99% of the domains in CATH are greater than or equal to this length. In turn, the shortest length considered for a two-domain assignment was 80 residues (i.e., an equal division yields two 40 residue domains). Similarly, the shortest length for predictions of three -or more domains is 120 residues.

Prediction of domain boundaries

For a sequence predicted as multidomain, random assignments were made for domain boundaries. For example, in the case of a two-domain protein, a window within the sequence was considered whereby 40 residues at the carboxy-terminal and amino-terminal extremes of the sequence were masked off. A random cut was then made in this window. In cases where the sequence length was exactly 80 residues, an equal partition was made. Similarly, when three -or more domains were predicted, random cuts were made to ensure that no domain was less than 40 residues in length.

Trivial boundary assignment procedure

Given that the number of domains for the target sequence has been predicted, one of the simplest ways to partition the sequence into domains is to divide it into equal fragments. Therefore, given a sequence length L and the predicted number of domains N, each domain length can be considered as L/(N − 1).

For all the random methods, random simulations were carried out 100 times, and the average success rate calculated.

Sequence alignment

An all–against–all alignment of sequences in the nonredundant set was carried out to predict both domain number and domain boundaries. FASTA (Pearson and Lipman 1988) was used to align each target sequence against all other sequences in the representative chain set. The sequence with the most significant alignment score was used to determine domain number. In cases where the top scoring hit was multidomain, the cutpoints were determined by mapping the known cutpoints of the template chain onto the target chain.

Absolute difference in length

The similarity of chain pairs was scored according to their absolute difference in sequence length, normalized by the maximum length. Domain number and boundaries were taken from the top scoring hit.

Domain Guess by Size (DGS)

The original DGS algorithm was implemented using the probability distributions as outlined by Wheelan et al. (2000) (here, defined as DGS-W). We also implemented the algorithm using probabilities generated from our own nonredundant dataset (here, defined as DGS-M). The cross-validation procedure outlined by Wheelan et al. (2000) was followed in both cases.

Secondary structure alignment (DomSSEA)

An all–against–all alignment of the secondary structure elements for each chain in the nonredundant set was carried out using a modified version of the dynamic programming algorithm previously developed by McGuffin et al. (2001) with a scoring scheme adapted from Przytycka et al. (1999). The use of both observed and predicted secondary structure was assessed. Top hits were taken as the pair with the highest alignment score. Domain boundaries were taken from the position to which the template domain boundary aligned to the target. Assignments were weighted to coil regions of chain, as previous studies revealed domain-linking regions are most commonly found in unstructured regions of chain (R. Marsden and D. Jones, unpubl. results).

Observed secondary structures for all chains were taken from DSSP assignments (Kabsch and Sander 1983). The eight structural states were simplified to three: E and B assignments were considered as strand, H and G assignments as helix, and the remaining states as coil.

Secondary structure predictions were made using PSIPRED (Jones 1999). Five sets of neural network weights were used to train the network, and in cases where a sequence was found to have homology to one of the sets of weights, the corresponding weight set was excluded. Q₃ and Sov (Zemla et al. 1999) scores were calculated to measure the prediction accuracy.

PUU / DDD

The DDD (http://www.embl-ebi.ac.uk/dali/) was used as an upper control for benchmarking the methods. The algorithm used by the DDD to assign domains from structural data is PUU (Holm and Sander 1994). PUU bases its assignments on the theory that domain regions contain more internal structural contacts than external contacts. A common set of chains found both in the representative set and in DDD was compiled, and the domain number and boundary definitions given in DDD were compared to the CATH assignments.

Homology filter

All top hit assignments for alignment methods were filtered further for any possible remaining homology detected by PSI-BLAST (Altschul et al. 1997) within the nonredundant set of chains. PSI-BLAST is one of the most successful methods for detecting remote sequence similarities when used in conjunction with a large nonredundant sequence database (Salamov et al. 1999). The use of sensitive sequence comparison tools is often one of the first steps in locating putative domains in a target sequence with no known structure. In this study it was important to establish a starting point when benchmarking the methods, in which all sequence homology was eradicated so as to simulate cases where sequence searching had been exhausted. It was important that correct assignments were not attributable to matches at the sequence level.

PSI-BLAST was run with default parameters for five iterations, or until convergence. A large nonredundant sequence database was used (containing sequences from PDB, SWISSPROT, and TREMBL, Bairoch and Apweiler 2000; PIR, Barker et al. 2001; ENSEMBL, Birney et al. 2001; WORMPEP, http://www.sanger.ac.uk/Projects/C_elegans/wormpep/; GENPEPT, ftp://ftp.ncifcrf.gov/pub/genpept/; as well as including the set of representative CATH chains used in this study). Each chain in the representative set was scanned against the sequence database and all significant pair-wise matches (E-value ≥0.01) found within the CATH representative set were recorded. This list was used to filter the top hits generated by each method. The same procedure was followed for the chimera set of chains.

Sensitivity measure

This study was undertaken with the aim of measuring the usefulness of prediction methods in terms of their application in automatic assignment algorithms. In terms of a typical Critical Assessment of Fully Automated Structure Prediction (CAFASP) (Fischer et al. 2001) assessment where automatic methods for fold recognition are assessed, the fold template with the highest score or top hit is taken to be the fold of a given target. In this study, we wanted to take a similar approach in assessing the domain assignment methods, basing the measurements on the presumption that they will be used to automatically analyze whole proteomes. Thus, the sensitivity of each domain assignment method was measured by calculating the number of correctly assigned top hits.

Sensitivity of domain number prediction

Measuring the success of a method at assigning the correct number of domains to a target chain was simply a question of how often the predicted number of domains matched the actual number of domains as assigned by CATH. In cases where two or more hits were found to have the same assignment score for a given target, the success rate was calculated to reflect this. For example, if a target was assigned three hits with identical scores, and two were correct predictions and one incorrect, the overall prediction for that particular target was given a sensitivity score of ⅔.

Sensitivity of domain boundary prediction

In terms of measuring domain boundary prediction accuracy, a correct assignment was given if the predicted cut fell within a given cutoff window around the boundary defined by CATH. A sliding scale of ±1–20 residues, either side of the CATH cut, was used to assess the accuracy of the boundary prediction. In cases where the target contained multiple boundaries, the correct number of boundaries had to be given with the assignments falling within the CATH boundaries for a prediction to be regarded as correct (for a given window cutoff). In cases where more than one hit shared the highest score, a random selection was made from the predictions. This was carried out 100 times to obtain an average of this randomization.

Consensus domain boundary prediction method

A consensus boundary prediction method was used to take into account predictions made by several methods used in the study, including DGS, DomSSEA (predicted secondary structure), difference in length, and the equal division procedure. Predicted cut points were grouped in terms of neighboring predictions and the average of the most populated group taken. Where no consensus could be reached, the assignment made by DomSSEA was used.

Comparison of the different methods

The comparison of the prediction methods was categorized into three main areas:

1. Correct prediction of the number of domains in a chain.

2. Correct prediction of domain boundaries. It is difficult to compare the overall top prediction given by DGS with the other methods and easily draw decisive conclusions from the results. To analyze the success rate of domain boundary delineation, each algorithm was assessed for its ability to predict the domain boundary for all the two-domain proteins in the nonredundant set (where each method was provided with the knowledge that the target chain was two domain). This procedure was necessary to provide a more level playing field for comparison of the methods in terms of boundary prediction accuracy. To achieve this for the alignment methods, a pair-wise comparison of the two-domain chains was undertaken.

3. Assessment of overall prediction accuracy. For a correct prediction, both domain number and domain boundaries (for a given cutoff) had to match the CATH assignments.