Abstract
The solution structures of two computationally designed core variants of the β1 domain of streptococcal protein G (Gβ1) were solved by 1H NMR methods to assess the robustness of amino acid sequence selection by the ORBIT protein design package under changes in protein backbone specification. One variant has mutations at three of 10 core positions and corresponds to minimal perturbations of the native Gβ1 backbone. The other, with mutations at six of 10 positions, was calculated for a backbone in which the separation between Gβ1's α-helix and β-sheet was increased by 15% relative to native Gβ1. Exchange broadening of some resonances and the complete absence of others in spectra of the sixfold mutant bespeak conformational heterogeneity in this protein. The NMR data were sufficiently abundant, however, to generate structures of similar, moderately high quality for both variants. Both proteins adopt backbone structures similar to their target folds. Moreover, the sequence selection algorithm successfully predicted all core χ1 angles in both variants, five of six χ2 angles in the threefold mutant and four of seven χ2 angles in the sixfold mutant. We conclude that ORBIT calculates sequences that fold specifically to a geometry close to the template, even when the template is moderately perturbed relative to a naturally occurring structure. There are apparently limits to the size of acceptable perturbations: In this study, the larger perturbation led to undesired dynamic behavior.
Keywords: Protein design, backbone design, core sidechain packing, dead-end elimination, ORBIT
It is now well known that protein backbones undergo small but global rearrangements to accommodate changes in hydrophobic core packing when core amino acid residues are mutated (Baldwin et al. 1993; Lim et al. 1994). Understanding this interplay between sequence and structure is particularly important for protein design. Most computational design methods presented to date presuppose a rigid backbone structure (for review, see Street and Mayo 1999), though several groups have reported efforts to treat both backbone structural variability and side-chain selection (Su and Mayo 1997; Harbury et al. 1998; Desjarlais and Handel 1999). In our approach, the global fold of a protein is decomposed via supersecondary structure parameterization. Variation of supersecondary structure parameter values then provides new fixed-backbone templates for input to a sequence selection algorithm.
In particular, we studied the immunoglobulin binding β1 domain of streptococcal protein G (Gβ1), a 56-residue domain comprising a four-stranded β-sheet and an α-helix. Four parameters were derived that fix the position and orientation of the helix with respect to the sheet: the distance between the helix center and the sheet plane, two angles defining the orientation of the helix axis with respect to the sheet plane, and an angle defining rotation about the helix axis. Each of these parameters was varied incrementally (up to ±1.5 Å for the helix-sheet distance and up to ±10° for the angles) to generate novel backbones. The backbones were then used as templates for core residue sequence selection calculations with the ORBIT (Optimization of Rotamers By Iterative Techniques) protein design programs, which utilize the dead-end elimination theorem to solve the rotamer space combinatorial optimization problem (Desmet et al. 1992; Pierce et al. 2000). The 10 most buried residues in the crystal structure of the wild-type protein (excluding glycines) were included in the calculation: backbone variation and subsequent sequence selection resulted in mutations at three to six of these positions (Su and Mayo 1997).
Gβ1 variants containing the optimal sequences calculated in this fashion were expressed and purified for analysis. Thermal stabilities were assessed by circular dichroism (CD) spectroscopy; fold specificities were evaluated by a qualitative consideration of chemical shift dispersion in 1D 1H nuclear magnetic resonance (NMR) spectra. It was found that small perturbations of the backbone yielded small changes in core sequence (three of 10 positions) and that the proteins containing those sequences were similar to Gβ1 in thermal stability and chemical shift dispersion. Many of the sequences calculated for more extensively displaced backbones also yielded well-folded proteins, judged by chemical shift dispersion. Several of these latter variants, however, are destabilized relative to the wild-type protein.
Analysis at this level establishes that the sequence selection algorithm is tolerant of small variations in backbone specification: when a nonnative but native-like backbone is used as a template, a sequence is calculated that yields a well-folded, thermostable protein. It is of considerable interest to know, further, how closely the folded protein matches the target structure and, particularly, how accurately the algorithm predicts core side-chain packing under backbone perturbations.
We report here the solution structures determined by 1H NMR, of two Gβ1 variants: one minimally perturbed (a threefold mutant) and one extensively perturbed (a sixfold mutant). When the native Gβ1 backbone is used as a template, the lowest-energy calculated sequence has three conservative mutations relative to the wild-type sequence: Y3F, L7I, and V39I (Dahiyat and Mayo 1997). These mutations have been rationalized in terms of the details of the calculation (Su and Mayo 1997). Experimentally, the protein containing this sequence (designated Δh0.9[+0.00 Å] in the previous study, referred to hereafter as Δ0) was found to be slightly more stable than wild type, with a melting temperature (Tm) of 91°C (Tm of Gβ1 is 89°C). The Δ0 sequence was also obtained by sequence selection with several different backbones in which the orientation of the helix with respect to the sheet was varied by small amounts. Thus Δ0 represents the optimal sequence for backbones close to the native fold. Displacement of the template helix from the sheet plane by +1.50 Å yields the sixfold mutant, which contains the three core substitutions of Δ0 plus F30L, A34I, and F52W. Among the extensively perturbed variants of the earlier study, this protein (previously designated Δh1.0[+1.50 Å], referred to hereafter as Δ1.5) was the best behaved, with chemical shift dispersion comparable to wild type and a Tm of 73°C.
Results and discussion
Standard sets of 2D 1H NMR data were collected for Δ0 and Δ1.5. Spin systems were assigned for all residues of Δ0. Core residue side chains were completely assigned; other side-chain assignments are >95% complete. Good dispersion of chemical shifts and narrow linewidths in the Δ0 spectra indicate that this protein favors a single conformation under the experimental conditions. The Δ1.5 data, by contrast, contain evidence of conformational dynamics. While resonance assignments for this protein are also ∼95% complete, no spin system was found for E27, and cross peaks to the backbone amide protons of T25, T51, and T53 are broadened and of low intensity. The chemical shifts of the ring protons of W52 are similar to random coil values, and the indole imino proton signal from this residue is absent, suggesting that its side chain is conformationally labile and accessible to solvent. Also, the Hɛ and Hζ ring protons of F3 could not be assigned definitively.
Families of structures consistent with the data were generated by standard distance geometry/simulated annealing methods (Nilges et al. 1988, 1991). The structures of both molecules are well defined, and their stereochemical quality is good (Table 1). Both proteins have the characteristic protein G fold. The Δ0 sequence adopts a fold quite similar to its template, that is, the native Gβ1 backbone (Fig. 1a ▶). The RMS deviation (RMSD) between atoms in the minimized mean experimental backbone and atoms in the crystallographic backbone is 0.92 Å (excluding two residues at the N terminus, for which few experimental restraints exist). Δ1.5 also closely matches the native Gβ1 structure, with a backbone atomic RMSD of 1.03 Å. With a backbone atomic RMSD of 1.26 Å (Fig. 1b ▶), Δ1.5 is somewhat less similar to its own target backbone.
Table 1.
Experimental restraints and structure statistics
| Δ0 | Δ1.5 | |
| NOE distance restraints | ||
| Intraresidue | 208 | 317 |
| Sequential | 145 | 146 |
| Medium range (2≤|i-j|≤4) | 67 | 73 |
| Long range (|i-j|≥5) | 176 | 161 |
| Hydrogen bond restraints | 28 | 36 |
| χ1 restraints | 0 | 10 |
| RMSDs from data | ||
| Distance restraints (Å) | 0.028 ± 0.001 | 0.029 ± 0.003 |
| χ1 restraints (°) | n/a | 0.57 ± 0.50 |
| RMSDs from ideal geometry | ||
| Bonds (Å) | 0.0031 ± 0.0001 | 0.0033 ± 0.0001 |
| Angles (°) | 0.55 ± 0.01 | 0.58 ± 0.01 |
| Impropers (°) | 0.41 ± 0.01 | 0.42 ± 0.01 |
| Ensemble atomic RMSDs (Å)a | ||
| Backbone | 0.23 | 0.23 |
| Heavy atoms | 0.74 | 0.60 |
| Ensemble Ramachandran statisticsb | ||
| Residues in most favored regions (%) | 77.7 | 80.4 |
| Residues in additionally allowed regions (%) | 20.7 | 19.3 |
| Residues in generously allowed regions (%) | 1.4 | 0.2 |
| Residues in disallowed regions (%) | 0.1 | 0.1 |
a Ensemble RMSDs were calculated for residues 2–56 of both proteins.
b Ramachandran analysis was performed with PROCHECK-NMR (Laskowski et al. 1996).
Fig. 1.
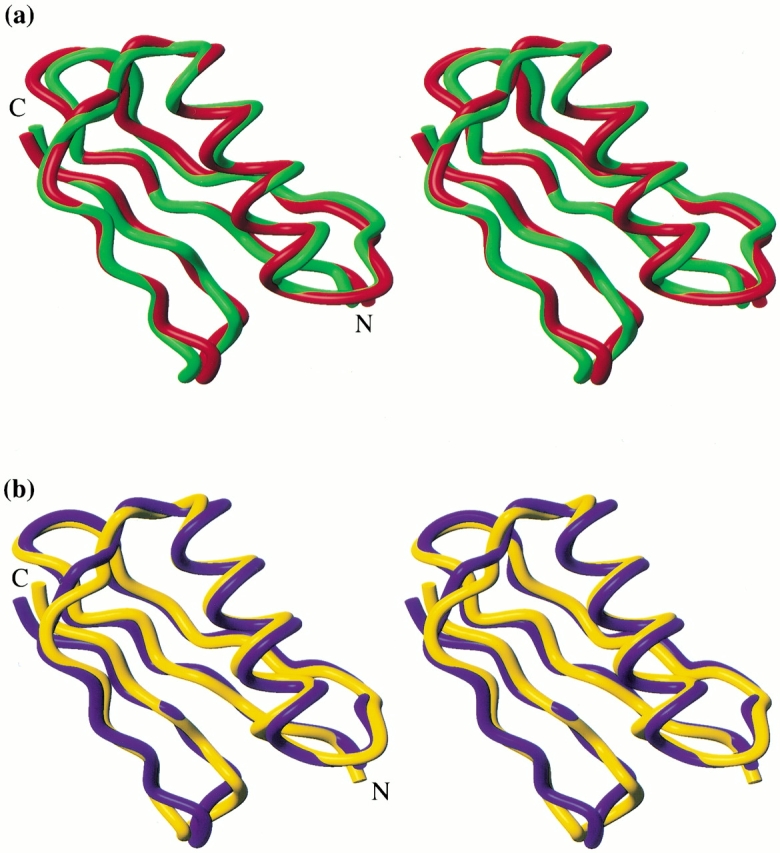
Stereoviews of experimental versus target structures of Gβ1 variants. (a) Superposition of the minimized mean experimental structure of Δ0 (green) and the crystal structure of Gβ1 (red), accession code 1pga (Gallagher et al. 1994). (b) Superposition of the minimized mean experimental (yellow) and calculated (blue) structures of Δ1.5. Incomplete N-terminal methionine processing results in mixtures of 56 and 57 amino acid proteins, with the 57-mer predominating for more stable variants. The structures presented are the 57-mer of Δ0 and the 56-mer of Δ1.5 (sequence numbering for the 56-mer is used throughout the text). Figures were generated using MOLMOL (Koradi et al. 1996).
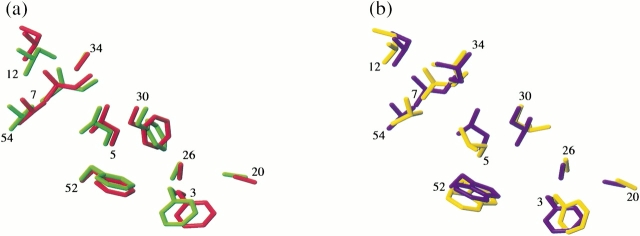
Prediction by ORBIT of core side-chain packing was found to be excellent (Fig. 2 ▶a,b). All of the nontrivial core residue χ1 angles were predicted correctly: the largest deviations between target and experimental structures were 22° (F30) in Δ0 and 35° (L5) in Δ1.5. Somewhat less robust was the χ2 angle prediction: five of six nontrivial χ2's were correctly predicted in Δ0, four of seven in Δ1.5. Closer examination of the Δ1.5 core reveals that the residues for which χ2 is mispredicted (F3, L5, L30) interact with side-chains that are dynamically disordered (E27 and W52, as described above). Misprediction of χ2 in these residues might be a further indication of conformational heterogeneity in this portion of the protein.
Fig. 2.
Sidechain packing in Gβ1 variants. (a) Core residue heavy atoms of the minimized mean experimental (green) and calculated (red) structures of Δ0. (b) Core residue heavy atoms of the minimized mean experimental (yellow) and calculated (blue) structures of Δ1.5. χ1 and χ2 angles in the ensemble of NMR structures were found in all cases to be well represented by the values in the minimized mean structures. Residue numbers are located near each residue's Cα atom.
A previous study found that Gβ1 variants with multiple core mutations form stable well-folded proteins (Gronenborn et al. 1996). We have extended this result herein, showing that a native-like fold is retained with changes at as many as six of 10 core positions. The Δ0 and Δ1.5 structures demonstrate, furthermore, that the sequences generated by ORBIT from perturbed backbone templates lead to correctly folded proteins and that ORBIT predicts core side-chain conformations in such proteins reasonably well. Similar success in predicting fold specificity and core packing has been demonstrated for the ROC algorithm in a study of a designed core variant of ubiquitin (Johnson et al. 1999). In that study, a detailed analysis of backbone and core sidechain dynamics showed small but significant differences between wild-type and variant proteins. Our sixfold mutant Δ1.5, the sequence obtained from the largest backbone perturbation we attempted, also shows unintended dynamic behavior. Much of this behavior may be caused by two aspects of the F52W mutation. First, the experimental Δ1.5 backbone more closely resembles the wild-type than the calculated backbone, so the core is overpacked. The bulk of the W52 side-chain must be compensated in ways (such as local structural fluctuations) other than global displacement of the helix from the sheet plane. Second, burial of the W52 imino proton in the hydrophobic core without a hydrogen-bonding partner may also contribute to the conformational exchange.
These results suggest several avenues for improvement of the design protocol. The method used to generate the Δ1.5 template neglected the loops connecting helix and sheet. Experimentally, we found that the Δ1.5 sequence does not achieve the helix–sheet separation specified in the Δ1.5 template; explicit consideration of loop length during backbone specification might enable us to achieve better agreement between target and experimental structures. In addition, further terms in the ORBIT scoring function, such as a penalty for burial of uncompensated polar hydrogens (implemented subsequent to this study), may lead to more favorable sequence selection and, hence, improved fold specificity.
Materials and methods
Designed proteins were expressed and purified as previously described (Su and Mayo 1997). For NMR experiments, 5–15 mg of lyophilized protein was dissolved in 700 μL buffer (50 mM sodium phosphate in either 90% H2O/10% D2O at pH 6.0 or 99.9% D2O, pD 6.0), yielding 1–3 mM protein concentration. NMR experiments were performed on a Varian UnityPlus 600-MHz spectrometer equipped with a Nalorac Z-axis gradient probe. DQF-COSY, TOCSY, and NOESY spectra were acquired at 25°C for the structure determinations. Additional data sets were acquired at 35°C to facilitate resonance assignments. TOCSY spectra were acquired with mixing times of 25 and 80 msec, NOESY spectra with mixing times of 75, 100, and 150 msec. The spectral width in all experiments was 7500 Hz. The TOCSY and NOESY spectra were recorded with 256t1 * 1024t2 complex points, the DQF-COSY spectra with 512t1 * 2048t2 complex points. Amide hydrogen exchange rates were measured by following the time course of the disappearance of amide-α proton crosspeaks in magnitude-mode COSY spectra (256t1 * 2048t2 points) for protiated, lyophilized protein resuspended in 99.9% D2O. E.COSY spectra were also acquired, with 625t1 * 2048t2 complex points. All spectra were processed with VNMR (Varian).
Resonance assignment was performed using ANSIG (Kraulis 1989) for the Δ0 data and NMRCOMPASS (MSI) for the Δ1.5 data. Cross peaks in the 75 msec mixing time NOESY spectra were assigned for use as distance restraints. Poorer dispersion in the Δ1.5 spectra than in the Δ0 spectra necessitated additional steps in assigning NOESY cross peaks, as follows. A table of putative NOESY cross-peak assignments was generated automatically in NMRCOMPASS. Proton pairs separated by >10 Å in the Δ1.5 template were discarded as possible assignments, yielding a partially assigned restraint set (Nilges et al. 1997). The subset of unambiguously assigned restraints taken from this set was used to calculate an initial ensemble of structures. The minimized mean of this ensemble was then used to calculate a new set of interproton distances, which were again used to filter the NOESY crosspeak assignments, this time with a 5-Å distance cutoff. After the second cycle of distance filtering, remaining ambiguous restraints were discarded. This approach resulted in a comparable number of distance restraints for the two proteins (Table 1). The χ1 restraints were obtained from coupling constant measurements in E.COSY spectra combined with patterns of intraresidue NOEs (Wagner et al. 1987). These angular restraints were found to improve the quality and precision of the ensemble of Δ1.5 structures but not that of the Δ0 structures. Hence, χ1 restraints were not used in refinement of the Δ0 ensemble. Handling of experimental restraints was otherwise as previously described (Malakauskas and Mayo 1998).
Standard hybrid distance geometry/simulated annealing protocols were used to find structures consistent with experimental restraints (Nilges et al. 1988, 1991). Distance geometry structures (100) were generated, regularized, and refined, resulting in ensembles of structures (68 for Δ0, 81 for Δ1.5) with no restraint violations >0.3 Å, RMSDs from idealized bond lengths <0.01Å, and RMSDs from idealized bond angles <1°. Statistics for the 40 lowest-energy structures of each of these ensembles are compiled in Table 1.
Electronic supplemental material
1H resonance assignments are provided for both proteins. Table S1 contains chemical shifts for Δ0. Table S2 contains chemical shifts for Δ1.5.
Acknowledgments
We thank Monica Breckow for assistance with molecular biology protocols. This work was supported by the Howard Hughes Medical Institute (S.L.M.). C.A.S. is partially supported by an NSF graduate research fellowship. Coordinates and NMR restraints have been deposited in the Protein Data Bank. Accession numbers for the coordinates are 1fd6 and 1fcl for Δ0 and Δ1.5, respectively.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at www.proteinscience.org/cgi/doi/10.1110/ps.32501
Supplemental material: See www.proteinscience.org.
References
- Baldwin, E.P., Hajiseyedjavadi, O., Baase, W.A., and Matthews, B.W. 1993. The role of backbone flexibility in the accomodation of variants that repack the core of T4 lysozyme. Science 262 1715–1718. [DOI] [PubMed] [Google Scholar]
- Dahiyat, B.I. and Mayo, S.L. 1997. Probing the role of packing specificity in protein design. Proc. Natl. Acad. Sci. 94 10172–10177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desjarlais, J.R. and Handel, T.M. 1999. Side-chain and backbone flexibility in protein core design. J. Mol. Biol. 289 305–318. [DOI] [PubMed] [Google Scholar]
- Desmet, J., De Maeyer, M., Hazes, B., and Lasters, I. 1992. The dead-end elimination theorem and its use in protein sidechain positioning. Nature 356 539–542. [DOI] [PubMed] [Google Scholar]
- Gallagher, T., Alexander, P., Bryan, P., and Gilliland, G.L. 1994. Two crystal structures of the β1 immunoglobulin-binding domain of streptococcal protein G and comparison with NMR. Biochemistry 33 4721–4729. [PubMed] [Google Scholar]
- Gronenborn, A.M., Frank, M.K., and Clore, G.M. 1996. Core mutants of the immunoglobulin binding domain of streptococcal protein G: Stability and structural integrity. FEBS Lett. 398 312–316. [DOI] [PubMed] [Google Scholar]
- Harbury, P.B., Plecs, J.J., Tidor, B., Alber, T., and Kim, P.S. 1998. High-resolution protein design with backbone freedom. Science 282 1462–1467. [DOI] [PubMed] [Google Scholar]
- Johnson, E.C., Lazar, G.A., Desjarlais, J.R., and Handel, T.M. 1999. Solution structure and dynamics of a designed hydrophobic core variant of ubiquitin. Structure 7 967–976. [DOI] [PubMed] [Google Scholar]
- Koradi, R., Billeter, M., and Wüthrich, K. 1996. MOLMOL: A program for display and analysis of macromolecular structures. J. Mol. Graph. 14 51–55. [DOI] [PubMed] [Google Scholar]
- Kraulis, P.J. 1989. ANSIG: A program for the assignment of protein 1H NMR spectra by interactive computer graphics. J. Magn. Reson. 84 627–633. [Google Scholar]
- Laskowski, R.A., Rullmann, J.A., MacArthur, M.W., Kaptein, R., and Thornton, J.M. 1996. AQUA and PROCHECK-NMR: Programs for checking the quality of protein structures solved by NMR. J. Biomol. NMR 8 477–486. [DOI] [PubMed] [Google Scholar]
- Lim, W.A., Hodel, A., Sauer, R.T., and Richards, F.M. 1994. The crystal structure of a mutant protein with altered but improved hydrophobic core packing. Proc. Natl. Acad. Sci. 91 423–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malakauskas, S.M. and Mayo, S.L. 1998. Design, structure, and stability of a hyperthermophilic protein variant. Nat. Struct. Biol. 5 470–475. [DOI] [PubMed] [Google Scholar]
- Nilges, M., Clore, G.M., and Gronenborn, A.M. 1988. Determination of three-dimensional structures of proteins from interproton distance data by hybrid distance geometry-dynamical simulated annealing calculations. FEBS Lett. 229 317–324. [DOI] [PubMed] [Google Scholar]
- Nilges, M., Kuszewski, J., and Brünger, A.T. 1991. Sampling and efficiency of metric matrix distance geometry. In Computational aspects of the study of biological macromolecules by NMR (ed. J.C. Hoch, et al.), pp. 451–457. Plenum, New York.
- Nilges, M., Macias, M.J., O'Donoghue, S.I., and Oschkinat, H. 1997. Automated NOESY interpretation with ambiguous distance restraints: The refined NMR solution structure of the pleckstrin homology domain from β-spectrin. J. Mol. Biol. 269 408–422. [DOI] [PubMed] [Google Scholar]
- Pierce, N.A., Spriet, J.A., Desmet, J., and Mayo, S.L. 2000. Conformational splitting: A more powerful criterion for dead-end elimination. J. Comp. Chem. 21 999–1009. [Google Scholar]
- Street, A.G. and Mayo, S.L. 1999. Computational protein design. Structure 7 R105–R109. [DOI] [PubMed] [Google Scholar]
- Su, A. and Mayo, S.L. 1997. Coupling backbone flexibility and amino acid sequence selection in protein design. Prot. Sci. 6 1701–1707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner, G., Braun, W., Havel, T.F., Schaumann, T., Go, N., and Wüthrich, K. 1987. Protein structures in solution by nuclear magnetic resonance and distance geometry—The polypeptide fold of the basic pancreatic trypsin-inhibitor determined using 2 different algorithms, DISGEO and DISMAN. J. Mol. Biol. 196 611–639. [DOI] [PubMed] [Google Scholar]