Stabilization of hen egg white lysozyme by a cavity-filling mutation

Abstract

Stabilization of a protein using cavity-filling strategy has hardly been successful because of unfavorable van der Waals contacts. We succeeded in stabilizing lysozymes by cavity-filling mutations. The mutations were checked by a simple energy minimization in advance. It was shown clearly that the sum of free energy change caused by the hydrophobicity and the cavity size was correlated very well with protein stability. We also considered the aromatic–aromatic interaction. It is reconfirmed that the cavity-filling mutation in a hydrophobic core is a very useful method to stabilize a protein when the mutation candidate is selected carefully.

Hydrophobic interaction is the major factor in the stabilization of the three-dimensional structure of a protein. In folded proteins, the side chains of hydrophobic amino acid residues are generally buried inside the protein molecules, packed efficiently, thus contributing to protein stability through hydrophobic interactions (Dill 1990). Many investigators have tried to improve hydrophobic interactions in hydrophobic cores of proteins to stabilize proteins. Protein stability increased with an increase of hydrophobicity at the specific residue of a protein (Yutani et al. 1987; Matsumura et al. 1988). Conversely, the increase in cavity size in the hydrophobic cores of proteins led to destabilization (Eriksson et al. 1992; Jackson et al. 1993; Buckle et al. 1996). The cavities exist commonly in all large proteins, even within the protein cores (Connolly 1986). Therefore, the cavity-filling mutation should be a highly convenient way to improve protein stability. However, protein stabilization by cavity-filling mutations was only successful in the stabilization attempt using ribonuclease HI (Ishikawa et al. 1993; Akasako et al. 1997). A few attempts of cavity-filling mutations (Karpusas et al. 1989; Eijsink et al. 1992) failed to improve their stabilities because of unfavorable vdW contacts at the mutated sites.

Although the cavities in the hydrophobic cores of proteins have been proven to affect protein stability, as has been shown in the previous reports, the method to stabilize a protein using a cavity-filling mutation is not considered to be definitive at this time.

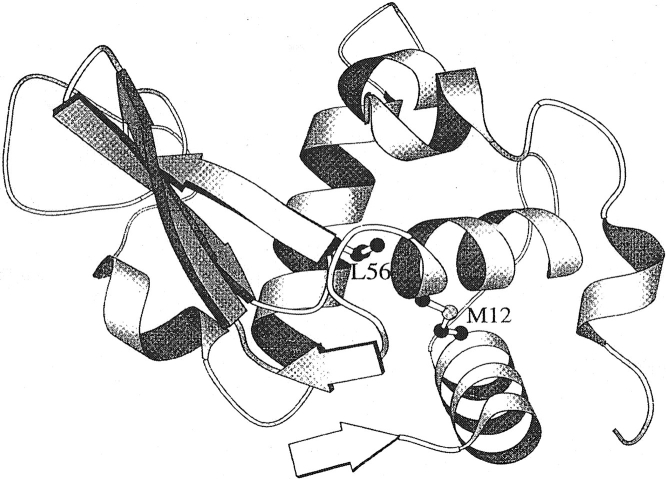
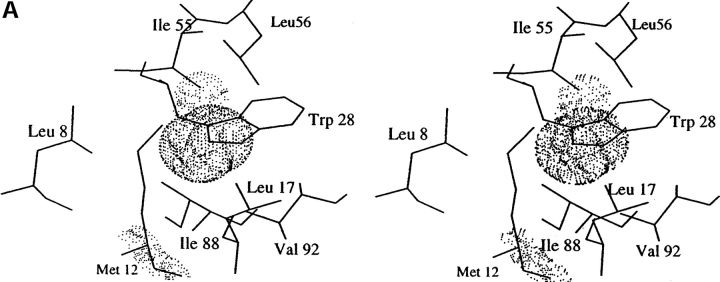
HEL is a small globular protein and the first enzyme whose three-dimensional structure was elucidated by X-ray crystallography (Fig. 1 ▶) Moreover, its crystallization is comparatively easy, it is a suitable protein for getting detailed information of the relationship between the three-dimensional structure and the stability. HEL has a cavity surrounded by a hydrophobic core, which consists of side-chain of residues 8, 12, 17, 28, 55, 56, 88, and 92 in the α-domain (Fig. 2B ▶). In this report, we have mutated Met12 (α-helix) and Leu56 (β-sheet), which face each other across a cavity in the hydrophobic core, to residues with higher hydrophobicity to stabilize the lysozyme molecule by cavity-filling mutation without unfavorable vdW contacts and have analyzed the relationship between the stabilities and the structures of the resulting mutant lysozymes.

Fig. 1.

Ribbon model of secondary and tertiary structures of HEL, showing the side chain of the hydrophobic core residues mutated in this study. The side chain is shown as a ball-and-stick model. This figure was made with the MOLSCRIPT program (Kraulis 1991).

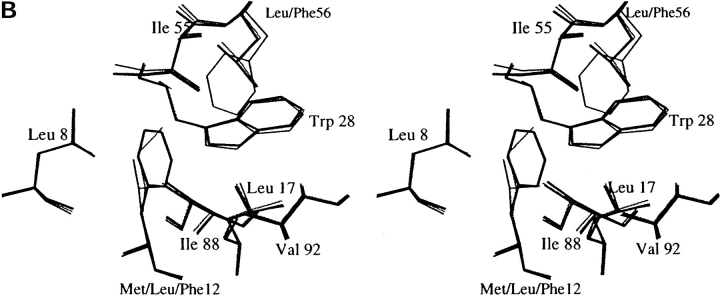
Fig. 2.

(A) Stereo view of space-filling model of cavities in the hydrophobic core of WT. (B) Comparisons of the core region in the refined structures of the mutants and WT. The alignments are based on the least-squares superposition of the main chain atoms. FL mutant (thick line) and LF mutant (thin line) versus WT (dotted line).

Results and discussion

The stabilities and crystal structures of the mutant lysozymes

Because Met12 is located closely to the cavity in the hydrophobic core (Fig. 2A ▶), we selected Met12 as a candidate residue to be mutated. The candidate residue to be substituted was selected to not give steric hindrance using a simple energy-minimization method that was calculated on the condition that all heavy atoms except the target residue were fixed. As a result, both mutant lysozymes where Met12 was mutated to Leu (LL mutant) and where Met12 was mutated to Phe (FL mutant) were prepared. From the analysis of thermal stability using differential scanning calorimetry (DSC), the melting temperature (Tm) of the WT was 66.0°C at pH 2.7 (Table 1). The LL mutant was less stable by 1.8°C (0.57 kcal/mol) than WT (Table 1). Conversely, the FL mutant was more stable by 0.8°C (0.28 kcal/mol) than WT. The crystal structures of both mutants indicated that their overall and local structures were very similar to those of WT (Fig. 2B ▶; LL mutant was omitted because of very similar structure to WT), and there were no unfavorable vdW contacts around their mutated site (data not shown). The difference in the volume of cavity (ΔVc) of all mutants was calculated from the individual X-ray coordinates (Table 1). The volume of cavity (Vc) of the LL mutant was 25.7 ų larger than that of WT, and the Vc of the FL mutant was 12.0 ų smaller than that of WT. The Vc value showed a tendency to be inversely proportional to the stability of HEL. This tendency was also observed in previous cavity-creating proteins (Karpusas et al. 1989; Eijsink et al. 1992). Therefore, the destabilization of the LL mutant was found to depend on the enlargement of the cavity in the hydrophobic core. Thus, even if the hydrophobicity of the substituted residue was increased by mutation, the cavity-creating mutation in the hydrophobic core was found to decrease the stability of a protein such as LL mutant in this study.

Table 1.

Thermal stabilities (pH 2.7) and Gdn-HCl denaturations (pH 5.5) of mutant lysozymes and the cavity volumes (Vc) and cavity surface areas (CSA) in their hydrophobic cores

	ΔTm(°C)a	ΔC1/2b	ΔVc(Å3)c	ΔCSA(Å2)c	ΔGtrd
ML (WT)	0 (0)e	0 (0)e	0 (0)f	0 (0)f	0
LL	−1.8 (−0.57)	−0.1 (−0.35)	25.7 (−0.62)	63.1 (−1.26)	+0.12
FL	+0.8 (+0.28)	+0.2 (+0.49)	−12.0 (+0.29)	−35.7 (+0.71)	+0.24
LF	+3.5 (+1.12)	+0.4 (+1.09)	−12.3 (+0.29)	−3.7 (+0.07)	+0.24
FF	+4.4 (+1.49)	+0.3 (+0.87)	−15.5 (+0.37)	−40.7 (+0.81)	+0.36

^a The difference in the Tm between WT and mutant lysozyme (ΔTm). The Tm value of WT was 66.0°C. ΔTm = Tm(mutant) − Tm(WT).

^b The difference in the C_1/2 between WT and mutant lysozyme (ΔC_1/2). The C_1/2 value of WT was 3.4 M. ΔC_1/2 = C_1/2(mutant) − C_1/2(WT). The unit is M.

^c The volume of the cavity (Vc) is the volume contained within the cavity surface (CSA) which is the area swept out by a sphere of radius 1.2 Å as it rolls over the cavity surface. The value of Vc or CSA in WT were 100.7 ų or 107.4 Ų, respectively. ΔVc = Vc(mutant) − Vc(WT). ΔCSA = CSA(mutant) − CSA(WT).

^d Virtual free energy of transfer of residues, from the exterior to interior of a sample of globular proteins, based on the fraction of the total number of residues that are 95% buried according to Chothia's criterion (1976). The unit is kcal/mol.

^e The numbers in parentheses show the difference in the Gibbs free energy values for thermostability (ΔΔGtm) and Gdn-HCl denaturation (ΔΔG_C1/2). The unit is kcal/mol.

^f The numbers in parentheses show the cavity-dependent energy term calculated by Eriksson's values (0.024 kcal/mol/ų and 0.020 kcal/mol/Ų). The unit is kcal/mol.

To construct a more stable mutant than FL, we prepared two double-mutant lysozymes: An LF mutant where Leu56 in the LL mutant is mutated to Phe and an FF mutant where Leu56 in the FL mutant is mutated to Phe.

The safeties for the mutations were also checked using the above energy minimization. We analyzed their thermostabilities and tertiary structures and the cavity sizes of the hydrophobic core. We found that the LF mutant and the FF mutant were more stable by 3.5°C (1.12 kcal/mol) and by 4.4°C (1.49 kcal/mol) than WT (Table 1), respectively. Both double mutants had similar overall and local structures to WT (Fig. 2B ▶; FF mutant was omitted because of very similar structure to WT). Moreover, there were no unfavorable vdW contacts in the structures of the double-mutant lysozymes (data not shown). Thus, our simple energy-minimization method was proved to be useful to avoid unfavorable vdW contacts. The cavities in both double mutants were observed to be smaller than that in WT (Table 1). We elucidated here that the decrease in the cavity size in the hydrophobic core of lysozyme molecule led to increase in the stability. Thus, filling up the cavity without unfavorable vdW contacts was shown to be a useful method to stabilize a protein.

The activities in mutant lysozymes

The molecular fluctuation of a protein is closely involved in the manifestation of protein activity (Imoto et al. 1994; Mine et al. 1999). Therefore, some mutations might have an influence on fluctuation coupled with the manifestation of the activity. The GC activities of all mutants decreased in the range from 40% to 80%.

Because there was no correlation between a decrease in the GC activity and an increase in the dissociation constant (data not shown), the decrease in GC activity for mutant lysozymes could not be explained by the change in binding ability. GC activity of each mutant against ΔVc or ΔΔGtm is plotted in Figure 3 ▶, A and B, respectively. They showed good correlations. Although the GC activities of all mutant lysozymes were lower than that of WT, the recovery of activity in mutant lysozyme was related to the increase in stability and to the decrease in cavity size. Therefore, this hydrophobic core would play a somewhat important role in lysozyme activity. Thus, the local structure in the hydrophobic core far from the active site cleft affected the manifestation of GC activity in the lysozyme.

Fig. 3.

Correlation between glycol chitin (GC) activity and ΔVc (A) and ΔΔGtm value (B).

The structure of mutant lysozymes possessing "swapped" residues

Interestingly, the "swapped" mutants (FL and LF), which have the same amino acid, only switching at position 12 and 56, had largely different stabilities (0.8 kcal/mol; Table 1). Swapped mutants tended to show the differences in protein stability because of the difference in the interactions around each swapped residue in folded structure, such as favorable or unfavorable vdW contacts and core repacking (Baldwin et al. 1996; Zhang et al. 1996).

As the stabilities of lysozymes evaluated by Gdn-HCl denaturation were similar to that evaluated by thermal denaturation (Table 1), it was suggested that the difference in stability between the swapped mutants was not caused by the difference in energy level of the unfolded states. This means that there existed a difference in a stabilizing factor in the folded states.

In general, a protein stability is largely influenced by vdW interaction. From the comparison of the crystal structures, there was no difference in static vdW interactions between the swapped mutants (data not shown).

Protein structure, however, is not rigid but is flexible. There is a possibility that molecular mobility caused the difference in vdW interaction. Therefore, we calculated the dynamic vdW energy on protein stability in the folded states using molecular dynamics (MD) simulation. Root-mean-square-fluctuation (RMSF) values calculated by simulation were compared with root-mean-square-fluctuation of B-factor (B-RMSF) values in all lysozymes. Although a value of correlation coefficient between RMSF and B-RMSF was ∼0.6, the plot of RMSF value versus residue was very similar to that of B-RMSF (data not shown). Therefore, MD simulations performed here were thought to reproduce molecular motions reasonably well. From the structures sampled during MD simulation, the dynamic vdW energies for the folded states of all lysozymes employed here were calculated (Table 2). The dynamic vdW energies in the swapped mutants were similar (Table 2), and it was confirmed that there was no difference in vdW energy between them in the folded states.

Table 2.

Van der Waals contact energy calculated using molecular dynamics simulation

	Residue 12 (kcal/mol)	Residue 56 (kcal/mol)	Total energy (kcal/mol)	ΔEnergya (kcal/mol)
ML (WT)	−2.65 (0.42)b	−2.77 (0.42)	−5.42 (0.66)	0
LL	−2.48 (0.45)	−2.08 (0.40)	−4.56 (0.58)	+0.86
FL	−7.58 (0.71)	−3.47 (0.33)	−11.06 (0.75)	−5.64
LF	−2.92 (0.41)	−8.29 (0.60)	−11.21 (0.77)	−5.81
FF	−9.23 (0.66)	−9.68 (0.61)	−18.91 (1.05)	−13.49

^a ΔEnergy = Total energy(mutant) − Total energy(WT).

^b The values in parentheses show standard deviations.

Consequently, it is likely that the large difference in stability between the swapped mutants was caused by other interactions which were independent of vdW interaction in the folded state. Since the propensities of phenylalanine for an α-helix and a β-sheet were very similar to those of leucine (Chou and Fasman 1978), it was expected that the mutations have little influence on the stability of secondary structure.

Aromatic–aromatic interactions form the fourth class of the forces stabilizing the native structure and are as important as hydrogen bonds, electrostatic interactions, and vdW interactions. An aromatic–aromatic interaction usually stabilizes a protein molecule by 0.6 ∼ 1.3 kcal/mol under the conditions that the preferential distance of the centroids of the two aromatic rings are ∼5.5 Å and that one aromatic ring is perpendicular to another aromatic ring (Burley and Petsko 1985). The effect of aromatic–aromatic interactions in protein structure was reported in previous studies (Serrano et al. 1991; Anderson et al. 1993).

Table 3 shows the geometry between aromatic ring pairs at residues 12, 28, and 56 in the FL, LF, and FF mutants. The aromatic ring pair in the FL mutant was residues 12 and 28. The effect of this aromatic–aromatic interaction on the stability in FL mutant was considered to be small because both aromatic rings were distant and were out of position. The aromatic ring pair in the LF mutant was residues 28 and 56. Aromatic rings of Trp28 and Phe56 formed a good edge–face interaction. A similar aromatic–aromatic interaction was also observed in the FF mutant.

Table 3.

The geometry of the aromatic–aromatic interaction in FL, LF, and FF mutants

	FL		LF		FF
	Distance (Å)	Angle (°)	Distance (Å)	Angle (°)	Distance (Å)	Angle (°)
12–56	—	—	—	—	5.38	18
12–28	6.81	75	—	—	7.09	75
28–56	—	—	6.03	72	6.09	73

Distances were calculated between the phenyl ring centroids in each pair of aromatic residues. Angles were calculated from the angle formed between the pair of aromatic rings.

Consequently, it would be reasonable to consider that the difference in stability between the swapped mutants would be caused by the presence or absence of an aromatic– aromatic interaction in the LF or the FL mutant, respectively.

The correlation between the stabilities of mutant lysozymes and the variations of cavities in the hydrophobic core

Eriksson et al. (1992) reported that the free energy change per size of cavity was 0.024 kcal/mol/ų for cavity volumes and 0.020 kcal/mol/Ų for cavity surface areas. The differences in free energy change with changes of cavity volume (ΔΔGvc) and that with changes of cavity surface (ΔΔG_CSA) are shown in Table 1. Plots of ΔΔGvc against ΔΔGtm did not give a good correlation. This may be because we have not considered the difference in the hydrophobicity of each residue at a mutated site and because of the aromatic–aromatic interactions in the LF mutant and the FF mutant. We amended the plot between stability and cavity-size using Chothia's ΔGtr (Table 1), which is virtual free energy of transfer of residues from the exterior to the interior of a sample set of globular proteins and each ΔΔGtm by deducting the effect of the aromatic–aromatic interaction in the LF and FF mutants (this value is ∼0.8 kcal/mol; LF′ and FF′ in Fig. 4 ▶, A and B). Replots of ΔΔGtm against the sum of ΔΔGvc and ΔGtr showed a good correlation (Fig. 4A, ▶r² = 0.95), and replots of ΔΔGtm against the sum of ΔΔG_CSA and ΔGtr also showed a good correlation (Fig. 4B ▶r,² = 0.92).

Fig. 4.

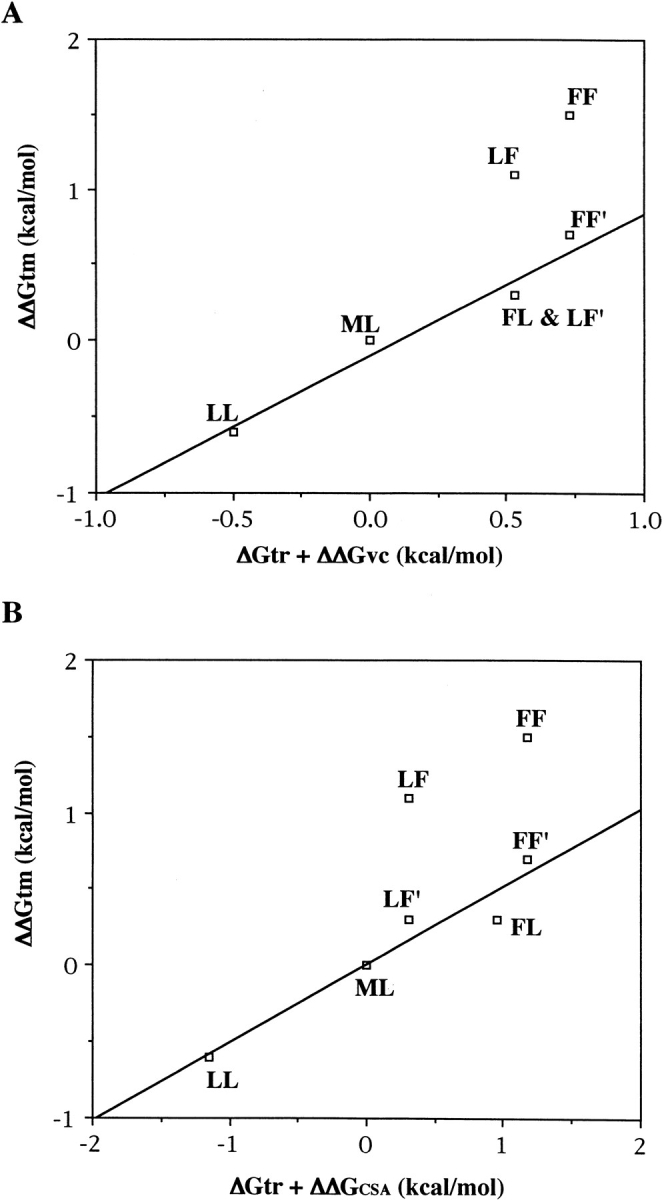
Correlation between ΔΔGtm value and the sum of ΔGtr and ΔΔGvc (A) and the sum of ΔGtr and ΔΔG_CSA (B). LF′ and FF′ are the corrected points for the aromatic–aromatic interaction in the LF mutant and the FF mutant, respectively.

Therefore, it was shown that the sum of the free energy change in the hydrophobicity and in the cavity size was correlated very well with protein stabilities.

Conclusion

In this study, we were successful in the premeditated stabilization of lysozyme by the cavity-filling mutation. It was shown clearly that both the sum of free energy change caused by hydrophobicity and the cavity size was correlated very well with protein stabilities, although two double mutations were further stabilized because of the aromatic–aromatic interaction and that the protein stability was influenced by the better cavity size than hydrophobicity, as seen in the result of the LL mutant. Thus, it is reconfirmed that the cavity-filling mutation in the hydrophobic core is a very useful method to stabilize a protein when the candidate of the mutation is selected carefully.

It is important to select suitable mutations. In previous studies (Karpusas et al. 1989; Eijsink et al. 1992), unexpected destabilizations of proteins were mainly caused by unfavorable vdW contacts. In this respect, our simple energy minimization was suitable to select a mutation in hydrophobic core, and we were successful in the stabilization of lysozyme by inquiring carefully into protein structure. It is very useful to know that our cavity-filling was successful in the stabilization of lysozyme.

Materials and methods

Materials

Restriction enzymes, T4 polynucleotide kinase, and DNA polymerase I (Klenow fragment) were purchased from either Takara Shuzo or New England Biolabs. DNA sequencing kits (Sequenase) were purchased from Amersham Japan. CM-toyopearl 650M, a cation-exchange resin for the purification of secreted hen lysozymes, was obtained from Tosoh.

Energy minimization

Energy minimizations were performed using the Discover simulation software package from Biosym Technologies. The following minimization strategies were used to predict the model for the cavity-filling mutants. All simulations were carried out using the CVFF force field (Dauber-Osguthorpe et al. 1988). First, to remove artifacts introduced by adding explicit hydrogens, the WT structure was energy minimized with the positions of all heavy atoms fixed using the methods of steepest descents for 100 steps. Next, Met12 was substituted for larger hydrophobic residues except Val (Leu, Ile, Phe, Tyr, and Trp), and the substituted structures were energy minimized with the positions of all heavy atoms fixed, except the mutated residues, by 2000 steps of conjugate gradients minimization. We selected a candidate of an amino acid residue to be substituted for the target residues using a simple energy minimization method where the calculation is performed on the condition that all heavy atoms except those in the substituted residue are fixed. After energy minimization, we selected such candidates for the substitution that have no heavy atoms with the distance between heavy atoms <3.4 Å in their energy-minimized structures.

Mutant lysozymes

Mutation of the lysozyme gene was carried out by site-directed mutagenesis as described previously (Hashimoto et al. 1996). Each transformant of Saccharomyces cerevisiae AH22 was cultivated at 30°C for 125 h for expression and secretion of the respective mutant lysozyme (Hashimoto et al. 1996).

Purification (ion-exchange chromatography) and identification (peptide mapping, amino acid sequencing, and amino acid composition) of the lysozymes were carried out as reported previously (Ueda et al. 1993).

Activities of the wild-type and mutant lysozymes

Activities against glycol chitin (GC) were measured in 0.1 M acetate buffer at pH 5.5 and 40°C as described elsewhere (Yamada and Imoto 1981).

Unfolding equilibrium

Unfolding equilibrium of lysozymes by Gdn-HCl was measured at pH 5.5 and 35°C by fluorescence at 360 nm (excited at 280 nm). The protein concentration was 0.9 x 10⁻⁷ M. The buffer used was 0.1 M sodium acetate adjusted to pH 5.5 with HCl. It has been found experimentally that the free energy of unfolding of proteins in the presence of Gdn-HCl is related linearly to the concentration of denaturant (Pace 1986). Details of the analysis were as described (Inoue et al. 1992), and the average m value of the wild-type and mutant lysozymes was employed. The differences in C_1/2 between WT and the mutant lysozymes (ΔC_1/2) are listed in Table 1.

Differential scanning calorimetry

DSC measurements were performed using VP-DSC calorimeters (MicroCal). DSC scans were performed at a rate of 1.0°C/min in a temperature range from 20° to 105°C. Protein concentrations ranged from 0.3 to 0.4 mg/mL in 0.05 M glycine hydrochloride (pH range 2.4–3.0). Data were analyzed with Origin software (MicroCal). DSC measurements of the mutant lysozymes were carried out from pH 2.4 to 3.0. Thermostabilities of these mutants were compared with that of WT based on the Tm value determined at pH 2.7 from each thermal denaturation curve. The differences in Tm between WT and the mutant lysozymes (ΔTm) are listed in Table 1.

X-ray analysis

Crystallization was carried out using a hanging drop vapor diffusion technique at pH 4.7. Intensity data collection for WT or the mutant lysozymes was carried out with an automated oscillation camera system, R-AXIS IIC (RIGAKU), equipped with an Imaging Plate detector, on a Cu rotating anode generator operated at 40 keV and 120 mA at room temperature. Refinement of the structure was carried out using both TURBO-FRODO (Roussel et al. 1990) and X-PLOR (Brunger 1992) installed on SGI Indigo2. The crystallographic data of the WT and the mutant lysozymes are shown in Table 4. Each sample was measured to a high resolution of 1.75–1.80 Å. R-merge was <8.2%, and data completeness was >88%.

Table 4.

Crystallographic data collection and refinement statistics

Lysozyme	ML (WT)	LL	FL	LF	FF
Data collection cell dimensions (Å):
a = b =	79.21	79.16	78.86	79.14	79.51
c =	37.97	37.97	38.02	37.90	37.95
Resolution (Å)	1.75	1.80	1.80	1.77	1.79
Unique reflections	11948	10397	10369	11379	10950
(F ≥ 1 σ [F])
Completeness (%)	93.2	88.7	88.6	91.8	91.1
R-merge (%)a	3.69	5.80	6.37	8.19	5.79
Refinement
R-factor (%)b	16.8	17.1	16.6	17.4	16.8
Δbond length (Å)	0.009	0.010	0.009	0.010	0.009
Δbond angle (°)	1.448	1.466	1.459	1.468	1.449

^a R-merge = (Σ(I − <I>)/ΣI).

^b R-factor = (Σ(F_o − F_c)/ΣF_o).

The refinement of the data for mutant lysozymes were carried out as described previously (Ohmura et al. 1997). As a result of the refinement, R-factors of all mutants fell to ∼17%. Coordinates for WT have been deposited in the Protein Data Bank (accession number 1RFP), and coordinates for all mutants (LL, FL, LF, and FF mutant) have been deposited in the Protein Data Bank (Brookhaven National Laboratory).

Molecular dynamics simulation

The crystal structure of lysozyme was used as the starting structure for MD simulations. This structure was refined to 1.75–1.80 Å resolution in this study and contained ∼100 crystallographically observed water molecules. Hydrogen atoms were added to this structure using the InsightII program (Biosym Technologies). About 300 water molecules were added to 3-Å thickness surrounding the protein structure. The oxygen atoms of all water molecules were tethered by 100 kcal/mol/Ų. MD simulation was carried out using the Discover program (Biosym Technologies) with CVFF (Dauber-Osguthprpe et al. 1988). The dielectric constant used was of a linear distance-dependent dielectric (1*r) equal to the interatomic separation, and a 14.0-Å cutoff was used for nonbonded interactions with a switching function that smoothly turns off the interaction over a range of 1.5 Å. The temperature of the system reached 300 K during the initial 0.1 ps of MD simulation. The rest of the simulation protocol was run for 50 ps at 300 K with a time step of 1 fs, and the molecular coordinates of the molecules were saved at every 0.1 ps.

Molecular dynamics data analysis

Time-dependent protein structures were evaluated in RMSD (data not shown) from the starting structure for all heavy atoms, and the RMSF was compared with the B-RMSF. The RMSD showed the standard perturbation in all MD simulations.

RMSF was calculated as the deviation from the average position of an atom in run time of MD simulation. B-RMSF was calculated from the B factor of each crystal structure by the following equations:

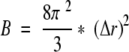where (Δr)² is the mean-square atomic fluctuation and B is the B factor. vdW energy of all proteins in the folded state was calculated as follows:

1. Selection of atomic pairs for vdW energy calculation.

2. Extraction of the distance of the atomic pairs.

3. Calculation of vdW energy of each atomic pairs.

   

   

   

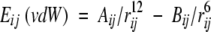
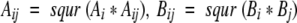
4. Summation of this calculated vdW energy in each sample structure. 5. The averaging of the calculated vdW energy of all sample structures.