Abstract
The net charge and isoelectric pH (pI) of a protein depend on the content of ionizable groups and their pK values. Ribonuclease Sa (RNase Sa) is an acidic protein with a pI = 3.5 that contains no Lys residues. By replacing Asp and Glu residues on the surface of RNase Sa with Lys residues, we have created a 3K variant (D1K, D17K, E41K) with a pI = 6.4 and a 5K variant (3K + D25K, E74K) with a pI = 10.2. We show that pI values estimated using pK values based on model compound data can be in error by >1 pH unit, and suggest how the estimation can be improved. For RNase Sa and the 3K and 5K variants, the solubility, activity, and stability have been measured as a function of pH. We find that the pH of minimum solubility varies with the pI of the protein, but that the pH of maximum activity and the pH of maximum stability do not.
Keywords: Ribonuclease Sa, isoelectric pH, net charge, electrostatic interactions, protein solubility, enzyme activity, protein stability
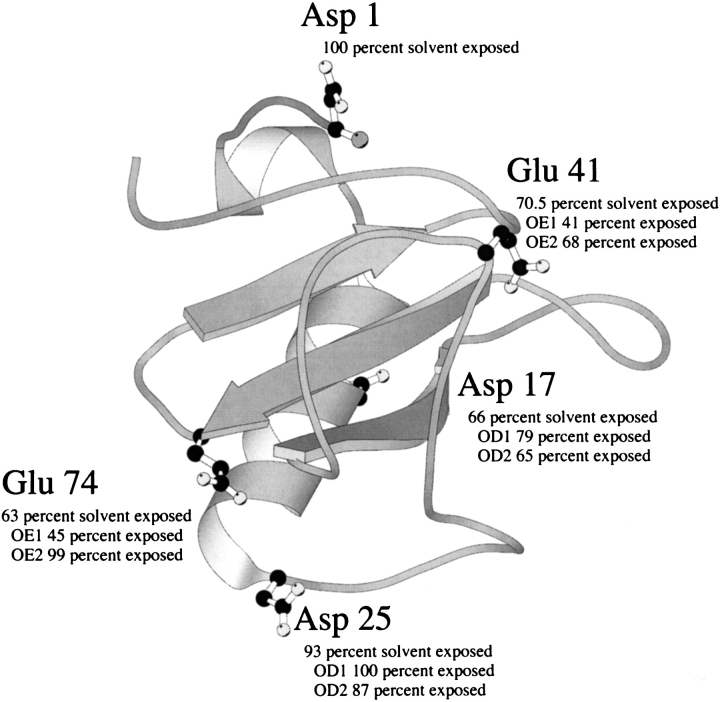
The net charge on a protein at any given pH is determined by the pK values (pKs) of the ionizable groups (Tanford 1962). The net charge on a protein is zero at the isoelectric point (pI), positive at pHs below the pI, and negative at pHs above the pI. Ribonuclease Sa (RNase Sa) has 7 Asp, 5 Glu, 2 His, 0 Lys, and 5 Arg residues. Consequently, the wild-type protein has an excess of acidic residues giving it a pI = 3.5 and a net charge ∼−7 at pH 7 (Hebert et al. 1997). We have previously reported studies of the thermodynamics of folding and conformational stability of RNase Sa (Pace et al. 1998) and several mutants (Hebert et al. 1998; Grimsley et al. 1999; Pace et al. 2000). In this study, we have replaced Asp and Glu residues with Lys residues singly and in combination to produce variants with different pIs. The residues selected for replacement, Asp 1, Asp 17, Asp 25, Glu 41, and Glu 74, are shown in Figure 1 ▶. All of these residues are well exposed to solvent and do not form ion pairs or hydrogen bonds. We report here the experimentally determined isoelectric points for RNase Sa (0K) and the 2K (D17K + E41K), 3K (2K + D1K), 4K (3K + D25K), and 5K (4K + E74K) variants, and we compare these values to the calculated isoelectric points. The addition of five lysines is expected to raise the pI to above 10 and reverse the net charge from −7 to +3 at pH 7. The ability to predict the pI of a protein is useful for developing methods to purify proteins by ion exchange chromatography (Janson andRyden 1989). We also report the dependence of solubility on pH for RNase Sa and the 3K and 5K variants. Theory predicts that the solubility of a protein will be minimal near the pI (Tanford 1961), and we test this in a system where the minimum possible changes in structure are used to vary the pI. Protein solubility is important in diseases such as Alzheimer's disease (Kaytor andWarren 1999), in the development of recombinant proteins for treating diseases such as fast-acting Lys-Pro insulin (Bakaysa et al. 1996), and to many biochemists, especially X-ray crystallographers (McPherson 1998) and NMR spectroscopists (Harris 1986). We also report the enzyme activity as a function of pH for RNase Sa and the 3K and 5K variants. This is of interest because the natural substrate for the ribonucleases is negatively charged and the net charge on the enzyme might influence the steady-state enzyme kinetics. Finally, we report the pH dependence of the thermodynamics of folding and the conformational stability of RNase Sa and the 3K and 5K variants. The pH dependence of protein stability depends both on the net charge of the protein and on the difference in pKs of the ionizable groups between the folded and unfolded states. Our system may allow us to assess the relative importance of these two effects. There is widespread interest in the pH dependence of protein stability (Tanford 1970; Matthew and Richards 1982; Anderson et al. 1990; Pace et al. 1990; Dao-Pin et al. 1991; Yang and Honig 1993; Antosiewicz et al. 1994; Barrick et al. 1994; Tan et al. 1995; Schaefer et al. 1998; Warwicker 1999; Pace et al. 2000; Whitten andGarcia-Moreno 2000).
Fig. 1.
Ribbon diagram of RNase Sa. The acidic residues changed to lysines are indicated in ball and stick representation. Also given is the percent solvent exposure of the side chain and the oxygens in the carboxyl groups estimated by the method of Lee and Richards ( 1971). The figure was generated with the program MOLSCRIPT (Kraulis 1991). The PDB identifier for RNase Sa is 1RGG (Sevcik et al. 1996).
Results
The measured and calculated pI values for RNase Sa and the 2K, 3K, 4K, and 5K variants are given in Table 1. The difference between the measured and calculated pI values will be discussed below.
Table 1.
Isoelectric points of RNase Sa and the 2K, 3K, 4K, and 5K variants
| Sa variant | Experimental pIa | Calculated pIb | Net charge at pH 7c |
| Wild type | 3.5 | 4.4 (3.9) | −7 |
| 2K | 4.6 | 5.3 (4.8) | −3 |
| 3K | 6.4 | 6.6 (6.5) | −1 |
| 4K | 8.4 | 8.2 (8.2) | +1 |
| 5K | 10.2 | 9.1 (9.1) | +3 |
a pIs of the wild-type and the 2K, 3K, and 4K variants were measured using isoelectric focusing gels and are accurate to ≈0.1 pH units. The pI of the 5K variant was estimated by determining the pH of immobility using continuous polyacrylamide gel electrophoresis and buffer systems recommended by McLellan (1982). This method is accurate to ≈0.3 pH units.b Obtained by calculating the titration curve of the protein using pK values for the amino acid side chains and the α-COOH and α-NH3+ termini determined from peptide/model compound studies: Asp = 4.1, Glu = 4.5 (Nozaki and Tanford, 1967); His = 6.6 (McNutt et al. 1990); Tyr = 9.6, Lys = 10.4, Arg = 12.5, α-COOH = 3.6, α-NH3+ = 7.8 (Tanford 1968). The values in parentheses were obtained using the average pK s for the side chains of Asp, Glu, and His measured in folded proteins: Asp = 3.4 ± 1.1, Glu = 4.1 ± 0.8 and His = 6.5 ± 0.9. The Asp and Glu values are based on >200 measured pK values in 24 proteins and they were compiled and kindly provided to us by William Forsyth and Andy Robertson at the University of Iowa. The His values are based on 58 measured pK values in 21 proteins and they were compiled and kindly proved by Steve Edgcomb and Kip Murphy at the University of Iowa.c Calculated using the pK values from the model compound data in the footnote above. The net change is rounded to the nearest integer.
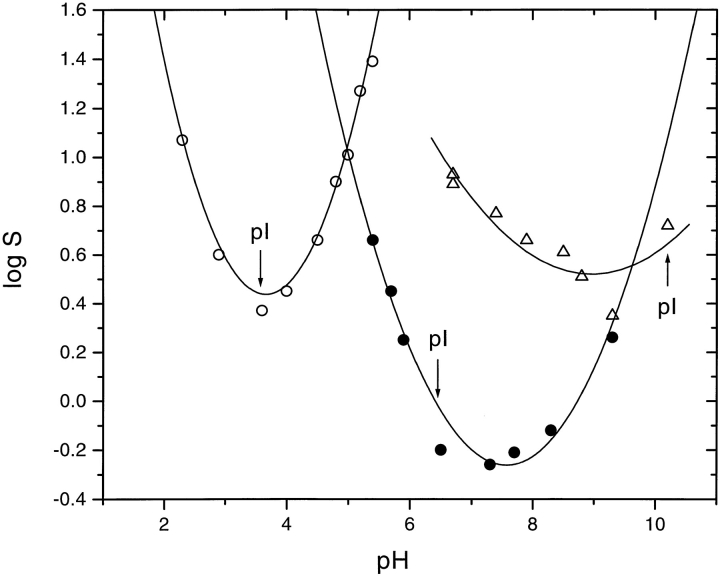
The solubilities of RNase Sa and the 3K and 5K variants are given in Table 2, and the pH dependences are shown in Figure 2 ▶. It is clear that the solubility minimum shifts with the pI of the protein from near pH 3.5 for RNase Sa to >pH 9 for the 5K variant. Despite this, the minimum solubility of RNase Sa and the 5K variant is about the same, ∼2 mg mL−1. In contrast, the 3K variant is less soluble, having a minimum solubility of 0.5 mg mL−1 near pH 7.
Table 2.
Solubility as a function of pH for RNase Sa and the 3K and 5K variants a
| Wild type | 3K | 5K | |||
| pH | S (mg mL−1) | pH | S (mg mL−1) | pH | S (mg mL−1) |
| 2.3 | 11.0 | 5.4 | 4.3 | 6.7 | 7.8 |
| 2.9 | 3.7 | 5.7 | 2.7 | 6.7 | 8.5 |
| 3.6 | 2.2 | 5.9 | 1.7 | 7.4 | 5.9 |
| 4.0 | 2.7 | 6.5 | 0.6 | 7.9 | 4.6 |
| 4.5 | 4.3 | 7.3 | 0.5 | 8.5 | 4.1 |
| 4.8 | 7.6 | 7.7 | 0.6 | 8.8 | 3.2 |
| 5.0 | 9.8 | 8.3 | 0.7 | 9.3 | 2.3 |
| 5.2 | 17.7 | 9.3 | 1.7 | 10.2 | 5.3 |
| 5.4 | 23.3 | ||||
a Measured at 25°C in the presence of 10 mM buffer as described in Materials and Methods.
Fig. 2.
Solubility of RNase Sa (○) and the 3K (•) and 5K (Δ) variants as a function of pH. The lines have no theoretical significance.
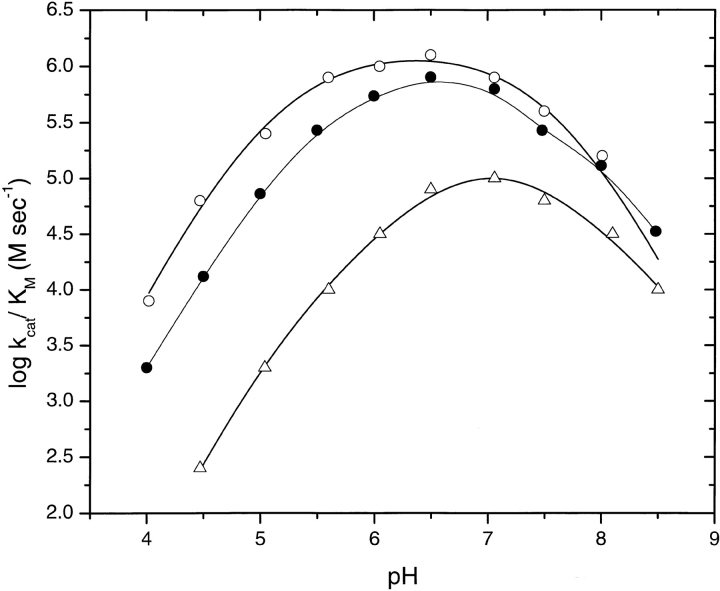
The steady-state kinetic parameters KM and kcat for the hydrolysis of poly inosinic acid (poly(I)) were determined as a function of pH for RNase Sa and the 3K and 5K variants. The results are given in Table 3. The pH dependence of log (kcat/KM) is shown in Figure 3 ▶. The pH of maximum activity is ∼6.5 for RNase Sa and the 3K variant, and ∼7.0 for the 5K variant. The 3K variant has somewhat less activity than wild-type RNase Sa, whereas the 5K variant is significantly less active than both. At the pH of optimum activity, (kcat/KM) is reduced from 1187 (mM sec)−1 for wild-type RNase Sa to 105 (mM sec)−1 for the 5K variant. The decrease in activity for both variants results entirely from a decrease in kcat.
Table 3.
Kinetic parameters characterizing the cleavage of poly(I) as a function of pH for RNase Sa and the 3K and 5K variants a
| pH | kcat(s−1) | KM (mM) | kcat/KM (mM s)− | |
| Wild type | 4.02 | 2.2 | 0.25 | 8.8 |
| 4.47 | 14.2 | 0.24 | 59 | |
| 5.05 | 59 | 0.21 | 281 | |
| 5.60 | 131 | 0.18 | 728 | |
| 6.05 | 175 | 0.16 | 1094 | |
| 6.50 | 178 | 0.15 | 1187 | |
| 7.06 | 146 | 0.19 | 768 | |
| 7.50 | 95 | 0.26 | 365 | |
| 8.01 | 42.1 | 0.29 | 145 | |
| 8.50 | 5.6 | 0.34 | 16 | |
| 3K | 4.00 | 1.5 | 0.75 | 3.3 |
| 4.50 | 7.5 | 0.57 | 13 | |
| 5.00 | 24 | 0.33 | 73 | |
| 5.50 | 70 | 0.26 | 269 | |
| 6.00 | 98 | 0.18 | 544 | |
| 6.50 | 112 | 0.14 | 800 | |
| 7.06 | 88 | 0.14 | 629 | |
| 7.48 | 51 | 0.19 | 268 | |
| 8.00 | 26 | 0.20 | 130 | |
| 8.48 | 8 | 0.24 | 33 | |
| 5K | 4.47 | 0.3 | 1.10 | 0.3 |
| 5.04 | 1.2 | 0.64 | 1.9 | |
| 5.60 | 4.7 | 0.47 | 10 | |
| 6.05 | 7.7 | 0.23 | 34 | |
| 6.50 | 11.1 | 0.13 | 85 | |
| 7.06 | 10.5 | 0.10 | 105 | |
| 7.50 | 6.7 | 0.10 | 67 | |
| 8.10 | 3.5 | 0.11 | 32 | |
| 8.50 | 1.3 | 0.14 | 9.3 |
a Measured at 25°C in the presence of 0.05 M Tris, 0.1 M potassium chloride and 0.05 M sodium acetate as described in Materials and Methods.
Fig. 3.
pH dependence of log (kcat/KM) for the cleavage of poly(I) by RNase Sa (○) and the 3K (•) and 5K (Δ) variants.
Thermal denaturation curves were determined by monitoring the circular dichroism at 234 nm. The curves for the variants are similar to those previously shown for wild-type RNase Sa (Pace et al. 1998). All curves were analyzed by assuming a two-state mechanism. The analysis yields the melting temperature, Tm, and the van't Hoff enthalpy change at Tm, ΔHm. These parameters and the differences in conformational stability, Δ(ΔG), at pH 7 in 30 mM MOPS are given in Table 4. We also show the calculated ΔΔG values obtained by summing the appropriate ΔΔG values of the single lysine variants. The good agreement between the measured and calculated ΔΔG values shows that the mutational effects are additive.
Table 4.
Parameters characterizing the thermal unfolding of RNase Sa and the charge reversal variants at pH 7 a
| Sa variant | Tmb (°C) | ΔHmc (kcal mole−1) | ΔΔGd (kcal mole−1) | ΔΔGe (kcal mole−1) |
| Wild type | 47.2 | 91 | — | — |
| D1K | 48.7 | 89 | 0.4 | — |
| D17K | 43.3 | 90 | −1.1 | — |
| D25K | 50.2 | 93 | 0.9 | — |
| E41K | 42.9 | 92 | −1.2 | — |
| E74K | 51.1 | 94 | 1.1 | — |
| 2K (E41K,D17K) | 39.5 | 83 | −2.2 | −2.3 |
| 3K (E41K,D17K,D1K) | 40.4 | 78 | −1.9 | −1.9 |
| 4K (E41K,D17K,D1K,D25K) | 44.4 | 84 | −0.8 | −1.0 |
| 5K (E41K,D17K,D1K,D25K,E74K) | 46.8 | 82 | −0.1 | 0.1 |
a pH 7, 30 mM MOPS.b Midpoint of the thermal unfolding curve. The standard deviation is ±0.3°C.c Enthalpy change at Tm. The standard deviation is ±5%.d ΔΔGmeas = ΔTm × ΔSm (wild type). See Becktel and Schellman (1987) or Pace and Scholtz (1997) for a discussion of this method. A positive sign indicates an increase in stability.e Calculated by summing the appropriate ΔΔG values of the single mutant variants.
The pH dependence of the conformational stability of RNase Sa and the 3K and 5K variants was also studied by thermal denaturation. Thermal denaturation curves were determined as a function of pH from pH 2 to pH 10 and analyzed by assuming a two-state mechanism as previously described (Pace et al. 1998). The thermodynamic parameters are summarized in Table 5. The free energy change for folding at any temperature, ΔG(T), can be calculated using the modified Gibbs-Helmholtz equation,
Table 5.
Parameters characterizing the thermal unfolding of RNase Sa and the 3K and 5K variants between pH 2 and 10
| Sa variant | pH | Tma (°C) | ΔHmb (kcal mole−1) | ΔSmc (cal K−1 mole−1) | ΔG (25°C)d (kcal mole−1) |
| Wild type | 2 | 27.3 | 56 | 186 | 0.42 |
| 3.3 | 42 | 85 | 270 | 3.88 | |
| 5 | 54.2 | 108 | 330 | 7.59 | |
| 7 | 47.2 | 91 | 284 | 5.11 | |
| 8.3 | 39.5 | 92 | 294 | 3.75 | |
| 9 | 35.4 | 78 | 253 | 2.36 | |
| 10 | 30.1 | 72 | 237 | 1.15 | |
| 3K | 2 | 27.9 | 60 | 199 | 0.56 |
| 3.3 | 44.4 | 83 | 261 | 4.15 | |
| 4 | 50.8 | 89 | 275 | 5.48 | |
| 5 | 49.4 | 91 | 282 | 5.44 | |
| 6 | 50.0 | 84 | 260 | 4.99 | |
| 7 | 40.7 | 77 | 245 | 3.24 | |
| 8.3 | 31.9 | 70 | 230 | 1.46 | |
| 9 | 29.1 | 62 | 205 | 0.80 | |
| 10 | 22.3 | 50 | 169 | −0.48 | |
| 5K | 2 | 25.6 | 62 | 208 | 0.12 |
| 3 | 41.4 | 77 | 245 | 3.31 | |
| 4 | 52.4 | 85 | 261 | 5.35 | |
| 5 | 53.3 | 87 | 267 | 5.62 | |
| 6 | 51.3 | 85 | 262 | 5.22 | |
| 7 | 47.3 | 82 | 256 | 4.50 | |
| 8 | 44.2 | 76 | 240 | 3.70 | |
| 9 | 42.7 | 72 | 228 | 3.50 | |
| 10 | 36.4 | 59 | 191 | 1.85 |
a Midpoint of the thermal unfolding curve. The standard deviation is ±0.3°C.b Enthalpy change at Tm. The standard deviation is ±5%.c ΔSm = ΔHm/Tm.d Calculated with Equation 1 using the Tm and ΔHm values in this table and a value of 1.52 kcal K−1 mole−1 for ΔCp (Pace et al. 1998).
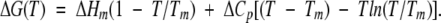 |
1 |
We use a value of 1.52 kcal mole−1 K−1 for ΔCp in Equation 1 to calculate ΔG(25°C), based on our earlier studies of the conformational stability of RNase Sa (Pace et al. 1998). Using the results in Table 5 between pH 2 and pH 5, where it is not necessary to correct for the ΔH for buffer ionization, gives ΔCp = 1.31 ± 0.18 kcal mole−1 K−1. This lower value of ΔCp would increase the ΔG values by, at most, 4%. Changes in amino acid side chains on the exterior of a protein are expected to have only a small effect on ΔCp because the side chains will be largely exposed to solvent in both the folded and unfolded conformations. Therefore we decided to use the more accurately determined value of 1.52 kcal mole−1 K−1. Note that all three proteins are maximally stable near pH 5, with stabilities (kcal mole−1) of 7.6 for RNase Sa, 5.4 for 3K RNase Sa, and 5.6 for 5K RNase Sa.
Discussion
Isoelectric points of RNase Sa and the charge reversal variants
Knowing the pI of a protein is helpful to protein chemists developing purification schemes or performing experiments in which the protein's solubility is a crucial factor. (As discussed below, proteins tend to be the least soluble near their pI.) The pI is usually determined experimentally by isoelectric focusing (Righetti et al. 1981); however, one can estimate a protein's pI by calculation if the amino acid composition and the pKs of the ionizable groups are known. Usually the pKs of the groups are not known, so values obtained from model compound studies are used for the calculation. Because these pKs may differ significantly from the pKs of groups in the folded protein, calculated pIs often disagree with experimentally measured pIs. A number of methods have been proposed for the theoretical determination of the pIs of proteins (Sillero andRibeiro 1989; Patrickios andYamasaki 1995). Typically, these methods give results that are within ±1 pH unit of the experimental pI.
In Table 1 we give the experimentally determined pIs for RNase Sa and the 2K, 3K, 4K, and 5K variants. The value of 3.5 obtained for RNase Sa is in exact agreement with our previously reported value (Hebert et al. 1997). Thus, RNase Sa is an acidic ribonuclease like RNase T1, which has a pI of 3.8 (Hebert et al. 1997). In contrast, barnase, another well-studied microbial ribonuclease, is a basic protein with a pI of 9.2 (Bastyns et al. 1996). Replacing three acidic residues with lysines (3K) raises the pI close to neutrality, and replacing five acidic residues with lysines (5K) raises the pI above 10. By reversing five charges on RNase Sa, we have changed it from one of the most acidic proteins to one of the most basic proteins. This is shown in Table 6, where we give the experimentally determined pIs and calculated pIs for a number of well-studied proteins.
Table 6.
pH of maximum stability, pHmax and isoelectric points of some well-studied proteins
| Protein | pHmax | Experimental pI | Calculated pIa |
| Pepsin | — | 2.9b | 3.2 |
| RNase Sa | ∼5.0c,d | 3.5c,e | 4.4 |
| RNase T1 | 4–5 | 3.8e | 4.3 |
| β-Lactoglobulin | — | 5.1b | 4.8 |
| RNase Sa2 | ∼4.5d | 5.3e | 7.4 |
| RNase Sa (3K) | 4–5c | 6.4c | 6.6 |
| RNase Sa3 | ∼5.5d | 7.2e | 6.2 |
| Whale myoglobin | ∼6.5g | 8.0b | 8.4 |
| RNase Ba | 5–6h | 9.2i | 9.0 |
| Horse cytochrome C | ∼7.5j | 9.4b | 9.7 |
| RNase A | 7–9f | 9.6b | 9.3 |
| Chymotrypsinogen A | — | 9.6b | 9.4 |
| Staph nuclease | ∼9.0k | >10.0k | 9.7 |
| RNase Sa (5K) | ∼5.0c | 10.2c | 9.1 |
| Human lysozyme | ∼4.5l | 10.5b | 10.3 |
| T4 lysozyme | ∼5.5m | >10.5n | 10.0 |
| BPTI | ∼5.0o | 10.6b | 10.2 |
| Hen lysozyme | 5–7p | 11.2b | 10.5 |
a Calculated using pK values determined from model compound studies as described in footnote b of Table 1.b From Table 3 of Patrickios and Yamasaki (1995).c From this paper.d From Pace et al. (1998).e From Hebert et al. (1997).f From Pace et al. (1990).g From Puett (1973).h From Pace et al. (1992).i From Bastyns et al. (1996).j From Walter Englander, personal communication.k From Whitten and Garcia-Moreno (2000).l From Takano et al. (2000).m From Dao-pin et al. (1991).n From Becktel and Base (1987).o From Makhatadze et al. (1993).p From Pfeil and Privalov (1976) and Schaefer et al. (1998).
When the pIs are calculated for RNase Sa and the 3K and 5K variants using pK values taken from model compound studies (Table 1), the pI is overestimated for RNase Sa and the 2K and 3K variants and underestimated for the 4K and 5K variants. When the calculation is performed using the average pKs for Asp, Glu, and His measured in folded proteins, the agreement between measured and calculated improves for RNase Sa and the 2K and 3K variants. The pKs of the ionizable groups of RNase Sa have been measured by NMR (D. Laurents, pers. comm. Similar measurements on the 5K variant are in progress.) When these values are used in the calculation, the pI = 3.7, in good agreement with the measured value. Similarly, if the pK values measured for RNase Sa are used for the 5K variant, the calculated pI = 10.1, again in excellent agreement with the measured pI. The calculated pI for the 5K variant in Table 1 is low because RNase Sa has eight Tyr that are largely buried and they all have pKs >11. This is much higher than the pK = 9.6 that is assumed for tyrosine -OH groups on the basis of model compound studies. This may be true with other proteins because Tyr side chains are 76% buried on average in a large sample of folded proteins (Lesser and Rose 1990).
The fact that the pKs of the ionizable groups in model compounds may differ significantly from the pKs of the same groups in folded proteins is reflected by the calculated and measured pI values shown in Table 6. In general, acidic proteins have their pIs overestimated and basic proteins have their pIs underestimated when calculated using pKs from model compound studies. This is expected. For Asp side chains, a pK = 4.1 is observed with uncharged model compounds, but a pK = 3.4 is the average value observed in proteins (See the footnotes to Table 1). This results mainly because proteins have a net positive charge in the region where Asp and Glu carboxyls titrate, and this will tend to lower their pKs relative to those measured in uncharged model peptides (Antosiewicz et al. 1996). The converse will be true for basic proteins, where the proteins will have a net negative charge above the pI that will tend to raise the pKs of the ionizable groups. In addition to net charge, other environmental effects can change pKs. For example, we have shown that the completely buried and hydrogen bonded carboxyl of Asp 76 in RNase T1 has a pK ∼0.5 (Giletto andPace 1999), but that the carboxyl group introduced in N44D in RNase T1 has a pK ∼5.7 (Hebert et al. 1998). Thus, it is always best to measure rather than estimate the pI of a protein unless the measured pKs of the ionizable groups are available.
Solubility of the RNase Sa and the 3K and 5K variants
Protein solubility has become increasingly important as it has become evident that many diseases result from the insolubility of proteins. For example, a genetic variant of α1-antitrypsin forms inclusion bodies in the liver and this can lead to early onset emphysema (Carrell andGooptu 1998). In addition, the plaques found in patients suffering form Alzheimer's disease are formed by the precipitation of Aβ1–42, a peptide generated by the inappropriate cleavage of amyloid precursor protein (Kaytor andWarren 1999). Solubility can also be important in treating diseases. The development of a fast-acting form of insulin (Lys-Pro insulin) was prompted by the fact that formulations of human insulin were not solubilized rapidly enough after they were injected (Bakaysa et al. 1996). Solubility is also important in both of the primary techniques used to determine the structure of proteins: X-ray crystallography (McPherson 1998) and NMR (Harris, 1986).
The relationship between protein solubility and pH has a long history in protein chemistry (Cohn and Edsall 1943; Tanford 1961; Arakawa and Timasheff 1985; Ries-Kautt and Ducruix 1997). To a first approximation, the solubility of a protein is proportional to the square of the net charge on the protein (Tanford 1961). Consequently, proteins are expected to be least soluble near their isoelectric points, and the solubility should increase as the pH is raised or lowered as the magnitude of the net charge increases. Our results support this. Figure 3 ▶ shows that the minimum solubility of RNase Sa and the 3K and 5K variants occurs within a pH unit of the pIs and the solubility increases markedly at both higher and lower pH.
Enzyme activity of RNase Sa and the 3K and 5K variants
Our hope was that the charge reversal mutants would retain most of their enzyme activity. Of the five Glu and Asp residues that were considered (Fig. 1 ▶), only Glu 41 appeared to be important to substrate binding or catalysis. Glu 41 in RNase Sa is conserved in all of the microbial ribonucleases where it forms hydrogen bonds to the guanine base of the nucleotide (Sevcik et al. 1990; Hebert et al. 1997). Thus, it is important to both specificity and binding. Previous studies have shown that the equivalent residues in barnase (Glu 60) and RNase T1 (Glu 46) were important to the activity. The value of kcat/Km for RNA hydrolysis is reduced by 30% in the E60Q mutant of barnase (Bastyns et al. 1994) and by 95% for the E46Q mutant of RNase T1 (Steyaert et al. 1991). It seemed likely that replacing Glu with Lys would be much more detrimental to the enzyme activity than replacing Glu with Gln. Thus, it was surprising that kcat/Km for the 3K variant is only reduced by ∼33%, and kcat/Km for the 5K variant is only reduced by 90% (Table 3). In both of these mutants, Glu 41 has been replaced by Lys. It is even more surprising that the decrease in activity is entirely caused by a decrease in kcat. Based on the Km value, these mutants appear to bind substrate better than wild-type RNase Sa. Perhaps, the loss of the hydrogen bond to the inosine base in E41K RNase Sa is compensated for by more favorable electrostatic interactions, because the net charge is ∼−6 for RNase Sa, ∼1 for the 3K variant, and ∼+4 for the 5K variant near pH 7 (using the measured pKs of all charged groups). The activity of the 5K variant is lower that that of RNase Sa and the 3K variant over the pH range pH 4– pH 8.5, but the pH of maximum activity is similar: ∼6.5 for RNase Sa and 3K variant, and ∼7 for the 5K variant (Fig. 3 ▶). Thus, unlike solubility, the pH dependence of the enzyme activity does not vary significantly with the pI of the enzyme. This is not surprising because the pKs of the ionizable groups on the enzyme actually involved in binding and catalysis will influence the pH dependence to a greater extent than the net charge on the protein (Fersht 1999).
Conformational stability of the single charge reversal mutants at pH 7
As shown in Figure 1 ▶, the Glu and Asp residues selected for charge reversal are highly accessible to solvent and not hydrogen bonded. In addition, when Lys residues are substituted for the Asp and Glu residues, calculations show that the -NH3 + group of the Lys residues should still be too far from any negative charges to form an ion pair. Thus, the main effect of these charge reversals on stability should be through a change in the long-range electrostatic interactions with the rest of the charged groups in RNase Sa. The actual net charge on RNase Sa at pH 7 will be ∼−6 based on the measured pKs of all charged groups (Laurents et al. unpubl.). Consequently, replacing a negative charge with a positive charge is expected to lead to an increase in stability. This is supported by calculations using Coulomb's law and a dielectric constant of 80 to sum up the electrostatic interactions. If we assume that electrostatic interactions are negligible in the unfolded states, then the predicted increases in stability are (kcal/mole): 2.9 for D1K, 3.2 for D17K, 2.5 for D25K, 1.2 for E41K, and 2.3 for E74K. The results in Table 4 show that, in fact, much smaller increases in stability are observed for three of the single variants and that a decrease in stability is observed for the other two. We have discussed some of these data and related results in two previous papers and reached the following conclusions. First, protein stability can sometimes be increased by improving the electrostatic interactions among charged groups on the surface of a protein (Grimsley et al. 1999). Second, the discrepancy between the observed and calculated changes in stability leads to the surprising suggestion that the free energy of the denatured state may be decreased more than that of the native state by these single charge reversal mutations (Pace et al. 2000). This makes it difficult to predict which charge reversals will be most likely to increase the stability of a protein.
Conformational stability of 2K, 3K, 4K, and 5K at pH 7
The observed ΔΔG values of the multiple mutants can be approximated remarkably well by summing the appropriate Δ(ΔG) values of the single mutants (Table 4). At first glance, this seems surprising. However, at pH 7 each charge is interacting with ∼19 other charges in both the folded and unfolded states of the protein so this is clearly a difficult problem to analyze. Note that even though RNase Sa is a very acidic protein (net charge ∼−6 at pH 7) and the 5K variant a very basic protein (net charge ∼+4 at pH 7) they have the same stability at pH 7. In contrast, the 3K variant is about 2 kcal mole−1 less stable than both RNase Sa and the 5K variant.
pH dependence of the conformational stability of RNase Sa and the 3K and 5K variants
In 1924, a model for the electrostatic interactions of a protein was proposed that smeared the net charge over the surface of a sphere with a dielectric constant, D, that was impenetrable to solvent (Linderstrom-Lang 1924). This model predicts that proteins should be most stable near their pIs, where their net charge is zero, because unfavorable electrostatic interactions resulting from either an excess of positive or negative charges will be minimized. Fig. 4 ▶ shows the conformational stabilities estimated from thermal denaturation curves, ΔG(25°C), as a function of pH for RNase Sa and the 3K and 5K variants. The maximum stability for all three proteins is near pH 5, and clearly does not shift with the pI of the protein. At pH 5, RNase Sa and the 3K and 5K variant have approximate net charges of −4, +2, and +5, respectively. Thus, the 3K variant is the least stable of the three proteins even though it has the net charge closest to 0 at this pH. Table 6 gives the pH of maximum stability, pHmax, for many of the proteins listed. It is interesting that the pHmax for eight of the 15 proteins is >2 pH units from their experimental pIs. These results show clearly that the Linderstrom-Lang model cannot account for the pH dependence of the stability of these proteins.
Fig 4.
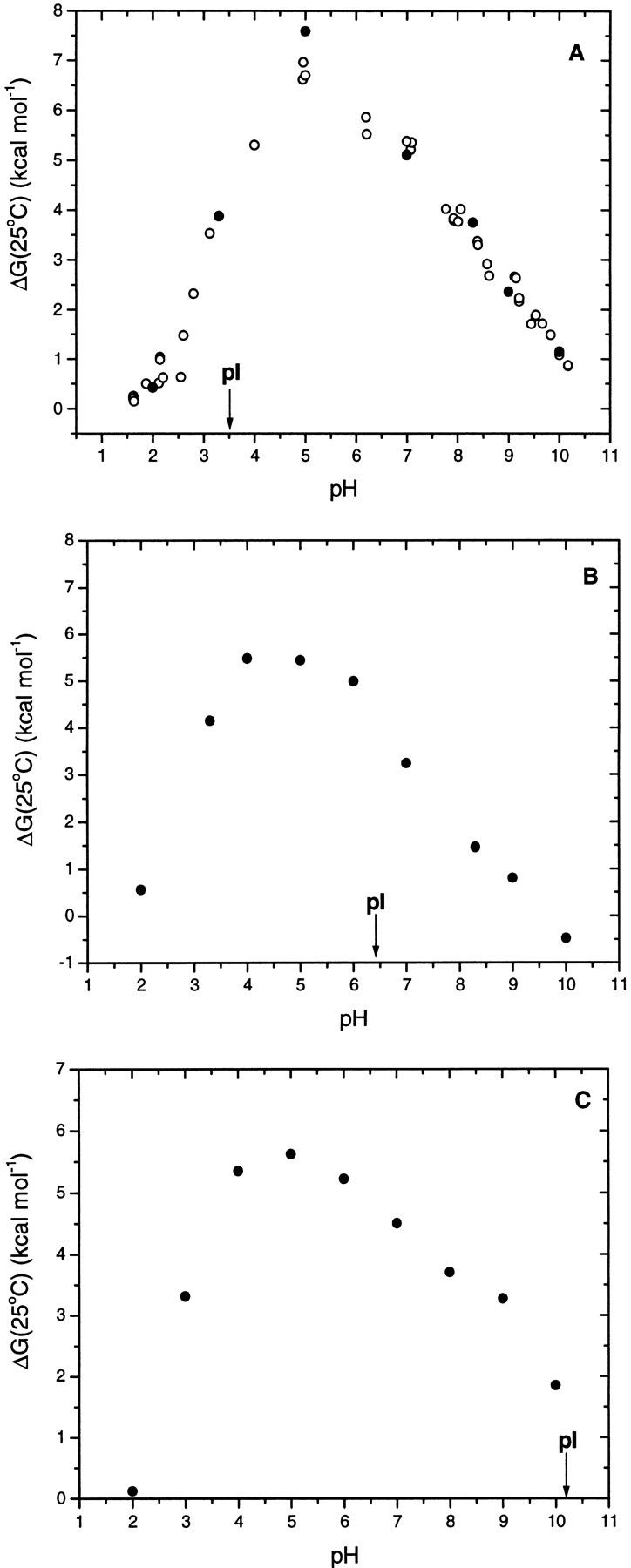
Conformational stability, ΔG(25°C), as a function of pH for RNase Sa (A), the 3K variant (B), and the 5K variant (C). ΔG(25°C) values represented by the closed symbols are from Table 5. The ΔG(25°C) values represented by the open circles are from (Pace et al. 1998). The pIs shown are the experimental values from Table 1.
The more important factor that determines the pH dependence of protein stability is the difference in the pK values of the ionizable groups in the folded and unfolded conformations of a protein. This subject has been discussed by several authors (Tanford 1962,Tanford 1970; Matthew and Gurd 1986; Yang and Honig 1993; Antosiewicz et al. 1994; Elcock 1998; Schaefer et al. 1998; Warwicker, 1999). Experimental studies of the pH dependence of stability have been reported for RNase A (Pace et al. 1990), RNase T1 (McNutt et al. 1990; Pace et al. 1990; Hu et al. 1992; Yu et al. 1994), T4 Lysozyme (Anderson et al. 1990; Dao-Pin et al. 1991), barnase (Pace et al. 1992; Makarov et al. 1993; Oliveberg et al. 1995), ovomucoid third domain (Swint-Kruse and Robertson, 1995), chymotrypsin inhibitor 2 (Tan et al. 1995), N-terminal domain of L9 (Kuhlman et al. 1999), and staphylococcal nuclease (Whitten andGarcia-Moreno 2000).
As shown in Figure 4 ▶, the maximum stability for RNase Sa and the 3K and 5K variants occurs near pH 5. We will first discuss the marked decrease in stability between pH 5 and 2. An analysis of this region shows that the three proteins take up ∼2 protons when they unfold. This shows that some of the groups in the unfolded protein have higher pKs than the same groups in the folded protein. The only groups that titrate in this pH range are the carboxyl groups. The pKs of carboxyl groups in folded proteins are generally considerably lower than observed in uncharged peptide models. The average pKs in folded proteins are less than in peptide models by 0.7 for Asp, 0.4 for Glu, and 0.1 for His (See footnote b in Table 1). The fact that the effect is larger for Asp than Glu reflects the fact that this is caused, in part, by the large positive charge that develops on proteins at low pH where the carboxyls titrate (Antosiewicz et al. 1996). In the unfolded protein, the pKs will be higher because the molecule expands and the effective dielectric constant increases. However, it is clear that the carboxyl pKs will still be less than in peptide models (Elcock 1998). Only in 6M GdnHCl or 8M urea in the presence of 1M salt do the pKs in unfolded proteins approach the pKs observed in model compounds (Whitten and Garcia-Moreno 2000).
RNase Sa has 13 carboxyls, and all but three have lower pKs than in model compounds (D. Laurents, unpubl.). The 3K and 5K variants have fewer carboxyls than does RNase Sa, but the carboxyls with the lowest pKs have not been removed. In addition, the 3K and 5K variants have greater positive charges at low pH than RNase Sa, so the pKs of the carboxyl groups are expected to be even lower. Consequently, the pH dependence is quite similar for RNase Sa and the 3K and 5K variants at low pH and can be explained by the difference in pKs between the groups in the folded and unfolded states of the protein.
Above pH 5, the dependence on pH is less and ∼0.8 protons are released when RNase Sa or the 3K or 5K variants unfold. Again, this is expected based on the pKs that we have measured in RNase Sa. Both the α-amino group and the side chain of His 53 have considerably higher pKs in folded RNase Sa than in model compounds and can easily account for the pH dependence observed above pH 5. We will attempt to account completely for the pH dependence of RNase Sa and the 5K variant when we have completed measurements of the pKs in the folded and unfolded states of these proteins.
Materials and methods
Glycine, diglycine, sodium acetate, MES (2–[N-morpholino]ethanesulfonic acid), and MOPS (3–[N-morpholino]propanesulfonic acid) were obtained from SIGMA. Enzymes for manipulation of DNA were from Promega Corporation. Oligonucleotides were made by Gene Technologies Laboratory at Texas A&M University. All other reagents were of analytical grade.
Wild-type RNase Sa and the variants were prepared as described in Hebert et al. ( 1997,1998), with some modifications. The Escherichia coli strain was RY1988 (MQ) FaraD139Δ(argFlac)U169rpsL150relA1flbB5301deoC1ptsF25rbsR, [λp1(CQ21)]). The wild-type protein was eluted from cellulose phosphate with a linear gradient generated using 500 mL of 20mM acetate buffer, pH 3.25, and 500 mL of the same buffer containing 0.5 M NaCl. Single lysine variants were purified like the wild-type protein. For the 3K variant, the periplasmic fraction was adjusted to pH 4 before being applied to the cellulose phosphate column, then eluted with a linear gradient generated using 500 mL of 20mM acetate buffer, pH 4.0, and 500 mL of the same buffer containing 1.0 M NaCl. The periplasmic fraction for the 5K variant was adjusted to pH 5.0, and then purified as the 3K variant.
The isoelectric points (pI) of wild-type RNase Sa and the 2K, 3K, and 4K variants were estimated at 4°C using the PhastSystem from Pharmacia with IEF precast gels with a pH range of 3– 9 (Pharmacia, PhastSystem Separation Technique File No. 100). The pI of the 5K variant was estimated by determining the pH of immobility, using polyacrylamide gel electrophoresis and the continuous electrophoresis buffers described by McLellan (1982).
Solubility experiments were performed using saturated protein solutions. Samples of 500 μL protein suspensions in buffer were mixed by vortexing, then incubated overnight in a 25°C water bath. After centrifugation, the pH of the samples was measured and an aliquot of the supernatant removed for dilution into the appropriate buffer. Protein concentrations were then determined using a molar absorption coefficient at 278 nm of 12,300 M−1 cm−1 (Hebert et al. 1997). The buffers used were 10 mM glycine from pH 2.0 to pH 3.5, 10 mM acetate from pH 3.5 to pH 5.5, 10 mM MES from pH 6.0 to pH 6.5, 10 mM MOPS from pH 7.0 to pH 8.0, 10 mM Tris from pH 8.5 to pH 10, and 10 mM CAPS for pHs >10.0.
Steady state kinetic parameters were determined for the hydrolysis of poly(I) at 25°C as described by Yakovlev et al. (1992). The initial velocities were measured by recording the change in absorbance at 248 nm. The buffer used was 0.05 M Tris, 0.1 M potassium chloride and 0.05 M sodium acetate titrated to the desired pH with acetic acid.
Thermal denaturation curves were determined by measuring changes in circular dichroism (CD) with an Aviv 62DS CD spectrophotometer as previously described (Hebert et al. 1998; Pace et al. 1998). The following buffers were used for all denaturations: pH 2 to pH 3.5 and pH 9.5 to pH 10 glycine; pH 3.5 to pH 5.5 acetate; pH 5.5 to pH 6.5 MES; pH 6.5 to pH 8.5 MOPS; pH 8.5 to pH 9.5 diglycine. The analysis of thermal denaturation curves for RNase Sa has been previously described (Pace and Scholtz, 1997; Hebert et al. 1998; Pace et al. 1998).
Acknowledgments
We thank William Forsyth, Steve Edgcomb, Andy Robertson, and Kip Murphy at the University of Iowa for providing the average pK values observed in folded proteins (Table 1). We thank Doug Laurents, Marta Bruix, and Manuel Rico at the Instituto de Estructura de la Materials in Madrid, Spain, for providing us with the pKs of RNase Sa. We thank Doug Laurents, Marty Scholtz, Richard Thurlkill, David Schell, Roy Alston, and Beatrice Huyghues-Despointes for helpful discussions. We thank Walter Baase, Bertrand Garcia-Moreno, Walter Englander, and Wesley Stites for providing the pHmax for some of the proteins in Table 6. We thank Vladmir Mitkevich for assistance in enzyme activity measurements. This work was supported by NIH Grant GM 37039, Robert A. Welch Foundation Grant A-1060, NIH FIRCA Grant TW01058, NATO Grant HTECH.LG 973299, RFBR Grant 99–04–48424, and the Tom and Jean McMullin Professorship.
The publication costs of this article were defrayed in part by payment of page charges.This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at www.proteinscience.org/cgi/doi/10.1110/
References
- Anderson, D.E., Becktel, W.J., and Dahlquist, F.W. 1990. pH-induced denaturation of proteins: a single salt bridge contributes 3-5 kcal/mol to the free energy of folding of T4 lysozyme. Biochemistry 29 2403–2408. [DOI] [PubMed] [Google Scholar]
- Antosiewicz, J., McCammon, J.A., and Gilson, M.K. 1994. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 238 415–436. [DOI] [PubMed] [Google Scholar]
- ———. 1996. The determinants of pKas in proteins. Biochemistry 35 7819–7833. [DOI] [PubMed] [Google Scholar]
- Arakawa, T. and Timasheff, S.N. 1985. Theory of protein solubility. Methods Enzymol. 114 49–77. [DOI] [PubMed] [Google Scholar]
- Bakaysa, D.L., Radzuik, J., Havel, H.A., Brader, M.L., Li, S., Dodd, S.W., Beals, J.M., Pekar, A.H., and Brems, D.N. 1996. Physicochemical basis for the rapid time-action of Lys B28 Pro B29 - Insulin: Dissociation of a protein-ligand complex. Protein Sci. 5 2521–2531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick, D., Hughson, F.M., and Baldwin, R.L. 1994. Molecular mechanisms of acid denaturation: The role of histidine residues in the partial unfolding of apomyoglobin. J. Mol. Biol. 237 588–601. [DOI] [PubMed] [Google Scholar]
- Bastyns, K., Froeyen, M., Diaz, J.F., Volckaert, G., and Engelborghs, Y. 1996. Experimental and theoretical study of electrostatic effects on the isoelectric pH and the pKa of the catalytic residue His-102 of the recombinant ribonuclease from Bacillus amyloliquefaciens (barnase). Proteins: Struct. Funct. Genet. 24 370–378. [DOI] [PubMed] [Google Scholar]
- Bastyns, K., Froeyer, M., Volckaert, G., and Engelborghs, Y. 1994. The role of Glu-60 in the specificity of the recombinant ribonuclease from Bacillus amyloliquefaciens (barnase) towards dinucleotides, poly(A) and RNA. Biochem. J. 300 737–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becktel, W.J. and Baase, W.A. 1987. Thermal denaturation of bacteriophage T4 lysozyme at neutral pH. Biopolymers. 26 619–623. [DOI] [PubMed] [Google Scholar]
- Becktel, W.J. and Schellman, J.A. 1987. Protein stability curves. Biopolymers. 26 1859–1877. [DOI] [PubMed] [Google Scholar]
- Carrell, R.W. and Gooptu, B. 1998. Conformational changes and disease-serpins,prions, and Alzheimer's. Curr. Opin. Struct. Biol. 8 799–809. [DOI] [PubMed] [Google Scholar]
- Cohn, E.J. and Edsall, J.T. 1943. Proteins, amino acids and peptides. Hafner Publishing Company, New York.
- Dao-Pin, S., Sauer, U., Nicholson, H., and Matthews, B.W. 1991. Contribution of engineered surface salt bridges to the stability of T4 lysozyme determined by directed mutagenesis. Biochemistry 30 7142–7153. [DOI] [PubMed] [Google Scholar]
- Dao-Pin, S., Soderlind, E., Baase, W.A., Wozniak, J.A., Sauer, U., and Matthews, B.W. 1991. Cumulative site-directed charge-change replacements in bacteriophage T4 lysozyme suggest that long-range electrostatic interactions contribute little to protein stability. J. Mol. Biol. 221 873–887. [DOI] [PubMed] [Google Scholar]
- Elcock, A.H. 1998. The stability of salt bridges at high temperatures: implications for hyperthermophilic proteins. J. Mol. Biol. 284 489–502. [DOI] [PubMed] [Google Scholar]
- Fersht, A. 1999. Structure and mechanism in protein science. W. H. Freeman and Company, New York.
- Giletto, A. and Pace, C.N. 1999. Buried, charged, non-ion-paired aspartic acid 76 contributes favorably to the conformational stability of ribonuclease T1. Biochemistry 38 13379–13384. [DOI] [PubMed] [Google Scholar]
- Grimsley, G.R., Shaw, K.L., Fee, L.R., Alston, R.W., Huyghues-Despointes, B.M.P., Thurlkill, R.L., Scholtz, J.M., and Pace, C.N. 1999. Increasing protein stability by altering long-range coulombic interactions. Protein Sci. 8 1843–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris, R.K. 1986. Nuclear magnetic resonance spectroscopy. Longman Scientific and Technical, Essex, England.
- Hebert, E.J., Giletto, A., Sevcik, J., Urbanikova, L., Wilson, K.S., Dauter, Z., and Pace, C.N. 1998. Contribution of a conserved asparagine to the conformational stability of ribonucleases Sa, Ba, and T1. Biochemistry 37 16192–16200. [DOI] [PubMed] [Google Scholar]
- Hebert, E.J., Grimsley, G.R., Hartley, R.W., Horn, G., Schell, D., Garcia, S., Both, V., Sevcik, J., and Pace, C.N. 1997. Purification of ribonucleases Sa, Sa2, and Sa3 after expression in Escherichia coli. Protein Express. Purificat. 11 162–168. [DOI] [PubMed] [Google Scholar]
- Hu, C.-Q., Sturtevant, J.M., Thomson, J.A., Erickson, R.E., and Pace, C.N. 1992. Thermodynamics of ribonuclease T1 denaturation. Biochemistry 31 4876–4882. [DOI] [PubMed] [Google Scholar]
- Janson, J.C. and Ryden, L. 1989. Protein purification: Principles, high resolution methods, and applications. Pharmacia, Uppsala, Sweden.
- Kaytor, M.D. and Warren, S.T. 1999. Aberrant protein deposition and neurological disease. J. Biol. Chem. 274 37507–37510. [DOI] [PubMed] [Google Scholar]
- Kraulis, P.J. 1991. MOLSCRIPT: A program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallog. 24 946–950. [Google Scholar]
- Kuhlman, B., Luisi, D.L., Young, P., and Raleigh, D.P. 1999. pKa values and the pH dependent stability of the N-terminal domain of L9 as probes of electrostatic interactions in the denatured state. Differentiation between local and nonlocal interactions. Biochemistry 38 4896–4903. [DOI] [PubMed] [Google Scholar]
- Lee, B. and Richards, F.M. 1971. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 55 379–400. [DOI] [PubMed] [Google Scholar]
- Lesser, G.J. and Rose, G.D. 1990. Hydrophobicity of amino acid subgroups in proteins. Proteins: Struct. Funct. Genet. 8 6–13. [DOI] [PubMed] [Google Scholar]
- Linderstrom-Lang, K.U. 1924. On the ionisation of proteins. C. R. Trav. Lab. Carlsberg. 15 1–29. [Google Scholar]
- Makarov, A.A., Protasevich, I.I., Kuznetsova, N.V., Fedorov, B.B., Korolev, S.V., Struminskaya, N.K., Bazhulina, N.P., Leshchinskaya, I.B., Hartley, R.W., and Kirpichnikov, M.P. 1993. Comparative study of thermostability and structure of close homologues-barnase and binase. J. Biomol. Struct. Dyn. 10 1047–1065. [DOI] [PubMed] [Google Scholar]
- Makhatadze, G.I., Kim, K-S., Woodward, C., and Privalov, P.L. 1993. Thermodynamics of BPTI folding. Protein Sci. 2 2028–2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthew, J.B. and Gurd, F.R. 1986. Stabilization and destabilization of protein structure by charge interactions. Methods Enzymol. 130 437–453. [DOI] [PubMed] [Google Scholar]
- Matthew, J.B. and Richards, F.M. 1982. Anion binding and pH-dependent electrostatic effects in ribonuclease. Biochemistry 21 4989–4999. [DOI] [PubMed] [Google Scholar]
- McLellan, T. 1982. Electrophoresis buffers for polyacrylamide gels at various pH. Anal. Biochem. 126 94–99. [DOI] [PubMed] [Google Scholar]
- McNutt, M., Mullins, L.S., Raushel, F.M., and Pace, C.N. 1990. Contribution of histidine residues to the conformational stability of ribonuclease T1 and mutant Glu58-Ala. Biochemistry 29 7572–7576. [DOI] [PubMed] [Google Scholar]
- McPherson, A. 1998. Crystallization of biological macromolecules. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Nozaki, Y. and Tanford, C. 1967. Intrinsic dissociation constants of aspartyl and glutamyl carboxyl groups. J. Biol. Chem. 242 4731–4735. [PubMed] [Google Scholar]
- Oliveberg, M., Arcus, V.L., and Fersht, A.R. 1995. pKa values of carboxyl groups in the native and denatured states of barnase: the pKa values of the denatured state are on average 0.4 units lower than those model compounds. Biochemistry 34 9424–9433. [DOI] [PubMed] [Google Scholar]
- Pace, C.N., Alston, R.W., and Shaw, K.L. 2000. Charge-charge interactions influence the denatured state ensemble and contribute to protein stability. Protein Sci. 9 1395–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace, C.N., Hebert, E.J., Shaw, K.L., Schell, D., Both, V., Krajcikova, D., Sevcik, J., Wilson, K.S., Dauter, Z., Hartley, R.W., and Grimsley, G.R. 1998. Conformational stability and thermodynamics of folding of ribonucleases Sa, Sa2 and Sa3. J. Mol. Biol. 279 271–286. [DOI] [PubMed] [Google Scholar]
- Pace, C.N., Laurents, D.V., and Erickson, R.E. 1992. Urea denaturation of barnase: pH dependence and characterization of the unfolded state. Biochemistry 31 2728–2734. [DOI] [PubMed] [Google Scholar]
- Pace, C.N., Laurents, D.V., and Thomson, J.A. 1990. pH dependence of the urea and guanidine hydrochloride denaturation of ribonuclease A and ribonuclease T1. Biochemistry 29 2564–2572. [DOI] [PubMed] [Google Scholar]
- Pace, C.N. and Scholtz, J.M. 1997. Measuring the conformational stability of a protein. In Protein Structure: a practical approach, 2nd ed. (ed. T.E. Creighton), pp. 299–321. IRL Press, Oxford.
- Patrickios, C.S. and Yamasaki, E.N. 1995. Polypeptide amino acid composition and isoelectric point: Comparison between experiment and theory. Anal. Biochem. 231 82–91. [DOI] [PubMed] [Google Scholar]
- Pfeil, W. and Privalov, P.L. 1976. Thermodynamic investigations of proteins. III. Thermodynamic description of lysozyme. Biophys. Chem. 4 41–50. [DOI] [PubMed] [Google Scholar]
- Puett, D. 1973. The equilibrium unfolding parameters of horse and sperm whale myoglobin:effects of guanidine hydrochloride, urea, and acid. J. Biol. Chem. 2484623–4634. [PubMed] [Google Scholar]
- Ries-Kautt, M. and Ducruix, A. 1997. Inferences drawn from physicochemical studies of crystallogenesis and precrystalline state. Methods Enzymol. 276 23–59. [DOI] [PubMed] [Google Scholar]
- Righetti, P.G., Tudor, G., and Ek, K. 1981. Isoelectric points and molecular weights of proteins: A new table. J. Chromatogr. 220 115–194. [DOI] [PubMed] [Google Scholar]
- Schaefer, M., van Vlijmen, H.W., and Karplus, M. 1998. Electrostatic contributions to molecular free energies in solution. Adv. Protein Chem. 51 1–57. [DOI] [PubMed] [Google Scholar]
- Sevcik, J., Dauter, Z., Lamzin, V.S., and Wilson, K.S. 1996. Ribonuclease from Streptomyces aureofaciens at atomic resolution. Acta Cryst. D. 52 257–271. [DOI] [PubMed] [Google Scholar]
- Sevcik, J., Sanishvili, R.G., Pavlovsky, A.G., and Polyakov, K.M. 1990. Comparison of active sites of some microbial ribonucleases: structural basis for guanylic specificity. Trends Biochem. Sci. 15 158–162. [DOI] [PubMed] [Google Scholar]
- Sillero, A. and Ribeiro, J.M. 1989. Isoelectric points of proteins: theoretical determination. Anal. Biochem. 179 319–325. [DOI] [PubMed] [Google Scholar]
- Steyaert, J., Opsomer, C., Wyns, L., and Stanssens, P. 1991. Quantitative analysis of the contribution of glu46 and asn98 to the guanosine specificity of ribonuclease T1. Biochemistry 30 494–499. [DOI] [PubMed] [Google Scholar]
- Swint-Kruse, L. and Robertson, A.D. 1995. Hydrogen bonds and the pH dependence of ovomucoid third domain stability. Biochemistry 34 4724–4732. [DOI] [PubMed] [Google Scholar]
- Takano, K.,Tsuchimori, K.,Yamagata, Y., and Yutani, K. 2000. Contribution of salt bridges near the surface of a protein to the conformational stability. Biochemistry 39 12375–12381. [DOI] [PubMed] [Google Scholar]
- Tan, Y.J., Oliveberg, M., Davis, B., and Fersht, A.R. 1995. Perturbed pKA-values in the denatured states of proteins. J. Mol. Biol. 254 980–992. [DOI] [PubMed] [Google Scholar]
- Tanford, C. 1961. Physical chemistry of macromolecules. John Wiley and Sons, Inc., New York.
- ———.1962. The interpretation of hydrogen ion titration curves of proteins. Adv. Protein Chem. 17 69–165. [Google Scholar]
- ———. 1968. Protein denaturation. Adv. Protein Chem. 23 121—282. [DOI] [PubMed] [Google Scholar]
- ———. 1970. Protein denaturation. C. Theoretical models for the mechanism of denaturation. Adv. Protein Chem. 24 1–95. [PubMed] [Google Scholar]
- Warwicker, J. 1999. Simplified methods for pKa and acid pH-dependent stability estimation in proteins: removing dielectric and counterion boundaries. Protein Sci. 8 418–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitten, S.T. and Garcia-Moreno, B.E. 2000. pH dependence of stability of staphylococcal nuclease: Evidence of substantial electrostatic interactions in the denatured state. Biochemistry 39 14292–14304. [DOI] [PubMed] [Google Scholar]
- Yakovlev, G.I., Moiseyev, G.P., Bezborodov, A.M., Both, V., and Sevcik, J. 1992. A comparative study on the catalytic properties of guanyl-specific ribonucleases. Eur. J. Biochem. 204 187–190. [DOI] [PubMed] [Google Scholar]
- Yang, A.-S. and Honig, B. 1993. On the pH dependence of protein stability. J. Mol. Biol. 231 459–474. [DOI] [PubMed] [Google Scholar]
- Yu, Y., Makhatadze, G.I., Pace, C.N., and Privalov, P.L. 1994. Energetics of ribonuclease T1 structure. Biochemistry 33 3312–3319. [DOI] [PubMed] [Google Scholar]